数与代数概念总汇
数与代数知识点

数与代数知识点数与代数是数学中非常重要的一个领域,它涵盖了从基础的数字运算到复杂的代数方程等广泛的内容。
无论是在日常生活中的计算,还是在科学、工程等领域的应用,数与代数都发挥着关键作用。
接下来,让我们一起深入了解数与代数的一些重要知识点。
一、数的概念1、自然数自然数是指从 0 开始,依次为 0、1、2、3、4……的整数。
它们是我们最早接触到的数,用于计数和表示物体的数量。
2、整数整数包括正整数、零和负整数。
例如-3、-2、-1、0、1、2、3 等。
整数的范围比自然数更广,用于表示具有相反意义的量,如温度的正负、海拔的高低等。
3、分数把单位“1”平均分成若干份,表示这样一份或几份的数叫做分数。
例如 1/2、3/4 等。
分数可以用来表示部分与整体的关系。
4、小数小数是分数的另一种表示形式。
例如 05 可以表示为 1/2,125 可以表示为 5/4。
小数在实际生活中的测量和计算中经常用到。
二、数的运算1、四则运算加法、减法、乘法和除法是基本的四则运算。
加法是将两个或多个数合并成一个数的运算;减法是已知两个数的和与其中一个加数,求另一个加数的运算;乘法是求几个相同加数和的简便运算;除法是已知两个因数的积与其中一个因数,求另一个因数的运算。
在进行四则运算时,需要遵循一定的运算顺序:先乘除,后加减;有括号时,先算括号内的。
2、运算定律加法交换律:a + b = b + a加法结合律:(a + b) + c = a +(b + c)乘法交换律:a × b = b × a乘法结合律:(a × b) × c = a ×(b × c)乘法分配律:a ×(b + c) = a × b + a × c这些运算定律可以帮助我们更简便地进行计算。
三、代数式1、用字母表示数用字母可以表示任意数、数量关系、运算定律和计算公式等。
例如,用 a 表示一个任意数,那么 a + 5 就可以表示比 a 大 5 的数。
初中数学知识归纳数与代数的基本概念和运算

初中数学知识归纳数与代数的基本概念和运算初中数学知识归纳:数与代数的基本概念和运算数学是一门抽象而又实用的学科,它是我们实际生活中不可或缺的一部分。
在初中阶段,数与代数是数学学习的基础,它们涉及了数的概念、数的分类以及代数运算等内容。
下面将介绍初中数学中与数与代数相关的基本概念和运算方法。
一、数的概念与分类数是用来计量事物多少的概念,是数学中最基本的要素。
在初中数学中,我们主要接触和学习到的数有自然数、整数、有理数和实数等。
1. 自然数:自然数是从1开始的正整数,用N表示。
自然数从1开始依次递增,是最基本的计数单位。
2. 整数:整数包括自然数和负整数,用Z表示。
整数集合包含了0和自然数,它们在数轴上分布开来,整数之间可以进行加减运算。
3. 有理数:有理数是可以表示为两个整数之比的数,用Q表示。
有理数包括正有理数、负有理数以及0,可以进行加减乘除等运算。
4. 实数:实数包括有理数和无理数,用R表示。
实数集合包含了所有的数,它们在数轴上密集分布,实数之间可以进行各种运算。
二、数的运算数的运算是数学中非常重要的一部分,能够帮助我们实现对数的操作和计算。
常见的数的运算包括加法、减法、乘法和除法。
1. 加法:加法是将两个数相加得到一个新的数。
在运算中,被加数加上加数,得到的结果称为和,符号用"+"表示。
2. 减法:减法是将一个数从另一个数中减去,得到差。
在运算中,被减数减去减数,得到的结果称为差,符号用"-"表示。
3. 乘法:乘法是两个数相乘得到一个新的数。
在运算中,被乘数乘以乘数,得到的结果称为积,符号用"×"表示。
4. 除法:除法是将一个数除以另一个数,得到商。
在运算中,被除数除以除数,得到的结果称为商,符号用"÷"表示。
数的运算是有法则和性质的,在实际运算中需要注意运算规则,特别是在运算的顺序和优先级上。
小学数学数与代数知识点汇总

小学数学数与代数知识点汇总一、数与运算1.数的认识:自然数、整数、有理数、实数2.顺序数的比较:大小比较、比大小的符号3.加法与减法:加法和减法的意义、加法和减法的性质、整数的加减法4.乘法与除法:乘法和除法的意义、乘法和除法的性质、整数的乘除法5.数的倍数和因数:整数的倍数、整数的因数、公倍数、最大公约数、最小公倍数6.小数:小数的读法、小数的比较、小数的四则运算7.分数:分数的意义、分数的大小比较、分数的加减法、分数的乘除法8.百分数:百分数的意义、百分数的相互转化、百分数的加减乘除二、代数式和方程1.代数式的认识:代数式的定义、代数式的运算、多项式2.代数式的计算:代数式的约分、代数式的化简、代数式的展开与因式分解3.代数式的应用:根据实际问题编写代数式、代数式的求值4.方程的认识:方程的定义、方程的解、解方程的意义、解方程的方法5.解一元一次方程:一元一次方程的解法、方程的意义、方程的实际应用6.解一元一次不等式:一元一次不等式的解法、不等式的意义、不等式的实际应用7.解一元一次方程组:一元一次方程组的解法、方程组的意义、方程组的实际应用三、数的性质和运算1.数的分类:分数、小数、整数及其运算2.数的性质:数的大小比较、数的相反数、数的绝对值、数的相反数与绝对值的关系3.定量关系:数与长度的关系、数与面积的关系、数与体积的关系4.倍数与公约数:整数的倍数和倍数的性质、整数的公约数和公约数的性质5.比例:比例的意义、比例的性质、比例的应用6.百分数:百分数的意义、百分数的相互转化、加减乘除百分数的方法7.降幂与乘方:降幂与升幂的意义、乘方及其运算法则、次乘方的意义和运算四、数据的应用1.数据的收集:问卷调查、实地调查、统计资料2.数据的整理:频数表、频数图、折线图3.数据的分析:数据的中心趋势、数据的离散程度、数据的比较4.数据的应用:数据的解读、数据的预测、数据的比较和判断五、几何基础1.点、线、面:基本图形的认识、基本图形的命名2.直线与线段:直线、线段、射线的认识和性质3.角的认识:角的定义、角的分类、角的性质4.三角形:三角形的分类、三角形的性质、等腰三角形、等边三角形5.四边形:平行四边形的性质、矩形的性质、菱形的性质、正方形的性质6.圆:圆的性质、圆的周长和面积7.空间几何图形:长方体、正方体、棱柱、棱锥、棱台、球体等的性质六、图形的应用1.图形的绘制:使用尺规作图仪器绘制图形2.图形的变换:平移、旋转、对称、放缩等图形的变换3.图形的投影:直线的平行投影、线段的视、上、右投影、线段的和、差投影以上是小学数学中的数与代数知识点汇总,希望对你的学习有所帮助。
数与代数主要知识点

数与代数主要知识点数与代数是数学的基础,是数学研究的重要分支。
它们在数学中扮演着重要的角色,涉及到许多重要的概念和方法。
本文将介绍数与代数的主要知识点,包括数的性质、代数方程、函数与图像等内容。
一、数的性质数是数学中最基本的概念,包括自然数、整数、有理数和实数等。
数的性质是研究数学问题的基础,它们具有以下重要性质:1. 数的比较性质:数可以比较大小,可以使用大于、小于和等于等符号进行比较。
2. 数的运算性质:数可以进行加法、减法、乘法和除法等运算,遵循相应的运算规则。
3. 数的性质:数具有交换律、结合律和分配律等性质,这些性质在数学中起到重要的作用。
二、代数方程代数方程是数与代数中的重要概念,它是一种含有未知数的等式。
代数方程的解是使得方程成立的未知数的值。
在代数方程中,我们可以使用代数的方法来求解未知数的值。
代数方程的求解过程中,可以运用因式分解、配方法、根号法等多种方法,求得方程的解。
三、函数与图像函数是数与代数中的重要概念,它描述了两个变量之间的关系。
函数可以用数学表达式表示,其中包含自变量和因变量。
函数的图像是函数在坐标系中的表示,它可以直观地展示函数的特点和性质。
函数的图像可以帮助我们理解函数的变化规律,找到函数的最大值、最小值和零点等重要信息。
四、等差数列与等比数列等差数列与等比数列是数与代数中常见的数列。
等差数列是指数列中相邻两项之间的差值相等的数列,它具有明显的规律性。
等差数列在数学中有广泛的应用,可以用于求和、推导等。
等比数列是指数列中相邻两项之间的比值相等的数列,它也具有明显的规律性。
等比数列在数学中也有重要的应用,可以用于求和、推导等。
五、复数复数是数与代数中的重要概念,它是由实数和虚数构成的数。
复数可以用复数形式表示,其中实部和虚部分别用实数表示。
复数在数学中有广泛的应用,可以用于求解代数方程、计算电路等。
复数具有加法、减法、乘法和除法等运算规则,也有自己的共轭和模等概念。
小学数学数与代数知识点整理

小学数学数与代数知识点整理一、数的大小和比较1.数的比较:数的大小关系,如大于、小于、等于。
2.数的顺序:自然数、整数、有理数的大小顺序。
二、数的性质和运算1.数的分类:自然数、整数、有理数、无理数。
2.数的性质:奇数、偶数、质数、合数。
3.数的运算:加法、减法、乘法、除法的基本概念和运算规则。
4.数的整除性:倍数、约数、公因数、最大公约数等概念。
三、数的分数表示和运算1.分数的概念:分子、分母、真分数、假分数。
2.分数与整数的运算:加法、减法、乘法、除法。
3.分数相比较:大小比较和等值判断。
四、数的小数表示和运算1.小数的定义:小数点的概念。
2.小数的读法和写法:整数、小数部分的读法和写法。
3.小数与分数的相互转化。
4.小数运算:加法、减法、乘法、除法。
五、数的倍数和约数1.倍数的概念:一个数能整除另一个数。
2.约数的概念:一个数能被另一个数整除。
3.最大公约数:两个数公共的约数中最大的那个数。
4.最小公倍数:两个数公共的倍数中最小的那个数。
六、数的代数式和数的应用1.代数式的概念:数、字母和运算符号的组合。
2.代数式的计算:代数式的加减乘除运算。
3.代数式的应用:通过代数式解决实际问题。
七、数的方程式1.方程式的概念:等号连接的代数式。
2.一元一次方程式:解方程的方法和步骤。
3.方程式的应用:通过方程式解决实际问题。
八、数的图形的认识与应用1.数的图形的概念:点、线、面。
2.平凡形的认识:正方形、长方形、三角形、圆形、梯形等。
3.图形的属性:边、角、面积、周长等。
4.图形的运算:图形的加法和减法。
总结:小学数学数与代数知识点主要包括数的大小和比较、数的性质和运算、数的分数表示和运算、数的小数表示和运算、数的倍数和约数、数的代数式和数的应用、数的方程式以及数的图形的认识与应用等内容。
在学习过程中,要注重理论与实践相结合,通过解决实际问题来巩固所学知识。
同时,要培养学生的计算和推理能力,让他们能够自主思考和解决问题。
(完整版)数与代数的知识点
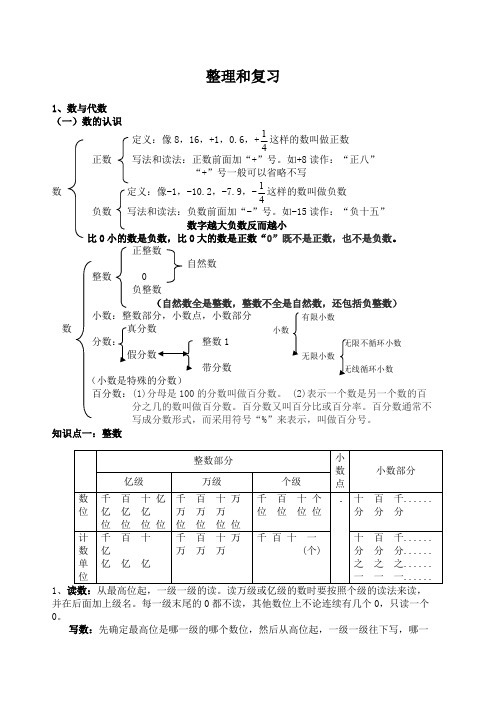
整理和复习1、数与代数(一)数的认识定义:像8,16,+1,0.6,+这样的数叫做正数41正数 写法和读法:正数前面加“+”号。
如+8读作:“正八” “+”号一般可以省略不写数 定义:像-1,-10.2,-7.9,-这样的数叫做负数41负数 写法和读法:负数前面加“-”号。
如-15读作:“负十五” 数字越大负数反而越小比0小的数是负数,比0大的数是正数“0”既不是正数,也不是负数。
正整数自然数 整数 0 数 (小数是特殊的分数)百分数:(1)分母是100的分数叫做百分数。
(2)表示一个数是另一个数的百分之几的数叫做百分数。
百分数又叫百分比或百分率。
百分数通常不写成分数形式,而采用符号“%”来表示,叫做百分号。
知识点一:整数1、读数:从最高位起,一级一级的读。
读万级或亿级的数时要按照个级的读法来读,并在后面加上级名。
每一级末尾的0都不读,其他数位上不论连续有几个0,只读一个0。
写数:先确定最高位是哪一级的哪个数位,然后从高位起,一级一级往下写,哪一整数部分亿级万级个级小数点小数部分数位千 百 十 亿亿 亿 亿位 位 位 位千 百 十 万万 万 万位 位 位 位千 百 十 个位 位 位 位十 百 千......分 分 分计数单位千 百 十 亿亿 亿 亿千 百 十 万万 万 万千 百 十 一 (个).十 百 千......分 分 分......之 之 之......一 一 一......位一个单位也没有,就在哪个数位上写0。
2、数的改写与求近似数:为了读写方便,常把较大的数简写成用“万”或“亿”作单位的数。
如:2365500=236.55万(改写用“万”作单位的数)。
如:2365500≈237万(省略万位后面的尾数,写成近似数),如:7.62983≈7.6(保留一位小数)。
知识点二:小数1、小数的意义: 把整数“1”平均分成10份,100份,1000份……这样的1份或几份是十分之几,百分之几,千分之几…可以用小数来表示。
数与代数知识点总结

数与代数知识点总结数与代数知识点总结11、像0,1,2,3,4,5,6……这样的数是自然数。
最小的自然数是0,没有最大的自然数,全部的自然数都是整数,整数不全是自然数。
2、像-3,-2,-1,0,1,2,3,……这样的数是整数。
〔注:整数包括自然数〕3、倍数和因数:倍数和因数是相互依存的。
如:4×5=20,就可以说20是4和5的倍数,4和5是20的因数。
判断题或填空题易出。
如:4×5=20,4是因数,20是倍数,这是错误的。
一个数的倍数有很多个,倍数的个数是无限的,而因数的个数是有限的。
一个数最大的因数和最小的倍数都是它本身。
4、找因数:找一个数的因数,一对一对有序地找,就不会重复和遗漏。
一个数最小的因数是1,最大的因数是它本身。
一个数因数的个数是有限的。
1的因数只有1个,就是1。
如:36的因数有:1,36,2,18,3,12,4,9,65、找倍数:从1倍开始有序地找,一个数没有最大的倍数,最小的倍数是它本身。
例:一个数最大的因数与最小的倍数是18,这个数是〔 18 〕。
6、奇数和偶数:是2的倍数的数叫偶数,特征是:个位上是0,2,4,6,8。
如:2,4,6,8等等。
不是2的倍数的数叫奇数。
特征是:个位上是1,3,5,7,9。
如:1,3,33,99等等。
7、质数:一个数只有1和它本身两个因数,这个数叫质数。
如:2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67 ,71,73,79,83,89,97等。
8、合数:一个数除了1和它本身以外还有别的因数,这个数叫合数。
合数至少有3个因数。
如:4,6,8,9,10,12,14,15,16,18,20等。
留意:1既不是质数也不是合数。
例:〔1〕最小的质数是2,最小的合数是4,最小的奇数1,最小的偶数是0。
〔2〕1、3、5、7、19、29、49、65、51当中是质数的有〔3,5,7,19,29 〕。
小学数学数与代数知识大全

小学数学数与代数知识大全数学是一门学科,其中包含了许多与数和代数相关的知识。
对于小学生来说,数与代数是他们日常学习中必须掌握的基础知识。
本文将介绍小学数学中与数与代数相关的重要概念和技巧。
一、基础数学知识1. 数的概念:数用来表示事物的多少,分为整数、分数和小数等不同类型。
整数包括正整数、负整数和零,分数由分子和分母组成,小数是指有限或无限循环小数。
2. 数的比较与排序:学习如何比较大小,使用比较符号(大于、小于、等于)进行数的比较;学习如何按照大小排序一组数。
3. 数的运算:学习加法、减法、乘法和除法的运算规则和性质,掌握基本的运算技巧与口算能力。
4. 四则运算:掌握加法、减法、乘法和除法的联合运算,灵活运用这些运算进行复杂的计算。
5. 数的倍数与因数:理解倍数和因数的概念,学习如何求一个数的倍数和因数,掌握最大公因数与最小公倍数的计算方法。
二、代数知识1. 代数符号:学习代数术语和代数符号的含义及使用方法,如:求和、求差、乘号、除号、等号等。
2. 字母代数:引入字母代表数,学习字母代数的含义和运算规则,能够进行简单的代数运算。
3. 简单方程:学习方程的概念和解方程的基本方法,掌握求解一元一次方程的技巧,如:凑项法、配方法等。
4. 分式运算:理解分式的概念和运算规则,能够进行分式的加、减、乘、除运算,学习简单分式方程的解法。
5. 代数式的展开与因式分解:学习代数式的展开与因式分解的方法,掌握公式展开与因式分解的技巧,如:二次方三项式的展开、二次差平方公式等。
三、数与代数技巧1. 应用题解决思路:学习运用数学知识解决实际问题的思维方式与方法,培养灵活运用数与代数知识的能力。
2. 逻辑推理与问题解决:发展逻辑思维,训练运用数与代数知识解决问题的能力,培养观察、分析、推理、判断和解决问题的能力。
3. 综合运用:通过综合运用所学的数与代数知识,解决综合性的数学问题,提高综合运算能力。
总结:小学数学的数与代数知识是学习数学的基础,掌握这些知识对于学生未来的学习和发展至关重要。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、自然数:
表示物体的数量的数,最小的白然数是“0”
白然数也是整数。
0是正整数与负整数的分界线。
2、质数
一个数除了1和它本身,不再有其它的约数(因数),这个数叫做质数(质数也叫做素数)。
质数:
只有“1和它本身两个约数的数。
最小的质数是“2;
3、合数
一个数除了1和它本身,还有别的约数,这个数叫做合数
注意:1只有一个约数,就是它本身,1既不是质数,也不是合数。
最小的质数是2,也是质数中唯一的一个偶数,其余的质数均为奇数。
合数:
除了“1和它本身以外还有别的约数的数。
最小的合数“4'
4、互质数:
只有公约数“1的两个数。
5、公约数:
两个数公有的约数。
6、公倍数:
两个数公有的倍数。
7、质因数:
把一个合数分解成几个质数相乘的形式,这几个质数叫作这个合数的质因
8、分解质因数:
把一个合数分解成几个质数相乘的形式,这个过程叫做分解质因数。
能被2整除数的特征:
个位上的数字是0, 2, 4, 6, 8
能被3整除数的特征:
各位上的数字之和是3的倍数
能被5整除数的特征:
个位上的数字是0, 5
能被9整除数的特征:
各位上的数字之和是9的倍数.
能被4或25整除数的特征:
末两位上的数是4或25的倍数.
能被8或125整除数的特征:
末三位数是8或125的倍数.
9、偶数
偶数就是可以被2整除的白然数(包括0)也叫做双数。
偶数通常用“2履示。
10、奇数
奇数就是不能被2整除的白然数,也叫做单数。
奇数通常用2k+1表示小数:
1、小数的基本性质:
在小数末尾添上”或去掉” 0;'小数的大小不变.
2、有限小数:
小数部分的位数是有限的。
3、无限小数:
小数部分的为数是无限的。
、无限循环小数:
小数部分的数位有规律的.
4、无限不循环小数:
小数部分没规律(又叫无理数)
5、纯循环小数:
从小数部分第一位开始循环'
6、混循环小数:
不是从小数部分第一位开始循环
7、循环节:
从小数部分的某一位起.开是依次不断重复一个或几个数字.这些数字叫做循环节.
分数
1、分数:
把单位“1平均分成若干份,表示这样的一份或几分的数,叫做分数。
2、分数的加减法则:
同分母的分数相加减,只把分子相加减,分母不变。
异分母的分数相加减,先通分,然后再加减。
3、、分数大小的比较:
同分母的分数相比较,分子大的大,分子小的小。
异分母的分数相比较,先通分然后再比较;若分子相同,分母大的反而小。
4、分数乘整数,用分数的分子和整数相乘的积作分子,分母不变。
5、分数乘分数,用分子相乘的积作分子,分母相乘的积作为分母。
6、分数除以整数(0除外),等于分数乘以这个整数的倒数。
7、真分数:
分子比分母小的分数叫做真分数。
8、假分数:
分子比分母大或者分子和分母相等的分数叫做假分数。
假分数大于或等于
1。
9、带分数:
把假分数写成整数和真分数的形式,叫做带分数。
10、分数的基本性质:
分数的分子和分母同时乘以或除以同一个数
(0除外),分数的大小不变。
11、一个数除以分数,等于这个数乘以分数的倒数。
12、甲数除以乙数(0除外),等于甲数乘以乙数的倒数。
14、分数的基本性质:
分数的分子和分母同时乘或除以一个数(0除外).分数的大小不变.
真分数v 1.假分数Al
15、约分:
将一个分数的分子与分母同时除以他们的最大公因数,这个过程叫约分.而得到的
这个分数叫最简分数.
16、最简分数:
分母与分子互质的时候.这个分数就叫最简分数.
17、通分:
将几个异分母的分数利用分数的基本性质将分母变成一样.这个过程叫通分.在分数大小的比较中会广泛遇到通分.
百分数
1、百分数:
表示一个数是另一个数的百分之几的数,叫做百分数。
百分数也叫做百分率或百分比。
2、、把小数化成百分数,只要把小数点向右移动两位,同时在后面添上百分号。
其实,把小数化成百分数,只要把这个小数乘以100%就行了。
把百分数化成小数,只要把百分号去掉,同时把小数点向左移动两位。
3、、把分数化成百分数,通常先把分数化成小数(除不尽时,通常保留三位小数),再把小数化成百分数。
其实,把分数化成百分数,要先把分数化成小数后,再乘以100%就行了。
把百分数化成分数,先把百分数改写成分数,能约分的要约成最简分数。
4、要学会把小数化成分数和把分数化成小数的化发。
5、利息=本金洌率用寸间(时间一般以年或月为单位,应与利率的单位相对应)
6、利率:
利息与本金的比值叫做利率。
一年的利息与本金的比值叫做年利率。
一月的利息与本金的比值叫做月利率。
比和方程:
1、什么叫比:
两个数相除就叫做两个数的比。
如:2+5或3:6或
比的前项和后项同时乘以或除以一个相同的数(0除外),比值不变。
2、什么叫比例:
表示两个比相等的式子叫做比例。
如3:6= 9:18
3、比例的基本性质:
在比例里,两外项之积等于两内项之积。
4、解比例:
求比例中的未知项,叫做解比例。
如3:疔9:18
5、正比例:
两种相关联的量,一种量变化,另一种量也随着化,如果这两种量中相对应的的比值(也就是商k)一定,这两种量就叫做成正比例的量,它们的关系就叫做正比例关系。
如:
y/x=k( k 一定)或kx=y
6、反比例:
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系就叫做反比例关系。
如:
x x y = k(K定)或k / x = y
7、么叫等式?等号左边的数值与等号右边的数值相等的式子叫做等式。
等式的基本性质:
等式两边同时乘以(或除以)一个相同的数,等式仍然成立。
8、什么叫方程式?答:
含有未知数的等式叫方程式。
9、什么叫一元一次方程式?答:
含有一个未知数,并且未知数的次数是一次的等式叫做一元一次方程式。
10、什么叫代数?代数就是用字母代替数。
11、什么叫代数式?用字母表示的式子叫做代数式。
如:3x = (a+b)*c运算定律:
1、加法交换律:
两数相加交换加数的位置,和不变。
2、加法结合律:
三个数相加,先把前两个数相加,或先把后两个数相加,再同第三个数相加,和不变。
3、乘法交换律:
两数相乘,交换因数的位置,积不变。
4、乘法结合律:
三个数相乘,先把前两个数相乘,或先把后两个数相乘,再和第三个数相乘,它们的积不变。
5、乘法分配律:
两个数的和同一个数相乘,可以把两个加数分别同这个数相乘,再把两个积相加,结果不变。
如:
(2+4) X 牝2X 5+4X 5
6、除法的性质:
在除法里,被除数和除数同时扩大(或缩小)相同的倍数,商不变。
O除以任何不是O的数都得O。
简便乘法:
被乘数、乘数末尾有O的乘法,可以先把O前面的相乘,零不参加运算,有几个零都落下,添在积的末尾。
