平移典型例题及练习含答案
三角函数的平移变换

函数)sin(A ϕω+=x y 的图像1、函数sin()y A x ωϕ=+的图像与sin y x =图像间的关系:① 函数sin y x =的图像纵坐标不变,横坐标向左(ϕ>0)或向右(ϕ<0)平移||ϕ个单位得()sin y x ϕ=+的图像;② 函数()sin y x ϕ=+图像的纵坐标不变,横坐标变为原来的1ω,得到函数()sin y x ωϕ=+的图像;③ 函数()s i n y x ωϕ=+图像的横坐标不变,纵坐标变为原来的A 倍,得到函数sin()y A x ωϕ=+的图像;要特别注意,若由()sin y x ω=得到()sin y x ωϕ=+的图像,则向左或向右平移应平移||ϕω个单位。
2、函数y =sin x 的图象经变换得到y =A sin(ωx +φ)的图象的步骤如下:【典型例题】例1将函数)3sin(2π+=x y 的图象上所有点的横坐标缩短到原来的21(纵坐标不变), 所得图象对应的表达式为A .)321sin(2π+=x y B .)621sin(2π+=x yC .)32sin(2π+=x yD .)322sin(2π+=x y 例2、110610. 将函数)32cos(4π-=x y 的图像向右平移6π个单位,所得图像的解析式是(A ))62cos(4π-=x y (B ))322cos(4π-=x y (C )x y 2cos 4= (D )x y 2sin 4=例3、080606.为了得到函数sin 23y x π⎛⎫=-⎪⎝⎭的图象,只需把函数sin 2y x =的图象( ) A . 向左平移3π个单位长度B . 向右平移3π个单位长度C . 向左平移6π个单位长度D . 向右平移6π个单位长度试题分析:因为sin 2sin 236y x x ππ⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭,所以只需将函数sin 2y x =的图像向右平移6π各单位即可得到函数sin 23y x π⎛⎫=- ⎪⎝⎭的图象;故D 正确.【会考真题】1、101213.为得到函数)42sin(π+=x y 的图像,只须将函数x y 2sin =上所有点( )(A )向右平移4π个单位 (B )向左平移4π个单位 (C )向右平移8π个单位 (D )向左平移8π个单位2、060615:要得到函数cos(2),3y x x R π=+∈的图像,只需把曲线cos 2y x =上所有的点( )(A )向左平行移动3π个单位长度 (B )向右平行移动3π个单位长度 (C )向左平行移动6π个单位长度 (D )向右平行移动6π个单位长度例4 、将函数的图像上所有的点向右平行移动个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图像的函数解析式是(A ) (B )(C ) (D ) 解析:将函数的图像上所有的点向右平行移动个单位长度,所得函数图象的解析式为y =sin (x -) 再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图像的函数解析式是.【答案】C1、100113:把函数3sin y x =的图像上每个点的横坐标伸长到到原来的两倍(纵坐标保持不变),然后再将整个图像向左平移3π个单位,所得图像的函数解析式是( )(A )3sin(2)6y x π=-(B )13sin()26y x π=+ (C )3sin(2)3y x π=- (D )13sin()23y x π=+2、070614或090113:将函数sin()()3y x x R π=-∈的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得到的图像向左平移3π个单位长度,则得到的图像的函数解析式是( )(A )1sin2y x = (B )1sin()23y x π=- (C )sin(2)6y x π=- (D )1sin()26y x π=-sin y x =10πsin(2)10y x π=-sin(2)5y x π=-1sin()210y x π=-1sin()220y x π=-sin y x =10π10π1sin()210y x π=-3、090614:把函数sin(2),4y x x R π=+∈的图像向右平移8π个单位长度,再把所得图像上各点的横坐标缩短到到原来的12倍(纵坐标不变),则所得图像对应的函数解析式为( ) (A )cos(4)8y x π=+(B )sin(4)8y x π=+ (C )cos 4y x = (D )sin 4y x =例5、为得到函数y =cos(2x +π3)的图象,只需将函数y =sin2x 的图象( )A .向左平移5π12个单位长度B .向右平移5π12个单位长度C .向左平移5π6个单位长度D .向右平移5π6个单位长度解析 y =cos(2x +π3)=sin[π2+(2x +π3)]=sin(2x +5π6).故要得到y =sin(2x +5π6)=sin2(x +5π12)的图象,只需将函数y =sin2x 的图象向左平移5π12个单位长度.。
小学平移图形试题及答案

小学平移图形试题及答案一、选择题(每题2分,共10分)1. 平移图形时,图形的()不变。
A. 形状B. 大小C. 位置D. 形状和大小答案:D2. 下列选项中,不属于平移性质的是()。
A. 对应点连线平行且相等B. 对应线段平行且相等C. 对应角相等D. 对应边相等答案:A3. 平移图形时,图形的()发生变化。
A. 形状B. 大小C. 位置D. 形状和大小答案:C4. 将一个图形向右平移5个单位,那么这个图形的()。
A. 形状不变B. 大小不变C. 位置不变D. 形状和大小都不变答案:D5. 平移图形时,图形的对应点的()。
A. 距离不变B. 角度不变C. 距离和角度都不变D. 距离和角度都变化答案:C二、填空题(每题2分,共10分)1. 平移图形时,图形的对应点之间的距离和方向都()。
答案:不变2. 将一个图形向上平移3个单位,那么这个图形的()也会向上移动3个单位。
答案:对应点3. 平移图形时,图形的()和()保持不变。
答案:形状;大小4. 一个图形向右平移6个单位,那么这个图形的()也会向右移动6个单位。
答案:对应线段5. 平移图形时,图形的对应角()。
答案:相等三、判断题(每题2分,共10分)1. 平移图形时,图形的位置会发生变化,但形状和大小不会变。
()答案:正确2. 平移图形时,图形的对应点连线不一定平行。
()答案:错误3. 平移图形时,图形的对应线段长度会发生变化。
()答案:错误4. 平移图形时,图形的对应角大小会发生变化。
()答案:错误5. 平移图形时,图形的对应点之间的距离和方向都会发生变化。
()答案:错误四、解答题(每题5分,共10分)1. 如图所示,将图形A向右平移5个单位,求平移后的图形B的坐标。
答案:假设图形A的坐标为(x, y),则平移后的图形B的坐标为(x+5, y)。
2. 已知图形C的坐标为(2, 3),将其向下平移4个单位,求平移后的图形D的坐标。
答案:图形C的坐标为(2, 3),向下平移4个单位后,图形D的坐标为(2, 3-4) = (2, -1)。
平移练习题(含答案)
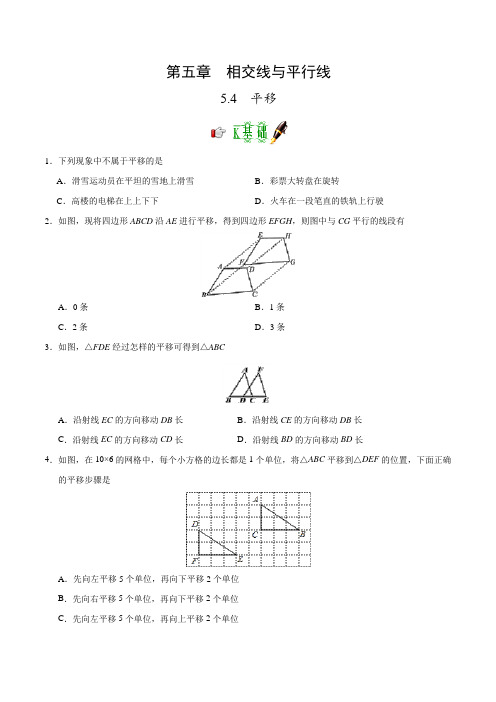
第五章相交线与平行线5.4 平移1.下列现象中不属于平移的是A.滑雪运动员在平坦的雪地上滑雪B.彩票大转盘在旋转C.高楼的电梯在上上下下D.火车在一段笔直的铁轨上行驶2.如图,现将四边形ABCD沿AE进行平移,得到四边形EFGH,则图中与CG平行的线段有A.0条B.1条C.2条D.3条3.如图,△FDE经过怎样的平移可得到△ABCA.沿射线EC的方向移动DB长B.沿射线CE的方向移动DB长C.沿射线EC的方向移动CD长D.沿射线BD的方向移动BD长4.如图,在10×6的网格中,每个小方格的边长都是1个单位,将△ABC平移到△DEF的位置,下面正确的平移步骤是A.先向左平移5个单位,再向下平移2个单位B.先向右平移5个单位,再向下平移2个单位C.先向左平移5个单位,再向上平移2个单位D .先向右平移5个单位,再向下平移2个单位5.如图,将△ABE 向右平移得到△DCF ,AE 与CD 交于点G ,其中45B ∠=︒,60F ∠=︒,则AGC ∠=A .75︒B .105︒C .125︒D .85︒6.如图,将△ABE 向右平移2 cm 得到△DCF ,如果△ABE 的周长是16 cm ,那么四边形ABFD 的周长是A .16 cmB .18 cmC .20 cmD .21 cm7.如图,把三角板的斜边紧靠直尺平移,一个顶点从刻度“5”平移到刻度“10”,则顶点C 平移的距离CC '=____.8.如图,三角形ADE 是由三角形DBF 沿BD 所在的直线平移得到的,AE ,BF 的延长线交于点C.若∠BFD =45°,则∠C 的度数是 ________9.如图,A B C '''△ 是△ABC 向右平移4 cm 得到的,已知∠ACB =30°,B ′C =3 cm ,则∠C ′=_________,B ′C ′=________cm.10.要在台阶上铺设某种红地毯,已知这种红地毯每平方米的售价是40元,台阶宽为3米,侧面如图所示.购买这种红地毯至少需要__________元.11.如图,△ABC沿直线BC向右移了3 cm,得△FDE,且BC=6 cm,∠B=40°.(1)求BE;(2)求∠FDB的度数;(3)找出图中相等的线段(不另添加线段);(4)找出图中互相平行的线段(不另添加线段).12.如图,将△ABC平移,可以得到△DEF,点B的对应点为点E,请画出点A的对应点D、点C的对应点F的位置,并作出△DEF.13.如图,在三角形ABC中,已知AB=3cm,AC=4cm,BC=5cm.现将三角形ABC沿着垂直于BC的方向平移6cm,到三角形DEF的位置,求三角形ABC所扫过的面积.14.如图,在6个边长为1的小正方形及其部分对角线构成的图形中,如图从A点到B点只能沿图中已有的线段走,那么从A点到B点的最短距离的走法共有A.1种B.2种C.3种D.4种15.多边形的相邻两边互相垂直,则这个多边形的周长为A.a+b B.2a+bC.2a+2b D.2b+a16.如图,平移△ABC可得到△DEF,如果∠C=60°,AE=7cm,AB=4cm,那么∠F= ______ 度,DB= ______ cm.17.如图,某宾馆在重新装修后,准备在大厅的主楼梯上铺上红色地毯,已知这种红色地毯的售价为每平方米32元,主楼梯宽为2 m,其侧面与正面如图所示,则购买地毯至少需要多少元?18.如图,在四边形ABCD中,AD∥BC,且AD<BC,△ABC平移到△DEF的位置.(1)指出平移的方向和平移的距离;(2)试说明AD+BC=BF.19.(2017•铜仁)如图,△ABC沿着BC方向平移得到△A′B′C′,点P是直线AA′上任意一点,若△ABC,△PB′C′的面积分别为S1,S2,则下列关系正确的是A.S1>S2B.S1<S2C.S1=S2D.S1=2S21.【答案】B【解析】A.滑雪运动员在平坦的雪地上滑雪,属于平移,故本选项错误;B.彩票大转盘在旋转,不属于平移,故本选项正确;C. 高楼的电梯在上上下下,属于平移,故本选项错误;D. 火车在一段笔直的铁轨上行驶,属于平移,故本选项错误.故选:B.4.【答案】A【解析】根据网格结构,观察对应点A,D,点A向左平移5个单位,再向下平移2个单位即可到达点D 的位置,所以平移步骤是:先把△ABC 向左平移5个单位,再向下平移2个单位,故选A . 5.【答案】B【解析】∵△ABE 向右平移得到△DCF ,∴AB ∥CD ,AE ∥DF ,∴∠DCF =∠B =45°,∴∠CDF =180°- 45°-60°=75°,∴∠AGC =∠DGE =180°-75°=105°,故选B . 6.【答案】C【解析】已知,△ABE 向右平移2 cm 得到△DCF ,根据平移的性质得到EF =AD =2 cm ,AE =DF ,又因△ABE 的周长为16 cm ,所以AB +BE +AE =16 cm ,则四边形ABFD 的周长=AB +BC +CF +DF +AD =16+2+ 2=20(cm ),故选C . 7.【答案】5【解析】∵把三角板的斜边紧靠直尺平移,一个顶点从刻度“5”平移到刻度“10”,∴三角板向右平移了5个单位,∴顶点C 平移的距离CC ′=5.故答案为:5. 8.【答案】45°【解析】∵△ADE 是由△DBF 沿BD 所在的直线平移得到的, ∴DE ∥BC ,∠BFD =∠AED , ∴∠AED =∠C ∴∠C =∠BFD =45°. 故答案是:45°. 9.【答案】30°,7【解析】∵A B C '''△ 是△ABC 向右平移4 cm 得到的, ∴BB ′=CC ′=4 cm ,∠C ′=∠ACB =30°, ∵B ′C =3 cm , ∴B ′C ′=4+3=7 cm . 故答案为:30°,7.12.【解析】如图:13.【解析】由题意可知,长方形BEFC的面积为5×6=30cm2,直角三角形ABC的面积为3×4÷2=6cm2,30+6=36cm2.∴三角形ABC所扫过的面积为36cm2.14.【答案】C【解析】如图,由题意和“两点之间线段最短”及“平行四边形的对边相等”可知,由A到B的最短距离的走法有下面三种:(1)由A→C→D→B;(2)由A→F→E→B;(3)由A→F→D→B,故选C.17.【解析】利用平移线段,把楼梯的横竖向上向左平移,构成一个长方形,长、宽分别为5米,3米,∴地毯的长度为5+3=8(米),∴地毯的面积为8×2=16(平方米),∴买地毯至少需要16×32=512(元).18.【解析】(1)平移的方向是点A到点D的方向,平移的距离是线段AD的长度;(2)∵△ABC平移到△DEF的位置,∴CF=AD,∵CF+BC=BF,∴AD+BC=BF.19.【答案】C【解析】∵△ABC沿着BC方向平移得到△A′B′C′,∴AA′∥BC′,∵点P是直线AA′上任意一点,∴△ABC,△PB′C′的高相等,∴S1=S2,故选C.。
《平移》练习题(含答案)

5.4 平移1.下列现象不属于平移的是( )A.飞机起飞前在跑道上加速滑行B.汽车在笔直的公路上行驶C.游乐场的过山车在翻筋斗D.起重机将重物由地面竖直吊起到一定高度2.下列所示的图案分别是奔驰、奥迪、大众、三菱汽车的车标,其中,可以看作由“基本图案”经过平移得到的是( )3.(2012·莆田)如图,△A′B′C′是由△ABC沿射线AC方向平移2 cm得到,若AC=3 cm,则A′C=__________.4.如图,方格中有一条美丽可爱的小金鱼.(1)若方格的边长为1,则小鱼的面积为__________;(2)画出小鱼向左平移3格后的图形(不要求写作图步骤和过程).5.在6×6方格中,将图1中的图形N平移后位置如图2所示,则图形N的平移方法中,正确的是( )A.向下移动1格B.向上移动1格C.向上移动2格D.向下移动2格6.如图,在10×6的网格中,每个小方格的边长都是1个单位,将△ABC平移到△DEF的位置,下面正确的平移步骤是( )A.先把△ABC向左平移5个单位,再向下平移2个单位B.先把△ABC向右平移5个单位,再向下平移2个单位C.先把△ABC向左平移5个单位,再向上平移2个单位D.先把△ABC向右平移5个单位,再向上平移2个单位7.(2014·邵阳)某数学兴趣小组开展动手操作活动,设计了如图所示的三种图形,现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是( )A.甲种方案所用铁丝最长B.乙种方案所用铁丝最长C.丙种方案所用铁丝最长D.三种方案所用铁丝一样长8.图中的4个小三角形都是等边三角形,边长为1.3 cm,你能通过平移三角形ABC得到其他三角形吗?若能,请说出平移的方向和距离.9.如图,凯瑞酒店准备进行装修,把楼梯铺上地毯,已知楼梯的宽度是2米,楼梯的总长度为8米,总高度为6米,已知这种地毯每平方米的售价是60元.请你帮助酒店老板算下,购买地毯至少需要多少元?10.(1)已知图1将线段AB向右平移1个单位长度,图2是将线段AB折一下再向右平移1个单位长度,请在图3中画出一条有两个折点的折线向右平移1个单位长度的图形;(2)若长方形的长为a,宽为b,请分别写出三个图形中除去阴影部分后剩下部分的面积;(3)如图4,在宽为10 m,长为40 m的长方形菜地上有一条弯曲的小路,小路宽度为1 m,求这块菜地的面积.参考答案1.C2.B3.1 cm4.(1)16(2)图略.5.D6.A7.D8.将△ABC沿着射线AF的方向平移1.3 cm得△FAE;将△ABC沿着射线BD的方向平移1.3 cm 得△ECD;将△ABC平移不能得到△AEC.9.图略,将竖直的线段都平移到BC上,将水平的线段都平移到AB上,由此可知折线AC的长等于AB与BC的和.故地毯的总长至少为8+6=14(米).所以购买地毯至少需要14×2×60=1 680(元).10.(1)图略.(2)三个图形中除去阴影部分后剩下部分的面积均为ab-b.(3)10×40-10×1=390(m2).。
小学二年级奥数题《图形的平移题目大全及答案》题库大全

小学二年级奥数题《图形的平移题目大全及答案》题库大全姓名:_____________ 年级:____________ 学号:______________题型选择题填空题解答题判断题计算题附加题总分得分评卷人得分1、下面的图形,平移哪些线段,就可以变成长方形,用笔画出来。
答案与解析:2、飞禽馆长颈鹿馆大象馆熊猫馆猴山(1)从入口向右平移5格是猴山。
(2)从猴山向上平移4格是熊猫馆。
(3)从熊猫馆向右平移3格是飞禽馆,再向右平移3格是长颈鹿馆。
(4)从长颈鹿馆向下平移6格是大象馆。
答案与解析:“略”3、电梯上下移动是()现象。
水龙头开关的转动是()现象。
(平移或旋转)答案与解析:平移;旋转4、画出平移后的图形。
答案与解析:5;5、请在()里填上“平移”或“旋转”(1)(2)(3)答案与解析:(1)平移;旋转;旋转(2)旋转;平移(3)旋转;旋转;平移;平移6、分别画出将向下平移3格和向右平移5格后得到的图形。
答案与解析:7、画出下图向左平移6格后的图形。
答案与解析:“略”8、画出下图向右平移8格得到的图形。
答案与解析:9、钟面上的指针是()现象。
(填“平移”或“旋转”)答案与解析:旋转10、把图案平移后的图形画出来。
答案与解析:“略”11、连线旋转平移答案与解析:旋转;平移12、把向左平移6格后得到的涂上颜色。
答案与解析:“略”13、下面的图形是平移的填“”,是旋转的填“○”。
(1)(2)(3)()()()(4)(5)(6)()()()(7)(8)(9)()()()答案与解析:(1)○;(2);(3)○;(4);(5)○;(6)○;(7);(8);(9)14、分别画出将凸向右平移5格,向下平移3格后得到的图形。
答案与解析:“略”15、下面现象中是平移的在()里打“”,是旋转的画“○”。
(1)建筑工地的升降机。
(2)直升机的螺旋桨。
()()(3)工作中的排气扇。
(4)行进中的滑雪板。
()()答案与解析:(1);(2)○;(3)○;(4)16、把可以平移到1号小鱼位置的小鱼涂上颜色。
【经典必考】二次函数图像平移30题含详细答案

○………○………二次函数图像平移30题含详细答案 一、单选题 1.将抛物线22y x =向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线为( ). A .22(2)3y x =++; B .22(2)3y x =-+; C .22(2)3y x =--; D .22(2)3y x =+-. 2.抛物线y=(x ﹣2)2﹣1可以由抛物线y=x 2平移而得到,下列平移正确的是( ) A .先向左平移2个单位长度,然后向上平移1个单位长度 B .先向左平移2个单位长度,然后向下平移1个单位长度 C .先向右平移2个单位长度,然后向上平移1个单位长度 D .先向右平移2个单位长度,然后向下平移1个单位长度 3.若抛物线2y x ax b =++与x 轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线1x =,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( ) A .()3,6-- B .()3,0- C .()3,5-- D .()3,1-- 4.将抛物线y=x 2向左平移2个单位,再向下平移5个单位,平移后所得新抛物线的表达式为( ) A .y=(x +2)2﹣5 B .y=(x +2)2+5 C .y=(x ﹣2)2﹣5 D .y=(x ﹣2)2+5 5.将抛物线y=﹣5x 2+1向左平移1个单位长度,再向下平移2个单位长度,所得到的抛物线为( ) A .y=﹣5(x+1)2﹣1 B .y=﹣5(x ﹣1)2﹣1 C .y=﹣5(x+1)2+3 D .y=﹣5(x ﹣1)2+3 6.如图,抛物线2145y x 7x 22=-+与x 轴交于点A 、B ,把抛物线在x 轴及其下方的部分记作1C ,将1C 向左平移得到2C ,2C 与x 轴交于点B 、D ,若直线1y x m 2=+与1C 、2C 共有3个不同的交点,则m 的取值范围是( )……○…………订※※装※※订※※线※※内※……○…………订A .455m 82-<<- B .291m 82-<<- C .295m 82-<<- D .451m 82-<<- 7.将抛物线23y x =-平移,得到抛物线23(1)2y x =---,下列平移方式中,正确的是( ) A .先向左平移1个单位,再向上平移2个单位 B .先向左平移1个单位,再向下平移2个单位 C .先向右平移1个单位,再向上平移2个单位D .先向右平移1个单位,再向下平移2个单位8.如图,将函数y =12(x ﹣2)2+1的图象沿y 轴向上平移得到一条新函数的图象,其中点A (1,m ),B (4,n )平移后的对应点分别为点A '、B '.若曲线段AB 扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )A .y =12(x ﹣2)2-2 B .y =12(x ﹣2)2+7C .y =12(x ﹣2)2-5 D .y =12(x ﹣2)2+49.在平面直角坐标系中,抛物线(5)(3)y x x =+-经过变换后得到抛物线(3)(5)y x x =+-,则这个变换可以是( )A .向左平移2个单位B .向右平移2个单位C .向左平移8个单位D .向右平移8个单位10.抛物线267y x x =++可由抛物线2y x 如何平移得到的( )A .先向左平移3个单位,再向下平移2个单位B .先向左平移6个单位,再向上平移7个单位C .先向上平移2个单位,再向左平移3个单位D .先回右平移3个单位,再向上平移2个单位11.将抛物线y=x 2﹣4x ﹣4向左平移3个单位,再向上平移5个单位,得到抛物线的函A .y=(x+1)2﹣13B .y=(x ﹣5)2﹣3C .y=(x ﹣5)2﹣13D .y=(x+1)2﹣3 12.若要得到函数y =(x+1)2+2的图象,只需将函数y =x 2的图象( ) A .先向右平移1个单位长度,再向上平移2个单位长度 B .先向左平移1个单位长度,再向上平移2个单位长度 C .先向左平移1个单位长度,再向下平移2个单位长度 D .先向右平移1个单位长度,再向下平移2个单位长度 13.将抛物线y=12x 2﹣6x+21向左平移2个单位后,得到新抛物线的解析式为( ) A .y=12(x ﹣8)2+5 B .y=12(x ﹣4)2+5 C .y=12(x ﹣8)2+3 D .y=12(x ﹣4)2+3 14.抛物线y=(x+2)2﹣3可以由抛物线y=x 2平移得到,则下列平移过程正确的是( )A .先向左平移2个单位,再向上平移3个单位B .先向左平移2个单位,再向下平移3个单位C .先向右平移2个单位,再向下平移3个单位D .先向右平移2个单位,再向上平移3个单位 15.把抛物线y=﹣2x 2先向右平移1个单位长度,再向上平移2个单位长度后,所得函数的表达式为( ) A .y=﹣2(x+1)2+2 B .y=﹣2(x+1)2﹣2 C .y=﹣2(x ﹣1)2+2 D .y=﹣2(x ﹣1)2﹣2 16.将抛物线223y x x =-+向上平移2个单位长度,再向右平移3个单位长度后,得到的抛物线解析式为( ) A .2(1)4y x =-+ B .2(4)4y x =-+ C .2(2)6y x =++ D .2(4)6y x =-+ 17.将抛物线2y x 向左平移2个单位长度,再向下平移3个单位长度,得到的抛物线的函数表达式为( ) A .2(2)3y x =+- B .2(2)3y x =++C .2(2)3y x =-+D .2(2)3y x =-- 18.如果将抛物线2y x 2=+向下平移1个单位,那么所得新抛物线的表达式是 A .()2y x 12=-+ B .()2y x 12=++ C .2y x 1=+ D .2y x 3=+ 19.将抛物线265y x x =-+向上平移两个单位长度,再向右平移一个单位长度后,得到的抛物线解析式是( ) A .2(4)6y x =-- B .2(1)3y x =-- C .2(2)2y x =-- D .2(4)2y x =--20.抛物线y =3x 2向右平移一个单位得到的抛物线是( )A .y =3x 2+1B .y =3x 2﹣1C .y =3(x+1)2D .y =3(x ﹣1)2 21.把函数212y x =-的图象,经过怎样的平移变换以后,可以得到函数()21112y x =--+的图象( )A .向左平移1个单位,再向下平移1个单位B .向左平移1个单位,再向上平移1个单位C .向右平移1个单位,再向上平移1个单位D .向右平移1个单位,再向下平移1个单位22.把抛物线y=﹣2x 2+4x+1的图象向左平移2个单位,再向上平移3个单位,所得的抛物线的函数关系式是( )A .y=﹣2(x ﹣1)2+6B .y=﹣2(x ﹣1)2﹣6C .y=﹣2(x+1)2+6D .y=﹣2(x+1)2﹣623.把抛物线y =﹣2x 2向上平移1个单位,再向右平移1个单位,得到的抛物线是( ) A .y =﹣2(x +1)2+1 B .y =﹣2(x ﹣1)2+1C .y =﹣2(x ﹣1)2﹣1D .y =﹣2(x +1)2﹣124.将抛物线y=x 2+2x+3向下平移3个单位长度后,所得到的抛物线与直线y=3的交点坐标是( )A .(0,3)或(﹣2,3)B .(﹣3,0)或(1,0)C .(3,3)或(﹣1,3)D .(﹣3,3)或(1,3)二、解答题 25.已知二次函数的图象以A (﹣1,4)为顶点,且过点B (2,﹣5) (1)求该函数的关系式; (2)求该函数图象与坐标轴的交点坐标; (3)将该函数图象向右平移,当图象经过原点时,A 、B 两点随图象移至A′、B′,求△O A′B′的面积. 26.已知二次函数2223y x mx m =-++(m 是常数) (1)求证:不论m 为何值,该函数的图像与x 轴没有公共点; (2)把该函数的图像沿x 轴向下平移多少个单位长度后,得到的函数的图像与x 轴只有一个公共点? 27.把二次函数y=a(x-h)2+k 的图象先向左平移2个单位,再向上平移4个单位,得到二次函数y=12(x+1)2-1的图象. (1)试确定a ,h ,k 的值; (2)指出二次函数y=a(x-h)2+k 的开口方向,对称轴和顶点坐标. 三、填空题 28.抛物线y =x 2-2x +3向上平移2个单位长度,再向右平移3个单位长度后,得到的抛物线的解析式为____________. 29.将抛物线2213y x =-向右平移3个单位,再向上平移3个单位,所得的抛物线的解析式为________________. 30.把抛物线y=x 2﹣2x+3沿x 轴向右平移2个单位,得到的抛物线解析式为 .参考答案1.B【分析】根据抛物线图像的平移规律“左加右减,上加下减”即可确定平移后的抛物线解析式.【详解】解:将抛物线22y x =向上平移3个单位长度,再向右平移2个单位长度,得到的抛物线的解析式为()2223y x =-+,故选B .【点睛】本题考查了二次函数的平移规律,熟练掌握其平移规律是解题的关键.2.D【解析】分析:抛物线平移问题可以以平移前后两个解析式的顶点坐标为基准研究.详解:抛物线y=x 2顶点为(0,0),抛物线y=(x ﹣2)2﹣1的顶点为(2,﹣1),则抛物线y=x 2向右平移2个单位,向下平移1个单位得到抛物线y=(x ﹣2)2﹣1的图象.故选D .点睛:本题考查二次函数图象平移问题,解答时最简单方法是确定平移前后的抛物线顶点,从而确定平移方向.3.B【解析】分析:根据定弦抛物线的定义结合其对称轴,即可找出该抛物线的解析式,利用平移的“左加右减,上加下减”找出平移后新抛物线的解析式,再利用二次函数图象上点的坐标特征即可找出结论.详解:∵某定弦抛物线的对称轴为直线x=1,∴该定弦抛物线过点(0,0)、(2,0),∴该抛物线解析式为y=x (x-2)=x 2-2x=(x-1)2-1.将此抛物线向左平移2个单位,再向下平移3个单位,得到新抛物线的解析式为y=(x-1+2)2-1-3=(x+1)2-4.当x=-3时,y=(x+1)2-4=0,∴得到的新抛物线过点(-3,0).故选B .点睛:本题考查了抛物线与x 轴的交点、二次函数图象上点的坐标特征、二次函数图象与几何变换以及二次函数的性质,根据定弦抛物线的定义结合其对称轴,求出原抛物线的解析式是解题的关键.4.A【分析】直接根据“上加下减,左加右减”的原则进行解答即可.【详解】抛物线y=x 2的顶点坐标为(0,0),先向左平移2个单位再向下平移5个单位后的抛物线的顶点坐标为(﹣2,﹣5), 所以,平移后的抛物线的解析式为y=(x +2)2﹣5.故选A .【点睛】本题考查了二次函数的图象与几何变换,熟知函数图象平移的法则是解答本题的关键. 5.A【解析】分析:直接利用二次函数图象与几何变换的性质分别平移得出答案.详解:将抛物线y=-5x 2+1向左平移1个单位长度,得到y=-5(x+1)2+1,再向下平移2个单位长度,所得到的抛物线为:y=-5(x+1)2-1.故选A .点睛:此题主要考查了二次函数图象与几何变换,正确记忆平移规律是解题关键. 6.C【分析】先求出点A 和点B 的坐标,然后再求出2C 的解析式,分别求出直线1y x m 2=+与抛物线2C 相切时m 的值以及直线1y x m 2=+过点B 时m 的值,结合图形即可得到答案. 【详解】抛物线2145y x 7x 22=-+与x 轴交于点A 、B , ∴2145x 7x 22-+=0, ∴x 1=5,x 2=9,()B 5,0∴,()A 9,0∴抛物线向左平移4个单位长度后的解析式21y (x 3)22=--, 当直线1y x m 2=+过B 点,有2个交点, 50m 2∴=+, 5m 2=-, 当直线1y x m 2=+与抛物线2C 相切时,有2个交点, 211x m (x 3)222∴+=--, 2x 7x 52m 0-+-=,相切,49208m 0∴=-+=,29m 8∴=-, 如图,若直线1y x m 2=+与1C 、2C 共有3个不同的交点, ∴--295m 82<<-, 故选C .【点睛】本题考查了抛物线与x 轴交点、二次函数图象的平移等知识,正确地画出图形,利用数形结合思想是解答本题的关键.7.D【解析】将抛物线y =-3x 2平移,先向右平移1个单位得到抛物线y =-3(x -1)2, 再向下平移2个单位得到抛物线y =-3(x -1)2-2.故选D.8.D【详解】∵函数()21212y x =-+的图象过点A (1,m ),B (4,n ), ∴m =()211212-+=32,n =()214212-+=3, ∴A (1,32),B (4,3), 过A 作AC ∥x 轴,交B ′B 的延长线于点C ,则C (4,32), ∴AC =4﹣1=3,∵曲线段AB 扫过的面积为9(图中的阴影部分),∴AC •AA ′=3AA ′=9,∴AA ′=3,即将函数()21212y x =-+的图象沿y 轴向上平移3个单位长度得到一条新函数的图象,∴新图象的函数表达式是()21242y x =-+. 故选D .9.B【分析】根据变换前后的两抛物线的顶点坐标找变换规律.【详解】y=(x+5)(x-3)=(x+1)2-16,顶点坐标是(-1,-16).y=(x+3)(x-5)=(x-1)2-16,顶点坐标是(1,-16).所以将抛物线y=(x+5)(x-3)向右平移2个单位长度得到抛物线y=(x+3)(x-5), 故选B .【点睛】此题主要考查了次函数图象与几何变换,要求熟练掌握平移的规律:左加右减,上加下减. 10.A【分析】先将抛物线267y x x =++化为顶点式,然后按照“左加右减,上加下减”的规律进行求解即可.【详解】因为()226732y x x x =++=+-,所以将抛物线2y x 先向左平移3个单位,再向下平移2个单位即可得到抛物线267y x x =++,故选A .【点睛】本题考查了抛物线的平移以及抛物线解析式的变化规律,熟练掌握“左加右减,上加下减”的规律是解题的关键.11.D【详解】因为y=x 2-4x-4=(x-2)2-8,以抛物线y=x 2-4x-4的顶点坐标为(2,-8),把点(2,-8)向左平移3个单位,再向上平移5个单位所得对应点的坐标为(-1,-3),所以平移后的抛物线的函数表达式为y=(x+1)2-3.故选D .12.B【分析】找出两抛物线的顶点坐标,由a 值不变即可找出结论.【详解】解:∵抛物线y=(x+1)2+2的顶点坐标为(-1,2),抛物线y=x 2的顶点坐标为(0,0), ∴将抛物线y=x 2先向左平移1个单位长度,再向上平移2个单位长度即可得出抛物线y=(x+1)2+2.故选B .【点睛】本题考查了二次函数图象与几何变换,通过平移顶点找出结论是解题的关键.13.D【解析】【分析】直接利用配方法将原式变形,进而利用平移规律得出答案.【详解】 y=12x 2﹣6x+21 =12(x 2﹣12x )+21 =12[(x ﹣6)2﹣36]+21 =12(x ﹣6)2+3, 故y=12(x ﹣6)2+3,向左平移2个单位后, 得到新抛物线的解析式为:y=12(x ﹣4)2+3. 故选D .【点睛】本题考查了二次函数图象与几何变换,熟记函数图象平移的规律并正确配方将原式变形是解题关键.14.B【解析】根据“左加右减,上加下减”的原则进行解答即可:∵23222y x y (x 2)y (x 2)3→+→+-向左平移个单位向下平移个单位===y =x 2,∴平移过程为:先向左平移2个单位,再向下平移3个单位.故选B .15.C【详解】解:把抛物线y=﹣2x 2先向右平移1个单位长度,再向上平移2个单位长度后,所得函数的表达式为y=﹣2(x ﹣1)2+2,故选C .16.B【分析】根据“左加右减、上加下减”的原则进行解答即可.【详解】将223y x x =-+化为顶点式,得2(1)2y x =-+.将抛物线223y x x =-+向上平移2个单位长度,再向右平移3个单位长度后,得到的抛物线的解析式为2(4)4y x =-+,故选B .【点睛】本题考查的是二次函数的图象与几何变换,要求熟练掌握平移的规律:左加右减,上加下减.17.A【分析】先确定抛物线y=x 2的顶点坐标为(0,0),再根据点平移的规律得到点(0,0)平移后所得对应点的坐标为(-2,-3),然后根据顶点式写出平移后的抛物线解析式.【详解】抛物线y=x 2的顶点坐标为(0,0),把点(0,0)向左平移1个单位,再向下平移2个单位长度所得对应点的坐标为(-2,-3),所以平移后的抛物线解析式为y=(x+2)2-3. 故选A .18.C【分析】根据向下平移,纵坐标相减,即可得到答案.【详解】∵抛物线y=x 2+2向下平移1个单位,∴抛物线的解析式为y=x 2+2-1,即y=x 2+1.故选C .19.D【分析】由平移可知,抛物线的开口方向和大小不变,顶点改变,将抛物线化为顶点式,求出顶点,再由平移求出新的顶点,然后根据顶点式写出平移后的抛物线解析式.【详解】解:()226534y x x x =-+=--,即抛物线的顶点坐标为()3,4-, 把点()3,4-向上平移2个单位长度,再向右平移1个单位长度得到点的坐标为()4,2-, 所以平移后得到的抛物线解析式为()242y x =--.故选D .【点睛】本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a 不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.20.D【解析】【分析】先确定抛物线y =3x 2的顶点坐标为(0,0),再利用点平移的坐标变换规律得到点(0,0)平移后对应点的坐标为(1,0),然后根据顶点式写出平移后的抛物线的解析式.【详解】y =3x 2的顶点坐标为(0,0),把点(0,0)右平移一个单位所得对应点的坐标为(1,0),所以平移后的抛物线解析式为y =3(x ﹣1)2.故选D .【点睛】本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a 不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.21.C【分析】根据抛物线顶点的变换规律作出正确的选项.【详解】 抛物线212y x =-的顶点坐标是00(,),抛物线线()21112y x =--+的顶点坐标是11(,), 所以将顶点00(,)向右平移1个单位,再向上平移1个单位得到顶点11(,), 即将函数212y x =-的图象向右平移1个单位,再向上平移1个单位得到函数()21112y x =--+的图象. 故选:C .【点睛】主要考查了函数图象的平移,要求熟练掌握平移的规律:左加右减,上加下减.并用规律求函数解析式.22.C【解析】∵抛物线y =﹣2(x ﹣1)2+3的顶点坐标为(1,3),∴向左平移2个单位,再向上平移3个单位后的顶点坐标是(﹣1,6)∴所得抛物线解析式是y =﹣2(x +1)2+6.故选C点睛:本题考查了二次函数图象的平移,其规律是是:将二次函数解析式转化成顶点式y=a (x -h )2+k ,确定其顶点坐标(h ,k ),在原有函数的基础上“ h 值正右移,负左移; k 值正上移,负下移”.23.B【解析】【详解】∵函数y=-2x 2的顶点为(0,0),∴向上平移1个单位,再向右平移1个单位的顶点为(1,1),∴将函数y=-2x 2的图象向上平移1个单位,再向右平移1个单位,得到抛物线的解析式为y=-2(x-1)2+1,故选B.【点睛】二次函数的平移不改变二次项的系数;关键是根据上下平移改变顶点的纵坐标,左右平移改变顶点的横坐标得到新抛物线的顶点.24.D【解析】【分析】先将抛物线y=x2+2x+3化为顶点式,找出顶点坐标,利用平移的特点即可求出新的抛物线,可求得与直线y=3的交点坐标.【详解】解:抛物线y= x2+2x+3=(x+1)2+2,顶点坐标(-1,2),再向下平移3个单位得到的点是(-1,-1).可得新函数的解析式为y=(x+1)2−1,当y=3时候,即:(x+1)2−1=3,得:(x+1)2=4,解得:x=1或x=-3,∴抛物线与直线y=3的交点坐标为(1,3)或(-3,3),故选D.【点睛】本题主要考查抛物线平移的规律与性质, 关键是得到所求抛物线顶点坐标,利用平移的规律解答.25.(1)y=﹣x2﹣2x+3;(2)抛物线与y轴的交点为:(0,3);与x轴的交点为:(﹣3,0),(1,0);(3)15.【解析】【分析】(1)已知了抛物线的顶点坐标,可用顶点式设该二次函数的解析式,然后将B点坐标代入,即可求出二次函数的解析式;(2)根据函数解析式,令x=0,可求得抛物线与y轴的交点坐标;令y=0,可求得抛物线与x轴交点坐标;(3)由(2)可知:抛物线与x轴的交点分别在原点两侧,由此可求出当抛物线与x轴负半轴的交点平移到原点时,抛物线平移的单位,由此可求出A′、B′的坐标.由于△OA′B′不规则,可用面积割补法求出△OA′B′的面积.【详解】解:(1)设抛物线顶点式y=a(x+1)2+4,将B(2,﹣5)代入得:a=﹣1,∴该函数的解析式为:y=﹣(x+1)2+4=﹣x2﹣2x+3;(2)令x=0,得y=3,因此抛物线与y轴的交点为:(0,3),令y=0,﹣x2﹣2x+3=0,解得:x1=﹣3,x2=1,即抛物线与x轴的交点为:(﹣3,0),(1,0);(3)设抛物线与x轴的交点为M、N(M在N的左侧),由(2)知:M(﹣3,0),N(1,0),当函数图象向右平移经过原点时,M与O重合,因此抛物线向右平移了3个单位,故A'(2,4),B'(5,﹣5),∴S△OA′B′=12×(2+5)×9﹣12×2×4﹣12×5×5=15.【点睛】本题考查了用待定系数法求抛物线解析式、函数图象与坐标轴交点、图形面积的求法等知识.熟练掌握待定系数法、函数图象与坐标轴的交点的求解方法、不规则图形的面积的求解方法等是解题的关键.26.(1)证明见解析;(2)3.【分析】(1)求出根的判别式,即可得出答案.(2)先化成顶点式,根据顶点坐标和平移的性质得出即可.【详解】(1)∵()()222224134412120m m m m ∆=--⨯⨯+=--=-<, ∴方程22230x mx m -++=没有实数解.∴不论m 为何值,该函数的图象与x 轴没有公共点.(2)∵()222233y x mx m x m =-++=-+,∴把函数2223y x mx m =-++的图象延y 轴向下平移3个单位长度后,得到函数()23y x m =-+的图象,它的顶点坐标是(m ,0).∴这个函数的图象与x 轴只有一个公共点.∴把函数2223y x mx m =-++的图象延y 轴向下平移3个单位长度后,得到的函数的图象与x 轴只有一个公共点.【点睛】本题考查了1.抛物线与x 轴的交点问题;2.一元二次方程根的判别式;3.二次函数图象与平移变换.27.(1)1,1,52a h k ===- (2)开口向下,对称轴是x=1的直线,顶点(1,-5) 【解析】试题分析:(1)二次函数的平移,可以看作是将二次函数y=12(x+1)2-1先向右平移2个单位,再向下平移4个单位得到二次函数y=a(x-h)2+k ,然后再按二次函数图象的平移法则,确定函数解析式,即可得到结论;(2),直接根据函数解析式,结合二次函数的性质,进行回答即可.试题分析:(1)∵二次函数y=a(x-h)2+k 的图象先向左平移2个单位,再向上平移4个单位,得到二次函数y=12(x+1)2-1, ∴可以看作是将二次函数y=12 (x+1)2-1先向右平移2个单位,再向下平移4个单位得到二次函数y=a(x-h)2+k ,而将二次函数y=12 (x+1)2-1先向右平移2个单位,再向下平移4个单位得到二次函数为:y=12(x-1)2-5,∴a=12,b=1,k=-5; (2)二次函数y=12 (x-1)2-5, 开口向上,对称轴为x=1,顶点坐标为(1,-5).28.y=x 2-8x+20.【分析】根据题意易得新抛物线的顶点,根据顶点式及平移前后二次项的系数不变可得新抛物线的解析式.【详解】2y 23x x =-+=()21x - +2,其顶点坐标为(1,2).向上平移2个单位长度,再向右平移3个单位长度后的顶点坐标为(4,4),得到的抛物线的解析式是y=()24x -+42820x x =-+.故答案为2y 820x x =-+.【点睛】本题考查二次函数图象与几何变换.29.22(3)23y x =-+ 【解析】【分析】先确定抛物线y 2213x =-的顶点坐标为(0,-1),再把点(0,-1)先向右平移3个单位,再向上平移3个单位后得到的点的坐标为(3,2),然后根据顶点式写出平移后抛物线的解析式.【详解】解:抛物线y=2213x -的顶点坐标为(0,-1),把点(0,-1)先向右平移3个单位,再向上平移3个单位后得到的点的坐标为(3,2),所以所得的抛物线的解析式为y=()22323x -+. 故答案为y=()22323x -+. 【点睛】本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.30.y=(x﹣3)2+2【解析】【分析】根据题意易得新抛物线的顶点,根据顶点式及平移前后二次项的系数不变可得新抛物线的解析式.【详解】解:y=x2﹣2x+3=(x﹣1)2+2,其顶点坐标为(1,2).向右平移2个单位长度后的顶点坐标为(3,2),得到的抛物线的解析式是y=(x﹣3)2+2,故答案为:y=(x﹣3)2+2.【点睛】此题主要考查了次函数图象与几何变换,要求熟练掌握平移的规律:左加右减,上加下减.。
平移练习题答案

平移练习题答案平移是数学中描述图形在平面上按照一定方向和距离移动的过程。
以下是一些平移练习题及其答案:练习题1:在平面直角坐标系中,点A的坐标为(3, 4)。
将点A向右平移5个单位,求新点的坐标。
答案:点A向右平移5个单位后,其x坐标增加5,变为3+5=8。
y坐标不变,仍为4。
因此,新点的坐标为(8, 4)。
练习题2:已知直线AB的方程为y = 2x + 3,若将直线AB向上平移3个单位,求新直线的方程。
答案:直线AB向上平移3个单位,其方程中的常数项需要增加3。
因此,新直线的方程为y = 2x + 3 + 3,即y = 2x + 6。
练习题3:在平面直角坐标系中,矩形ABCD的顶点坐标分别为A(1, 2),B(1, 6),C(5, 6),D(5, 2)。
将矩形ABCD向右平移4个单位,求新矩形的顶点坐标。
答案:将矩形ABCD向右平移4个单位,每个顶点的x坐标都增加4。
因此,新矩形的顶点坐标为:- 新A点:(1+4, 2) = (5, 2)- 新B点:(1+4, 6) = (5, 6)- 新C点:(5+4, 6) = (9, 6)- 新D点:(5+4, 2) = (9, 2)练习题4:已知三角形PQR的顶点坐标分别为P(-2, 3),Q(-2, -1),R(2, 1)。
将三角形PQR向下平移2个单位,求新三角形的顶点坐标。
答案:将三角形PQR向下平移2个单位,每个顶点的y坐标都减少2。
因此,新三角形的顶点坐标为:- 新P点:(-2, 3-2) = (-2, 1)- 新Q点:(-2, -1-2) = (-2, -3)- 新R点:(2, 1-2) = (2, -1)练习题5:在平面直角坐标系中,圆心O的坐标为(0, 0),半径为5。
将圆心O向左平移3个单位,向上平移2个单位,求新圆的方程。
答案:圆心O向左平移3个单位,向上平移2个单位后,新的圆心坐标为(-3, 2)。
新圆的方程为(x+3)^2 + (y-2)^2 = 5^2,即(x+3)^2 + (y-2)^2= 25。
平移的练习题答案

平移的练习题答案平移是一种几何变换,指的是在平面内,将一个图形沿着某一方向移动一定的距离,而图形的形状和大小保持不变。
下面是一些关于平移的练习题及其答案。
练习题1:若一个点A(3,4)沿x轴正方向平移5个单位,求平移后的新坐标。
答案:点A沿x轴正方向平移5个单位后,x坐标增加5,y坐标不变。
因此,新坐标为(3+5, 4) = (8, 4)。
练习题2:一个矩形的顶点坐标为(1,2), (1,6), (5,6), (5,2)。
如果这个矩形沿y轴负方向平移3个单位,求平移后矩形的顶点坐标。
答案:沿y轴负方向平移3个单位,即每个顶点的y坐标减少3。
所以,平移后的顶点坐标为:(1, 2-3), (1, 6-3), (5, 6-3), (5, 2-3) = (1, -1), (1, 3), (5, 3), (5, -1)。
练习题3:如果一个三角形的顶点坐标为A(2,5), B(4,1), C(-1,3),求这个三角形沿向量<3,2>平移后的新顶点坐标。
答案:沿向量<3,2>平移,即每个顶点的x坐标增加3,y坐标增加2。
因此,新顶点坐标为:A'(2+3, 5+2) = (5, 7)B'(4+3, 1+2) = (7, 3)C'(-1+3, 3+2) = (2, 5)练习题4:一个平行四边形的顶点坐标为D(0,0), E(4,0), F(4,3), G(0,3)。
如果这个平行四边形沿y轴正方向平移4个单位,求平移后平行四边形的顶点坐标。
答案:沿y轴正方向平移4个单位,即每个顶点的y坐标增加4。
因此,平移后的顶点坐标为:D'(0, 0+4), E'(4, 0+4), F'(4, 3+4), G'(0, 3+4) = (0, 4), (4, 4), (4, 7), (0, 7)。
练习题5:一个圆的圆心坐标为H(-3,-3),半径为2。
求这个圆沿向量<-1,1>平移后的新圆心坐标。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平移一、知识点复习知识点1:平移的定义:在平面内,一个图形沿某个方向移动一定的距离,这种图形的变换叫做平移。
知识点2:平移的要素1.平移的方向:原图上的点指向它的对应点的射线方向;2.平移的距离:连接原图与平移后图形上的一对对应点的线段的长度。
知识点3:平移的性质1.性质(1)平移只改变图形的位置,不改变图形的形状和大小。
(2)平移后的图形与原图形上对应点连成的线段,①数量关系是相等 .②位置关系是平行或在同一条直线上。
2.判断一组图形能不能通过平移得到的方法(1)看对应点连线是否平行或在同一条直线上;(2)看它的形状、大小是否发生变化,位置的变化是否由平移产生。
★★★特别注意:平移是由平移的方向和距离决定的,平移必须指明平移的方向和距离;平移是在平面内,整个图形沿着某一直线平行移动的过程,原图上的每个点都沿同一方向移动相同的距离;平移的距离不能为0;平移的方向是任意的,但就一次平移而言,只能有一个方向,一次平移完成后可以改变方向进行下一次平移。
二、典型例题题型1:生活中平移现象【例题1】(2017春•乌海期末)下列运动属于平移的是()A.荡秋千 B.推开教室的门 C.风筝在空中随风飘动 D.急刹车时,汽车在地面上的滑动【例题2】:(2016春•淮安期中)下列现象:①电梯的升降运动,②飞机在地面上沿直线滑行,③风车的转动,④冷水加热过程中气泡的上升.其中属于平移的是()A.①② B.①③ C.②③ D.③④题型2:平移的性质【例题4】:(2016春•沧州期末)在下列说法中:①△ABC在平移过程中,对应线段一定相等;②△ABC 在平移过程中,对应线段一定平行;③△ABC在平移过程中,周长保持不变;④△ABC在平移过程中,对应边中点所连线段的长等于平移的距离;⑤△ABC在平移过程中,面积不变,其中正确的有()A.①②③④ B.①②③④⑤ C.①②③⑤ D.①③④⑤题型3:与平移有关的计算【例题5】:(2015春•石家庄期末)如图,将△ABC沿射线BC方向移动,使点B移动到点C,得到△DCE,连接AE,若△ABC的面积为2,则△ACE的面积为()A.2 B.4 C.8 D.16【例题6】:(2017秋•兴化市期末)如图,将△ABE向右平移2cm得到△DCF,AE、DC交于点G.如果△ABE的周长是16cm,那么△ADG与△CEG的周长之和是 cm。
例题6 例题7【例题7】(2017春•高密市期末)如图,大矩形长是10厘米,宽是8厘米,阴影部分宽为2厘米,则空白部分面积是()A.36平方厘米 B.40平方厘米 C.32平方厘米 D.48平方厘米【例题8】(2017春•孝南区期末)如图所示,某住宅小区内有一长方形地块,想在长方形地块内修筑同m.样宽的两条”之”字路,余下部分绿化,道路的宽为2米,则绿化的面积为2例题8 例题9【例题9】如图所示,平移△ABC 可得到△DEF,如果∠A=50°,∠C=60°2 AB ,那么∠E=•____度, ∠EDF=_____度,∠F=______度,∠DOB=_______度,DE= .题型4:平移作图【例题10】按要求作图:将三角形ABC 向右平移8格;题型5:综合题型【例题11】:(2016春•莱芜期末)已知:BC ∥OA ,∠B=∠A=100°,试回答下列问题:(1)如图①,OB 与AC 平行吗为什么?(2)如图②,若点E 、F 在BC 上,且满足∠FOC=∠AOC ,并且OE 平分∠BOF .求∠EOC 的度数;(3)在(2)的条件下,若平行移动AC ,如图③,那么∠OCB 与∠OFB 之间的关系并说明理由.三、课堂检测一、选择题1.(2018春•潮州期中)如图所示,四幅汽车标志设计中,能通过平移得到的是()A. B. C. D.2.(2014春•陆丰市校级期中)如图所示,由△ABC平移得到的三角形的个数是()A.5 B.15 C.8 D.63.(2018春•天心区校级期末)平移后的图形与原来的图形的对应点连线()A.相交 B.平行 C.平行或在同一条直线上且相等 D.相等4.如图所示,△DEF经过平移可以得到△ABC,那么∠C的对应角和ED的对应边分别是( )A.∠F, ACB.∠BOD, BAC.∠F, BAD.∠BOD, AC5. 如图10-4-8所示,A、B、C、D四幅图案中,能通过平移图案(1)得到的是()6.下列运动属于平移的是()A.风车的转动B.冷水加热过程中小气泡上升成为大气泡。
C.急刹车是汽车在地面上滑行。
D.随手抛出的小石子的运动。
7.(2018春•宜兴市期中)如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为20cm,则四边形ABFD的周长为()A.20cm B.22cm C.24cm D.26cm二、填空题8.在平移过程中,平移后的图形与原来的图形________和_________都相同,•因此对应线段和对应角都________.9.如图10-4-5所示,已知线段DE由线段AB平移而得, AB=DC=4cm,EC=5cm,则△DCE的周长是____ cm.10.(2017秋•绍兴期末)某小区有一块长方形的草地(如图),长18米,宽10米,空白部分为两条宽度m.均为2米的小路,则草地的实际面积2三、解答题11.(2016春•定陶县期末)如图,两个大小一样的直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=10,DH=4,平移距离为6,求阴影部分的面积。
四、课后作业一、选择题1.(2015春•利川市校级月考)下面生活中的物体的运动情况可以看成平移的是()(1)摆动的钟摆.(2)在笔直的公路上行驶的汽车.(3)随风摆动的旗帜.(4)摇动的大绳.(5)汽车玻璃上雨刷的运动.(6)从楼顶自由落下的球(球不旋转).A.(1)(2) B.(1)(3)(4) C.(3)(4)(5) D.(2)(6)2.(2017秋•姜堰区期末)如图图形中,把△ABC平移后能得到△DEF的是()A. B. C. D.3.如图所示,△FDE经过怎样的平移可得到△ABC.( )A.沿射线EC的方向移动DB长;B.沿射线EC的方向移动CD长C.沿射线BD的方向移动AD长;D.沿射线BD的方向移动DC长4.(2017秋•鸡西期末)如图,在10×6的网格中,每个小正方形的边长都是1个单位,将三角形ABC平移到三角形DEF的位置,下面正确的平移步骤是()A.先向左平移5个单位,再向下平移2个单位 B.先向右平移5个单位,再向下平移2个单位C.先向左平移5个单位,再向上平移2个单位 D.先向右平移5个单位,再向上平移2个单位5.下列说法错误的是()A.一个三角形沿某一个方向平移后,所得的三角形与原来的三角形形状,大小都一样。
B.一个图形平移后对应点的连线平行且相等。
C.一个圆平移后得到一个椭圆D.若两个三角形的形状和大小完全一样,则这两个三角形不一定是平移得到的。
6.如图,△ABC平移到△EFG,则图中共有平行线()对对对对7.(2017•莱西市一模)如图,面积为6cm2的△ABC纸片沿BC方向平移至△DEF的位置,平移的距离是BC 长的2倍,则△ABC纸片扫过的面积为()A.18cm2 B.21cm2 C.27cm2 D.30cm2二、填空题8.图形的平移是由_________和_________决定的,图形平移后它的__________和_________没有发生变化。
9.观察图10-4-1中的正六边形A BCDEF,线段AB平移后能得到的线段是,EF是线段平移得到的。
10.如果△ABC沿着北偏东50°的方向移动了4cm,那么△ABC的一条高AD上的中点M向__________方向移动了______________.11.如图10-4-3,在长方形ABCD中,AB=10cm,BC=6cm,将长方形ABCD沿着BC方向平移____________才能使平移后的长方形与原来的长方形ABCD重叠的部分面积为20cm2.12.如图10-4-4所示,△A′B′C′是由△ABC沿BC方向平移3个单位得到的,则点A与点A′的距离等于个单位.13.(2017春•农安县期末)如图,在一块长方形ABCD草地上,AB=10,BC=15,有一条弯曲的柏油小路(小路任何地方的水平宽度都是2个单位),空白部分表示的草地面积是。
三、解答题14.(2017秋•灵石县期末)如图,已知直线AB∥CD,∠A=∠C=100°,E,F在CD上,且满足∠DBF=∠ABD,BE平分∠CBF.(1)求证:AD∥BC;(2)求∠DBE的度数;(3)若平行移动AD,在平行移动AD的过程中,是否存在某种情况,使∠BEC=∠ADB若存在,求出其度数;若不存在,请说明理由.平移参考答案:二.典型例题题型1:生活中平移现象【例题1】(2017春•乌海期末)下列运动属于平移的是()A.荡秋千 B.推开教室的门 C.风筝在空中随风飘动 D.急刹车时,汽车在地面上的滑动参考答案:D【例题2】:(2016春•淮安期中)下列现象:①电梯的升降运动,②飞机在地面上沿直线滑行,③风车的转动,④冷水加热过程中气泡的上升.其中属于平移的是()A.①② B.①③ C.②③ D.③④参考答案:A题型2:平移的性质【例题4】:(2016春•沧州期末)在下列说法中:①△ABC在平移过程中,对应线段一定相等;②△ABC 在平移过程中,对应线段一定平行;③△ABC在平移过程中,周长保持不变;④△ABC在平移过程中,对应边中点所连线段的长等于平移的距离;⑤△ABC在平移过程中,面积不变,其中正确的有()A.①②③④ B.①②③④⑤ C.①②③⑤ D.①③④⑤参考答案:D题型3:与平移有关的计算【例题5】:(2015春•石家庄期末)如图,将△ABC沿射线BC方向移动,使点B移动到点C,得到△DCE,连接AE,若△ABC的面积为2,则△ACE的面积为()A.2 B.4 C.8 D.16参考答案:A【例题6】:(2017秋•兴化市期末)如图,将△ABE向右平移2cm得到△DCF,AE、DC交于点G.如果△ABE的周长是16cm,那么△ADG与△CEG的周长之和是 cm。
【例题7】(2017春•高密市期末)如图,大矩形长是10厘米,宽是8厘米,阴影部分宽为2厘米,则空白部分面积是()A .36平方厘米B .40平方厘米C .32平方厘米D .48平方厘米参考答案:D【例题8】(2017春•孝南区期末)如图所示,某住宅小区内有一长方形地块,想在长方形地块内修筑同样宽的两条”之”字路,余下部分绿化,道路的宽为2米,则绿化的面积为 2m .参考答案:540【例题9】如图所示,平移△ABC 可得到△DEF,如果∠A=50°,∠C=60°2 AB ,那么∠E=•____度, ∠EDF=_____度,∠F=______度,∠DOB=_______度,DE= .题型4:平移作图按要求作图:将三角形ABC 向右平移8格;题型5:综合题型(2016春•莱芜期末)已知:BC ∥OA ,∠B=∠A=100°,试回答下列问题:(1)如图①,OB 与AC 平行吗为什么?(2)如图②,若点E 、F 在BC 上,且满足∠FOC=∠AOC ,并且OE 平分∠BOF .求∠EOC 的度数;(3)在(2)的条件下,若平行移动AC ,如图③,那么∠OCB 与∠OFB 之间的关系并说明理由.【解答】(1)证明:∵BC ∥OA , ∴∠B+∠O=180°, ∴∠O=180°-∠B=80°,而∠A=100°, ∴∠A+∠O=180°, ∴OB ∥AC ;(2)解:∵OE 平分∠BOF , ∴∠BOE=∠FOE ,而∠FOC=∠AOC , ∴∠EOF+∠COF=21∠AOB=21×80°=40°; (3)结论为:∠OFB=2∠OCB ;∵BC ∥OA , ∴∠OCB=∠AOC ,∠OFB=∠AOF ,∵∠FOC=∠AOC , ∴∠AOF=2∠AOC , ∴∠OFB=2∠OCB . 三、课堂检测一、选择题1.(2018春•潮州期中)如图所示,四幅汽车标志设计中,能通过平移得到的是()A. B. C. D.参考答案:A2.(2014春•陆丰市校级期中)如图所示,由△ABC平移得到的三角形的个数是()A.5 B.15 C.8 D.6参考答案:A3.(2018春•天心区校级期末)平移后的图形与原来的图形的对应点连线()A.相交 B.平行 C.平行或在同一条直线上且相等 D.相等参考答案:C4.如图所示,△DEF经过平移可以得到△ABC,那么∠C的对应角和ED的对应边分别是( )A.∠F, ACB.∠BOD, BAC.∠F, BAD.∠BOD, AC参考答案:C5. 如图10-4-8所示,A、B、C、D四幅图案中,能通过平移图案(1)得到的是()参考答案:B6.下列运动属于平移的是()A.风车的转动B.冷水加热过程中小气泡上升成为大气泡。
