12.1全等三角形-优质PPT课件
合集下载
12-1 全等三角形 课件(共26张PPT)

时,对应的顶点放在对应的位置上.
知识梳理
例题 1:如图所示,△ ≌△ ,指出所有的对应边和对应角.
AB与DC,AC与DB,BC与CB是对应边;
∠ABC与∠DCB,∠A与∠D,∠ACB与∠DBC是对应角。
【解答】(1)已知△ABC≌△DCB,故公共边BC和CB
是对应边,它们所对的∠A和∠D是对应角,最短边
【结论】本题考查了全等三角形的性质及
比较角的大小,解题的关键是找到两全等
三角形的对应角、对应边.
80°
.
知识梳理
例题4:如图,将长方形ABCD沿AE折叠,使D点落在BC边上的F点处,
如果∠BAF = 60°,那么∠DAE= 15°
角
例题5:如图,△ ABC ≌△ ADE,则AB = AD ,∠E =
知识梳理
把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合
的边叫做对应边,重合的角叫做对应角。例如,图中的△ 和△
全等,记作△ ≌ ,其中点和点,点和点,点
和点是对应顶点;和,和,和是对应边;∠和
∠,∠和∠,∠和∠是对应角.
∠BAE = 130°,∠BAD = 50°,则∠BAC=
。
80°
∠C
,若
知识梳理
例题6:如图,已知△ ABC ≌△ EBF,AB ⊥ CE,ED ⊥ AC,∠A = 24°,
则:(1)AB =
EB ,BC = BF ,∠C = 66 °,∠EFB = 66 °;
(2)若AB = 5cm,BC = 3cm,则AF = 2cm 。
AB和DC是对应边,它们所对的∠ACB和∠DBC是对应
角,余下的一对边和一对角分别是对应边和对应角.
(2)根据书写规范可知点A和点D,点B和点C,点C
知识梳理
例题 1:如图所示,△ ≌△ ,指出所有的对应边和对应角.
AB与DC,AC与DB,BC与CB是对应边;
∠ABC与∠DCB,∠A与∠D,∠ACB与∠DBC是对应角。
【解答】(1)已知△ABC≌△DCB,故公共边BC和CB
是对应边,它们所对的∠A和∠D是对应角,最短边
【结论】本题考查了全等三角形的性质及
比较角的大小,解题的关键是找到两全等
三角形的对应角、对应边.
80°
.
知识梳理
例题4:如图,将长方形ABCD沿AE折叠,使D点落在BC边上的F点处,
如果∠BAF = 60°,那么∠DAE= 15°
角
例题5:如图,△ ABC ≌△ ADE,则AB = AD ,∠E =
知识梳理
把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合
的边叫做对应边,重合的角叫做对应角。例如,图中的△ 和△
全等,记作△ ≌ ,其中点和点,点和点,点
和点是对应顶点;和,和,和是对应边;∠和
∠,∠和∠,∠和∠是对应角.
∠BAE = 130°,∠BAD = 50°,则∠BAC=
。
80°
∠C
,若
知识梳理
例题6:如图,已知△ ABC ≌△ EBF,AB ⊥ CE,ED ⊥ AC,∠A = 24°,
则:(1)AB =
EB ,BC = BF ,∠C = 66 °,∠EFB = 66 °;
(2)若AB = 5cm,BC = 3cm,则AF = 2cm 。
AB和DC是对应边,它们所对的∠ACB和∠DBC是对应
角,余下的一对边和一对角分别是对应边和对应角.
(2)根据书写规范可知点A和点D,点B和点C,点C
初中数学《全等三角形》课件PPT

(来自《点拨》)
知2-练
1 说出图12.1-2 (2)、图12.1-2 (3)中两个全等三角形 的 对应边、对应角.
(2)(3)图 1源自.1-2(来自教材)知2-练
解:在教材图12.12(2)中,AB和DB,BC和BC,AC和 DC是对应边;∠A和∠D,∠ABC和∠DBC, ∠ACB和∠DCB是对应角. 在教材图12.12(3)中,AB和AD,BC和DE,AC和 AE是对应边;∠BAC和∠DAE,∠B和∠D,∠C 和∠E是对应角.
知1-导
知1-讲
一个图形经过平移,翻折,旋转后,位置变化了, 但_形_状_和_大_小_都没有改变,即平移,翻折, 旋转前后的图形___完__全__重__合__ . 定义 形状、大小相同的图形放在一起能够完全重合.
能够完全重合 的两个图形叫做全等形.
(来自《教材》)
知1-讲
例1 下列图中是全等形是 ①和⑨、②和③、④和⑧、⑪和⑫ .
例2 如图,已知△ABD≌△CDB,∠ABD=∠CDB, 写出其对应边和对应角.
知2-讲
导引:在△ABD和△CDB中,∠ABD=∠CDB,则 ∠ABD,∠CDB所对的边AD与CB是对应边,公共 边BD与DB是对应边,余下的一对边AB与CD是对 应边.由对应边所对的角是对应角可确定其他两组 对应角.
(来自《典中点》)
知1-练
3 下列说法:①两个图形全等,它们的形状相同;
②两个图形全等,它们的大小相同;③面积相
等的两个图形全等;④周长相等的两个图形全
等.其中正确的个数为( B )
A.1个
B.2个
C.3个
D.4个
(来自《典中点》)
知识点 2 全等三角形及对应元素
知2-导
能够完全重合的两个三角形,叫做_全__等__三__角__形___.
知2-练
1 说出图12.1-2 (2)、图12.1-2 (3)中两个全等三角形 的 对应边、对应角.
(2)(3)图 1源自.1-2(来自教材)知2-练
解:在教材图12.12(2)中,AB和DB,BC和BC,AC和 DC是对应边;∠A和∠D,∠ABC和∠DBC, ∠ACB和∠DCB是对应角. 在教材图12.12(3)中,AB和AD,BC和DE,AC和 AE是对应边;∠BAC和∠DAE,∠B和∠D,∠C 和∠E是对应角.
知1-导
知1-讲
一个图形经过平移,翻折,旋转后,位置变化了, 但_形_状_和_大_小_都没有改变,即平移,翻折, 旋转前后的图形___完__全__重__合__ . 定义 形状、大小相同的图形放在一起能够完全重合.
能够完全重合 的两个图形叫做全等形.
(来自《教材》)
知1-讲
例1 下列图中是全等形是 ①和⑨、②和③、④和⑧、⑪和⑫ .
例2 如图,已知△ABD≌△CDB,∠ABD=∠CDB, 写出其对应边和对应角.
知2-讲
导引:在△ABD和△CDB中,∠ABD=∠CDB,则 ∠ABD,∠CDB所对的边AD与CB是对应边,公共 边BD与DB是对应边,余下的一对边AB与CD是对 应边.由对应边所对的角是对应角可确定其他两组 对应角.
(来自《典中点》)
知1-练
3 下列说法:①两个图形全等,它们的形状相同;
②两个图形全等,它们的大小相同;③面积相
等的两个图形全等;④周长相等的两个图形全
等.其中正确的个数为( B )
A.1个
B.2个
C.3个
D.4个
(来自《典中点》)
知识点 2 全等三角形及对应元素
知2-导
能够完全重合的两个三角形,叫做_全__等__三__角__形___.
人教版八年级上册第十二章 12.1全等三角形 课件(共18张PPT)

今日任务—— 课堂作业:课本P31-32习题1、2 家庭作业:3、4
寻找对应边对应角的规律
(1)有公共边的,公共边是对应边; (2)有公共角的,公共角是对应角; (3)有对顶角的,对顶角是对应角; (4)最大边与最大边(最小边与最小边) 为
对应边;最大角与最大角(最小角与最小角)为对 应角;
(5)对应角所对的边为对应边;对应边所对 的角为对应角;
(6)根据书写规范,按照对应顶点找对应边 或对应角.
△ABC≌△BAD的对应边和
角∴
AB∠-BAACE= ∠=AEBFD-EA AF∠=ABEB=C_=_6_-2∠_=_B4AD
对应角
角 ∠C= ∠D
等式的性质1
谈谈你这节课的收获
全等三角形
(1)能够完全重合的两个三角形叫做全等三角形; (2)全等三角形的性质:对应边相等、对应角相等; (3)全等三角形用符号“≌”表示,且一般对应顶点写在对应位置上.
人教版八年级数学上册
12.1全等三角形
教学目标
知识与能力
1.知道什么是全等形、全等三角形及全等三角形的对应元素; 2.知道全等三角形的性质,能用符号正确地表示两个三角形全等.
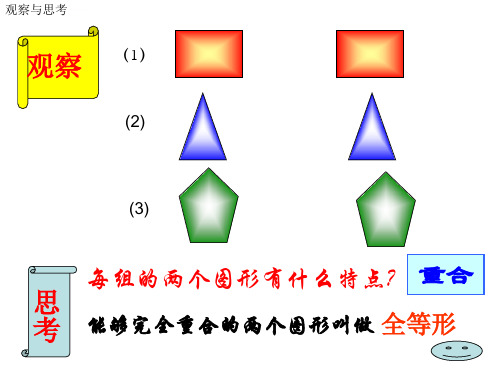
观察 (1)
(2)
(3)
每组的两个图形有什么特点? 重合
思 考 能够完全重合的两个图形叫做 全等形
2021年8月12日星期四
F
如图:∵△ABC≌△DEF ∴AB=DE,BC=EF,AC=DF ( 全等三角形的对应边相等 )
∠A=∠D,∠B=∠E,∠C=∠F ( 全等三角形的对应角相等 )
A
D
随堂练习:
B
CE
F
第二题图
1、若△ ABC≌ △ DEF,则∠B= ∠E , ∠BAC= ∠EDF ,
第十二章12.1全等三角形.1全等三角形课件ppt
1、有公共边
A
B
D
A
D B
A
D
B
C
CLeabharlann C2、有公共角 、对顶角
D
A O
A
D
O
A
E
D
C B
C
B
C
B
让我们记住找对应边、对应角的方法
活动5:展示才华 认识到了贫困户贫困的根本原因,才能开始对症下药,然后药到病除。近年来国家对扶贫工作高度重视,已经展开了“精准扶贫”项目
A
填一填:
1、已知△ABC≌△ADE,
认识到了贫困户贫困的根本原因,才 能开始 对症下 药,然 后药到 病除。 近年来 国家对 扶贫工 作高度 重视, 已经展 开了“ 精准扶 贫”项 目
同一张底片洗出的照片
形状、大小相同的图形放在一起能够完全重合。 能够完全重合的两个图形叫做全等形.
认识到了贫困户贫困的根本原因,才 能开始 对症下 药,然 后药到 病除。 近年来 国家对 扶贫工 作高度 重视, 已经展 开了“ 精准扶 贫”项 目
F
全等三角形的性质: 1、全等三角形的对应边相等,
2、全等三角形的对应角相等。 ∵△ABC≌△DEF (已知)
∴ AB=DE,BC=EF,AC=DF(全等三角形的对应边相等)
∠A=∠D,∠B=∠E,∠C=∠F(全等三角形的对应角相等)
例1
认识到了贫困户贫困的根本原因,才 能开始 对症下 药,然 后药到 病除。 近年来 国家对 扶贫工 作高度 重视, 已经展 开了“ 精准扶 贫”项 目
C
D
A
B
认识到了贫困户贫困的根本原因,才 能开始 对症下 药,然 后药到 病除。 近年来 国家对 扶贫工 作高度 重视, 已经展 开了“ 精准扶 贫”项 目
A
B
D
A
D B
A
D
B
C
CLeabharlann C2、有公共角 、对顶角
D
A O
A
D
O
A
E
D
C B
C
B
C
B
让我们记住找对应边、对应角的方法
活动5:展示才华 认识到了贫困户贫困的根本原因,才能开始对症下药,然后药到病除。近年来国家对扶贫工作高度重视,已经展开了“精准扶贫”项目
A
填一填:
1、已知△ABC≌△ADE,
认识到了贫困户贫困的根本原因,才 能开始 对症下 药,然 后药到 病除。 近年来 国家对 扶贫工 作高度 重视, 已经展 开了“ 精准扶 贫”项 目
同一张底片洗出的照片
形状、大小相同的图形放在一起能够完全重合。 能够完全重合的两个图形叫做全等形.
认识到了贫困户贫困的根本原因,才 能开始 对症下 药,然 后药到 病除。 近年来 国家对 扶贫工 作高度 重视, 已经展 开了“ 精准扶 贫”项 目
F
全等三角形的性质: 1、全等三角形的对应边相等,
2、全等三角形的对应角相等。 ∵△ABC≌△DEF (已知)
∴ AB=DE,BC=EF,AC=DF(全等三角形的对应边相等)
∠A=∠D,∠B=∠E,∠C=∠F(全等三角形的对应角相等)
例1
认识到了贫困户贫困的根本原因,才 能开始 对症下 药,然 后药到 病除。 近年来 国家对 扶贫工 作高度 重视, 已经展 开了“ 精准扶 贫”项 目
C
D
A
B
认识到了贫困户贫困的根本原因,才 能开始 对症下 药,然 后药到 病除。 近年来 国家对 扶贫工 作高度 重视, 已经展 开了“ 精准扶 贫”项 目
全等三角形ppt课件

动学生的学习积极性,使学生勇于提出问题,乐于探索问题,同时 注重培养学生善于合作交流的良好情感和积极向上的学习态度. 学习重难点
1、重点:全等三角形的概念、性质及对应元素的确定. 2、难点:全等三角形对应元素的确定.
活动一:
1、观察:下列各组图形的形状与大小有什么特点?
2、小结:
能够完全重合的两个图形称为全等形。
第十二章 全等三角形
人教版八年级数学(上)
12.1 全等三角形
学习目标 1、了解全等三角形的概念,通过动手操作,体会平移、翻折、
旋转是考察两三角形全等的主要方法. 2、能准确确定全等三角形的对应元素,掌握全等三角形的性
质. 3、通过找出全等三角形的对应元素,培养学生的识图能力. 4、通过构建和谐的课堂教学氛围,激发学生的学习兴趣,调
A.AC=DE B.∠BAD=∠CAE C.AB=AE D.∠ABC=∠AED
4、下列说法正确的是( ) A. 两个周长相等的圆是全等图形。 B. 两个面积相等的三角形是全等图形。 C. 两个长方形是全等图形。 D. 两个正方形是全等图形。
5、一个三角形的三边为2、7、x,另一个三角形的三边为y、2、6, 若这两个三角形全等,则x+y=______ .
D A图形经过平移、旋转或翻折等变换后,所得
到的新图形一定与原图形全等.
A
(2)全等三角形的性质: 全等三角形的对应边相等。
全等三角形的对应角相等。 B
CE
(3)推论: 全等三角形的面积相等。 全等三角形的周长相等。
D F
3、思考:把一个三角形平移、旋转、翻折,变换前后的两个三角形 全等吗?若全等,找出全等图形的对应元素。
(2)∠NAB、∠NMC、∠MNC的度数。
1、重点:全等三角形的概念、性质及对应元素的确定. 2、难点:全等三角形对应元素的确定.
活动一:
1、观察:下列各组图形的形状与大小有什么特点?
2、小结:
能够完全重合的两个图形称为全等形。
第十二章 全等三角形
人教版八年级数学(上)
12.1 全等三角形
学习目标 1、了解全等三角形的概念,通过动手操作,体会平移、翻折、
旋转是考察两三角形全等的主要方法. 2、能准确确定全等三角形的对应元素,掌握全等三角形的性
质. 3、通过找出全等三角形的对应元素,培养学生的识图能力. 4、通过构建和谐的课堂教学氛围,激发学生的学习兴趣,调
A.AC=DE B.∠BAD=∠CAE C.AB=AE D.∠ABC=∠AED
4、下列说法正确的是( ) A. 两个周长相等的圆是全等图形。 B. 两个面积相等的三角形是全等图形。 C. 两个长方形是全等图形。 D. 两个正方形是全等图形。
5、一个三角形的三边为2、7、x,另一个三角形的三边为y、2、6, 若这两个三角形全等,则x+y=______ .
D A图形经过平移、旋转或翻折等变换后,所得
到的新图形一定与原图形全等.
A
(2)全等三角形的性质: 全等三角形的对应边相等。
全等三角形的对应角相等。 B
CE
(3)推论: 全等三角形的面积相等。 全等三角形的周长相等。
D F
3、思考:把一个三角形平移、旋转、翻折,变换前后的两个三角形 全等吗?若全等,找出全等图形的对应元素。
(2)∠NAB、∠NMC、∠MNC的度数。
《12.1 全等三角形》课件(3套)

∴∠A=∠F, ∠B=∠D, ∠ACB= ∠FED.
DDDDDDDDD
B
规律五:一对最大的角是对应角 一对最小的角是对应角
已知△A0B≌△COD 指出图中 两三角形的对应边和对应角
A
D O B
C
已知△ABC≌△DCB 指出图 中两三角形的对应边和对应角
A B
D O
C
找一找:请指出下列全等三角形的对应边和对应角
解:在△ABC中,∠ACB=180°-30°-50°= 100°.∵△ABC≌△DEF,∴∠DFE=∠ACB=100°,EF=BC,∴EC =BF=2
10.如图,Rt△ABC沿直角边BC所在的直线向右平移得到△DEF,下 列结论中错误的是( D )
A.△ABC≌△DEF B.∠DEF=90° C.AC=DF D.EC=CF
1.不能准确确定全等三角形的对应关系. 2.对应关系考虑不全面而出错.
观察 (1)
(2)
(3)
每组的两个图形有什么特点? 重合 思 考 能够完全重合的两个图形叫做全等形
观察下面两组图形,它们是不是全等图形?为什么?与同伴进行交流。
形状
1
相同
大小 相同
2
全等图形的特征: 全等图形的形状和大小都相同
3.如图,将△ABC沿CB方向平移得到△DFE,则△ABC≌△__D_F_E, ∠ABC的对应角是 ∠DFE,∠C的对应角是 ∠DEF,BC的对应边是 _F__E_.
4.如图,将△ABC绕点A顺时针方向旋转得到△ADE,那么∠BAC的 对应角是∠__D_A_,E ∠B的对应角是_∠__D_,AC的对应边是__A_E_,BC的对应边 是__D_E_.
典型例题
例3:如图,若ΔABC≌ΔAEF, AB=AE,∠B=∠E,则下列
DDDDDDDDD
B
规律五:一对最大的角是对应角 一对最小的角是对应角
已知△A0B≌△COD 指出图中 两三角形的对应边和对应角
A
D O B
C
已知△ABC≌△DCB 指出图 中两三角形的对应边和对应角
A B
D O
C
找一找:请指出下列全等三角形的对应边和对应角
解:在△ABC中,∠ACB=180°-30°-50°= 100°.∵△ABC≌△DEF,∴∠DFE=∠ACB=100°,EF=BC,∴EC =BF=2
10.如图,Rt△ABC沿直角边BC所在的直线向右平移得到△DEF,下 列结论中错误的是( D )
A.△ABC≌△DEF B.∠DEF=90° C.AC=DF D.EC=CF
1.不能准确确定全等三角形的对应关系. 2.对应关系考虑不全面而出错.
观察 (1)
(2)
(3)
每组的两个图形有什么特点? 重合 思 考 能够完全重合的两个图形叫做全等形
观察下面两组图形,它们是不是全等图形?为什么?与同伴进行交流。
形状
1
相同
大小 相同
2
全等图形的特征: 全等图形的形状和大小都相同
3.如图,将△ABC沿CB方向平移得到△DFE,则△ABC≌△__D_F_E, ∠ABC的对应角是 ∠DFE,∠C的对应角是 ∠DEF,BC的对应边是 _F__E_.
4.如图,将△ABC绕点A顺时针方向旋转得到△ADE,那么∠BAC的 对应角是∠__D_A_,E ∠B的对应角是_∠__D_,AC的对应边是__A_E_,BC的对应边 是__D_E_.
典型例题
例3:如图,若ΔABC≌ΔAEF, AB=AE,∠B=∠E,则下列
121全等三角形上课用 ppt课件
26
(三)拓展与应用
1、全等对应元素的找法 A
D
小组活动
O
C
小组方案
B B
A
DD
方法提练
B
C
B
2020/12/15
A
D C
A
EC
27
寻找对应元素的规律
(1)有公共边的,公共边是对应边;
(2)有公共角的,公共角是对应角;
(3)有对顶角的,对顶角是对应角;
(4)两个全等三角形最大的边是对应边, 最小的边也是对应边;
动脑筋:两个等边三角形全等吗?两个正方 形全等吗?为什么?
2020/12/15
22
1.概念:能够完全重合的两个图形叫全等形。
2.表示:全等多边形对应顶点要写在对应的位 置上。 3.性质:全等多边形对应边、对应角分别相等。 4.识别:边、角对应相等的两个多边形全等。
2020/12/15
23
课堂小测:
11.1 全等三角形
2020/12/15
1
观
同一张底片冲洗出来的两张照片
察
形状和大小有什么特征?
2020/12/15
2
精品资料
• 你怎么称呼老师? • 如果老师最后没有总结一节课的重点的难点,你
是否会认为老师的教学方法需要改进? • 你所经历的课堂,是讲座式还是讨论式? • 教师的教鞭 • “不怕太阳晒,也不怕那风雨狂,只怕先生骂我
2020/12/15
15
在找全等三角形的对应元素时 一般有什么规律?
A
2020/12/15
C
A
C
E
O
D
B
D
B
有公共角的,公共角是对应角.
人教版八年级数学上册全等三角形精品课件PPT
•
2、人物作为支撑影片的基本骨架,在 影片中 发挥着 不可替 代的作 用,也 是影片 的灵魂 ,阿甘 是影片 中的主 人公, 是支撑 起整个 故事的 重要人 物,也 是给人 最大启 示的人 物。
•
3、在生命的每一个阶段,阿甘的心中 只有一 个目标 在指引 着他, 他也只 为此而 踏实地 、不懈 地、坚 定地奋 斗,直 到这一 目标的 完成, 又或是 新的目 标的出 现。
•
4、让学生有个整体感知的过程。虽然 这节课 只教学 做好事 的部分 ,但是 在研读 之前我 让学生 找出风 娃娃做 的事情 ,进行 板书, 区分好 事和坏 事,这 样让学 生能了 解课文 大概的 资料。
•
5、人们都期望自我的生活中能够多 一些快 乐和顺 利,少 一些痛 苦和挫 折。可 是命运 却似乎 总给人 以更多 的失落 、痛苦 和挫折 。我就 经历过 许多大 大小小 的挫折 。
A组: B组: C组:
第十二章 全等三角形 12.1 全等三角形
人教版八年级数学上册 12.1 全等三角形 课件
1、理解图形全等的概念和特征, 能识别全等形; 2、掌握全等三角形的性质,并能 进行简单的推理和计算。
人教版八年级数学上册 12.1 全等三角形 课件
人教版八年级数学上册 12.1 全等三角形 课件
人教版八年级数学上册 12.1 全等三角形 课件
找出下面的全等形。
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
解:(1)和(9)、(2)和(8)、 (3)和(6)
人教版八年级数学上册 12.1 全等三角形 课件
人教版八年级数学上册 12.1 全等三角形 课件
人教版数学八年级上册12.1 全等三角形课件(共24张PPT)
图 (1)
图 (2)
图 (3)
12.1 全等三角形
一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有 改变,即平移、翻折、旋转前后的图形全等.
图 (1)
图 (2)
图 (3)
12.1 全等三角形
把两个全等的三角形重合到一起,
重合的顶点叫做对应顶点,
A
D
重合的边叫做对应边,
重合的角叫做对应角.
除颜色外形状、大小完全一样. 能够完全重合.
12.1 全等三角形
归纳
可以看到,形状、大小相同的图形放在一起能够完全重合,我们把能够 完全重合的两个图形叫作全等形.
能够完全重合的两个三角形叫作全等三角形.
12.1 全等三角形
思考
我们将买来的一面三角彩旗的三个顶点分别标为A、B、C, 在图 (1) 中,把△ABC 沿直线 BC 平移,得到△DEF. 在图 (2) 中,把△ABC 沿直线 BC 翻折180°,得到△DBC. 在图 (3) 中,把△ABC 绕点 A 旋转,得到△ADE. 各图中的两个三角形全等吗?
A
D
B
CE
F
注意:记两个三角形全等时,通常把表示对应顶点的字母写在 对应的位置上.
12.1 全等三角形 例1 说出图 (2)(3) 中两个全等三角形的对应顶点、对应边和对应角,并 写成△***≌△***的形式.
解:△ABC≌△DBC. 对应顶点:点 A 和点 D,点 B 和点 B,点 C 和点 C ; 图 (2) 对应边:AB 和 DB,BC 和 BC,AC 和 DC; 对应角:∠A 和∠D,∠ABC 和∠DBC,∠ACB 和∠DCB .
的是△DEF,若△ABC≌△DEF,对应边有什么关系?对应角呢?
数学人教版八年级上册12.1 全等三角形.1 全等三角形(共47张PPT)
BD
C
想一想: 能否根据下列全等式说出两个
三角形的对应边和对应角
1.△BDC ≌ △FHG
BD=FH DC=HG BC=FG ∠B=∠F ∠D=∠H ∠C=∠G
2.△AOC ≌ △BOD
AO=BO OC=OD AC=BD ∠A=∠B ∠O=∠O ∠C=∠D
请小心:在具体图形中,有时角不能用一个 大写字母表示。
沿BC方向平移一个单位得
到△DEF,则四边形ABFD的
周长为_1_0_____
BE C F
如图△ABD≌ △EBC, AB=3cm,BC=5cm,求DE的长.
D
E
A
B
C
课堂小结
1.能够重合的两个图形叫做 全等形。 互相重合的顶点叫做 对应顶点 。
其中 互相重合的边叫做 对应边 。 互相重合的角叫做 对应角 。
请观察,并说出你看到的现象
请观察,并说出你看到的现象 结论:这两个三角形重合
学习目标 1.掌握全等形及全等三角形的相关 概念。
2.会找全等三角形的对应顶点、对 应角及对应边。
3.理解并掌握全等三角形的性质。
“全等”用符号≌“
A
”来表示 读作“全等于”
D
B
CE
F
三角形ABC 全等于三角形DEF
A
B
● O
D
C
思考题:
如图,已知⊿ABC≌⊿ADE,且∠CAD=
100,∠DFB=900,∠B=250,求∠E和
∠DGB的度数。
A
E
F G
C
B D
提问与解答环节
Questions And Answers
谢谢聆听
·学习就是为了达到一定目的而努力去干, 是为一个目标去 战胜各种困难的过程,这个过程会充满压力、痛苦和挫折
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
你能指出上面 两个全等三角 形的对应顶点、 对应边
C
E
F
3、全等三角形的表示法
记作△ABC≌ △DEF,读作△ABC全等于△DEF 对应的顶点要写在对应的位置
“全等”用符号“≌ ”,表示图中的△ABC和△DEF全等,
注意
全等三角形的性质.
全等三 角形的 性质
A
C O
M
S
O
D
B
C
寻找对应边、对应角有什么规律?
寻找对应边、对应角的规律
在全等三角形中,一般是: 1.有公共边,则公共边为对应边 2.有公共角,则公共角为对应角 (对顶角为对应角) 3.最大边与最大边(最小边与最小边) 为 对应边;最大角与最大角(最小角与最小角) 为对应角
4.对应角的对边为对应边; 对应边的对角为对应角。
下列各组图形的形状 与大小有什么特点?
同一张底片洗出的照片
下列各组图形的形状 与大小有什么特点?
下列各组图形的形状 与大小有什么特点?
下列各组图形的形状 与大小有什么特点?
思考:他们能完全重合吗?
下列各组图形的形状 与大小有什么特点?
思考:他们能完全重合吗?
每组的两个图 形有什么特点?
A
B
祝大家学习愉快
• 形状、大小相同的图形放在 一起能够完全重合。 • 能够完全重合的两个图形叫 做全等形 • 能够完全重合的两个三角形 叫做全等三角形
D
∠BDA= ∠CEA
B
C
3、若△ABC≌△CDA,AB= ∠BAC= ∠DCA
CD A
D
公共边
B C
请你利用两个全等三角形拼出有公共
顶点或公共边或公共角的图形。
用全等符号表示这两个全等三角形,并 写出全等三角形的对应边、对应角。
1、有公共边
A A A D B C D
D
B
B
C
C
2、有公共点
D A A O O E B B B C D C B C D A E A D
发现:全等三角形的对应边相等; N
全等三角形的对应角相等.
T
全等三角形性质的几何语言
A D
B
C
E
F
∵△ABC≌△DEF(已知) ∴AB=DE, AC=DF,BC=EF(全等三角形对应边相等) ∠A=∠D, ∠B=∠E, ∠C=∠F(全等三角形对应角相等)
请填空
公共点
A O B
A E
D
1、若△AOC≌△BOD,AC= BD ∠ A= ∠ B C 公共角 2、若△ABD≌△ACE,BD=CE ,
完全重合
能够完全重合的两个图形称为全等形
各图中的两个三角形是全等形吗?
A D
B
A
C
C
E
M O
F
S
O B
解后思:
D N T
平移、翻折、旋转前后的两个三角形的位置改变, 但形状、大小不变。
大家来探索新知!
1、能够完全重合的两个三角形,叫做 全等三角形.
A D
B
C
E
F
2、把两个全等的三角形重叠到
一起时,重合的顶点叫做对应顶 点,重合的边叫做对应边,重合 的角叫做对应角
5.根据书写规范,按照对应 顶点找对应边或对应角。
[例1]如图,△OCA≌△OBD,C 和B,A和D是对应顶点,• 说出这 两个三角形中相等的边和角
.
[例2]如图,已知△ABE≌△ACD, ∠ADE=∠AED,∠B=∠C,•指出其他 的对应边和对应角.
A
B
D
E C
拓展训练共提高 (4)如右图,已知△ABD≌△ACE, 且∠C=45°,AC = 8,AE = 5,则 3 . ∠B = 45° , DC =
A
B (2)已知△ABC≌△CDA, 则AC边的对应边为 CA C F (3)已知△ABC≌△DEF,
D A B C
则AB边的对应边为 DE E
D
∠C的对应角为
∠F
拓展训练共提高
2、请选择
(1) △ABC≌ △BAD,点A和点B、点C和点D是对应点, 如果AB=6cm,BD=5cm,AD=7cm,那么BC的长是 ( )A (A)7cm (B)6cm (C)5cm ( D)无法确定 (2)在上题中, ∠CAB的对应角是( B ) (A)∠DAB (B) ∠ DBA D C (C) ∠ DBC (D) ∠ CAD
8
D
5
C
A
5
E
B
大家一起来说说:
我的收获……
1、知识点:了解全等形、全等三角形的有 关概念,会找全等三角形的对应元素; 2、学习方式:动手实验(平移、旋转、 翻折)、合作交流。 3、情感上:快乐学习,勤于思考, 体验成功。
A
D
课堂检测
(1)已知△ABC≌△DEF, 则∠A的对应角为 ∠D
B
E
C
F
