杨氏双缝实验
杨氏双缝实验

实验六 杨氏双缝实验一、实验目的1.观察杨氏双缝干涉现象,认识光的干涉。
2.了解光的干涉产生的条件,相干光源的概念。
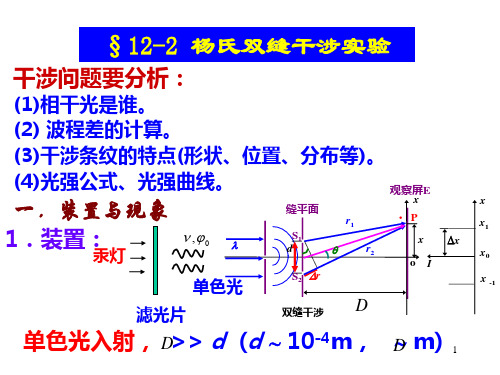
二、实验原理(一)杨氏双缝实验由光源发出的光照射在单缝S 上,使单缝S 成为实施本实验的缝光源。
在单缝S 前面放置两个相距很近的狭缝S 1和S 2,且S 1和S 2与S 之间的距离均相等。
S 1和S 2是由同一光源S 形成的,满足振动方向相同、频率相同、相位差恒定的相干条件。
故S 1和S 2为相干光源。
当S 1和S 2发出的光在空间相遇,将产生干涉现象,在屏幕P 上将出现明、暗交替的干涉条纹。
1. 分波阵面获得相干光,满足振动方向相同,相位差恒定,频率相同的干涉条件。
2. 干涉明暗条纹的位置P 点处的波程差,12r r -=δ∆,(空气的折射率 n = 1 ) 在 D >>d , D >>x ,即θ 很小时,D xd d d r r =≈≈-=θθδtan sin 12 (其中Dx=θtan ) (1)双缝干涉的明暗纹条纹干涉相消暗纹干涉相长明纹 ,2,1,0,2,1,0)12(==⎩⎨⎧+±±==k k k k x D dλλδ(2)干涉明暗纹的位置,2,1,02)12(,2,1,0=+±==±=k dD k x k d D kx ,暗纹,明纹λλ两相邻明纹或暗纹的间距都是dD x λ=∆ 其它 x 点的亮度介于明纹和暗纹之间,逐渐变化 综上所述,杨氏双缝干涉的特点:(1) 用分振幅法获得相干光,两束光初相位相同,均无半波损失;(2) 干涉明暗纹是等间距分布,相邻明纹间的距离与入射光的波长成正比,波长越小,条纹间距越小;(3) 若用白光照射,则在中央明纹(白光)的两侧将出现彩色条纹。
(二) 杨氏双缝干涉的光强分布狭缝S 1和S 2发出的光波单独到达屏上任一点B 处的振幅分别为A 1和A 2,光强分别为I 1和I 2,则根据叠加原理,两光波叠加后的振幅为:)cos(212212221ϕϕ-++=A A A A A两光波叠加后的光强为:)cos(2122121ϕϕ-++=I I I I I其中: λδπϕϕ212=-。
杨氏双缝实验实验报告

一、实验目的1. 通过杨氏双缝实验,观察光的干涉现象,验证光的波动性。
2. 理解光的干涉条件,包括相干光源的概念。
3. 掌握实验仪器的操作方法,包括光源、狭缝、透镜和屏幕等。
4. 学习如何测量光波的波长。
二、实验原理杨氏双缝实验是由英国物理学家托马斯·杨于1801年提出的,该实验通过观察光通过两个狭缝后在屏幕上形成的干涉条纹,验证了光的波动性。
实验原理基于以下两个假设:1. 光是一种波动现象。
2. 当两束相干光波相遇时,会发生干涉现象。
在杨氏双缝实验中,光通过两个狭缝后,在屏幕上形成一系列明暗相间的干涉条纹。
这些条纹的形成是由于两束光波相遇时发生干涉,即两束光波的振幅相加,导致某些区域光强增强(亮条纹),而另一些区域光强减弱(暗条纹)。
根据杨氏双缝实验的原理,可以推导出干涉条纹间距的公式:\[ \Delta x = \frac{\lambda L}{d} \]其中,\(\Delta x\) 是相邻两条亮条纹或暗条纹之间的距离,\(\lambda\) 是光波的波长,\(L\) 是屏幕到双缝的距离,\(d\) 是两个狭缝之间的距离。
三、实验仪器1. 激光器:提供单色光源。
2. 狭缝板:包含两个平行的狭缝。
3. 透镜:将激光束聚焦到狭缝板上。
4. 屏幕板:用于观察干涉条纹。
5. 支架:用于固定实验仪器。
四、实验步骤1. 将激光器、狭缝板、透镜和屏幕板按照实验要求放置在支架上。
2. 调整透镜,使激光束聚焦到狭缝板上。
3. 调整狭缝板,使两个狭缝平行且距离适中。
4. 调整屏幕板,使屏幕与狭缝板平行,并观察屏幕上的干涉条纹。
5. 记录屏幕上的干涉条纹间距,并计算光波的波长。
五、实验结果与分析1. 在实验过程中,成功观察到屏幕上的干涉条纹,验证了光的波动性。
2. 根据干涉条纹间距的测量结果,计算出光波的波长。
3. 通过实验结果,可以得出以下结论:- 光是一种波动现象。
- 干涉现象是光波的基本特性之一。
波动光学实验系列之杨氏双缝干涉

波动光学实验系列之杨氏双缝干涉
一、引言
波动光学实验一直是光学领域中的重要研究方向,其中杨氏双缝干涉实验是一种经典的实验现象。
本文将介绍杨氏双缝干涉实验的原理、实验装置及其应用。
二、实验原理
杨氏双缝干涉实验是利用光的波动性质进行研究的实验。
在这个实验中,一束光线通过两个密接的缝隙后,形成交替明暗条纹的干涉图样。
这种干涉现象可以用光的波动理论来解释,根据叠加原理,两个波的相位差会决定光的干涉效应。
三、实验装置
杨氏双缝干涉实验的实验装置主要包括光源、双缝光栅、透镜和屏幕。
光源产生一束平行光,通过双缝光栅后,光线经过透镜成像在屏幕上,观察者可以看到干涉条纹的形成。
四、实验过程
在进行杨氏双缝干涉实验时,首先需要调整光源和双缝光栅的位置,使得光线通过双缝形成干涉条纹。
然后调整透镜的位置和焦距,使得干涉条纹清晰可见。
最后观察屏幕上的干涉条纹,并记录实验现象。
五、实验应用
杨氏双缝干涉实验不仅是一种经典的光学实验,还具有广泛的应用价值。
在现代科学研究中,杨氏双缝干涉实验常被用于测量光波的波长、验证光的波动性质,以及研究干涉现象对光学元件的影响等方面。
六、结论
通过对杨氏双缝干涉实验的介绍,我们可以更深入地了解光的波动性质和干涉现象。
这一实验不仅展示了光学的精彩世界,还为我们理解光的本质提供了重要的实验依据。
希望通过这篇文档,读者能够对光学实验有一个更加全面的认识。
以上是关于波动光学实验系列之杨氏双缝干涉的简要介绍,希望能为您带来有价值的信息。
杨氏双缝干涉实验

D 解 (1)由双缝干涉明纹条件 x k ,可得 d
x15
D x5 x1 (k5 k1 ) d
杨氏双缝干涉实验
d x15 4 10 6 10 6.0 107 m(橙色) 11 D (k5 k1 ) 1 (5 1)
(2)当 4000 A时,相邻两明纹间距为
杨氏双缝干涉实验
D (1)d 、 一定时,若 变化, x 变化情况
4
杨氏双缝干涉实验
(2)、D 一定时,条纹间距 x 与 d 的关系
5
杨氏双缝干涉实验
二、其他分波阵面干涉装置
6
1.菲涅耳双面镜
装置 S点光源(或线光源,与两镜交线平行);M1和M2:镀 银反射镜,夹角很小; 两反射镜把S发出的光分成两 部分,可以看作缝干涉实验
相位分析
7
同一光源,分波面, 有固定的位相差。从两虚 光源看,位相差为
2 S1 p S 2 p
条纹位置 可直接利用Young双缝干涉的结果。
杨氏双缝干涉实验
2、洛埃镜 洛埃(H.Lloyd)镜的装置如图,它是一个平面镜.从狭缝
S1发出的光,一部分直接射向屏E,另一部分以近90° 的入射角掠射到镜面ML上,然后反射到屏幕E上.
(2k 1)
2
k 0,1, 2,
x
D (2k 1) d 2
D k d
k 0,1,2,
暗纹
杨氏双缝干涉实验
白光照射时,出现彩色条纹。
3
讨论
条纹间距
D x xk 1 xk d
d 、 一定时, D
条纹间距 与 的关系 ;
若 变化 , x 将怎样变化?
B3-2杨氏双缝干涉实验

(1.51)d5 d106m
例8 钠光灯作光源,波长 0.5,8屏9与m 3双缝的距离
D=500mm,(1)d=1.2mm和d=10mm,相邻明条纹间距分别
为多大?(2) 若相邻明条纹的最小分辨距离为0.065mm,能
分辨干涉条纹的双缝间距是多少?
解 {1}d= 1.2 mm
例2、根据条纹移动求缝后所放介质片的厚度
当双缝干涉装置的一条狭缝S1后面盖上折射率为n=1.58
的云母片时,观察到屏幕上干涉条纹移动了9个条纹间距,
已知波长λ=5500A0,求云母片的厚度。
P
S1 r1
x
d S2
r2
O
解:没有盖云母片时,零级明条纹在O点; 当S1缝后盖上云母片后,光线1的光程增大。 由于零级明条纹所对应的光程差为零,所以这时零级明条
d
可利用此公式求波长
一般称到达屏上某点的两条相干光线间的夹角为相干光束
的会聚角,记为
当 dD 且 x, yD 有 d D
P
S1
r1
x
则 e
d
r2
O
S2
条纹间距正比于相干光的波长,反比于相干光束的会聚角
任何两条相邻的明(或暗)条纹所对应的光程差之差一定
等于一个波长值。 m (m1) 2 上式中的m为干涉条纹的级次。
例3 一双缝装置的一个缝为折射率1.40的薄玻璃片遮盖,另 一个缝为折射率1.70的薄玻璃片遮盖,在玻璃片插入以后, 屏上原来的中央极大所在点,现在为原来的第五级明纹所占
据。假定λ=480nm,且两玻璃片厚度均为t,求t值。
解:两缝分别为薄玻璃片遮盖后,两束相干光到达O点处
的光程差的改变为
P
杨氏双缝干涉
k 1,2,.....
2)、用波程差表示: k 0,1,2,3.....
d sin
2k .....加强(明).....
x2 d. {(2k 1) 减弱(暗).......(12.8)
D2
k——条纹级次
k 1,2,3.....
3
(2)干涉明纹和暗纹中心的位置: 1)明纹中心的位置:
x D k D ......(12 9) k 0,1,2,.....
d
d
2)暗纹中心的位置:
x D (2k 1) D ......(12 10) k 1,2,3,.....
d
d2
3)k=0时,x 0即在屏中央出现明纹—称为零级
明纹。
如D、不变,而d减小,某级条纹的位置如何
变化?
明纹: k (整数级)
暗纹:(2k-1)/2(半整数级) 5
观察屏
x
(4)相邻两明纹或相邻两暗纹间的距离:
亮纹位置:
xk
D d
k
xk 1
D d
(k
1)
暗纹 +2级
+1级
0级亮纹 -1级 -2级
相邻亮纹间距:
x
xk 1
xk
D d
相邻两明纹中心或相邻两暗纹中心间的距离:
x
D d
.........(12.11)
(2)、相位差: 2 ......(1)
——相干光的波长。
2
2、干涉明暗条纹的位置和条件:
· (1)、干涉明暗条纹的条件:
r1
Px x
1)、用相位差表示:
k 0,1,2,.....
d
r2
r
D
x o x0
第三讲 杨氏双缝干涉实验

4、条纹间距
y
yk 1
yk
(k
1)
D d
k
D d
D d
① 等距离分布,与级数无关;
② D>>d可分辨;
r1
p
d
θ
r2
光强的分布
I
β
I β
D
医学物理学
复色光:中央白色、两侧内紫外红条纹
若用复色光源,则干涉条纹是彩色的。
k D
d
k 3 k 1 k 1 k 3
k 2
k 2医学物理学医 Nhomakorabea物理学实际上,第10级明纹已看不清楚,例:
k=10;λ=5×10-7 m;d = 10-4 m
d sin k
Bp
sin
10 5107 104
0.05
s1
s do
s2
o
30
r
D
D d
D d,sin tan y
D
r2
r1
d
sin
d
y D
医学物理学
3、条纹位置
d sin d y k , y k D k 0,1, 2,3
杨氏双缝干涉(Young’s double-slit interference)
1、装置与原理
S1 S
S2
2、条纹分布规律
(mm)
实 验
d
s1
s
r 1 r 2
装
o
置
s2
r
D d
D(m)
Bp
y
o
d sin k
明条纹
d sin (2k 1)
k 0,1, 2,
暗条纹
2
杨氏双缝实验

2 干涉减弱
明纹中心
x
D 2k 2a 2
D (2k 1) 2a 2
k 0,1,2,
暗纹中心
每一条纹都对应着一定的波程差(相位差), 如第三级明纹对应的波程差为3。
太原理工大学物理系
4 干涉条纹形状及间距 形状:明暗相间的直条纹(平行于缝) 间距:条纹均匀分布 相邻两条明纹或暗纹的距离: 观察屏 暗纹 +2级 +1级 0级亮纹 -1级 -2级
k红 k 1 紫 ( )
紫 4000 k 1 3 红 紫 7000 4000
未重叠的清晰光谱只有一级。 太原理工大学物理系
条纹形态: 平行于缝的等亮度、等间距、明暗相间条纹
条纹亮度:
I max 4I1
x D d
I min 0
条纹宽度:
条纹变化:
2
k
( n 1)e
太原理工大学物理系
7
缝光源垂直于轴上、下移动对干涉条纹的影响。
1 2
x
S’ S 单 缝
S1
o 0
S2 双缝
0
如图:光源 S 向上移动到 S 则干涉条纹怎么变化
,
屏
条纹将向下平移
太原理工大学物理系
例3 在双缝干涉实验中,单色光源 S 到两缝 S 和 S 1 2 的距离分别为 l1和l2,并且 l l 3 , 为入射
问:(1)中央明纹两测第十级明纹的距离
(2)第十条明纹的位置 (3)用厚度为 e 6.6 106 m ,折射率n=1.58 的玻璃片盖住一缝后,问零级明纹移动了第几 级明纹处? 太原理工大学物理系
D D D D 解: x10 ,10 10 ( 10 ) 20 20 2a 2a 2a d 2 5.5 107 20 1.1102 2 104
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验六 杨氏双缝实验
一、实验目的
1.观察杨氏双缝干涉现象,认识光的干涉。
2.了解光的干涉产生的条件,相干光源的概念。
二、实验原理
(一)杨氏双缝实验
由光源发出的光照射在单缝S 上,使单缝S 成为实施本实验的缝光源。
在单缝S 前面放置两个相距很近的狭缝S 1和S 2,且S 1和S 2与S 之间的距离均相等。
S 1和S 2是由同一光源S 形成的,满足振动方向相同、频率相同、相位差恒定的相干条件。
故S 1和S 2为相干光源。
当S 1和S 2发出的光在空间相遇,将产生干涉现象,在屏幕P 上将出现明、暗交替的干涉条纹。
1. 分波阵面获得相干光,满足振动方向相同,相位差恒定,频率相同的干涉条件。
2. 干涉明暗条纹的位置
P 点处的波程差,12r r -=δ∆,(空气的折射率 n = 1 ) 在 D >>d , D >>x ,即θ 很小时,D xd d d r r =≈≈-=θθδtan sin 12 (其中D
x
=θtan ) (1)双缝干涉的明暗纹条纹
干涉相消
暗纹干涉相长
明纹 ,2,1,0,2,1,0)12(==⎩⎨⎧+±±==
k k k k x D d
λ
λδ
(2)干涉明暗纹的位置
,2,1,02)12(,2,1,0=+±==±=k d
D k x k d D k
x ,暗纹,明纹λ
λ
两相邻明纹或暗纹的间距都是d
D x λ
=
∆ 其它 x 点的亮度介于明纹和暗纹之间,逐渐变化 综上所述,杨氏双缝干涉的特点:
(1) 用分振幅法获得相干光,两束光初相位相同,均无半波损失;
(2) 干涉明暗纹是等间距分布,相邻明纹间的距离与入射光的波长成正比,波长越小,条纹间距越小;
(3) 若用白光照射,则在中央明纹(白光)的两侧将出现彩色条纹。
(二) 杨氏双缝干涉的光强分布
狭缝S 1和S 2发出的光波单独到达屏上任一点B 处的振幅分别为A 1和A 2,光强分别为I 1和I 2,则根据叠加原理,两光波叠加后的振幅为:
)cos(212212
221ϕϕ-++=A A A A A
两光波叠加后的光强为:
)cos(2122121ϕϕ-++=I I I I I
其中: λ
δ
π
ϕϕ212=-。
当A 1=A 2=A 0,则I 1=I 2=I 0,两光波叠加后的光强为
,2,1,04,2,1,0)12(0
====⎩
⎨⎧+±±=I k I I k k k 光强暗纹光强明纹 λλδ
(三) 缝宽对干涉条纹的影响 空间相干性
在双缝干涉实验中,如果逐渐增加光源狭缝S 的宽度,则屏幕P 上的条纹和会变得逐渐模糊起来,最后干涉条纹完全消失。
这是因为单缝S 内所包含的各小部分S '、S "等非相干波源;它们互不相干,且S '发出的光与S "发出的光通过双缝到达点B 的波程差并不相等,即S '、S "发出的光将各自满足不同的干涉条件。
比如,当S '发出的光经过双缝后恰在点B 形成干涉极大的光强时,S "发出的光可能在点B 形成干涉较小的光强。
由于S '、S "是非相干光源,它们在点B 形成的合光强只是上述结果的简单相加,即非相干叠加。
所以,缝S 愈宽,所包含的非相干子波源愈多,合光强的分布就愈偏离图17-的样式,结果是最暗的光强不为零,使最亮和最暗的差别缩小,从而造成干涉条纹的模糊甚至消失。
只有当光源S 的线度较小时,才能获得较清晰的干涉条纹,这一特性称为光场的空间相干性。
强调:空间相干性是指光源不同位置发出的光在屏幕上形成的干涉条纹是非相干叠加,是光源不同点的波列相遇在空间同一点;而时间相干性是指光源同一点发出的不同时刻波列相遇在空间同一点,不能相干。
三、主要仪器及耗材
1:钠灯(加圆孔光阑) 9:延伸架(SZ-09)
2:透镜L1(f '=50 mm ) 10:测微目镜架
3:二维架(SZ-07) 11:测微目镜M
4:可调狭缝S (SZ-27) 12:二维平移底座 (SZ-02) 5:透镜架(SZ-08,加光阑) 13:二维平移底座 (SZ-02)
6:透镜L2 (f '=150mm) 14:升降调节座(SZ-03)
7:双棱镜调节架 (SZ-41) 15:二维平移底座(SZ-02) 8:双缝D 16:升降调节座(SZ-03)
四、实验内容和步骤
1、使钠光通过透镜L1会聚到狭缝S 上,用透镜L2将S 成像于测微目镜分划板M 上,然后将双缝D 置于L2近旁。
在调节好S ,D 和M 的mm 刻线的平行,并适当调窄S 之后,目镜视场出现便于观测的杨氏条纹。
2、用测微目镜测量干涉条纹的间距△x ,用米尺测量双缝至目镜焦面的距离l ,用显微
镜测量双缝的间距d,根据
d l x λ
=
∆计算钠黄光的波长λ。
五、数据处理与分析
1、分析实验结果,讨论误差形成原因;
2、自拟表格记录实验数据。
六、实验注意事项
1、先后改变双棱镜和目镜的位置,分别观察干涉条纹的变化并作定性解释。
2、仔细观察双棱镜干涉场,是否受到衍射的影响,如何解释?
3、从光具座上取下滤光片,观察干涉条纹的变化,说明其特征。
七、思考题
1、狭缝s 的存在有没有必要?
2、狭缝s 的极限宽度是多少?
3、为什么白光也能产生双缝干涉?
4、试用杨氏双缝实验说明干涉与衍射区别与联系?
图6-4。
