7-2安培定律
合集下载
2安培环路定理
v µ0I v B 1 ⋅ d l1 = dα 2π
v B1
v B2
v d l1
r1
dα
v dl2
θ1
I
●
r2
2
o θ
L
v v µ0I B2 ⋅ dl2 = − dα 2π
v µ0I v B 1 ⋅ d l1 = dα 2π v v µ0I B2 ⋅ dl2 = − dα 2π
v B1
v B2
L1
L
µ0 I
0
（闭合回路包围电流） 闭合回路包围电流） 闭合回路不包围电流） （闭合回路不包围电流）
表明：沿闭合环路的线积分，等于穿过以闭合环路 表明：沿闭合环路的线积分， 为边界的所围曲面的所有电流的代数和乘以 为边界的所围曲面的所有电流的代数和乘以 代数和
µ0
如果闭合回路不在垂直长直电流平面内， 如果闭合回路不在垂直长直电流平面内， 情况又如何？ 情况又如何？
r r ∫ B ⋅ d l ≠ 0 说明稳恒磁场不是保守场
L
——磁场是“有旋场” 磁场是“有旋场” 磁场是
例：如图，流出纸面的电流为 2I ， 如图， 流进纸面的电流为 I ， 则下述各式中那一个是正确的? 则下述各式中那一个是正确的 r r r r (B) ∫ L 2 B ⋅ d l = µ 0 I (A) ∫ L B ⋅ d l = 2µ0 I r r r r (C) ∫ L B ⋅ d l = − µ0 I (D) ∫ L B ⋅ d l = − µ 0 I
如图， 如图，闭合曲线 L 不在垂直直电流的平面内
L
o
v dl||
v dl
v dl⊥
v v v dl = dl|| + dl⊥
L⊥
v B1
v B2
v d l1
r1
dα
v dl2
θ1
I
●
r2
2
o θ
L
v v µ0I B2 ⋅ dl2 = − dα 2π
v µ0I v B 1 ⋅ d l1 = dα 2π v v µ0I B2 ⋅ dl2 = − dα 2π
v B1
v B2
L1
L
µ0 I
0
（闭合回路包围电流） 闭合回路包围电流） 闭合回路不包围电流） （闭合回路不包围电流）
表明：沿闭合环路的线积分，等于穿过以闭合环路 表明：沿闭合环路的线积分， 为边界的所围曲面的所有电流的代数和乘以 为边界的所围曲面的所有电流的代数和乘以 代数和
µ0
如果闭合回路不在垂直长直电流平面内， 如果闭合回路不在垂直长直电流平面内， 情况又如何？ 情况又如何？
r r ∫ B ⋅ d l ≠ 0 说明稳恒磁场不是保守场
L
——磁场是“有旋场” 磁场是“有旋场” 磁场是
例：如图，流出纸面的电流为 2I ， 如图， 流进纸面的电流为 I ， 则下述各式中那一个是正确的? 则下述各式中那一个是正确的 r r r r (B) ∫ L 2 B ⋅ d l = µ 0 I (A) ∫ L B ⋅ d l = 2µ0 I r r r r (C) ∫ L B ⋅ d l = − µ0 I (D) ∫ L B ⋅ d l = − µ 0 I
如图， 如图，闭合曲线 L 不在垂直直电流的平面内
L
o
v dl||
v dl
v dl⊥
v v v dl = dl|| + dl⊥
L⊥
大学物理7-2磁场的源
q
+
r
v
B
q
r
v
B
例4 半径为 R 的带电薄圆盘的电荷面密度为 ，并 以角速度 绕通过盘心垂直于盘面的轴转动，求圆盘 中心的磁感应强度。
解法一 ：圆电流的磁场
dq 2 rdr dI rdr T 2 / dB
R o r
0 dI
2r
0
2
dr
7.2
magnetic field and magnetic induction
磁力——电流和磁体之间的相互作用。 (1) 磁铁与磁铁之间的相互作用力 磁铁
同极相斥 异极相吸
注意：如果把一条磁铁折成数段，不论段数 多少或各段的长短如何，每一小段仍将形成 一个很小的磁铁，仍具有N、S两极，即 N 极与 S 极相互依存而不可分离。但是，正电 荷或负电荷却可以独立存在，这是磁现象和 电现象的基本区别。
(1) 将电流分解为无数个电流元 Idl (2) 由电流元求dB (据毕—萨定律)
(3) 将 dB 在坐标系中分解，并用磁场叠加原理做对称 性分析，以简化计算步骤 (4) 对 dB 积分求 B = dB
Bx dBx , B y dB y , Bz dBz
L L L
矢量合成： B B i B j B k x y z
2
x
C
o
0 I B （cos 1 cos 2 ） 4 r
方向：电流与磁感强度成 右手螺旋定则 注意：从直电流始端沿电 流方向积分到末端。 ◆ 无限长载流长直导线 的磁场
z
D
2
B
I
o
x
C
r
电磁学几大定律
1、安培定则，也叫右手螺旋定则，是表示电流和电流激发磁场的磁感线方向间
关系的定则。
（1）通电直导线中的安培定则（安培定则一）：用右手握住通电直导线，让大拇指指向电流的方向，那么四指的指向就是磁感线的环绕方向；
（2）通电螺线管中的安培定则（安培定则二）：用右手握住通电螺线管，使四指弯曲与电流方向一致，那么大拇指所指的那一端是通电螺线管的N极。
2、左手定则：通电导体放入磁场，
伸开左手，让磁场垂直穿过手掌，四指指向电流方向，则大拇指指的方向即为通电导体所受磁场力的方向。
左手定则可称“电动机定则”，是判断通电导线在磁场中的受力方向的法则，说的是磁场对电流的作用力，或者是磁场对运动电荷的作用力。
其内容是：将左手放入磁场中，使四个手指的方向与导线中的电流方向一致，那么大拇指所指的方向就是受力方向。
无论是直流发电机还是交流发电机，它们的工作原理都是相同的，区别是直流发电机有换向器，而交流发电机则没有换向器
3、右手定则
导体切割磁感线，产生感应电动势。
伸开右手，让磁场垂直穿过手掌，则大拇指指向运动方向，则四指指向即为电流方向。
CH07-2安培环路定理
L3
方向：顺时针，与L2同。 注意： 10管内的磁场是不均匀的。
0 NI B 0 nI 2 r
例3、求无限长均匀载流圆柱体（I、R）内、外的磁场。
I
解：与轴等距离的圆环上B相等，方向如图。
R
L2
r>R时：作环路 L1
L1
B1 dl 0 I i
0 I B1 2 r
I
d B
L
B dl
L
B cos dl Br d
r
p
dl
推广，得安培环路定理：
B dl 0 I i
L
0 I rd 0 I 0 2r
2
安培环路定理： 表示： B d l I 0 i
d
3
c
B1 dl B1 ab ab
ab
bc
cd
da
右：0 Ii
左边=右边：
0 (nab)I
I 为正
Bab 0 nabI
B 0 nI
均匀的场！
例2、求螺绕环（I、N）内的磁场。
解：在环内r处作L2，其上B处处大小相等， 方向与“L2”一致。
根据
20在截面很小的情况下：
30管外（如L1、L3 处）B 0
40螺绕环的截面不一定是圆。
L1
L2
B dl 0 I i
L
安培环路定理：
r
B
B 2 r 0 NI 0 NI B 2 r
方向：沿L1
L1
r
朱卫华《大学物理》2-安培环路定律与安培定律和带电粒子的作用和磁介质2014
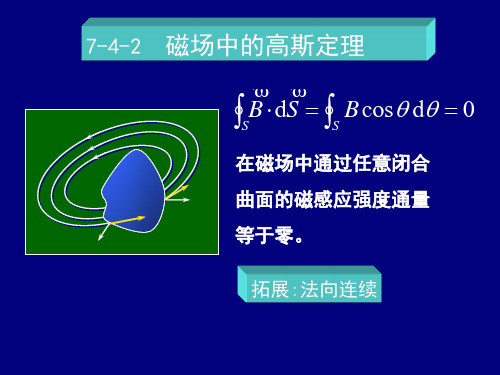
v 2eV m
电子束打在屏幕中央的条件： v E B
E 2eV Bm
e m
E2 2VB 2
电子的比荷： e 1.75881962(53) 1011 C kg 1 m
电子的质量： m 9.1093897(54) 1031 kg
v E B
7 质谱仪原理
R mv qB0
mE qB0 B
不同的粒子质量分布在不同的位置
液体中观察原子图象
下图所示的是在电解液中得到的硫酸根离子吸附在 铜单晶(111)表面的STM图象。
5 . 电子荷质比的测定
控制极 阳极
阴
极
U
⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙
B l
调节B 使比值
l n v0 xT
控制极 阳极
阴
极
U
⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙⊙
B l
T 2π m qB
安培环路定理：
B B onI
a
bB
d
c
2. 螺线环内的磁感应强度
B dl L
o I
B 2 r oNI
B oNI 2 r
环路 L
磁感应 线
无限大电流平面的磁场----与电场作类比
E
2 0
B
0
j 2
???
电场高斯定理和磁场安培环 路定理应用总结
注意
B dl L
0
Ii
1. 安培环路定理表达式中的
电流强度是指闭合曲线所包
I4
围，并穿过的电流强度，不
包括闭合曲线以外的电流。
I3 I2 I1
L
2. 安培环路定理表达式中的磁感应强度B是闭合曲线
内外所有电流产生的磁感应强度。
安培环路定理
(1)管内:取L矩形回路 abcda
边在轴上，两边与轴平行,另
aP b
两个边垂直于轴。
LB dl Bab ab Bcd cd Bab ab
e
Q
f
0I 0nI ab
d
c
∞
B内 onI 其方向与电流满足右手螺旋.
(2)管外 :
取回路efbae同理可证，无限长直螺线管外任一点的磁场为
A(rQ )
0I 2
ln
r Q
r P
A(rP )
A(rQ
)
0I 2
ln
r Q
r
-I
r P
P
两式相加,得:
A(rP )
A(rQ )
0I 2
ln
rQ rP
rP rQ
0I 2
ln
rP rP
A(rP )
A(rQ )
0I 2
ln
r P
r P
若选Q点的矢势为零,则
A(rP )
0I 2
ln
r P
r P
例2.一无限长载流圆柱导体,半径为R, 电流I均匀分布
ldr
0I 2
l
ln
rQ r
A(rP ) A(rQ )
0I 2
ln
rQ rP
+I
Q
若选Q点的矢势为零,则
A(rp
)
0I 2
ln
rQ rP
r P
注意:若选Q点在无穷远处或导线
上,磁矢势将无意义.
讨论:两根平行的载流直导线,电流大 小相等方向相反,求磁矢势.
选Q点在两直线电流之间垂线的中点处.
A(rP )
B dS 0
安培力知识点
安培力知识点
1、安培力是通电导线在磁场中受到的作用力。
2、注意：安培力F垂直于B磁场F垂直于I电流
3、注意：当通电导线与磁场方向平行时，通电导线不受安培力。
也就是电流与磁场平行时
这个电流垂直纸面向内磁场垂直纸面向外都垂直纸面所以不受安培力
4、安培力方向的判断----左手定则
1、伸出左手，使拇指与其余四指垂直，并且跟手掌都在同一平面内。
2、让磁感线垂直穿过手心，并且四指指向电流方向。
3、这时大拇指所指方向就是通电导线在磁场中所受安培力的方向。
4、两条平行导线通上电流：同向电流相互吸引，反向电流相互排斥。
5、安培力的大小
F=BILsinθθ表示导线中电流方向与磁场方向之间的夹角。
7-2 安培定律
此式的适用范围是：直导线，均匀磁场。
B
Idl
×
a
Idl
9
I
dF
B
F
Idl
例 均匀磁场中放置一半圆形导线, 电流为I， ab 与 B 夹角a=30°
求:此段圆弧形通电导线所受 到的磁力。 解
7-2
安培定律
I
ab
B
1. 任取电流元
Idl
2. 电流元所受的安培力:
dF Idl B
1. 均匀磁场B 中长为l的载流导线受力 F dF ( I dl ) B
l l
2. 非均匀磁场中载流导线受力
Fx dFx , Fy dFy , Fz dFz
l l l
F Fxi Fy j Fk k
7
7-2
安培定律
M m B
0M 0 M M max 2 M 0
稳定平衡 力矩最大
非稳定平衡
15
7-2
安培定律
en
en
en
0, M 0 稳定平衡
/2
/ 2 M最大
en
en
/2
16 , M 0 不稳定平衡
dF Idl B
dFx IBdl sin IBdy
y
× dF ×
O
×
Idl
L I
dFy IBdl cos IBdx
Fx 0 IBdy 0
0
F
×
A x
Fy 0 IBdx IBL
L
FI
dl B I OA B
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
7-2 安培定律
第七章
稳恒磁场
1
本章内容
7-1 磁感应强度 磁场的高斯定理 7-2 安培定律 7-3 毕奥-萨伐尔定律 7-4 安培环路定理 7-5 介质中的磁场
7-2 安培定律
2
7-2 安培定律
7-2 安培定律
3
7-2 安培定律
教学基本要求
一、掌握磁感应强度的概念，理解洛伦兹力公式。 二、了解用磁感应线形象描述磁感应强度的方法，会计算简单情况下的磁
Fcd
d (c)
l2
B
en
14
定义磁矩： m NISen
M
m
B
7-2 安培定律
结论
在匀强磁场中，平面线圈所受的安培力合力
为零，仅受磁力矩的作用：
M
m
B
讨论 (1)线圈所受的力矩 ——运动趋势
M
m
B
0M 0
2
M
M max
M 0
稳定平衡 力矩最大 非稳定平衡 15
7-2 安培定律
安培定律
dF Idl B
B
有限长载流导线所受的安培力:
F ldF l Idl B
7-2 安培定律
I Idl S
dl
5
安培定律的微观解释
洛伦兹力：
Fm
qv
B
7-2 安培定律
电流“受力”
载流子通过“碰撞”把“力”传递给导体
载流导体受力（安培力）
电流元相当于运动的电荷元：
Idl
s(nev)dl
8
7-2 安培定律
安培力 F BIl sina
此式的适用范围是：直导线，均匀磁场。
v B
Idl
I
×v a
F
r dF
v B
r Idl
9
例 均匀磁场中放置一半圆形导线,
电流为I， ab 与 B 夹角a=30°
Id l
I
7-2 安培定律
B
求:此段圆弧形通电导线所受
到的磁力。
解 1. 任取电流元 Idl
F Fxi Fy j Fkk
Fz l dFz
7
例 一根长度为 l，电流为 I的 载流导线，放入均匀磁场中，
求该导线所受到的磁场力。
Idl
解
任取电流元 Idl
r r
a Idl , B
电流元所受磁场力： dF Idl B
7-2 安培定律
v B
I
a
×v F
整个导线受力： F BIl sina
六、理解磁场的安培环路定理，理解用安培环路定理计算磁感应强度的条件 和方法并能作简单计算。
七、了解介质的磁化现象及对磁场分布的影响，了解各向同性介质中磁场 强度和磁感应强度的关系，了解铁磁质的特性及应用。
*八、了解介质中的安培环路定理。
4
一、安培定律
由实验总结出磁场对电流元的作用力
dF IdlBsin θ
7-2 安培定律
讨论：
（1）均匀磁场中，若载流导线闭合回路所在的平面与磁感 强度垂直，则该闭合回路所受磁场力合力为零。此结论， 适用于任意形状闭合回路。
（2） 均匀磁场中，任意形状的平面载流导线所受磁场力， 跟与其始末位置相同的载流直导线所受磁场力是相等的。
×× × × ×
×
×× × × ×
×
o× × × × ×
×P
12
7-2 安培定律
二、均匀磁场对载流线圈的作用力矩
将平面载流线圈放入均匀磁场中，
Fda Fbc Il2B cos
Fab Fcd Il1B
a
Fda与Fbc大小相等方向相反，
l1
作用在一条直线上，为一对平衡力。
b Fab与Fcd大小相等方向相反，不在 Fab
一条直线上，不能抵消，为一对力偶，
dqv
在磁场中，“运动电荷”受力：dF
dq(v
B)
dF Idl B
6
7-2 安培定律
有限长载流导线所受的安培力:
F ldF l Idl B
1. 均匀磁场B 中长为l的载流导线受力
F l dF (I l dl ) B
2. 非均匀磁场中载流导线受力
Fx l dFx, Fy l dFy ,
产生力矩。
o
Fda
d
Fcd
I
B
c en
l2 o'
Fbc
13
作俯视图可看出线圈受到的力矩大小为
M
2 Fab
l2 2
sin
2
Il1
B
l2 2
sin
l2 sin
2
o
Il1l2B sin
如果为N匝平面线圈，则
I
a (b )
M NIl1l2B sin
NISBsin
Fab
S为平面线圈面积
7-2 安培定律
dF Idl B
dFx IBdl sin IBdy
dFy IBdl cos IBdx
y
××
dF
I
Idl
× F×
0
Fx 0 IBdy 0
O
L
Ax
L
Fy 0 IBdx IBL
F I dl B I OA B
相当于一根与其始末位置相同载流直导线在匀强磁场所受的力 11
ab
2. 电流元所受的安培力: dF Idl B
3. 整个通电导线受力
场均匀
(b)
F Idl B I dl B I ab B
l
(a)
10
7-2 安培定律
例 在均匀磁场中放置一任意形状的导线，电流强度为I 求: 此段载流导线所受到的磁力。
解
在电流上任取电流元 Idl
en
en
en
0, M 0 稳定平衡
en
/2
/ 2 M最大
en
/2
, M 0 不稳定平16衡
7-2 安培定律
(2)任意形状载流小线圈受的磁力矩
dM
IdSen
B
M
dM
Ien
B
dS
IS B
M
m
B
B
en
I
适用于任意形状的平面载流线圈的 方向上。
通量，理解磁场高斯定理的内涵。 三、理解洛伦兹关系式，能分析点电荷在均匀电场或均匀磁场中的运动，
了解洛仑兹力关系的应用。
四、理解安培定律，了解磁矩的概念，能计算简单几何形状载流导体和载 流平面线圈中所受的力和力矩。
五、理解毕奥-萨伐尔定律，理解磁场叠加原理，能计算一些简单电流分布 产生的磁场的磁感应强度。
17
磁电式电流计原理:
线圈所受磁力矩：
N
游丝M给线圈N的BI反S 抗力矩：
M a
a —游丝的扭转常数
M M NBIS a
I a k
NBS
k a NBS
— 常量
表示线圈偏转单位角度需 通过的电流。
7-2 安培定律
S 磁铁
18
第七章
稳恒磁场
1
本章内容
7-1 磁感应强度 磁场的高斯定理 7-2 安培定律 7-3 毕奥-萨伐尔定律 7-4 安培环路定理 7-5 介质中的磁场
7-2 安培定律
2
7-2 安培定律
7-2 安培定律
3
7-2 安培定律
教学基本要求
一、掌握磁感应强度的概念，理解洛伦兹力公式。 二、了解用磁感应线形象描述磁感应强度的方法，会计算简单情况下的磁
Fcd
d (c)
l2
B
en
14
定义磁矩： m NISen
M
m
B
7-2 安培定律
结论
在匀强磁场中，平面线圈所受的安培力合力
为零，仅受磁力矩的作用：
M
m
B
讨论 (1)线圈所受的力矩 ——运动趋势
M
m
B
0M 0
2
M
M max
M 0
稳定平衡 力矩最大 非稳定平衡 15
7-2 安培定律
安培定律
dF Idl B
B
有限长载流导线所受的安培力:
F ldF l Idl B
7-2 安培定律
I Idl S
dl
5
安培定律的微观解释
洛伦兹力：
Fm
qv
B
7-2 安培定律
电流“受力”
载流子通过“碰撞”把“力”传递给导体
载流导体受力（安培力）
电流元相当于运动的电荷元：
Idl
s(nev)dl
8
7-2 安培定律
安培力 F BIl sina
此式的适用范围是：直导线，均匀磁场。
v B
Idl
I
×v a
F
r dF
v B
r Idl
9
例 均匀磁场中放置一半圆形导线,
电流为I， ab 与 B 夹角a=30°
Id l
I
7-2 安培定律
B
求:此段圆弧形通电导线所受
到的磁力。
解 1. 任取电流元 Idl
F Fxi Fy j Fkk
Fz l dFz
7
例 一根长度为 l，电流为 I的 载流导线，放入均匀磁场中，
求该导线所受到的磁场力。
Idl
解
任取电流元 Idl
r r
a Idl , B
电流元所受磁场力： dF Idl B
7-2 安培定律
v B
I
a
×v F
整个导线受力： F BIl sina
六、理解磁场的安培环路定理，理解用安培环路定理计算磁感应强度的条件 和方法并能作简单计算。
七、了解介质的磁化现象及对磁场分布的影响，了解各向同性介质中磁场 强度和磁感应强度的关系，了解铁磁质的特性及应用。
*八、了解介质中的安培环路定理。
4
一、安培定律
由实验总结出磁场对电流元的作用力
dF IdlBsin θ
7-2 安培定律
讨论：
（1）均匀磁场中，若载流导线闭合回路所在的平面与磁感 强度垂直，则该闭合回路所受磁场力合力为零。此结论， 适用于任意形状闭合回路。
（2） 均匀磁场中，任意形状的平面载流导线所受磁场力， 跟与其始末位置相同的载流直导线所受磁场力是相等的。
×× × × ×
×
×× × × ×
×
o× × × × ×
×P
12
7-2 安培定律
二、均匀磁场对载流线圈的作用力矩
将平面载流线圈放入均匀磁场中，
Fda Fbc Il2B cos
Fab Fcd Il1B
a
Fda与Fbc大小相等方向相反，
l1
作用在一条直线上，为一对平衡力。
b Fab与Fcd大小相等方向相反，不在 Fab
一条直线上，不能抵消，为一对力偶，
dqv
在磁场中，“运动电荷”受力：dF
dq(v
B)
dF Idl B
6
7-2 安培定律
有限长载流导线所受的安培力:
F ldF l Idl B
1. 均匀磁场B 中长为l的载流导线受力
F l dF (I l dl ) B
2. 非均匀磁场中载流导线受力
Fx l dFx, Fy l dFy ,
产生力矩。
o
Fda
d
Fcd
I
B
c en
l2 o'
Fbc
13
作俯视图可看出线圈受到的力矩大小为
M
2 Fab
l2 2
sin
2
Il1
B
l2 2
sin
l2 sin
2
o
Il1l2B sin
如果为N匝平面线圈，则
I
a (b )
M NIl1l2B sin
NISBsin
Fab
S为平面线圈面积
7-2 安培定律
dF Idl B
dFx IBdl sin IBdy
dFy IBdl cos IBdx
y
××
dF
I
Idl
× F×
0
Fx 0 IBdy 0
O
L
Ax
L
Fy 0 IBdx IBL
F I dl B I OA B
相当于一根与其始末位置相同载流直导线在匀强磁场所受的力 11
ab
2. 电流元所受的安培力: dF Idl B
3. 整个通电导线受力
场均匀
(b)
F Idl B I dl B I ab B
l
(a)
10
7-2 安培定律
例 在均匀磁场中放置一任意形状的导线，电流强度为I 求: 此段载流导线所受到的磁力。
解
在电流上任取电流元 Idl
en
en
en
0, M 0 稳定平衡
en
/2
/ 2 M最大
en
/2
, M 0 不稳定平16衡
7-2 安培定律
(2)任意形状载流小线圈受的磁力矩
dM
IdSen
B
M
dM
Ien
B
dS
IS B
M
m
B
B
en
I
适用于任意形状的平面载流线圈的 方向上。
通量，理解磁场高斯定理的内涵。 三、理解洛伦兹关系式，能分析点电荷在均匀电场或均匀磁场中的运动，
了解洛仑兹力关系的应用。
四、理解安培定律，了解磁矩的概念，能计算简单几何形状载流导体和载 流平面线圈中所受的力和力矩。
五、理解毕奥-萨伐尔定律，理解磁场叠加原理，能计算一些简单电流分布 产生的磁场的磁感应强度。
17
磁电式电流计原理:
线圈所受磁力矩：
N
游丝M给线圈N的BI反S 抗力矩：
M a
a —游丝的扭转常数
M M NBIS a
I a k
NBS
k a NBS
— 常量
表示线圈偏转单位角度需 通过的电流。
7-2 安培定律
S 磁铁
18