2016年高考江苏卷
2016年江苏高考语文试卷及答案(完整版-包括附加题)

2016年普通高等学校招生统一考试(江苏卷)语文I试题一、语言文字运用(15分)1.在下面一段话的空缺处依次填入词语,最恰当的一组是(3分)人人都希望自己____________,却很少有人能沉静下来用心对待生活。
其实生活很____________,你是不是诚心待它,它一眼就能分辨出来。
你越____________,越想得到,距离目标就越远;你努力振作,默默耕耘,惊喜往往就会悄然而至。
A.与众不同机敏焦躁B.与众不同敏锐浮躁C.标新立异机敏浮躁D.标新立异敏锐焦躁2.下列熟语中, 没有使用借代手法的一项是(3分)A.人为刀俎,我为鱼肉B.人皆可以为尧舜C.化干戈为玉帛D.情人眼里出西施3.下列各句中,所引诗词不符合语境的一项是(3分)A.“闲云潭影日悠悠,物换星移几度秋”,往事历历,所有的记忆都在时光里发酵,散发出别样的味道。
B.“拣尽寒枝不肯栖,寂寞沙洲冷”,正是这种难言的孤独,使他洗去人生的喧闹,去寻找无言的山水,远逝的古人。
C.“长风破浪会有时,直挂云帆济沧海”,青葱少年总是信心满满,跃跃欲试,渴望在未来的岁月中大显身手。
D.“帘外雨潺潺,春意阑珊”,初春的细雨渐渐沥沥,撩拨了无数文人墨客心中关于江南的绵绵情思。
4.某同学从自己所写的文章里选出一下三组,为每组文章拟一标题,编成集子。
所拟标题与各组文章对应最恰当的一项是(3分)第一组:《看见<看见>》《书虫诞生记》《对话苏东坡》《家有书窝》第二组:《同桌的你》《伴我同行》《奔跑吧,兄弟》《没有麦田的守望者》第三组:《感悟青春》《我的“离经叛道”的话》《扪心自问》《当我发呆时我在想些什么》A.读书万卷寸草春晖我思我在B.悦读生活寸草春晖指点江山C.悦读生活那些花儿我思我在D.读书万卷那些花儿指点江山5.文化宫为评书、古琴、昆曲、木偶戏四个文艺演出专场各准备了一副对联,对联与演出专场对应恰当的一项是(3分)①假笑啼中真面目新笙歌里古衣冠②疑雨疑云颇多关节绘声绘影巧合连环③白雪阳春传雅曲高山流水觅知音④开幕几疑非傀儡舞台虽小有机关A.①古琴②评书③昆曲④木偶戏B.①昆曲②评书③古琴④木偶戏C.①古琴②木偶戏③昆曲④评书D.①昆曲②木偶戏③古琴④评书二、文言文阅读(18分)阅读下面的文言文,完成6~9题。
2016年江苏省高考语文试题及参考答案

绝密★启用前2016年普通高等学校招生全国统一考试(江苏卷)语文注意事项:1.答题前,考生在答题卡上务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚,并贴好条形码,请认真核准条形码上的准考证号、姓名和科目。
2.每小题选出答案后,用2B铅笔把答题卡上对应题目标号涂黑,如需改动,用橡皮擦干净后,再选择其他答案标号,在试卷上作答无效。
3.第I卷共10小题,每小题3分,共30分。
在每小题给出的四个选项中,只有一项符合题目要求。
一、语言文字运用(15分)1.在下面一段话的空缺处依次填入词语,最恰当的一组是(3分)人人都希望自己____________,却很少有人能沉静下来用心对待生活。
其实生活很____________,你是不是诚心待它,它一眼就能分辨出来。
你越____________,越想得到,距离目标就越远;你努力振作,默默耕耘,惊喜往往就会悄然而至。
A.与众不同机敏焦躁B.与众不同敏锐浮躁C.标新立异机敏浮躁D.标新立异敏锐焦躁2.下列熟语中,没有使用借代手法的一项是(3分)A.人为刀俎,我为鱼肉B.人皆可以为尧舜C.化干戈为玉帛D.情人眼里出西施3.下列各句中,所引诗词不符合语境的一项是(3分)A.“闲云潭影日悠悠,物换星移几度秋”,往事历历,所有的记忆都在时光里发酵,散发出别样的味道。
B.“拣尽寒枝不肯栖,寂寞沙洲冷”,正是这种难言的孤独,使他洗去人生的喧闹,去寻找无言的山水,远逝的古人。
C.“长风破浪会有时,直挂云帆济沧海”,青葱少年总是信心满满,跃跃欲试,渴望在未来的岁月中大显身手。
D.“帘外雨潺潺,春意阑珊”,初春的细雨渐渐沥沥,撩拨了无数文人墨客心中关于江南的绵绵情思。
4.某同学从自己所写的文章里选出一下三组,为每组文章拟一标题,编成集子。
所拟标题与各组文章对应最恰当的一项是(3分)第一组:《看见<看见>》《书虫诞生记》《对话苏东坡》《家有书窝》第二组:《同桌的你》《伴我同行》《奔跑吧,兄弟》《没有麦田的守望者》第三组:《感悟青春》《我的“离经叛道”的话》《扪心自问》《当我发呆时我在想些什么》A.读书万卷寸草春晖我思我在B.悦读生活寸草春晖指点江山C.悦读生活那些花儿我思我在D.读书万卷那些花儿指点江山5.文化宫为评书、古琴、昆曲、木偶戏四个文艺演出专场各准备了一副对联,对联与演出专场对应恰当的一项是(3分)①假笑啼中真面目新笙歌里古衣冠②疑雨疑云颇多关节绘声绘影巧合连环③白雪阳春传雅曲高山流水觅知音④开幕几疑非傀儡舞台虽小有机关A.①古琴②评书③昆曲④木偶戏B.①昆曲②评书③古琴④木偶戏C.①古琴②木偶戏③昆曲④评书D.①昆曲②木偶戏③古琴④评书二、文言文阅读(18分)阅读下面的文言文,完成6~9题。
2016年江苏语文高考试卷及答案word版

2016年江苏语文高考试卷及答案word版13.第④段中会明为什么逢人就问何时开火?请简要概括。
(6分)14.文中两处画线句分别表现了会明什么样的精神状态?请简要分析。
(4分)15.文中多处写到“插军旗”,请说明这个细节在全文中的主要作用。
(4分)16.请探究小说结尾“微笑的意义”的意蕴。
(6分)六、现代文阅读(二)(18分)阅读下面的作品,完成17-19题。
成人不自在郭英德《西游记》记录了孙悟空从出生、成长、奋斗,直到成为“斗战圣佛”的曲折过程,揭示了一个深刻的人生哲理:成人不自在。
孙悟空的出生,和普通人大不一样,他是从石头缝里蹦出来的,摆脱了人与生俱有的社会关系。
用小说的话,就是“不服麒麟辖,不服凤凰管,又不服人间王位约束”。
那么,作为一个原生态的人,他是不是就获得了真正的“自在”呢?这还不行。
他发现自己生活的环境太狭隘了,来来回回就在花果山上,交往的就是些猴兄猴弟。
他想要拥有更大的空间和世界,所以去寻仙问道,有了种种法力。
一个筋斗云翻出十万八千里,生活空间如此之大,可以为所欲为,来去自如。
有了这么广阔的生存空间,就获得真正的“自在”了吗?还是不行。
孙悟空有一天突然悲叹起来,他看到老猴死去,想到自己迟早也要死去,于是到阎罗殿去把自己的名字从生死符中勾掉,从而拥有了绝对意义上的“自在”。
但是对社会人来说,这却触犯了规范,社会不允许没有经过任何修炼就得到这种绝对自由。
孙悟空扰乱了正常的秩序,这必定要受到惩罚。
社会要么剿灭他,要么改造他。
小说采用了寓意性的写法,用“如来佛的掌心”代表一种无所不能的社会规范,个人有再大的能耐也逃不出如来佛的手掌心。
“个体人”一旦步入社会,就不可能再有绝对的自由自在了。
孙悟空遇到唐僧,投身西天取经的事业,这是偶然的事情吗?不完全是。
小说有一个寓意性的写法——“金箍儿”。
金箍儿是有形的东西,但却有无形的含义。
孙悟空头上的金箍儿是怎么戴上的?是他自己戴上的。
他看到藏着金箍儿的花帽子漂亮,就自己给自己戴上了。
2016年普通高等学校招生统一考试高考语文试卷(江苏卷)

2016年普通高等学校招生统一考试高考语文试卷(江苏卷)各位读友大家好,此文档由网络收集而来,欢迎您下载,谢谢2016年普通高等学校招生统一考试高考语文试卷(江苏卷)语文I试题一、语言文字运用(15分)1.在下面一段话的空缺处依次填入词语,最恰当的一组是(3分)人人都希望自己____________,却很少有人能沉静下来用心对待生活。
其实生活很____________,你是不是诚心待它,它一眼就能分辨出来。
你越____________,越想得到,距离目标就越远;你努力振作,默默耕耘,惊喜往往就会悄然而至。
A.与众不同机敏焦躁B.与众不同敏锐浮躁C.标新立异机敏浮躁 D.标新立异敏锐焦躁下列熟语中, 没有使用借代手法的一项是(3分)A人为刀俎,我为鱼肉 B.人皆可以为尧舜C.化干戈为玉帛 D.情人眼里出西施A.“闲云潭影日悠悠,物换星移几度秋B.“拣尽寒枝不肯栖,寂寞沙洲冷”,正是这种难言的孤独,使他洗去人生的喧闹,去寻找无言的山水,远逝的古人。
C.“长风破浪会有时,直挂云帆济沧海”,青葱少年总是信心满满,跃跃欲试,渴望在未来的岁月中大显身手。
D.“帘外雨潺潺,春意阑珊”,初春的细雨渐渐沥沥,撩拨了无数文人墨客心中关于江南的绵绵情思。
4.某同学从自己所写的文章里选出一下三组,为每组文章拟一标题,编成集子。
所拟标题与各组文章对应最恰当的一项是(3分)第一组:《看见》《书虫诞生记》《对话苏东坡》《家有书窝》第二组:《同桌的你》《伴我同行》《奔跑吧,兄弟》《没有麦田的守望者》第三组:《感悟青春》《我的“离经叛道”的话》《扪心自问》《当我发呆时我在想些什么》A.读书万卷寸草春晖我思我在 B.悦读生活寸草春晖指点江山C.悦读生活那些花儿我思我在D.读书万卷那些花儿指点江山5.文化宫为评书、古琴、尾曲、木偶戏四个文艺演出专场各准备了一副对联,对联与演出专场对应恰当的一项是(3分)①假笑啼中真面目②疑雨疑云颇多关节③白雪阳春传雅曲④开幕几疑非傀儡A.①古琴②评书③昆曲④木偶戏①昆曲②评书③古琴④木偶戏①古琴②木偶戏③昆曲④评书①昆曲②木偶戏③古琴④评书阅读下面的文言文,完成6~9题。
2016年江苏语文高考试卷含答案和解析

2016年江苏语文高考试卷语文I试题一、语言文字运用(15分)1.在下面一段话的空缺处依次填入词语,最恰当的一组是(3分)人人都希望自己▲,却很少有人能沉静下来用心对待生活。
其实生活很▲,你是不是诚心待它,它一眼就能分辨出来。
你越▲,越想得到,距离目标就越远;你努力振作,默默耕耘,惊喜往往就会悄然而至。
A.与众不同机敏焦躁B.与众不同敏锐浮躁C.标新立异机敏浮躁D.标新立异敏锐焦躁2.下列熟语中, 没有..使用借代手法的一项是(3分)A.人为刀俎,我为鱼肉B.人皆可以为尧舜C.化干戈为玉帛D.情人眼里出西施3.下列各句中,所引诗词不符合...语境的一项是(3分)A.“闲云潭影日悠悠,物换星移几度秋”,往事历历,所有的记忆都在时光里发酵,散发出别样的味道。
B.“拣尽寒枝不肯栖,寂寞沙洲冷”,正是这种难言的孤独,使他洗去人生的喧闹,去寻找无言的山水,远逝的古人。
C.“长风破浪会有时,直挂云帆济沧海”,青葱少年总是信心满满,跃跃欲试,渴望在未来的岁月中大显身手。
D.“帘外雨潺潺,春意阑珊”,初春的细雨渐渐沥沥,撩拨了无数文人墨客心中关于江南的绵绵情思。
4.某同学从自己所写的文章里选出一下三组,为每组文章拟一标题,编成集子。
所拟标题与各组文章对应最恰当的一项是(3分)第一组:《看见<看见>》《书虫诞生记》《对话苏东坡》《家有书窝》第二组:《同桌的你》《伴我同行》《奔跑吧,兄弟》《没有麦田的守望者》第三组:《感悟青春》《我的“离经叛道”的话》《扪心自问》《当我发呆时我在想些什么》A.读书万卷寸草春晖我思我在B.悦读生活寸草春晖指点江山C.悦读生活那些花儿我思我在D.读书万卷那些花儿指点江山5.文化宫为评书、古琴、昆曲、木偶戏四个文艺演出专场各准备了一副对联,对联与演出专场对应恰当的一项是(3分)①假笑啼中真面目新笙歌里古衣冠②疑雨疑云颇多关节绘声绘影巧合连环③白雪阳春传雅曲高山流水觅知音④开幕几疑非傀儡舞台虽小有机关A.①古琴②评书③昆曲④木偶戏B.①昆曲②评书③古琴④木偶戏C.①古琴②木偶戏③昆曲④评书D.①昆曲②木偶戏③古琴④评书二、文言文阅读(18分)阅读下面的文言文,完成6~9题。
2016年高考语文江苏卷(含详细答案)

语文试卷 第1页(共10页)语文试卷 第2页(共10页)绝密★启用前2016年普通高等学校招生全国统一考试(江苏卷)语文本试卷共10页,包括选择题(第1题~第7题,共7题)、非选择题(第8题~第20题,共13题)两部分。
本卷满分为160分。
考试时间为150分钟。
考试结束后,请将本试卷和答题卡一并交回。
考生注意:1. 答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在试卷及答题卡的规定位置。
2. 请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符。
3. 作答选择题(第1题~第7题),必须用2B 铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案。
作答非选择题,必须用0.5毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效。
一、语言文字运用(15分)1. 在下面一段话的空缺处依次填入词语,最恰当的一组是(3分)( )人人都希望自己____________,却很少有人能沉静下来用心对待生活。
其实生活很____________,你是不是诚心待它,它一眼就能分辨出来。
你越____________,越想得到,距离目标就越远;你努力振作,默默耕耘,惊喜往往就会悄然而至。
A. 与众不同 机敏 焦躁 B. 与众不同 敏锐 浮躁 C. 标新立异 机敏 浮躁D. 标新立异 敏锐 焦躁2. 下列熟语中,没有使用借代手法的一项是(3分)( )A. 人为刀俎,我为鱼肉B. 人皆可以为尧舜C. 化干戈为玉帛D. 情人眼里出西施3. 下列各句中,所引诗词不符合语境的一项是(3分)( )A. “闲云潭影日悠悠,物换星移几度秋”,往事历历,所有的记忆都在时光里发酵,散发出别样的味道。
B. “拣尽寒枝不肯栖,寂寞沙洲冷”,正是这种难言的孤独,使他洗去人生的喧闹,去寻找无言的山水、远逝的古人。
C. “长风破浪会有时,直挂云帆济沧海”,青葱少年总是信心满满,跃跃欲试,渴望在未来的岁月中大显身手。
2016年江苏数学高考试卷含答案和解析
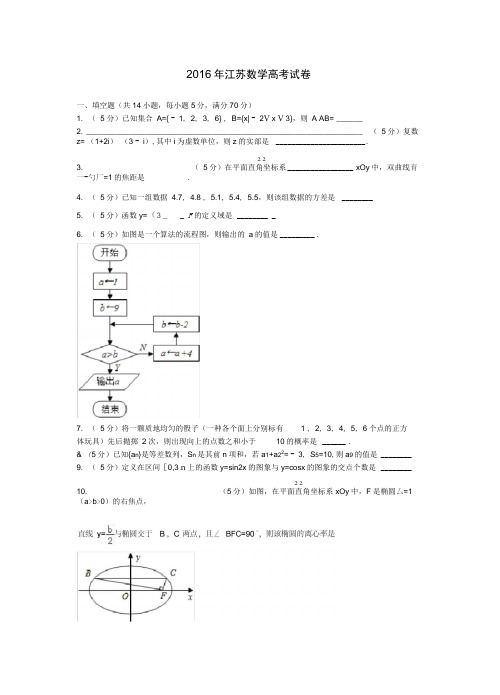
2016年江苏数学高考试卷一、填空题(共14小题,每小题5分,满分70分)1. (5 分)已知集合A={ - 1, 2, 3, 6} , B={x| - 2V x V 3},则A AB= ______2. ________________________________________________________________ (5分)复数z= (1+2i)(3 - i),其中i为虚数单位,则z的实部是_______________________ .2 23. (5分)在平面直角坐标系_________________ xOy中,双曲线育一-勺厂=1的焦距是.4. (5分)已知一组数据4.7, 4.8 ,5.1, 5.4, 5.5,则该组数据的方差是________5. (5分)函数y=(3 _ _ F的定义域是________ _6. (5分)如图是一个算法的流程图,则输出的a的值是_________ .7. (5分)将一颗质地均匀的骰子(一种各个面上分别标有 1 , 2, 3, 4, 5, 6个点的正方体玩具)先后抛掷2次,则出现向上的点数之和小于10的概率是______ .& (5分)已知{a n}是等差数列,S n是其前n项和,若a1+a22= - 3, S5=10,则a9的值是 ________ 9. (5分)定义在区间[0,3 n上的函数y=sin2x的图象与y=cosx的图象的交点个数是________2 210. (5分)如图,在平面直角坐标系xOy中,F是椭圆厶=1 (a>b>0)的右焦点,14. (5分)在锐角三角形 ABC 中,若sin A=2si nBsi nC ,贝U tan Ata nBta nC 的最小值是 二、解答题(共6小题,满分90分)415. (14 分)在厶 ABC 中,AC=6 , cosB=—, (1 )求AB 的长; (2 )求 cos (A )的值.616. (14分)如图,在直三棱柱 ABC - A 1B 1C 1中,D , E 分别为AB , BC 的中点,点 F 在 侧棱B 1B 上,且 B 1D 丄A 1F , A 1C 1丄A 1B 1 .求证: (1) 直线 DE //平面 A 1C 1F ; (2) 平面B 1DE 丄平面A 1C 1F .17. (14分)现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥 P -A 1B 1C 1D 1,下部的形状是正四棱柱 ABCD - A 1B 1C 1D 1 (如图所示),并要求正四棱柱的高 010是正四棱锥的高 PO 1的4倍.(1 )若AB=6m , PO 1=2m ,则仓库的容积是多少?11. (5分)设f (x )是定义在 R 上且周期为2的函数,在区间[-1, 1) 上, f (x )L o<^<r其中a € R , 若 f (-寻)=f (鲁),则f (5a )的值是12.( 5分)已知实数x , x -y 满足」2x+y - 2>03K - y 3<0,则x 2+y 2的取值范围是13. ( 5分)如图,在△ ABC 中,D 是BC 的中点,E, F 是AD 上的两个三等分点,一.? .=4, “? ' =- 1则_L.r I .的值是C —(2)若正四棱锥的侧棱长为 6m ,则当PO 1为多少时,仓库的容积最大?18. ( 16分)如图,在平面直角坐标系 xOy 中,已知以M 为圆心的圆M :x 2+y 2- 12x - 14y+60=0 及其上一点A (2, 4).(1) 设圆N 与x 轴相切,与圆 M 外切,且圆心 N 在直线x=6上,求圆N 的标准方程; (2) 设平行于 OA 的直线I 与圆M 相交于B 、C 两点,且BC=OA ,求直线I 的方程; (3) 设点T (t , 0)满足:存在圆 M 上的两点P 和Q ,使得“〔+「=/,求实数t 的取值① 求方程f (x ) =2的根;② 若对于任意x € R ,不等式f (2x )> mf ( x )- 6恒成立,求实数 m 的最大值; (2)若O v a v 1, b > 1,函数g (x ) =f (x )- 2有且只有1个零点,求ab 的值. 20. (16分)记U={1, 2,…,100},对数列{a n } (n € N *)和U 的子集T ,若T=?,定义S T =0;若 T={ t 1, t 2,…,t k },定义 S T =g 十 +% +•• +斗.例如:T={1,3,66}时,S r =a 1+a 3+a 66.现 设{a n } (n € N *)是公比为3的等比数列,且当 T={2, 4}时,S T =30. (1) 求数列{a n }的通项公式;(2) 对任意正整数 k ( K k w 100),若 T? {1, 2,…,k },求证:S T V a k+1 ; (3) 设 C? U , D? U , So S D ,求证:S c +S cro >2S D .附加题【选做题】本题包括 A 、B 、C 、D 四小题,请选定其中两小题,并在相应的答题区 域内作答,若多做,则按作答的前两小题评分,解答时应写出文字说明、证明过程或演算 步骤.A .【选修4—1几何证明选讲】21. (10分)如图,在△ ABC 中,/ ABC=90 ° BD 丄AC , D 为垂足,E 为BC 的中点,求 证:/EDC= / ABD .f (x )(1 )设 a=2, b=±.=a x +b x(a >0, b >0, 1, b ^ 1).C.【选修4—4:坐标系与参数方程】23. 在平面直角坐标系 xOy 中,已知直线I 的参数方程为(B 为参数),设直线I 与椭圆C 相交于A , B 两点,求线段 AB 的24. 设 a > 0, | x - 1| V — , | y - 2| <一,求证:| 2x+y - 4| v a .附加题【必做题】225. (10分)如图,在平面直角坐标系 xOy 中,已知直线I : x - y - 2=0 ,抛物线C : y 2=2px (p > 0).(1) 若直线I 过抛物线C 的焦点,求抛物线 C 的方程; (2) 已知抛物线C 上存在关于直线I 对称的相异两点 ① 求证:线段PQ 的中点坐标为(2- p , - p ); ② 求p 的取值范围.22. (10分)已知矩阵 A=,矩阵B 的逆矩阵B -1,求矩阵AB .(t 为参数),椭圆C 的参数方程为 B.【选修4—2:矩阵与变换】(n+1) C 咋(m+1) C 吧.rtn+2(2)设 m , n € N *, n 》m ,求证:(m+1) CJU+ (m+2) C :::+ (m +3)C . +*26. (10 分)(1 )求 7C -4C 的值;2016年江苏数学参考答案与试题解析一、填空题(共14小题,每小题5分,满分70分)1. ( 5 分)已知集合 A={ - 1, 2, 3, 6} , B={x| - 2V x V 3},则 A AB= { - 1, 2}.【分析】根据已知中集合 A={ - 1 , 2, 3, 6} , B={x| - 2V x v 3},结合集合交集的定义可 得答案. 【解答】 解:•••集合 A={ - 1, 2, 3, 6}, B={x| - 2v x v 3}, ••• A n B={ - 1 , 2}, 故答案为:{ - 1, 2}【点评】本题考查的知识点是集合的交集及其运算,难度不大,属于基础题.2.( 5分)复数z= (1+2i ) (3 - i ),其中i 为虚数单位,贝U z 的实部是 5 .【分析】利用复数的运算法则即可得出. 【解答】 解:z= (1+2i ) (3 - i ) =5+5i , 则z 的实部是5, 故答案为:5.【点评】 本题考查了复数的运算性质,考查了推理能力与计算能力,属于基础题.2 2I 解答】解:双曲线】-_ 中, a 「,b=「,双曲线 —-2—=1的焦距是2 In. 故答案为:2 III.【点评】本题重点考查了双曲线的简单几何性质,考查学生的计算能力,比较基础.4. ( 5分)已知一组数据 4.7, 4.8 ,5.1, 5.4, 5.5,则该组数据的方差是 0.1 .【分析】先求出数据4.7, 4.8, 5.1 , 5.4, 5.5的平均数,由此能求出该组数据的方差.【解答】 解:•••数据4.7, 4.8, 5.1 , 5.4, 5.5的平均数为:•该组数据的方差:3. ( 5分)在平面直角坐标系 xOy 中,双曲线 【分析】确定双曲线的几何量,即可求出双曲线=1的焦距是/ III=1的焦距.(4.7+4.8+5.1+5.4+5.5) =5.1 ,s2=±[ (4.7 - 5.1) 2+ (4.8 - 5.1) 2+ ( 5.1 - 5.1) 2+ ( 5.4 - 5.1) 2+ ( 5.5- 5.1) 2]=0.1.5故答案为:0.1.【点评】本题考查方差的求法,是基础题,解题时要认真审题,注意方差计算公式的合理运用.5. ( 5分)函数y= : J 厂的定义域是[-3, 11 . 【分析】根据被开方数不小于0,构造不等式,解得答案.【解答】解:由3-2x - x2> 0得:X2+2X-3< 0,解得:x € [ —3, 1 ],故答案为:[-3, 1]【点评】本题考查的知识点是函数的定义域,二次不等式的解法,难度不大,属于基础题.6. ( 5分)如图是一个算法的流程图,则输出的a 的值是9 .【分析】根据已知的程序框图可得,该程序的功能是利用循环结构计算并输出变量a的值, 模拟程序的运行过程,可得答案.【解答】解:当a=1, b=9时,不满足a> b,故a=5, b=7,当a=5, b=7 时,不满足a>b,故a=9, b=5当a=9, b=5时,满足a> b,故输出的a值为9,故答案为:9【点评】本题考查的知识点是程序框图,当循环次数不多,或有规律可循时,可采用模拟程序法进行解答.7. ( 5分)将一颗质地均匀的骰子(一种各个面上分别标有1 , 2, 3, 4, 5, 6个点的正方体玩具)先后抛掷2次,则出现向上的点数之和小于10的概率是学 .—6-【分析】出现向上的点数之和小于10的对立事件是出现向上的点数之和不小于10,由此利用对立事件概率计算公式能求出出现向上的点数之和小于10的概率.【解答】 解:将一颗质地均匀的骰子(一种各个面上分别标有 1, 2, 3, 4, 5, 6个点的正方体玩具)先后抛掷 2次, 基本事件总数为 n=6 X 6=36,出现向上的点数之和小于 10的对立事件是出现向上的点数之和不小于 10,出现向上的点数之和不小于 10包含的基本事件有:(4, 6), (6, 4), (5 , 5), (5 , 6), (6 , 5), (6 , 6),共 6 个, •••出现向上的点数之和小于 10的概率:故答案为:电.6【点评】本题考查概率的求法, 的合理运用.&( 5分)已知{a n }是等差数列,S n 是其前n 项和,若a 1+a 22= - 3 , S 5=10,则a 9的值是 20 【分析】利用等差数列的通项公式和前 n 项和公式列出方程组,求出首项和公差,由此能求 出a 9的值.2【解答】 解:••• {a n }是等差数列,S n 是其前n 项和,a 1+a 2=-3, S 5=10,g ] + (屯 + d) ‘二 _ 35心 ,5有+七丄左10 L 乙 解得a 仁-4, d=3 ,…a 9= — 4+8 X 3=20 .故答案为:20.【点评】本题考查等差数列的第 9项的求法,是基础题,解题时要认真审题,注意等差数列 的性质的合理运用.9. (5分)定义在区间[0, 3 n 上的函数y=s in 2x 的图象与y=cosx 的图象的交点个数是 7【分析】画出函数y=sin2x 与y=cosx 在区间[0, 3刃上的图象即可得到答案. 【解答】 解:画出函数y=sin2x 与y=cosx 在区间[0, 3 n 上的图象如下:故答案为:7.【点评】 本题考查正弦函数与余弦函数的图象,作出函数 y=sin2x 与y=cosx 在区间[0, 3冗]上的图象是关键,属于中档题.65366 p=1 - 是基础题,解题时要认真审题,注意对立事件概率计算公式5 9 2【分析】设右焦点F ( c , 0),将y=b 代入椭圆方程求得 B , C 的坐标,运用两直线垂直的\2\条件:斜率之积为-1,结合离心率公式,计算即可得到所求值. 【解答】解:设右焦点F (c , 0), 将代入椭圆方程可得 x= ± a'■ = ± a ,3V 4b 22可得 B (-£!a , +), C 哼a , —), 由/ BFC=90 ° 可得 k BF ?k CF =— 1 , b_ b_2亠 2即有:?——化简为 b 2=3a 2 — 4c 2, 由 b 2=a 2 — c 2,即有 3c 2=2a 2, 由e=£,可得 e 2=E —=丄,& ¥ 3 , 可得e=',3 故答案为:''.【点评】本题考查椭圆的离心率的求法,注意运用两直线垂直的条件:斜率之积为- 查化简整理的运算能力,属于中档题.11. (5分)设f (x )是定义在 R 上且周期为2的函数,在区间[-1 , 1)上,f (x )0心<],其中R 若f (—豆)=f (京)则f ( 5a )的值是I 分析】根据已知中函数的周期性,结合f(一)=f (「可得a值,进而得到f (5a )的值.10. ( 5分)如图,在平面直角坐标系 -V-1,考xOy 中, (a > b > 0)的右焦点,4,13],【解答】解:f (x )是定义在R 上且周期为2的函数,在区间[-1,1) 上, f (x ) 卅弘-0U T K• f (-◎) =f (-±|) =-土+a ,2f号=f 伶=1亍囱 ••• f (5a ) =f(3) =f (- 1) = - 1+三=52 5【点评】本题考查的知识点是分段函数的应用,函数的周期性,根据已知求出 的关键.【分析】作出不等式组对应的平面区域, 利用目标函数的几何意义, 结合两点间的距离公式以及点到直线的距离公式进行求解即可. 【解答】 解:作出不等式组对应的平面区域,设z=x 2+y 2,则Z 的几何意义是区域内的点到原点距离的平方, 由图象知A 到原点的距离最大,点0到直线BC : 2x+y - 2=0的距离最小,,即 A ( 2, 3),此时 Z =22+32=4+9=13 ,故Z 的取值范围是[ 故答案为:[L o<^<r2 1 W,故答案为:a 值,是解答12. ( 5分)已知实数x ,x -y 满足」2x+y - 2>0 3K - y 3<0,则x 2+y 2的取值范围是[,13]5s=2 y —3点0到直线BC : 2x+y - 2=0的距离|-2|-电则 z=d 2=(2涉及距离的计算,利用数形结合是解决本题的关键.13. ( 5分)如图,在△ ABC 中,D 是BC 的中点,E, F 是AD 上的两个三等分点,―.? .=4,【分析】由已知可得歸二歸+丽,可=-冠5+丽,刚环+菽,冠=-M +頑,祝=i5+丽,I I 2丄,苛2—,可得答案.【解答】 解:••• D 是BC 的中点,E , F 是AD 上的两个三等分点, ...1・=二+十,卜=-.「+ 卜,_._-=' i+3 L 」,'■ .|^.= - 1+3 卜, ••• |・?厂=:卩2- ; I 2=- I , ';? '「.=9 下2 -才 2=4, • 124,訂2=丄,又•••祝=丽麺,CE =-面+2丽, •侦?还=4帀2-乔=*, 故答案为:丄O【点评】本题考查的知识是平面向量的数量积运算,平面向量的线性运算,难度中档.7_? =- 5 ■?' 的值是——'=-11+2.I I ,结合已知求出【点评】本题主要考查线性规划的应14. (5分)在锐角三角形 ABC 中,若sinA=2sinBsinC ,贝U tanAtanBtanC 的最小值是 8【分析】 结合三角形关系和式子 sinA=2sinBsinC 可推出sinBcosC+cosBsinC=2sinBsinC ,进 而得到tanB+tanC=2tanBtanC ,结合函数特性可求得最小值.【解答】 解:由 sinA=sin ( n — A ) =sin ( B+C ) =sinBcosC+cosBsinC , sinA=2sinBsinC , 可得 sinBcosC+cosBsinC=2sinBsinC ,①由三角形ABC 为锐角三角形,则 cosB >0, cosC >0,在① 式两侧同时除以 cosBcosC 可得tanB+tanC=2tanBtanC , 又 tanA= — tan ( n — A ) = — tan (B+C ) = — :-1 丨 1:- ②,1 - tarBt anC则 tanAtanBtanC= -' -:11- ' ?tanBtanC ,1一 tanBt anC由 tanB+tanC=2tanBtanC 可得 tanAtanBtanC=—令 tanBtanC=t ,由 A , B , C 为锐角可得 tanA >0, tanB >0, tanC > 0, 由② 式得1 — tanBtanC v 0,解得t > 1,当且仅当t=2时取到等号,此时 tanB+tanC=4 , tanBtanC=2,解得 tanB=2+.二,tanC=2 — . ?, tanA=4 ,(或 tanB , tanC 互换),此时 A , B , C 均为锐角. 【点评】本题考查了三角恒等式的变化技巧和函数单调性知识,有一定灵活性. 二、解答题(共6小题,满分90分)415. (14 分)在厶 ABC 中,AC=6 , cosB=—, (1 )求AB 的长;(2 )求 cos (A — ------ )的值.6【分析】(1)禾U 用正弦定理,即可求 AB 的长; (2)求出cosA 、sinA ,利用两角差的余弦公式求 【解答】 解:(1):公ABC 中,cosB^,5 ••• si nB=厶,5」丄—二 sinC _sinB '1 一 tanBtanCtan Ata nBta nC=— 2—1 _ L ,丄,由t > i 得, 4v 0,2因此tanAtanBtanC 的最小值为8,cos (A —)的值.(2) cosA= - cos (C+B ) =sinBsinC - cosBcosC=-T A 为三角形的内角,/• sinA=—'・二10cos (A -—) = COSA+丄sinA=:6 2 2 20【点评】本题考查正弦定理,考查两角和差的余弦公式,16. (14分)如图,在直三棱柱 ABC - A 1B 1C 1中,D , E 分别为AB , BC 的中点,点 F 在 侧棱B 1B 上,且 B 1D 丄A 1F , A 1C 1丄A 1B 1 .求证: (1) 直线 DE //平面 A 1C 1F ; (2) 平面B 1DE 丄平面A 1C 1F .【分析】(1)通过证明DE // AC ,进而DE // A 1C 1,据此可得直线 DE //平面A 1C 1F 1;(2 )通过证明A 1F 丄DE 结合题目已知条件 A 1F 丄B 1D ,进而可得平面 B 1DE 丄平面A 1C 1F . 【解答】解:(1)T D , E 分别为AB , BC 的中点, .DE ABC 的中位线, .DE // AC ,T ABC - A 1B 1C 1 为棱柱,.AC // A 1C 1, ••• DE // A 1C 1,T A 1C 1?平面 A 1C 1F ,且 DE?平面 A 1C 1F ,• DE // A 1C 1F ;(2 )T ABC - A 1B 1C 1 为直棱柱, • AA 1 丄平面 A 1B 1C 1, • AA 1 丄 A 1C 1,又 T A 1C 1 丄 A 1B 1,且 AA 1Q A 1B 仁A 1, AA 1、A 1B 1?平面 AA 1B 1B , • A 1C 1 丄平面 AA 1B 1B , •/ DE // A 1C 1, • DE 丄平面 AA 1B 1B,考查学生的计算能力,属于基础题.又••• A 1F?平面 AA 1B 1B , ••• DE 丄 A I F ,又:A 1F 丄 B I D , DE Q B 1D=D ,且 DE 、B I D?平面 B I DE ,•- A IF 丄平面 B 1DE ,又:A I F?平面 A i C i F ,•平面B IDE 丄平面A 1C 1F .【点评】本题考查直线与平面平行的证明, 以及平面与平面相互垂直的证明, 把握常用方法最关键,难度不大.17.( 14分)现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥 P -A 1B 1C 1D 1,下部的形状是正四棱柱 ABCD - A 1B 1C 1D 1 (如图所示),并要求正四棱柱的高010是正四棱锥的高 PO 1的4倍.(1 )若AB=6m ,P0i =2m ,则仓库的容积是多少?(2)若正四棱锥的侧棱长为 6m ,则当P01为多少时,仓库的容积最大?【分析】(1)由正四棱柱的高 010是正四棱锥的高 P01的4倍,可得P01=2m 时,010=8m , 进而可得仓库的容积;(2)设 P01=xm ,贝U 010=4xm ,A 101= 一「 - m ,A 1B 1=;』E ? 一「 - m ,代入体积公式,求出容积的表达式,利用导数法,可得最大值.(2 )若正四棱锥的侧棱长为 6m ,设 P01=xm ,则 0〔0=4xm , A 101=,, -m ,A 1B 1=i :F? i, , - m ,则仓库的容积 V 圣 X “?(36- F ) 2?x+ (血?伽-F ) 2?4x=—W+312X ,(0 R-4J*v x v 6),• V = - 26x 2+312,( 0v x v 6 ),当O v x v 2.1时,V '> 0,V ( x )单调递增; 当2 「Vx v 6时,V'v 0,V (x )单调递减;故当x=2 _ ;时,V (x )取最大值; 即当P01=2 . ■: m 时,仓库的容积最大.【点评】 本题考查的知识点是棱锥和棱柱的体积,导数法求函数的最大值,难度中档.【解答】解: •- 010=8m , •仓库的容积(1)T P01=2m ,正四棱柱的高 010是正四棱锥的高 P01的4倍.X 62X 2+62X 8=312m 318. (16分)如图,在平面直角坐标系xOy中,已知以M为圆心的圆M :x2+y2- 12x - 14y+60=0 及其上一点A (2, 4).(1)设圆N与x轴相切,与圆M外切,且圆心N在直线x=6上,求圆N的标准方程;(2)设平行于OA的直线I与圆M相交于B、C两点,且BC=OA,求直线I的方程;(3)设点T (t, 0)满足:存在圆M上的两点P和Q,使得「+ ^ ;= 一I,求实数t的取值(x - 6) 2+(y- n) 2=n2, n>0,从而得到| 7- n| =| n|+ 5, (2)由题意得OA=2 口,k oA=2,设I : y=2x+b,则圆心M到直线I的距离:d=由此能求出直线I的方程.I〔1= j | -I -,又 |丨J| 三10,得t€ [2-2『||, 2+2. | ],对于任意t€ [2-2 . 一 | , 2+2 . 一| ],欲使•,只需要作直线TA的平行线,使圆心到直线的距离为.,「:一__,由此能求出实数t的取值范围.【解答】解:(1)v N在直线x=6上,•••设N (6, n),•••圆N 与x 轴相切,•圆N 为:(x - 6) 2+ (y - n) 2=n2, n>0,又圆N 与圆M 外切,圆M : x2+y2- 12x - 14y+60=0,即圆M : ((x - 6) 2+ (x- 7) 2=25 , •-1 7 - n| =| n|+ 5,解得n=1 ,•••圆N的标准方程为(x- 6) 2+ ( y- 1) 2=1 .(2)由题意得OA=2 口,k OA=2,设I : y=2x+b,则圆心M到直线I的距离:d= ——=」V22+l V5则|BC|=2 —.」2 _」:,'''■', BC=2 口,即2匸‘川」=2. 7解得b=5或b= - 15,•直线I的方程为:y=2x +5或y=2x - 15.(3) ^1 ' = '11,即■- < - •宀即| /=| 丨,| ,E =J(t - 2),+ 八,又 I FQ I w 10,即 — 2严 + 4輕 10,解得 t € [2-2何,2+2阿], 对于任意t € [2-2 - | , 2+2-[],欲使|上I'n,此时,| J < 10,只需要作直线TA 的平行线,使圆心到直线的距离为 祐 F ,必然与圆交于P 、Q 两点,此时|「| =|丨則,即丨;-丨I-J,因此实数t 的取值范围为t € [2 - 2j[. |, 2+2「],【点评】本题考查圆的标准方程的求法, 考查直线方程的求法, 考查实数的取值范围的求法, 是中档题,解题时要认真审题,注意圆的性质的合理运用. 19. ( 16 分)已知函数 f (x ) =a x +b x (a >0, b >0, 1, 1).(1 )设 a =2, b兮.① 求方程f (x ) =2的根;② 若对于任意x € R ,不等式f (2x )> mf ( x )- 6恒成立,求实数 m 的最大值; (2)若0v a v 1, b > 1,函数g (x ) =f (x )- 2有且只有1个零点,求ab 的值. 【分析】(1)①利用方程,直接求解即可.②列出不等式,禾U 用二次函数的性质以及函数 的最值,转化求解即可.(2)求出g (x ) =f (x ) - 2=a x +b x - 2,求出函数的导数,构造函数h (x )=出)x ,a Inb 求出g(x )的最小值为:g (x o ).同理①若g (X 0)v 0, g (x )至少有两个零点,与条件 矛盾.②若g (X 0)> 0,禾ij 用函数g (x ) =f (x )- 2有且只有1个零点,推出g (x 0) =0, 然后求解ab=1.【解答】 解:函数 f (x ) =a x +b x (a >0, b >0, a ^ 1, b ^ 1). (1 )设 a=2, b=t .即:m 2- 16w 0 或 m W 4, m € (-汽 4]. 实数m 的最大值为:4.①方程f (x ) =2;即:"=2,可得 x=0 . 2X②不等式f (2x )> mf (x )- 6恒成立,即 令 t=F , t > 2 .不等式化为:t 2- mt+4>0在t >2时,恒成立.可得:22 - 2iud-4>0> m6恒成立.(2) g (x ) =f (x )- 2=a x +b x - 2,Inb0 v a v 1, b > 1 可得—“a 1, a可得 【点评】本题考查函数与方程的综合应用,函数的导数的应用,基本不等式的应用,函数恒 成立的应用,考查分析问题解决问题的能力.20. (16分)记U={1, 2,…,100},对数列{a n } (n € N )和U 的子集T ,若T=?,定义 S T =0;若 T={ t 1, t 2, •••, t k },定义 S T =% + 色弋 +・・ + 自十.例如:T={1,3,66}时,S T =a 1+a 3+a 66.现 设{a n } (n € N *)是公比为3的等比数列,且当 T={2, 4}时,S T =30. (1) 求数列{a n }的通项公式;(2) 对任意正整数 k ( K k w 100),若 T? {1, 2,…,k },求证:S T V a k+1 ; (3) 设 C? U , D? U , S C > S D ,求证:SC+S CCD >2S D .【分析】(1)根据题意,由 S T 的定义,分析可得 S T =a 2+a 4=a 2+9a 2=30,计算可得a 2=3,进 而可得a 1的值,由等比数列通项公式即可得答案;(2)根据题意,由S T 的定义,分析可得 ST w a 1+a 2+・・a k =1+3+32+・・+3k -1,由等比数列的前n 项和公式计算可得证明;(3 )设A=?C ( C A D ), B=?D ( C A D ),则A QB=?,进而分析可以将原命题转化为证明 S C>2S B ,分2种情况进行讨论: ①、若B=?,②、若B 丰?,可以证明得到 S A >2S B ,即可 得证明.【解答】 解:(1)当 T={ 2, 4}时,S T =a 2+a 4=a 2+9a 2=30, 因此 a 2=3,从而 a 1==1,n — 1故 a n =3Il 旦+(b 尸]Inb ,' ag ' (x ) =a x |na+b x lnb=a x [ Inb,则 (x )是递增函数,而,Ina v 0, Inb >0,lnba)时, h (x 0) =0,因此x €x €( x 0, 则 g xm, x 0)时,h (x ) v 0, a Inb >0,则 g ' (x )v 0.)时,h (x ) > 0,在(-a, x0)递减, ①若 g (x 0)v 0, x v log a 2 时,a x lnb > 0,则 g'( x ) > 0,(x°, +a)递增, x 、■' a > -“=2, 因此g (x )的最小值为:g (x O ). b x >0,贝U g (x )> 0,因此 x 1 V Iog a 2,且 x 1v x 0 时,g (x 1) 则g (x )至少有两个零点,与条件矛盾.②若 g (x 0)> 0,函数 g (x ) =f (x ) 可得 由g g (X 0) =0,(0) =a °+b °- 2=0, 因此 X 0=0,因此: 亠一- )=0,> 0,因此 g (乂)在(x 1 , x 0)有零点, -2有且只有1个零点,g (x )的最小值为g (x 0), =1,即 Ina+lnb=0, In (ab ) =0,则 ab=1.ab=1.2k - l£— 1 k(2) S T W a i +a 2+・・a k =1+3+3+・・+3 =v 3 =a k+i ,2(3 )设 A=?c ( C A D ), B=?D ( C A D ),则 A QB=?,分析可得 S c =S A +S CAD , S D =S B +S CAD ,贝y S C +S CAD - 2S D =SA - 2S B , 因此原命题的等价于证明S O 2S B ,由条件S O S D ,可得S A > SB ,① 、若 B=?,贝y S B =0,故 S A > 2S B ,② 、若B 丰?,由S A > S B 可得A 丰?,设A 中最大元素为I , B 中最大元素为 m , 若m 》l+1,则其与S A v a i+i w a m < SB 相矛盾, 因为A QB=?,所以I 工m ,贝U I > m+1,综上所述,S A > 2S B , 故 S C +S CHD > 2S D .【点评】本题考查数列的应用, 涉及新定义的内容, 解题的关键是正确理解题目中对于新定 义的描述.附加题【选做题】本题包括 A 、B 、C 、D 四小题,请选定其中两小题,并在相应的答题区 域内作答,若多做,则按作答的前两小题评分,解答时应写出文字说明、证明过程或演算 步骤.A .【选修4—1几何证明选讲】21. (10分)如图,在△ ABC 中,/ ABC=90 ° BD 丄AC ,D 为垂足,E 为BC 的中点,求 证:/ EDC= / ABD .得/ ABD= / C ,从而可证得结论.【解答】 解:由BD 丄AC 可得/ BDC=90 ° 因为E 为BC 的中点,所以 DE=CE 冷BC , 则:/ EDC= / C ,由/ BDC=90 ° 可得/ C+Z DBC=90 ° 由/ ABC=90 ° 可得Z ABD+Z DBC=90 ° 因此Z ABD= Z C ,而Z EDC= Z C , 所以,Z EDC= Z ABD .【点评】本题考查三角形的性质应用, 利用Z C+Z DBC= Z ABD +Z DBC=90 °证得Z ABD=Z C 是关键,属于中档题.B.【选修4—2:矩阵与变换】1_3皿-1=222 S B W a i +a 2+-a m =1+3+32+"+3m ,即 S A > 2S B ,质可求得答案.【点评】 本题考查逆变换与逆矩阵,考查矩阵乘法的性质,属于中档题.C.【选修4—4:坐标系与参数方程】23.在平面直角坐标系 xOy 中,已知直线I 的参数方程为分别化直线与椭圆的参数方程为普通方程, 然后联立方程组,求出直线与椭圆的交 代入两点间的距离公式求得答案.代入①并整理得,:'.K=COS B2两式平方相加得H 11 -1~2.0 2【解答】解:T B 「122. (10分)已知矩阵 A=1 2 0 -2_ 1矩阵B 的逆矩阵B,求矩阵AB .【分析】依题意,利用矩阵变换求得21_T70 1 .2 2],再利用矩阵乘法的性_ 1 _ 1 • B= (B ')'1 2_7 2*20 1 2 2,又 A=••• AB=114d 5= 1「 0斗_o -1_ _2 J(t 为参数),椭圆C 的参数方程为y=2sin 9(B 为参数),设直线I 与椭圆C 相交于A , B 两点,求线段 AB 的长.【分析】 点【解答】 解:由*,由②得y=2sin 9,得rsln0B= ( B ^1) 一1【点评】本题考查直线与椭圆的参数方程, 考查了参数方程化普通方程, 置关系的应用,是基础题. ,| y - 2| v 二,求证:| 2x+y -4| v a .3【分析】 运用绝对值不等式的性质:|a+b| w |a|+| b|,结合不等式的基本性质,即可得证. 【解答】 证明:由a > 0, |x - 1| v —, |y - 2| V —,可得 | 2x+y - 4| =| 2 (x - 1) + (y - 2) | <2| x - 1|+| y - 2| v 亘+^=a ,3 3则| 2x+y - 4| v a 成立.【点评】本题考查绝对值不等式的证明, 注意运用绝对值不等式的性质, 以及不等式的简单性质,考查运算能力,属于基础题. 附加题【必做题】225. (10分)如图,在平面直角坐标系 xOy 中,已知直线I : x - y - 2=0 ,抛物线C : y =2px (p > 0).(1)若直线I 过抛物线C 的焦点,求抛物线 C 的方程; (2)已知抛物线 C 上存在关于直线I 对称的相异两点 P 和Q . ① 求证:线段PQ 的中点坐标为(2- p , - p ); ② 求p 的取值范围.【分析】(1)求出抛物线的焦点坐标,然后求解抛物线方程.(2):①设点P ( X 1, y 1) , Q (x 2, y 2),通过抛物线方程,求解 k PQ ,通过P , Q 关于直线I 对称,点的k PQ =- 1,推出一 ,■, PQ 的中点在直线 可证明线段PQ 的中点坐标为(2 - p ,- p ); ②利用线段PQ 中点坐标(2 - p ,- p ).推出4p=0,有两个不相等的实数根,列出不等式即可求出p 的范围.【解答】 解:(1).T : x -y - 2=0,A I 与x 轴的交点坐标(2, 0),,解得八—i 或厂X- 联立显+piy=L■丄T -gyi 考查直线与椭圆位24.设 a > 0, | x - 1| v2 2,得到关于y +2py+4p -:IA Bi 彳出)沁+学屮二平•I 上,推出=2 - p ,:+ (n +1) C '=(m+1)m+2n+2即抛物线的焦点坐标(2, 0).•••抛物线 C : y 2=8x .(2)证明:①设点 P (x i , y i ), Q (x 2, y 2),贝 V :r ?珀-亍"k _ ¥广冬.力n , k PQ = g g =y 2 _ v tv )+y 2又••• P , Q 关于直线l 对称,•线段PQ 的中点坐标为(2- p ,- p ); ②因为Q 中点坐标(2 - p , - p ).•严+『厂力卜1卩2二4子-绑2 2• △> 0, (2p )- 4 (4p - 4p )> 0,•p €〔o, £).【点评】本题考查抛物线方程的求法,直线与抛物线的位置关系的应用,考查转化思想以及 计算能力.(2)设 m , n € N , n 》m ,求证:(m+1) C "■ +JIL(n +1) C ' = (m+1) C J_n.n+2【分析】(1)由已知直接利用组合公式能求出 7 t ..:■的值.(2)对任意m € N *,当n=m 时,验证等式成立;再假设 n=k (k >m )时命题成立,推导 出当n=k+1时,命题也成立,由此利用数学归纳法能证明(m+1)C +(m+2)C +(m+3)又PQ 的中点在直线■ '. =2 - p,2即:屮专Mi即」y l + y 2=_ 为乜/二力-4/,即关于y 2+2py+4p 2- 4p=0,有两个不相等的实数根, 26. (10 分)(1 )求 7C-4C 的值;k PQ = - 1,即 y 1+y 2= - 2p ,=_i ,严 + 一 :'',右边=「一 十=(k+2 八:「二阳)c 覺+0£十为鬲1= (m+1) c 祭,•••左边=右边,••• n=k + 1时,命题也成立,• m , n € N , n 》m , ( m+1) C 二 + ( m+2) C 二n. m+1【点评】本题考查组合数的计算与证明, 是中档题,解题时要认真审题,注意组合数公式和数学归纳法的合理运用.【解答】解:(1) 7 ,,|:空空土 _ 4X 7X6X£X4 3X2X1 4X3X2X 1 =7X 20 _ 4 X 35=0 .证明:(2)对任意m € N *,① 当 n=m 时,左边=(m+1) cm =m+1, R右边=m)曲訓+1,等式成立. ② 假设n=k (k > m )时命题成立, 即(m+1) C m + (m+2) C m + (m+3) m ihMC 朮n+2(m+1)C 驀,当n=k+1时, %+7kf +(k+1)璋 +(k+2)也(m+1)[(m+1)x (k+3)!G^2) ' £k - nrf-1) !(k+2) 1(rrH-2) I (k - nr+1) I(k*M !]I ! :i 〕.[k+3 _( k _ m+1)](k+2)(出)!ml (k - 硏1〕\+ (m+3) C 加+ (n+1)C■= (m+1)左边=(m+1)(m+2)C :+ [+ ( m+3)。
2016年江苏高考试卷附答案(word)

绝密★启封并使用完毕前试题类型:2016年普通高等学校招生全国统一考试(江苏卷)物理注意事项:考生在答题前请认真阅读本注意事项及各题答案要求1.本试卷共8页,包含选择题(第1题~第9题,共9题)和非选择题(第10题~第15题,共6题)两部分。
本卷满分为120分,考试时间为100分钟。
考试结束后,请将本卷和答题卡一并交回。
2.答题前,考生务必将自己的姓名、准考证号用0.5毫米黑色水笔填写在试卷和答题卡规定位置。
3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号和本人是否相符。
4.作答选择题,必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再涂选其他答案。
做大非选择题,必须用0.5毫米黑色的签字笔在答题卡上的指定位置做大,在其他位置作答一律无效。
5.如需作图,需用2B铅笔绘、写清楚,线条、符号等需加黑、加粗。
第Ⅰ卷一、单项选择题:本题共5小题,每小题3分,共计15分,每小题只有一个选项符合题意。
1.一轻质弹簧原厂为8 cm,在4 N的拉力作用下伸长了2 cm,弹簧未超出弹性限度,则该弹簧的劲度系数为(A)40 m/N (B)40 N/m(C)200 m/N (D)200 N/m2.有A、B两小球,B的质量为A的两倍。
现将它们以相同速率沿同一方向跑出,不计空气阻力。
图中①为A的运动轨迹,则B的运动轨迹是(A)①(B)②(C)③(D)④3.一金属容器置于绝缘板上,带电小球用绝缘细线悬挂于容器中,容器内的电场线分布如图所示。
容器内表面为等势面,A、B为容器内表面上的两点,下列说法正确的是(A)A点的电场强度比B点的大(B)小球表面的电势比容器内表面的低(C)B点的电场强度方向与该处内表面垂直(D)将检验电荷从A点沿不同路径到B点,电场力所做的功不同4.一自耦变压器如图所示,环形铁芯上只饶有一个线圈,将其接在a、b间作为原线圈。
通过滑动触头取该线圈的一部分,接在c、d间作为副线圈。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
根据以下材料,选取角度,自拟题目,写一篇不少于800字的文章;文体不限,诗歌除外。
俗话说,有话则长,无话则短。
有人却说,有话则短,无话则长——别人已说的我不必再说,别人无话可说处我也许有话要说。
有时这是个性的彰显,有时则是创新意识的闪现。
作文题材料由三句话构成。
第一句话中,“有话则长,无话则短”作为一句俗语,是公认的说话准则。
第二句话中,“有话则短,无话则长”是材料所要表达的核心内容,破折号之后则是具体解释,从另一维度对“有话”“无话”及其长短进行阐述。
第三句话,是对“有话则短,无话则长”这种行为的思考与界定,进一步拓展和丰富了材料内涵。
第二句话的内容,体现了一种逆向思维和创新意识。
“有话则短”即“别人已说的我不必再说”,是不走寻常路、避免无谓的重复之意;“无话则长”即“别人无话可说处我也许有话要说”,是在众人无所发现处有所发现和思考,于无疑处有疑,是在众人觉得“无话可说处”别出机杼、大说特说,从而有所创新的表达。
不单说话,科学、文学、艺术等领域的创造也应于“别人无话可说处”,本着自己的慧心、慧眼,作深度的挖掘。
现实生活中彰显个性的现象很多,可以从正面解读其展现出的独特魅力,也可从反面显示出其怪异的取向。
关键是看待的角度。
立意的时候,考生可以抓住关键句“别人已说的我不必再说,别人无话可说处我也许有话要说”“有时这是个性的彰显,有时则是创新意识的闪现”来确定立意,比如“彰显个性”“创新与守规”等。
选用文体的时候,考生可以选择记叙文,从正面彰显人的个性魅力和创新意识,也可以从反面用讽喻的形式发人深思;同样考生也可以选择议论文,借助论述阐述“创新”和个性的魅力。
烟火蓝边碗今早喝粥时我用的是一只白底素净的蓝边碗,你或许会问,如此平淡无奇的碗有什么好说?错矣!此中考究可大着呢,且听我慢慢道来。
(自然切入材料)新居落成,我与父母前往景德镇购买瓷器布置新居。
这里瓷器种类繁多,有“白如玉,明如镜,薄如纸,声如磬”的白瓷;有造型精致小巧的骨瓷;有绚丽多彩的斗彩……让人眼花缭乱,美不胜收。
买什么好呢?有人说:只要票子够多尽选造型独特的买,显得荣华富贵的买,精工极致的买,这还不简单?又错啦!器皿的选择体现了主人的生活态度。
不可不慎重。
(及时升华,提升高度)有的瓷器过于大件且富丽堂皇,赤红、明黄、宝蓝与我家简约的装修风格不符;有的过于小巧,家人并无英国绅士贵妇那般品下午茶的闲情;有的瓷器上绘有泼墨山水工笔花鸟,我们一行人中并无行家,不知如何鉴赏……如此看来,竟无我们能买的瓷器了!突然,这平淡无奇得突兀的蓝边碗闯入我的眼帘。
如此简陋的碗会在这里出售?我要走,爸爸却在这碗前驻足许久。
为何?这是上世纪七八十年代家家户户都用的碗,这是盛放了父亲的记忆的碗。
据销售人员介绍,这蓝边碗在传统蓝边碗上加以细节上的改良与创新。
我拿起一只仔细端详,发现手感极好,分量厚重让人踏实。
底足的角度略微加大,让碗显得端庄典雅不失大气。
而且这碗极易打理,深受妈妈的喜欢。
(恰到好处的描写)蓝边碗没有繁复精致的花纹修饰,没有绚丽的色彩,没有复杂的工艺。
可当你凝视它,就会情不自禁地想起一家人围在一起乐呵呵地吃热腾腾的饭菜的情景,就会想起苦日子里生活精打细算的不易,就会想起寻常百姓家人间烟火的温度……(切题并照应题目中的“烟火”)蒋勋曾在《品味四讲》中说“纯棉衬衫就像爱人”,让我感动了好久,一件物品使用久了,就会产生难以割舍的情感,对我来说,蓝边碗亦是如此。
景德镇作为瓷都,常有瓷器新品推出,我却独爱这蓝边碗并歌颂它。
因它注重在细节上的改良,把创新的点子用在提升人们的生活上而不是争一时的噱头。
距离人的生活太远的创意并不是人真正想要的。
新鲜感过后便如失了灵性般只能束之高阁。
(议论高超,思维显风姿)每日捧着这只蓝边碗吃饭,不但手感好,我仿佛还能听到它无声的诉说,谆谆教诲我认真踏实地生活的真谛。
听我如此道来,你可有话反驳?本文见微知著,主旨深刻。
此文为议论性散文,朴素而有韵味,寓丰腴于平淡之中。
本来面对一只白底素净的蓝边碗,应该是“无话可说”,可考生却“无话则长”,表达了富有启示意义的主旨:选择应该适合自己,生活应该认真踏实。
另外,构思独特,语言有味。
构思有特色,“错矣”“又错啦”“如此看来,竟无我们能买的瓷器了”,可谓多重蓄势,层层铺垫。
“蓝边碗”前加上“烟火”二字,暗示对比,激发联想,实属灵光一闪,巧慧之举。
我言秋日胜春朝无意中翻到马远的《寒江独钓图》,几点水纹,几抹残云。
一扁舟,一钓叟,除此之外,满卷皆虚空。
这叫留白,是中国水墨画中荡开的浓重一笔。
全卷只有几处重点物象是细心勾勒的,其余只是略作铺垫,甚至不沾半点墨。
全卷意蕴于是从二维纸面伸展成了无限。
(以名画开篇,起笔不凡,显从容之态)留白是与前人的叫板。
南宋马远与夏圭,人称马一角、夏半边,尤善留白。
而宋代的山水画师,大多是事无巨细,皆一一列举下来。
怕是远处草丛中几块石子,几块污秽的牛粪,前人也会一丝不苟的记录下来,装裱以登大雅之堂。
布满画纸的山水,自有它的美,碧水蓝天,枯藤怪石,强烈的视觉冲击,喂饱了千年来中国人的审美。
仿照古人的《清明上河图》,一千多个人物,雕梁画栋,飞桥屋檐,美、大气。
但马远与夏圭,偏不爱这耗尽精力体力的活儿。
再者,前人已经留下大量如此详尽的山水,再走这条路,恐怕历史上只会多两个无名的山水画师,却少了“马一角”“夏半边”!(在画史中进行比较,突出“留白”手法的创新,为下文的议论做准备)古诗云:“自古秋风悲寂寥,我言秋日胜春朝!”这是乐观与通达,也是个性与创新。
自古太多的悲秋怀古,似乎一到秋天,日历一撕下,人的心境也会转凉,尽管那炎热还未曾褪去。
“前人之述备矣!”秋,承载了太多的悲伤情怀,有“天凉好个秋”,也有“物换星移几度秋”,“秋色连波,波上寒烟翠”。
只有这一声啼鸣,唤起了后世对秋新的审美。
“晴空一鹤排云上,便引诗情到碧霄”,那成排的雁、鹤不同于以往,成了欣欣向荣的象征,成了最美的秋词。
(由画到诗,充满艺术气息)这便是“唱反调”“叫板”之类,有些话,别人也说过,我便不必再附庸风雅;只有别人无话可说时,才是我的主场,我的黄金时代。
(联系材料,水到渠成)国学大师陈寅恪不正是这样的人吗?面对一个妓女,他不像别人一样心怀芥蒂,以别样眼光看她,而是在眼盲情况下口述了百万字巨著《柳如是别传》,这是个性与创新,也是对人性的敬重。
(以学术大师为例,进一步揭示个性与创新的价值)同样,韩干,那个画马的宫廷画师,亲身入马厩,与马儿共同生活,不听从老师的劝诫,才成就了《照夜白》。
韩干的马,大多腰体肥圆,怒目圆睁,没了以往画师的瘦马。
鲁迅先生的话犹在耳边萦绕:“这世上本没有路,走的人多了,也便成了路。
”是的,只有于杂草丛生处辟蹊径,才能避免在他人的康庄大道上流于平庸,才能成为为人记住的开路人,才能成为有个性的个体,才能成为马远、夏圭、陈寅恪和韩干……(联结全文所有论据,美珠成串)只愿在不断流淌的长河中,尽管洪流碾过,巨山平偃而下,我却依旧能听到“我言秋日胜春朝”亦或更响亮,更不同于他的啼鸣。
(结尾点题)作者闲处落笔,悠闲从容地从《寒江独钓图》起笔漫谈,材料援引丰富而妥帖,从马远、夏圭、韩干到陈寅恪、鲁迅等,古今史料,尽显风流,可贵的是文章不是脱离材料空谈道理,也并非生搬硬套堆砌事例,而是在精当的列举,巧妙的引用之后,恰到好处地加以议论,自然地勾连了题旨,用“留白”“唱反调”“叫板”“独辟蹊径”等词,生动地诠释了题目材料中的“有话则短,无话则长”,意蕴丰富,颇有新意。
以文而论,作者胸中有墨,故清词丽句汩汩而来,行文徐徐从容,又节奏分明。
修钟长脊蜿蜒,垂脊错落,红墙沥粉,鎏金飞檐。
这儿是故宫,老王工作的地方。
(四字短语组成阵列开篇,可谓流光溢彩。
文字典雅切合故宫环境,也与古玩修复的工作内容贴切)先打了一盆热水,老王便紧闭上了西三所的红门。
“嗨!王老师回来了!快来看看这件宝物!”徒弟小林招呼着便掀开了工作台上的白席——一座金光璀璨的大型钟表,原来是乾隆帝的音乐永法钟。
老王细细赏了一番,着实精美巧妙。
欧式建筑中式亭台并列其上更添韵味。
“老师,这件宝贝还算完好,我们几个着手修复没有问题。
”小林自信满满地和老王保证道。
老王点点头坐在一旁,花猫懒沐在细碎的阳光下,半眯着眼朝老王笑。
老王不再盯着徒弟们干活,只觉得院子里的猫儿一颦一动之间也不乏趣味。
(可谓颊上三毛,显出人物和文章的神采)不出半日,小林就出来交差了,除锈见新后的器物更显出皇家的雍容华贵,钟盘走时精准,不愧为前辈们巧夺天工之作,几个小徒弟和隔壁木器组的同事们都对它赞不绝口,老王却觉得钟表虽美,但除了时刻运转的表针太过死板,还少了灵动的韵味。
几位看客正大赞表台之上栩栩如生的装饰动物和银箔仿制的溪水,老王却蹙起了眉头。
(眉头蹙起源于老王独到之眼光)“王老师怎么不说话?也和我们几个门外汉分享一下高见呀!”几位同事调侃道。
“此钟虽美,但多为静止之物,装饰的堆砌在你们看来是盛美之处,我倒觉得此处可以作文章。
”“大家都是干这行的,修复文物的工作能做到复原便可,你何必自增烦恼啊!”老王摇摇头反驳道:“人人赞此物华美,我不必再说。
但你们眼中的完美之处我还真有话可说!”说罢,老王拆了钟表的上盘,用铁丝将装饰品和钟内的传统系统一一连接起来;将银箔尾端捻做银丝扣于动轴之上;再取银丝上连纺车、风车。
合上上盘后,老王欣慰一笑,原本沉寂之物此时动了起来!转鸭,吠犬,还有那潺潺的流水:真如大型表演,运转精准,具体而微。
在场的各位连声叫好,老王看着门槛边的小花猫,轻轻地笑了,徒弟们求老王传授经验,老王从容道:“你们啊,只会做千篇一律的工作;别人的溢美之处你何必多言?众人无话之处或许你有话可说,此时大做文章岂不快哉?”于老王而言,文物修复仍有可创新之处,工匠必有慧眼识得旁人忽视之处。
(处处着笔切合材料,老王的笑显出创新的魅力)老王骑车下班,又锁上了西三所的红门。
一句秦腔传来:“红门里的故事多……”这是一篇优秀的记叙文。
首先,构思新颖别致。
通过老王修钟的故事,突出人物的鲜明个性。
在众人觉得“无话可说处”“无所发现处”独出机杼,有所创发和表达,彰显了工匠的创新意识。
主人公个性鲜明,形象丰满。
其次,事件过程描述详细、具体。
思路清晰,脉络分明,层次感强。
故事情节发展前后勾连映衬,相互照应。
另外,文中不乏情趣生动的细节,尤其是结尾处的秦腔,余味悠长。
