新人教版初中数学三角形的中位线定理优质课课件完美版
合集下载
八年级数学-三角形中位线定理ppt课件-人教版
是AC的中点。
则有:DE∥BC, DE= 1 BC. 2
A
能说出理由
吗?
D
E
B
C
采用PP管及配件:根据给水设计图配置好PP管及配件,用管件在 管材垂 直角切 断管材 ,边剪 边旋转 ,以保 证切口 面的圆 度,保 持熔接 部位干 净无污 物
如图:在△ABC中,D是AB的中点,E
是AC的中点。
则有:DE∥BC, DE= 1 BC.
B
F
C
HG//AC,HG= AC
2
所以EF//HG,EF=HG
所以四边形EFGH是平行四边形
采用PP管及配件:根据给水设计图配置好PP管及配件,用管件在 管材垂 直角切 断管材 ,边剪 边旋转 ,以保 证切口 面的圆 度,保 持熔接 部位干 净无污 物
从例1中你能得到什么结论?
顺次连接四边形各边中点的 线段组成一个平行四边形 演示2
画出三角形的所有中线并说
出中位线和中线的区别.
A
D
F
B
C
E
采用PP管及配件:根据给水设计图配置好PP管及配件,用管件在 管材垂 直角切 断管材 ,边剪 边旋转 ,以保 证切口 面的圆 度,保 持熔接 部位干 净无污 物
观察猜想
在△ABC中,中位线 DE和边BC什么关系?
A
演示1
D
E
B
C
DE和边BC关系
aห้องสมุดไป่ตู้
A
B
同样, 线段BD的长是点 B 到
直线 b 的距离, 且 AC = BD. b
C
D
因此 , 如果两条直线平行 , 则其中一条直线上任意一 点到另一条直线的距离相等 .
这个距离称为平行线之间的距离..
人教版八年级数学下册:三角形的中位线【精品课件】

(2)由(1)知DE=CF,又∵AD=BC,
∴Rt△DAE≌Rt△CBF,∴∠A=∠B.
10. 如图,四边形ABCD是平行四边形, ∠ABC=70°,BE平分∠ABC且交AD于点E,
DF∥BE且交BC于点F. 求∠1的大小.
解:∵四边形ABCD是平行四边形, ∠ABC=70°,∴∠ADC=∠ABC=70°,
解:分别取AC,BC的中点D,E, 连接DE,并量出DE的长,则 AB=2DE.
根据三角形的中位线平行于三角 形的第三边,且等于第三边的一半.
误区 诊断
误区 错误认识中点四边形 一 1.下列说法①任意四边形的四边中点的连线所 形成的四边形是平行四边形;②一个四边形的四边 中点的连线所形成的四边形是平行四边形,则这个 四边形一定是平行四边形;③平行四边形四边中点 的连线所形成的四边形是平行四边形.其中正确的是 ()
B
C
如图,在△ABC中,BD、CE分别是AC、AB 上的中线,BD与CE相交于点O,试探究BO与OD 的大小关系.(提示:分别取OB、OC的中点M、N)
解:OB=2OD, 如图,取OB、OC的中点M、 N,连接EM、MN、ND.∵E、D 分别为△ABC的中点,
∴ED∥BC,ED=
1 2
BC,
∵M、N是△OBC的中点,
A
D
理由:因为光线AD∥BC,纸板
对边AB∥CD,所以光线与纸板所形
B
C
成的四边形ABCD是平行四边形,而平行四边形对角
相等,所以∠2=∠1.
3.如图, ABCD的对角线AC,BD相交于点
O,且AC+BD=36,AB=11,求△OCD的周长.
解:∵ ABCD的对角线互相平分,
(OC=
三角形中位线定理PPT教学课件

三角形的中位线定理
2021/01/21
1
什么叫三角形的中位线?
连结三角形两边中点的线段叫三角形的中位线
如图: D、E分别是AB、AC边的中点, DE就是△ABC的中位线。
A
一个三角形共有几条中位线? D
E
答:三条
2021/01/21
B
F
C
2
三角形的中位线与三角形的中线有
什么区别? A
A
D
E
B
CB
边形是平行四边形。
已知:E、F、G、H分别是四边形ABCD中
AB、BC、CD、DA的中点。求证:EFGH是平
行四边形。
A
H
D
E
G B
F
2021/01/21
C
5
任意四边形四边中点连线所得的四边形 一定是平行四边形。
2021/01/21
6
例2:顺次连结矩形各边中点所得的四边形是 菱形。
已知:E、F、G、H分别是矩形ABCD中 AB、BC、CD、DA边的中点。求证:EFGH是 菱形。
A
H
D
2021/01/21
E G
B
F
C
7
ቤተ መጻሕፍቲ ባይዱ
例3:已知 ABCD中,AC、BD相交于点 O,E、F、G、H分别是AB、OB、CD、OD的 中点。求 证:∠HEF= ∠FGH。
A
E F
B
D H
O
G
C
2021/01/21
8
例4:已知如图:在△ABC中,AB、BC、
CA的中点分别是E、F、G,AD是高。求 证:
∠EDG= ∠EFG。
分析:EF是△ABC的中位线
EF 1 AC
2021/01/21
1
什么叫三角形的中位线?
连结三角形两边中点的线段叫三角形的中位线
如图: D、E分别是AB、AC边的中点, DE就是△ABC的中位线。
A
一个三角形共有几条中位线? D
E
答:三条
2021/01/21
B
F
C
2
三角形的中位线与三角形的中线有
什么区别? A
A
D
E
B
CB
边形是平行四边形。
已知:E、F、G、H分别是四边形ABCD中
AB、BC、CD、DA的中点。求证:EFGH是平
行四边形。
A
H
D
E
G B
F
2021/01/21
C
5
任意四边形四边中点连线所得的四边形 一定是平行四边形。
2021/01/21
6
例2:顺次连结矩形各边中点所得的四边形是 菱形。
已知:E、F、G、H分别是矩形ABCD中 AB、BC、CD、DA边的中点。求证:EFGH是 菱形。
A
H
D
2021/01/21
E G
B
F
C
7
ቤተ መጻሕፍቲ ባይዱ
例3:已知 ABCD中,AC、BD相交于点 O,E、F、G、H分别是AB、OB、CD、OD的 中点。求 证:∠HEF= ∠FGH。
A
E F
B
D H
O
G
C
2021/01/21
8
例4:已知如图:在△ABC中,AB、BC、
CA的中点分别是E、F、G,AD是高。求 证:
∠EDG= ∠EFG。
分析:EF是△ABC的中位线
EF 1 AC
三角形的中位线ppt课件

∴AB= + = + =13.
∵点 D,E 分别是直角边 BC,AC 的中点,
∴DE 是 Rt△ABC 的中位线.
∴DE= AB=6.5.
三角形中位线的两个作用
位置关系: ∵ ,分别为,
⇒
的中点, ∴ ∥ .
数量关系: ∵ ,分别为,
的中点, ∴ = .
新知应用
1.如图所示,在△ABC中,点D,E分别为AB,AC的中点,若DE=2,则BC的长
为( D
)
A.1
B.2
C.3
D.4
2.如图所示,在Rt△ABC中,∠A=90°,AB=3,AC=4,D,E,F分别是边
AB,BC,AC的中点,连接DE,DF,EF,∠ADF的度数为53°.求:
A.1
B.2
C.3
D.4
4.如图所示,在四边形ABCD中,AC⊥BD,AC=6,BD=8,点E,F分别是边AD,BC
5
的中点,连接EF,则EF的长是
.
5.如图所示,在△ABC中,AB=AC,点D是边AB上一点,DE∥BC交AC于点E,连
接BE,点F,G,H分别为BE,DE,BC的中点.求证:FG=FH.
点D,E,F,G依次连接,得到四边形DEFG.求证:四边形DEFG是平行四边形.
证明:∵AB,OB,OC,AC 的中点分别为 D,E,F,G,
∴DG 是△ABC 的中位线,EF 是△OBC 的中位线.
∴DG∥BC,DG= BC,EF∥BC,EF= BC.∴DG∥EF,DG=EF.
∴四边形 DEFG 是平行四边形.
到点D,使AB=2AD,连接DE,DF,AE,EF,AF与DE交于点O.试说明AF与DE互相
∵点 D,E 分别是直角边 BC,AC 的中点,
∴DE 是 Rt△ABC 的中位线.
∴DE= AB=6.5.
三角形中位线的两个作用
位置关系: ∵ ,分别为,
⇒
的中点, ∴ ∥ .
数量关系: ∵ ,分别为,
的中点, ∴ = .
新知应用
1.如图所示,在△ABC中,点D,E分别为AB,AC的中点,若DE=2,则BC的长
为( D
)
A.1
B.2
C.3
D.4
2.如图所示,在Rt△ABC中,∠A=90°,AB=3,AC=4,D,E,F分别是边
AB,BC,AC的中点,连接DE,DF,EF,∠ADF的度数为53°.求:
A.1
B.2
C.3
D.4
4.如图所示,在四边形ABCD中,AC⊥BD,AC=6,BD=8,点E,F分别是边AD,BC
5
的中点,连接EF,则EF的长是
.
5.如图所示,在△ABC中,AB=AC,点D是边AB上一点,DE∥BC交AC于点E,连
接BE,点F,G,H分别为BE,DE,BC的中点.求证:FG=FH.
点D,E,F,G依次连接,得到四边形DEFG.求证:四边形DEFG是平行四边形.
证明:∵AB,OB,OC,AC 的中点分别为 D,E,F,G,
∴DG 是△ABC 的中位线,EF 是△OBC 的中位线.
∴DG∥BC,DG= BC,EF∥BC,EF= BC.∴DG∥EF,DG=EF.
∴四边形 DEFG 是平行四边形.
到点D,使AB=2AD,连接DE,DF,AE,EF,AF与DE交于点O.试说明AF与DE互相
三角形的中位线课件(优秀课件)

B
F
C
C
∴四边形EFGH是平行四边形.
结论:中点四边形是平行四边形.
图形变式,应用定理
中点四边形的周长与原四边形的关系.
中点四边形的面积与原四边形面积的关系.
AEH∽ ABD SAEH EH
同理:SCFG
E14FSBSCDAHBDG
BD1 2
2 1 4
AC
S AEH
1 4
S ABD
A
1 1 EH FG BD SAEH SCFG 4 S四边形ABCD
A
H
D
A
变式
F
E
G
E
B
D
C
B
C
F
图形变式,应用定理
例题 已知:在四边形ABCD中,点E、F、G、H分别是AB、BC、CD、DA的
中点.
求证:四边形EFGH是平行四边形.
A
H
思证路明:分连析结AC A
H
D
化归思∵∴想同AHH理G=∥EHFAD∥C,,ACCHG,G=EGFD12A1CACDG
E
G
2
∴HG∥EF且HG=EF
灵活运用,回归生活
课堂练习2
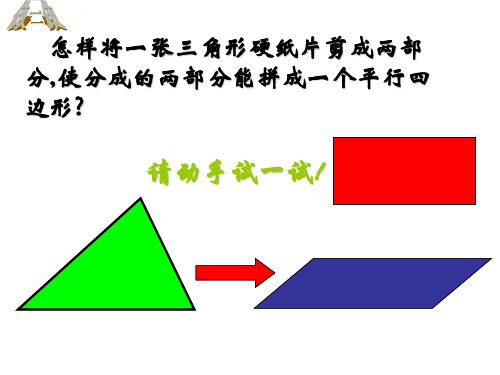
2.利用“剪”、“拼”的方法将任意一个三角形纸片变成一个与 原三角形面积相等的平行四边形纸片,并证明你的做法的合理
性.(教材94页5题)
课后思考: 你能将一个平行四边形纸片利用“剪”、“拼”的
方法变成一个面积相等三角形纸片吗?
剪一刀
剪 两 刀?
灵活运用,回归生活
课堂练习2
2 同理 :
SBEF
S DHG
1 4
S四边形ABCD
E
S四边形EFGH
人教版八年级数学下册《三角形的中位线定理》精品课件

人教版 八年级下册
三角形的中 位线定理
导入新课 判断下列条件能否判定一个四边形是平行四边形。 A.一组对边平行,另一组对边相等。 不能 B.一组对角相等,另一组对角互补。 不能 C.一组对角相等,一组邻角互补。 能 D.一组对边平行,一组对角互补 不能
新课学习
三角形的中位线定理
如图,画出△ABC的AB、AC边中点D、E,连接DE.
知识巩固 1.如图,在△ABC中,D、E分别是AB,AC的中点, AC=12,F是DE上一点,连接AF,CF,若∠AFC=90°,
EF=3DF,则BC的长为( D )
A.13B.14 C.15 D.16
分析:根据直角三角形的性质得到EF=6,根据EF=3DF,得 到DF=2,求出DE,根据三角形中位线定理解答即可。
角或
平行四边形
截长补短 线段相等
新课学习
证明:延长DE到F,使EF=DE,连接FC、DC、AF
∵AE=EC,EF=DE
∴四边形ADCF是平行四边形
∴ CF∥DA,CF=DA ∴ CF∥BD,CF=BD
∴四边形DBCF是平行四边形
∴ DF∥BC,DF=BC
又DE= 12DF
∴DE∥BC且DE=
1 2
拓展提升 解析:如图,取BC边的中点G,连接EG,FG. ∵E、F分别是AB、CD的中点,
∴EG∥AC,EG= 12AC, 同理:FG∥BD,FG= 12BD, ∵AC=BD,∴EG=FG,∴∠GEF=∠GFE. ∵EG∥AC,∴∠OMN=∠GEF. 同理,∠ONM=∠GFE.∴∠OMN=∠ONM, ∴OM=ON.即△MON是等腰三角形
课堂小结
1、三角形的中位线 2、三角形的中位线定理 三角形的中位线平行于三角形的第三边,且等于第三边的 一半。
三角形的中 位线定理
导入新课 判断下列条件能否判定一个四边形是平行四边形。 A.一组对边平行,另一组对边相等。 不能 B.一组对角相等,另一组对角互补。 不能 C.一组对角相等,一组邻角互补。 能 D.一组对边平行,一组对角互补 不能
新课学习
三角形的中位线定理
如图,画出△ABC的AB、AC边中点D、E,连接DE.
知识巩固 1.如图,在△ABC中,D、E分别是AB,AC的中点, AC=12,F是DE上一点,连接AF,CF,若∠AFC=90°,
EF=3DF,则BC的长为( D )
A.13B.14 C.15 D.16
分析:根据直角三角形的性质得到EF=6,根据EF=3DF,得 到DF=2,求出DE,根据三角形中位线定理解答即可。
角或
平行四边形
截长补短 线段相等
新课学习
证明:延长DE到F,使EF=DE,连接FC、DC、AF
∵AE=EC,EF=DE
∴四边形ADCF是平行四边形
∴ CF∥DA,CF=DA ∴ CF∥BD,CF=BD
∴四边形DBCF是平行四边形
∴ DF∥BC,DF=BC
又DE= 12DF
∴DE∥BC且DE=
1 2
拓展提升 解析:如图,取BC边的中点G,连接EG,FG. ∵E、F分别是AB、CD的中点,
∴EG∥AC,EG= 12AC, 同理:FG∥BD,FG= 12BD, ∵AC=BD,∴EG=FG,∴∠GEF=∠GFE. ∵EG∥AC,∴∠OMN=∠GEF. 同理,∠ONM=∠GFE.∴∠OMN=∠ONM, ∴OM=ON.即△MON是等腰三角形
课堂小结
1、三角形的中位线 2、三角形的中位线定理 三角形的中位线平行于三角形的第三边,且等于第三边的 一半。
《三角形的中位线》 精选优质课件

书是甜的,快翻开你的书,在书的海洋中遨游,去尝一尝书的蜜糖吧。
位线。 书犹如冬日里的阳光,带给我春的温暖;
对我来说,读书就和吃饭一样,已经成为我生命中最重要的组成部分,一餐不吃感觉饿,一天不读感觉慌。
或是说,只有他才能使我们的血液流动,促进心脏的呼吸,只有他才能使我们活在这个世界上,我们要读好书、好读书、读好书把冰 心的言论铭记在心。 我说爸爸你要我还是要她你说一声,进考场的时候我回看了父亲一眼,他哭了,甚至鼻涕都流到了嘴边。
小学生读书心得(三): 读书让我快乐地成长
如果我是一棵小树,那么书就是灿烂的 阳光, 它照耀 着我, 让我快 乐地成 长;如 果我是 一条小 鱼,那 么书就 是清清 的溪流 ,它滋 润着我 ,让我 快乐的 成长; 如果我 是一只 小鸟, 那么书 就是碧 蓝的天 空,它 支撑着 我,让 我快乐 的成长! 从小,我就很喜欢看书。记得还在幼儿 园时, 我便早 早地学 起了a、 o、e。 为什么 只是为 了能早 点捧起 我心爱 的书本 ,在书 的世界 中翱翔 。小学 生读书 心得。 那时, 书就像 一个缤 纷世界 ,让我 流连忘 返。在 书中, 我和小 鸟一齐 飞上蓝 天,和 小精灵 一齐唱 歌跳舞 ,和蝴 蝶们一 齐玩 捉迷藏 随着时 光的流 逝,我 一天天 地长大 ,一本 本书更 是成了 我的好 伙伴:我 捧起了 童话故 事,捧 起了科 幻小说 ,捧起 了百科 全书, 捧起了 世界名 著。我 常常静 静地坐 在书桌 旁,时 而深思 ,时而 幻想, 时而快 乐,时 而忧伤 。在《 水浒传 》里, 我结识 了忠义 宽容的 宋江; 在《三 国演义 》里, 我认识 了足智 多谋的 诸葛亮 ;在《 鲁滨逊 漂流记 》里, 我懂得 了遇事 要坚强 ;在《 钢铁是 怎样炼 成》里 ,我汲 取了战 胜困难 的力量!读《中 华国宝 》和《 中华国 恨》, 让我明 白了中 华民族 以前有 过的辉 煌历史 ,也让 我明白 了中华 民族以 前遭受 的屈辱!更让我 在心中 立下了 和周恩 来总理 一样的 志愿为 中华之 崛起而 读书!努力读 书,振 兴中华!书是无 穷的宝 藏,为 我增添 了丰富 的知识 ;书是 快乐的 天堂, 让我忘 记了所 有的忧 伤。书 犹如冬 日里的 阳光, 带给我 春的温 暖;书 又似沙 漠里的 绿洲, 给予我 新的期 望!就这 样,书 陪伴我 度过了 一年又 一年, 我在书 香中渐
位线。 书犹如冬日里的阳光,带给我春的温暖;
对我来说,读书就和吃饭一样,已经成为我生命中最重要的组成部分,一餐不吃感觉饿,一天不读感觉慌。
或是说,只有他才能使我们的血液流动,促进心脏的呼吸,只有他才能使我们活在这个世界上,我们要读好书、好读书、读好书把冰 心的言论铭记在心。 我说爸爸你要我还是要她你说一声,进考场的时候我回看了父亲一眼,他哭了,甚至鼻涕都流到了嘴边。
小学生读书心得(三): 读书让我快乐地成长
如果我是一棵小树,那么书就是灿烂的 阳光, 它照耀 着我, 让我快 乐地成 长;如 果我是 一条小 鱼,那 么书就 是清清 的溪流 ,它滋 润着我 ,让我 快乐的 成长; 如果我 是一只 小鸟, 那么书 就是碧 蓝的天 空,它 支撑着 我,让 我快乐 的成长! 从小,我就很喜欢看书。记得还在幼儿 园时, 我便早 早地学 起了a、 o、e。 为什么 只是为 了能早 点捧起 我心爱 的书本 ,在书 的世界 中翱翔 。小学 生读书 心得。 那时, 书就像 一个缤 纷世界 ,让我 流连忘 返。在 书中, 我和小 鸟一齐 飞上蓝 天,和 小精灵 一齐唱 歌跳舞 ,和蝴 蝶们一 齐玩 捉迷藏 随着时 光的流 逝,我 一天天 地长大 ,一本 本书更 是成了 我的好 伙伴:我 捧起了 童话故 事,捧 起了科 幻小说 ,捧起 了百科 全书, 捧起了 世界名 著。我 常常静 静地坐 在书桌 旁,时 而深思 ,时而 幻想, 时而快 乐,时 而忧伤 。在《 水浒传 》里, 我结识 了忠义 宽容的 宋江; 在《三 国演义 》里, 我认识 了足智 多谋的 诸葛亮 ;在《 鲁滨逊 漂流记 》里, 我懂得 了遇事 要坚强 ;在《 钢铁是 怎样炼 成》里 ,我汲 取了战 胜困难 的力量!读《中 华国宝 》和《 中华国 恨》, 让我明 白了中 华民族 以前有 过的辉 煌历史 ,也让 我明白 了中华 民族以 前遭受 的屈辱!更让我 在心中 立下了 和周恩 来总理 一样的 志愿为 中华之 崛起而 读书!努力读 书,振 兴中华!书是无 穷的宝 藏,为 我增添 了丰富 的知识 ;书是 快乐的 天堂, 让我忘 记了所 有的忧 伤。书 犹如冬 日里的 阳光, 带给我 春的温 暖;书 又似沙 漠里的 绿洲, 给予我 新的期 望!就这 样,书 陪伴我 度过了 一年又 一年, 我在书 香中渐
三角形中位线课件

三角形中位线的定理
• 定理:三角形的中位线定理是指三角形的中位线长度等于 第三边长度的一半,并且平行于第三边。
三角形中位线的性质定理
01
02
03
性质定理1
三角形的中位线将相对边 分为两段,且这两段长度 相等。
性质定理2
三角形的中位线与第三边 平行,且长度为第三边的 一半。
性质定理3
三角形的中位线将相对顶 点与对边中点连接,且该 连线长度为中位线长度的 一半。
电路设计
在电路设计中,三角形中位线可以用来平衡电流,防止电流过大导致设备损坏或 火灾等安全事故。
05 总结与思考
三角形中位线的重要性和意义
几何构造的基础
在实际生活中的应用
三角形中位线是几何学中的基础概念 ,对于理解几何图形的构造和性质至 关重要。
在建筑、工程和设计等领域,三角形 中位线的应用广泛,例如在测量、绘 图和计算面积等方面。
02 三角形中位线的 性质与判定
三角形中位线的性质
三角形中位线平行于第三边
01
三角形中位线与第三边平行,这是三角形中位线的基本性质。
三角形中位线长度为第三边的一半
02
三角形中位线的长度是第三边长度的一半,这是三角形中位线
的长度性质。
三角形中位线将相对边等分
03
三角形中位线将相对边等分,这是三角形中位线的等分性质。
在解题中的应用
解题辅助
在解决一些几何问题时,三角形中位线可以作为一个重要的解题工具,帮助我 们找到解题的突破口。
证明定理
通过三角形中位线,我们可以证明一些重要的几何定理,如“三角形中位线定 理”等。
在生活中的实际应用
建筑测量
在建筑行业中,三角形中位线被广泛应用于测量和计算角度、长度等参数,决几何证明问题
