拉普拉斯行列式展开例题
行列式典型例题

第二讲 行列式综合训练第一部分例2.1 计算行列式,其中对角线上元素都是a ,未写出的元素都是零.n D =11aa解 这道题可以用多种方法进行求解,充分应用了行列式的各种性质. 方法1 利用性质,将行列式化为上三角行列式.n D 11c nc a-⋅=101a aaa-=11()n a a a--=n a -2n a - 方法2 仍然是利用性质,将行列式化为上三角行列式.n D n 1r r -=111a aa --1nc c +=111a aa +-=na -2n a-方法3 利用展开定理,将行列式化成对角行列式.n D 1c 展开=1n aaa -+11001(1)0n n a a +--而 11001(1)0n n a a+--最后列展开=21(1)n +-2n aa -=2n a--n D =1n a a -⋅-2n a -=n a -2n a -方法4 利用公式A O OB=A B .将最后一行逐行换到第2行,共换了2n -次;将最后一列逐列换到第2列,也共换了2n -次.n D =2(2)(1)n --11a aa=11a a2n aa -=na -2n a-方法5 利用公式A O OB=A B .例2.2 计算n 阶行列式:11212212n n n n na b a a a a b a D a a a b ++=+ (120n b b b ≠)解 采用升阶(或加边)法.该行列式的各行含有共同的元素12,,,n a a a ,可在保持原行列式值不变的情况下,增加一行一列,适当选择所增行(或列)的元素,使得下一步化简后出现大量的零元素.1211212212100n n n n n na a a ab a a D a a b a a a a b +=++升阶213111n r r r r r r +---=121211001010n na a ab b b --- 1112,,1jj c c b j n -+=+=111211121000000000n na a a a ab b b b b +++=1121(1)nn na ab b b b b +++这个题的特殊情形是121212n n n n a x a a a a x a D a a a x++=+=11()nn i i xx a -=+∑可作为公式记下来.例2.3 计算n 阶行列式:12111111111n na a Da ++=+其中120n a a a ≠.解 这道题有多种解法. 方法1 化为上三角行列式nD 12,,i r r i n-==1121111na a a a a +--112,,j ja c c a j n+==21100nb a a其中11211n i i b a a a ==++∑1111ni i a a =⎛⎫=+ ⎪⎝⎭∑,于是n D 12111nn i i a a a a =⎛⎫=+ ⎪⎝⎭∑.方法2 升阶(或加边)法121111011101110111n naD a a +=++升阶12,3,,1i r r i n -=+=121111100101na a a --- 11111121,2,,1121111111j jni jc c a nn j n i i na a a a a a a a +=+=-=+⎛⎫==+⎪⎝⎭∑∑方法3 递推法.将n D 改写为1211101110111n na a D a ++++=+n=按c 拆开12111111111a a +++1211011011na a a ++由于12111111111a a ++1,,1i n r r i n -=-=12111a a 121n a a a -=1211011011na a a ++n =按c 展开1n n a D -因此n D =1n n a D -121n a a a -+为递推公式,而111D a =+,于是n D =1n n a D -121n a a a -+=12n a a a 11211n n n D a a a a --⎛⎫+ ⎪⎝⎭=12n a a a 2122111n n n n D a a a a a ---⎛⎫++ ⎪⎝⎭==12n a a a 11211n D a a a ⎛⎫+++⎪⎝⎭=12n a a a 121111n a a a ⎛⎫++++⎪⎝⎭例2.4 设343123211211)(------=x x x x x x x f ,证明存在),1,0(∈ζ使0)(='ζf . 证 因为()f x 是关于x 的二次多项式多项式,在[]1,0上连续,(0,1)内可导,且0331221111)0(=------=f ,101(1)1110121f =-=-由罗尔定理知,存在)1,0(∈ζ,使0)(='ζf .例2.5 计算D =222244441111ab c d a b c d a b c d . 解 这不是范得蒙行列式,但可借助求解范得蒙行列式进行求解.方法1 借助于求解范得蒙行列式的技巧进行求解:从下向上,逐行操作.D 2433221r a r r ar r ar ---=222222222111100()()()0()()()b ac ad ab b ac c ad d a b b a c c a d d a ---------1c 展开=()()()b ac ad a ---222111()()()b c d b b a c c a d d a +++ 3r 拆开=()()()b a c a d a ---(333111bc d b c d +222111a b c d b c d )其中333111b cd b c d 23221r b r r br --=222211100()()c bd b c c b d d b ---- =()()c bd b --11()()c c bd d b ++=()()c b d b --[()()]d d b c c b +-+由于222111bcd b c d 是范德蒙行列式,故222111b c d b c d =()()()c b d b d c --- D =()a b c d +++()()()b a c a d a ---()()()c b d b d c --- 方法2 D 213141c c c c c c ---=222222244444441000ab ac ad aa b a c a d a a b a c a d a --------- 1r 展开=()()()b ac ad a ---222222111()()()()()()b ac ad a b a b a c a c a d a d a +++++++++ 2131c c c c --=()()()b ac ad a ---221()()b a c b d b b a b a x y+--++ 1c 展开=()()()b ac ad a ---c b d b xy--其中222()()x c b a b c ac bc ab =-+++++,222()()y d b a b c ad bd ab =-+++++D =()a b c d +++()()()b a c a d a ---()()()c b d b d c ---=()a b c d +++()()()a b a c a d ---()()()b c b d c d ---方法3 用升阶法.由于行列式中各列元素缺乏3次幂的元素,在D 中添加3次幂的一 行元素,再添加一列构成5阶范得蒙行列式:5D =22222333334444411111a b c d x a b c d x a b c d x a b c d x 5D 按第5列展开得到的是x 的4次多项式,且3x 的系数为4545(1)A D D +=-=-又利用计算范得蒙行列式的公式得5D =()()()()b a c a d a x a ----()()()c b d b x b ---()()()d c x c x d ---=()()()b a c a d a ---()()c b d b --()d c -[()()()()]x a x b x c x d ----=()()()b a c a d a ---()()c b d b --()d c -43[()]x a b c d x -++++其中3x 的系数为()()()b a c a d a ----()()c b d b --()d c -()a b c d +++由3x 的系数相等得:D =()a b c d +++()()()b a c a d a ---()()()c b d b d c --- 例2.6 设4322321143113151||-=A ,计算A 41 + A 42 + A 43 + A 44 = ? 其中A 4j (j= 1, 2, 3, 4)是|A |中元素a 4j 的代数余子式.解 直接求代数余子式的和工作量大.可将414243A A A A +++改写为4142431111A A AA ⋅+⋅+⋅+⋅,故A 41 + A 42 + A 43 + A 44 1111321143113151-=1602102310121000-==41602(1)023012+--=62100320261=-- 例2.7 求解方程:11111111()01121111(1)x f x x nx-==---解 方法1()f x 12,,i r r i n-==111100000100(2)x xn x-=---=)2()1()1(1+----n x x x n由题设知0)2()1()1()(1=+---=-n x x x x f n所以2,,1,0121-===-n x x x n 是原方程的解.方法2 由题设知,当2,,2,1,0-=n x 时,由于行列式中有两列对应元素相同,行列式值为零,因此)(x f 可写成)2()1()(+--=n x x Ax x f于是原方程0)2()1()(=+--=n x x Ax x f 的解为:2,,1,0121-===-n x x x n例2.8 计算元素为a ij = | i -j |的n 阶行列式. 解 方法1 由题设知,11a =0,121a =,1,1,n a n =-,故01110212n n n D n n --=--1,1,,2i i r r i n n --=-=11111111n ----1,,1j n c c j n +=-=1211021(1)2(1)20001n n n n n n ------=----其中第一步用的是从最后一行起,逐行减前一行.第二步用的每列加第n 列.方法2 011102120n n n D n n --=--11,2,,111111112i i r r i n n n +-=----=--12,,1001201231j c c j nn n n +=---=---=12(1)2(1)n n n ----例2.9 计算行列式221111220000000b d b d c a c a D =. 解 方法1 按第一列展开:1121120000a c D a d b b =-0000111122b d c a c d =111122b d c ab a -111122b d c a c d=(22b a -111122b d c a c d )=(22b a -)22c d (11b a -)11c d方法2 本题也可利用拉普拉斯展开定理进行计算,选定第2、3行,有:11232311(1)a c D d b +++=-2222a c db =(11b a 11dc -)(22b a 22d c -)例2.10 计算2n D =1111nnnna b a b c d c d ,其中未写出的元素都是0.解 方法1 利用公式A O OB=A B .采用逐行操作,将最后一行逐行和上行进行对换,直到换到第2行(作22n -次相邻对换);最后一列逐列和上列换,换到第2列(作22n -次相邻对换),得到2n D =2(22)(1)n --1111111100000n n n n n n n n a b c d a b a b c d c d ----=2D 2(1)n D -=()n n n n a d b c -2(1)n D -=()n n n n a d b c -1111()n n n n a d b c -----2(2)n D -==()n n n n a d b c -1111()n n n n a d b c -----1111()a d b c -=1()ni i i i i a d b c =-∏方法2 利用行列式展开定理进行求解.2n D 1r 展开=11111111n n nn n na b a b a c d c d d ----+12(1)n n b +-111111110n n n n na b a b c d c d c ----上面第1个行列式是A O OB的形式,而第2个行列式按第1列展开,所以2n D =2112222(1)n n n n n n n a d D b c D -+---- =()n n n n a d b c -2(1)n D - ==1()ni i i i i a d b c =-∏例2.11 计算5100011000110001100011a a aa D a a a a a ---=------. 解 方法1 采用递推的方法进行求解.5D 125c c c ++=1000010001100011011a a aa a a aaa-------- 1c 展开=1001100110011a a a a a a a -------+51000100()(1)110011a a a a a a aa+------- 即 51454()(1)D D a a +=+--, 41343()(1)D D a a +=+--,31232()(1)D D a a +=+--, 221D a a =-+故 234551D a a a a a =-+-+-方法2 采用降阶的方法进行求解.5D 12(1)r a r +-=2210011000110001100011a a a a a a a a a a a -+---------213(1)r a a r +-+=232301011000110001100011a a a a a a a a a a a a a-+--+--------2314(1)r a a a r +-+-=23423400111000110001100011a a a a a a a a a a a a a a a-+-+-+---------23415(1)r a a a a r +-+-+=23450001110001100011011a a a a a a a a aa a a-+-+---------1r 展开=2345514(1)(1)(1)a a a a a +-+-+-⋅--=23451a a a a a -+-+-例2.12 证明D n =121100010nn n xxa a a xa ----+=111n n n n x a x a x a --++++证 方法1 递推法 按第1列展开,有D n = x D 1-n +(-1)1+n a n11111n xxx-----= x D 1-n + a n由于D 1= x + a 1,2211x D a x a -=+,于是D n = x D 1-n + a n =x (x D 2-n +a 1-n )+ a n =x 2D 2-n + a 1-n x + a n== x1-n D 1+ a 2x2-n + + a 1-n x + a n =111n n n n x a x a x a --++++方法2 第2列的x 倍,第3列的x 2倍, ,第n 列的x1-n 倍分别加到第1列上12c xc n D +=2112101001000n n n n x x xa xa a a xa -----++213c x c +=3212123110000100010n n n n n n x xx a xa x a a a a x a--------+++==111x fx---n r =按展开1(1)n f+-1111n xxx----=f其中111n n n n f a a x a x x --=++++或 D n21123n nc xc x c x c -++++=122110000100001n n x x fa a ax a -----+1=按c 展开1(1)n f +-1111n x xx----=11(1)(1)n n f +---=f其中111n n n n f a a x a x x --=++++方法3 利用性质,将行列式化为上三角行列式.D n21321111n n c c x c c xc c x-+++=112200000000n n nnn n nx x x a a a a a a k xx x---+++n =按c 展开x1-n k n = x1-n (1-n n x a + 21--n n x a + +x a 2+a 1+x)=111n n n n a a x a x x --++++ 方法4n r nD =按展开1(1)n na +-1000101x x ---+21(1)n n a +--000010001x x --+ +212(1)n a --1000001x x --+21(1)()n a x -+10000000x x x-=(-1)1+n (-1)1-n a n +(-1)2+n (-1)2-n a 1-n x+ +(-1)12-n (-1)a 2x2-n +(-1)n2( a 1+x) x1-n= 111n n n n a a x a x x --++++例2.13 计算n阶“三对角”行列式Dn=001000101αβαβαβαβαβαβ++++解 方法1 递推法.D n1=按c 展开()αβ+D 1-n —(1)0000101n αβαβαβαβ-++1=按r 展开()αβ+D 1-n -αβD 2-n即有递推关系式 D n =()αβ+D 1-n -αβD 2-n (n ≥3) 故 1n n D D α--=12()n n D D βα---递推得到 1n n D D α--=12()n n D D βα---=223()n n D D βα---==221()n D D βα--而1()D αβ=+,2D =β+α1αββ+α=22ααββ++,代入上式得1n n n D D αβ--=1n n n D D αβ-=+ (2.1)由递推公式得1n n n D D αβ-=+=12()n n n D ααββ--++=α2D2-n +1n n αββ-+==n α+1n αβ-+ +1n nαββ-+=时=,当时,当--βαβα1)α(n αβαβ111≠⎪⎩⎪⎨⎧++++n n n方法2 把D n 按第1列拆成2个n 阶行列式D n =000100010001ααβαβαβαβαβ++++00010001000001βαβαβαβαβαβαβαβ+++上式右端第一个行列式等于αD 1-n ,而第二个行列式00010001000001βαβαβαβαβαβαβαβ+++12,,i i c ac i n--==00010000101ββββ=βn于是得递推公式1n n n D D αβ-=+,已与(2.1)式相同.方法3 在方法1中得递推公式D n =()αβ+D 1-n -αβD 2-n又因为当αβ+时 D 1=αβ+=βαβα--2221D αβαβαβ+=+=2()αβ+-αβ=22ααββ++=βαβα--33 D 3=βααββααββα+++110=3()αβ+-2αβ()αβ+ = ()αβ+22()αβ+=βαβα--44于是猜想11n n n D αβαβ++-=-,下面用数学归纳法证明.当n=1时,等式成立,假设当n ≤k 时成立. 当n=k+1是,由递推公式得D 1+k =()αβ+D k -αβD 1-k=()αβ+βαβα--++11k k —αββαβα--k k =βαβα--++22k k所以对于n ∈N +,等式都成立.第二部分这一部分的题是与矩阵、向量、特征值等后续内容有关的题,感觉困难的同学可以放到相关内容学习后再看.但应注意考研题中关于行列式内容的出题,往往与后续内容联系较多.例2.14 设A 为3×3矩阵, |A | =-2, 把A 按行分块为123A A A A ⎛⎫ ⎪= ⎪ ⎪⎝⎭, 其中(1,2,3)i A i =是A 的第i 行, 则行列式312122A A A A -=______.解312122A A A A -=312122A A A A -=3212A A A =12322||4A A A A -=-=例2.15 判断题(1) 若B A ,是可乘矩阵,则=AB B A . ( ) (2) 若B A ,均为n 阶方阵,则A B A B -=-. ( )解 (1) 错误,因为B A ,不一定是方阵,即不一定有对应的行列式.(2) 错误,例如取3003A ⎛⎫= ⎪⎝⎭,2002B ⎛⎫= ⎪⎝⎭,15A B A B -=≠-=.例2.16 证明:奇数阶反对称矩阵的行列式为零.证 ||||)1(||||||,A A A A A A A n T T -=-=-==-=(n 为奇数). 所以|A | = 0.例2.17 (数四,01,3分)设矩阵111111111111kk A k k ⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭,且秩()R A =3,则k = 解 由于111111111111k k A k k =124r r r ++=3333111111111k k k k k k k++++=1111111(3)111111k k k k +=11110100(3)00100001k k k k -+-- =3(3)(1)k k +-由()R A =3,知A =0,而1k =时,()R A =1,故必有3k =-.例2.18 若B A ,,C 均为3阶可逆方阵,1-=A ,2=B ,计算C B A C T 211)(2--.解 C B A C T 211)(2--=23112T C A BC -- =223112TC A BC-=22312A B=2例2.19 设3阶方阵B A ,满足方程 E B A B A =--2,试求矩阵B 以及行列式B ,其中101020201A ⎛⎫⎪= ⎪ ⎪-⎝⎭. 解 由E B A B A =--2,得E A B E A +=-)(2,即 ()()A E A E B A E +-=+由于 201030202A E ⎛⎫⎪+= ⎪ ⎪-⎝⎭,180A E +=≠ 001010200A E ⎛⎫ ⎪-= ⎪ ⎪-⎝⎭,20A E -=≠ 111()()()()B A E A E A E A E ---=-++=-1001001/2010010200100--⎛⎫⎛⎫⎪ ⎪== ⎪ ⎪⎪ ⎪-⎝⎭⎝⎭所以2/1||=B .例2.20 设A 为3阶方阵,A =2,求1*1()32A A --的值. 解 方法1 化为关于*A 的形式进行计算.利用公式111()A A λλ--=,*1A A A-=,1n A A -*=有1*1()32A A --=1*23A A --=**23A A A -=**3A A -=*2A -=3*(2)A -=23(2)A -=32-方法2 化为关于1A -的形式计算. 利用公式111()A A λλ--=,*1A A A -=,1A -=1A,有 1*1()32A A --=1123A A A ---=14A --=3(4)-1A=32- 例2.21 (数四,98,3分)设B A ,均为n 阶方阵,A =2,B =-3,求1*2-B A 的值.解 1*2-BA =1*2-BA n =n21-n AB1⋅=n 212-n 31-=3212--n 例 2.22 若21321,,,,ββααα都是4维列向量,且4阶行列式n =3221,,,αβαα,m =1321,,,βααα,计算4阶行列式32112,,,αααββ+的值.解 如果行列式的列向量组为n ααα,,,21 ,则此行列式可表示为n ααα,,,21 ,利用行列式的性质,有=+21123,,,ββααα3211,,,αααβ+3212,,,αααβ=1231,,,αααβ--3221,,,ααβα=1231,,,αααβ-+1223,,,ααβα=n m -例2.23 计算行列式OB AO B A ,,||||,其中12112(1)121121n n x n x n A x n n x n n -+⎛⎫⎪-+ ⎪⎪=⎪+- ⎪ ⎪+-⎝⎭, 100002000010000B n n ⎛⎫⎪ ⎪⎪=⎪- ⎪ ⎪⎝⎭ 解 ||A =12112(1)121121n n x n x nx n nx n n-+-++-+-12,,12100000ir ri nn n x x x x x x x-=-+-=--1,,1n j c c j n +=-=(1)12120000000n n n x x x x +-+这是逆对角的上三角行列式,所以(1)12(1)(1)()2n n n n n A x x --+=-+ 又!||n B =,故12)1(!)2)1(()1(2-+-++-=n n n n x n x n n O B A O .注 这里用了公式:若A 为m 阶方阵,B 为n 阶方阵,则O AB O=(1)mn -A B .例2.24 若A 为n 阶方阵,E 为单位矩阵,满足TAA E =,0A <,求 A E +. 解 方法1 由TAA E =有A E +=T A AA +=()T A E A +=()T A E A +=A ()TE A +=A E A +=A A E +即(1)A -A E +=0,而(1)A -0>,所以A E +=0.方法2 因为 ()T A E A +=T T AA A +=TE A +=A E +即 A E +A =A E +有(1)A -A E +=0,而(1)A -0>,所以A E +=0.方法 3 由TAA E =知矩阵A 为正交矩阵,即T AA =1,2A =1,又因为0A <,所以有1A =-,故A E +=A 1E A -+=T E A -+=E A -+即2A E +=0,A E +=0.例2.25 若A 为n 阶正定矩阵,E 为n 阶单位矩阵,证明A E +的行列式大于1. 证 方法1 因为A 为正定矩阵,因此所有的特征值大于零.设A 的n 个特征值为1,1,2,,i i n λ==,且0i λ>,由特征值的性质知,A E +的n 个特征值为1,1,2,,i i n λ+=,于是1(1)(1)1n λλ++>.方法2 因为正定矩阵是对称矩阵,因此A 可对角阵,且所有的特征值大于零,故存在可逆阵P 有11n P AP λλ-⎛⎫⎪=⎪⎪⎝⎭ (0,1,2,,i i n λ>=)即 11n A P P λλ-⎛⎫⎪= ⎪ ⎪⎝⎭111n A E P P PP λλ--⎛⎫ ⎪+=+⎪ ⎪⎝⎭=1111n P P λλ-+⎛⎫⎪ ⎪ ⎪+⎝⎭A E +=1111n PP λλ-++=1(1)(1)1n λλ++>例2.26 设11112222aa A nn n n a +⎛⎫⎪+⎪= ⎪⎪+⎝⎭,求A解 利用特征值法进行求解,即利用公式12n A λλλ=.11112222aa A nn n n a +⎛⎫ ⎪+⎪= ⎪⎪+⎝⎭=100000000a ⎛⎫⎪⎪ ⎪⎪⎝⎭+11112222a nn n n a ⎛⎫ ⎪+ ⎪ ⎪⎪+⎝⎭==11112222aE n n nn ⎛⎫ ⎪⎪+ ⎪⎪⎝⎭矩阵11112222n n n n⎛⎫⎪⎪⎪⎪⎝⎭的秩为1,由第十三讲的注意(7)知它特征值为11122nna a aλ=++=(1)2n n+,23nλλλ====0所以A特征值为(1),,,2n na a a++,故A=1(1)[]2nn na a-++.21。
第8节 拉普拉斯定理

它们的代数余子式为
A1 ( 1)1 31 2 0 1 0, 0 1 A3 ( 1)
1 3 2 3
A2 ( 1)1 3 2 4 1 1 2, 1 1 A4 ( 1)
1 31 2
1 2 5, 1 3
0 1 0, 0 1
A5 ( 1)411 3 0 2 0, 0 3
a11 a1n 0 an1 ann 0 1 b11 1 bn1
0 0 0 0 0 0 1 b1n 1 bnn
c11 c n1 b11 bn1
c1n cn1 b1n bnn
注释1 ① 一个行列式的k 级子式和余子式有很多。 ② k=1时A的行列式的每个元素都是一个1级子式, k=n时A本身是一个n级子式(没有余子式)。
二、Laplace定理
定理8.3 在矩阵A中取定k行,则这k行确定的所有k
阶子式和它们的代数余子式的乘积和等于 A .
注释2
① 理解引理和Laplace定理以及会用定理即可 ② k=1时Laplace定理就是行列式按行(列)展开法则 ③ Laplace定理不适合计算一般行列式(见下例)
2 2 2 D a11 a12 a1n 2 2 2 a21 a22 a2n
n
作业:P130 Ex 1 (2), (4), 2 (1)(3)
2 2 2 an1 an 2 ann
2 nD aij 0. i 1 j 1
n
n
因此,由上面两方面知,结论成立。
到第k 行, j , k 1,2,, n.
a11 a1n 0 an1 ann 0 1 b11 1 bn1 0 0 0 0 0 0 1 b1n 1 bnn c11 c n1 b11 bn1 c1n cn1 b1n bnn
行列式典型例题ppt课件 (2)

例3
计算n阶行列式
x1 a2 a3 an
a1 x2 a3 an
D n
a1
a2
x3
an
a1 a2 a3 xn
加边法:行列式的每行或每列除对角线上元素 外分别是某个数的倍数.
8
x1 a2 a3 an
a1 x2 a3 an
D n
a1
a2
x3
an
a1 a2 a3 xn (n)
1 0 0 0 0
1 1 1 1
1
2
2 2 2
n1
Vn n! 1
3
32
3
n1 .
1
n
n n 2
n1
6
上面等式右端行列式为n阶范德蒙行列式,由 范德蒙行列式知
V n n! (ai a j) 1 j i n n!(2 1)(3 1)(n 1) • (3 2)(4 2)(n 2)[n (n 1)] n!(n 1)!(n 2)! 2!1!.
xa a a a a a a
0 x a a a x a
Dn 0 a x a a a a
0 a a x a a x
即
D n (x a )D n 1 a (x a )n 1
(1)
14
利用类似的方法,可得
xa a
0x
Dn
0 a
a a a a
a a x a
x a a x
行列式,它必可利用行列式性质化为三角形行 列式而求得其值,所以
10
1
1
1 Dn
1
1
a1
a2
a3
an
a1 x1 a2 x2 a3 x3
an xn
1
2-3(拉普拉斯展开定理)
21
a2 b2 a2 b3 a2 bn 0 b1 a2 a2 b3 a2 bn Dn 0 b1 an an b3 an bn a b a b a b
n 2 n 3 n n
a1 b2 a1 b3 a1 bn
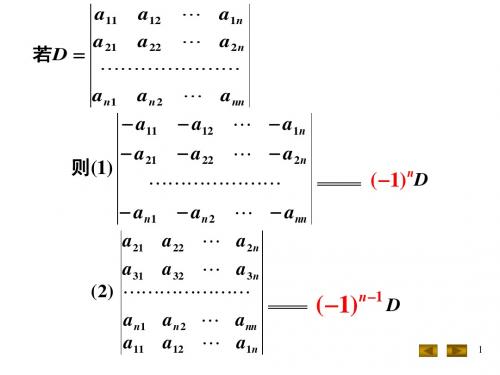
__ a 23 d , 则 2a21 2a22 2a23 6d a11 a12 a13 a 33
2
§ 2.3 拉普拉斯展开定理
1. k阶子式:
在 n 阶行列式D 中任取k 行 k 列( k n), 1
位于这 行k列交叉处的 个元素 ( 不改变它们 k k
2
的相对位置 ) 所构成的行列式S, 称为D的一个 k 阶子式.
BZ DY DC
W 0,
1
Z B 1 DC 1 ,
Y C 1 ,
B 1 B 1 DC 1 1 A . 1 C O
14
作业 P74 1.(1)
15
计算行列式常用方法
1.利用行列式性质化为三角行列式.
2.降阶法---按某一行(列)展开. 3.升阶法---加边法. 4.利用范德蒙德行列式. 5.递推法. 6.数学归纳法.(通常用在证明题中)
1
A1 1 , 1 At
1 At . 1 A1
A1 A t
1
12
小 结 1. 拉普拉斯定理 在行列式D中任取k(1≤k≤n-1)行 (列),由这k行(列)元所组成的一切k阶子式分 别与它们的代数余子式的乘积之和,等于行列式D. 2. 分块行列式
左 ( 1)
1 2 m ( n 1 ) ( n 2 ) ( n m )
行列式觧法

0 0 2 2 0
1 3 3 2 0
0 0 4 0 0
2⎤ 0⎥ ⎥ 5 ⎥. ⎥ 0⎥ 3⎥ ⎦
选择在第 4 行下之拉普拉斯展开式的行列式之值为:
det( A) = ∑ (−1) i + 4 ai 4 det( Ai 4 ) = ( −1) 3+ 4 a34 det( A34 )
i =1
5
0 1 2⎤ 0 3 0⎥ ⎥ 2 2 0⎥ ⎥ 0 0 3⎦ Use Sarrus’s rule Expand down column 2 ⎡ 1 1 2⎤ ⎥ = −4 ⋅ −2 ⋅ (9 + 27 − 30) = 48 = −4 ⋅ −2 ⋅ det ⎢ − 9 3 0 ⎢ ⎥ ⎢ ⎣ 5 0 3⎥ ⎦
a12 a 22 M ai 2 M an2
L L L L
a1 j a2 j M a ij M a nj
L L L L
a1 n ⎤ a2n ⎥ ⎥ ⎥ ⎥. a in ⎥ M ⎥ ⎥ a nn ⎥ ⎦
因此利用子行列式,则矩阵 A 之行列式之值 det(A),可写为
det(A) = a11 det(A11) − a12 det(A12 ) + a13 det(A13 )
定义: 沙乐氏规则( Sarrus’s rule) 求解 3x3 矩阵 A 之行列式值为,将矩阵 A 之第一及第二行元素复制至第 三行之右边,然后沿着六个对角化元素做相乘运算,其方式如下:
-
⎡ a11 ⎢a ⎢ 21 ⎢ ⎣ a31
a12 a22 a32
-
-
a13 ⎤ a11 a23 ⎥ ⎥ a21 a33 ⎥ ⎦ a31
例题 6: 使用拉普拉斯展开式,求解下列矩阵之行列式值?
行列式的展开(知识点,例题,习题,答案)

( 1)
1 3
6
2
5 5
8 0
2 5
40.
例2
证明范德蒙德(Vandermonde)行列式
1 x1 1 x2
2 x2
1 xn
2 xn
2 Dn x1 n 1 x1
n i j 1
( xi x j ).
(1)
n 1 n 1 x2 xn
a11 a22a33 a23a32 a12 a23a31 a21a33 a13 a21a32 a22a31
a11
a22 a23 a32 a33
a12
a21 a23 a31 a33
a13
a21 a23 a31 a33
在 n 阶行列式中,把元素 a ij 所在的第 i 行和第 j 列划去后,留下来的 n 1 阶行列式叫做元素 a ij 的余子式,记作 M ij .
n
1 ,当 i j, 其中 ij 0 ,当 i j .
3 5 3
例3 计算行列式 D 0 7 解 按第一行展开,得
D 3 1 0 7 2 5 0 0 7 2
1 0 7 2
3
0 1 7 7
27.
5 1
例4 计算行列式
3 7
1 2 0 2 5 2 3 3 1 0 5 0
ann
aij ij anj
0
0 ann
于是有 ai 1, j ai 1, j 1 ai 1,n aij Mij ,
a n , j 1
aij 0 0 a ij 故得 i j D 1 ai 1, j ai 1, j 1 ai 1,n 1i j aij M ij . anj an , j 1 ann
拉普拉斯行列式公式

关于行列式的拉普拉斯定理又称为子式的代数余子式定理,其内容是:设在n(n≥2)阶行列式D中任取定k(1≤k<n)行(列),且用这k行(列)作出的所有k阶子式为N1,N2,…, Nt,相应的代数余子式依次为A1,A2,…,At,则D=N1A1+N2A2+…+NtAt.其中t=C(n,k)=n!/[k!(n-k)!].拉普拉斯定理可以用来求行列式的值。
从定理的内容来看,第一步,也是最重要的一步就是要找到最合适的行列,其这些行或列的所有子式。
这些子式中,当然0越多越好了。
这样就可以大大的减少运算量。
然后分别取定那些非0的子列的代数余子式。
因为从定理的内容来看,等于0的子列和它的代数余子式的积,一定等于0,因此并不需要考虑等于0的子列的代数余子式。
最后将各非0子列分别乘以它们的代数余子式,并求这些积的和,就得到原行列式的值了。
下面举一个运用拉普拉斯定理计算行列式的实例。
计算五阶行列式(元素间用逗号分隔,行与行之间用分号分隔):D=|2,5,0,0,0;1,3,0,1,0;0,1,1,0,0;0,0,2,1,5;0,0,1,0,3|.我们可以取定第1行和第2行,其非0的子式有N1=|2,5;1,3|=1;N2=|2,0;1,1|=2以及N3=|5,0;3,1|=5。
对应的代数余子式分别为:A1=(-1)^(1+2+1+2)|1,0,0;2,1,5;1,0,3|=3;A2=(-1)^(1+2+1+4)|1,1,0;0,2,5;0,1,3|=1;A3=(-1)^(1+2+2+4)|0,1,0;0,2,5;0,1,3|=0.因此,D=N1A1+N2A2+N3A3=3+2+0=5.想要熟悉掌握运用拉普拉斯定理求行列式的值的方法,还必须多做相关的练习。
虽然我们还有其它更简单便的求行列式的值的方法,但是不能因为这种方法复杂,就不掌握。
因为在运用拉普拉斯定理求行列式的值的过程中,还可以熟练很多与行列式相关的知识。
自动控制原理--拉普拉斯变换的4个例题讲解

2
4 3 12
F(s)
Cm (s-p1 )m
C m- 1 (s-p1 )m-1
C1 s-p1
Cm1 s-pm1
Cn s-pn
(s-p1 )m F(s) Cm Cm-1(s-p1 ) Cm-2(s-p1 )2 C1(s-p1 )m1
Cm1(s-p1 )m Cn(s-p1 )m
s-pm1
C(s)
bm sm ansn
bm1sm1 ... b1s b0 an1sn1 ... a1s a0
R(s)
r(t ) (t )
C(s)
bm sm ansn
bm1sm1 ... b0 an1sn1 ... a0
C1
s 1
C2
s 2
Cn
s n
L1 : c(t ) L1[C(s)] C1e1t C2e2t Cnent
F(s)
Cm (s-p1 )m
C m- 1 (s-p1 )m-1
C1 s-p1
Cm1 s-pm1
Cn s-pn
C
m
lim (s
s p1
p1
)m .F(s)
C m- 1
1 lim
1! s p1
d ds
(s
p1 )m .F(s)
C m-j
1
d( j)
j!
lim
s p1
ds j
(s
p1 )m .F(s)
f(t) 1 et 1 e3t 22
例3
已知 F (s)
s2 5s 5 s2 4s 3
,求
f (t) ?
解.
F(s)
(s2 4s 3) (s 2) s2 4s 3
