高二数学 三垂线定理
三垂线定理及逆定理

三垂线定理及逆定理三垂线定理是一个重要的几何定理,它掌握着许多几何形状的性质。
在这里,我们将介绍这个定理及其逆定理,并讨论它们在几何学中的应用。
三垂线定理:对于任意三角形ABC,它的边AB,AC通过C点的垂线BD,CD相交于点D。
那么,D点同时也在BC边上的垂线上。
这个定理的意思是,如果我们在三角形的两侧都有一条垂直线,它们都通过三角形的另一个点,在尖角处相交,那么这个交点也必须在三角形底边上的垂直线上。
这个定理可以用来进行几何证明,以及解决几何运算问题。
为了更好地理解这个定理,让我们看一看下面这张图。
在这个三角形ABC中,我们可以看到点D是通过边AB和边AC的垂线相交而成的。
根据三垂线定理,D点也应该在BC边上的垂线上。
在图中,我们可以看到BC的垂线DE,它与AD相交于点F。
因此,根据三垂线定理,D点也应该在DE线上。
三垂线定理的逆定理是另一个重要的几何定理。
逆定理的意思是,如果我们能够证明一个点同时在三角形的底边上的垂线和其他两条垂直线上,我们就可以推断出这三条线相交于同一个点。
逆定理的表述如下:三垂线定理的逆定理:对于任意三角形ABC,如果BC的垂线DE与AD相交于点F,且DF和EF是三角形底边BC的垂线,则D、E、F三点共线。
这个逆定理与三垂线定理是完全相反的。
它表明,如果我们知道某个点在三条互相垂直的线上,则这些线都必须相交于同一个点。
这个定理可以帮助我们解决几何证明和运算问题。
总之,三垂线定理及其逆定理是几何学中重要的定理。
如果我们能够掌握它们的应用,就可以顺利解决许多三角形的几何问题。
无论是在学术上还是在生活中,这些定理都具有非常大的指导和应用价值。
高中立体几何 三垂线定理

三垂线定理说明( 三垂线定理说明(6)
• 平行于平面α的直线a,如果垂直于 平行于平面α的直线a
斜线OP在平面α内的射影OA,那么 斜线OP在平面α内的射影OA,那么 直线a也垂至于斜线OP,它在解某些 直线a也垂至于斜线OP,它在解某些 较复杂的问题时可能化难为易
P a
立体几何——三垂线定理 立体几何——三垂线定理
写在前面的话
• 高三同学在对立体几何的基本知识进行了系统
的复习之后,对于比较重要的定理、概念以及 在学习过程中感到难于掌握的问题进行综合性 的专题复习是很必要的。在专题复习中应通过 分类、总结,提高对所学内容的认识和理解。 今天我和大家共同探讨高中立体几何中的三垂 线问题。
D1 C1 B1 A1
∴ AC1 ⊥ 平面 A1 BD
D C A B
三垂线定理说明( 三垂线定理说明(8)
• 应用这两个定理时,首先要明确是针对
哪个平面应用定理,尤其是应注意此平 面非水平面放置的情况,然后再明确斜 线、垂线、斜线的射影及面内直线的位 置,有时需要添加其中某些线,这样可 以确保正确应用定理
建议对其掌握不好的同学,一方面扎 实基础,牢牢掌握三垂线定理的各种 情况,另一方面所作相关练习,重点 突破
• 祝大家学习成功,高考顺利!
连结CD,由三垂线定理可知,CD ⊥ AB, ∴ CD为 ABC中AB边上的高线且满足垂足在AB内, 同理可证 ABC中BC边、AC边上的高线的垂足也在BC、AC内 ∴ ABC的垂心在 ABC内,故 ABC为锐角三角形
P A D B C
一些例子
• 判定空间中两条直线相互垂直 证明:由余弦定理,
b2 + c2 − a 2 cos ∠CAB = 2bc ( x2 + z 2 ) + ( x2 + y2 ) − ( y 2 + z 2 ) = 2 x2 + z 2 x2 + y 2 = 2x 2 x +z
高二数学三垂线定理和逆定理
D1 (3) 在正方体AC1中,
C1
B1
求证:A1C⊥BC1 , A1C⊥B1D1
证明: ∵在正方体AC1中 A1B1⊥面BCC1B1且BC1 ⊥B1C
A1
D
A D1 B1 D A B B
C
∴B1C是A1C在面BCC1B1上的射影 由三垂线定理知 A1 A1C⊥BC1
C1
同理可证, A1C⊥B1D1
(3) 已知:在正方体AC1中,求证:A1C⊥B1D1,A1C⊥BC1
P A O B C D A
P
D1
C1
A1
C
B1 D
C
(1)
(2)
M B
A (3)
B
(1) PA⊥正方形ABCD所在平
P A B D
面,O为对角线BD的中点,
求证:PO⊥BD,PC⊥BD 证明: ∵ PA⊥平面ABCD ∴ AO是PO在平面ABCD上的射影 ∵ABCD为正方形 O为BD的中点 ∴ AO⊥BD 又 BD
O
a
α
A
三垂线定理
说明:
1、三垂线定理描述的是PO(斜线)、AO(射
影)、a(直线)之间的垂直关系。 2、a与PO可以相交,也可以异面。 3、三垂线定理的实质是平面的一条斜线和 平面内的一条直线垂直的判定定理。
例1 直接利用三垂线定理证明下列各题:
(1) 已知:PA⊥正方形ABCD所在平面,O为对角线BD的中点 求证:PO⊥BD,PC⊥BD (2) 已知:PA⊥平面PBC,PB=PC,M是BC的中点, 求证:BC⊥AM
?
?
?
A
C 结 论 成 立
三垂线定理
小
结
三垂线定理:在平面内的一条直线,如果
三垂线定理

1.直接利用三垂线定理证明下列各题:
(1) PA⊥正方形ABCD所在平面,O为对角线BD的中点 求证:PO⊥BD,PC⊥BD (2) 已知:PA⊥平面PBC,PB=PC,M是BC的中点, 求证:BC⊥AM
(3) 在正方体AC1中,求证:A1C⊥B1D1,A1C⊥BC1
P
P
D1
C1
A
D
O
A
B
C
(1)
∴ ∠AFC= ∠MDF , ∴ ∠DMF+∠AFC=∠DMF+∠MDF= 90°,
∴ DM ⊥AF,又ABC-DEF为直三棱柱,∴ CF⊥EF,又EF⊥DF,∴ EF⊥平面AF,由三 垂线定理知AE⊥DM
能力拓展:
2、过Rt ∆BPC的直角顶点P作线段PA ⊥平面BPC,求证: ∆ABC的垂心H是P点在平面ABC内的射影。
3. 如果一个角所在平面外一点到角的两边距离相等 那么这一点在平面上的射影在这个角的平分线上。
已知:∠BAC在平面内,点P,PE⊥AB,PF⊥AC,
PO⊥ ,垂足分别是E、F、O,PE=PF
求证:∠BAO=∠CAO
P
分析: 要证 ∠BAO=∠CAO
只须证OE=OF, OE⊥AB,OF⊥AC
?
?
?
A
三垂线定理

三垂线定理,平面内的一条直线,如果与穿过这个平面的一条斜线在这个平面上的射影垂直,那么它也和这条斜线垂直。
线面垂直证明
已知:如图,PO在上的射影OA垂直于a。
求证:OPa
证明:过P做PA垂直于
∵PA且a
aPA
又aOA
OAPA=A
a平面POA
aOP
用向量证明
1.已知:PO,PA分别是平面的垂线,斜线,OA是PA在内的射影,向量b包含于,且向量b垂直于OA,求证:向量b垂直于PA
证明:∵PO垂直于,PO垂直于b,又∵OA垂直b,向量PA=(向量PO+向量OA)
向量PA向量b=(向量PO+向量OA)向量b=(向量PO向量b)+(向量OA向量b )=0,PA 向量b。
2.已知三个平面OAB,OBC,OAC相交于一点O,AOB=BOC=COA=60度,求交线OA与平面OBC所成的角。
解:∵向量OA=(向量OB+向量AB),O是内心,又∵AB=BC=CA,OA与平面OBC所成的角是30。
三余弦定理
三余弦定理:平面内的一条直线与该平面的一条斜线所成角的余弦值,等于斜线与平面所成角的余弦值乘以斜线在平面上的射影与该直线所成角的余弦值。
例如:OP是平面OAB的一条斜线,且OP在面上的射影是OC。
若POC=(斜线与平面
所成角),AB与OC所成角为(射影与直线所成角),OP与AB所成角为(直线与斜线所成角),则cos=coscos
显然,三垂线定理就是当=90的情况。
直线垂直射影有cos=0,因此cos=0,即直线与斜线也垂直。
三垂线定理证明过程

三垂线定理证明过程三垂线定理是解决三角形垂心位置的一个重要定理。
在本文中,我们将通过证明过程来探讨三垂线定理的原理和应用。
让我们来介绍一下三垂线定理的概念。
在任意三角形ABC中,我们可以通过顶点A、B、C分别作边BC、AC、AB的垂线,分别得到D、E、F三个垂足点。
三垂线定理指出,这三条垂线所交于一点H,该点被称为三角形ABC的垂心。
为了证明三垂线定理,我们将分两步进行推理。
首先,我们需要证明垂心H在BC上。
假设垂线AD与BC的交点是H,我们将证明H在BC上。
根据垂直线的性质,可知∠ABH=90°。
同理,由于垂线CE与AB垂直,我们可以得出∠CBH=90°。
因此,∠ABH和∠CBH都是直角,那么∠ABH+∠CBH=180°。
由此可知,点H在直线BC上。
接下来,我们继续证明垂心H在AC和AB上。
我们已经得出点H在BC上,现在我们需要证明H也在AC上。
假设垂线BE和AC的交点是H',我们将证明H'和H是同一个点。
根据垂直线的性质,可知∠BAH'=90°。
同理,由于垂线CF与AB垂直,我们可以得出∠CAH'=90°。
因此,∠BAH'和∠CAH'都是直角,那么∠BAH'+∠CAH'=180°。
由此可知,点H'在直线AC上。
同样地,我们可以通过证明垂线CF与AB的交点是H来得出结论,点H也在直线AB上。
我们已经证明了三垂线定理。
在任意三角形ABC中,通过连接顶点A、B、C和分别作边BC、AC、AB的垂线,得到的三个垂足点D、E、F所确定的垂心H是在三角形的三条边上的。
三垂线定理在几何学中有着重要的应用。
通过垂心的位置,我们可以推导出很多与三角形相关的性质。
例如,垂心到三角形三边的距离相等,垂心到三个顶点的连线会互相垂直等等。
这些性质可以帮助我们解决许多与三角形相关的问题,如求三角形的面积、判断三角形的类型等。
高中数学 三垂线定理以及应用

O
B
C
解题回顾
关于三垂线定理的应用,关键是找出平面(基准 面)以及垂线。射影就可以由垂足、斜足来确定。 从三垂线定理的证明中得到证明a⊥b的一个程 序:一垂、二射、三证。即 第一、找平面(基准面)及平面垂线。
第二、找射影线,这时a、b便成平面上的一条 直线与一条斜线。
第三、证明射影线与直线a垂直,从而得出a与b 垂直。
三垂线定理
P O A
a
α
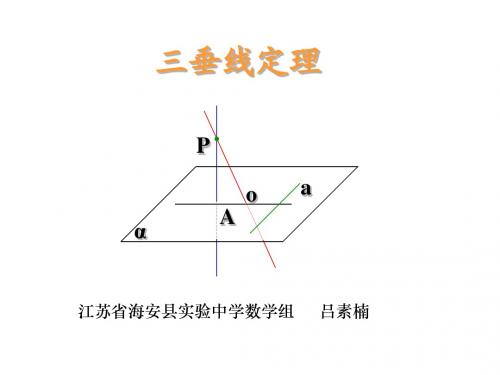
复习:平面的斜线、垂线、射影
PA是平面α的斜线,
P
O
A为斜足; PO是平面α 的垂线, O为垂足; AO
A
a
是PA在平面α内的射 影. 如果a α, a⊥AO, 思考a与PA的位置关 系如何?
α
a⊥PA
为什么呢?
三垂线定理:在平面内的一条直线,如果和这个平面的 一条斜线的射影垂直,那么它也和这条斜线垂直。
A
a
O
A
a
直线和平 面垂直
平面内的直线 和平面一条斜 线的射影垂直
平面内的直线 和平面的一条 斜线垂直
三垂线定理:在平面内的一条直线,如果和这个平面的 一条斜线的射影垂直,那么它也和这条斜线垂直。
对三垂线定理的说明: 1.三垂线定理描述的是斜线(PA)、射影(AO)、 直线(a)之间的垂直关系。 P 2.三垂线定理的实质 a 是平面的一条斜线和平面 内的一条直线垂直的判定 O A α 定理。其中直线a与PA可以 相交,也可以异面。 3. 三垂线定理中垂线、斜线、射影、直线都是 相对于一个平面而言,即四线一面,所以把该平面 称为基准平面。 但基准 平面不一定是水平的。
A A1 D1 B1 C1
D
B
C
三垂线定理
三垂线定理

三垂线定理定义:在平面内的一条直线,如果和这个平面的一条斜线在这个平面内的射影垂直,那么它也和这条斜线垂直。
三垂线定理的逆定理:在平面内的一条直线,如果和这个平面的一条斜线垂直,那么它也和这条斜线在平面的射影垂直。
具体如下:1,三垂线定理描述的是PO(斜线),AO(射影),a(直线)之间的垂直关系.2,a与PO 可以相交,也可以异面.3,三垂线定理的实质是平面的一条斜线和平面内的一条直线垂直的判定定理.关于三垂线定的应用,关键是找出平面(基准面)的垂线.至于射影则是由垂足,斜足来确定的,因而是第二位的.从三垂线定理的证明得到证明a⊥b的一个程序:一垂,二射,三证.即第一,找平面(基准面)及平面垂线第二,找射影线,这时a,b便成平面上的一条直线与一条斜线.第三,证明射影线与直线a垂直,从而得出a与b垂直。
扩展资料:三垂线定理与逆定理的核心就是两两垂直。
其中射影就是斜线的一端到另一端到平面的垂线段的连线。
三垂线定理:影垂不怕线斜(形影不离),即垂直射影垂斜线。
三垂线定理逆定理:斜垂影随其身(影随其身),即:垂直斜线垂射影。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
证明: PO , a ,
PO a.
又 PA a, PA PO P,
P
O
A
a
a 平面PAO. a AO
α
例题分析:
例1、已知点O是△ABC的BC边的高上的任 意一点,且PO⊥平面ABC,求证PA ⊥BC。
证明: ∵PO⊥平面ABC
P
A ∴ OA是PA在平面 O ABC内的射影, B 又∵BC⊥OA, ∴BC ⊥PA(三垂线定理)
AB OE, AC OF PE PF , PO PO,
OE OF .
Rt PEO Rt PFO.
又AO AO, Rt EAO RtFAO.
(三垂线定理的逆定理)
P
B E
BAO CAO.
A F
O C
课堂练习
如图,PD⊥平面ABC,AC=BC,D为AB 1、
OA是PA在内的射影,a ,且a OA.
证明: PO , a ,
PO a.
又 a OA, PO OA O,
P O A
求证:a PA.
a 平面POA. a PA.
a
α
三垂线定理
对三垂线定理的说明: 1、三垂线定理描述的是 PA(斜线)、OA(射影)、a(直线) α 之间的垂直关系,它们都是相对 同一个平面而言的。
三垂线定理
复习回顾
下图中哪些直线是平面的斜线、直线的射影?
已知直线PO是平面α的垂线, O为垂足;
直线PA是平面α的斜线, A 为斜足; 直线OA是PA在平 面α内的射影.
P
A
a
α
O
如果a , a OA,
那么a与PA 的位置关系 如何呢?
新课讲解
三垂线定理:在平面内的一条直线,如果和这个平面的 一条斜线的射影垂直,那么它也和这条斜线垂直。 已知: PO、PA分别是平面的垂线、斜线,
又 BC AB,AB为PB在平面 ABCD的射影 BC PB PBC是直角三角形 B 同理, PDC也是直角三角形.
A
D
C
课时小结
三垂线定理
三垂线定理
a PO a PA a OA
a , PO a OA a PA
C
三垂线定理
已知:∠BAC在平面α内,点P ,PE⊥AB, PF⊥AC,PO ⊥α,垂足分别是E、F、O,PE=PF。
例2 求证: 如果一个角所在平面外一点到角的 两边的距离相等,那么这点在平面内的射影在 这个角的平分线上.
求证:∠BAO = ∠CAO. 证明: PO , PE AB, PF AC,
判定定理
三垂线定理的逆定理 a PO a OA a PA
垂射必垂斜 垂斜必垂射
性质定理
线线垂直
线面垂直
三垂线定理 三垂线定理 的逆定理
线线垂直
线线垂直
线线垂直
的中点,求证AB⊥PC。
P
证明: ∵AC=BC,D是BC的中点,
∴AB⊥CD, ∵PD⊥平面ABC,
A D C
B
∴CD是PC在平面ABC内的射影, ∴ AB⊥PC(三垂线定理)
2.如图,ABCD是矩形,PA⊥平面AC,连结PB、PC、P 指出图中有哪些三角形是直角三角形,并说明理由.
解: PA 平面AC, PA AB,PA AD. P PAB, PAD都是直角三角形.
P O (1) a A
2、a与PA可以异面,也可以相交。
P a O (2)
P
a A (3) O A
α
α
(4)
三垂线定理
三垂线定理的逆定理:在平面内的一条直线如果和 这个平面的一条斜线垂直,那么它也和这条斜线的 射影垂直. 已知: PO、PA分别是平面的垂线、斜线,
OA是PA在内的射影,a ,且a PA. 求证 : a PA.
