江西2015年高考文科数学二轮专项训练之函数2Word版含答案
2015年江西省高考 .doc

2015年江西省高考 文科数学 模拟样卷注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.答卷前,考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上.2. 回答第Ⅰ卷时.选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动.用橡皮擦干净后,再选涂其它答案标号.写在本试卷上无效.3.回答第Ⅱ卷时.将答案写在答题卡上.写在本试卷上无效.4.考试结束后.将本试卷和答且卡一并交回.第I 卷一.选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{|05}A x x =<<,2{|230}B x x x =-->,则AB =R ðA. (0,3)B. (3,5)C. (1,0)-D.(0,3]2.复数1(i)(0)z a a a a=+∈≠R 且对应的点在复平面内位于A .第一、二象限B .第一、四象限C .第二、四象限D .第二、三象限 3.命题“2,x x x ∀∈≠R ”的否定是A .2,x x x ∀∉≠R B .2,x x x ∀∈=R C . 2,x x x ∃∉≠R D .2,x x x ∃∈=R4.已知函数2()f x x -=,3()tan g x x x =+,那么A. ()()f x g x ⋅是奇函数B. ()()f x g x ⋅是偶函数C. ()()f x g x +是奇函数D. ()()f x g x +是偶函数 5.已知等比数列{}n a 中,2109a a =,则57a a +A. 有最小值6B. 有最大值6C. 有最小值6或最大值-6D.有最大值-6 6.下列程序框图中,则输出的A 的值是A .128B .129C .131D .1347.已知数列{}n a 中,122,8a a ==,数列1{2}n n a a +-是公比为2的等比数列,则下列判断正确的是A. {}n a 是等差数列B. {}n a 是等比数列C. {}2n n a 是等差数列 D. {}2nna 是等比数列 8.已知抛物线:C 24y x =,那么过抛物线C 的焦点,长度为整数且不超过2015的弦的条数是A . 4024B . 4023C .2012D .2015 9.已知函数()sin()f x x ωϕ=+(0,2πωϕ><)的部分图像如图所示,则()y f x = 的图象可由cos 2y x = 的图象A .向右平移3π个长度单位B .向左平移3π个长度单位C .向右平移6π个长度单位D .向左平移6π个长度单位10.已知函数1()ln 2xf x x =-(),若实数x 0满足01188()log sinlog cos88f x ππ>+,则0x 的取值范围是A .(,1)-∞B .(0,1)C .(1,)+∞D .1(,)2+∞11.已知函数232,31,()1ln ,13x x x f x x x ⎧-+--≤≤⎪=⎨<≤⎪⎩,若()|()|g x ax f x =-的图像与x 轴有3个不同的交点,则实数a 的取值范围是A. ln 31[,)3eB. 1(0,)2eC. 1(0,)eD. ln 31[,)32e12.某几何体三视图如图所示,则该几何体的体积为 A .23 B .1 C .43 D .32第Ⅱ卷本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须作答,第22-2正视图侧视图俯视图ABCD A 1B 1C 1第24题为选考题,考生根据要求作答. 二.填空题:本大题共4小题,每小题5分.13. 已知回归直线斜率的估计值为2,样本点的中心为点(4,5),则回归直线的方程为 . 14.已知=a,)k =b ,且a 与b 的夹角为3π,则k = . 15.若变量y x ,满足约束条件1,,3215x y x x y ≥⎧⎪≥⎨⎪+≤⎩,则42x yw =⋅的最大值是 .16.对椭圆有结论一:椭圆2222:1(0)x y C a b a b +=>>的右焦点为(,0)F c ,过点2(,0)a P c的直线l交椭圆于,M N 两点,点M 关于x 轴的对称点为'M ,则直线'M N 过点F .类比该结论,对双曲线有结论二,根据结论二知道:双曲线22':13x C y -=的右焦点为F ,过点3(,0)2P 的直线与双曲线'C 右支有两交点,M N ,若点N的坐标是,则在直线NF 与双曲线的另一个交点坐标是__________.三、解答题:解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)已知函数2()sin cos sin f x a x x b x =+,x R ∈,且()112f π=,()16f π=. (Ⅰ)求函数()f x 的单调递增区间; (Ⅱ)若3()25f α=,(,)3παπ∈-,求sin α的值. 18.某校男女篮球队各有10名队员,现将这20名队员的身高绘制成如下茎叶图(单位:cm ).男队员身高在180cm 以上定义为“高个子”,女队员身高在170cm 以上定义为“高个子”,其他队员定义为“非高个子”.用分层抽样的方法,从“高个子”和“非高个子”中共抽取5名队员.(Ⅰ)从这5名队员中随机选出2名队员,求这2名队员中有“高个子”的概率;(Ⅱ)求这5名队员中,恰好男女“高个子”各1名队员的概率.19.(本小题满分12分)如图,已知在直三棱柱111ABC A B C -中, 12AB AA ==,3ACB π∠=,点D 是线段BC 的中点.(Ⅰ)求证:1A C ∥平面1AB D ;(Ⅱ)当三棱柱111ABC A B C -的体积最大时,求三棱锥11A AB D -的体积.20.(本小题满分12分)FED CBA已知椭圆2222:1(0)x y C a b a b+=>>的左右焦点分别是12(1,0),(1,0)F F -,直线l 的方程是4x =,点P 是椭圆C 上动点(不在x 轴上),过点2F 作直线2PF 的垂线交直线l 于点Q ,当1PF 垂直x 轴时,点Q 的坐标是(4,4). (Ⅰ)求椭圆C 的方程;(Ⅱ)判断点P 运动时,直线PQ 与椭圆C 的公共点个数,并证明你的结论. 21.(本小题满分12分) 已知函数ln ()a x bf x x+=(其中0a <),函数()f x 在点(1,(1))f 处的切线过点(3,0). (Ⅰ)求函数()f x 的单调区间;(Ⅱ)若函数()f x 与函数2()2g x a x x=+--的图像在(0,2]有且只有一个交点,求实数a 的取值范围.请考生在第22,23,24题中任选一题做答,如果多做,则按所做的第一题计分, 做答时请写清题号.22.(本小题满分10分)选修41-:几何证明选讲如图,圆内接四边形ABCD 的边BC 与AD 的延长线交于点E ,点F 在BA 的延长线上. (Ⅰ)若21,31==EA ED EB EC ,求ABDC的值; (Ⅱ)若CD EF //,证明:FB FA EF ⋅=2.23.(本小题满分10分)选修44-;坐标系与参数方程在直角坐标系xoy 中,以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,已知某圆的极坐标方程为:24cos 20ρρθ-+=. (Ⅰ)将极坐标方程化为普通方程;(Ⅱ)若点P (x ,y )在该圆上,求x +y 的最大值和最小值. 24.(本小题满分10分)选修45-:不等式选讲 已知函数()||f x x =,()|4|g x x m =--+ (Ⅰ)解关于x 的不等式[()]20g f x m +->;(Ⅱ)若函数()f x 的图像在函数()g x 图像的上方,求实数m 的取值范围.。
江西2015届高中数学二轮复习高效专项检测题54Word版含答案

指数函数、对数函数、幂函数一、选择题1. (2013·大纲版全国卷高考文科·T6)与(2013·大纲版全国卷高考理科·T5)相同函数)0)(11(log )(2>+=x xx f 的反函数()1=f x -( )A.()1021x x >- B.()1021xx ≠- C.()21xx R -∈ D.()210x x ->【解题指南】首先令)11(log 2xy +=求出x ,然后将y x ,互换,利用反函数的定义域为原函数的值域求解.【解析】选A.由)11(log 2xy +=,0>x ,得函数的值域为0>y ,又x y 112+=,解得121-=y x ,所以()1=f x -121-x )0(>x 2.(2013·北京高考理科·T5)函数f(x)的图象向右平移1个单位长度,所得图象与曲线y=e x 关于y 轴对称,则f(x)= ( ) A.e x+1 B.e x-1 C.e -x+1 D.e -x-1 【解题指南】把上述变换过程逆过来,求出y=e x 关于y 轴对称的函数,再向左平移1个单位长度得到f(x).【解析】选D.与y=e x 关于y 轴对称的函数应该是y=e -x ,于是f(x)可由y=e -x 向左平移1个单位长度得到,所以f(x)=e -(x+1)=e -x-1. 3.(2013·广东高考文科·T2)函数lg(1)()1x f x x +=-的定义域是( )A .(1,)-+∞B .[1,)-+∞C .(1,1)(1,)-+∞D .[1,1)(1,)-+∞ 【解题指南】函数的定义域有两方面的要求:分母不为零,真数大于零,据此列不等式即可获解.【解析】选C. 解不等式10,10x x +>-≠可得1,1x x >-≠是定义域满足的条件.4.(2013·山东高考文科·T5)函数()f x =的定义域为( )A.(-3,0]B.(-3,1]C.(,3)(3,0]-∞--D.(,3)(3,1]-∞--【解题指南】定义域的求法:偶次根式为非负数,分母不为0.【解析】选A. ⎩⎨⎧>+≥-03021x x ,解得03≤<-x .5.(2013·陕西高考文科·T3)设a, b, c 均为不等于1的正实数, 则下列等式中恒成立的是 ( )A . ·log log log a c c b a b = B. b a b c c a log log log =⋅ C. c b bc a a a log log )(log ⋅=D. ()log g og o l l a a a b b c c +=+【解题指南】a, b,c ≠1,掌握对数两个公式:abb y x xyc c a a a a log log log ,log log log =+= 并灵活转换即可得解.【解析】选B.对选项A: bab a b bc c a c c a log log log log log log =⇒=⋅,显然与第二个公式不符,所以为假。
江西2015届高考数学二轮专题复习之专项检测19Word版含答案

19 三角函数化简与求值策略1.若sin(π+α)=-12,则cos α=________. 答案 ±32解析 由sin(π+α)=-12,得-sin α=-12, 即sin α=12, ∴cos α=±1-sin 2α=±32. 2.设tan α,tan β是方程x 2-3x +2=0的两根,则tan(α+β)的值为________.答案 -3解析 tan α+tan β=3,tan α×tan β=2,所以tan(α+β)=tan α+tan β1-tan α×tan β=-3. 3.sin(65°-x )cos(x -20°)+cos(65°-x )·cos(110°-x )的值为________.答案 22解析 sin(65°-x )cos(x -20°)+cos(65°-x )cos(110°-x )=sin(65°-x )cos(x -20°)+cos(65°-x )[-cos(70°+x )]=sin(65°-x )cos(x -20°)+cos(65°-x )sin(x -20°)=sin(65°-x +x -20°)=sin 45°=22.4. sin 47°-sin 17°cos 30°cos 17°的值是________. 答案 12解析 原式=sin (30°+17°)-sin 17°cos 30°cos 17°=sin 30°cos 17°+cos 30°sin 17°-sin 17°cos 30°cos 17°=sin 30°cos 17°cos 17°=sin 30°=12. 5.若0<α<π2,-π2<β<0,cos ⎝⎛⎭⎫π4+α=13,cos ⎝⎛⎭⎫π4-β2=33,则cos ⎝⎛⎭⎫α+β2=________. 答案 539解析 ∵cos ⎝⎛⎭⎫π4+α=13,0<α<π2, ∴sin ⎝⎛⎭⎫π4+α=223.又∵cos ⎝⎛⎭⎫π4-β2=33,-π2<β<0, ∴sin ⎝⎛⎭⎫π4-β2=63, ∴cos ⎝⎛⎭⎫α+β2=cos ⎣⎡⎦⎤⎝⎛⎭⎫π4+α-⎝⎛⎭⎫π4-β2 =cos ⎝⎛⎭⎫π4+αcos ⎝⎛⎭⎫π4-β2+sin ⎝⎛⎭⎫π4+αsin ⎝⎛⎭⎫π4-β2 =13×33+223×63=539. 6.(2014·课标全国Ⅰ改编)设α∈(0,π2),β∈(0,π2),且tan α=1+sin βcos β,则2α-β=________. 答案 π2解析 由tan α=1+sin βcos β得sin αcos α=1+sin βcos β, 即sin αcos β=cos α+cos αsin β,∴sin(α-β)=cos α=sin(π2-α). ∵α∈(0,π2),β∈(0,π2), ∴α-β∈(-π2,π2),π2-α∈(0,π2), ∴由sin(α-β)=sin(π2-α),得α-β=π2-α, ∴2α-β=π2. 7.已知tan α=2,则sin 2α+cos 2(π-α)1+cos 2α的值为________. 答案 52解析 sin 2α+cos 2(π-α)1+cos 2α=2sin αcos α+cos 2α2cos 2α =2sin α+cos α2cos α=tan α+12=52. 8.cos 2α1+sin 2α·1+tan α1-tan α的值为________. 答案 1 解析 原式=cos 2α-sin 2α(sin α+cos α)2·1+sin αcos α1-sin αcos α=cos α-sin αsin α+cos α·sin α+cos αcos α-sin α=1. 9.已知sin θ+cos θ=713,θ∈(0,π),则tan θ=________.答案 -125解析 方法一 因为sin θ+cos θ=713,θ∈(0,π), 所以(sin θ+cos θ)2=1+2sin θcos θ=49169, 所以sin θcos θ=-60169. 由根与系数的关系,知sin θ,cos θ是方程x 2-713x -60169=0的两根, 所以x 1=1213,x 2=-513. 又sin θcos θ=-60169<0, 所以sin θ>0,cos θ<0.所以sin θ=1213,cos θ=-513. 所以tan θ=sin θcos θ=-125. 方法二 同法一,得sin θcos θ=-60169, 所以sin θcos θsin 2θ+cos 2θ=-60169. 齐次化切,得tan θtan 2θ+1=-60169, 即60tan 2θ+169tan θ+60=0,解得tan θ=-125或tan θ=-512. 又θ∈(0,π),sin θ+cos θ=713>0, sin θcos θ=-60169<0. 所以θ∈(π2,3π4),所以tan θ=-125. 10.已知sin θ+cos θ=43(0<θ<π4),则sin θ-cos θ的值为________. 答案 -23解析 ∵sin θ+cos θ=43, ∴(sin θ+cos θ)2=1+2cos θsin θ=169, ∴2cos θcos θ=79, ∴(sin θ-cos θ)2=1-79=29, 又θ∈(0,π4),∴sin θ<cos θ,∴sin θ-cos θ=-23. 11.已知cos α=17,cos(α-β)=1314,且0<β<α<π2. (1)求tan 2α的值;(2)求β.解 (1)由cos α=17,0<α<π2,得 sin α=1-cos 2α= 1-(17)2=437. ∴tan α=sin αcos α=437×71=43, 于是tan 2α=2tan α1-tan 2α=2×431-(43)2=-8347. (2)由0<β<α<π2,得0<α-β<π2, 又∵cos(α-β)=1314, ∴sin(α-β)=1-cos 2(α-β)= 1-(1314)2=3314. 由β=α-(α-β), 得cos β=cos [α-(α-β)]=cos αcos(α-β)+sin αsin(α-β)=17×1314+437×3314=12, ∴β=π3. 12.已知向量a =(3sin α,cos α),b =(2sin α,5sin α-4cos α),α∈(3π2,2π),且a ⊥b . (1)求tan α的值;(2)求cos(α2+π3)的值. 解 (1)∵a ⊥b ,∴a ·b =0.而a =(3sin α,cos α),b =(2sin α,5sin α-4cos α),∴a ·b =6sin 2α+5sin αcos α-4cos 2α=0,∵cos α≠0,∴6tan 2α+5tan α-4=0. 解得tan α=-43或tan α=12. ∵α∈(3π2,2π),∴tan α<0, ∴tan α=-43. (2)∵α∈(3π2,2π),∴α2∈(3π4,π). 由tan α=-43, 求得tan α2=-12或tan α2=2(舍去). ∴sin α2=55,cos α2=-255,∴cos(α2+π3)=cos α2cos π3-sin α2sin π3 =-255×12-55×32=-25+1510.。
江西2015届高考数学二轮专题复习之专项检测39Word版含答案

39 二项式定理的两类重点题型——求和与求展开项1.(2014·四川改编)在x (1+x )6的展开式中,含x 3项的系数为________.答案 15解析 因为(1+x )6的展开式的第r +1项为T r +1=C r 6x r ,x (1+x )6的展开式中含x 3的项为C 26x3=15x 3,所以系数为15.2.(2014·浙江改编)在(1+x )6(1+y )4的展开式中,记x m y n 项的系数为f (m ,n ),则f (3,0)+f (2,1)+f (1,2)+f (0,3)=________.答案 120解析 因为f (m ,n )=C m 6C n 4,所以f (3,0)+f (2,1)+f (1,2)+f (0,3)=C 36C 04+C 26C 14+C 16C 24+C 06C 34=120.3.设⎝⎛⎭⎫5x -1x n 的展开式的各项系数之和为M ,二项式系数之和为N ,若M -N =240,则展开式中x 的系数为________.答案 150解析 M =⎝⎛⎭⎫5×1-11n =4n ,N =2n ⇒4n -2n =240⇒2n =16⇒n =4,T r +1=(-1)r C r 4·54-r ·342rx - ⇒r =2,则(-1)2C 24·52=150. 4.设a ∈Z ,且0≤a <13,若512 012+a 能被13整除,则a 的值为________.答案 12解析 化51为52-1,用二项式定理展开.512 012+a =(52-1)2 012+a =C 02 012522 012-C 12 012522 011+…+C 2 0112 012×52×(-1)2 011+C 2 0122 012×(-1)2 012+a .因为52能被13整除,所以只需C 2 0122 012×(-1)2 012+a 能被13整除, 即a +1能被13整除,因为0≤a <13,所以a =12.5.若(1+x )(2-x )2 013=a 0+a 1x +a 2x 2+…+a 2 013x 2 013+a 2 014x 2 014,则a 2+a 4+…+a 2 012+a 2 014=________.答案 1-22 013解析 采用赋值法,令x =1,得a 0+a 1+a 2+…+a 2 013+a 2 014=2,令x =-1,得a 0-a 1+a 2-…-a 2 013+a 2 014=0,把两式相加,得2(a 0+a 2+…+a 2 014)=2,所以a 0+a 2+…+a 2 014=1,又令x =0,得a 0=22 013,所以a 2+a 4+…+a 2 012+a 2 014=1-22 013.6.设f (x )是⎝⎛⎭⎫x 2+12x 6展开式的中间项,若f (x )≤mx 在区间⎣⎡⎦⎤22,2上恒成立,则实数m 的取值范围是______.答案 [5,+∞) 解析 由于T r +1=C r 6⎝⎛⎭⎫12r x 12-3r ,故展开式中间的一项为T 3+1=C 36·⎝⎛⎭⎫123·x 3=52x 3,f (x )≤mx ⇔52x 3≤mx 在⎣⎡⎦⎤22,2上恒成立,即m ≥52x 2,又52x 2≤5,故实数m 的取值范围是m ≥5. 7.(2014·大纲全国)⎝⎛⎭⎫x y-y x 8的展开式中x 2y 2的系数为________.(用数字作答) 答案 70解析 由T r +1=C r 8(x y )8-r (-y x)r =(-1)r C r 8x 8-3r 2y 32r -4知, 要求x 2y 2的系数,则⎩⎨⎧ 8-3r 2=2,32r -4=2,解得r =4,∴x 2y 2的系数为(-1)4C 48=70.8.(2014·山东)若(ax 2+b x)6的展开式中x 3项的系数为20,则a 2+b 2的最小值为________. 答案 2解析 (ax 2+b x )6的展开式的通项为T r +1=C r 6(ax 2)6-r ·(b x)r =C r 6a 6-r b r x 12-3r , 令12-3r =3,得r =3,由C 36a 6-3b 3=20得ab =1, 所以a 2+b 2≥2ab =2,故a 2+b 2的最小值为2.9.已知(x +a x)6(a >0)的展开式中常数项为240,则(x +a )(x -2a )2的展开式中x 2项的系数为________.答案 -6解析 (x +a x )6的二项展开式的通项T r +1=C r 6x 6-r (a x)r =C r 6a r x 6-3r 2,令6-3r 2=0,得r =4,则其常数项为C 46a 4=15a 4=240,则a 4=16,由a >0,故a =2.又(x +a )(x -2a )2的展开式中,x2项为-3ax 2,故x 2项的系数为(-3)×2=-6.10.已知f (x )=(1+x )m +(1+2x )n (m ,n ∈N *)的展开式中x 的系数为11,当x 2的系数取得最小值时,f (x )展开式中x 的奇次幂项的系数之和为________.答案 30解析 由已知得C 1m +2C 1n =11,∴m +2n =11,x 2的系数为C 2m +22C 2n =m (m -1)2+2n (n -1)=m 2-m 2+(11-m )⎝⎛⎭⎫11-m 2-1=⎝⎛⎭⎫m -2142+35116. ∵m ∈N *,∴m =5时,x 2的系数取得最小值22,此时n =3.∴f (x )=(1+x )5+(1+2x )3. 设这时f (x )的展开式为f (x )=a 0+a 1x +a 2x 2+…+a 5x 5,令x =1,a 0+a 1+a 2+a 3+a 4+a 5=25+33,令x =-1,a 0-a 1+a 2-a 3+a 4-a 5=-1,两式相减得2(a 1+a 3+a 5)=60,故展开式中x 的奇次幂项的系数之和为30.11.已知(1+2x )n 的展开式中,某一项的系数是它前一项系数的2倍,而又等于它后一项系数的56. (1)求展开后所有项的系数之和及所有项的二项式系数之和;(2)求展开式中的有理项.解 根据题意,设该项为第r +1项,则有⎩⎪⎨⎪⎧ C r n 2r =2C r -1n 2r -1,C r n 2r =56C r +1n 2r +1,即⎩⎪⎨⎪⎧C r n =C r -1n ,C r n =53C r +1n , 亦即⎩⎪⎨⎪⎧ n =2r -1,n !r !(n -r )!=53×n !(r +1)!(n -r -1)!, 解得⎩⎪⎨⎪⎧r =4,n =7. (1)令x =1得展开式中所有项的系数之和为(1+2)7=37=2 187.所有项的二项式系数之和为27=128.(2)展开式的通项为T r +1=C r 72r x r 2,r ≤7且r ∈N . 于是当r =0,2,4,6时,对应项为有理项,即有理项为T 1=C 0720x 0=1,T 3=C 2722x =84x ,T 5=C 4724x 2=560x 2,T 7=C 6726x 3=448x 3.12.已知⎝⎛⎭⎫12+2x n . (1)若展开式中第5项、第6项与第7项的二项式系数成等差数列,求展开式中二项式系数最大的项的系数;(2)若展开式前三项的二项式系数和等于79,求展开式中系数最大的项.解 (1)因为C 4n +C 6n =2C 5n ,所以n 2-21n +98=0,解得n =7或n =14.当n =7时,展开式中二项式系数最大的项是T 4和T 5.所以T 4的系数为C 37⎝⎛⎭⎫124×23=352, T 5的系数为C 47⎝⎛⎭⎫123×24=70. 当n =14时,展开式中二项式系数最大的项是T 8.所以T 8的系数为C 714⎝⎛⎭⎫12727=3 432. (2)因为C 0n +C 1n +C 2n =79,所以n =12或n =-13(舍去).设T k +1项的系数最大.因为⎝⎛⎭⎫12+2x 12=⎝⎛⎭⎫1212(1+4x )12, 所以⎩⎪⎨⎪⎧C k 124k ≥C k -1124k -1C k 124k ≥C k +1124k +1,所以9.4≤k ≤10.4. 又因为0≤k ≤12且k ∈N ,所以k =10.所以展开式中系数最大的项为T 11.T 11=⎝⎛⎭⎫1212C 1012410x 10=16 896x 10.。
江西省上饶市2015届高三第二次高考模拟试题数学【文】试题及答案

2
14.以抛物线 y =20x 的焦点为圆心,且与双曲
x2
y2 1的
16 9
两条渐近线都相切的圆的方程为
15.把正奇数依次按第一个括号 1 个数,第二个括号 2 个数,第三个括号 3 个数,第四个括号 1
பைடு நூலகம்
个数, …… 如此循环为( 1),( 3, 5),( 7, 9, 11),( 13),( 15, 17),( 19, 21, 23),…… 。则
请考生在第 22、 23 题中任选一题作答。若多做,则按所做的第一题计分。 22.(本小题 10 分)选修 4-4:参数方程选讲
极坐标系与直角坐标系 xOy 有相同的长度单位,以原点 O 为极点,以 x 轴正半轴为极轴。已知
曲线 C1 的极坐标方程为
2 2 sin(
) ,曲线 C2 的极坐标方程为 sin 4
成.若. x1.y1 x2.y2 x3. y3 x4.y4 的所有可能取值中的最小值为
A.
3
2
B.
3
C.
2
8.设变量 x, y 满足约束条件
yx x 3y 4, 则 z=|x--3y| 的取值范围为 x2
2
4 a ,则 a 与 b 的夹角为
D.
6
A . [2,8]
9.已知函数 f ( x)
B.[0,8]
用分层抽样的方法,每个人被抽中的概率是
51
,
20 4
1
所以选中的“高个子”有 8
2 人,设这两个人为 A,B ;
4
1
“ 非高个子”有 12
3 人 , 设这三个人 C,D,E. -------------------------------------- 2 分
江西2015届高中数学二轮复习高效专项检测题36Word版含答案

双曲线一、选择题1.(2013²湖北高考文科²T2)已知π04θ<<,则双曲线1C :22221sin cos x y θθ-=与2C :22221cos sin y x θθ-=的( ) A .实轴长相等 B .虚轴长相等 C .离心率相等 D .焦距相等【解题指南】分别表示出双曲线1C 和2C 的实轴,虚轴,离心率和焦距,最后比较即可.【解析】选 D. 双曲线1C 的实轴长为2sin θ,虚轴长为2cos θ,焦距为2=,离心率为1sin θ;双曲线2C 的实轴长为2cos θ,虚轴长为2sin θ,焦距为2=,离心率为1cos θ,故只有焦距相等.故答案为D.2.(2013²福建高考理科²T3)双曲线1422=-y x 的顶点到渐进线的距离等于( ) A.52 B.54C. 552 D.554【解题指南】先求顶点,后求渐近线方程,再用距离公式求解.【解析】选 C.双曲线的右顶点为(20),,渐近线方程为20x y -=,则顶点到渐近线的距离为= 3.(2013²福建高考文科²T4)双曲线x 2-y 2=1的顶点到其渐近线的距离等于 ( )A .12B .2C .1D .【解题指南】先求顶点,后求渐近线方程,再用距离公式. 【解析】选B.顶点错误!未找到引用源。
到渐近线y=x 的距离为错误!未找到引用源。
.4. (2013²新课标Ⅰ高考文科²T4)与(2013²新课标Ⅰ高考理科²T4)相同已知双曲线C :12222=-by a x 错误!未找到引用源。
= 1(a>0,b>0)的离心率为错误!未找到引用源。
,则C 的渐近线方程为( ) A.y=±错误!未找到引用源。
x B.y=±错误!未找到引用源。
x C.y=±错误!未找到引用源。
x D.y=±x 【解题指南】 根据题目中给出离心率确定a 与c 之间的关系,再利用222b a c +=确定a 与b 之间的关系,即可求出渐近线方程.【解析】选C.因为25==a c e ,所以4522=a c ,又因为222b a c +=,所以45222=+a b a ,得=22a b 41,所以渐近线方程为x y 21±= 5.(2013²天津高考理科²T5)已知双曲线22221(0,0)x y a b a b -=>>的两条渐近线与抛物线y 2=2p x(p >0)的准线分别交于A,B 两点,O 为坐标原点.若双曲线的离心率为2,△AOB 的面积为错误!未找到引用源。
2015年全国Ⅱ高考数学试题及答案(文)

2015年全国Ⅱ高考数学试题(文)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}|12A x x =-<<,{}|03B x x =<<,则AB =A .()1,3-B .()1,0-C .()0,2D .(2,3)2.若a 为实数,且231aii i+=++,则a = A .-4 B .-3 C .3 D .43.根据下面给出的2004年至2013年我国二氧化硫年排放量(单位:万吨)柱形图,以下结论中不正确的是A .逐年比较,2008年减少二氧化硫排放量的效果最显著B .2007年我国治理二氧化硫排放显现成效C .2006年以来我国二氧化硫年排放量呈减少趋势D .2006年以来我国二氧化硫年排放量与年份正相关 4.向量(1,1),(1,2)a b =-=-,则(2)a b a +=A .-1B .0C .1D .25.已知n S 是等差数列{}n a 的前n 项和,若1353a a a ++=,则5S =A .5B .7C .9D .116.一个正方体被一个平面截去一部分后,剩余部分的三视图如右图,则截去部分体积与剩余部分体积的比值为A .18B .17C .16D .152004年 2005年 2006年 2007年 2008年 2009年 2010年 2011年 2012年 2013年7.已知三点(1,0)A,B,C ,则△ABC 外接圆的圆心到原点的距离为A .53B.3CD .438.右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的,a b 分别为14,18,则输出的a =A .6B .2C .4D .149.已知等比数列{}n a 满足114a =,3544(1)a a a =-,则2a A .2B .1C .12D .1810.已知,A B 是球O 的球面上的两点,90AOB ∠=,C 为该球面上的动点,若三棱锥O ABC -体积的最大值为36,则球O 的表面积为A .36πB .64πC .144πD .256π11.如图,长方形ABCD 的边2AB =,1BC =,O 是AB 的中点,点P 沿着边,BC CD 与DA 运动,记BOP x ∠=,将动点P 到A 、B 两点距离之和表示为x 的函数()f x ,则()y f x =的图象大致为A .B .C .D .12.设函数21()ln(1||)1f x x x=+-+,则使得()(21)f x f x >-成立的x 的取值范围是 A .1,13⎛⎫ ⎪⎝⎭B .()1,1,3⎛⎫-∞+∞ ⎪⎝⎭424424424424C .11,33⎛⎫- ⎪⎝⎭D .11,,33⎛⎫⎛⎫-∞-+∞ ⎪⎪⎝⎭⎝⎭第Ⅱ卷(非选择题共90分)注意事项:用钢笔或圆珠笔直接答在答题卡上.二、填空题:本大题共4小题,每小题5分,共20分,把答案填在题中横线上.13.已知函数3()2f x ax x =-的图像过点(1,4)-,则a = .14.若,x y 满足约束条件50,210,210,x y x y x y +-≤⎧⎪--≥⎨⎪-+≤⎩则2z x y =+的最大值为 .15.已知双曲线过点(,且渐近线方程为12y x =±,则该双曲线的标准方程为 . 16.已知曲线ln y x x =+在点(1,1)处的切线与曲线2(2)1y ax a x =+++相切,则a = .三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.17.(本小题满分12分)△ABC 中,D 是BC 上的点,AD 平分BAC ∠,2BD DC =. (1)求sin sin BC∠∠;(2)若60BAC ∠=,求B ∠.18.(本小题满分12分)某公司为了解用户对其产品的满意度,从,A B 两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得到A 地区用户满意度评分的频率分布直方图和B 地区用户满意度评分的频数分布表。
2015年普通高等学校招生全国统一考试(新课标Ⅱ卷)文数答案解析(正式版)(原卷版)
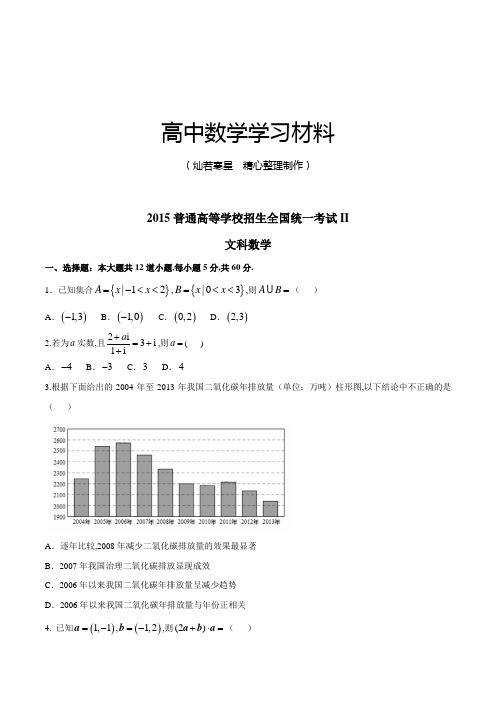
高中数学学习材料(灿若寒星 精心整理制作)2015普通高等学校招生全国统一考试II文科数学一、选择题:本大题共12道小题,每小题5分,共60分.1.已知集合{}|12A x x =-<<,{}|03B x x =<<,则AB =( ) A .()1,3- B .()1,0-C .()0,2D .()2,32.若为a 实数,且2i 3i 1ia +=++,则a =( ) A .4- B .3- C .3 D .43.根据下面给出的2004年至2013年我国二氧化碳年排放量(单位:万吨)柱形图,以下结论中不正确的是( )A .逐年比较,2008年减少二氧化碳排放量的效果最显著B .2007年我国治理二氧化碳排放显现成效C .2006年以来我国二氧化碳年排放量呈减少趋势D .2006年以来我国二氧化碳年排放量与年份正相关4. 已知()1,1=-a ,()1,2=-b ,则(2)+⋅=a b a ( )A .1-B .0C .1D .25. 设n S 是等差数列{}n a 的前n 项和,若1353a a a ++=,则5S =( )A .5B .7C .9D .116. 一个正方体被一个平面截去一部分后,剩余部分的三视图如下图,则截去部分体积与剩余部分体积的比值为( )1A.8 1B.7 1C.6 1D.57. 已知三点(1,0),(0,3),(2,3)A B C ,则△ABC 外接圆的圆心到原点的距离为( )5A.3 21B.3 25C.3 4D.38. 右边程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的,a b 分别为14,18,则输出的a 为( )A.0B.2C.4D.149.已知等比数列{}n a 满足114a =,()35441a a a =-,则2a =( ) A.2 B.1 1C.2 1D.810. 已知B A ,是球O 的球面上两点,︒=∠90AOB ,C 为该球面上的动点.若三棱锥ABC O -体积的最大值为36,则球O 的表面积为( )A.π36B. π64C.π144D. π25611. 如图,长方形的边AB =2,BC =1,O 是AB 的中点,点P 沿着边BC ,CD 与DA 运动,记BOP x ∠= ,将动点P 到A ,B 两点距离之和表示为x 的函数()f x ,则的图像大致为( )A .B .C .D .12. 设函数21()ln(1||)1f x x x =+-+,则使得()(21)f x f x >-成立的x 的取值范围是( ) A .1,13⎛⎫ ⎪⎝⎭ B .()1,1,3⎛⎫-∞+∞ ⎪⎝⎭ C .11,33⎛⎫-⎪⎝⎭ D .11,,33⎛⎫⎛⎫-∞-+∞ ⎪ ⎪⎝⎭⎝⎭ 二、填空题:本大题共4小题,每小题5分,共20分13. 已知函数()32f x ax x =-的图像过点(-1,4),则a = . 14. 若x ,y 满足约束条件50210210x y x y x y +-≤⎧⎪--≥⎨⎪-+≤⎩,则z =2x +y 的最大值为 .15. 已知双曲线过点()4,3,且渐近线方程为12y x =±,则该双曲线的标准方程为 . 16.已知曲线ln y x x =+在点()1,1 处的切线与曲线()221y ax a x =+++ 相切,则a = .三、解答题17(本小题满分12分)△ABC 中D 是BC 上的点,AD 平分∠BAC ,BD =2DC .(I )求sin sin B C∠∠ ;(II )若60BAC ∠=,求B ∠.18. (本小题满分12分)某公司为了了解用户对其产品的满意度,从A ,B 两地区分别随机调查了40个用户,根据用户对其产品的满意度的评分,得到A 地区用户满意度评分的频率分布直方图和B 地区用户满意度评分的频率分布表.A 地区用户满意度评分的频率分布直方图(I )在答题卡上作出B 地区用户满意度评分的频率分布直方图,并通过此图比较两地区满意度评分的平均值及分散程度.(不要求计算出具体值,给出结论即可)B 地区用户满意度评分的频率分布直方图(II )根据用户满意度评分,将用户的满意度评分分为三个等级:估计那个地区的用户的满意度等级为不满意的概率大,说明理由.19. (本小题满分12分)如图,长方体1111ABCD A B C D -中AB =16,BC =10,18AA =,点E ,F 分别在1111,A B D C 上,11 4.A E D F ==过点E ,F 的平面α与此长方体的面相交,交线围成一个正方形.(I )在图中画出这个正方形(不必说明画法与理由);(II )求平面α把该长方体分成的两部分体积的比值.20. (本小题满分12分)已知椭圆()2222:10x y C a b a b +=>> 的离心率为22,点()2,2在C 上. (I )求C 的方程;(II )直线l 不经过原点O ,且不平行于坐标轴,l 与C 有两个交点A ,B ,线段AB 中点为M ,证明:直线OM 的斜率与直线l 的斜率乘积为定值.21. (本小题满分12分)已知()()ln 1f x x a x =+-.(I )讨论()f x 的单调性;(II )当()f x 有最大值,且最大值大于22a -时,求a 的取值范围.请考生在22、23、24题中任选一题作答,如果多做,则按所做的第一题计分,作答时请写清题号22. (本小题满分10分)选修4-1:几何证明选讲如图O 是等腰三角形AB C 内一点,圆O 与△ABC 的底边BC 交于M ,N 两点,与底边上的高交于点G ,且与AB ,AC 分别相切于E ,F 两点.(I )证明EF BC ;(II )若AG 等于圆O 半径,且23AE MN == ,求四边形EBCF 的面积.23. (本小题满分10分)选修4-4:坐标系与参数方程在直角坐标系xOy 中,曲线1cos ,:sin ,x t C y t αα=⎧⎨=⎩(t 为参数,且0t ≠ ),其中0απ≤<,在以O 为极点,x 轴正半轴为极轴的极坐标系中,曲线23:2sin ,:23cos .C C ρθρθ== (I )求2C 与3C 交点的直角坐标;(II )若1C 与 2C 相交于点A ,1C 与3C 相交于点B ,求AB 最大值.24.(本小题满分10分)选修4-5:不等式证明选讲设,,,a b c d 均为正数,且a b c d +=+.证明:(I )若ab cd > ,则a b c d +>+; (II )a b c d +>+是a b c d -<-的充要条件.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一.基础题组 1. 【上海市长宁、嘉定区2014届高三4月第二次模拟考试数学(文)试题】对于任意),1()1,0(∞+∈ a ,函数)1(log 111)(--=x x f a 的反函数)(1x f-的图像经过的定点的坐标是______________.2. 【上海市长宁、嘉定区2014届高三4月第二次模拟考试数学(文)试题】已知偶函数)(x f 对任意R∈x 都有)2(2)()4(f x f x f =-+,则)2014(f 的值等于……………………………………( )A .2B .3C .4D .03. 【上海市崇明县2014届高三高考模拟考试(二模)数学(文)试卷】已知函数()21x f x =+的反函数为1()y f x -=,则1()0f x -<的解集是 .【解析】4. 【上海市崇明县2014届高三高考模拟考试(二模)数学(文)试卷】如果函数(]()210,1()311,ax x f x ax x ⎧-∈⎪=⎨-∈+∞⎪⎩,2()log g x x =,关于x 的不等式()()0f x g x ⋅≥,对于任意(0,)x ∈+∞ 恒成立,则实数a 的取值范围是 .5. 【上海市奉贤区2014届下学期高三二模数学试卷(文科)】函数()()42lg -=x x f 的定义域为________.6. 【上海市虹口区2014届高三4月高考练习(二模)数学(文)试题】 函数2()41f x x x =-++([]1,1x ∈-)的最大值等于 .7. 【上海市虹口区2014届高三4月高考练习(二模)数学(文)试题】 已知函数()y f x =是函数x y a =(0a >且1a ≠)的反函数,其图像过点2(,)a a ,则()f x = .8. 【上海市虹口区2014届高三4月高考练习(二模)数学(文)试题】若函数()1f x ax =+在区间(1,1)-上存在一个零点,则实数a 的取值范围是( ).A 1a > .B 1a <- .C 1a <-或1a > .D 11a -<<9. 【上海市黄浦区2014年高考模拟(二模)数学(文)试题】函数xxy -+=11log 2的定义域是 .10. 【上海市黄浦区2014年高考模拟(二模)数学(文)试题】函数)1,0(|log |)(≠>=a a x x f a 且的单调递增区间是 .11. 【上海市黄浦区2014年高考模拟(二模)数学(文)试题】函数)0()(2≤-=x x x f 的反函数是)(1x f -,则反函数的解析式是=-)(1x f .12. 【上海市黄浦区2014年高考模拟(二模)数学(文)试题】方程1)34(log 2+=-x x 的解=x .13. 【上海市静安、杨浦、青浦、宝山四区2014高考模拟(文科)数学】已知1log log 22=+y x ,则y x +的最小值为_____________.14. 【上海市徐汇、金山、松江区2014届高三第二学期学习能力诊断数学(文)试题】函数()22y x x x=+≥的值域是____________.二.能力题组 1. 【上海市崇明县2014届高三高考模拟考试(二模)数学(文)试卷】已知二次函数2()()f x x ax a x =-+∈R 同时满足:①不等式()0f x ≤的解集有且只有一个 元素;②在定义域内存在120x x <<,使得不等式12()()f x f x >成立.设数列{}n a 的前n 项和为n S ,且()n S f n =.规定:各项均不为零的数列{}n b 中,所有满足10i i b b +⋅<的正整数i 的个数称为这个数列{}n b 的变号数.若令1n nab a =-(n ∈*N ),则数列{}n b 的变号数等于 .2. 【上海市奉贤区2014届下学期高三二模数学试卷(文科)】定义在(0,)+∞上的函数()f x 满足:①当[1,3)x ∈时,1,12,()3,23,x x f x x x -≤≤⎧=⎨-<<⎩②(3)3()f x f x =,设关于x 的函数()()1F x f x =-的零点从小到大依次记为123,,,x x x ⋅⋅⋅,则123x x x ++=________.【解析】3. 【上海市静安、杨浦、青浦、宝山四区2014高考模拟(文科)数学】()f x 的定义域为实数集R,⎪⎩⎪⎨⎧<≤--≤≤=.01,1)21(,1,)(xxxxfx对于任意的x R∈都有(1)(1)f x f x+=-.若在区间[1,3]-上函数()()g x f x m x m=--恰有四个不同的零点,则实数m的取值范围是 .【解析】4.【上海市闵行区2014届高三下学期教育质量调研(二模)数学(文)试题】对于函数[]sin,0,2()1(2),(2,)2x xf xf x xπ⎧∈⎪=⎨-∈+∞⎪⎩,有下列4个命题:①任取[)120,x x∈+∞、,都有12()()2f x f x-≤恒成立;②()2(2)f x kf x k=+*()k∈N,对于一切[)0,x∈+∞恒成立;③函数()ln(1)y f x x=--有3个零点;④对任意0x>,不等式2()f xx≤恒成立.则其中所有真命题的序号是.考点:函数的综合应用.三.拔高题组1. 【上海市长宁、嘉定区2014届高三4月第二次模拟考试数学(文)试题】设a 是实数,函数|2|4)(a x f xx-+=(R ∈x ).(1)求证:函数)(x f 不是奇函数;(2)当0≤a 时,解关于x 的方程2)(a x f =;(3)当0>a 时,求函数)(x f y =的值域(用a 表示).(2)因为02>x ,04>x ,所以当0≤a 时,a x f xx -+=24)(, ……………(1分)2. 【上海市崇明县2014届高三高考模拟考试(二模)数学(文)试卷】设121()log1axf x x x -=+-为奇函数,a 为常数. (1)求a 的值;(2)判断函数()f x 在(1,)x ∈+∞上的单调性,并说明理由; (3)若对于区间[]3,4上的每一个x 值,不等式1()()2x f x m >+恒成立,求实数m 的取值范围.3. 【上海市奉贤区2014届下学期高三二模数学试卷(文科)】已知函数9()||f x x a a x=--+,[1,6]x ∈,a R ∈.(1)若1a =,试判断并用定义证明函数()f x 的单调性;(2)当()3,1∈a 时,求函数()f x 的最大值的表达式()M a .证明:当13a <≤时,()f x 在[1,]a 上是增函数(过程略) 11分4. 【上海市黄浦区2014年高考模拟(二模)数学(文)试题】 某通讯公司需要在三角形地带OAC 区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域BOC 内,乙中转站建在区域AOB 内.分界线OB 固定,且OB =(1百米,边界线AC 始终过点B ,边界线OC OA 、满足00075,30,45AOC AOB BOC ∠=∠=∠=.设OA x =(36x ≤≤)百米,OC y =百米.(1)试将y 表示成x 的函数,并求出函数y 的解析式;(2)当x 取何值时?整个中转站的占地面积OAC S ∆最小,并求出其面积的最小值.助于三角形有面积,OAC OAB OCB S S S ∆∆∆=+,从这个等式中,解出y ,即得要求的函数式;(2)有5. 【上海市静安、杨浦、青浦、宝山四区2014高考模拟(文科)数学】某公司承建扇环面形状的花坛如图所示,该扇环面花坛是由以点O 为圆心的两个同心圆弧AD 、弧BC 以及两条线段AB 和CD 围成的封闭图形.花坛设计周长为30米,其中大圆弧AD 所在圆的半径为10米.设小圆弧BC 所在圆的半径为x 米(100<<x ),圆心角为θ弧度.(1)求 关于x的函数关系式;(2)在对花坛的边缘进行装饰时,已知两条线段的装饰费用为4元/米,两条弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用的比为y,当x为何值时,y取得最大值?6. 【上海市静安、杨浦、青浦、宝山四区2014高考模拟(文科)数学】设函数x x g 3)(=,x x h 9)(=.(1)解方程:0)1()(8)(=--h x g x h ;(2)令3)()()(+=x g x g x p ,求证:22013)20142013()20142012()20142()20141(=++++p p p p ; (3)若bx g a x g x f +++=)()1()(是实数集R 上的奇函数,且 0))(2()1)((>⋅-+-x g k f x h f 对任意实数x 恒成立,求实数k 的取值范围.又因为)(x f 在实数集上单调递增,所以2)(1)(-⋅>-x g k x h。
