谢处方电磁场与电磁波(第三版)规范标准答案
电磁场与电磁波习题(第三版)习题解答第1-2章
ˆ y ˆ 2 yz z ˆ 的旋度。 1.33 计算矢量场 F xxy
解：
ˆ x F x Fx
ˆ y y Fy
ˆ ˆ z x z x Fz xy
ˆ y y 2 yz
ˆ z z 1
ˆ 2 y xz ˆ x
ˆ yx ˆ ，计算 A A 。 1.35 已知 A xy
2
电磁场与电磁波习题答案 chapter 1～2
Copyright @ ShengQian
dE x, y
S dx '
1/ 2
ˆ x x ' yy ˆ x
1/ 2
2 2 2 0 x x ' y 2 x x ' y 2 ˆ x x ' yy ˆ S x dx ' 2 2 2 0 x x ' y ˆ a 2 S x ˆ x x ' yy dx ' E x, y 2 a 2 2 2 0 x x ' y a 2 ˆ ˆ a2 S y x x x' y S dx ' dx ' 2 2 2 a 2 a 2 2 0 2 0 x x ' y x x ' y 2
D 0 E 0
当r a时
Sa D1n D2 n r a 0
当r b时
C 0C a a
Sb D1n D2 n r b 0
0C C b b
分析，本 题求解面电荷分布时， 法线方向和 D1 , D2 关系不要弄 混，这里公式
电磁场与电磁波(第三版)课后标准答案谢处方
JS v ω r ez era
e a sin
e
Q 4 a
sin
将球面划分为无数个宽度为 dl a d 的细圆环，则球面上任一个宽度为 dl a d 细
.-
圆环的电流为
d
I
JS
dl
Q 4
sin
d
细圆环的半径为 b a sin ，圆环平面到球心的距离 d a cos ，利用电流圆环的轴线上
.-
第二章习题解答
2.1
一个平行板真空二极管内的电荷体密度为
4 9
0U0d 4
3 x 2
3
，式中阴极板位
于 x 0 ，阳极板位于 x d ，极间电压为 U0 。如果 U0 40 V 、 d 1cm 、横截面
S 10cm2 ，求：（1） x 0 和 x d 区域内的总电荷量 Q ；（2） x d 2 和 x d 区域内
解 电偶极子 p1 在矢径为 r 的点上产生的电场为
E1
1 4 0
[3(
p1 r)r r5
p1 r3
]
所以 p1 与 p 2 之间的相互作用能为
We
p2
E1
1 [3( p1 4 0
r)( p2 r5
r)
p1 r
p2
3
]
因为1 r, p1 ，2 r, p2 ，则
p1 r p1r cos1
处的电场强度 E 中，有一半是有平面上半径为 3z0 的圆内的电荷产生的。
解 半径为 r 、电荷线密度为 l d r 的带电细圆环在 z 轴上 z z0 处的电场强度为
d
E
ez
r z0 d r 20 (r 2 z02 )3
2
故整个导电带电面在 z 轴上 z z0 处的电场强度为
电磁场与电磁波(西安交大第三版)第8章课后答案
第八章 电磁辐射与天线8.1 由（8.1-3）式推导(8.1-4)及(8.1-5)式。
解)sin ˆcos ˆ(4θθθπμ-=-rrIdle A jkrρ (8.1-3) 代入A H ρρ⨯∇=μ1，在圆球坐标系ˆsin ˆˆsin 112θ∂ϕ∂∂θ∂∂∂ϕθθθμμrA A rr r rr A H r=⨯∇=ρρ)]cos ()sin ([4ˆ])([sin sin ˆ2r e e r r Idl A rA r r r jkr jkr r θθθπϕθθμθϕθ--∂∂--∂∂=∂∂-∂∂=可求出H ρ的3个分量为jkre kr kr j Idl k H -+=))(1(sin 422θπϕ (8.1-4) 0==θH H r将上式代入E j H ρρωε=⨯∇，可得到电场为H j E ρρ⨯∇=ωε1ϕθ∂ϕ∂∂θ∂∂∂ϕθθθωεH r rr r rr j sin 0ˆsin ˆˆsin 12=代入ϕH 得jkrr e kr kr j Idl k j E -+-=))(1)((cos 2323θπωε jkr e kr jkr kr j Idl k E --+=))()(1(sin 4323θπωεθ (8.1-5) 0=ϕE8.2 如果电流元yIl ˆ放在坐标原点，求远区辐射场。
解 解1 电流元yIl ˆ的矢量磁位为 jkr e rIl y A -=πμ4ˆρ 在圆球坐标系中jkry r e rIl A A -==πϕθμϕθ4sin sin sin sinjkry e rIl A A -==πϕθμϕθθ4sin cos sin cosjkry e rIl A A -==πϕμϕϕ4cos cos由A H ρρ⨯∇=μ1，对远区辐射场，结果仅取r1项，得jkre rIl jH -=λϕθ2cos jkre r Il j H --=λϕθϕ2sin cos根据辐射场的性质，E r ZH ρρ⨯=ˆ1得 jkre r Il jZ E --=λϕθθ2sin cosjkre r Il jZ E --=λϕϕ2cos解2 根据 jkR e RR l Id j H -⨯=λ2ˆρρ (8.1-13) RH Z E ˆ⨯=ρρ (8.1-14) ϕϕϕθθϕθcos ˆsin cos ˆsin sin ˆˆˆ++==r y lr Rˆˆ≈ ϕθϕθϕcos ˆsin cos ˆˆˆ+-=⨯rl ϕϕϕθθcos ˆsin cos ˆˆ)ˆˆ(--=⨯⨯r rl jkRer Idl j H -=λ2ρ)cos ˆsin cos ˆ(ϕθϕθϕ+- 2jkR Idl E jZ erλ-=r )cos ˆsin cos ˆ(ϕϕϕθθ--8.3 三副天线分别工作在30MHz,100MHz,300MHz,其产生的电磁场在多远距离之外主要是辐射场。
电磁场与电磁波(第三版)课后答案第6章
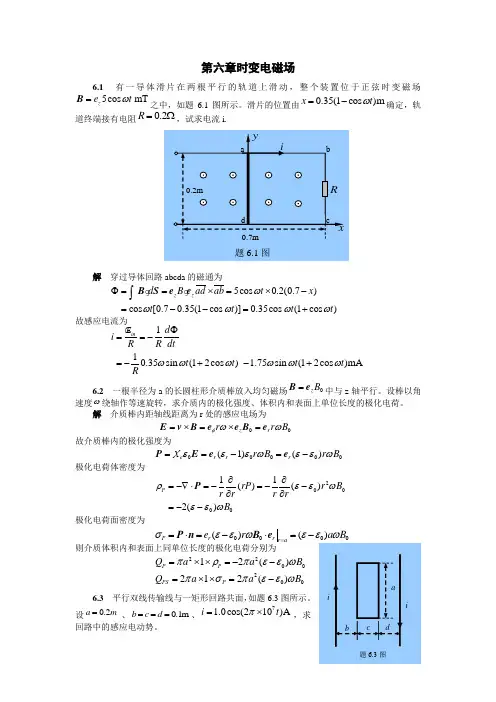
第六章时变电磁场6.1 有一导体滑片在两根平行的轨道上滑动，整个装置位于正弦时变磁场5cos mT z e t ω=B 之中，如题6.1图所示。
滑片的位置由0.35(1cos )m x t ω=-确定，轨道终端接有电阻0.2R =Ω，试求电流i.解 穿过导体回路abcda 的磁通为5cos 0.2(0.7)cos [0.70.35(1cos )]0.35cos (1cos )z z d B ad ab t x t t t t ωωωωωΦ==⨯=⨯-=--=+⎰ B S e e故感应电流为110.35sin (12cos ) 1.75sin (12cos )mAin d i R R dt t t t t R ωωωωωωΦ==-=-+-+E6.2 一根半径为a 的长圆柱形介质棒放入均匀磁场0z B =B e 中与z 轴平行。
设棒以角速度ω绕轴作等速旋转，求介质内的极化强度、体积内和表面上单位长度的极化电荷。
解 介质棒内距轴线距离为r 处的感应电场为 00z r r r B φωω=⨯=⨯=E v B e e B e故介质棒内的极化强度为 00000(1)()e r r r r B r B εεεωεεω==-=-P E e e X极化电荷体密度为2000011()()2()P rP r B r r r rB ρεεωεεω∂∂=-∇⋅=-=--∂∂=--P极化电荷面密度为00()()P r r r a e r a B σεεωεεω==⋅=-⋅=-P n B e 则介质体积内和表面上同单位长度的极化电荷分别为220020012()212()P P PS P Q a a B Q a a B πρπεεωπσπεεω=⨯⨯=--=⨯⨯=-6.3 平行双线传输线与一矩形回路共面，如题6.3图所示。
设0.2a m =、0.1m b c d ===、71.0cos(210)A i t π=⨯，求回路中的感应电动势。
《电磁场与电磁波》第版谢处方编课后习题答案高等教育出版社
S
1 2
R1 2 R 2 3
1 2
R 1 2 R
2 312 1 7
69
1 7 . 1 3
1.3 求 P(3,1, 4) 点到 P(2, 2,3) 点的距离矢量 R 及 R 的方向。
解 rP ex 3 ey ez 4 ， rP ex 2 ey 2 ez 3 ，
则
RPP rP rP ex 5 ey 3 ez
Ax ) y
ez
dS
S
y2
dS
a 2 00
r2 sin2 r d d r
a4 4
1.23 证明：（1） R 3 ；（2） R 0 ；（3）(A R) A 。其中 R ex x ey y ez z ， A 为一常矢量。
解 （1） R x y z 3 x y z
（2）
ex ey ez R 0
2
2
2
2
解
A d l xd x x d x 22 d y 0d y 8
C
0
0
0
0
ex ey ez
又
A x y
z
ex 2 yz ez 2x
x x2 y2z
22
所以
A d S (ex 2yz ez 2x) ez d x d y 8
S
00
故有
A dl 8 A dS
2 a
r d 3r2 sin d r d d 4 a3
0 00
1.21 求矢量 A ex x ey x2 ez y2z 沿 xy 平面上的一个边长为 2 的正方形回路的线 积分，此正方形的两边分别与 x 轴和 y 轴相重合。再求 A 对此回路所包围的曲面积分，
验证斯托克斯定理。
电磁场与电磁波(西安交大第三版)第2章课后答案
第2章习题2-1.已知真空中有四个点电荷q C11=，q C22=，q C34=，q C48=，分别位于(1,0,0)，(0,1,0)，(-1,0,0,)，(0,-1,0)点，求(0,0,1)点的电场强度。
解：zyrzxrzyrzxrˆˆ;ˆˆ;ˆˆ;ˆˆ4321+=+=+-=+-=84ˆ15ˆ6ˆ3)ˆˆˆˆ(412444233322222111πεπεzyxrrqrrqrrqrrqE++=+++=2-2.已知线电荷密度为ρl的均匀线电荷围成如图所示的几种形状，求P点的电场强度。
题2-2图解：(a) 由对称性04321=+++=EEEEE(b) 由对称性0321=++=EEEE(c) 两条半无限长线电荷产生的电场为yayxyxaEEE llaˆ2)}ˆˆ()ˆˆ{(421περπερ-=+--=+=半径为a的半圆环线电荷产生的电场为yaE lbˆ2περ=总电场为0=+=baEEE2-3.真空中无限长的半径为a的半边圆筒上电荷密度为ρs，求轴线上的电场强度。
解:在无限长的半边圆筒上取宽度为ϕad的窄条,,电荷线密度为ϕρρadsl=,对ϕ积分,可得真空中无限长的半径为a的半边圆筒在轴线上的电场强度为ydxyad r aE sssˆ)ˆcosˆsin(22ˆ0000⎰⎰-=--==πππερϕϕϕπερπεϕρ题2-3图题2-4图2-4.真空中无限长的宽度为a的平板上电荷密度为ρs，求空间任一点上的电场强度。
解:在平板上'x处取宽度为'dx的无限长窄条，可看成无限长的线电荷，电荷线密度为'dxslρρ=，在点),(yx处产生的电场为ρρρπε'ˆ21),(dxyxEd s=其中22)'(y x x +-=ρ；22)'(ˆˆ)'(ˆyx x y y xx x +-+-=ρ对'x 积分可得无限长的宽度为a 的平板上的电荷在点),(y x 处产生的电场为 )}2/2/(2ˆ)2/()2/(ln ˆ{4),(22220y a x arctg y a x arctg y ya x y a x x y x E s --+++-++=περr 为场点到坐标原点的距离，a ，b 为常数。
电磁场与电磁波(西安交大第三版)第7章课后规范标准答案
习题7-1、如果E z ，H z 已知，由无源区的麦克斯韦方程，求圆柱坐标系中E ,E ,H ,H 与E z ,H z 的关系。
解：设 EE 0（ , ）e jkzZ ； H H 0（ , ）e jkzZEH则一jk z E ； 一jk z Hzz在圆柱坐标系中展开无源区的麦克斯韦方程jZ式中k C k 2k ；1 H zjk z H1 E zjk z Ejk z HH zjk z EE z由以上几式得1 k c 2（jk z E zE z H z右（k z E zk c 2（jE zjk7-2证明（7.2-6 ）式为（7.2-4）式的解。
证明:由( 7.2-6 )式V(z) V o e z V o e可得：V (z) (V o e V o e z) V(z) 2因此dz22V 0 即(7.2-4)7-2、从图7.2-2的等效电路，求（7.2-和（7.2-6）式对应的传输线方程的时域形式。
解:图7.2-2dV(z) dz dl(z) dzZ i l(z) Y i V(z)串联支路上的电压为V iRidz心V dV 并联支路上的电流为由（dVdidui uG i dz C i dz——i i dt1 ）和（2）式得(iR i L i 为dzdt/d II(uG i C i —)dz dt两边同除dz得dV di—(iR i L i 石)dz dt di / c c du —(uG i C idz dt(uG i C i（5 ）、（6）式就是（7.2-7-3、(7.2-3)解: 代入di(3)(4)(5)(6)和(7.2-6)、(7.2-4)式对应的传输线方程的时域形式。
和(7.2- 9 )式推导(7.2- 11 )和(7.2- 1 2)式。
Z iY iR iG ij L ij C iJZ i Y i并等式两边平方得2 j2 R i G i 2L i C i j (C i R i L i G i)令等式两边实部和虚部分别相等，得2 2R i G i 2 L i C i(C i R i L i G i)解以上两方程，得2C i2) (R i G i 2L i C i)] ⑺ 2- 11 )2d V(z) dz27-5、同轴线内导体外径为 d 3.04mm ,外导体内径为7mm ,内外导体之间为r2.2的非磁性介质，求特性阻抗。
电磁场与电磁波课后答案谢处方
第二章习题解答2.1 一个平行板真空二极管内的电荷体密度为43230049U d x ρε--=-，式中阴极板位于0x =，阳极板位于x d =，极间电压为0U 。
如果040V U =、1cm d =、横截面210cm S =，求：（1）0x =和x d =区域内的总电荷量Q ；（2）2x d =和x d =区域内的总电荷量Q '。
解 （1） 43230004d ()d 9dQ U d x S x τρτε--==-=⎰⎰110044.7210C 3U S dε--=-⨯ （2）4320024d ()d 9dd Q U d x S x τρτε--''==-=⎰⎰11004(10.9710C 3U S d ε--=-⨯ 2.2 一个体密度为732.3210C m ρ-=⨯的质子束，通过1000V 的电压加速后形成等速的质子束，质子束内的电荷均匀分布，束直径为2mm ，束外没有电荷分布，试求电流密度和电流。
解 质子的质量271.710kg m -=⨯、电量191.610C q -=⨯。
由21mv qU = 得 61.3710v ==⨯ m s 故 0.318J v ρ== 2A m26(2)10I J d π-== A2.3 一个半径为a 的球体内均匀分布总电荷量为Q 的电荷，球体以匀角速度ω绕一个直径旋转，求球内的电流密度。
解 以球心为坐标原点，转轴（一直径）为z 轴。
设球内任一点P 的位置矢量为r ，且r 与z 轴的夹角为θ，则P 点的线速度为sin r φωθ=⨯=v r e ω球内的电荷体密度为343Qa ρπ=故 333sin sin 434Q Q r r a aφφωρωθθππ===J v e e 2.4 一个半径为a 的导体球带总电荷量为Q ，同样以匀角速度ω绕一个直径旋转，求球表面的面电流密度。
解 以球心为坐标原点，转轴（一直径）为z 轴。
设球面上任一点P 的位置矢量为r ，且r 与z 轴的夹角为θ，则P 点的线速度为sin a φωθ=⨯=v r e ω球面的上电荷面密度为24Q a σπ=故 2sin sin 44S Q Q a a aφφωσωθθππ===J v e e 2.5 两点电荷18C q =位于z 轴上4z =处，24C q =-位于y 轴上4y =处，求(4,0,0)处的电场强度。
电磁场与电磁波第三版课后答案
电磁场与电磁波第三版课后答案本文是对《电磁场与电磁波》第三版的课后习题答案的整理与解答。
本书是电磁场与电磁波领域的经典教材，其中的习题对于巩固和加深对电磁场与电磁波知识的理解非常重要。
以下是本文对第三版的习题答案的详细解析。
第一章电磁场基本概念1.1 电磁场基本概念习题答案：1.电磁场的基本概念是指在空间中存在着电场和磁场，它们相互作用产生相互关联的现象；它们是由带电粒子的运动而产生的，是物理学的基本概念之一。
2.宏观电荷位移是指电荷在物体内部的移动；它的存在使得物体表面或其周围的电场产生变化，从而产生an内部电磁场。
3.电磁场的基本方程是麦克斯韦方程组，由四个方程组成：高斯定律、法拉第电磁感应定律、法拉第电磁感应定律的积分形式和安培环路定律。
1.2 矢量分析习题答案：1.根据题目所给的向量，求两个向量的点乘积：$\\vec{A}\\cdot\\vec{B}=A_{x}B_{x}+A_{y}B_{y}+A_{z}B_{ z}$2.根据题目所给的向量，求两个向量的叉乘积：$\\vec{A}\\times\\vec{B}=(A_{y}B_{z}-A_{z}B_{y})\\hat{i}+(A_{z}B_{x}-A_{x}B_{z})\\hat{j}+(A_{x}B_{y}-A_{y}B_{x})\\hat{k}$3.定义标量和矢量场，然后利用高斯定理得出结论。
1.3 电场与静电场习题答案：1.静电场是指电场的源是静止电荷，不会随时间变化，不产生磁场。
2.在静电场中，高斯定律表示为：$\ abla \\cdot\\vec{E} = \\frac{1}{\\varepsilon_0}\\rho$，其中$\ abla\\cdot \\vec{E}$表示电场的散度，$\\varepsilon_0$表示真空介电常数，$\\rho$表示电荷密度。
3.电场的位移矢量$\\vec{D}$定义为$\\vec{D} =\\varepsilon_0 \\vec{E} + \\vec{P}$，其中$\\varepsilon_0$表示真空介电常数，$\\vec{E}$表示电场强度，$\\vec{P}$表示极化强度。
电磁场与电磁波第三版 郭辉萍 第2章习题答案
（2-1-5）
第2章 静电场分析
2. 分布电荷的电场强度
上述的分析， 我们假设电荷是集中在一个点上， 从宏观的角度讲， 电荷是连续的分布在一段线上、 一 个面上或一个体积内的， 因此， 我们先定义电荷分布。 线电荷密度（Charge Line Density）： 当电荷分布 在一细线（其横向尺寸与长度的比值很小）上时， 定 义线电荷密度为单位长度上的电荷
第2章 静电场分析
第2章 静电场和恒定电场
2.1 电场强度与电位函数
2.2 真空中静电场的基本方程 2.3 电介质的极化与介质中的场方程 2.4 导体间的电容与电耦合 2.5 静电场的边界条件
2.6 恒定电场
习 题
第2章 静电场分析
2.1 电场强度与电位函数
2.1.1 库仑定律 库仑定律（Coulom's Law）是静电现象的基本实验定 律， 它表明固定在真空中相距为R的两点电荷q1与q2之间 的作用力：正比于它们的电荷量的乘积； 反比于它们之 两点电 间距离的平方；作用力的方向沿两者间的连线；
（2-1-7）
第2章 静电场分析
P(r) R
dV
V
r
r
O
图2 - 3 体电荷产生的场
第2章 静电场分析
体电荷密度（Charge Volume Density）： 如果电 荷分布在一个体积空间内， 定义体电荷密度为单位体 积内的电荷
q V lim V 0 V
式中， Δq是体积元ΔV内所包含的电荷。
荷同性为斥力， 异性为吸力（如图2-1所示）， 表达式为
第2章 静电场分析
q1q2 q1q2 F12 a R R 2 3 4 0 R 4 0 R
F12 q2 R
电磁场与电磁波第三版课后答案 谢处方
第一章习题解答1.1 给定三个矢量A 、B 和C 如下： 23x y z =+-A e e e4y z =-+B e e52x z =-C e e求：（1）A a ；（2）-A B ；（3）A B ；（4）AB θ；（5）A 在B 上的分量；（6）⨯A C ；（7）()⨯A BC 和()⨯A BC ；（8）()⨯⨯A BC 和()⨯⨯A B C 。
解 （1）23A x y z+-===e e e A a ee e A （2）-=A B (23)(4)x y z y z +---+=e e e e e 64x y z +-e e e （3）=A B (23)x y z +-e e e (4)y z -+=e e －11 （4）由cos AB θ=14-==⨯A B A B ，得1cos ABθ-=(135.5= （5）A 在B 上的分量 B A =A cos AB θ=1117=-A B B （6）⨯=A C 123502xy z-=-e e e 41310x y z ---e e e （7）由于⨯=B C 041502x yz-=-e e e 8520x y z ++e e e⨯=A B 123041x y z-=-e e e 1014x y z ---e e e所以 ()⨯=A B C (23)x y z +-e e e (8520)42x y z ++=-e e e ()⨯=A B C (1014)x y z ---e e e (52)42x z -=-e e（8）()⨯⨯=A B C 1014502x y z---=-e e e 2405x y z -+e e e()⨯⨯=A B C 1238520x y z -=e e e 554411x y z --e e e1.2 三角形的三个顶点为1(0,1,2)P -、2(4,1,3)P -和3(6,2,5)P 。
（1）判断123PP P ∆是否为一直角三角形； （2）求三角形的面积。
电磁场与电磁波第三版答案第四章
《电磁场与电磁波》——习题详解第四章 静态场的解4-1 一个点电荷 Q 与无穷大导体平面相距为 d ,如果把它移动到无穷远处,需要 作多少功? 解: 用镜像法, 相当于两个电荷关于 y = 0 平面向相反方向离开,当 Q 移到 y 处时,受到 的电场力为:y Qdy y xdF= Q2 4πε 0 (2 y ) 2-Q 此时移动 d y 需对电荷做功图 4-1dw = Fd y =移到无穷远处做的总功为:Q2 16πε 0 y 2dyW = dw = Fd y =d∫∫∞∫∞ dQ216πε 0 y 2dy=Q2 16πε 0 d当用外力将电荷 Q 移动到无穷远处时,同时也要将镜像电荷移动到无穷远处,所以在整个过程中,外力作的总功为Q2 8πε 0 d也可以用静电能计算,在移动以前,系统的静电能等于两个点电荷之间的相互 作用能:W=1 1 1 1 Q Q Q2 + (Q) q11 + q2 2 = Q = 2 2 2 4π ε 0 (2d ) 2 4π ε 0 (2d ) 8π ε 0 d移动点电荷到无穷远以后,系统的静电能为零.因此,在这个过程中,外力作 功等于系统静电能的增量,即外力作功为Q2 8πε 0 d.43习题四4-2 一个点电荷放在直角导体内部(如图 4-2),求出所有镜像电荷的位置和大小y-q r2 d r3O r1 r4rq ax -qq图 4-2 解:假设如图所示三个镜像电荷,则空间电荷分布为φ (r ) =v1 1 1 1 ( + ) 4πε 0 r1 r2 r3 r4q经检验:在 y = 0 平面上 φ ( r ) = 0 ,在 x = 0 平面上vφ (r ) = 0所以上述解为原问题的解.因此求得镜像电荷的位置和大小如图 4-2 所示,即vq 2 = q 位置 ( a, d ) , q3 = q 位置 ( a, d ) , q 4 = q 位置 (a, d )4-3 证明:一个点电荷 q 和一个带有电荷 Q ,半径为 R 的导体球之间的作用力为Rq Q + D q DRq F= 2 4π ε 0 D 2 (D R 2 ) 2 其中 D 是 q 到球心的距离 ( D > R ) . 证明:使用镜像法分析.由于导体球不接地,本身又带电 Q ,必须在导体球内 加上两个镜像电荷来等效导体球对外的影响.在距离球心 b = R / D 处,镜像电荷2为 q′ = Rq / D ;在球心处,镜像电荷为 q2 = Q q′ = Q + Rq / D .点电荷 q 受导 体球的作用力就等于球内两个镜像电荷对 q 的作用力,即44《电磁场与电磁波》——习题详解F= q2 q′ D 2 + ( D b) 2 4π ε 0 q Rq Rq Q + D q D = + R2 2 4π ε 0 D 2 2 (D ) D Rq Q + D DRq = 2 4π ε 0 D 2 (D R 2 ) 2 q4-4 两个点电荷 + Q 和 Q 位于一个半径为 a 的接地导体球的直径的延长线上, 分 别距离球心 D 和 D . (1) (2) 证明:镜像电荷构成一电偶极子,位于球心,偶极矩为 2a Q / D . 令 Q 和 D 分别趋于无穷,同时保持 Q / D 不变,计算球外的电场. 使用导体球面的镜像法和叠加原理分析.在球内加上两个镜像电荷:2 2 3 2解:(1)一个是 Q 在球面上的镜像电荷, 1 = aQ / D , q 距离球心 b1 = a / D ; 第二个是 Q 在球面上的镜像电荷, q2 = aQ / D ,距离球心 b2 = a / D .当距离较大时,镜像2电荷间的距离很小,等效为一个电偶极子,电偶极矩为p = q 1 (b1 b2 ) =(2) 2a 3Q D2球外任意点的电场等于四个点电荷产生的电场的叠加.设 + Q 和 Q 位于2坐标 z 轴上,当 Q 和 D 分别趋于无穷,同时保持 Q / D 不变时,由 + Q 和 Q 在空 间产生的电场相当于均匀平板电容器的电场,是一个均匀场,均匀场的大小为v 2Q / 4π ε 0 D 2 ,方向在 ez ,由镜像电荷产生的电场可以由电偶极子的公式计算.v E=p 4π ε 0 r3v v (er 2 cos θ + eθ sin θ )45习题四=4-5 2 a 3Q v v (er 2 cos θ + eθ sin θ ) 3 2 4π ε 0 r D接地无限大导体平板上有一个半径为 a 的半球形突起,在点 (0,0, d ) 处有一个 点电荷 q (如图 4-3),求导体上方的电z dq a bq2 -bq3-dq1 图 4-3位. 解:计算导体上方的电位时,要保持导 体平板部分和半球部分的电位都为零.先找平 面导体的镜像电荷 q1 = q ,位于 (0,0, d ) 处.再找球面镜像电荷 q2 = aq / d ,位于(0,0, b) 处,b = a 2 / d .当叠加这两个镜像电荷和原电荷共同产生的电位时,在导体平面上位于 (0,0,b) 处. 和球面上都不为零, 应当在球内再加上一个镜像电荷 q3 = aq / d , 这时,三个镜像电荷和原电荷共同产生的电位在导体平面和球面上都为零,而且三 个镜像电荷在要计算的区域以外. 导体上方的电位为四个点电荷电位的叠加,即=其中 q q1 q2 q3 + + + 4π ε 0 R r1 r2 r3 1R = [ x 2 + y 2 + ( z d ) 2 ]1 2 r1 = [ x 2 + y 2 + ( z + d ) 2 ]1 2 r2 = [ x 2 + y 2 + ( z b) 2 ]1 2 r3 = [ x 2 + y 2 + ( z + b) 2 ]1 24-6 求截面为矩形的无限长区域( 0 < x < a , 0 < y < b )的电位,其四壁的电位 为 ( x,0) = ( x, b) = 0 ,46《电磁场与电磁波》——习题详解 (0, y ) = 0U 0 y b , ( a, y ) = y U 0 (1 ), b 0 < y ≤ b/ 2 b/ 2 < y < b解:法一:由边界条件 ( x,0) = ( x, b) = 0 知,方程的基本解在 y 方向应该 为周期函数,且仅仅取正弦函数,即Yn = sin k n y(k n =nπ ) b在 x 方向,考虑到是有限区域,选取双曲正弦函数和双曲余弦函数,使用边界 (0, y ) = 0 条件,得出仅仅选取双曲正弦函数,即X n = sh nπ x b将基本解进行线性组合,得 = ∑ Cn shn =1∞nπ x nπ y sin b b待定常数由 x = a 处的边界条件确定,即 (a, y ) = ∑ Cn shn =1∞nπ a nπ y sin b b使用正弦函数的正交归一性质,有b nπ a C n sh = 2 b∫ (a, y) sin0bnπ y dy bb/2∫b/2 02 U0 y U b nπ y by nπ y nπ y sin d y = 0 cos sin b b b nπ b nπ b 0=U0 b b nπ b2 nπ cos sin 2 2nπ 2 nπ 2∫y nπ y U 0 1 sin dy b b/2 bb47习题四b 2 b nπ y U b nπ y by nπ y 0 = U 0 cos cos sin nπ b b / 2 b nπ b nπ b bb/2b nπ U 0 b nπ = U 0 sin + cos nπ cos 2 b nπ 2 nπ +化简以后得2U 0 b2 U b b nπ cos nπ 0 cos 2 b nπ b nπ 2b nπ a = C n sh b 2∫ (a, y) sin0bnπ y b nπ d y = 2U 0 2 2 sin b 2 nπ求出系数,代入电位表达式,得nπ 4U 2 sin nπ y sh nπ x = ∑ 2 02 nπ a b b n =1 n π sh b 4-7 一个截面如图 4-4 所示的长槽,向 y 方向无限延伸,两侧的电位是零,槽内∞siny → ∞ , → 0 ,底部的电位为 ( x,0) = U 0求槽内的电位. 解:法一:令 ( x, y ) = X ( x)Y ( y ) = 0 , 因边界条件y =0 =0 = U0 (0, y ) = (a, y ) = 0a图 4-4x所以 X(x) = Acos K x x + B sin K x xQ X ( x) = X (a) = 0求得A = 0 , Kx =nπ a( n = 1,2,3L )X ( x) = Bn sinnπ x ( n = 1,2,3L ) a48《电磁场与电磁波》——习题详解由 Kx + Ky = 0 得 所以 Y ( y ) = C n enπ y a22K y = K x K y = ± j22nπ a( n = 1,2,3L )+ Dn e nπ y a nyπ a nyπ a ( x, y ) =∑n =1 ∞∞(C n e+ Dn e )Bn sinnπ x a=∑n =1 ′ (C n enyπ a′ + Dn e nyπ a) sinnπ x a′ 由边界条件 ( x,+∞) = 0 可得 C n = 0所以 ( x, y ) =∑n =1∞′ Dn enπ y asinnπ x a再由边界条件 ( x,0) = U 0 代入可得∑n =1∞′ Dn e nπ 0 asinnπ x= a∑ D′ sinn n =1∞nπ x = U0 a再两边同乘以 sinmπ x ,并从 0 到 a 积分得 a 4U 0 2U 0 ′ Dn = (1 cos mπ ) = mπ mπ 0 所以槽内电位为∞m = 1,3,5L m = 2,4,6L ( x, y ) =4U 0 myπ mπ e a sin x mπ a m =1, 3, 5....∑=∑n =1∞( 2 n 1) yπ 4U 0 (2n 1)π a x e sin a (2n 1)π法二:由于在 x = 0 和 x = a 两个边界的电位为零,故在 x 方向选取周期解, 且仅仅取正弦函数,即X n = sin k n xnπ kn = a 49习题四在 y 方向,区域包含无穷远处,故选取指数函数,在 y → ∞ 时,电位趋于零,所以 选取Yn = e kn y由基本解的叠加构成电位的表示式为nπ x nπa y e = C n sin a n =1∑∞待定系数由 y = 0 的边界条件确定.在电位表示式中,令 y = 0 ,得U 0 = ∑ Cn sinn =1∞nπ x aCna = 2∫a0U 0 sinaU 0 nπ x dx = (1 cos nπ ) nπ a当 n 为奇数时, Cn =4U 0 ,当 n 为偶数时, Cn = 0 .最后,电位的解为 nπnπ y a=4-84U nπ x ∑,5 nπ0 sin a e n =1, 3∞若上题的底部的电位为 ( x,0) = U 0 sin重新求槽内的电位3π x a解:同上题,在 x 方向选取正弦函数,即 X n = sin k n x , k n = 向选取 Yn = e kn y nπ ,在 y 方 a .由基本解的叠加构成电位的表示式为 = ∑ Cn sinn =1∞nπ x e anπ y a将 y = 0 的电位代入,得 U 0 sinnπ x 3π x ∞ = ∑ Cn sin a a n =1其余系数 Cn = 0 , 应用正弦级数展开的惟一性, 可以得到 n = 3 时,C3 = U 0 ,50《电磁场与电磁波》——习题详解所以 = U 0 sin4-93π x e a3π y a一个矩形导体槽由两部分构成, 如图 4-5 所示, 两个导体板的电位分别是 U 0 和 零,求槽内的电位. 解: 将原问题的电位看成是两个电位的叠加. 一个电位与平行板电容器的电位相同(上板电位为 U 0 ,下板电位为零 ),另一个电位为 U ,即=U0 y +U a y = 0 ,U = 0 y = a ,U = 0 a a 2y其中,U 满足拉普拉斯方程,其边界条件为 = U0 =0x图 4-5x = 0 时, U0 U 0 a y, U0 y= U = (0, y ) U a 0 y, a a < y<a 2 a 0< y< 2x → ∞ 时,电位 U 应该趋于零. U 的形式解为 nπ y e U = ∑ Cn sin a n =1待定系数用 x = 0 的条件确定.∞ ∞ nπ x aU (0, y ) = ∑ Cn sinn =1nπ y anπ y dy aa/2a C = 2 n∫a 0U (0, y ) sin∫a/2 02 U0 y U 0 a nπ y nπ y a nπ y sin dy = y cos sin a a a nπ a nπ a 051习题四U = 0 a a 2 nπ a 2 nπ cos + sin 2 2nπ 2 nπ a∫y nπ y a nπ y U 0 1 sin d y = U 0 cos a a/2 nπ a aaa/2 aU 0 a a 2 nπ y ay nπ y cos sin a nπ a nπ nπ U0 a sin + 2 a nπ 2a/2= U 0a nπnπ cos nπ cos 2 +化简后,得到U a a U0 a2 nπ cos nπ 0 cos 2 a nπ 2 a nπ U a nπ y nπ d y = 0 cos a nπ 2a C = 2 n∫a0U (0, y ) sin只有偶数项系数不为零.将系数求出,代入电位的表达式,得=4-10∞ U0 y 2U 0 nπ nπ y + ∑ cos sin e a a 2 n = 2 , 4 ,L nπnπ x a将一个半径为 a 的无限长导体管平分成两半,两部分之间互相绝缘,上半(0 < φ < π ) 接电压 U 0 ,下半 (π < φ < 2π ) 电位为零,如图 4-6,求管内的电位. 解:圆柱坐标的通解为 (r , φ ) = ( A0φ + B0 )(C0 ln r + D0 ) + ∑ r n ( An cos nφ + Bn sin nφ )n =1∞+ ∑ r n (Cn cos nφ + Dn sin nφ )n =1∞由于柱内电位在 r = 0 点为有限值,通解中不能有 ln r 和 rn项,即有52《电磁场与电磁波》——习题详解Cn = 0 , Dn = 0 , C0 = 0 (n = 1,2, L)柱内电位是角度的周期函数, A0 = 0 .因此,该题的通 解取为 r = U0 φx (r , φ ) = B0 D0 + ∑ r ( An cos nφ + Bn sin nφ )n n =1∞ =0图 4-6各项系数用 r = a 处的边界条件来定. (a, φ ) = B0 D0 + ∑ a n ( An cos nφ + Bn sin nφ ) = n =1∞ U0, 0 < φ < π 0, π < φ < 2πB 0 D0 =a n An =U 1 2π (a, φ ) d φ = 0 2π 0 2∫1π1∫ ∫0 (a, φ ) cos nφ d φ = 02π2πa n Bn =柱内的电位为π0 (a, φ ) sin nφ d φ =U0 (1 cos nπ ) nπ2U U (r , φ ) = 0 + 0 2 π4-111r ∑5L n a sin nφ n =1, 3,∞n半径为无穷长的圆柱面上,有密度为 ρ S = ρ S 0 cos φ 的面电荷,求圆柱面内, 外的电位. 解:由于面电荷是余弦分布,所以柱内,外的电位也是角度的偶函数.柱外的电位不应有 r 项,柱内电位不应有 r 是角度的周期函数.故柱内电位选为nn项.柱内,外的电位也不应有对数项,且1 = A0 + ∑ r n An cos nφn =1∞柱外电位选为 2 = C0 + ∑ r nCn cos nφn =1∞53习题四假定无穷远处的电位为零,定出系数 C0 = 0 . 在界面 r = a 上, 1 = 2 , ε0∞ 2 + ε0 1 = ρ S 0 cos φ r r∞即A0 + ∑ a n An cos nφ = ∑ a nCn cos nφn =1 n =1 ε0 ∑ na n 1Cn cos nφ + ε0 ∑ na n 1 An cos nφ = ρ S 0 cos φn =1 n =1∞∞解之得A0 = 0 , A1 =ρS 0 a2 ρS 0 , C1 = 2ε 2ε 0(n > 1)An = 0 , Cn = 0最后的电位为 ρS0 2ε r cos φ , = 2 0 a ρ S 0 cos φ , 2ε 0 r 3-12r<a r>a将一个半径为 a 的导体球置于均匀电场 E0 中,求球外的电位,电场. 解:采用球坐标系求解,设均匀电场沿正 z 方向,并设原点为电位零点(如图v4-7) . 因 球 面 是 等 位 面 , 所 以 在 r = a 处 , = 0 ; 在 r → ∞ 处 , 电 位 应 是 = E0 r cos θ ,球坐标中电位通解具有如下形式: (r ,θ ) = ∑ ( An r n + Bn r n 1 ) Pn (cos θ )n =0∞用无穷远处的边界条件 r → ∞ 及 = E0 r cos θ ,得到 A1 = E0 ,其余An = 0 .再使用球面上 ( r = a ) 的边界条件54《电磁场与电磁波》——习题详解∞ (a,θ ) = E0 a cos θ + ∑ Bn a n 1 Pn (cos θ ) = 0n =0上式可以改写为E0 a cos θ = ∑ Bn a n 1 Pn (cos θ )n =0∞因为勒让德多项式是完备的,即将任意的函数展开成勒让德多项式的系数是 惟 一 的 , 比 较 上 式 左 右 两 边 , 并 注 意 P (cos θ ) = cos θ , 得 E0 a = B1a 12,即B1 = E0 a 3 ,其余的 Bn = 0 .故导体球外电位为 = 1 电场强度为a3 E0 r cos θ r3 rE0θz图 4-7Er = 2a 3 = E0 1 + 3 cos θ r r a = E0 1 3 sin θ r rθ 3Eθ = 4-13将半径为 a , 介电常数为 ε 的无限长介质圆柱放置于均匀电场 E0 中, E0 沿 设vvx 方向,柱的轴沿 z 轴,柱外为空气,如图 4-8,求任意点的电位,电场.解: 选取原点为电位参考点, 1 表示柱内电位, 2 表示柱外电位. r → ∞ 用 在 处,电位 2 = E0 r cos φ因几何结构和场分布关于 y = 0 平面对称, 故电位表 示式中不应有 φ 的正弦项.令rE0φε ε0图 4-8x1 = A0 + ∑ ( An r n + Bn r n ) cos nφn =1∞55习题四∞ 2 = C0 + ∑ (Cn r n + Dn r n ) cos nφn =1因在原点处电位为零,定出 A0 = 0 , Bn = 0 .用无穷远处边界条件 r → ∞ 及 2 = E0 r cos φ ,定出 C1 = E0 ,其余 Cn = 0 .这样,柱内,外电位简化为 1 = ∑ An r n cos nφn =1∞ 2 = C1r cos φ + ∑ Dn r n cos nφn =1∞再用介质柱和空气界面 ( r = a ) 的边界条件 1 = 2 及 ε 1 = ε 0 2 ,得 r r∞ ∞ n n ∑ An a cos nφ = E0 a cos φ + ∑ Dn a cos nφ n =1 n =1 ∞ ∞ ∑ εnAn a n 1 cos nφ = ε 0 E0 cos φ ∑ ε 0 nDn a n 1 cos nφ n =1 n =1 比较左右 n = 1 的系数,得A1 解之得D1 D1 = E0 , ε A1 + ε 0 2 = ε 0 E0 2 a aA1 = 2ε 0 ε ε0 E0 , D1 = E0 a 2 ε + ε0 ε + ε0比较系数方程左右 n > 1 的各项,得An Dn D = 0 , ε An + ε 0 2n = 0 2n a a n由此解出 An = Dn = 0 .最终得到圆柱内,外的电位分别是1 = E02ε 0 r cos φ , ε + ε0ε ε0 a2 2 = E0 r cos φ + E0 cos φ ε + ε0 r56《电磁场与电磁波》——习题详解电场强度分别为v v 2ε 0 v 2ε 0 E1 = 1 = er E0 cos φ eφ E0 sin φ ε + ε0 ε + ε0v v ε ε 0 a2 v ε ε 0 a2 1 + E0 cos φ eφ 1 E2 = 2 = er ε + ε r 2 E0 sin φ ε + ε0 r2 0 4-14 在均匀电场中,设置一个半径为 a 的介质球,若电场的方向沿 z 轴,求介质 球内,外的电位,电场(介质球的介电常数为 ε ,球外为空气). 解:设球内,外电位解的形式分别为1 = ∑ ( An r n + Bn r n 1 ) Pn (cos nθ ) ,n =0 ∞∞ 2 = ∑ (Cn r n + Dn r n 1 ) Pn (cos nθ )n =0在 选取球心处为电位的参考点, 则球内电位的系数中 A0 = 0 ,Bn = 0 . r → ∞ 处,电位 2 = E0 r cos θ ,则球外电位系数 Cn 中,仅仅 C1 不为零,即 C1 = E0 , 其余为零.因此,球内,外解的形式分别简化为1 = ∑ An r n Pn (cos nθ ) ,n =0∞ 2 = E0 r cos θ + ∑ Dn r n 1 Pn (cos nθ )n =0∞再用介质球面 ( r = a ) 的边界条件 1 = 2 及 ε1 = ε 0 2 ,得 r r∞ ∞ n An a Pn (cos nθ ) = E 0 a cos θ + Dn a n 1 Pn (cos nθ ) n =1 n =1 ∞ ∞ εnA a n 1 P (cos nθ ) = ε E cos θ ε 0 (n + 1) Dn a n 2 Pn (cos nθ ) n n 0 0 n =1 n =1 ∑ ∑∑∑比较上式的系数,可以知道,除了 n = 1 以外,系数 An , Dn 均为零,且A1a = E0 a + D1a 2 , ε A1 = ε 0 E0 2ε 0 D1a 357习题四由此,解出系数A1 = 3ε 0 ε ε0 E0 , D1 = E0 a 3 ε + 2ε 0 ε + 2ε 0 3ε 0 r cos θ , ε + 2ε 0最后得到电位,电场1 = E0 2 = E0 r cos θ + E0v v E1 = 1 = erε ε 0 a3 cos θ ε + 2ε 0 r 23ε 0 v 3ε 0 E0 cos θ eθ E0 sin θ ε + 2ε 0 ε + 2ε 0v ε ε 0 a3 ε ε 0 a3 v v 1 + 2 E0 cos θ eθ 1 E2 = 2 = er ε + 2ε r 3 E0 sin θ ε + 2ε 0 r 3 0 4-15 已知球面 ( r = a ) 上的电位为 = U 0 cos θ ,求球外的电位. 解:设球外电位解的形式为 = ∑ ( An r n + Bn r n 1 ) Pn (cos nθ )n =0∞在无穷远处,应该满足自然边界条件,即电位趋于零.这样确定系数 An = 0 ,球外 电位的形式解简化为 = ∑ Bn r n 1 Pn (cos nθ )n =0∞使用球面 ( r = a ) 的边界条件,有U 0 cos θ = ∑ Bn a n 1 Pn (cos nθ )n =0∞由于勒让德多项式 Pn (cos nθ ) 是线性无关的,考虑到 P (cos θ ) = cos θ ,比较上式 1 左右的系数,得到 B1 = U 0 a , Bn = 02(n = 0,2,3,L) .所以,球外的电位分布为58《电磁场与电磁波》——习题详解 = U04-16a2 cos θ r2求无限长矩形区域 (0 < x < a,0 < y < b) 第一类边值问题的格林函数(即矩形 槽的四周电位为零,槽内有一与槽平行的单位线源,求槽内电位,如图 4-9). 解:这个问题的格林函数满足的方程为 2G 2G 1 + 2 = δ( x x′) δ( y y′) 2 x y ε0格林函数的边界条件是,在矩形区域的四周为零,即 x = 0 或 x = a , G = 0 ,y = 0 或 b = 0 , G = 0 .用分离变量法求这个问题的格林函数.考虑到格林函数在x = 0 , x = a 时的边界条件,将格林函数表示为y b(x',y')G = ∑Ψ n ( y ) sinn =1∞nπ x a将其代入格林函数方程,得a x 2 nπ 2 nπ x 1 = δ( x x′) δ( y y′) Ψ n ( y ) sin 图 4-9 ∑ y 2 a ε0 a n =1 nπ x 上式左右乘以 sin , 并在 0 < x < a 区间积分, 利用正弦函数的正交性和 δ 函数 a∞的积分性质,得函数Ψ n ( y ) 满足的微分方程为2 d2 nπ x ′ 2 nπ sin δ( y y ′) Ψn ( y ) = 2 a ε 0a dy a 在确定函数Ψ n ( y ) 时,将原来的区域分为两个区域,并注意到边界条件,设nπ An sh a (b y ), Ψ n ( y) = nπ Bn sh y, a 在 y = y′ 处,电位连续,即y > y′ y < y′An shnπ nπ (b y′) = Bn sh y′ a a59习题四对于函数Ψ n ( y ) 满足的微分方程,在点源附近积分,得∫y′+ 0 y′0d2 nπ Ψn ( y ) d y 2 dy a 2∫y′+ 0 y′0Ψ0 ( y ) d y = nπ x 2 sin ε 0a a因为电位连续,故上式左边第二项的积分为零,从而有d d nπ x′ 2 sin Ψ n ( y) Ψ n ( y) = dy dy a ε 0a y = y′ y = y′ + 代入函数Ψ n ( y ) 的形式,得nπ nπ nπ nπ x′ nπ 2 (b y′) sin An ch Bn ch y′ = a a a a ε 0a a将上式与 An shnπ nπ (b y′) = Bn sh y′ 相互联立求解,得 a a nπ 2 1 An = sh y′ , nπ ε 0 sh nπ b a a nπ 2 1 Bn = sh (b y′) nπ ε 0 sh nπ b a asin最后得到矩形区域的格林函数为nπ x ′ n π x nπ nπ sin y ≤ y′ sh a (b y′) sh a y, 2 a a = G= nπ ∑ nπ nπ b ε 0π n =1 sh y′ sh (b y ), y ≥ y′ n sh a a a 4-17 推导无限长圆柱区域内(半径为 a )第一类边值问题的格林函数. 解:使用镜像法及其格林函数的定义计算.在半径为 a 的导体圆柱内部离轴 线 r ′ 处,放置一个线密度为 1 单位,与导体圆柱平行的无穷长线电荷,并且维持导∞体柱面的电位为零,求出柱内的电位,这个电位就是柱内的格林函数.当原电荷位 于 r 处,需要在 r ′ 的镜像位置 r ′′ 处,加一个线密度为 1 的线电荷.此时,圆柱内 的电位是v v G (r , r ′) =1 2π εln1 1 1 ln +C R1 2π ε R2R1 和 R2 分别是从 r ′ 和 r ′′ 到 r 的距离(如图 4-10),C 是常数.由柱面上的电位为零,60《电磁场与电磁波》——习题详解可以定出这个常数的值.最后得到柱内的格林函数为v v G (r , r ′) =1 2π εlnR2 r ′ R1 a yrR1 r'R2 r'' x =0 = U0图 4-10 4-18d图 4-11x两个无限大导体平板间距离为 d ,其间有体密度 ρ =ρ 0 x / d 的电荷,极板的电位如图 4-11 所求,用格林函数法求极板之间的电位. 解:先用直接积分法求解.电位仅仅是 x 的函数,故其满足如下方程:ρ x d2 ρ = = 0 2 dx ε0 ε 0d对以上方程积分得ρ x2 ρ x3 d = C1 0 , = C2 + C1 x 0 dx 2ε 0 d 6ε 0 d由 x = 0 及 = 0 , 可 定 出 系 数 C2 = 0 ; 由 x = d 及 = U 0 , 可 定 出 系 数C1 =U 0 ρ0d + ,从而,得到电容器内的电位为 d 6ε 0 =ρ0 x3 6ε 0 dU ρ d + 0 + 0 x d 6ε 0 再用格林函数法求解.这个问题的格林函数为 d x′ x < x′ ε d x, 0 G ( x, x′) = x′ (d x), x > x′ ε 0d 为了计算方便,将这个问题分解为两个:一个是平板电容器内有电荷,而两极板的61习题四电位为零,即奇次边界条件,记电位 1 ;另一个是无电荷分布,极板的电位维持原 来的电位,记电位 2 .用格林函数法计算奇次边界条件时的电位 1 :1 = ρ ( x ′)G ( x, x ′) d x ′0∫d= ρ ( x ′)G ( x, x ′) d x ′ + ρ ( x ′)G ( x, x ′) d x ′0 x∫x∫d=∫x 0ρ 0 x ′ x ′(d x) d x′ + d ε 0d∫d xρ 0 x ′ (d x ′) x d x′ d ε 0dρ 0 (d x) x 3 ρ 0 x 1 2 2 1 (d x )d + (d 3 x 3 ) = + 2 2 3 ε 0d 2 3 ε 0d =ρ0 3 ρ0d x + x 6ε 0 d 2 6ε 0至于电位 2 ,容易得出 2 = (U 0 / d ) x .故所求电位为 = 1 + 2 = 4-192ρ0 2 U 0 ρ0d x + d + 6ε x 6ε 0 d 0 分析复变函数 w = z 能够表示的静电场. 解: w = u + j v = z = ( x + j y ) = x y + j 2 xy2 2 2 2u = x 2 y 2 , v = 2 xy实部的等值线是双曲线 x y = C1 ;虚部的等值线也是双曲线,其方程为2 22 xy = C2 .因此,这个函数能够表示极板形状为双曲线的导体附近的静电场.如果用虚部表示电位函数,在 x = 0 或 y = 0 处,电位为零,可以表示接地的直角导体拐 角附近的静电场. 4-20 分析复变函数 w = arccos z 能够表示哪些情形的静电场.62《电磁场与电磁波》——习题详解解: z = x + j y = cos(u + j v) = cos u ch v j sin u sh vx = cos u ch v , y = sin u sh vx2 y2 x2 y2 + 2 = 1, 2 =1 ch 2 v sh v cos 2 u sin u可见,虚部的等值线是一簇椭圆,实部的等值线是一簇双曲线.当用虚部表示 电位时,能够表示两个共焦点的椭圆柱体之间的场;当用实部表示电位时,能够表 示两个共焦点的双曲线柱体之间的场. 4-21 用有限差分法求图 4-12 所示区域中各个节点的电位. 解:1 4 1 2 = (1 + 4 + 100) 4 1 3 = (1 + 4 ) 4 1 4 = ( 2 + 3 ) 41 = ( 2 + 3 + 100)解这一方程组,得到1 = 2 = 37.5 V , 3 = 4 = 12.5 V100V 1 0V 3 4 2 0V0V 图 4-1263。
电磁场与电磁波(第三版)课后答案第3章
第三章习题解答3.1 真空中半径为a 的一个球面，球的两极点处分别设置点电荷q 和q -，试计算球赤道平面上电通密度的通量Φ(如题3.1图所示)。
解 由点电荷q 和q -共同产生的电通密度为33[]4q R R π+-+-=-=R R D 22322232()(){}4[()][()]r z r z r z a r z a q r z a r z a π+-++-+-++e e e e 则球赤道平面上电通密度的通量d d zz SSS Φ====⎰⎰D S D e22322232()[]2d 4()()aq a arr r a r a ππ--=++⎰ 221201)0.293()aqa q q r a =-=-+ 3.2 1911年卢瑟福在实验中使用的是半径为a r 的球体原子模型，其球体内均匀分布有总电荷量为Ze -的电子云，在球心有一正电荷Ze （Z 是原子序数，e 是质子电荷量），通过实验得到球体内的电通量密度表达式为02314ra Ze r r r π⎛⎫=- ⎪⎝⎭D e ，试证明之。
解 位于球心的正电荷Ze 球体内产生的电通量密度为 124rZer π=D e 原子内电子云的电荷体密度为 333434a a Ze Zer r ρππ=-=- 电子云在原子内产生的电通量密度则为32234344r r ar Ze rr r ρπππ==-D e e 故原子内总的电通量密度为 122314ra Ze r r r π⎛⎫=+=- ⎪⎝⎭D D D e 3.3 电荷均匀分布于两圆柱面间的区域中，体密度为30C m ρ, 两圆柱面半径分别为a 和b ，轴线相距为c )(a b c -<，如题3.3图()a 所示。
求空间各部分的电场。
解 由于两圆柱面间的电荷不是轴对称分布，不能直接用高斯定律求解。
但可把半径为a 的小圆柱面内看作同时具有体密度分别为0ρ±的两种电荷分布，这样在半径为b 的整个圆柱体内具有体密度为0ρ的均匀电荷分布，而在半径为a 的整个圆柱体内则具有体密度为0ρ-的均匀电荷分布，如题3.3图()b 所示。
《电磁场与电磁波第三版》课后答案
ˆ cos ˆ cos sin ˆ F2 (r , , ) sin sin , F2 ( , , z ) 3 用直角坐标系中的坐标分 1.9 将圆柱坐标系中的矢量场 F1 ( , , z ) 2
量表示。 解：根据
习题
ˆ 3y ˆz ˆ y ˆ 2z ˆ; B x ˆ ，求:(a) A 和 B 的大小（模） 1.1 已知 A 2 x ； (b) A 和 B 的单位
矢量；(c) A B ；(d) A B ；(e)A 和 B 之间的夹角；(f) A 在 B 上的投影。 解：(a) A 和 B 的大小
ˆ sin ˆ cos cos ˆ F1 (r , , ) sin cos Fr 2 sin cos F 2 cos cos F 2 sin sin cos cos cos sin sin sin cos sin cos sin sin cos sin cos cos Fx 2 sin Fy 2 0 Fz 2 cos 0 sin sin sin 1 cos sin 0 0 cos
ˆ Ay y ˆ A Ax x ˆ By y ˆ B Bx x ˆ x
ˆ y By Cy
ˆ z ˆ ( Bz C x Bx C z ) y ˆ ( Bx C y B y C x ) z ˆ Bz ( B y C z Bz C y ) x Cz
ˆ 12 y ˆz ˆ 3y ˆz ˆ 和 2x ˆ ，求从 P 点到 Q 点的距离矢 1.6 P 点和 Q 点的位置矢量分别为 5 x
电磁场与电磁波》第 版 谢处方 编 课后习题答案 高等教育出版社
S
2 1 2 1 2
2 1 2 1 2
1 2 1 2 2x2 (1)2 d x dz 1 2 1 2 2x2 ( 1)2 d x dz
1 2 1 2
2
1 2 1 2
2
ቤተ መጻሕፍቲ ባይዱ
1 2 1 2 24x2 y2 (1)3 d x dy 1 2 1 2 24x2 y2 ( 1)3 d x dy 1
Ax ) y
ez
dS
S
y2
dS
a 2 00
r2 sin2 r d d r
a4 4
1.23 证明：（1） R 3 ；（2） R 0 ；（3）(A R) A 。其中 R ex x ey y ez z ， A 为一常矢量。
解 （1） R x y z 3 x y z
（2）
ex ey ez R 0
1 2 1 2
2
1 2 1 2
2
24
故有
Ad
1 24
S
A
d
S
1.19 计算矢量 r 对一个球心在原点、半径为 a 的球表面的积分，并求 r 对球体积
的积分。
2
解
r d S r er d S d aa2 sin d 4 a3
S
S
0
0
又在球坐标系中，
r
1 r2
r
(r2r)
3 ，所以
ey Ay
ez Az
A
一径向矢量场 F er f (r) 表示，如果 F 0 ，那么函数 f (r) 会有什么特点
解 在圆柱坐标系中，由 可得到
F 1 d [rf (r)] 0 r dr
f (r) C r
C 为任意常数。
电磁场与电磁波(西安交大第三版)第6章课后答案
第六章 平面电磁波 1.在εr=2, μr=1的理想介质中,频率为f =150MHZ 的均匀平面波沿y 方向传播,y=0处,E =zˆ10V/m,求E , E (y,t), H ,H (y,t) ,S c,υp.解：s m c cv rr p /2==εμ，m f c fv p 222===λπλπ22==kyj jkye z eE E π2010ˆ--==Z=120π/2Z e z yZ E k H yj /10ˆˆ/ˆ2π-⨯=⨯==-xˆ（2/12π）yj e π2-E (y,t)= zˆ102cos(2π*150*106t-2πy) H (y,t)= -xˆ/6πcos(2π*150*106t-2πy) Sc=*H E ⨯=yˆ52/6π2.在真空中H =xˆx H =x ˆ0H zj e π2求E ,E (z,t), λ, f ,Z, S c.解：Z=120πE =kH Z ˆ⨯=z j e H z x ππ20120)ˆ(ˆ-⨯=y ˆ120π0H z j e π2 k=2πλ=k π2=1m ，Hz c v f p 8103⨯===λλ Sc=*H E⨯=-zˆ120π0H 23.在理想介质中E (x,t)= y ˆ80π2cos(10*107πt+2πx)H (x,t)= -z ˆ2cos(10*107πt+2πx)求: f , εr, μr ,λ.解：71010⨯=πω，f =πω2=5*107Hz π2=k ，λ=kπ2=1m,m f c 60==λ由: k=2π=ω (εrμr)2/1及 Z=80π=120π(μr /εr)2/1 得：εr=9 ,μr=44.均匀平面电磁波在真空中沿kˆ=1/2(yˆ+z ˆ)方向传播, 0E =10x ˆ,求E ,E (y,z,t),H ,H (y,z,t), Sc解：则k=2π,E =0E r k j e ∙-=xˆ10))(2(z y j e +-πH =1/Z*⨯kˆE =2/24π(yˆ-z ˆ))(2z y j e +-πE (y,z,t)= xˆ102cos(2πc/λt-（2π）(y+z)) H (y,z,t)= 1/12π(y ˆ-z ˆ)cos(2πc/λt-（2π）(y+z)) Sc=*H E ⨯=（5/62π)(yˆ+z ˆ)5、在均匀理想介质中)sin(2ˆ)cos(2ˆ)(00kz t E y kz t E xt E -+-=ωω. 求)(t H及平均坡印亭矢量。
谢处方电磁场与电磁波(第三版)答案
(A B)A (A A)B (A C)A (A A)C
由于 A B A C ，于是得到 (A A)B (A A)C
故
BC
1.7 如果给定一未知矢量与一已知矢量的标量积和矢量积，那么便可以确定该未知矢
量。设 A 为一已知矢量， p A X 而 P A X ， p 和 P 已知，试求 X 。 解 由 P A X ，有
ex ey ez 解 A B 2 3 4 ex13 ey 22 ez10
6 4 1
所以 A B 在 C 上的分量为
(A B)C
(A B) C
C
25 3
14.43
1.6 证明：如果 A B A C 和 A B AC ，则 B C ； 解 由 A B AC ，则有 A (A B) A (AC) ，即
E
25 r2
且 RPP 与 x 、 y 、 z 轴的夹角分别为
x
cos1( ex RPP RPP
)
cos1(
5 ) 32.31 35
y
cos1(ey RPP ) cos1( RPP
3 ) 120.47 35
z
cos1( ez RPP RPP
)
cos 1 (
1 ) 99.73 35
1.4 给定两矢量 A ex 2 ey 3 ez 4 和 B ex 4 ey 5 ez 6 ，求它们之间的夹角和
故该点的直角坐标为 (2, 2 3, 3) 。
（2）在球坐标系中 r 42 32 5 、 tan1(4 3) 53.1 、 2 3 120 故该点的球坐标为 (5,53.1 ,120 )
1.9
用球坐标表示的场 E
er
25 r2
，
（1）求在直角坐标中点 (3, 4, 5) 处的 E 和 Ex ；
电磁场与电磁波(西安交大第三版)第2章课后答案
第2章习题2-1.已知真空中有四个点电荷q C 11=，q C 22=，q C 34=，q C 48=，分别位于(1,0,0)，(0,1,0)，(-1,0,0,)，(0,-1,0)点，求(0,0,1)点的电场强度。
解：z y r z x r z y r z xr ˆˆ;ˆˆ;ˆˆ;ˆˆ4321+=+=+-=+-=84ˆ15ˆ6ˆ3)ˆˆˆˆ(41024442333222221110πεπεz y xr r q r r q r r q r r q E ++=+++=2-2.已知线电荷密度为ρl 的均匀线电荷围成如图所示的几种形状，求P 点的电场强度。
题2-2图解：(a) 由对称性04321=+++=E E E E E(b) 由对称性0321=++=E E E E(c) 两条半无限长线电荷产生的电场为yay x y x a E E E ll a ˆ2)}ˆˆ()ˆˆ{(40021περπερ-=+--=+=半径为a 的半圆环线电荷产生的电场为y a E lb ˆ20περ=总电场为0=+=b a E E E2-3.真空中无限长的半径为a 的半边圆筒上电荷密度为ρs ，求轴线上的电场强度。
解:在无限长的半边圆筒上取宽度为ϕad 的窄条,,电荷线密度为ϕρρad s l =,对ϕ积分,可得真空中无限长的半径为a 的半边圆筒在轴线上的电场强度为y d x y a d r a E ss s ˆ)ˆcos ˆsin (22ˆ00000⎰⎰-=--==πππερϕϕϕπερπεϕρ题2-3图 题2-4图2-4.真空中无限长的宽度为a 的平板上电荷密度为ρs ，求空间任一点上的电场强度。
解: 在平板上'x 处取宽度为'dx 'dx s l ρρ=，在点),(y x 处产生的电场为ρρρπε'ˆ21),(0dx y x E d s =其中22)'(y x x +-=ρ；22)'(ˆˆ)'(ˆyx x y y xx x +-+-=ρ对'x 积分可得无限长的宽度为a 的平板上的电荷在点),(y x 处产生的电场为)}2/2/(2ˆ)2/()2/(ln ˆ{4),(22220y a x arctg y a x arctg y ya x y a x x y x E s --+++-++=περ 2-5.已知真空中电荷分布为r a ，b 为常数。
电磁场与电磁波习题解 谢处方 饶克谨编(第三版)
C
C
∫= 2π (−a2 cosφ sinφ + a4 cos2 φ sin2 φ )dφ = π a4
0
4
∫ ∫ S
∇×
� AidS
=
S
� ez
(
∂Ay ∂x
−
∂Ax ∂y
)ie�z dS
∫ ∫ ∫ = y2dS = a 2π r2 sin2 φrdφdr = π a4
S
00
4
∫ � � �
1.19 给定矢量函数 E = ex y + e y x ，试求从点 P1(2,1, −1) 到点 P2 (8, 2, −1) 的线积分
�� Eidl ：
� （1）沿抛物线 x = y2 ；（ 2）沿连接该两点的直线。这个 E 是保守场吗？
��
解（1） ∫ Eidl = ∫ Exdx + Eydy = ∫ ydx + xdy
C
C
C
2
2
∫ ∫ = yd(2 y2 ) + 2 y2dy = 6 y2dy = 14
1
1
（2）连接点 P1(2,1, −1) 到点 P2 (8, 2, −1) 直线方程为
−1/ 2 −1/ 2
2
−1/ 2 −1/ 2
2
=1 24
故有
�
∫ ∇iAdτ
τ
=
1 24
=
�∫
S
�� AidS
1.14
计算矢量
� r
对一个球心在原点、半径为
a
的球表面的积分，并求
∇ir�
对球体积的积分。
解
�∫
r�idS
=
�∫
电磁场与电磁波第三版课后答案 谢处方
第一章习题解答1.1 给定三个矢量A 、B 和C 如下：23x y z =+-A e e e4y z =-+B e e52x z =-C e e求：（1）A a ；（2）-A B ；（3）A B g ；（4）AB θ；（5）A 在B 上的分量；（6）⨯A C ；（7）()⨯A B C g 和()⨯A B C g ；（8）()⨯⨯A B C 和()⨯⨯A B C 。
解 （1）23A x y z +-===-e e e A a e e e A（2）-=A B (23)(4)x y z y z +---+=e e e ee 64x y z +-=e e e （3）=A B g (23)x y z +-e e e (4)y z -+=e e g －11（4）由cos AB θ===A B A B g ，得1cos AB θ-=(135.5=o（5）A 在B 上的分量 B A =A cos AB θ==A B B g（6）⨯=A C 123502xy z-=-e e e 41310x y z ---e e e（7）由于⨯=B C 041502x y z-=-e e e 8520x y z ++e e e⨯=A B 123041xyz-=-e e e 1014x y z ---e e e所以 ()⨯=A B C g (23)x y z +-e e e g (8520)42x y z ++=-e e e()⨯=A B C g (1014)x y z ---e e e g (52)42x z -=-e e（8）()⨯⨯=A B C 1014502x y z---=-e e e 2405x y z -+e e e()⨯⨯=A B C 1238520x y z -=e e e 554411x y z --e e e1.2 三角形的三个顶点为1(0,1,2)P -、2(4,1,3)P -和3(6,2,5)P 。
（1）判断123PP P ∆是否为一直角三角形； （2）求三角形的面积。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
AA
1.8 在圆柱坐标中，一点的位置由 (4, 2 ,3) 定出，求该点在：（1）直角坐标中的坐 3
标；（2）球坐标中的坐标。
解 （1）在直角坐标系中 x 4cos(2 3) 2 、 y 4sin(2 3) 2 3 、 z 3
故该点的直角坐标为 (2, 2 3, 3) 。
（2）在球坐标系中 r 42 32 5 、 tan1(4 3) 53.1 、 2 3 120
则
RPP rP rP ex 5 ey 3 ez
且 RPP 与 x 、 y 、 z 轴的夹角分别为
x
cos1( ex RPP RPP
)
cos 1 (
5 ) 32.31 35
y
cos1(ey RPP ) cos1( RPP
3 ) 120.47 35
z
cos1( ez RPP RPP
)
cos 1 (
1 ) 99.73 35
1.4 给定两矢量 A ex 2 ey 3 ez 4 和 B ex 4 ey 5 ez 6 ，求它们之间的夹角和
A 在 B 上的分量。
解 A 与 B 之间的夹角为
AB
cos 1 (
A A
B B
)
cos 1 (
31 ) 131 29 77
A 在 B 上的分量为
2
解
r d S r er d S d aa2 sin d 4 a3
S
S
0
0
又在球坐标系中，
r
1 r2
r
(r2r)
3 ，所以
2 a
r d 3r2 sin d r d d 4 a3
0 00
1.15 求矢量 A exx ey x2 ez y2z 沿 xy 平面上的一个边长为 2 的正方形回路的线
Az z)
ex Ax
ey Ay
ez Az
A
一径向矢量场 F er f (r) 表示，如果 F 0 ，那么函数 f (r) 会有什么特点
解 在圆柱坐标系中，由 可得到
F 1 d [rf (r)] 0 r dr
在球坐标系中，由
f (r) C r
C 为任意常数。
F
1 r2
d dr
[r2
f
,.
第一章习题解答
1.1 三个矢量 A 、 B 和 C 如下：
A ex ey 2 ez 3 B ey 4 ez C ex5 ez 2 求：（1） aA ；（2） A B ；（3） A B ；（4）AB ；（5） A 在 B 上的分量；（6） AC ； （7） A (B C) 和 ( A B) C ；（8） (A B)C 和 A (B C) 。
sin1 sin2 cos(1 2 ) cos1 cos2
1.11 一球面 S 的半径为 5 ，球心在原点上，计算： (er 3sin ) d S 的值。 S
,.
2
解 (er 3sin ) d S (er 3sin ) er d S d 3sin 52 sin d 75 2
S
S
0
故该点的球坐标为 (5,53.1 ,120 )
1.9
用球坐标表示的场
E
er
25 r2
，
（1）求在直角坐标中点 (3, 4, 5) 处的 E 和 Ex ；
（2）求在直角坐标中点 (3, 4, 5) 处 E 与矢量 B ex 2 ey 2 ez 构成的夹角。 解 （1）在直角坐标中点 (3, 4, 5) 处， r2 (3)2 42 (5)2 50 ，故
故
BC
1.7 如果给定一未知矢量与一已知矢量的标量积和矢量积，那么便可以确定该未知矢
,.
量。设 A 为一已知矢量， p A X 而 P A X ， p 和 P 已知，试求 X 。
解 由 P A X ，有
A P A(A X ) (A X )A (A A)X pA (A A)X
故得
X pA A P
S
S
4 2
5 2
52 5d d z 2 4r d r d 1200
00
00
故有
Ad 1200 A d S
S
1.13 求（1）矢量 A ex x2 ey x2 y2 ez 24x2 y2z3 的散度；（2）求 A 对中心在原
点的一个单位立方体的积分；（3）求 A 对此立方体表面的积分，验证散度定理。
B ) cos1(19 B
(10 32
2)) 153.6
1.10 球坐标中两个点 (r1,1,1) 和 (r2 ,2 ,2 ) 定出两个位置矢量 R1 和 R2 。证明 R1 和 R2 间夹角的余弦为
解由
cos cos1 cos2 sin1 sin2 cos(1 2 ) R1 exr1 sin1 cos1 eyr1 sin1 sin 1 ezr1 cos1
解
（1） aA
A A
ex ey 2 ez 3 12 22 (3)2
ex
1 14
ey
2 14
ez
3 14
（2） A B (ex ey 2 ez 3) (ey 4 ez ) ex ey 6 ez 4 53
（3） A B (ex ey 2 ez 3) (ey 4 ez ) －11
（4）由
cosAB
A B 11 11
A B 14 17
238
AB cos1 (
11 ) 135.5 238
（5） A 在 B 上的分量
AB
A
cos AB
A B B
11 17
，得
ex （6） AC 1
5
ey ez 2 3 ex 4 ey13 ez10 0 2
ex ey ez （7）由于 BC 0 4 1 ex 8 ey 5 ez 20
5 0 2
ex A(BC) 1
8
ey ez 2 3 ex 55 ey 44 ez11 5 20
1.2 三角形的三个顶点为 P1(0,1, 2) 、 P2 (4,1, 3) 和 P3(6, 2, 5) 。 （1）判断 P1P2P3 是否为一直角三角形；
,.
（2）求三角形的面积。
解 （1）三个顶点 P1(0,1, 2) 、 P2 (4,1, 3) 和 P3(6, 2, 5) 的位置矢量分别为
0
1.12 在由 r 5 、 z 0 和 z 4 围成的圆柱形区域，对矢量 A err2 ez 2z 验证散
度定理。
解 所以
在圆柱坐标系中
A 1 (rr2 ) (2z) 3r 2
r r
z
4 2 5
Ad d z d (3r 2)r d r 1200
0
0
0
又
A dS (err2 ez 2z) (er d Sr e d S ez d Sz )
R2 exr2 sin2 cos2 eyr2 sin2 sin 2 ezr2 cos2
得到
cos R1 R2 R1 R2
sin1 cos1 sin2 cos2 sin1 sin1 sin2 sin2 cos1 cos2
sin1 sin2 (cos1 cos2 1 sin1 sin2 ) cos1 cos2
所以
A d S (ex 2yz ez 2x) ez d x d y 8
S
00
故有
A dl 8 A dS
C
S
1.16 求矢量 A ex x ey xy2 沿圆周 x2 y2 a2 的线积分，再计算 A 对此圆面
积的积分。
解
A d l x d x xy2 d y 2 (a2 cos sin a4 cos2 sin2 ) d a4
AB A
B B
31 3.532 77
1.5 给 定 两 矢 量 A ex 2 ey 3 ez 4 和 B ex 6 ey 4 ez ， 求 A B 在 C ex ey ez 上的分量。
ex ey ez 解 A B 2 3 4 ex13 ey 22 ez10
6 4 1
所以 A B 在 C 上的分量为
r1 ey ez 2 ， r2 ex 4 ey ez 3 ， r3 ex 6 ey 2 ez 5
则
R12 r2 r1 ex 4 ez ，
R23 r3 r2 ex 2 ey ez 8 ，
R31 r1 r3 ex 6 ey ez 7
由此可见
R12 R23 (ex 4 ez ) (ex 2 ey ez 8) 0
25 1
E
er r2
2
Ex
ex
E
E
cosrx
1 3 2 52
3 2 20
（2）在直角坐标中点 (3, 4, 5) 处， r ex 3 ey 4 ez 5 ，所以
E 25 25r ex 3 ey 4 ez 5
r2 r3
10 2
故 E 与 B 构成的夹角为
EB
cos1( E E
(r)]
0
,.
可得到
f
(r)
C r2
1.19 给定矢量函数 E ex y ey x ，试求从点 P1(2,1, 1) 到点 P2 (8, 2, 1) 的线积分
E d l ：（1）沿抛物线 x y2 ；（2）沿连接该两点的直线。这个 E 是保守场吗？
解 （1） E d l Ex d x Ey d y y d x x d y
故 P1P2P3 为一直角三角形。
（2）三角形的面积
1
1
1
S 2
R12 R23
2
R12
R23
2
17
69 17.13
1.3 求 P(3,1, 4) 点到 P(2, 2,3) 点的距离矢量 R 及 R 的方向。