信号与系统冲激信号尺度变换的证明
信号与系统重点概念公式总结

信号与系统重点概念公式总结Last updated on the afternoon of January 3, 2021信号与系统重点概念及公式总结:第一章:概论1.信号:信号是消息的表现形式。
(消息是信号的具体内容)2.系统:由若干相互作用和相互依赖的事物组合而成的具有特定功能的整体。
第二章:信号的复数表示:1.复数的两种表示方法:设C 为复数,a 、b 为实数。
常数形式的复数C=a+jba 为实部,b 为虚部;或C=|C|e j φ,其中,22||b a C +=为复数的模,tan φ=b/a ,φ为复数的辐角。
(复平面)2.欧拉公式:wt j wt e jwt sin cos +=(前加-,后变减) 第三章:正交函数集及信号在其上的分解1.正交函数集的定义:设函数集合)}(),(),({21t f t f t f F n =如果满足:n i K dt t f j i dt t f t f i T T i T T j i 2,1)(0)()(21212==≠=⎰⎰则称集合F 为正交函数集如果n i K i ,2,11==,则称F 为标准正交函数集。
如果F 中的函数为复数函数条件变为:ni K dt t f t f j i dt t f t f i T T i i T T j i 2,1)()(0)()(2121**==⋅≠=⋅⎰⎰其中)(*t f i 为)(t f i 的复共轭。
2.正交函数集的物理意义:一个正交函数集可以类比成一个坐标系统;正交函数集中的每个函数均类比成该坐标系统中的一个轴;在该坐标系统中,一个函数可以类比成一个点;点向这个坐标系统的投影(体现为该函数与构成坐标系的函数间的点积)就是该函数在这个坐标系统中的坐标。
3.正交函数集完备的概念和物理意义:如果值空间中的任一元素均可以由某正交集中的元素准确的线性表出,我们就称该正交集是完备的,否则称该正交集是不完备的。
如果在正交函数集()()()()t g n ,t g ,t g ,t g 321之外,不存在函数x (t )()∞<<⎰2120t t dt t x ,满足等式:()()⎰=210t t i dt t g t x ,则此函数集称为完备正交函数集。
信号与系统4.3拉氏变换的性质

T
T2
2
E(2 )
T
s2 ( 2 )2
E(2 )
[
s2
T
( 2
)2
sT
]e 2
T
T
E(2 )
T
s2 ( 2 )2
(1
sT
e2
)
T
第4章 拉普拉斯变换、连续时间系统的S域分析
例4-4 试求图4.4所示的正弦半波周期信号的拉氏变换。
f (t)
E
…
0
TT
2T
t
2
图4.4 例 4―4图
解: 在例4―3中我们已求得从t=0开始的单个正弦半波(亦即
0 24
t
图4.5 例4-5图
e2(t2)e4u(t 2) e2(t4)e8u(t 4)
于是
F (s) L[ f (t)] e4L[e2t ]e2s e8L[e2t ]e4s
e2(s2) e4(s2) s2
第4章 拉普拉斯变换、连续时间系统的S域分析
4、s域平移特性
若 f (t) F(s)
t)u(t) E sin[ T
(t )]u(t )
2
2
第4章 拉普拉斯变换、连续时间系统的S域分析
应用拉氏变换的时移特性,有
F (s) L[ f (t)] L[ fa (t)] L[ fb (t)]
L[E sin(2 t)u(t)] L{E sin[ 2 (t T )]u(t T )}
本题第一个周期的波形)的拉氏变换为
F1(s)
L[
f
(t)]
E(2 )
T
s2 ( 2 )2
(1
sT
e2
)
T
第4章 拉普拉斯变换、连续时间系统的S域分析
信号与系统常用变换对及性质梳理
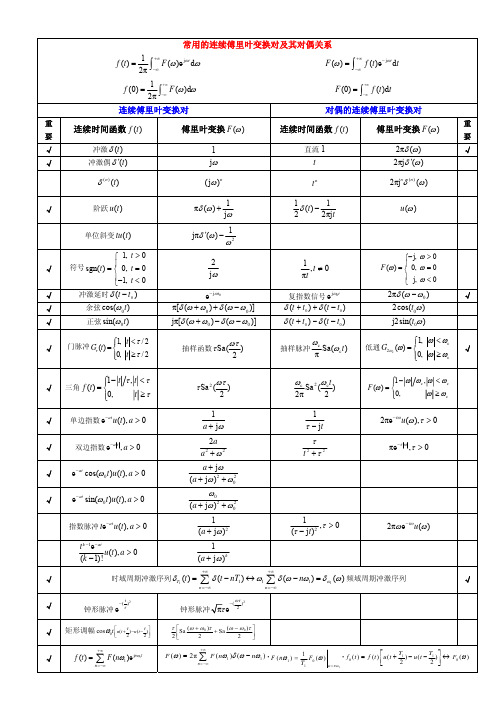
√ √ √ √
时域周期冲激序列 δ T1 (t ) =
t − ( )2
n =−∞
∑ δ (t − nT1 ) ↔ ω1 ∑ δ (ω − nω1 ) = δω (ω ) 频域周期冲激序列
n =−∞
1
+∞
+∞
√
钟形脉冲 e
τ
钟形脉冲 πτ e
τ ⎡
2⎢ ⎣ Sa
−(
ωτ
2
)2
矩形调幅 cos ω0t ⎡u(t +τ ) −u(t −τ )⎤ ⎢ ⎥
√ √ √ √
F (t ) ↔ 2πf (−ω ) f (t )e jω0 t (− jt ) f (t ) πf (0)δ (t ) + f (t ) p(t ) f (t ) − jt F (ω − ω 0 ) F '(ω )
f (t − t 0 ) f '(t )
F (ω )e− jωt0 jω F (ω ) πF (0)δ (ω ) + F (ω ) jω
jω0 t
√ √ √ √ √
⎧ 1, t > 0 ⎪ 符号 sgn(t ) = ⎨ 0, t = 0 ⎪−1, t < 0 ⎩
冲激延时 δ (t − t 0 ) 余弦 cos(ω0 t ) 正弦 sin(ω0 t )
⎧− j, ω > 0 ⎪ F (ω ) = ⎨ 0, ω = 0 ⎪ ⎩ j, ω < 0
(n + 1)a n u (n) (n + 1)! a n u ( n) (n + k − 1)!k !
z , z > a z−a
z , z > a ( z − a) 2 z2 , z > a ( z − a) 2 z k +1 , z > a ( z − a ) k +1
《信号与系统》课程实验报告

《信号与系统》课程实验报告《信号与系统》课程实验报告一图1-1 向量表示法仿真图形2.符号运算表示法若一个连续时间信号可用一个符号表达式来表示,则可用ezplot命令来画出该信号的时域波形。
上例可用下面的命令来实现(在命令窗口中输入,每行结束按回车键)。
t=-10:0.5:10;f=sym('sin((pi/4)*t)');ezplot(f,[-16,16]);仿真图形如下:图1-2 符号运算表示法仿真图形三、实验内容利用MATLAB实现信号的时域表示。
三、实验步骤该仿真提供了7种典型连续时间信号。
用鼠标点击图0-3目录界面中的“仿真一”按钮,进入图1-3。
图1-3 “信号的时域表示”仿真界面图1-3所示的是“信号的时域表示”仿真界面。
界面的主体分为两部分:1) 两个轴组成的坐标平面(横轴是时间,纵轴是信号值);2) 界面右侧的控制框。
控制框里主要有波形选择按钮和“返回目录”按钮,点击各波形选择按钮可选择波形,点击“返回目录”按钮可直接回到目录界面。
图1-4 峰值为8V,频率为0.5Hz,相位为180°的正弦信号图1-4所示的是正弦波的参数设置及显示界面。
在这个界面内提供了三个滑动条,改变滑块的位置,滑块上方实时显示滑块位置代表的数值,对应正弦波的三个参数:幅度、频率、相位;坐标平面内实时地显示随参数变化后的波形。
在七种信号中,除抽样函数信号外,对其它六种波形均提供了参数设置。
矩形波信号、指数函数信号、斜坡信号、阶跃信号、锯齿波信号和抽样函数信号的波形分别如图1-5~图1-10所示。
图1-5 峰值为8V,频率为1Hz,占空比为50%的矩形波信号图1-6 衰减指数为2的指数函数信号图1-7 斜率=1的斜坡信号图1-8 幅度为5V,滞后时间为5秒的阶跃信号图1-9 峰值为8V,频率为0.5Hz的锯齿波信号图1-10 抽样函数信号仿真途中,通过对滑动块的控制修改信号的幅度、频率、相位,观察波形的变化。
信号与系统 拉普拉斯变换的基本性质

L
f
(at
b)u(at
b)
1
F
(
s
)
sb
ea
(a 0,b 0)
aa
信号与系统
四.s 域平移
若 L f (t) F(s)
则 L f (t) eαt F (s α)
证明:
L f (t) eαt
f (t) eαtestd t f (t) e(αs)td t F (s α)
sF (s)
f
(0 )
证明: f (t) estd t f (t) est [sf (t) est ]d t
0
0
0
推广:
f (0) sF(s)
L
d
f 2 (t)
dt2
s
L
d
f (t)
dt
f
(0 )
ssF(s)
f
(0 )
f
(0 )
s2F (s) sf (0 ) f (0 )
s0
f
(0
)
lim
s0
d f (t) estd t 0 d t
f
(0
)
lim
t
f
(t)
f (0 )
lim f (t) t
信号与系统
九.初值定理和终值定理
例:确定下列拉普拉斯变换所对应的时域因果信号的初值和终值
I(s) s 2 s(s 2)
H(s)
s2
8 10s
169
V(s)
2s3 10 s3 (s 1)
t0 0
证明:
L f (t t0 )u(t t0 )
0
f
(t
t0 )u(t
信号与系统第一章重点

是线性系统,否则是非线性系统 否则是非线性系统。 则系统 H[•] 是线性系统 否则是非线性系统。 注意:外加激励与系统非零状态单独处理。 注意:外加激励与系统非零状态单独处理。
判断下述微分方程所对应的系统是否为线性系统? 判断下述微分方程所对应的系统是否为线性系统
dr(t) +10r(t) + 5 = e(t) t > 0 dt
∞
(2)奇偶性 δ (−t) = δ (t)
δ ′(t)dt = δ (t) −∞
∞
(3)比例性 −∞ 1 δ (at) = δ (t ) f (t)δ ′(t) = f (0)δ ′(t) − f ′(0)δ (t) a (6)卷积性质 (4)微积分性质 du(t) t f (t) ∗δ (t ) = f (t ) δ (t) = ∫−∞δ(τ )dτ = u(t) dt
不同) ( 与 f (t)δ (t) = f (0)δ (t) 不同 )
X
1 δ (at) = δ (t) a
冲激偶的标度变换
1 1 δ ′(at ) = ⋅ δ ′(t ) a a
1 1 (k ) δ (at ) = ⋅ k δ (t ) a a
(k )
定义看: 从δ (t) 定义看:
p(t ) 1
δ (t) f (t)dt = f (0) −∞
δ (−t) f (t)dt = −∞
+∞
t =−τ
+∞
故 , δ (t) =δ(−t)
∫
−∞
+∞
δ (τ ) f (−τ )d(−τ )
= ∫ δ (τ ) f (−τ )dτ = f (0)
−∞
+∞
为 t 又因 δ (t)只在 = 0有 值
信号与系统课后习题与解答第三章
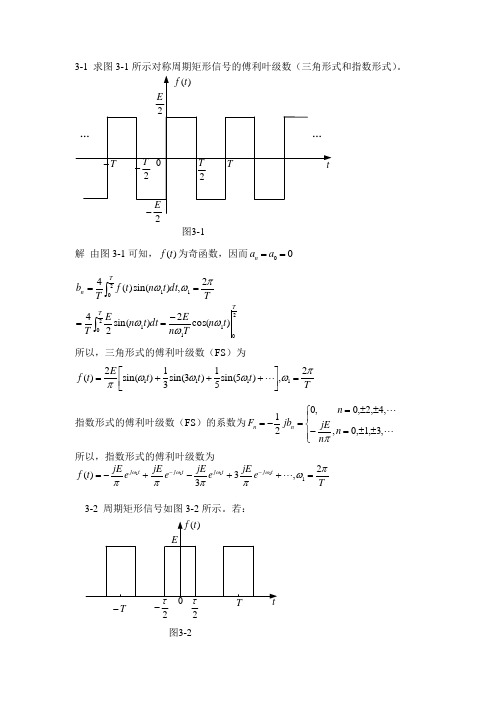
3-1 求图3-1所示对称周期矩形信号的傅利叶级数(三角形式和指数形式)。
图3-1解 由图3-1可知,)(t f 为奇函数,因而00==a a n2112011201)cos(2)sin(242,)sin()(4T T T n t n T n Edt t n E T T dt t n t f T b ωωωπωω-====⎰⎰所以,三角形式的傅利叶级数(FS )为T t t t E t f πωωωωπ2,)5sin(51)3sin(31)sin(2)(1111=⎥⎦⎤⎢⎣⎡+++=指数形式的傅利叶级数(FS )的系数为⎪⎩⎪⎨⎧±±=-±±==-= ,3,1,0,,4,2,0,021n n jE n jb F n n π所以,指数形式的傅利叶级数为T e jE e jE e jE e jE t f t j t j t j t j πωππππωωωω2,33)(11111=++-+-=--3-2 周期矩形信号如图3-2所示。
若:图3-22τT-2τ-重复频率kHz f 5= 脉宽 s μτ20=幅度 V E 10=求直流分量大小以及基波、二次和三次谐波的有效值。
解 对于图3-2所示的周期矩形信号,其指数形式的傅利叶级数(FS )的系数⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛====⎰⎰--22sin 12,)(1112212211τωττωππωττωωn Sa T E n n E dt Ee T T dt e t f T F tjn TT t jn n则的指数形式的傅利叶级数(FS )为∑∑∞-∞=∞-∞=⎪⎭⎫ ⎝⎛==n tjn n tjn n e n Sa TE eF t f 112)(1ωωτωτ其直流分量为TE n Sa T EF n ττωτ=⎪⎭⎫ ⎝⎛=→2lim100 基波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-2sin 2111τωπEF F 二次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-22sin 122τωπEF F 三次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-23sin 32133τωπE F F 由所给参数kHz f 5=可得s T s rad 441102,/10-⨯==πω将各参数的值代入,可得直流分量大小为V 110210201046=⨯⨯⨯--基波的有效值为())(39.118sin 210101010sin 210264V ≈=⨯⨯⨯- πππ二次谐波分量的有效值为())(32.136sin 251010102sin 21064V ≈=⨯⨯⨯- πππ三次谐波分量的有效值为())(21.1524sin 32101010103sin 2310264V ≈=⨯⨯⨯⨯- πππ3-3 若周期矩形信号)(1t f 和)(2t f 的波形如图3-2所示,)(1t f 的参数为s μτ5.0=,s T μ1= ,V E 1=; )(2t f 的参数为s μτ5.1=,s T μ3= ,V E 3=,分别求:(1))(1t f 的谱线间隔和带宽(第一零点位置),频率单位以kHz 表示; (2))(2t f 的谱线间隔和带宽; (3))(1t f 与)(2t f 的基波幅度之比; (4))(1t f 基波与)(2t f 三次谐波幅度之比。
信号与系统MATLAB常见信号的表示及运算

信号与系统——实验指导实验一 常见信号的表示及运算一、实验目的1.熟悉常见信号的意义、特性及波形2. 掌握用matlab软件产生基本信号的方法.3. 应用matlab软件实现信号的加、减、乘、反褶、移位、尺度变换及卷积运算。
二、实验原理1. 信号的表示方法● 常用信号:连续函数()θω+=t t f sin )(, at Ae t f =)(,ttt Sa sin )(= 离散信号()n n f 0sin )(ω=,njw e n f 0)(=,)()(n u a n f n =● 奇异信号:连续函数:冲激函数)(t δ,阶跃函数)(t u ,斜坡函数)(t R 离散信号:冲激函数)(n δ,阶跃函数)(n u ,斜坡函数)(n R2.卷积连续函数的卷积:⎰∞∞--=τττd t f f t g )()()(21离散函数的卷积:∑∞-∞=-=m m n fm f n g )()()(21三、实验要求1.预习实验原理;2.对实验内容编写程序(M文件),上机运行;3.绘出运算或变换后信号的波形.四.实验内容1. 熟悉matlab 工作环境(1) 运行matlab.exe ,进入matlab 工作环境,如图(1)所示。
图1 matlab工作环境(2) matlab工作环境由Command Window(命令窗口)、Current Direcroty(当前目录)、workspace(工作空间)、command History(历史命令)和Editor(文件编辑器)5部分组成。
其中所有文件的编辑和调试、运行在Editor编辑窗口下进行。
程序的运行也可以在命令窗口进行。
程序调试的信息显示在命令窗口。
(3) 程序文件的产生:点击菜单file下的New下的M_files,进入编辑器界面,如图2。
图2 M文件编辑器(4) 在m文件编辑器下键入程序代码,保存程序文件(命名规则同C语言)。
如果所定义的是函数文件,则要求函数名为M文件名。
