作业(二)答案:单自由度机械系统动力学等效转动惯量等效力矩
【大二学习笔记】机械原理第八章 机械的运转及其速度波动的调节

ω
ωmax
ωmin
平均角速度:m
1
T
T d
0
φ
T
工程上常采用算术平均值:
ωm=(ωmax +ωmin)/2
ωmax-ωmin 表示了机器主轴速度波动范围的大小,称为
绝对不均匀度。
定义:δ=(ωmax-ωmin)/ ωm 为机器运转速度不均匀系数, 它表示了机器速度波动的程度。
由ωm=(ωmax +ωmin)/2 以及上式可得:
力矩所作功及动能变化:
Md Mr
ab c d E
e a' φ
φ ω
φ
区间
a-b b-c c-d
d-e
e-a’
外力矩所作功
Md<Mr 亏功“-”
Md>Mr Md<Mr 盈功“+”亏功“-”
Md>Mr Md<Mr 盈功“+” 亏功“-”
主轴的ω
↓
↑
↓
↑
↓
动能E
↓
↑
↓
↑
↓
机械运转的平均速度和不均匀系数
已知主轴角速度:ω=ω( )
二、机械运转过程的三个阶段
稳定运转阶段的状况有:
①匀速稳定运转:ω=常数
②周期变速稳定运转:ω(t)=ω(t+T) 注意:Wd = Wr
③非周期变速稳定运转
m
m
t
起动 稳定运转 停车
起动
稳定运转
t
停车
二、机械运转过程的三个阶段
阶段
名称
运动特征
功能关系
起 动
稳定 运转
停 车
角速度ω由零逐渐上升至 稳定运转时的平均角速 Wd Wr
第七章 机械系统的动力学分析

§7-2 单自由度机械系统动力学分析
3、等效动力学模型的意义
等效力学模型
等效构件 + 等效质量(转动惯量) + 等效力(力矩)
Je
Me
注意: 、、S、V是某构件的真实运动;
Me是系统的等效力矩;
Je是系统的等效转动惯量。
Fe
me
ve
Fe是系统的等效力; me是系统的等效质量。
例题:图示机构。已知z1=20,J1;z2=60,质量中心在B点,
§7-1 概 述
机构力分析的目的和方法
目的: 1)求驱动力。用以确定所需功率,选择合适的电动机。
2)求生产阻力。根据原动件上驱动力的大小,确定机
械所能克服的生产阻力。 3)求机构运动副中的反力。该力大小和性质是零件设
计计算和强度计算的重要依据。
方法:图解法和解析法
§7-1 概 述
二、机械的运转过程 机械运转中的功能关系 Wd - Wc = E2 – E1 其中:Wc = Wr+ Wf 1、 起动阶段: ω=0,↗ωm , 则:E1 =0,↗E2, W= E=E2-E1 >0 故:Wd > Wc = Wr +Wf 主动件作加速运动。
启
动
Wd-Wc=E2-E1>0
稳定运行
Wd-Wc=E2-E1=0
停
车
原动件速度从正常工作速 度值下降到零
Wd-Wc=E2-E1<0
§7-2 单自由度机械系统动力学分析
为了便于讨论机械系统在外力作用下作 功和动能变化,将整个机械系统多个构件运
动问题根据能量守恒原理转化成对某个构件
的运动问题进行研究。为此引入等效转动惯
等效力可以根据等效前后功率相等的原则求取。
机械原理习题及答案
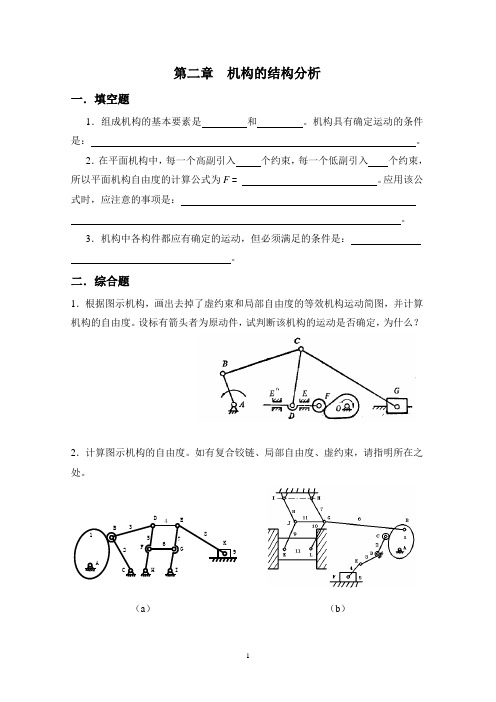
第二章 机构的结构分析一.填空题1.组成机构的基本要素是 和 。
机构具有确定运动的条件是: 。
2.在平面机构中,每一个高副引入 个约束,每一个低副引入 个约束,所以平面机构自由度的计算公式为F = 。
应用该公式时,应注意的事项是: 。
3.机构中各构件都应有确定的运动,但必须满足的条件是: 。
二.综合题1.根据图示机构,画出去掉了虚约束和局部自由度的等效机构运动简图,并计算机构的自由度。
设标有箭头者为原动件,试判断该机构的运动是否确定,为什么?2.计算图示机构的自由度。
如有复合铰链、局部自由度、虚约束,请指明所在之处。
(a ) (b )ADECHGF IBK1234567893.计算图示各机构的自由度。
(a)(b)(c)(d)(e)(f)4.计算机构的自由度,并进行机构的结构分析,将其基本杆组拆分出来,指出各个基本杆组的级别以及机构的级别。
(a)(b)(c)(d)5.计算机构的自由度,并分析组成此机构的基本杆组。
如果在该机构中改选FG 为原动件,试问组成此机构的基本杆组是否发生变化。
6.试验算图示机构的运动是否确定。
如机构运动不确定请提出其具有确定运动的修改方案。
(a)(b)第三章平面机构的运动分析一、综合题1、试求图示各机构在图示位置时全部瞬心的位置(用符号P直接在图上标出)。
ij2、已知图示机构的输入角速度ω1,试用瞬心法求机构的输出速度ω3。
要求画出相应的瞬心,写出ω3的表达式,并标明方向。
3、在图示的齿轮--连杆组合机构中,试用瞬心法求齿轮1与3的传动比ω1/ω2。
4、在图示的四杆机构中,AB l =60mm, CD l =90mm, AD l =BC l =120mm, 2ω=10rad/s ,试用瞬心法求:(1)当ϕ=165°时,点C 的速度c v ;(2)当ϕ=165°时,构件3的BC 线上速度最小的一点E 的位置及其速度的大小; (3)当0c v =u u u v时,ϕ角之值(有两个解)。
第7章机械动力学
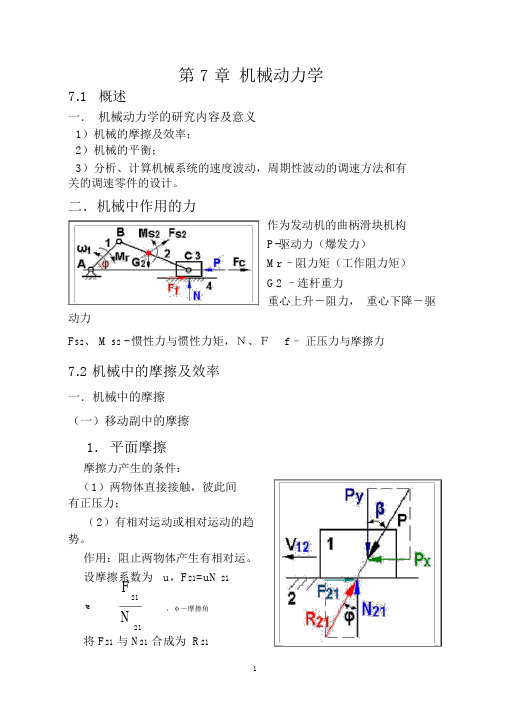
第 7 章机械动力学7.1概述一.机械动力学的研究内容及意义1)机械的摩擦及效率;2)机械的平衡;3)分析、计算机械系统的速度波动,周期性波动的调速方法和有关的调速零件的设计。
二.机械中作用的力作为发动机的曲柄滑块机构P-驱动力(爆发力)Mr –阻力矩(工作阻力矩)G2 –连杆重力重心上升-阻力,重心下降-驱动力F S2、 M S2 - 惯性力与惯性力矩,N、F f –正压力与摩擦力7.2 机械中的摩擦及效率一.机械中的摩擦(一)移动副中的摩擦1.平面摩擦摩擦力产生的条件:(1)两物体直接接触,彼此间有正压力;(2)有相对运动或相对运动的趋势。
作用:阻止两物体产生有相对运。
设摩擦系数为u,F21=uN 21F21tg,φ-摩擦角N21将 F21与 N21合成为 R21R21-总反力(全反力)P X P分解为 P和 P ,tgX Y P Y( P X P sin、 P Y P cos )F21P X,有F21tgY 方向平衡: Py=N 21,即:tg tg P Xtg讨论:①总反力 R21恒与相对速度V 12成 90° +φ②当β >φ, P X > F21,滑块作加速运动;当β =φ, P X = F21,动则恒动,静则恒静;当β <φ, P X < F21,原来运动,作减速运动,原来静止,永远静止,称自锁。
③ 自锁条件:β≤φβ=φ,条件自锁(静止);β<φ,无条件自锁。
2.斜面摩擦斜面机构如图,滑块置于升角α的斜面上,摩擦角为φ,作用于滑块上的铅垂力为Q,求滑块等速上升和下降时所需水平平衡力P 和 P’。
(1)求等速上升水平平衡力 PP-驱动力, Q-阻力PQ R 21 0 ,tg ()P,P Qtg () (1)Q( 2)求等速下降水平平衡力 P ’Q -驱动力, P ’-阻力P'Q R 21 0 ,tg () P ',P 'Qtg () (2)Q讨论:① 欲求下滑 (反行程) P ’,只需将式 ( 1)中 P →P ’,φ→ (-φ )② 下滑时,当α >φ, P ’为平衡力α <φ, P ’为负,成为驱动力的一部分,该条件下,若无 P ’,则无论 Q 多大,滑块不下滑,称自锁,自锁条件:α≤φ。
结构动力学习题解答

然后积分求初始速度
̇̇ d t = θ̇0 = θ 0
0+ 0+ 0+
∫
0
∫ hδ ( t ) d t = h ∫ δ ( t ) d t = h
0 0 0+
;
再积分求初位移
̇̇ d t == h )d t = 0 ; θ0 = θ 0
0+
∫
0
∫
0
̇̇ 、 θ̇ 和 θ 的瞬态响应 这样方程(6)的解就是系统对于初始条件 θ 0 0 0
1.6 求图 1-35 所示系统的固有频率。图中磙子半径为 R,质量为 M,作纯滚动。弹簧刚度 为K 。 解:磙子作平面运动, 其动能 T=T 平动 +T 转动 。
K R M 图 1-35 x
T平动 = T转动
1 ̇2; Mx 2 2 2 ̇ ⎞ 1 ⎛ MR 2 ⎞ ⎛ x ̇⎞ 1 ⎛x = I⎜ ⎟ = ⎜ ⎟⎜ ⎟ ; 2 ⎝R⎠ 2 ⎝ 2 ⎠⎝ R ⎠
U= r 2 1 1 1 1⎛ K A ϕ A 2 + K B ϕ B 2 = K Aϕ A 2 + K B ϕ B 2 = ⎜ K A + K B A 2 2 2 2 2⎜ rB ⎝
(
)
⎞ 2 ⎟ϕ ; ⎟ A ⎠
系统的机械能为
T +U = r 2 1 1⎛ ̇ A2 + ⎜ K A + K B A (m A + m B )rA 2ϕ 4 2⎜ rB 2 ⎝
d (T + U ) = 0 ,进一步得到系 dt
统的运动微分方程; (3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。 1.2 叙述用衰减法求单自由度系统阻尼比的方法和步骤。 用衰减法求单自由度系统阻尼比的方法有两个:衰减曲线法和共振法。 方法一:衰减曲线法。 求解步骤: (1)利用试验测得单自由度系统的衰减振动曲线,并测得周期和相邻波峰和波谷 的幅值 Ai 、 Ai +1 。 (2)由对数衰减率定义 δ = ln(
第一章单自由度机械系统动力学建模解析

静力分析(static) 动态静力分析(kinetio-static) 动力分析(dynamic) 弹性动力分析(elastodynamic)
1 静力分析
对低速机械,运动中产生的惯性可以忽略不计,对机 械的运动过程中的各个位置,可以用静力学方法求出 为平衡载荷而需在驱动构件上施加的驱动力或力矩, 以及各运动副中的约束反力,可用此进行原动机功率 的计算、构件和运动副承载能力的计算。
v32
(M1
1
v3
F3 )v3
me
n i 1
mi
vsi v
2
等 J效si质 量vi
2 me
Fe
n i 1
Fi
程,其维数等于机构的自由度数目; 另一类是含运动副约束反力的代数与微分混合型
方程,其维数大于机构的自由度数目。
机构动力学分析的发展与现状
建立复杂机构动力学模型的常用力学方法有: * 牛顿-欧拉(Newton-Euler)法 * 拉格朗日(Lagrange)法 * 虚功原理法 * 凯恩(Kane)法 * 旋量法和R-W法等。
机械系统动力学
绪论
机械系统动力学是应用力学的基本理论解决 机械系统中动力学问题的一门学科,其核心 问题是建立机械系统的运动状态与其内部参 数、外部条件之间的关系,找到解决问题的 途径
三体机械臂
可伸展卫星太阳能电池板
汽车
五轴并联机床
机械动力学研究内容 :
机械原理由三部分组成:
机械结构学、机构运动学和机械动力学
4 弹性动力分析
随着机械系统向高速轻质化发展,构件的柔度加大,惯 性力急剧加大,构件的弹性变形可能给机械的运动输出 带来误差。机械系统柔度 系统的固有频率 ,机械 运转速度 激振频率 可能会发生共振,破坏运动精度 ,影响疲劳强度,引发噪声。
作业(二)答案:单自由度机械系统动力学等效转动惯量等效力矩

作业(二)单自由度机械系统动力学等效转动惯量等效力矩1.如题图1所示的六杆机构中,已知滑块5的质量为m 5=20kg ,l AB =l ED =100mm ,l BC =l CD =l EF =200mm ,φ1=φ2=φ3=90o ,作用在滑块5上的力P=500N .当取曲柄AB 为等效构件时,求机构在图示位置的等效转动惯量和力P的等效力矩.图1答案:解此题的思路是:①运动分析求出机构处在该位置时,质心点的速度及各构件的角速度.②根据等效转动惯量,等效力矩的公式求出.做出机构的位置图,用图解法进行运动分析.V C =V B =ω1×l AB ω2=0V D =V C =ω1×l AB 且ω3=V C /l CD =ω1V F =V D =ω1×l AB (方向水平向右) ω4=0由等效转动惯量的公式:e J =m 5(V F /ω1)2=20kg ×(ω1×l AB /ω1)2=0.2kgm 2由等效力矩的定义: e M =500×ω1×l AB ×cos180o/ω1=-50Nm (因为VF 的方向与P方向相反,所以α=180o )2.题图2所示的轮系中,已知各轮齿数:z 1=z 2’=20,z 2=z 3=40,J 1=J 2’=0.01kg ·m 2,J 2=J 3=0.04kg ·m 2.作用在轴O3上的阻力矩M3=40N ·m .当取齿轮1为等效构件时,求机构的等效转动惯量和阻力矩M3的等效力矩.图2答案:该轮系为定轴轮系.i 12=ω1/ω2=(-1)1z 2/z 1∴ ω2=-ω1/2=-0.5×ω1ω2’=ω2=-0.5×ω1i 2’3=ω2’/ω3=(-1)1z 3/z 2’ ∴ ω3=0.25×ω1根据等效转动惯量公式e J = J 1×(ω1/ω1)2+J 2×(ω2/ω1)2+J 2’×(ω2’/ω1)2+J 3×(ω3/ω1)2 ∑=+=n i i Si Si i e J v m J 12121]()([ωωω∑=±=n i i i i i i e M v F M 111)]()(cos [ωωωα∑=+=n i i Si Si i e J v m J 12121]()([ωωω=J 1+J 2/4+J 2’/4 +J 3/16=0.01+0.04/4+0.01/4+0.04/16=0.025 kg ·m 2根据等效力矩的公式: e M =M 3×ω3/ω1=40×0.25ω1/ω1=10N ·m3.在题图3所示减速器中,已知各轮的齿数:z 1=z 3=25,z 2=z 4=50,各轮的转动惯量J 1=J 3=0.04kg ·m 2,J 2=J 4=0.16kg ·m 2,(忽略各轴的转动惯量),作用在轴Ⅲ上的阻力矩M 3=100N ·m .试求选取轴Ⅰ为等效构件时,该机构的等效转动惯量J 和M 3的等效阻力矩M r .图3答案:i 12=ω1/ω2=z 2/z 1 ω2=ω1/2 ω3=ω2=ω1/2 i 34=ω3/ω4=z 4/z 3ω4=ω1/4等效转动惯量:J=J 1(ω1/ω1)2+J 2(ω2/ω1)2+J 3(ω3/ω1)2+J 4(ω4/ω1)2=0.042+0.16×(1/2)2+0.04×(1/2)2+0.16×(1/4)2=0.04+0.04+0.01+0.01=0.1 kg ·m 2等效阻力矩:M r =M 3×ω4/ω1=100/4=25(N ·m)4.题图4所示为一简易机床的主传动系统,由一级带传动和两级齿轮传动组成.已知直流电动机的转速n 0=1500r/min ,小带轮直径d =100mm ,转动惯量J d =0.1kg ·m 2,大带轮直径D =200mm ,转动惯量J D =0.3kg ·m 2.各齿轮的齿数和转动惯量分别为:z 1=32,J 1=0.1kg ·m 2,z 2=56,J 2=0.2kg ·m 2,z 2’=32,J 2’=0.4kg ·m 2,z 3=56,J 3=0.25kg ·m 2. 要求在切断电源后2秒,利用装在轴上的制动器将整个传动系统制动住.求所需的制动力矩M 1.图4∑=±=n i i i i i i e M v F M 111()(cos [ωωωα答案:电机的转速n0=1500r/min其角速度ω0=2π×1500/60=50π(rad/s)三根轴的转速分别为:ω1=d×ω0/D=25π(rad/s)ω2=z1×ω1/z2=32×25π/56=1429π(rad/s)ω3=z2’×ω2/z3=32×1429π/56=816π(rad/s)轴的等效转动惯量:J V=J d×(ω0/ω1)2+J D×(ω1/ω1)2+J1×(ω1/ω1)2+J2×(ω2/ω1)2+ J2’×(ω2/ω1)2+ J3×(ω3/ω1)2∴J V=0.1×(50π/25π)2+0.3×12+0.1×12+(0.2+0.1)×(14.29π/25π)2+0.25×(8.16π/25π)2=0.4+0.4+0.098+0.027=0.925 (kg·m2)轴制动前的初始角速度ω1=25π,制动阶段做减速运动,即可求出制动时的角加速度∴ωt=ω0-εt即0=25π-2εε=12.5π则在2秒内制动,其制动力矩M为:M=J V×ε=0.925×12.5=36.31 (kg·m)5.在题图5所示定轴轮系中,已知各轮齿数为:z1=z2’=20,z2=z3=40;各轮对其轮心的转动惯量分别为J1=J2’=0.01kg·m2,J2=J3=0.04kg·m2;作用在轮1上的驱动力矩M d=60N·m,作用在轮3上的阻力矩M r=120N·m.设该轮系原来静止,试求在M d和M r作用下,运转到t=15s时,轮1的角速度ω1和角加速度α1.图5答案:i12=ω1/ω2=(-1)1×z2/z1 ω2=-ω1/2i13=ω1/ω3=(-1)2×z2×z3/z1×z2’ω3=20×20×ω1/40×40=ω1/4轮1的等效力矩M为:M=M d×ω1/ω1+M r×ω3/ω1 =60×1-120/4=30 N·m轮1的等效转动惯量J为:J=J1(ω1/ω1)2+(J2’+J2)(ω2/ω1)2+J3(ω3/ω1)2=0.01×1+(0.01+0.04)/4+0.04/16=0.025 (kg·m2)∵M=J ×ε∴角加速度ε=M/J=1200 (rad/s2)初始角速度ω0=0 ∴ω1=ω0+ε×tω=1200×1.5=1800(rad/s)。
单自由度机械系统动力学——牛头刨床运动例题

单自由度机械系统动力学作业题目:图1所示为一牛头刨床。
各构件长度为:1110L mm =,3540L mm =,4135L mm =;尺寸580H mm =,1380H mm =。
导杆3重量3200G N =,质心3S 位于导杆中心,导杆绕3S 的转动惯量23 1.1J kg m =⋅。
滑枕5的重量5700G N =。
其余构件重量均可不计。
电动机型号为Y100L2-4,电动机轴至曲柄1的传动比23.833i =,电动机转子及传动齿轮等折算到曲柄上的转动惯量21133.3J kg m =⋅。
刨床的平均传动效率0.85η=。
空行程时作用在滑枕上的摩擦阻力50f F N =,切削某工件时的切削力和摩擦阻力如图2所示。
1)求空载启动后曲柄的稳态运动规律; 2)求开始刨削工件的加载过程,直至稳态。
图1 牛头刨床 图2 牛头刨床加工某工件时的负载图 解:(1)运动分析可以用解析法列出各杆角速度、各杆质心速度的表达式。
但为简便起见,现调用改自课本附录Ⅰ中的Matlab 子程序来进行计算。
图1中给出了构件和运动副的编号。
先调用子程序crank 分析点②的运动学参数,再调用子程序vosc 进行滑块2—导杆3这一杆组的运动学分析,然后再调用子程序vguide 进行小连杆4—滑枕5这一杆组的运动学分析。
这一段的Matlab 程序如下:crank(1,2,L(1),TH(1),W(1)); vosc(2,3,4,L(3)); vguide(4,5,L(4)); 其中:L(i)、TH(i)、W(i)分别表示第i 个杆的长度、位置角、角速度。
(2)等效转动惯量和等效力矩取曲柄1为等效构件,等效转动惯量为2223335513111()()()S e J J J G v G v g g ωωωω=+++ (a) 式中:g 为重力加速度,3S v 为导杆3质心的速度,5v 为滑枕的速度。
等效驱动力矩可由电动机机械特性导出,设m M 、de M 分别为电动机输出力矩和等效驱动力矩,两者有如下关系:de m M iM = (b)式中i 为电动机轴和曲轴间的传动比。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
作业(二)单自由度机械系统动力学等效转动惯量等效力矩
1.如题图1所示的六杆机构中,已知滑块5的质量为m 5=20kg ,l AB =l ED =100mm ,l BC =l CD =l EF =200mm ,φ1=φ2=φ3=90o ,作用在滑块5上的力P=500N .当取曲柄AB 为等效构件时,求机构在图示位置的等效转动惯量和力P的等效力矩.
图1
答案:解此题的思路是:①运动分析求出机构处在该位置时,质心点的速度及各构件的角速度.
②根据等效转动惯量,等效力矩的公式求出.
做出机构的位置图,用图解法进行运动分析.
V C =V B =ω1×l AB ω2=0
V D =V C =ω1×l AB 且ω3=V C /l CD =ω1
V F =V D =ω1×l AB (方向水平向右) ω4=0
由等效转动惯量的公式: e J =m 5(V F /ω1)2=20kg ×(ω1×l AB /ω1)2=0.2kgm 2
由等效力矩的定义: e M =500×ω1×l AB ×cos180o /ω1=-50Nm (因为VF 的方向与P方向相反,所以α=180o )
∑=+=n i i Si Si i e J v m J 121
21])()(
[ωωω∑=±=n i i i i i i e M v F M 11
1)]()(
cos [ωωωα
2.题图2所示的轮系中,已知各轮齿数:z 1=z 2’=20,z 2=z 3=40,J 1=J 2’=0.01kg ·m 2,J 2=J 3=0.04kg ·m 2.作用在轴O3上的阻力矩M3=40N ·m .当取齿轮1为等效构件时,求机构的等效转动惯量和阻力矩M3的等效力矩.
图2
答案:该轮系为定轴轮系.
i 12=ω1/ω2=(-1)1z 2/z 1 ∴ ω2=-ω1/2=-0.5×ω1 ω2’=ω2=-0.5×ω1
i 2’3=ω2’/ω3=(-1)1z 3/z 2’ ∴ ω3=0.25×ω1 根据等效转动惯量公式
e J = J 1×(ω1/ω1)2+J 2×(ω2/ω1)2+J 2’×(ω2’/ω1)2+J 3×(ω3/ω1)2 =J 1+J 2/4+J 2’/4 +J 3/16
=0.01+0.04/4+0.01/4+0.04/16
=0.025 kg ·m 2
根据等效力矩的公式: e M =M 3×ω3/ω1=40×0.25ω1/ω1=10N ·m
3.在题图3所示减速器中,已知各轮的齿数:z 1=z 3=25,z 2=z 4=50,各轮的转动惯量J 1=J 3=0.04kg ·m 2,J 2=J 4=0.16kg ·m 2,(忽略各轴的转动惯量),作用在轴Ⅲ上的阻力矩M 3=100N ·m .试求选取轴
∑=+=n i i Si Si i e J v m J 121
21])((
[ωωω∑=±=n i i i i i i e M v F M 11
1)]()(
cos [ωωωα
Ⅰ为等效构件时,该机构的等效转动惯量J和M3的等效阻力矩M r.
图3
答案:i12=ω1/ω2=z2/z1ω2=ω1/2 ω3=ω2=ω1/2
i34=ω3/ω4=z4/z3ω4=ω1/4
等效转动惯量:
J=J1(ω1/ω1)2+J2(ω2/ω1)2+J3(ω3/ω1)2+J4(ω4/ω1)2
=0.042+0.16×(1/2)2+0.04×(1/2)2+0.16×(1/4)2
=0.04+0.04+0.01+0.01
=0.1kg·m2
等效阻力矩:
M r=M3×ω4/ω1=100/4=25(N·m)
4.题图4所示为一简易机床的主传动系统,由一级带传动和两级齿轮传动组成.已知直流电动机的转速n0=1500r/min,小带轮直径d=100mm,转动惯量J d=0.1kg·m2,大带轮直径D=200mm,转动惯量J D=0.3kg·m2.各齿轮的齿数和转动惯量分别为:z1=32,
J1=0.1kg·m2,z2=56,J2=0.2kg·m2,z2’=32,J2’=0.4kg·m2,z3=56,J3=0.25kg·m2.
要求在切断电源后2秒,利用装在轴上的制动器将整个传动系统制动住.求所需的制动力矩M1.
图4
答案:电机的转速n0=1500r/min
其角速度ω0=2π×1500/60=50π(rad/s)
三根轴的转速分别为:
ω1=d×ω0/D=25π(rad/s)
ω2=z1×ω1/z2=32×25π/56=1429π(rad/s)
ω3=z2’×ω2/z3=32×1429π/56=816π(rad/s)
轴的等效转动惯量:
J V=J d×(ω0/ω1)2+J D×(ω1/ω1)2+J1×(ω1/ω1)2+J2×(ω2/ω1)2+ J2’×(ω2/ω1)2+ J 3×(ω3/ω1)2
∴J V=0.1×(50π/25π)2+0.3×12+0.1×12+(0.2+0.1)×(14.29π/25π)2+0.25×(8.16π/25π)2
=0.4+0.4+0.098+0.027
=0.925 (kg·m2)
轴制动前的初始角速度ω1=25π,制动阶段做减速运动,即可求出制动时的角加速度
∴ωt=ω0-εt即0=25π-2ε
ε=12.5π
则在2秒内制动,其制动力矩M为:
M=J V×ε=0.925×12.5=36.31 (kg·m)
5.在题图5所示定轴轮系中,已知各轮齿数为:z1=z2’=20,z2=z3=40;各轮对其轮心的转动惯量分别为J1=J2’=0.01kg·m2,J2=J3=0.04kg·m2;作用在轮1上的驱动力矩M d=60N·m,作用在轮3上的阻力矩M r=120N·m.设该轮系原来静止,试求在M d和M r 作用下,运转到t=15s时,轮1的角速度ω1和角加速度α1.
图5
答案:i12=ω1/ω2=(-1)1×z2/z1 ω2=-ω1/2
i13=ω1/ω3=(-1)2×z2×z3/z1×z2’ω3=20×20×ω1/40×40=ω1/4
轮1的等效力矩M为:
M=M d×ω1/ω1+M r×ω3/ω1 =60×1-120/4=30 N·m
轮1的等效转动惯量J为:
J=J1(ω1/ω1)2+(J2’+J2)(ω2/ω1)2+J3(ω3/ω1)2=0.01×1+(0.01+0.04)/4+0.04/16=0.025 (kg·m2)
∵M=J ×ε∴角加速度ε=M/J=1200 (rad/s2)
初始角速度ω0=0 ∴ω1=ω0+ε×t
ω
=1200×1.5=1800(rad/s)。
