研究生《机械系统动力学》试卷及答案

机械考研试题与答案

第三章螺纹联接与螺旋传动1.常用螺纹有哪几类哪些用于联接，哪些用于传动，为什么哪些是标准螺纹常用的有：三角螺纹，矩形螺纹，梯形螺纹和锯齿形螺纹。

三角螺纹用于联接，其余用于传动。

因三角螺纹自锁性好，其它螺纹传动效率高。

除矩形螺纹外，其余均为标准螺纹。

2.何谓螺纹联接的预紧，预紧的目的是什么预紧力的最大值如何掌握螺纹联接的预紧是指在装配时拧紧，是联接在承受工作载荷之前预先受到预紧力的作用。

预紧的目的是增加螺纹联接的刚度、保证联接的严密性和牢靠性〔防松力量〕。

拧紧后，预紧应力的大小不得超过材料屈服极限σS的80%。

3.螺纹联接有哪些根本类型适用于什么场合螺纹联接有 4 中根本类型。

螺栓联接：用于被联接件不太厚且两边有足够的安装空间的场合。

螺钉联接：用于不能承受螺栓联接〔如被联接件之一太厚不宜制成通孔，或没有足够的装配空间〕，又不需要常常拆卸的场合。

双头螺柱联接：用于不能承受螺栓联接且又需要常常拆卸的场合。

紧定螺钉联接：用于传递力和力矩不大的场合。

4.紧螺栓联接的强度也可以按纯拉伸计算，但须将拉力增大30%，为什么考虑拧紧时的扭剪应力，因其大小约为拉应力的30%。

5.提高螺纹联接强度的措施有哪些1〕改善螺纹牙间的载荷安排不均；2〕减小螺栓的应力幅；3〕减小螺栓的应力集中；4〕避开螺栓的附加载荷〔弯曲应力〕；5〕承受合理的制造工艺。

6.为什么螺母的螺纹圈数不宜大于10 圈〔使用过厚的螺母不能提高螺纹联接强度〕由于螺栓和螺母的受力变形使螺母的各圈螺纹所担当的载荷不等，第一圈螺纹受载最大，约为总载荷的1/3，逐圈递减，第八圈螺纹几乎不受载，第十圈没用。

所以使用过厚的螺母并不能提高螺纹联接强度。

7.联接螺纹能满足自锁条件，为什么还要考虑防松依据防松原理，防松分哪几类由于在冲击、振动、变载以及温度变化大时，螺纹副间和支承面间的摩擦力可能在瞬间减小或消逝，不再满足自锁条件。

这种状况屡次重复，就会使联接松动，导致机器不能正常工作或发生严峻事故。

合肥工业大学机械动力学基础试题(含部分答案)

1 1 2 m2 x2 J eq 2 ， 2 2
②由动能定理可知： E = m1 x12
1 2
其中 x1 a , x2 b , 为杆转过的角度. J eq m1a 2 m2b2 再求等效刚度， keq x 2
1 2
1 2 1 2 2 kx2 kb keq kb2 2 2
④推导出用单元节点位移表示的单元应变、单元应力表达式，再利用虚功方程建立单元节点力阵与节点位移列阵之间的关系，形成单元的刚度方程式。 ⑤根据系统的动能与势能，得到各单元的刚度矩阵和质量矩阵。 ⑥考虑整体结构的约束情况，修正整体刚度方程，求解单元节点的运动方程。 ⑦由单元节点的运动方程“装配”成为全系统的运动方程。（6）简述机械系统的三要素及动力学模型。（2012）答：三要素：惯性、弹性、阻尼. 动力学模型：①集中参数模型,由惯性元件、弹性元件和阻尼元件等离散元件组成；②有限单元模型，由有限个离散单元组成，每个单元则是连续的；③连续弹性体模型将实际结构简化成质量和刚度均匀分布或按简单规律分布的弹性体. 3. 试求图示振动系统的运动微分方程和固有频率。（图 3、图 5 作纯滚动）
不作用外载荷时的力矩平衡可列为： ∴系统固有频率为：
M J
eq
keq 0
keq J eq

kb 2 . m1a 2 m2b 2
③由于 m作纯滚动，则运动微分方程可表示为： J kx r 0 ，其中 J 为 m相对于接地点的转动惯量， J
kk mx kx 0 ，即： mx 1 2 k3 cos 2 x 0 k1 k2
∴系统固有频率为：n
k m
k1k2 k3 cos 2 k k k (k k 2 ) cos 2 k1 k 2 . = 1 2 3 1 m m(k1 k 2 )

第14章知识资料机械系统动力学(1)

2
m m (vv ) 等效质量：
n
e i 1
J
si
(i
v
)2
n
i 1
i
si
F F v 等效力：
n
e i 1
M（i vi )
(
iห้องสมุดไป่ตู้
si
v
)
c
osi
机械系统运动方程式的建立
等效构件为回转件时机械系统的运动方程简化式为：
经过推导，可得M以ed微分 M形e式dt表示d的J e机2 械2 系统运动方程式为：
Wm a x
m2 J
20 π 202 0.3
0.52
max
m
(1
) 2
25.2
rad/s
m in
m (1
)
2
14.8
rad/s
ωmax发生在 32处；
ωmin 发生在
处。
五、试题自测及答案（1 、2、3、4）
1.一重力G1=450N的飞轮支承在轴径直径d＝80 mm的轴
承上，在轴承中摩擦阻力矩作用下，飞轮转速在 14s 内从 200 r/min 均匀地下降到150 r/min。若在飞轮轴上再装上
以积分方式表示的机械系统运动方程式为：
F s
s0
e
ds
s s0
(Fd
Fr
)ds
1 2
mv2
1 2
m0v02
以上两个公式在具体应用时要看使用哪个方程更简单。
机器运转的速度波动
机器速度波动的原因是其驱动功与阻抗功并不时时相等。或者说，其等效驱动力矩与等效阻力矩并不时时相等，其转动惯量也不能随等效力矩作相应的变化，致使机器出现盈功或亏功，产生速度的波动。

作业(二)答案：单自由度机械系统动力学等效转动惯量等效力矩

作业（二）单自由度机械系统动力学等效转动惯量等效力矩1．如题图1所示的六杆机构中，已知滑块５的质量为m 5=20kg ，l AB =l ED =100mm ，l BC =l CD =l EF =200mm ，φ1=φ2=φ3=90o ，作用在滑块５上的力Ｐ＝500N ．当取曲柄AB 为等效构件时，求机构在图示位置的等效转动惯量和力Ｐ的等效力矩．图1答案：解此题的思路是：①运动分析求出机构处在该位置时，质心点的速度及各构件的角速度．②根据等效转动惯量，等效力矩的公式求出．做出机构的位置图，用图解法进行运动分析．V C =V B =ω1×l AB ω2=0V D =V C =ω1×l AB 且ω3=V C /l CD =ω1V F =V D =ω1×l AB (方向水平向右) ω4=0由等效转动惯量的公式：e J =m 5(V F /ω1)2=20kg ×(ω1×l AB ／ω1)2=0．2kgm 2由等效力矩的定义： e M =500×ω1×l AB ×cos180o／ω1＝－50Nm （因为ＶF 的方向与Ｐ方向相反，所以α＝180o ）2．题图2所示的轮系中，已知各轮齿数：z 1=z 2’=20，z 2=z 3=40，J 1=J 2’=0．01kg ·m 2，J 2=J 3=0．04kg ·m 2．作用在轴Ｏ3上的阻力矩Ｍ3＝40N ·m ．当取齿轮１为等效构件时，求机构的等效转动惯量和阻力矩Ｍ3的等效力矩．图2答案：该轮系为定轴轮系．i 12=ω1/ω2=(-1)1z 2/z 1∴ ω2=－ω1/2=－0．5×ω1ω2’=ω2=－0．5×ω1i 2’3=ω2’/ω3=(-1)1z 3/z 2’ ∴ ω3=0．25×ω1根据等效转动惯量公式e J = J 1×(ω1/ω1)2＋J 2×(ω2/ω1)2＋J 2’×(ω2’/ω1)2＋J 3×(ω3/ω1)2 ∑=+=n i i Si Si i e J v m J 12121]()([ωωω∑=±=n i i i i i i e M v F M 111)]()(cos [ωωωα∑=+=n i i Si Si i e J v m J 12121]()([ωωω＝J 1＋J 2／４＋J 2’／４＋J 3／16＝0．01＋0．04／4+0．01／4+0．04／16＝0．025 kg ·m 2根据等效力矩的公式： e M =M 3×ω3/ω1=40×0．25ω1/ω1=10N ·m3．在题图3所示减速器中，已知各轮的齿数：z 1=z 3=25，z 2=z 4=50，各轮的转动惯量J 1=J 3=0．04kg ·m 2，J 2=J 4=0．16kg ·m 2，（忽略各轴的转动惯量），作用在轴Ⅲ上的阻力矩M 3=100N ·m ．试求选取轴Ⅰ为等效构件时，该机构的等效转动惯量J 和M 3的等效阻力矩M r ．图3答案：i 12=ω1／ω2=z 2/z 1 ω2=ω1/2 ω3=ω2=ω1/2 i 34=ω3/ω4=z 4/z 3ω4＝ω1/4等效转动惯量：J=J 1(ω1/ω1)2+J 2(ω2/ω1)2+J 3(ω3/ω1)2+J 4(ω4/ω1)2=0．042+0．16×(1/2)2+0．04×(1/2)2+0．16×(1/4)2=0．04+0．04+0．01+0．01=0．1 kg ·m 2等效阻力矩：M r =M 3×ω4/ω1=100/4=25(N ·m)4．题图4所示为一简易机床的主传动系统，由一级带传动和两级齿轮传动组成．已知直流电动机的转速n 0＝1500r/min ，小带轮直径d =100mm ，转动惯量J d =0．1kg ·m 2，大带轮直径D ＝200mm ，转动惯量J D =0．3kg ·m 2．各齿轮的齿数和转动惯量分别为：z 1=32，J 1=0．1kg ·m 2，z 2=56，J 2=0．2kg ·m 2，z 2’=32，J 2’=0．4kg ·m 2，z 3=56，J 3=0．25kg ·m 2．要求在切断电源后２秒，利用装在轴上的制动器将整个传动系统制动住．求所需的制动力矩M 1．图4∑=±=n i i i i i i e M v F M 111()(cos [ωωωα答案：电机的转速n0＝1500r/min其角速度ω0＝2π×1500/60=50π(rad/s)三根轴的转速分别为：ω1=d×ω0/D=25π(rad/s)ω2=z1×ω1/z2=32×25π/56=1429π(rad/s)ω3=z2’×ω2/z3=32×1429π/56=816π(rad/s)轴的等效转动惯量：J V=J d×(ω0/ω1)2+J D×(ω1/ω1)2+J1×(ω1/ω1)2+J2×(ω2/ω1)2+ J2’×(ω2/ω1)2+ J3×(ω3/ω1)2∴J V=0．1×(50π/25π)2+0．3×12+0．1×12+(0．2+0．1)×(14．29π/25π)2+0．25×(8．16π/25π)2=0．4+0．4+0．098+0．027=0．925 (kg·m2)轴制动前的初始角速度ω1＝２５π，制动阶段做减速运动，即可求出制动时的角加速度∴ωt=ω0－εt即０＝25π－2εε=12．5π则在２秒内制动，其制动力矩Ｍ为：M=J V×ε=0．925×12．5=36．31 (kg·m)5．在题图5所示定轴轮系中，已知各轮齿数为：z1=z2’=20，z2=z3=40；各轮对其轮心的转动惯量分别为J1=J2’=0．01kg·m2，J2=J3=0．04kg·m2；作用在轮１上的驱动力矩M d=60N·m，作用在轮３上的阻力矩M r=120N·m．设该轮系原来静止，试求在M d和M r作用下，运转到t=15s时，轮１的角速度ω1和角加速度α1．图5答案：i12=ω1/ω2=(-1)1×z2/z1 ω2=－ω1/2i13=ω1/ω3=(-1)2×z2×z3/z1×z2’ω3=20×20×ω1/40×40=ω1/4轮１的等效力矩Ｍ为：Ｍ＝M d×ω1/ω1+M r×ω3/ω1 =60×1－120/4=30 N·m轮１的等效转动惯量Ｊ为：Ｊ=J1(ω1/ω1)2+(J2’+J2)(ω2/ω1)2+J3(ω3/ω1)2=0．01×1+(0．01+0．04)/4+0．04/16=0．025 (kg·m2)∵M=J ×ε∴角加速度ε＝Ｍ／Ｊ＝1200 (rad/s2)初始角速度ω0=0 ∴ω1=ω0+ε×tω=1200×1．5=1800(rad/s)。

2012机械系统动力学基础考试试卷A答案

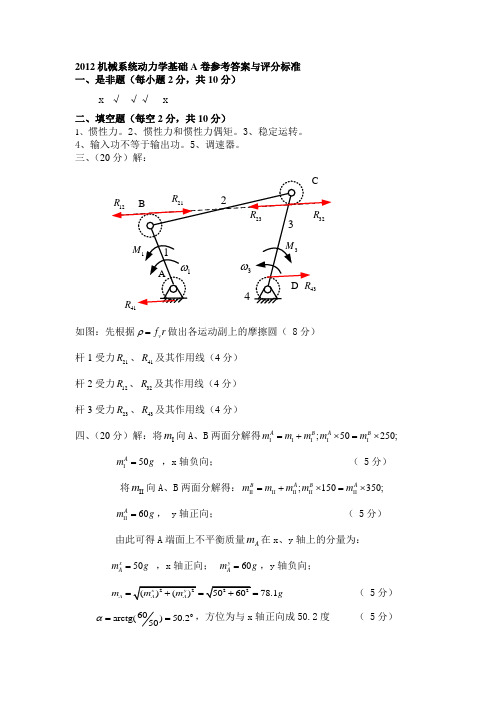
2012机械系统动力学基础A 卷参考答案与评分标准一、是非题（每小题2分，共10分）x √ √√ x二、填空题（每空2分，共10分）1、惯性力。

2、惯性力和惯性力偶矩。

3、稳定运转。

4、输入功不等于输出功。

5、调速器。

三、（20分）解：如图：先根据v f r ρ=做出各运动副上的摩擦圆（ 8分）杆1受力21R 、41R 及其作用线（4分）杆2受力12R 、32R 及其作用线（4分）杆3受力23R 、43R 及其作用线（4分）四、（20分）解：将m I 向A 、B 两面分解得;50250;A B A B m m m m m I I I I I =+⨯=⨯50A m g I = ，x 轴负向；（ 5分）将m II 向A 、B 两面分解得：;150350;B A B Am m m m m II II II II II =+⨯=⨯60Am g II =， y 轴正向；（ 5分）由此可得A 端面上不平衡质量A m 在x 、y 轴上的分量为：50x A m g = ，x 轴正向； 60yA m g =，y 轴负向；78.1A m g = （ 5分）060arctg()50.250α==，方位为与x 轴正向成50.2度（ 5分）五、（20分）解：1、解法一：上升时P=Qsin λ+f Qcos λ为驱动力，Q 为生产阻力； P 0= Qsin λ （4分）0PP η== sin λ/（ sin λ+fcos λ）=0.54；（6分）下降时P '=Qsin λ-fQcos λ为生产阻力，Q 为驱动力；0P '= Qsin λ （4分）0P P η'='=（sin λ－fcos λ）/sin λ= 0.15 （6分） 2、解法二：Qλϕ+Pλ-Qλϕ-P0λ-上升时：P 为驱动力下降时：P 为阻力0sin()sin(90)P Qλφφ+=-， 0sin()sin(90)P Q λφφ-=+0sin P Q λ= （4分） 0s i n P Q λ=（4分）00sin sin(90)sin()P P λφηλφ-==+ （6分） 00s i n ()s i n s i n (90)P P λφηλφ-'==+（6分） =sin λ/（ sin λ+fcos λ）=0.54 =（sin λ－fcos λ）/sin λ= 0.15 六、（20分）解：31=0.5ωω，21=0ωω，211s v l ω=，（6分）220.110.10.3(1/2)0.185v J =+⨯+⋅= （5分） 1012/24v M =-= （5分） 1/21.62v v M J ε== （4分）。

2022机械动力学试题答案

2022机械动力学试题答案一、判断题1.考虑效率时，等效力大小与效率值大小成反比。

2.某机械的广义坐标数为5，则该机械的广义力一定少于5个。

3.某机械系统自由度为4，那么其惯性系数J33一定不小于零。

4.定轴轮系在匀速转动时，等效力矩一定等于零。

5.在考虑弹性时，铰链四杆机构中单元杆的节点变形数一定等于系统的节点变形数。

1．某2．某3．√4．√5．某二、如图所示机构在水平面上运转，件1为原动件，转角为已知杆1长l0.8m，其绕A点转动惯量J1A0.2kgm2，件2质量m21.2kg，其质心为B2点，杆3质量m32kg，杆1受驱动力矩M，杆3受力F作用。

试求：1.以件1为等效件建立机构动力学方程。

2.该机构由静止起动时45，那么若F20N，M至少应大于多少才能启动机构。

3.若F20N，M15Nm，求90时，解：1、Slcov31linMvMFv31MFlinv322mJmlmlin31A23122JvJ1AvB2m212dJv由MvJv2d得:MFlinJ1Am2l2m3lin2ml322inco2、M200.8in450M11.3Nm3、MFlinJ1Am2l2m3lin2ml322inco9.34rad2图示轮系中，轮4转角为4，系杆转角为H，各件转动惯量:J10.4kgm2,J21.8kgm2，J3J62.1kgm2，J4J50.6kgm2，JH0.5kgm2。

各轮齿数：z120，z260，z4z530，z3z660，各件所受力矩大小：MH30Nm，M120Nm，M430Nm，M640Nm，方向如图所示。

忽略各件质量及重力，现选定q1=H，q24，试求H。

解：iH1=1,iH2=0，i410,i421，i11533151,i12，i21,i22，i61,i6222224422222J11J1i11(J2J3J5)i21J6i61JHiH116.4kgm2222J22J1i12(J2J3J5)i22J6i62J4i423.15kgm2J12J1i11i12(J2J3J5)i21i22J6i61i62-1.22kgm2Q1MHM1i11M6i6130NmQ2M4M1i12M6i6210Nm设M向上为正1J12q2Q1J11q得：H2.13rad/21J22q2Q2J21q图示机构中，件1受驱动力F1，件4受驱动力矩M4，件3受F3作用，方向如图，取广义坐标q1S1，q24。

2014级研究生《机械系统动力学》试题B

太原理工大学研究生试题B姓名：学号：专业班级：机械工程2014级1 求图1系统的当量刚度，钢丝绳的刚度为K 1，滑轮的质量忽略不计。

(10分)2 系统如图2所示，圆盘的转动惯量为I ，其旋转轴线与垂直方向成α角安装，圆盘上有一偏心质量m ，偏心距为a ，求系统微幅振动的频率。

(10分)3 试求图3所示系统的固有频率。

略去转轴和中间齿轮的转动惯量，已知：I1=235.2kg.cm2,I2=98kg.cm2, L1=75cm, L2=75cm, D1=15cm, D2=7.5cm, d1=5cm, d2=4cm 。

(10分)4 重量为W 的薄板挂在弹簧的下端，在空气中上下振动时，周期为T 1；在液体中上下振动时，周期为T 2。

假定空气阻尼略去不计，液体阻力表示为，其中2A 为薄板的总面积，为其运动速度。

试证明液体的粘性系数：2122212T T T AgT W -=πμ，见图4。

(10分) 5 如图5所示的单摆，其质量为m ，摆杆是无质量的刚性杆，长为L 。

它在粘性液体中摆动，粘性阻尼系数为r ，悬挂点O 的运动x(t)=Asin ωt ，试写出单摆微幅摆动的方程式并求解。

(15分)6 机器和机座由弹簧和阻尼支承如图6所示。

机器产生的惯性激振力频率ω=43rad ／s ，机器与机座的重量为2450N,选择阻尼系数r=2.94N.s ／cm 的材料制作隔振器(即阻尼器的阻尼系数r=2.94N.s ／cm)。

问隔振系数η＜0.1时，弹簧刚度K 应该多大? (15分)7 统如图7所示，其滑轮质量为M ，忽略绳的弹性和M 的转动（只考虑M 的上下振动），试用能量法确定系统的固有频率。

(15分)8如图8所示的振动系统，其支承的振动位移t H x H ωsin =，试求支承的最大振动力幅0Q 。

(15分)太原理工大学研究生试题纸图1 图2 图3图4 图5 图6图7 图8。

机械硕士考研试题及答案

机械硕士考研试题及答案一、选择题（每题2分，共10分）1. 机械设计中，齿轮传动的主要失效形式是（）。

A. 磨损B. 疲劳C. 腐蚀D. 变形答案：B2. 在材料力学中，下列哪项不是材料的力学性能指标？A. 弹性模量B. 屈服强度C. 硬度D. 密度答案：D3. 根据机械原理，四杆机构中，若最短杆长度等于最长杆长度的一半，则机构为（）。

A. 双曲柄机构B. 双摇杆机构C. 曲柄摇杆机构D. 摇杆曲柄机构答案：A4. 在液压系统中，下列哪个元件不是用来控制液体流动方向的？A. 单向阀B. 溢流阀C. 换向阀D. 节流阀答案：D5. 机械制造中，数控加工精度的提高主要依赖于（）。

A. 刀具材料B. 加工工艺C. 控制系统D. 机床刚度答案：C二、填空题（每题2分，共10分）1. 在机械设计中，为了提高齿轮的使用寿命，通常采用_________进行热处理。

答案：渗碳2. 材料的疲劳强度与其_________有关。

答案：循环次数3. 四杆机构中，若最短杆长度大于最长杆长度的一半，则机构为_________。

答案：双摇杆机构4. 液压系统中，_________的作用是防止系统压力超过设定值。

答案：溢流阀5. 数控加工中，刀具的_________直接影响加工精度。

答案：磨损三、简答题（每题5分，共20分）1. 简述机械设计中，轴承的选型原则。

答案：轴承的选型应考虑轴承的承载能力、转速、工作温度、安装空间、经济性等因素。

2. 说明材料力学中，材料的弹性模量与屈服强度的区别。

答案：弹性模量是材料在弹性阶段内应力与应变比值的物理量，而屈服强度是材料开始产生塑性变形时的应力值。

3. 描述四杆机构中，曲柄摇杆机构的工作原理。

答案：曲柄摇杆机构中，曲柄通过连杆驱动摇杆，实现往复运动与旋转运动的转换。

4. 解释液压系统中，单向阀的作用。

答案：单向阀的作用是允许液体单向流动，防止液体反向流动，确保系统安全。

四、计算题（每题10分，共20分）1. 已知一齿轮传动系统，主动齿轮的转速为1000转/分钟，传动比为3:1，求从动齿轮的转速。

西北工业大学机械系统动力学试题(含答案)

考试科目：机械系统动力学课程编号：056022 开课学期： 2014-2015学年第二学期考试时间：2015/07/08 说明：所有答案必须写在答题册上,否则无效。

共6 页第 1页1. 用加速度计测出某结构按频率82 Hz 简谐振动时的最大加速度为50g (2/980s cm g =). 求该振动的振幅及最大速度.解答: 已知振动频率 82f Hz =，最大加速度max 50a g =,振动角频率2164f ωππ==rad/s将简谐振动表述为正弦函数 sin()x A t ωϕ=+ ，则其速度为 cos()x A t ωωϕ=+ ，加速度为 2sin()x A t ωωϕ=-+振幅 m a x 22509.80.185(164)a A cm ωπ⨯=== 最大速度 max 1.8516495.1/v A cm s ωπ==⨯=2. 一个机器内某零件的振动规律为0.4sin 0.3cos x t t ωω=+，x 的单位是cm ，10/s ωπ=。

这个振动是否简谐振动? 求出它的振幅、最大速度及最大加速度，并用旋转矢量表示这三者之间的关系。

解答：频率相同的简谐振动合成的振动仍是简谐振动，显然该振动为简谐振动。

0.4sin 0.3cos sin()x t t A t ωωωϕ=+=+其中，振幅 0.5A == ，相角为 10.3370.4tg ϕ-==︒ 最大速度 max 0.5105v A ωππ==⨯=最大加速度 22max 0.5(10)500a A ωπ==⨯=振幅、最大速度和最大加速度之间的旋量关系可表示为图0 所示：图0 振幅、最大速度和最大加速度间的旋量关系表示3. 将图1所示的锯齿波展为富里叶级数, 并画出频谱图.考试科目：机械系统动力学课程编号：056022 开课学期： 2014-2015学年第二学期考试时间：2015/07/08 说明：所有答案必须写在答题册上,否则无效。

【2017年整理】机械动力学复习题

机械动力学复习试题1、试求图1-1所示系统的等效弹簧常数，并导出其运动微分方程。

2、一无质量的刚性杆铰接于O ，如图2-1所示。

试确定系统振动的固有频率，给出参数如下：k 1=2500磅/英寸(4.3782×105N/m ），K 2=900磅/英寸(1.5761×105N/m ）， m=1磅*秒2/英寸（175.13kg ）， a=80英寸 (2.03m)， b=100英寸（2.54m ）。

2k图3-1图2-13、试求出图3-1所示系统的固有频率。

弹簧是线性的，滑轮对中心0的转动惯量为I。

设R=2500磅/英寸（4.3782×105N/m），I=600磅*英寸*秒2（67.79N*m*s2），m=2.5磅*秒2/英寸（437.82kg），R=20英寸（0.5/m）4、一台质量为M的机器静止地置于无质量的弹性地板上，如图4-1所示。

当一单位载荷作用于中心点时的挠度为x st。

今在机器上放有一总质量为ｍｓ并带有两个旋转的不平衡质量的振动器提供一铅垂的谐波力mlw2sinwt，这里，转动的频率w是可以改变的。

试说明怎样用此振动器来测定系统弯曲振动的固有频率。

5,、图5-1中所示的系统模拟一在粗糙道路上运动的车辆，速度为均匀，即V=常数。

试计算其响应Z(t)和传给车辆的力。

图5-16,、试导出如图6-1所示系统的运动微分方程，并求解位移X1(t)。

图6-17、转动惯量分别为I1和I2的两个圆盘安装在扭转刚度分别为GJ1和GJ2的圆轴上如图7-1。

导出这两个圆盘的转动微分方程。

8、导出图8-1所示系统当θ为微小角时的运动微分方程。

GJ 1GJ 21()t θ2()t θM 2(t)M 1(t)I 1I 29、如图9-1所示在风洞中试验的机翼截面。

设机翼的总质量为m，绕其质心C 的转动惯量为I C，试导出器运动微分方程。

K1C O图9-1C图10-110、导出图10-1所示的三重摆的运动方程。

机械系统动力学试题a2008答案

机械系统动力学试题A平分标准1 填空（20）（每空2分）离散线性系统的数学模型可用线性常微分方程描述。

LTI系统为线性时不变系统。

静态设计主要考虑静态载荷作用，动态设计主要考虑振动与动态载荷作用。

系统有离散系统和连续系统。

确定性系统在随机激励下，响应是随机的。

重力场的势函数为-mgy 。

广义坐标为完全决定系统状态的独立参数。

牛顿力学的主要不便是处理约束反力不方便。

连续系统的自由度数为无穷多。

2 用拉格朗日方程建立单摆运动方程(20)。

解：3 写出建立拉格朗日方程的步骤(20)。

解：（1）确定系统自由度数，选取广义坐标（5）；（2）计算系统动能E（5）;（3）计算系统的广义力Q（5）；（4）将动能和广义力代入格郎日方程，得系统运动微分方程（5）。

4如图，推导杆的纵向振动微分方程(20)。

解：微元所受的合力为：dx x F F T ∂∂=（2）因为 xu AE A F T ∂∂==σ（3）所以 dx xu AE dx x F F T 22∂∂=∂∂=（5）微元的质量为：dx A M ρ=（2）代入牛顿定律得：dx tu A dx x u AE 2222∂∂=∂∂ρ（3） 222221t u c x u ∂∂=∂∂即（4） ρE c =2其中（1）5 等效力学模型微分方程中，已知等效转动惯量为常数，等效力矩为)(ϖe e M M =，0=t 时，0=ϖ，求时间和角速度的关系(20)。

解：等效力学模型微分方程为：e e e M dt d d dJ dt d J =⎪⎭⎫ ⎝⎛+22221ϕϕϕ（5）因等效转动惯量为常数，故有：e e M dtd J =22ϕ（2）即：e e M dtd J =ω，)(ϖe e M M =（3）分离变量得：)(ϖωe e M d J dt =（5）积分并应用初始条件，得：⎰=ωϖω0)(e e M d J t （5）。

《机械动力学答案》

共 6 页，第 3页
A、急停阶段 B、启动阶段 C、稳定运转阶段 D、停车阶段 72、在动力分析中，主要涉及的力是（）。 A、驱动力 B、重力 C、摩擦力 D、生产阻力 73、以下选项中，与等效力有关的是（）。 A、外力 B、传动比 C、ωj/v D、vk/v 74、以下选项中，与等效力矩有关的是（）。 A、外力据 B、传动比 C、ωj/ω D、vk/ω 75、以下选项中，可归为阻尼的有（）。 A、物体的内力 B、物体表面间的摩擦力 C、周围介质的阻力 D、材料的内摩擦四、填空题（每空 2 分，共 30 空，共 60 分） 76、从惯性载荷被平衡的程度看，平衡可分为、和。 77、机械动力学的分析方法按功能分类可分为和。 78、动力学的分析方法按水平分类，可分为、、和。 79、用质量再分配实现摆动力的完全平衡，其分析方法主要有、、和。 80、机械系统运转的全过程可分为、和这几个阶段。 81、机器人动力学是机器人、和的基础。 82、工业机器人通常由、、和组成。 83、二自由度系统的等效转动惯量是系统的、、和的函数。 84、实现摆动力完全平衡的方法有、和。 76、部分平衡、完全平衡、优化综合平衡 77、动力学反问题、动力学正问题 78、静力分析、动态静力分析、动态分析、弹性动态分析 79、广义质量代换法、线性独立矢量法、质量矩替代法、有限位置法 80、启动阶段、稳定运转阶段、停车阶段 81、操作机设计、控制器设计、动态性能分析 82、执行机构、驱动装置、控制系统、传感系统 83、时间、惯性参数、几何参数、广义坐标 84、加配重、合理布置机构、设置附加机构五、计算题（第 85、86 题各 30 分，第 87 题 10 分，第 88 题 20 分，共 90 分） 85、如图所示为一对心曲柄滑块机构。曲柄以转速度 ω1 作等速回转运动，曲柄与水平方向夹角为 θ1 ，曲柄长度为 r ，质心与其回转中心 A 重合。连杆长度 l ，连杆与水平方向夹角为 θ 2 ，连杆质心 S2 到铰链 B 的距离 BS 2 = L ，连杆质量 m 2 ，对其质心的转动惯量 J 2 。滑块质量 m3 ，其质心与铰链 C 重合。1)画出曲柄、连杆和滑块的受力分析图；2）写出曲柄、连杆和滑块的平衡方程。

[机械系统动力学考试题2014年]

机械系统动力学课程第一部分开卷考试题(2014年硕士研究生课适用、共六题)一、下图所示为一对心曲柄滑块机构。

曲柄以转速ω1=100 rad / s 作等速回转运动，曲柄长度r = 50.8 mm ，质心与其回转中心A 重合。

连杆长度l =203 mm ，连杆质心S 2到铰链B 的距离mm BS 8.502=，连杆质量kg m 36.12=，对其质心的转动惯量220102.0m kg J •=。

滑块质量kg m 907.03=，其质心与铰链C 重合。

（1）列出动态静力分析方程，绘出摆动力对A 点的摆动力矩与惯性载荷相对应的那一部分平衡力矩随曲柄位置1θ变化的情况；（2）对计算结果的某些现象、或各尺寸参数、质量分布等问题，提出一个讨论问题，并阐述自己的观点。

（15分）二、列出曲柄导杆机构（右下图）的完全平衡方程，并推出平衡条件，写出在杆1和3上所加项式运动规律。

要求有详细的推导步骤；（2）试简述使用高次方多项式作为凸轮从动件运动规律有何特点？（10分）五、已知一曲柄压机简图如题三图所示，l 1 =50 mm ，l 2 =300 mm ，J 1 = 8 kgm 2 , m 3 = 2 kg ，不计杆2质量，曲柄受驱动力矩M 1 = 158.5-10ω N •m ，工作阻力F 3为：⎩⎨⎧=)(m N)(m N 160F 333向上运动向下运动设当φ1 = 0°时，ω1 = 15.5 1/s 。

现求以杆1为等效构件，用经典四阶龙格库塔法，以Δφ =5°计算φ1 =0°～720°对应的ω1，dt d 1ω的值，绘出线图。

（10分）打印格式：No. φ1 ω1 dω1/dt0 0 15.5 · 1 5 · ·2 10 · ·六、请检索文献，完成一篇3000字左右的“综述”，内容是平面连杆机构弹性动力学分析近年来的研究方法和应用。

机械系统动力学习题2010.

⎨ ⎪⎩−KB1
+ (2K
−
2mω2
)B2
=
P0
得
解该方程组，
B1
=
(2K
−
KP0 mω2)(2K −
2mω2 )
−
K
2
B2
=
(2K
−
(2K − mω2 )P0 mω2)(2K − 2mω2) − K
2
所以，受迫响应为
x1
=
(2K
−
KP0 mω2)(2K −
2mω2 )
−
K
2
sinωt
及
x2
=
(2K
所以碰撞后的系统可视为低阻尼状态
•
碰撞初始位置： x0 = 0, x0 = v = 0
•
所以 A =
x0
+
x0
+ξwn x0 wd
=
x0 = 0.082 m wn 1 −ξ2
Td
2π ==
wd
wn
2π 1−ξ2
= 1.4
s
所以在相撞后的约 Td ≈0.35 s 达到最大振幅 Ae−ξwnt ≈0.07 m
整理，得
ωn4
−
1 M
[k
(M +
+ l
m)
g
]ωn
2
+
kg Ml
=0
解：取质量块的位移 x1 , x2 为广义坐标，对 m1, m2 分别进行受力分析，根据牛顿定律，有
⎧ ••
⎪m1 x1 = K2 ( x2 − x1 ) − K1 x1
⎨
⎪ ⎩
m2
••
x2
=

(完整word版)西北工业大学机械系统动力学试题(含答案)(word文档良心出品)

考试科目：机械系统动力学课程编号：056022 开课学期： 2014-2015学年第二学期考试时间：2015/07/08 说明：所有答案必须写在答题册上,否则无效。

共6 页第 1页1. 用加速度计测出某结构按频率82 Hz 简谐振动时的最大加速度为50g (2/980s cm g =). 求该振动的振幅及最大速度.解答: 已知振动频率 82f Hz =，最大加速度max 50a g =,振动角频率2164f ωππ==rad/s将简谐振动表述为正弦函数 sin()x A t ωϕ=+ ，则其速度为 cos()x A t ωωϕ=+ ，加速度为 2sin()x A t ωωϕ=-+振幅 m a x 22509.80.185(164)a A cm ωπ⨯=== 最大速度 max 1.8516495.1/v A cm s ωπ==⨯=2. 一个机器内某零件的振动规律为0.4sin 0.3cos x t t ωω=+，x 的单位是cm ，10/s ωπ=。

这个振动是否简谐振动? 求出它的振幅、最大速度及最大加速度，并用旋转矢量表示这三者之间的关系。

解答：频率相同的简谐振动合成的振动仍是简谐振动，显然该振动为简谐振动。

0.4sin 0.3cos sin()x t t A t ωωωϕ=+=+其中，振幅 0.5A == ，相角为 10.3370.4tg ϕ-==︒ 最大速度 max 0.5105v A ωππ==⨯=最大加速度 22max 0.5(10)500a A ωπ==⨯=振幅、最大速度和最大加速度之间的旋量关系可表示为图0 所示：图0 振幅、最大速度和最大加速度间的旋量关系表示3. 将图1所示的锯齿波展为富里叶级数, 并画出频谱图.考试科目：机械系统动力学课程编号：056022 开课学期： 2014-2015学年第二学期考试时间：2015/07/08 说明：所有答案必须写在答题册上,否则无效。

机械系统动力学试题

机械系统动力学试题一、简答题：1．机械振动系统的固有频率与哪些因素有关？关系如何？2．简述机械振动系统的实际阻尼、临界阻尼、阻尼比的联系与区别。

3．简述无阻尼单自由度系统共振的能量集聚过程。

4. 简述线性多自由度系统动力响应分析方法。

5. 如何设计参数，使减振器效果最佳？二、计算题：1、单自由度系统质量Kg m 10=, m s N c /20∙=, m N k /4000=, m x 01.00=,00=∙x ,根据下列条件求系统的总响应。

（a ）作用在系统的外激励为t F t F ωcos )(0=,其中N F 1000=，s rad /10=ω。

（b ） 0)(=t F 时的自由振动。

2、质量为m 的发电转子，它的转动惯量J 0的确定采用试验方法：在转子径向R 1的地方附加一小质量m 1。

试验装置如图2所示，记录其振动周期。

a ）求发电机转子J 0。

b ）并证明R 的微小变化在R 1=（m/m 1+1）·R 时有最小影响。

3、如图3所示扭转振动系统，忽略阻尼的影响J J J J ===321，K K K ==21（1）写出其刚度矩阵；（2）写出系统自由振动运动微分方程；（2）求出系统的固有频率；（3）在图示运动平面上，绘出与固有频率对应的振型图。

1θ（图2）（图3）4、求汽车俯仰振动（角运动）和跳振（上下垂直振动）的频率以及振动中心（节点）的位置（如图4）。

参数如下：质量m=1000kg，回转半径r=0.9m，前轴距重心的距离l1=0.1m,后轴距重心的距离l2=1.5m,前弹簧刚度k1=18kN/m,后弹簧刚度k2=22kN/m（图4）5、如5图所示锻锤作用在工件上的冲击力可以近似为矩形脉冲。

已知工件，铁锤与框架的质量为m1=200 Mg，基础质量为m2=250Mg，弹簧垫的刚度为k1=150MN/m，土壤的刚度为k2=75MN/m.假定各质量的初始位移与速度均为零，求系统的振动规律。

大学考研机械原理试题答案

大学考研机械原理试题答案一、选择题1. 机械原理中，关于连杆机构的基本描述，以下哪项是正确的？A. 连杆机构是由若干刚性杆件通过转动副或滑动副连接而成的B. 连杆机构的输入和输出均为转动运动C. 连杆机构的传动比是恒定不变的D. 连杆机构不能实现复杂的运动规律答案：A2. 在平面四杆机构中，以下哪种类型的机构可以实现直线运动输出？A. 曲柄摇杆机构B. 双曲柄机构C. 双摇杆机构D. 曲柄滑块机构答案：D3. 关于凸轮机构的描述，以下哪项是错误的？A. 凸轮机构可以实现间歇运动B. 凸轮机构中的凸轮是固定的，从动件作直线运动C. 凸轮机构可以实现复杂的运动规律D. 凸轮机构中的从动件可以是滚子或平面推块答案：B4. 机械系统中，用于减少冲击和振动的元件是？A. 弹簧B. 阻尼器C. 减振器D. 缓冲器答案：A5. 在机械原理中，机构的自由度与哪些因素有关？A. 构件的数量B. 运动副的类型C. 构件的形状和尺寸D. 所有上述因素答案：D二、填空题1. 在平面四杆机构中，当最短杆与最长杆之和小于其余两杆之和时，机构具有_________副。

答案：两转动2. 凸轮机构中，从动件的位移曲线是由凸轮的_________轮廓决定的。

答案：基圆3. 机械系统的动力学分析中，通常采用_________法来求解系统的动态响应。

答案：牛顿第二定律4. 机械原理中，用于描述机构运动特性的参数包括速度比、传动比和_________。

答案：压力角5. 在机械设计中，为了提高机构的承载能力，常常采用_________来调整构件的受力状况。

答案：平衡三、简答题1. 简述曲柄滑块机构的工作原理及其应用。

答：曲柄滑块机构是一种将曲柄的转动运动转换为滑块的直线往复运动的机构。

工作原理是：曲柄通过转动副与连杆连接，连杆的另一端与滑块相连，滑块在导轨内作直线运动。

当曲柄转动时，通过连杆的传递，使得滑块在导轨内往复移动。

这种机构广泛应用于各种往复运动的机械装置中，如内燃机、压力机、自动化装置等。

山东机械考研试题及答案

山东机械考研试题及答案一、单选题（每题2分，共20分）1. 下列关于机械设计的说法，错误的是（）。

A. 机械设计需要考虑材料的力学性能B. 机械设计可以不考虑成本C. 机械设计需要满足功能要求D. 机械设计需要考虑环境适应性答案：B2. 机械加工中，螺纹的螺距是指（）。

A. 螺纹的直径B. 相邻两个螺纹之间的距离C. 螺纹的深度D. 螺纹的宽度答案：B3. 机械制图中，尺寸线通常采用（）。

A. 虚线B. 点划线C. 粗实线D. 细实线答案：D4. 动平衡的目的是减少（）。

A. 静不平衡B. 动不平衡C. 静摩擦D. 动摩擦答案：B5. 机械系统中，轴承的主要作用是（）。

A. 传递力B. 承受压力C. 减少摩擦D. 增加摩擦答案：C6. 下列材料中，不属于金属材料的是（）。

A. 钢B. 铝C. 塑料D. 铜答案：C7. 机械制造中，热处理的目的是（）。

A. 提高材料的硬度B. 降低材料的韧性C. 增加材料的脆性D. 减少材料的强度答案：A8. 机械传动中，齿轮的传动比是指（）。

A. 齿轮的齿数之比B. 齿轮的直径之比C. 齿轮的宽度之比D. 齿轮的中心距之比答案：A9. 机械设计中，强度计算的目的是（）。

A. 确保机械的美观B. 确保机械的尺寸C. 确保机械的强度D. 确保机械的重量答案：C10. 机械制图中，三视图包括（）。

A. 正视图、侧视图、俯视图B. 正视图、侧视图、仰视图C. 正视图、侧视图、立体图D. 正视图、侧视图、剖视图答案：A二、多选题（每题3分，共15分）1. 下列属于机械加工方法的有（）。

A. 车削B. 铸造C. 铣削D. 焊接答案：A、C2. 机械设计中，常用的材料性能指标包括（）。

A. 硬度B. 韧性C. 导电性D. 耐腐蚀性答案：A、B、D3. 机械制图中，常用的线型有（）。

A. 实线B. 虚线C. 点线D. 双点划线答案：A、B、C、D4. 机械系统中，常见的传动方式有（）。