一阶电路的零输入响应和零状态响应
2012-2013学年一学期电路基础复习题参考答案

电路基础复习题(一)一、简答题1、什么叫基尔霍夫电流定律?什么叫基尔霍夫电压定律?答:电流定律:任一时刻在电路的任一结点上,所有支路电流的代数和恒等于零。
电压定律:在任一时刻,沿任一回路各段电压的代数和恒等于零。
2、什么是电路的开路状态、短路状态、空载状态、过载状态、满载状态?答;电源与负载未构成闭合电路,即电路处于开路状态;短路是指电路中电位不等的两点,由于某种原因而短接在一起的现象。
当电源没接负载时称为空载;当电源输出的电压为额定值时:电流等于额定电流,称为满载,电流小于额定电流,称为轻载,电流超过额定电流,称为过载。
3、什么是谐振现象?答:如果电源的频率和电路参数满足一定的条件,使电路中的总电压和总电流的相位相等,则整个电路呈现纯电阻性,这种现象称为谐振现象。
4、电路产生动态过程的原因有哪些?答:电路产生动态过程有内、外两种原因,内因是电路中纯在储能元件L和C;外因是电路的结构或参数发生改变。
5、什么叫叠加定理?答:线性电阻电路中,任一电压或电流都是电路中各个独立电源单独作用时,在该处产生的电压或电流的叠加。
6、什么叫等效变换?答:选取电路中的某一部分电路作为研究对象,这部分电路与其他部分电路通过端子进行连接,当被选取的部分电路变换成另一种连接形式时,各个端子处的电压和电流与变换前一致,则称选取电路部分的变换为等效变换。
二、填空题1、为了分析方便,常把电路分为内电路和外电路;从电源一端经过负载再回到电源另一端的这部分电路称为(外电路);电源内部的通路称为(内电路)。
2、电流的实际方向规定为(正电荷)的运动方向;衡量电流大小的物理量是(电流强度);电流的国际单位是(安培)。
3、在电压电流参考方向关联时,直流W电路功率的计算公式为(P=t或P=UI),若电压电流的参考方向非关联,功率的计算公式应为(P=-UI)。
4、电阻元件是一种对电流表现“阻碍”作用的(电路元件),它的主要参数是电阻,用字母(R)表示,单位为(Ω或欧姆)。
一阶动态电路暂态过程的研究
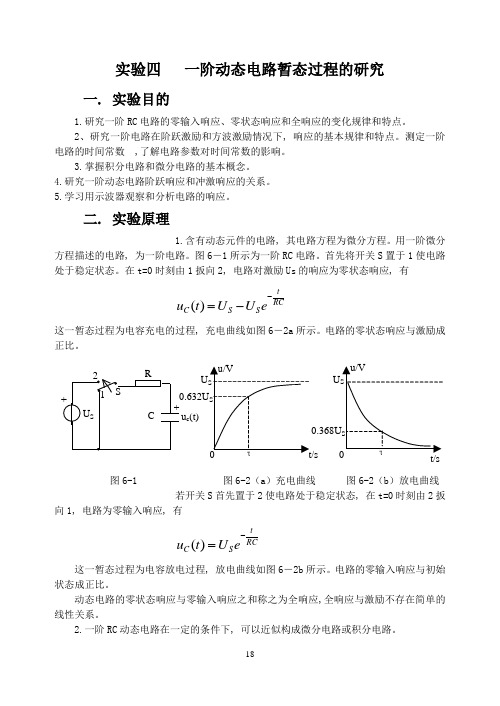
实验四 一阶动态电路暂态过程的研究一. 实验目的1.研究一阶RC 电路的零输入响应、零状态响应和全响应的变化规律和特点。
2、研究一阶电路在阶跃激励和方波激励情况下, 响应的基本规律和特点。
测定一阶电路的时间常数 ,了解电路参数对时间常数的影响。
3.掌握积分电路和微分电路的基本概念。
4.研究一阶动态电路阶跃响应和冲激响应的关系。
5.学习用示波器观察和分析电路的响应。
二. 实验原理1.含有动态元件的电路, 其电路方程为微分方程。
用一阶微分方程描述的电路, 为一阶电路。
图6-1所示为一阶RC 电路。
首先将开关S 置于1使电路处于稳定状态。
在t=0时刻由1扳向2, 电路对激励Us 的响应为零状态响应, 有RCt S S C eU U t u --=)(这一暂态过程为电容充电的过程, 充电曲线如图6-2a 所示。
电路的零状态响应与激励成正比。
U U u c (t) 图6-1 图6-2(a )充电曲线 图6-2(b )放电曲线若开关S 首先置于2使电路处于稳定状态, 在t=0时刻由2扳向1, 电路为零输入响应, 有RCt S C eU t u -=)(这一暂态过程为电容放电过程, 放电曲线如图6-2b 所示。
电路的零输入响应与初始状态成正比。
动态电路的零状态响应与零输入响应之和称之为全响应,全响应与激励不存在简单的线性关系。
2.一阶RC 动态电路在一定的条件下, 可以近似构成微分电路或积分电路。
当时间常数 (=RC)远远小于方波周期T 时, 图6-3(a)所示为微分电路。
输出电压u0(t)与方波激励uS(t)的微分近似成比例, 输入输出波形如6-3(b)所示。
从中可见, 利用微分电路可以实现从方波到尖脉冲波形的转变。
+ u O_uC图6-3(a ) 图6-3(b )当时间常数 (=RC)远远大于方波周期T 时, 图6-4(a)所示为积分电路, 输出电压uO(t)与方波激励uS 的积分近似成比例。
输入、输出波形如图6-4(b)所示。
一阶电路的过渡过程

一阶电路的过渡过程1、一阶电路的零输入响应零输入响应:换路后动态电路中没有外施激励,电路响应由动态元件所储藏的能量引起。
一阶电路的零输入响应包括有RC放电电路和RL 放电电路。
2、RC放电电路RC电路的时间常数:对于含有电容的一阶电路,电路的时间常数定义为,时间常数,其中为一阶电路中,除电容以外的含源一端口网络或无源一端口网络的等效电阻。
如:在图1电路中,电阻、电容以及电压源全部为已知参数,开关S 在t=0时刻从位置1合到位置2,开关移动之前电路处于稳态,换路后的、以及流过电路中的电流为:,,图1 RC放电电路图2 电容电压、电阻电压和电路电流随时间的变化根据所求得的、和,可得它们随时间的变化规律如图2所示。
从图22中电压和电流随时间的变化规律,可得结论:1)电流和电压都按照同样的指数规律变化,因电路的特征方程和特征根仅取决于电路的结构和元件的参数,而与变量的选择无关。
2)由于特征根是负值,电流和电压都按同样的指数规律衰减,最终趋于零。
从上可以看出,电压和电流的衰减的快慢取决于指数中的大小。
反映了一阶电路过渡过程的进展速度,越小,过渡过程越快,是讨论过渡过程的一个重要参数。
3、RL放电电路RL电路的时间常数:对于含有电感的一阶电路,电路的时间常数定义为,时间常数,其中为一阶电路中,除电感以外的含源一端口网络或无源一端口网络的等效电阻。
利用微分方程的求解,RL电路响应的电压和电流随时间的变化规律,可得出与RC电路相同的结论。
4、一阶电路的零状态响应零状态响应:换路后动态电路中动态元件所储藏的能量为零,电路响应是由外施激励引起。
零状态响应的时间常数与零输入响应的时间常数的求解相似。
且零状态响应的过渡过程变化规律主要也是由时间常数来决定。
实验报告RC一阶电路的响应测试

实验报告实验题目:RC 一阶电路的响应测试 实验目的1. 测定RC 一阶电路的零输入响应、零状态响应及完全响应。
2. 学习电路时间常数的测量方法。
3. 掌握有关微分电路和积分电路的概念。
4. 进一步学会用示波器观测波形。
实验原理1. 动态网络的过渡过程是十分短暂的单次变化过程。
要用普通示波器观察过渡过程和测量有关的参数,就必须使这种单次变化的过程重复出现。
为此,我们利用信号发生器输出的方波来模拟阶跃激励信号,即利用方波输出的上升沿作为零状态响应的正阶跃激励信号;利用方波的下降沿作为零输入响应的负阶跃激励信号。
只要选择方波的重复周期远大于电路的时间常数τ,那么电路在这样的方波序列脉冲信号的激励下,它的响应就和直流电接通与断开的过渡过程是基本相同的。
2.图1(b)所示的 RC 一阶电路的零输入响应和零状态响应分别按指数规律衰减和增长,其变化的快慢决定于电路的时间常数τ。
3. 时间常数τ的测定方法:用示波器测量零输入响应的波形如图1(a)所示。
根据一阶微分方程的求解得知u c =U m e-t/RC=U m e-t/τ。
当t =τ时,Uc(τ)=0.368U m 。
此时所对应的时间就等于τ。
亦可用零状态响应波形增加到0.632 U m 所对应的时间测得,如图1(c)所示。
(a) 零输入响应 (b) RC 一阶电路 (c) 零状态响应图 14. 微分电路和积分电路是RC 一阶电路中较典型的电路, 它对电路元件参数和输入信号的周期有着特定的要求。
一个简单的 RC 串联电路, 在方波序列脉冲的重复激励下,当满足τ=RC<<2T时(T 为方波脉冲的重复周期),且由R 两端的电压作为响应输 出,这就是一个微分电路。
因为此时电路的输出信号电压与输入信号电压的微分成正比。
如图2(a)所示。
利用微分电路可以将方波转变成尖脉冲。
(a) 微分电路 (b) 积分电路图2若将图2(a )中的R 与C 位置调换一下,如图2(b )所示,由 C 两端的电压作为响应输出。
初始值的计算,零输入响应,零状态响应,全响应及三要素公式的推导(1)

i R 0 u L 0
, u 0 uS(0+)
R
NR
, i 0 iS(0+) c
uC(0+) iL(0+)
(b)t=0+时等效电路
电路分析基础
3.8 电路初始值的计算
9
计算非独立初始值的具体方法: A、画出t =0+电路,
a、若 若
uc (0 ) uc (0 ) U cs ,
6
以电容上电压为未知变量列写电路的方程。
换路后由图(b)可知,其KVL方程为:
uczi (t ) uRzi (t ) 0
而uRzi(t)=izi(t) R,
izi ( t )
C
d u C zi ( t dt
)
,代入上式可得:
RC
duCzii (0+ )= RI S
则电容用一个电压源UCS代替;
uc (0 ) 0 , 则电容用短路线代替。
b、若 iL (0 ) iL (0 ) ILs ,
则电感用一个电流源ILS 代替; 若 iL (0 ) 0 , 则电感作开路处理。
B、现在可用求解电阻电路的各种方法来求解指定的非独立初始值。
电路分析基础
3.8 电路初始值的计算
(或称内部激励)共同作用引起的响应。
f t 0
N
y t
xk 0 0 k1,2,,n
实际上,由线性电路的性质知:
全响应 零输入响应 零状态响应
即:
y t yzi t yzs t
电路分析基础
xk 0 0 k 1,2,,n
3.4 电感的串联和并联
6
思考题
1. 解释电路零输入响应的定义; 2. 解释电路零状态响应的定义; 3. 解释电路全响应的定义;
一阶电路的零输入响应零状态响应

2 0
WR
i2Rdt
0
0(I0eL/tR)2Rdt
I02R
0
e
2t
L/Rdt
I02R(L2/ReR2tC)| 0
1 2
LI 0 2
上页 下页
例1 t=0时 , 打开开关K,求uv。 电压表量程:50V
K(t=0) R=10
10V
+
uV
–
V RV 10k
有一过渡期
0
t1新的稳定状态 t
过渡状态
上页
下页
(t →)
i
K 未动作前,电路处于稳定状态
K
R+
US
uL L
–
iU S R, uL0
K US
i
R+
uL L
–
K 断开瞬间
i0, uL
注意工程实际中的过电压过电流现象
上页 下页
换路
支路接入或断开 电路结构、状态发生变化
电路参数变化
过渡过程产生的原因
(1) 由0-电路求 uC(0-)或iL(0-)
例1 求 iC(0+)
10k
+
10V -
10k 40k
+ uC(0-) -电
+
i
40k iC
+ uC
- 10V k
-
uC(0)8V
(2) 由换路定律
容 开 路
+ 10V
-
i 10k iC (0+)
0+等效电路
uC(0)uC(0)8V
+
8V
(3) 由0+等效电路求 iC(0+)
零状态全响应三要素

uc
t
t
uC US (1 e ) U0e t 0
零状态响应
US
零输入响应
U0
全响应 零状态响应
t 0
零输入响应
暂态+稳态
t
uC U S (U0 U S )e 电路响应与其工作状态
t0
之间的关系
零输入+零状态
t
t
uC US (1 e ) U0e
激励与响应的因果关系
t0
A=4
L 0.1s
R1 R2
i (4e10t 2)A t 0
uL
L
di dt
24e V 10t
t0
解法二 全响应 i =零输入响应i ′+ 零状态响应i"
i(0 ) i(0 ) 6A
0.1s
1. i 6e 10t A t 0
t
( f (t ) f (0 )e )
i() 2A
状态,再根据元件的VAR ,便可一求出其他各个电压、电流。
3. 一阶电路的零状态响应和激励成正比,称为零状态线性。
RC零状态响应电路
uC (0+)= uC (0-)=0
=RC
t
uC U S (1 - e RC ) t 0
iC
US R
t
e RC
t0
t
uR USe RC
t0
RL零状态响应电路
iL(0+)= iL(0-)=0
2. i 2(1 e10t )A t 0
t
( f (t) f ()(1 e ))
i i i (4e10t 2) A t 0
uL
L di dt
24e V 10t
RC一阶电路的响应测试实验内容

实验五RC—阶电路的响应测试一、实验目的1.测定RC-阶电路的零输入响应、零状态响应及全响应。
2.掌握有关微分电路和积分电路的概念。
3.学会时间常数T的测定方法。
4.进一步学会用示波器观测波形。
二、原理说明图5」所示的矩形脉冲电压波5可以看成是按照一定规律定时接通和关断的直流电压源U。
若将此电压5加在RC串联电路上(见图5.2),则会产生一系列的电容连续充电和放电的动态过程,在5的上升沿为电容的充电过程,而在5 的下降沿为电容的放电过程。
它们与矩形脉冲电压5的脉冲宽度匕及RC串联电路的时间常数T有十分密切的关系。
当5不变时,适当选取不同的参数,改变时间常数T,会使电路特性发生质的变化。
图5.1矩形脉冲电压波形图5.2 RC串联电路图1 • RC 一阶电路的零状态响应所有储RC喚+ u - U °的电路%(t) = U 卢响应。
电路的微分方程为:RC dt +%-U叫其解为(• 忒八一丿,式中,T=RC为该电路的时间常数。
2.RC-阶电路的零输入响应电路在无激励情况下,由储能元件的初始状态引起的响应称为零输入响应。
电路达到'* ciu c- •'器经R放I V各响应为零输入响应。
电路的微分方程为:RC盂十%"其解为%(t)= U m e \RC —阶电路的零输入响应和零状态响应分别按指数规律衰减和增长(如图5.3 所示),其变化的快慢决定于电路的时间常数T。
3.时间常数T的测定方法方法一:在已知电路参数的条件下,时间常数可以直接由公式计出,T=RC。
方法二:对充电曲线(零状态响应),电容的端电压达到最大值的1二(约0.632)倍时所需要的时间即是时间常数T。
如图5.3 (a)所示,用示波器观测响应波形, 取上升曲线中波形幅值的0.632倍处所对应的时间轴的刻度,计算出电路的时间常数:丫 =扫描时间X 0P其中,扫描时间是示波器上x轴扫描速度开关“t/div”的大小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3) 求一阶电路的零输入响应,就是 找初始值及特征根(或时间常数)。 (4) 因 e 1 =0.368,所以 是零输入响 应衰减到初始值的0.368时的时间。
如果电路中有多个电阻或含受控源, 则 =RC中的R应是动态元件两端 的戴维宁电阻R0 。
二、RL电路的零输入响应
t=0 2 iL
1
uR uc U0 i( t ) e R R R
uc t
U0 R
t
,t >0
U0
i t
0 0 由上述结果可看出: (1) 特征根为负(即 为正)的零输入响 应是从初始值开始随时间单调衰减的指数函数。 所经历的过渡过程的长短取决于RC(即时间常 数),R和C↑,过程会↑。
(2) RC电路零输入响应变化过程的实质 是电容的贮能逐渐被R所消耗的过程。
§8-1 零输入响应
一、 RC电路的零输入响应 对下图电路,求换路以后 ( t 0) 的 uc ( t ),i ( t ),uR ( t )。
R0
t=0 i + + R uR C uc -
+ -
U0
R0
t=0 i + + R uR C uc C + uc -
i + R uR -
+ -
U0
1、换路前后,电路的物理过程
st
因特征方程为
1 RCS 1 0 则 S RC t uc (t) Ke RC
在上式中令 t=0,得K= uC(0) =U0
t U 0e RC t
则 uc ( t )
U0 e ,t 0
1 式中 RC ,称为RC电路的时间常数 S
又
iL
R
I0
R
L
+ L uL t 0, i L ( 0 ) I 0
R 由特征方程 LS R 0 S L 1 L 且令 称为RL电路的时间常数。
diL L RiL 0 以 iL为变量的方程: dt iL ( 0 ) I 0
S
R
, t0 t di L RI 0e t >0 及 uL (t ) L , dt iL u
t 0, uc (0) U 0
t 0 时,uc ( 0 ) U0,i ( 0 ) 0,uR ( 0 ) 0
t=0+时,uc(0+)=uc(0-)=U0,
i(0+)= U 0 , R
1 2 CU Wc(0)= 0 2
uR(0+)=U0,
t > 0 时, C 放出能量(放电), uc ( t ) , uR ( t ) uc ( t ) i(t ) R t , uc uR 0 , i 0 ,放电结束,电路 达到稳态。
(若电路中有多个电阻或受控源,式中R0 为 t 0 时动态元件两端的戴维宁等效电 阻。)
3. 零输入响应满足线性性 (即比例性 和叠加性)。
例 求 t 0 时 的i1、i2、i3。
a t = 0 10 + b - 10V 10 i3 i1
1H
20
i3 i1
i2
20
i2
1 H
20
t0
+ u R + + US C uc (t = 0+)
ic
uc(0- ) = 0
1. 电路的物理过程 t=0- 时, uc (0) 0,ic (0) 0 t = 0+ 时,uc (0) uc (0) 0 ,电容等效 为短路,
Us 为最大值, ic ( 0 ) uR (0) US 最大值。 R duc ic (0 ) 随t↑,∵ uC(t)↑, > ,∴ 0 dt t 0 C ic R uR(t) ↓, ic↓。 + + US C uc 当t→∞时,ic→0, t0 uR→0,uc→Us 达到最 ic R + uR 大值,此时电容相当于 + + US C uc 开路,电路达到稳态。 -
2. 电路的微分方程及其求解
i
设响应为 uc(t) + + uc uR 0 C uc R uR duc uR Ri RC t 0, uc (0) U 0 dt duc RC uc 0,t (齐次微分方程) 0 dt 及uc ( 0) U 0 一阶齐次微分方程的解为 uc ( t ) Ke 式中K是由初始条件确定的待定常数,S 是特征方程的特征根。
(t )
uc(t)的微分方程及其求解 R duc RC uc U s + 由KVL dt US uc ( 0) 0
非齐次一阶微分方程的解为:
10 t
20
20
t0 A,t 0 1 10 t i 2 (t ) i 3 (t ) i 1 (t ) 0.5e A,t 0 2
§8-2零状态响应
初始状态为零,仅由外加激励引起的响应称 为零状态响应。
一、 RC电路的零状态响应 R ic t=0 + u R + + uc C US R
。而 L
放电时间↓,所以
1 。 R
三、小结
1. 一阶电路零输入响应的通式
t
f ( t ) f ( 0 )e
, t >0
即只需求得 f (0 ) 和τ,就可 得出 一阶电路的零输入响应。
2 . f ( 0 ) 由动态元件的性质及KVL、 KCL确定;τ由电路本身参数确定: R0C 或 L R0 。
I0
iL ( t ) I 0 e
R t L
I0e
t
0
L
t
0.368I0
0
t - RI 0
可见,当s <0时,RL电路的零输入响应也是按指 数规律衰减,衰减的快慢取决于时间常数 。
L 何以 ? R
这是因为在同样的初始电流时,L↑,贮 能↑,过渡过程将愈长。即 初始电流一定时,R↑,消耗的功率↑,
a + 10V t = 0-
解:这是பைடு நூலகம்零输入响应,先 t 求
10 i1(0- )
i1 ( t ) i1 ( 0 )e
由t =0-的电路,
i1 (0) 1 A i1 (0)
又∵ R0=20∥20=10
i3
i2 i1
1 H
L 1 则 S R 10
∴ i 1 (t ) e
