一阶电路的零输入响应
06-3 一阶电路的零输入响应-应用举例课件

t ≥ 0+ 电路
电压表损坏!!
一阶电路零输入响应——举例
例4:如图所示汽轮发电机励磁电路,t=0时开关S打开,
打开前已达稳态, 电压表是否会损坏? 电压表量程:100V
+ 24V _
S
iL
R=4Ω
L=0.1H
+
RV V uV 10k _
iL (0+ ) = 6A
+ 24V _
S
iL
R=4Ω
L=0.1H
S
US=12V
+ Us_
R i
+ u_L L
火花塞 气隙
工作原理
①点火开关S闭合, 经过一段时间,电路达到稳态,电感
线圈电流为:
i=US/R
②开关S断开, 电感两端会形成很高的电压,产生电弧
实现汽车点火
6Ω
20mF
+ u+_C 18V_
解: 求初始值 u C(0+) = uC(0-)
3Ω 6Ω
2Ω 20mF
+ u_C(0-)
t = 0 - 电路
一阶电路零输入响应——举例
例3:如图所示电路,开关S在t=0时打开,打开前电路
已达稳态,试求uC(t) (t ≥0+) ,并计算电容器初始储能。
3Ω S(t =0)
+ 24V _
S
iL
R=4Ω
L=0.1H
+
RV V uV 10k _
+ 24V _
S
iL
R=4Ω
L=0.1H
+
RV V uV 10k _
解: 求初始值
t = 0 - 电路
一阶电路的零输入响应

dt
50 1 e1500t 0.05 1500 e1500t
50 25e1500tV
第17页/共26页
§10.4 一阶电路的全响应 一、全响应的分解
全响应:电路中输入激励和储能元件的储能共同产生的响应。
R
+
+ uR – i
–US
C
uC 0 U0
电路方程
ui US
+u US-U0 C
一、RC电路的零输入响应
12 i
uC i
特征根
p
1
+ U0
—
R0
+ C uC
—
+ R uR
—
U0
U0
R
uC
i
0
RC
t
uC Ae RC t 0
确定积分常数
t
uC 0 U0
uC 0 U0
电路方程
uR uC 0
电压与电流的关系
u R iR
电路方程
RC
duC dt
uC
0
t>0
通解
uC Aept
二、全响应的分解
1.全响应可分解为稳态分量和瞬态分量。
t
uC = uC′+ uC″ = US + (U0 - US)e
τ
稳态分量 瞬态分量
强制分量 自由分量
2.全响应可分解为零输入响应和零状态响应。
t
t
uc = uc1 + uc2 = U0e τ + US(1-e τ )
零输入响应 零状态响应
uC US
+ uR –
uR uC i
+
R+i
(电路分析)一阶电路的零输入响应
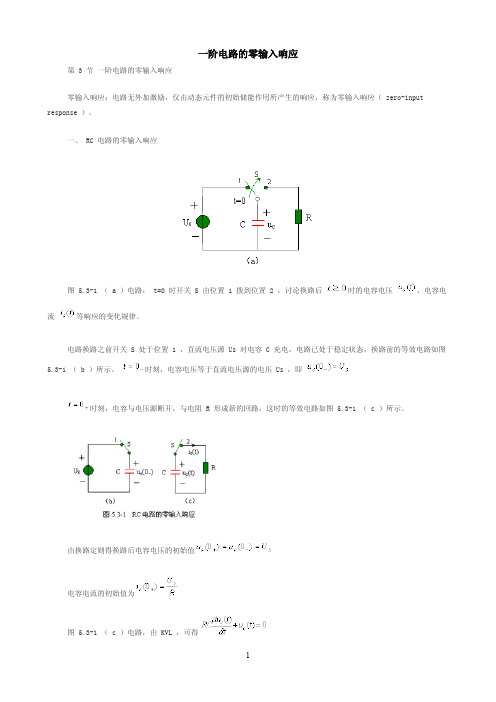
一阶电路的零输入响应第 3 节一阶电路的零输入响应零输入响应:电路无外加激励,仅由动态元件的初始储能作用所产生的响应,称为零输入响应( zero-input response )。
一、 RC 电路的零输入响应图 5.3-1 ( a )电路, t=0 时开关 S 由位置 1 拨到位置 2 ,讨论换路后时的电容电压、电容电流等响应的变化规律。
电路换路之前开关 S 处于位置 1 ,直流电压源 Us 对电容 C 充电,电路已处于稳定状态,换路前的等效电路如图5.3-1 ( b )所示。
时刻,电容电压等于直流电压源的电压 Us ,即时刻,电容与电压源断开,与电阻 R 形成新的回路,这时的等效电路如图 5.3-1 ( c )所示。
由换路定则得换路后电容电压的初始值电容电流的初始值为图 5.3-1 ( c )电路,由 KVL ,可得用积分变量分离法进行求解,得式中,为 RC 电路的时间常数( time constant ),当 R 的单位为Ω, C 的单位为 F 时,τ的单位是秒( s )。
时间常数:时间常数是反映一阶电路过渡过程进展快慢的一个重要的参数,其大小仅取决于电路的结构和参数。
τ越大,响应衰减的速度就越慢;τ越小,响应衰减的速度就越快。
用表示电路换路后的响应,用表示该响应的初始值,则 RC 一阶电路的零输入响应可表示为RC 电路零输入响应的规律RC 电路换路后,各处的零输入响应都是从初始值开始,按指数规律衰减。
衰减得快慢由时间常数τ决定。
二、 RL 电路的零输入响应图 5.3-3 ( a )是 RL 动态电路。
电路换路之前开关 S 处于位置 1 , t=0 时开关 S 由位置 1 拨到位置 2 。
下面讨论换路后时的电感电流、电感电压等响应的变化规律。
时刻,电路换路之前开关 S 处于位置 1 ,直流电流源 Is 对电感 L 充电,电路已处于稳定状态,换路前的等效电路如图 5.3-3 ( b )所示。
t=0 时,开关 S 拨到位置 2 ,时,电感与电流源断开,而与电阻 R 形成新的回路,这时的等效电路如图5.3-3 ( c )所示。
一阶RC电路的零状态与零输入响应

2022/9/10
2022/9/10
一 四、一过阶渡R过C程电路零输入响应的实例
解: 在开关由位置1拨向位置2的瞬间,电容电压不能越变,因此可得
uC (0 ) uC (0 ) 6V
将连接于电容两端的电阻等效为一个电阻,其阻值为
R 8 6 3 10k 63
的电流为 I0 US R1,
电感中储存一定的 能量。在 t 0,开 关S由位置1拨向位 置2处。
一 三、一过阶渡R过L程电路的零输入响应的分析
一阶RL电路的零输入响应的定性分析
在换路的瞬间,由于电感的电流不能突变,即 iL (0 ) iL (0 ) I0 , 此时电阻 端电压 uR (0 ) I 0 R 。根据KVL可知,电感上的电压立即从换路前的零值突变
得到如图(b)所示电路,其时间常数为
RC 10103 5106 5102 s 0.05s
uC
t
U0e
6e V 20t
iC
U0
t
e
R
- 6 e20t 10 10 3
0.6e20t mA
一 四、一过阶渡R过C程电路零输入响应的实例
例:电路如下图所示,t 0 时开关由位置1拨向位置2,求 t 0 时
而电阻消耗的能量为
Q
0 uC dq
U 0
S
CuC
duC
1 2
CU
2 S
WR
i 2 Rdt
0
U
2 S
0R
2t
e RC dt
1 2
CU
2 S
由此可见,在充电过程中电源所提供的能量,一半储存在电容的电场中, 一半消耗在电阻上。且电阻上消耗的能量与R无关,充电效率总是50%。
一阶电路零状态响应公式

一阶电路零状态响应公式在电路理论中,一阶电路是指由一个电感或一个电容和一个电阻组成的电路。
它是电路理论中最基本的电路之一,也是我们学习电路的起点。
在分析一阶电路时,我们经常需要计算电路的零状态响应,即在初始时刻电路中没有任何电流或电压的情况下,当输入信号突然改变时电路的响应。
一阶电路的零状态响应公式可以通过求解电路的微分方程得到。
对于一个由电感、电阻和输入电压源组成的串联电路,我们可以根据基尔霍夫电压定律和欧姆定律建立如下的微分方程:L di/dt + Ri = Vin其中,L是电感的感值,单位是亨利;R是电阻的阻值,单位是欧姆;Vin是输入电压源的电压,单位是伏特;i是电路中的电流,单位是安培;t是时间,单位是秒。
为了求解这个微分方程,我们可以使用分离变量法。
首先,将方程两边除以L,得到:di/dt + (R/L)i = Vin/L接下来,我们可以将这个微分方程进行变换,使得左边只有i的导数,右边只有t和Vin。
具体的变换方法是将方程两边乘以e^(Rt/L),得到:e^(Rt/L)di/dt + (R/L)e^(Rt/L)i = (Vin/L)e^(Rt/L)这样,左边的第一项可以通过链式法则转化为:d(e^(Rt/L)i)/dt右边的第一项可以通过乘法法则转化为:(Vin/L)e^(Rt/L)现在,我们可以将方程重新写成:d(e^(Rt/L)i)/dt = (Vin/L)e^(Rt/L)接下来,我们对方程两边进行积分,得到:∫d(e^(Rt/L)i) = ∫(Vin/L)e^(Rt/L)dt对于左边的积分,我们可以使用积分的基本性质,得到:e^(Rt/L)i = ∫(Vin/L)e^(Rt/L)dt + C其中,C是积分常数。
最后,我们可以解出i的表达式:i = (1/L)e^(-Rt/L)∫(Vin/L)e^(Rt/L)dt + Ce^(-Rt/L)这就是一阶电路的零状态响应公式。
通过这个公式,我们可以计算出在初始时刻电路中没有任何电流或电压的情况下,当输入信号突然改变时电路的响应。
一阶电路的零输入响应零状态响应

2 0
WR
i2Rdt
0
0(I0eL/tR)2Rdt
I02R
0
e
2t
L/Rdt
I02R(L2/ReR2tC)| 0
1 2
LI 0 2
上页 下页
例1 t=0时 , 打开开关K,求uv。 电压表量程:50V
K(t=0) R=10
10V
+
uV
–
V RV 10k
有一过渡期
0
t1新的稳定状态 t
过渡状态
上页
下页
(t →)
i
K 未动作前,电路处于稳定状态
K
R+
US
uL L
–
iU S R, uL0
K US
i
R+
uL L
–
K 断开瞬间
i0, uL
注意工程实际中的过电压过电流现象
上页 下页
换路
支路接入或断开 电路结构、状态发生变化
电路参数变化
过渡过程产生的原因
(1) 由0-电路求 uC(0-)或iL(0-)
例1 求 iC(0+)
10k
+
10V -
10k 40k
+ uC(0-) -电
+
i
40k iC
+ uC
- 10V k
-
uC(0)8V
(2) 由换路定律
容 开 路
+ 10V
-
i 10k iC (0+)
0+等效电路
uC(0)uC(0)8V
+
8V
(3) 由0+等效电路求 iC(0+)
一阶电路的零输入响应
3、原始能量增大A倍,则零输入响应将相应增大A倍,这种原始能量与零输 入响应的线性关系称为零线性。
零输入响应就是无电源一阶线性电路,在初始储能作用下产生的响应,
其形式表示为:
f (t) f (0) et
t 0
式中 f (0) 为变量的初始值 uC (0 ) 或 iL (0 )
为时间常数 RC (电容)
L R
(电感)
一、RC电路的零输入响应
如右图,已知uc(0-)=U0,K于t=0 时刻闭合,分析t≧0时uc(t) 、 i(t)的变化规律。
0
一阶常系数齐次微分方程
其特征根方程:
S 1 0
特征根
RC
1
S
RC
uc (t )
Ae st
1t
Ae RC (t
0)
又有初始条件: uc(0+) = uc(0-) =U0 (换路定理)
1t
uc (t ) U0e RC (t 0)
i(t ) C duc
U0
1t
e RC (t
0)
dt
R
i(t)
E
uL(t)的变化规律。
R0 K R
iL
+ L uL
-
(a) 分析:t<0时已达稳态,L中电流为I0=E/R0
t≧0时,电感以初始储能来维持电流iL (t)(放电)
①
换路后( t≧0),由KVL有:
L diL dt
RiL (t ) 0
即:
diL dt
R L
iL (t )
0
特征根:
零状态全响应三要素
uc
t
t
uC US (1 e ) U0e t 0
零状态响应
US
零输入响应
U0
全响应 零状态响应
t 0
零输入响应
暂态+稳态
t
uC U S (U0 U S )e 电路响应与其工作状态
t0
之间的关系
零输入+零状态
t
t
uC US (1 e ) U0e
激励与响应的因果关系
t0
A=4
L 0.1s
R1 R2
i (4e10t 2)A t 0
uL
L
di dt
24e V 10t
t0
解法二 全响应 i =零输入响应i ′+ 零状态响应i"
i(0 ) i(0 ) 6A
0.1s
1. i 6e 10t A t 0
t
( f (t ) f (0 )e )
i() 2A
状态,再根据元件的VAR ,便可一求出其他各个电压、电流。
3. 一阶电路的零状态响应和激励成正比,称为零状态线性。
RC零状态响应电路
uC (0+)= uC (0-)=0
=RC
t
uC U S (1 - e RC ) t 0
iC
US R
t
e RC
t0
t
uR USe RC
t0
RL零状态响应电路
iL(0+)= iL(0-)=0
2. i 2(1 e10t )A t 0
t
( f (t) f ()(1 e ))
i i i (4e10t 2) A t 0
uL
L di dt
24e V 10t
电路理论:一阶电路的零输入响应
零输入响应(Zeroinput response ):激励(电源)为零,由初 始储能引起的响应。
一、 RC电路的零输入响应 (C对R放电)
S(t=0) i
+
C uC
–
+
R uC
–
i C duC dt
uC
RC duC dt
0
uC (0)=U0
解答形式 uC(t)=uC"=Aept (特解 uC'=0)
1
p
从理论上讲 t 时,电路才能达到稳态. 单实际上一般认
为经过3 5 的时间, 过渡过程结束,电路已达到新的稳态。
t 0
2
3
4 5
t
uc U0e
U0
0.368U0
0.135U0
0.05U0
0.02U0
0.007 U0
能量关系:
C
R
C的能量不断释放, 被R吸收, 直到
全部储能消耗完毕.
WR
由特征方程
Lp+R=0
得
pR L
由初值 i(0+)=i(0)= I0 得 i(0+)=A= I0
解答
Rt
iL(t) I0e L
(t 0)
Rt
iL(t) I0e L
(t 0)
I0 iL
uL(t)
L diL dt
R t
RI 0e L
(t
0)
O uL
t
O
(1) iL, uL 以同一指数规律衰减到零;
iL I0e L
R
R
t
t
uV RiL RV I0e L 875e L kV
一阶电路的零输入响应
一阶电路的零输入响应所谓零输入响应就是没有外部激励输入,仅仅依靠动态元件中的储能产生的响应。
换句话说,就是求解微分方程在初始条件不为零时的齐次解。
1 RC 电路的零输入响应如图1-4-5(a)所示的电路中:t<0 时,开关在位置1,电容被电流源充电,电路已处于稳态,电容电压uC(0-)=RIS;在t=0 时,开关按箭头方向动作;在t≥0 时,电容将对R 放电,电路如图1-4-5(b)所示,电路中形成电流i。
故t>0 后,电路中无电源作用,电路的响应均是由电容的初始储能而产生,故属于零输入响应。
换路后得图1-4-5(b),根据KVL有uR +uC=0,而代入上式可得图1-4-5 RC电路的零输入这是一个一阶齐次方程,根据换路定理,可知初始条件uC (0+)=uC(0-)=u。
方程的通解为将初始条件uC (0+)=RIS代入式(1-4-12),求出积分常数A为将uC (0+)代入式(1-4-12),得到满足初始值的微分方程的通解为放电电流为令τ=RC,它具有时间的量纲,即故称τ为时间常数,这样式(1-4-13)、(1-4-15)可分别写为。
由于,为负,故uC和i均按指数规律衰减,它们的最大值分别为初始值uC (0+)=RIS,以及,当t→∞时,uC和i衰减到零。
其变化曲线如图1-4-6所示。
图1-4-6 RC 电路零输入响应电压电流波形图关于零输入响应曲线的几点说明:(1)时间常数是体现一阶电路电惯性特性的参数,它只与电路的结构与参数有关,而与激励无关。
(2)对于含电容的一阶电路,τ=RC;对于含电感的一阶电路,。
(3)τ越大,电惯性越大,相同初始值情况下,放电时间越长。
(4)一阶电路方程的特征根为时间常数的相反数;它具有频率的量纲,称为“固有频率”(natural frequency)。
理论上认为t→∞、uC →0 时,电路达稳态;工程上认为t=(3-5)τ、uC→0,电容放电基本结束。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
R1
R3
R3
+ US
–
解: ⑴
+ uR2
+ uR3– R2
–
L iL
+ uL
–
C
iC +
+ uR2
uC
–
–
iL(0+)
+ uR3 – R2
+ uL
–
确定独立初始值
iC
+ uC(0+)
–
⑵ 确定相关初始值
uR2 0 R2iL 0 55 25V
iL 0
US R1 R2
50 55
5A
uC 0 R 2iL 0 5 5 25V
0
uC U0
0.368U0
uC
0
τ
uC
U0
uC2uC3 0.368U0 uC1
t
0 τ1 τ2 τ3
τ3>τ2>τ1
第5页/共26页
t
uC U0e
t
i
U0
t
e
R
WC
1 2
Cu
2 C
RC
一组C=40µF的电容器从高压电路断开,断开时电容器电压U0=5.77kV, 断开后,电容器经过它本身的漏电阻放电。电容器的漏电阻R=100MΩ, 试问断开后经过多长时间,电容器的电压衰减为1KV。
24 230 250
0.05A
继电器电流为
得
t
i 0.05e A 0.01
t 0.01 ln 0.05 0.025s 0.004
第10页/共26页
RL
图示为汽轮发电机的励磁回路,已知励磁绕组的电阻R=1.4Ω,电感L=8.4H,
初始值的计算
1. 根据换路定律求独立初始值。
2. 根据独立初始值和电路基本定律求相关初始值。 复杂电路可画出 t = 0+时的等效电路
电容元件
+ uc(0+) –
+ uc(0+) –
电感元件
C
iL(0+)
L
iL(0+)
第2页/共26页
计算初始值
图示电路中,电压源电压US=50V, R1=R2=5Ω, R3=20Ω。电路原以稳定。 在t=0时断开开关。试求t=0+时的iL、uC、uR2、uR3、iC、uL。
1kΩ 1 2 i
3mA
+
2kΩ 1µF uC
3kΩ
﹣
解
uC 0 uC 0 310 3 2 103 6V
时间常数 RC 3103 1106 0.03s
得
i
U0
t
e
6
e
t 0.003
2e333t mA
R
3
uC
t
U0e
t
6e 0.003
6e333t V
第7页/共26页
RC
如图所示,开关闭合前电路已处于稳态。在t=0时将开关闭合, 试求t > 0时电压uC和电流ic、i1及i2 。
解 电路的时间常数为
RC 100106 40106 4000s
t
t
uC U0e 5.77e 4000 kV
把Uc=1kV代入
t
1 5.77e 4000kV
t 4000ln 5.77 7011s
第6页/共26页
RC
如图所示,开关长期接在位置1上,如在t=0时把它接在位置2上, 试求电容电压uC及放电电流i的表达式。
uL
L
di dt
uR Ri
代入方程得
L di Ri 0 t>0
dt
由初始条件求出 A I0
得出
令 L
R
t
i I0e t 0
R t
i I0e L
uL
L di dt
R t
RI 0e L
t>0
uR
Ri
R t
RI 0e L
t
0
t
u L RI 0e
t
u R RI 0e
第9页/共26页
A U0
电容零输入响应电压
t
uC U0e RC t 0
i C duC dt
特征方程
RCP 1 0
i C duC
U0
t
e RC
dt R
t>0
第4页/共26页
时间常数τ
❖ RC电路中,电阻R与电容C的乘积称为RC电路的时间常数 。
τ= RC
t
0
1τ 2τ 3τ 4τ 5τ …
∞
t
U0e τ U0 0.368U0 0.135U0 0.05U0 0.015U0 0.007U0 …
§10.1换路定律和初始条件的计算
一、换路定律
❖ 换路: 电路中支路的接通、切断、短路,电源或电路参数的突然改变及
电路结构的改变等统称为换路。
t = O 时换路
0- 0+
t
0
换路前的最后一刻(未换路)
换路后的最初一刻(已换路)
换路定律内容:在换路瞬间,电容电压不能跃变,电感电流不能跃变。
ห้องสมุดไป่ตู้
u
US
0
t
uC(0+)= uC(0-)
iC 0 iL 0 5A uR30 R3iC 0
20 5 100 V
iL 0 iL 0 5A
uL 0 uR2 0 uR30 uC 0
uC 0 uC 0 25V
25100 25 100V
第3页/共26页
§10.2一阶电路的零输入响应
零输入响应: 电路中输入激励为零,仅由动态元件的初始储能引起的响应。
i C duC
dt
WC
1 2
Cu 2
iL(0+)= iL(0-)
uL
L
diL dt
WL
1 2
Li2
第1页/共26页
二、初始值的计算
初始值: 响应在换路后的最初一瞬间(即 t = 0+)时的值称为初始值。
独立初始值:电容电压的初始值uC(0+)和电感电流的初始值iL(0+)。 相关初始值:其他可跃变的量的初始值。
i1 iC i2 1.5e1.7105 tA
第8页/共26页
二、RL电路的零输入响应
R
+ uR – i
R1
+
+
uL L
US
–
–
ui
RI0 I0
uR
i
0 uL
-RI0
通解为 i Aept
特征根
t
pR L
Rt
i Ae L
t 0
i0
US R1 R
I0
电路方程
uL uR 0
元件电压与电流的关系
一、RC电路的零输入响应
12 i
uC i
特征根
p
1
+
U0
+
+
—
C uC R uR
R0
—
—
U0
U0
R
uC
i
RC
t
uC Ae RC t 0
确定积分常数
0
t
uC 0 U0
uC 0 U0
电路方程
uR uC 0
电压与电流的关系
u R iR
电路方程
RC
duC dt
uC
0
t>0
通解
uC Aept
RL
图示电路中,一个继电器线圈的电阻R=250Ω,电感L=2.5H,电源电压
U=24V, R1=230Ω,已知此继电器释放电流为0.004A,试问开关闭合后, 经多少时间,继电器才能释放?
R1
i
+
R
U
–
L
解 时间常数为
L 2.5 0.01s R 250
电流的初始值为
i0 i0
U R1 R
1Ω +
2Ω i1 iC +
i2
解
u
C
0
u
C
0
1
6 2
3
3
3V
6V ﹣
5μF ﹣uC
3Ω
23 5106 6106s
23
得
uC
t
U0e
3e
t 6106
3e1.7105 t V
iC
U0 R
t
e
3 e1.7105 t 1.2
2.5e1.7105 t A
i2
uC 3
e A 1.7105 t
