《圆》单元测试
人教版小学六年级数学第5单元《圆》单元测试卷(附参考答案)

人教版小学六年级数学第5单元《圆》单元测试卷一、填空题。
1.半径决定圆的(),圆心决定圆的()。
2.画一个周长是18.84 cm的圆,圆内最长的线段是()cm,所画出的圆的面积是()cm2。
3.淘气用一个圆规画一个直径是 6 厘米的圆,圆规针尖的位置是圆的(),圆规两脚之间的距离是()厘米,这个圆的周长是()厘米,面积是()平方厘米。
4.自行车的车轮溶动一周,所行的路程就是车轮的()。
5.一个圆的直径扩大到原来的 3 倍,它的周长扩大到原来的()倍,面积就扩大到原来的()倍。
6.有一个钟面,它的分针长3分米,时针长2分米。
从6时到9时,分针的针尖走过的路程是()分米;时针扫过的面积是()平方分米。
7.已知一个挂钟的时针长度是分针的3,转动一小时后,时针扫过的面积是分4针的()。
8.大圆的半径与小圆的直径相等,那么大小两个圆的周长比是(),它们的面积比是()。
9.画一个圆,圆规两脚间的距离是3cm,那么,这个圆的周长是(),面积是()。
10.一个圆的周长是12.56厘米,它的面积是()。
二、选择题。
1.把一个直径是2cm 的圆分割成两个半圆形后,每个半圆形的周长是( )cm。
A.6.28 B.3.14 C.4.14 D.5.142.圆的()是圆中最长的线段。
A.周长B.直径C.半径3.画圆时,圆规两脚间的距离是圆的()。
A.半径B.直径C.周长4.一个圆的直径由原来的 3 厘米增加到 7 厘米,周长增加了()厘米。
A.6.28 B.12.56 C.25.12 D.50.245.将一个圆形纸片沿着它的直径剪成两半,它的面积和周长()。
A.面积不变周长增加B.面积增加周长不变C.面积周长都不变D.面积周长都增加6.在一个长 5 cm ,宽 3 cm 的长方形中画一个最大的半圆,这个半圆的直径是()。
A.1.5 cm B.3 cm C.5 cm D.6 cm7.一个圆的直径与周长的比是()A.1:2πB.1:πC.2:π8.淘气和笑笑分别在本子上画了一个大圆和小圆,两个圆的圆周率()A.淘气的大B.笑笑的大C.一样大D.无法比较9.用圆规画一个周长是6.28cm的圆,这个圆的半径是()cm。
数学九年级上学期《圆》单元检测卷(带答案)

∵OP=1,∠POE=45°,
∴OE=PE= ,即点P的坐标为( , ),
则第2秒P点为(0,1),
根据题意可知,第3秒P点为(- , ),第4秒P点为(-1,0),第5秒P点为(- ,- ),第6秒P点为(0,-1),
第7秒P点为( ,- ),第8秒P点为(1,0),
2018÷8=252……2,
A. B. πC. πD. π
11.如图,A B是⊙O的直径,C,D是圆上两点,连接A C,B C,A D,C D.若∠C A B=55°,则∠A D C的度数为( )
A. 55°B. 45°C. 35°D. 25°
12.如图,在矩形A B C D中,A B=3,B C=4,O为矩形A B C D对角线的交点,以D为圆心1为半径作⊙D,P为⊙D上的一个动点,连接AP、OP,则△AOP面积的最大值为()
A. 44°B. 54°C. 62°D. 72°
3.如图,A B、C D分别与半圆OO切于点A,D,B C切⊙O于点E,若A B=4,C D=9,则⊙O 半径为( )
A. 12B. C. 6D. 5
4.如图,△A B C是⊙O的内接三角形,A B为⊙O的直径,点D为⊙O上一点,若∠A C D=40°,则∠B A D的大小为( )
16.如图,Rt△A B C中,A B⊥B C,A B=6,B C=4,P是△A B C内部的一个动点,且满足∠PA B=∠PB C,则线段CP长的最小值为_____.
17.如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接A D,则图中阴影部分面积是_____.
九年级上学期数学《圆》单元检测题含答案

A.5B. C.5 D.5
[答案]D
[解析]
试题解析:连接OA、OB、OP,
∵∠C=30°,∴∠APB=∠C=30°,∵PB=A B,∴∠PA B=∠APB=30°
A.π+1B.π+2C.2π+2D.4π+1
8.如图,△A B C是⊙O的内接三角形,∠C=30°,⊙O的半径为5,若点P是⊙O上的一点,在△A BP中,PB=A B,则PA的长为()
A. 5B. C. 5 D. 5
9.如图是某公园的一角,∠AOB=90°,弧A B的半径OA长是6米,C是OA的中点,点D在弧A B上,C D∥OB,则图中休闲区(阴影部分)的面积是()
23.如图,点I是△A B C的内心,AI的延长线和△A B C的外接圆相交于点D,与B C相交于点E.
(1)求证:DI=D B;
(2)若AE=6Cm,ED=4Cm,求线段DI的长.
24.如图,已知扇形AOB的圆心角为直角,正方形OC DE内接于扇形AOB.点C、E、D分别在OA、OB、弧A B上,过点A作AF⊥DE交ED的延长线于F,如果正方形的边长为1,求阴影部分M、N的面积和.
点睛:本题考查了圆周角定理,圆周角的度数等于它所对的弧所对的圆心角度数的一半,圆的弦所对的圆周角分两种,一种是优弧所对的圆周角,一种是劣弧所对的圆周角,它们是互补的关系.
4.⊙O的半径r=5Cm,直线l到圆心O的距离D=4,则l与⊙O的位置关系是( )
A.相离B.相切C.相交D.重合
[答案]C
[解析]
3.正六边形内接于圆,它的边所对的圆周角是( )
数学九年级上册《圆》单元综合检测含答案

C.圆上任意两点之间的线段长度不大于
D.圆上任意两点之间的部分可以大于
8.已知⊙O和直线l相交,圆心到直线l的距离为10cm,则⊙O的半径可能为().
A.10cmB.6cmC.12cmD.以上都不对
9.已知 的半径为 ,点 不在 内,则点 到圆心 的距离 满足()
详解】解:连接 , ,作 于点 ,
∵ 的半径为 ,则 的内接正八边形的中心角为: ,
∴ ,
∴ ,
∴ 正八边形 ,
故答案为 .
【点睛】本题考查了正多边形和圆的知识,题目中没有作出边心距求面积是解答本题的亮点,难度一般.
15.正多边形的一个中心角为 度,那么这个正多边形的一个内角等于________度.
三、解答题(本题共计 8 小题 ,共计60分 ,)
21.作一个圆,使它经过已知点 和 ,并且圆心在已知直线 上.
(1)当直线 和 相交时,可作几个?
(2)当直线 和 垂直但不经过 的中点时,可作出几个?
(3)你还能提出不同于(1),(2)的问题吗?
22.如图,过圆锥 顶点 和底面圆的圆心 的平面截圆锥得截面 ,其中 , 是圆锥底面圆 的直径,已知 , ,求截面 的面积.
5. 如图,A、B、C是⊙O上的三点,且∠ABC=70°,则∠AOC的度数是( )
A. 35°B. 140°C. 70°D. 70°或140°
6.在⊙O中, 所对的圆心角为60°,半径为5cm,则 的长为()
A. B. C. D.
7.关于半径为 的圆,下列说法正确的是()
A.若有一点到圆心的距离为 ,则该点在圆外
A. 个B. 个C. 个D. 个
3.正六边形半径为 ,则它的边长、边心距、面积分别为()
《圆》单元测试

(一)课题:第一单元圆的测试题1.请写出元的直径和半径的关系(用字母表示):2.圆的周长公式用字母表示为(1)(2)3.圆的面积公式用字母表示为:4.求出下列圆的周长和面积:直径为20cm 半径为4dm 直径为80mm 半径3m周长:面积:1.画一个半径是1.5厘米的圆。
(1)用字母标出圆心、半径和直径(2)画出它的一条对称轴2.计算3.14×2= 3.14×5= 3.14×4= 3.14×6=3.14×8= 3.14×3= 3.14×9= 3.14×7=2.日本富士山是世界最著名的火山之一,底座直径约40千米,富士山的占地面积约是多少平方千米?3.天坛公园中的回音壁呈圆形。
它的内圆半径是32.5米,周长是多少米?4.一粒小石子投到平静的水中,水波大约可传5米;一片落叶掉到水中,水波大约可传1米。
哪种物体产生的水波面积大?大多少?5.餐厅有两种圆桌,小圆桌桌面直径是1.6米,是大圆桌的4/5。
(1)小圆桌与大圆桌周长比是多少?(2)大圆桌面积比小圆桌大约大多少平方米?(得数保留两位小数)6.一个圆形花坛,原来直径是15米,扩建后的直径与原来的比是4:3.扩建后花坛的周长和面积各是多少?(二)新青岛版(五四制)小学五年级下册数学完美的图形圆的综合测试题一、填空1.一个圆形桌面的直径是 2米,它的面积是()平方米。
2.已知圆的周长c,求d=(),求r=()。
3.圆的半径扩大2倍,直径就扩大()倍,周长就扩大()倍,面积就扩大()倍。
4.用圆规画一个周长50.24厘米的圆,圆规两脚尖之间的距离应是()厘米,画出的这个圆的面积是()平方厘米。
5.大圆半径是小圆半径的4倍,大圆周长是小圆周长的()倍,小圆面积是大圆面积的()。
6.一个半圆的周长是20.56分米,这个半圆的面积是()平方分米。
7.在一个面积是16平方厘米的正方形内画一个最大的圆,这个圆的面积是()平方厘米;再在这个圆内画一个最大的正方形,正方形的面积是()平方厘米。
人教版数学九年级上册《圆》单元检测卷(带答案)

【点睛】本题考查了圆柱的计算,解题的关键是熟知圆柱的侧面积的计算方法.
11. 在直角坐标系中的位置如图所示,若将 绕点 旋转,点 的对应点为点 ,其中 , , , ,则旋转后点 的对应点 的坐标为()
A. B. C. D.
【答案】D
【解析】
分析】
根据旋转的性质作出旋转后的图形,写出点A对应点的坐标即可得解.
【详解】连结BC.
∵OB=OC,∴∠OBC=∠OCB.
∵∠ABO=∠ACO,∴∠ABC=∠ACB,∴AB=AC,∴ = = ,故A、B、C正确,不符合题意;
∠BOC的度数无法求出,故D错误,符合题意.
故选D.
【点睛】本题考查了圆心角、弧、弦的关系定理:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等;同时考查了等腰三角形的判定与性质.
指出其旋转中心和旋转的角度
求 的长度;
与 的位置关系如何?说明理由.
24.想一想:如图称为太极图,圆形图案由两条形状和大小完全一样的白鱼和黑鱼组成,也称为“阴阳鱼”,若太极图的直径为 ,你能算出一条白鱼或黑鱼的面积吗?
25.已知 是 的直径,点 是 延长线上一点, , 是 的弦, .
(1)求证:直线 是 的切线;
设圆心角为n,有 =2πr=πR,
∴n=180°.
故选B.
考点:圆锥的计算
8.如图,直线 经过 的圆心,与 相交于 、 两点,点 在 上,且 度.点 是直线 上的一个动点(与点 不重合),直线 交 于 ,则使 的点 共有()
A.1个B.2个C.3个D.4个
【答案】C
【解析】
【分析】
作图,根据等腰三角形的性质和三角形的内角和、外角的性质求解即可.
第三章《圆》单元测试(含答案)
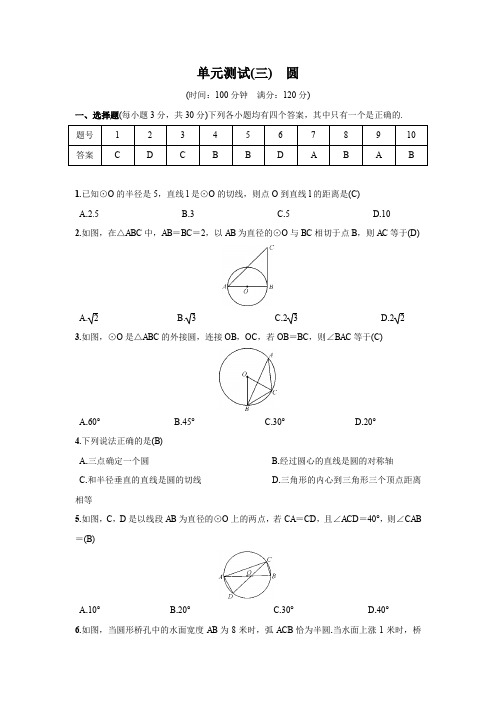
单元测试(三)圆(时间:100分钟满分:120分)一、选择题(每小题3分,共30分)下列各小题均有四个答案,其中只有一个是正确的.1.已知⊙O的半径是5,直线l是⊙O的切线,则点O到直线l的距离是(C)A.2.5B.3C.5D.102.如图,在△ABC中,AB=BC=2,以AB为直径的⊙O与BC相切于点B,则AC等于(D)A. 2B. 3C.2 3D.2 23.如图,⊙O是△ABC的外接圆,连接OB,OC,若OB=BC,则∠BAC等于(C)A.60°B.45°C.30°D.20°4.下列说法正确的是(B)A.三点确定一个圆B.经过圆心的直线是圆的对称轴C.和半径垂直的直线是圆的切线D.三角形的内心到三角形三个顶点距离相等5.如图,C,D是以线段AB为直径的⊙O上的两点,若CA=CD,且∠ACD=40°,则∠CAB =(B)A.10°B.20°C.30°D.40°6.如图,当圆形桥孔中的水面宽度AB为8米时,弧ACB恰为半圆.当水面上涨1米时,桥孔中的水面宽度A′B′为(D)A.15米B.4米C.217米D.215米7.如图,AB是⊙O的直径,P A切⊙O于点A,连接PO并延长交⊙O于点C,连接AC,AB =10,∠P=30°,则AC的长度是(A)A.5 3B.5 2C.5D.5 28.如图,AP为⊙O的切线,P为切点,若∠A=20°,C、D为圆周上的两点,且∠PDC=60°,则∠OBC等于(B)A.55°B.65°C.70°D.75°9.如图,在△ABC中,∠A=60°,BC=6,它的周长为16.若⊙O与BC,AC,AB三边分别切于点E,F,D,则DF的长为(A)A.2B.3C.4D.610.如图,将正六边形ABCDEF放置在平面直角坐标系内,A(-2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2 018次翻转之后,点C的坐标是(B)A .(4 038,0)B .(4 034,0)C .(4 038,3)D .(4 034,3)二、填空题(每小题3分,共15分)11.如图,在⊙O 中,已知∠AOB =120°,则∠ACB =60°.12.如图,在矩形ABCD 中,AB =3,AD =4,若以点A 为圆心,以4为半径作⊙A ,则点A ,点B ,点C ,点D 四点中在⊙A 外的是点C .13.如图,AB 是⊙O 的直径,C 、D 是⊙O 上的点,∠CDB =20°,过点C 作⊙O 的切线交AB 的延长线于点E ,则∠E =50°.14.如图,在△ABC 中,CA =CB ,∠ACB =90°,AB =22,点D 为AB 的中点,以点D 为圆心作圆心角为90°的扇形DEF ,点C 恰好在弧EF 上,则图中阴影部分的面积为π2-1(结果保留π).15.如图,半圆O 的半径为2,E 是半圆上的一点,将E 点对折到直径AB 上(EE ′⊥AB ),当被折的圆弧与直径AB 至少有一个交点时,则折痕的长度取值范围是三、解答题(本大题共8个小题,满分75分)16.(8分)如图,以正六边形ABCDEF 的边AB 为边,在内部作正方形ABMN ,连接M C.求∠BCM 的大小.解:∵六边形ABCDEF 为正六边形,∴∠ABC =120°,AB =B C. ∵四边形ABMN 为正方形,∴∠ABM =90°,AB =BM . ∴∠MBC =120°-90°=30°,BM =B C. ∴∠BCM =∠BM C.∴∠BCM =12×(180°-30°)=75°.17.(9分)如图,在⊙O 中,AB ︵=AC ︵,∠ACB =60°,求证:∠AOB =∠BOC =∠AO C.证明:∵AB ︵=AC ︵, ∴AB =A C.∴△ABC 是等腰三角形. ∵∠ACB =60°, ∴△ABC 是等边三角形. ∴AB =BC =A C.∴∠AOB =∠BOC =∠AO C.18.(9分)如图,在平面直角坐标系中,已知点A (1,3)、B (3,3)、C (4,2). (1)请在图中作出经过点A 、B 、C 三点的⊙M ,并写出圆心M 的坐标; (2)若D (1,4),则直线BD 与⊙M 的位置关系是相切.解:如图所示,圆心M 的坐标为(2,1).19.(9分)如图,⊙O 的半径OD ⊥弦AB 于点C ,连接AO 并延长交⊙O 于点E ,连接E C.若AB =8,CD =2,求EC 的长.解:∵OD ⊥AB ,AB =8,∴AC =BC =12AB =4.设⊙O 的半径为r ,则OC =r -2.在Rt △AOC 中,OA 2=AC 2+OC 2,即r 2=42+(r -2)2,解得r =5.∴AE =2r =10. 连接BE .∵AE 是⊙O 的直径,∴∠ABE =90°.在Rt △ABE 中,∵AE =10,AB =8,∴BE =AE 2-AB 2=102-82=6. 在Rt △BCE 中,∵BE =6,BC =4, ∴CE =BE 2+BC 2=62+42=213.20.(9分)如图,在△ABC 中,以AB 为直径的⊙O 分别与BC ,AC 相交于点D ,E ,BD =CD ,过点D 作⊙O 的切线DF 交边AC 于点F . (1)求证:DF ⊥AC ;(2)若⊙O 的半径为5,∠CDF =30°,求BD ︵的长.(结果保留π)解:(1)证明:连接O D.∵DF 是⊙O 的切线,D 为切点,∴OD ⊥DF .∴∠ODF =90°. ∵BD =CD ,OB =OA ,∴OD 是△ABC 的中位线. ∴OD ∥A C.∴∠CFD =∠ODF =90°. ∴DF ⊥A C.(2)∵∠CDF =30°,∠ODF =90°, ∴∠ODB =180°-∠CDF -∠ODF =60°. ∵OB =OD ,∴△OBD 是等边三角形. ∴∠BOD =60°.∴l BD ︵=60π×5180=53π.21.(10分)如图,AB 是⊙O 的直径,点P 是AB 下方的半圆上不与点A ,B 重合的一个动点,点C 为AP 中点,延长CO 交⊙O 于点D ,连接AD ,过点D 作⊙O 的切线交PB 的廷长线于点E ,连接CE .(1)求证:△DAC ≌△ECP ; (2)填空:①当∠DAP =45°时,四边形DEPC 为正方形;②在点P 运动过程中,若⊙O 的半径为5,∠DCE =30°,则AD证明:∵DE 为切线, ∴OD ⊥DE .∴∠CDE =90°. ∵点C 为AP 的中点,∴DC ⊥AP .∴∠DCA =∠DCP =90°. ∵AB 是⊙O 直径, ∴∠APB =90°.∴四边形DEPC 为矩形.∴DC =EP .在△DAC 和△ECP 中,⎩⎪⎨⎪⎧AC =CP ,∠ACD =∠CPE ,DC =EP ,∴△DAC ≌△ECP (SAS ).22.(10分)如图,在平面直角坐标系xOy 中,以点O 为圆心的圆分别交x 轴的正半轴于点M ,交y 轴的正半轴于点N .劣弧MN ︵的长为65π,直线y =-43x +4与x 轴,y 轴分别交于点A ,B.(1)求证:直线AB 与⊙O 相切;(2)求图中所示的阴影部分的面积.(结果保留π)解:(1)证明:作OD ⊥AB 于D.∵劣弧MN ︵的长为65π,∴90π·OM 180=6π5.解得OM =125.故⊙O 的半径为125.∵直线y =-43x +4与x 轴,y 轴分别交于点A ,B ,当y =0时,x =3;当x =0时,y =4,∴A (3,0),B (0,4).∴OA =3,OB =4.∴AB =32+42=5. ∵S △AOB =12AB ·OD =12OA ·OB ,∴OD =OA·OB AB =125.∴OD 为⊙O 的半径. ∴直线AB 与⊙O 相切.(2)S 阴影=S △AOB -S 扇形OMN =12×3×4-90π×(125)2360=6-3625π.23.(11分)问题背景:如图1,在四边形ACBD 中,∠ACB =∠ADB =90°,AD =BD ,探究线段AC ,BC ,CD 之间的数量关系.小吴同学探究此问题的思路:将△BCD 绕点D 逆时针旋转90°到△AED 处,点B ,C 分别落在点A ,E 处(如图2),易证点C ,A ,E 在同一条直线上,且△CDE 是等腰三角形,所以CE =2CD ,从而得出结论:AC +BC =2C D. 简单应用:(1)在图1中,若AC =2,BC =22,则CD =3;(2)如图3,AB 是⊙O 的直径,点C ,D 在⊙O 上,AD ︵=BD ︵,若AB =13,BC =12,求CD 的长;(3)如图4,∠ACB =∠ADB =90°,AD =BD ,若AC =m ,BC =n (m <n ),求CD 的长.(用含m ,n 的代数式表示)图1 图2 图3 图4解:(2)连接AC ,BD ,AD ,∵AB 是⊙O 直径, ∴∠ADB =∠ACB =90°. ∴AC =AB 2-BC 2=5. ∵AD ︵=BD ︵, ∴AD =B D.将△BCD 绕点D 顺时针旋转90°到△AED , ∴∠EAD =∠DB C. ∵∠DBC +∠DAC =180°, ∴∠EAD +∠DAC =180°. ∴E ,A ,C 三点共线. ∵BC =AE ,∴CE =AE +AC =BC +AC =17. ∵∠EDA =∠CDB ,∴∠EDA +∠ADC =∠CDB +∠ADC , 即∠EDC =∠ADB =90°.∵CD =ED ,∴△EDC 是等腰直角三角形. ∴CE =2C D. ∴CD =1722.(3)以AB 为直径作⊙O ,连接DO 并延长交⊙O 于点D 1,连接D 1A ,D 1B ,D 1C. 由(2)可知:AC +BC =2D 1C , ∴D 1C =2(m +n )2. 又∵D 1D 是⊙O 的直径, ∴∠DCD 1=90°. ∵AC =m ,BC =n ,∴由勾股定理可求得:AB 2=m 2+n 2. ∴D 1D 2=AB 2=m 2+n 2. ∵D 1C 2+CD 2=D 1D 2,∴CD 2=m 2+n 2-(m +n )22=(m -n )22.∵m<n,∴CD=2(n-m)2.。
人教版数学九年级上册《圆》单元综合检测(附答案)

人教版数学九年级上学期《圆》单元测试(满分120分,考试用时120分钟)一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分)1.在同圆或等圆中,如果弧AB的长度=弧CD的长度,则下列说法正确的个数是()弧AB的度数等于弧CD的度数;所对的圆心角等于弧CD所对的圆心角;弧AB和弧CD是等弧;弧AB所对的弦的弦心距等于弧CD所对的弦的弦心距.A. 1个B. 2个C. 3个D. 4个2.、是直线上的两个不同的点,且,的半径为,下列叙述正确的是()A. 点在外B. 点在外C. 直线与一定相切D. 若,则直线与相交3. 如图,已知⊙O的半径为5,点O到弦AB的距离为2,则⊙O上到弦AB所在直线的距离为3的点有()A. 1个B. 2个C. 3个D. 4个4.如图,在中,已知,是圆周上的一点,则为()A. B. C. D.5.如图,正六边形内接于圆,圆的半径为,则这个正六边形的边心距和的长分别为()A. 、B. 、C. 、D. 、6.高速公路的隧道和桥梁最多.如图是一个隧道的横截面,若它的形状是以为圆心的圆的一部分,路面米,净高米,则此圆的半径A. 米B. 米C. 米D. 米7.已知和三点、、,的半径为,,,,经过这三点中的一点任意作直线总是与相交,这个点是()A. B. C. D. 或8.如图,,是的直径,的半径为,,以为圆心,以为半径作,则与围成的新月形的面积为()平方单位.A. B. C. D.9.如图,已知:是的直径,、是上的三等分点,,则是()A. B. C. D.10.如图,点,,在上,点在圆外,则下列结论正确的是()A. ∠C>∠DB. ∠C<∠DC. ∠C=∠DD. ∠C=2∠D二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分)11.在,,,,点是的外心,现在以为圆心,分别以、、为半径作,则点与的位置关系分别是________.12.如下图,在以为圆心的两个同心圆中,大圆的弦交小圆于和两点,,,则长为________.13.已知:如图,为半的直径,、、为半圆弧上的点,,,则的度数为________度.14.如图,边长为的正方形的顶点、在一个半径为的圆上,顶点、在圆内,将正方形沿圆的内壁逆时针方向作无滑动的滚动.当点第一次落在圆上时,点运动的路径长为________.15.已知中,,,,直线过点且与平行,若以为轴将旋转一周,则所得的几何体的表面积为________.(不求近似值)16.如图,已知是的直径,为弦,度.过圆心作交于点,连接,则________度.17.如图,的边位于直线上,,,,若由现在的位置向右无滑动地旋转,当第次落在直线上时,点所经过的路线的长为________(结果用含有的式子表示)18.如图,圆柱底面半径为,高为,点、分别是圆柱两底面圆周上的点,且、在同一母线上,用一棉线从顺着圆柱侧面绕圈到,求棉线最短为________.19.以矩形的顶点为圆心作,要使、、三点中至少有一点在内,且至少有一点在外,如果,,则的半径的取值范围为________.20.如图,在中,是弦,,,那么圆心到的距离是________,弦的长是________.三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分)21.一圆柱形排水管的截面如图所示,已知排水管的半径为,水面宽为.由于天气干燥,水管水面下降,此时排水管水面宽变为,求水面下降的高度.22.如图,在中,弦、于点,且.求证:.23.如图,在中,,,求分别以、、为圆心,以为半径画弧,三条弧与边所围成的阴影部分的面积.24.已知:如图,的外接圆,弦的长为,,求圆心到的距离.25.如图,已知为的直径,是弦,于,于,.求证:;求证:;若,,设,求值及阴影部分的面积.26.如图,内接于,,,.求的度数;将沿折叠为,将沿折叠为,延长和相交于点;求证:四边形是正方形;若,,求的长.参考答案一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分)1.在同圆或等圆中,如果弧AB的长度=弧CD的长度,则下列说法正确的个数是()弧AB的度数等于弧CD的度数;所对的圆心角等于弧CD所对的圆心角;弧AB和弧CD是等弧;弧AB所对的弦的弦心距等于弧CD所对的弦的弦心距.A. 1个B. 2个C. 3个D. 4个【答案】D【解析】【分析】由在同圆或等圆中,的长度=的长度,根据弧长公式得到它们所对的圆心角相等,再根据在同圆或等圆中,如果两个圆心角以及它们对应的两条弧、两条弦中有一组量相等,则另外两组量也对应相等,即可对选项进行判断.【详解】∵在同圆或等圆中,的长度=的长度,∴弧AB和弧CD所对的圆心角相等,∴的度数等于的度数;∴和是等弧;∴所对的弦的弦心距等于所对的弦的弦心距.故选D.【点睛】本题考查了在同圆或等圆中,如果两个圆心角以及它们对应的两条弧、两条弦中有一组量相等,则另外两组量也对应相等.在圆中经常利用此结论把圆心角、弧、弦之间进行转化.2.、是直线上的两个不同的点,且,的半径为,下列叙述正确的是()A. 点在外B. 点在外C. 直线与一定相切D. 若,则直线与相交【答案】D【解析】【分析】由P、Q是直线l上的两个不同的点,且OP=5,⊙O的半径为5,可得点P在⊙O上,直线l与⊙O相切或相交;若OQ=5,则直线l与⊙O相交.【详解】∵OP=5,⊙O的半径为5,∴点P在⊙O上,故A错误;∵P是直线l上的点,∴直线l与⊙O相切或相交;∴若相切,则OQ>5,且点Q在⊙O外;若相交,则点Q可能在⊙O上,⊙O外,⊙O内;故B、C错误.∴若OQ=5,则直线l与⊙O相交;故D正确.故选D.【点睛】此题考查了直线与圆的位置关系,注意掌握分类讨论思想的应用是解题关键.3. 如图,已知⊙O的半径为5,点O到弦AB的距离为2,则⊙O上到弦AB所在直线的距离为3的点有()A. 1个B. 2个C. 3个D. 4个【答案】C【解析】考点:垂径定理;勾股定理.分析:根据垂径定理计算.解答:解:如图OD=OA=OB=5,OE⊥AB,OE=3,∴DE=OD-OE=5-3=2cm,∴点D是圆上到AB距离为2cm的点,∵OE=3cm>2cm,∴在OD上截取OH=1cm,过点H作GF∥AB,交圆于点G,F两点,则有HE⊥AB,HE=OE-OH=2cm,即GF到AB的距离为2cm,∴点G,F也是圆上到AB距离为2cm的点.故选C.点评:本题利用了垂径定理求解,注意圆上的点到AB距离为2cm的点不唯一,有三个.4.如图,在中,已知,是圆周上的一点,则为()A. B. C. D.【答案】B【解析】【分析】首先根据题画出图形,然后在优弧上取点D,连接AD,BD,根据圆周角的性质,即可求得∠ADB的度数,又由圆的内接四边形的性质,即可求得∠ACB的度数.【详解】如图:在优弧上取点D,连接AD,BD,∵∠AOB=100°,∴∠ADB=∠AOB=55°,∵四边形ADBC是⊙O的内接四边形,∴∠ADB+∠ACB=180°,∴∠ACB=125°.故选B.【点睛】此题考查了圆周角定理与圆的内接四边形的性质,根据题意作出图形,掌握数形结合思想的应用及圆周角定理是解题关键.5.如图,正六边形内接于圆,圆的半径为,则这个正六边形的边心距和的长分别为()A. 、B. 、C. 、D. 、【答案】D【解析】试题解析:连接OC,OD,∵正六边形ABCDEF是圆的内接多边形,∴∠COD=60°,∵OC=OD,OM⊥CD,∴∠COM=30°,∵OC=6,∴OM=6cos30°=3,∴=2π故选D.考点:1.正多边形和圆;2.弧长的计算.6.高速公路的隧道和桥梁最多.如图是一个隧道的横截面,若它的形状是以为圆心的圆的一部分,路面米,净高米,则此圆的半径A. 米B. 米C. 米D. 米【答案】B【解析】【分析】根据垂径定理可知AD的长,设半径为r,利用勾股定理列方程求出r的值即可.【详解】∵CD⊥AB,∴由垂径定理得AD=6米,设圆的半径为r,则OD2+AD2=OA2,即(9-r)2+62=r2,解得r=米.故选B.【点睛】考查了垂径定理、勾股定理.根据题意构造一个由半径、半弦、弦心距组成的直角三角形进行计算是解题关键.7.已知和三点、、,的半径为,,,,经过这三点中的一点任意作直线总是与相交,这个点是()A. B. C. D. 或【答案】A【解析】【分析】根据⊙O的半径为3,OP=2,OQ=3,OR=4,可以知道点P在圆内,点Q在圆上,点R在圆外,因而这三点中P的一点任意作直线总是与⊙O相交.【详解】∵的半径为,,,,∴Q点在圆上;R点在圆外;P点在圆内,∴经过P点任意作直线总是与⊙O相交.故选A.【点睛】本题考查了对点与圆的位置关系的判断.设点到圆心的距离为d,则当d=R时,点在圆上;当d>R 时,点在圆外;当d<R时,点在圆内.准确判断P、Q、R三点与⊙O的位置关系是解决本题的关键.8.如图,,是的直径,的半径为,,以为圆心,以为半径作,则与围成的新月形的面积为()平方单位.A. B. C. D.【答案】B【解析】【分析】新月形ACED的面积是圆O半圆的面积-弓形CED的面积,弓形CED的面积又=扇形BCD面积-三角形BCD 的面积,然后依面积公式计算即可.【详解】∵OC=OB=R,,∴BC=R,)∴新月形ACED的面积=S半圆-(S扇形BCD-S△BCD=-(-)=R2.故选B.【点睛】本题的关键是看出:新月形ACED的面积是圆O半圆的面积-弓形CED的面积,然后逐一求面积即可.9.如图,已知:是的直径,、是上的三等分点,,则是()A. B. C. D.【答案】C【解析】【分析】先求出∠BOE=120°,再运用“等弧对等角”即可解.【详解】∵∠AOE=60°,∴∠BOE=180°-∠AOE=120°,∴的度数是120°,∵C、D是上的三等分点,∴弧CD与弧ED的度数都是40度,∴∠COE=80°,故选:C.【点睛】本题主要考查圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.熟练掌握圆周角定理是解题关键.10.如图,点,,在上,点在圆外,则下列结论正确的是()A. ∠C>∠DB. ∠C<∠DC. ∠C=∠DD. ∠C=2∠D【答案】A【解析】【分析】根据三角形外角的性质得到∠BEC>∠BDC,根据圆周角定理得到∠BAC=∠BEC,得到答案【详解】如图:连接AE,∵∠BEA是△ADE的外角,∴∠BEA>∠D,∵∠C=∠BEA,∴∠C>∠D,故A选项正确,则B、C、错误,∵不确定D点的位置,∴∠C不一定等于2∠D,故D选项错误,故选A.【点睛】本题考查的是圆周角定理和三角形的外角的性质的应用,掌握同弧所对的圆周角相等和三角形的一个外角大于与它不相邻的任何一个内角是解题的关键.二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分)11.在,,,,点是的外心,现在以为圆心,分别以、、为半径作,则点与的位置关系分别是________.【答案】圆外,圆上,圆内【解析】【分析】由点是的外心,可知O为△ABC的外接圆的圆心,因为∠C=90°,由圆周角定理可知AB为外接圆的直径,根据勾股定理可求出AB的长,根据直角三角形斜边中线等于斜边一半可知OC的长度,根据半径的长判断点C的位置即可.【详解】∵,点是的外心,∴AB为⊙O的直径,且O为AB中点,∵,,∴AB==5,∴OC=2.5,∵2.5>2;2.5=2.5; 2.5<3,∴以、、为半径作,则点与的位置关系分别是圆外、圆上、圆内.故答案为:圆外、圆上、圆内【点睛】本题考查了对点与圆的位置关系的判断.设点到圆心的距离为d,则当d=R时,点在圆上;当d>R 时,点在圆外;当d<R时,点在圆内.根据圆周角定理确定O点的位置是解题关键.12.如下图,在以为圆心的两个同心圆中,大圆的弦交小圆于和两点,,,则长为________.【答案】【解析】【分析】如图:作OE⊥AB于E,根据垂径定理可知CE=CD,AE=AB,根据AC=AE-CE求出AC的长即可.【详解】如图:作OE⊥AB于E,∴根据垂径定理得:CE=CD=3,AE=AB=5,∴AC=AE-CE=2.故答案为:2【点睛】本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧,熟练掌握垂径定理是解题关键.13.已知:如图,为半的直径,、、为半圆弧上的点,,,则的度数为________度.【答案】【解析】【分析】根据同圆中,等弧所对的圆心角相等可知∠BOC的度数,即可求出∠AOC的度数.【详解】∵,∠BOE=55°,∴∠COD=∠DOE=∠BOE=55°,∴∠BOC=165°,∴∠AOC=180°-165°=15°,故答案为:15【点睛】本题考查圆周角定理,在同圆或等圆中,如果两个圆心角以及它们对应的两条弧、两条弦中有一组量相等,则另外两组量也对应相等.在圆中经常利用此结论把圆心角、弧、弦之间进行转化.14.如图,边长为的正方形的顶点、在一个半径为的圆上,顶点、在圆内,将正方形沿圆的内壁逆时针方向作无滑动的滚动.当点第一次落在圆上时,点运动的路径长为________.【答案】【解析】【分析】设圆心为O,连接AO,BO,AC,AE,易证三角形AOB是等边三角形,确定∠GFE=∠EAC=30°,再利用弧长公式计算即可.【详解】如图所示:设圆心为O,连接AO,BO,AC,AE,∵AB=,AO=BO=,∴AB=AO=BO,∴△AOB是等边三角形,∴∠AOB=∠OAB=60°同理:△FAO是等边三角形,∠FAB=2∠OAB=120°,∠DAF=120°-90°=30°,即旋转角为30°,∴∠EAC=30°,∠GFE=∠FAD=120°-90°=30°,∵AD=AB=,∴AC=2,∴当点C第一次落在圆上时,点C运动的路径长为=()π;故答案为:()π【点睛】本题考查了正方形的性质、旋转的性质、等边三角形的判定和性质、勾股定理的运用以及弧长公式的运用,题目的综合性较强,解题的关键是正确的求出旋转角的度数.15.已知中,,,,直线过点且与平行,若以为轴将旋转一周,则所得的几何体的表面积为________.(不求近似值)【答案】【解析】【分析】根据,,,可求出△ABC的其余边长,表面积为一个圆锥的侧面积+一个圆的底面积+圆柱的侧面积,按照公式计算即可.【详解】∵Rt△ABC中,∠C=90°,∠A=30°,AB=10,∴BC=5,AC=5,∴所得几何体的表面积为:π×5×10+π×52+2π×5×5=75π+50.故答案为75π+50.【点睛】考查圆锥的计算;画出相关图形,判断出表面积的组成是解决本题的关键.16.如图,已知是的直径,为弦,度.过圆心作交于点,连接,则________度.【答案】【解析】【分析】先根据直角三角形两锐角互余求出∠BOD,再根据圆周角定理∠DCB=∠BOD即可得答案.【详解】∵OD⊥BC交弧BC于点D,∠ABC=30°,∴∠BOD=90°-∠ABC=90°-30°=60°,∴∠DCB=∠BOD=30°.故答案为:30【点睛】本题主要考查圆周角定理,在同圆或等圆中同弧所对的圆周角的度数是圆心角的一半,熟练掌握圆周角定理是解题关键.17.如图,的边位于直线上,,,,若由现在的位置向右无滑动地旋转,当第次落在直线上时,点所经过的路线的长为________(结果用含有的式子表示)【答案】【解析】【分析】根据含30度的直角三角形三边的关系得到BC=1,AB=2BC=2,∠ABC=60°;点A先以B点为旋转中心,顺时针旋转120°到A1,再以点C1为旋转中心,顺时针旋转90°到A2,然后根据弧长公式计算两段弧长,从而得到点A第3次落在直线上时,点A所经过的路线的长.【详解】∵Rt△ABC中,AC=,∠ACB=90°,∠A=30°,∴BC=1,AB=2BC=2,∠ABC=60°;∵Rt△ABC由现在的位置向右无滑动的翻转,且点A第3次落在直线l上时,有3个的长,2个的长, ∴点A经过的路线长=×3+×2=(4+)π.故答案为:(4+)π.【点睛】本题考查了旋转的性质与弧长的计算,解题的关键是熟练的掌握旋转的性质与弧长的计算方法. 18.如图,圆柱底面半径为,高为,点、分别是圆柱两底面圆周上的点,且、在同一母线上,用一棉线从顺着圆柱侧面绕圈到,求棉线最短为________.【答案】【解析】【分析】将圆柱体展开,然后利用两点之间线段最短解答即可.【详解】圆柱体的展开图如图所示:用一棉线从A顺着圆柱侧面绕3圈到B的运动最短路线是:AC→CD→DB;即在圆柱体的展开图长方形中,将长方形平均分成3个小长方形,A沿着3个长方形的对角线运动到B的路线最短;∵圆柱底面半径为2cm,∴长方形的宽即是圆柱体的底面周长:2π×2=4πcm;又∵圆柱高为9πcm,∴小长方形的一条边长是3πcm;根据勾股定理求得AC=CD=DB=5πcm;∴AC+CD+DB=15πcm;故答案为:15π.【点睛】本题主要考查了圆柱的计算、平面展开--路径最短问题.圆柱的侧面展开图是一个长方形,此长方形的宽等于圆柱底面周长,长方形的长等于圆柱的高.本题就是把圆柱的侧面展开成长方形,“化曲面为平面”,用勾股定理解决.19.以矩形的顶点为圆心作,要使、、三点中至少有一点在内,且至少有一点在外,如果,,则的半径的取值范围为________.【答案】【解析】【分析】先求出矩形对角线的长,然后由B、C、D与⊙A的位置,确定⊙A的半径的取值范围.【详解】根据题意画出图形如下所示:∵AB=CD=5,AD=BC=12,∴AC=BD==13.∵B、C、D中至少有一个点在⊙A内,且至少有一个点在⊙A外,∴点B在⊙A内,点C在⊙A外.∴5<r<13.故答案是:5<r<13.【点睛】本题考查的是点与圆的位置关系,要确定点与圆的位置关系,主要根据点与圆心的距离与半径的大小关系来进行判断.当d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内.20.如图,在中,是弦,,,那么圆心到的距离是________,弦的长是________.【答案】(1). (2).【解析】【分析】过O作OC⊥AB交AB于C点,根据垂径定理可知OC垂直平分AB,根据OA=OB,∠AOB=120°可求出∠OAB=30°,根据30°角所对直角边等于斜边一半即可求得圆心到的距离;根据勾股定理求出AC的长即可求出AB的长.【详解】过O作OC⊥AB交AB于C点,如图所示:由垂径定理可知,OC垂直平分AB,∵OA=OB,∠AOB=120°∴∠OAB=30°∴OC=OA=cm∴由勾股定理可得:AC= =cm∴AB=2AC=5cm.故答案为:;5;【点睛】本题考查垂径定理,垂直于弦的直径,平分弦且平分这条弦所对的两条弧,熟练掌握垂径定理是解题关键.三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分)21.一圆柱形排水管的截面如图所示,已知排水管的半径为,水面宽为.由于天气干燥,水管水面下降,此时排水管水面宽变为,求水面下降的高度.【答案】水面下降了米.【解析】【分析】如图:过点O作ON⊥CD于N,交AB于M,先根据垂径定理求得AM、CN,然后根据勾股定理求出OM、ON的长,即可得出结论【详解】如图,下降后的水面宽CD为6m,连接OA,OC,过点O作ON⊥CD于N,交AB于M.∴∠ONC=90°.∵AB∥CD,∴∠OMA=∠ONC=90°.∵AB=8m,CD=6m,∴AM=AB=4,CN=CD=3,在Rt△OAM中,∵OA=5,∴OM==3.同理可得ON=4,∴MN=ON-OM=1(米).答:水面下降了1米.【点睛】本题考查的是垂径定理的应用以及勾股定理的应用,熟知垂直于弦的直径平分弦,并且平分这条弦所对的两条弧是解答此题的关键.22.如图,在中,弦、于点,且.求证:.【答案】见解析【解析】【分析】根据,可证明,进而证明AC=BD,通过证明即可证明结论.【详解】∵,∴,,∴在与中,∵,∴,∴.【点睛】本题考查的是圆心角、弧、弦的关系及全等三角形的判定与性质,熟练掌握,圆心角、弧、弦的关系是解题关键.23.如图,在中,,,求分别以、、为圆心,以为半径画弧,三条弧与边所围成的阴影部分的面积.【答案】.【解析】【分析】由于三条弧所对的圆心角的和为180°,根据扇形的面积公式可计算出三个扇形的面积和,而三条弧与边AB 所围成的阴影部分的面积=S△ABC-三个扇形的面积和,再利用三角形的面积公式计算出△ABC的面积,然后代入即可得到答案.【详解】∵∠C=90°,CA=CB=2,∴AC=1,S△ABC==2,∵三条弧所对的圆心角的和为180°,三个扇形的面积和==,∴三条弧与边AB所围成的阴影部分的面积=S△ABC-三个扇形的面积和=2-,【点睛】本题考查扇形面积,熟练掌握面积公式并明确三条弧所对的圆心角的和为180°是解题关键.24.已知:如图,的外接圆,弦的长为,,求圆心到的距离.【答案】圆心到的距离为.【解析】【分析】连接,,过点作于点,根据圆周角定理可知∠BOC=60°,进而证明△OBC是等边三角形,根据垂径定理可知CD的长度,利用勾股定理求出OD的长即【详解】连接,,过点作于点,∵,∴.∵,∴是等边三角形,∴,∵OD⊥BC,∴CD=BC=2,∴=,即圆心到的距离为.【点睛】本题考查圆周角定理及垂径定理,在同圆中,同弧所对的圆周角的度数等于圆心角的一半,垂直于弦的直径,平分弦且平分这条弦所对的两条弧,熟练掌握定理是解题关键.25.如图,已知为的直径,是弦,于,于,.求证:;求证:;若,,设,求值及阴影部分的面积.【答案】(1)见解析;(2)见解析;(3)x=5,.【解析】【分析】(1)根据直径所对的圆周角是90°可知∠ACB=∠AFO=90°,由平行线判定定理即可证明OF//BC;(2)由可知∠CBE=∠FOA,利用,,即可证明;(3)在Rt△OCE中,利用勾股定理列方程即可求出x的值,根据OC=2OE可知∠OCE=30°,即可求出∠COD的度数,利用扇形面积及三角形面积公式求出阴影面积即可.【详解】证明:∵为的直径,∴又∵∴证明:∵∴∠CBE=∠FOA∵,,∴解:连接.设,∵∴.在中,,根据勾股定理可得:解得:,即,∵OC=5+5=10,∴OC=2OE,∴∠OCE=30°,∴,∴扇形的面积是:的面积是:∴阴影部分的面积是:.【点睛】本题考查圆周角定理、垂径定理及扇形面积,熟练掌握定理和公式是解题关键.26.如图,内接于,,,.求的度数;将沿折叠为,将沿折叠为,延长和相交于点;求证:四边形是正方形;若,,求的长.【答案】(1);(2)见解析;(3).【解析】【分析】(1)连接和,由OE=BC,可知OE=BE,进而可知∠OBE=45°,同理可证∠OCE=45°,即可证明∠BOC=90°,根据圆周角定理即可求得∠BAC的度数;(2)由折叠性质可知AG=AD=AF,∠AGH=∠AFH=90°,∠DAC=∠CAF,∠BAD=∠BAG,由∠BAD+∠DAC=45°,可证明∠GAF=90°,即可证明四边形AFHG 是正方形;(3)由折叠性质可知,;由(2)可知∠BHC=90°,设AD长为x,利用勾股定理列方程求出x的值即可得解.【详解】(1)连接和;∵,∴;∵,∴,∴;∵,∴;由折叠可知,,,,,∴;∴;∴四边形是正方形;解:由得,,,,;设的长为,则,.在中,,∴;解得,,(不合题意,舍去);∴.【点睛】本题主要考查圆周角定理及折叠性质,在同圆中,同弧所对的圆周角的度数等于圆心角的一半;折叠后的图形与原图形全等,熟练掌握折叠的性质是解题关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《圆》单元测试
、填空
1.从圆心到圆上任意一点的线段叫()。
通过()并且()都在()的线段叫做直径。
圆的位置是由
()确定的,圆的大小决定于()的长短。
2.在同一个圆里,所有的半径(
),所有的()也
3.圆周率表示同一圆内()和()的倍数关系,
都相等,直径等于半径的()
它用字母()表示,保留两位小数后的近似值是()
4.在同一个圆内可以画()条直径;如果用圆规画一个直径是
10厘米的圆,圆规的两脚间的距离应该是()厘米。
5.在长6厘米,宽4厘米的长方形内剪下一个最大的圆,这个圆的
周长是(),面积是(),还剩下面积()。
6.—个圆环,外圆半径是6分米,内圆半径4分米,圆环的面积是
()。
7.甲圆直径长8厘米,是乙圆直径的40%。
乙圆的周长是()。
3
8.—个圆的半径是8厘米,这个圆面积的4是()平方厘米。
9.大圆的半径等于小圆直径,则大圆面积是小圆面积的()倍,
小圆周长是大圆周长的()。
10.在一张长32厘米,宽16厘米的长方形内画半径是4厘米的圆,
这样的圆最多能画()个,这些圆的面积和是()。
11.圆是()图形,它有()对称轴。
正方形有
()条对称轴,长方形有()条对称轴,等边三角形有()
条对称轴。
12.填表:
二、判断题。
1.圆的周长是它的直径的n倍。
()
2.半径为1厘米的圆的周长是
3.14厘米。
()
3.—个圆的周长是12.56厘米,面积是12.56平方厘米。
()
4.圆的半径由6分米增加到9分米,圆的面积增加了45平方分米。
()
5.当长方形、正方形、圆的周长相等时,圆的面积最大。
()
6.水桶是圆形的。
()
7.半个圆的周长就是圆周长的一半。
()
8.所有的直径都相等。
()
9.n = 3.14。
(
3. 画出下列图形的所有对称轴
--------- K ----------- K ----------- K
二、画一画。
1. 以0为圆心,画一个直径是
4厘米的圆。
2.
下面是正方形,在它的内 部画一个最大的圆。
1 .直径是6厘米 2. 半径是5分米
四、计算下列各圆的周长
五、计算下列各圆的面积(6 分)
1 .半径是8厘米 2. 周长9.4
2 米(n 取3.14 )
六、求下面阴影部分的面积(单位:厘米)
u 2 -1 ---------- S ------------ 1- 2」
七、应用题。
1.一个圆形养鱼池,直径是4米,这个养鱼池的周长是多少米?占
地面积是多少平方米?
2512 米的桥,大约需要几分钟?(车身的长度忽略不计)
2.一辆自行车的车轮半径是40厘米,车轮每分钟转100圈,要通过
3.一根铁丝可以围成一个半径是3 厘米的半圆。
这根铁丝有多长?它所围成半圆的面积有多大?
4.用席子围成一个地面周长是18.84 米的圆柱形粮囤。
这个粮囤占地面积有多大?
5.公园里有一个直径为16米的圆形花圃,在它的周围环绕着一条2
米宽的走道。
现将走道也改成花圃,现在花圃的面积是多少?
6.一块正方形草地,边长8 米。
用一根长3.5 米的绳拴住一只羊到
草地上吃草。
羊最多能吃到多少面积的草?
7.一个铁环直径是60 厘米,从操场东端沿直线滚到西端转了90 圈,另一个铁环的直径是40 厘米,它从东端也沿直线滚到西端要转多少圈?。
