二次函数的综合运用
第六篇 二次函数综合应用
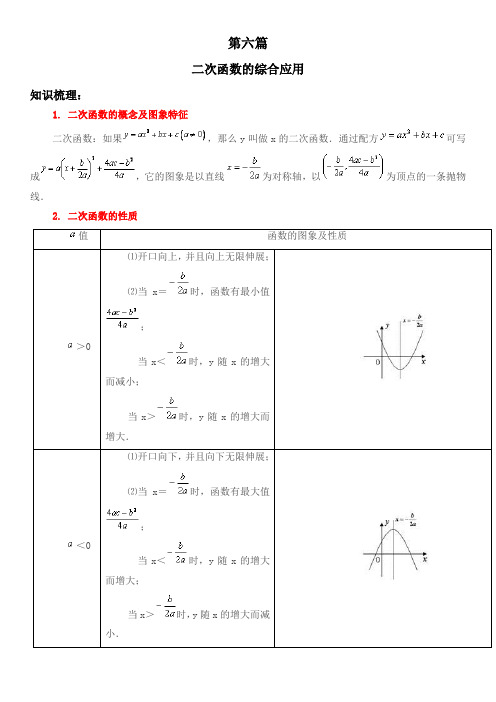
∵直线 交 轴于A点,交 轴于B点,
∴A点坐标为(-1,0)、B点坐标为(0,3).
又∵抛物线经过A、B、C三点,
∴ ,解得: ,
∴抛物线的关系式为:y=-x2+2x+3.
(2)∵y=-x2+2x+3= ,∴该 抛物线的对称轴为x=1.
设Q点坐标为(1,m),则 ,又 .
当x> 时,y随x的增大而增大.
<0
⑴开口向下,并且向下无限伸展;
⑵当x= 时,函数有最大值 ;
当x< 时,y随x的增大而增大;
当x> 时,y随x的增大而减小.
3.二次函数图象的平移规律
抛物线 可由抛物线 平移得到.由于平移时,抛物线上所有的点的移动规律都相同,所以只需研究其顶点移动的情况.因此有关抛物线的平移问题,需要利用二次函数的顶点式 来讨论.简单地说:“左正右负 上正下负”
因为当x=47时,利润y有最大值,而超过47时,利润y反而减少。
要想卖的越多赚的越多,即 随 的增大而增大,
由二次函数性质可知,x≤47,
所以当x=47时,最低售价应定为60-0.1(47-10)=56.3元.
题型四、面积和周长问题最值
例题1、已知二次函数y=mx2-5mx+1(m为常数,图像的对称轴对称.
c>0,与y轴的交点在y轴的正半轴上;
c=0,抛物线经过原点;
c<0,与y轴的交点在y轴的负半轴上.
⑷b2-4ac→决定抛物线与x轴交点的个数:
①当b2-4ac>0时,抛物线与x轴有两个交点;
②当b2-4ac=0时,抛物线与x轴有一个交点;
③当b2-4ac<0时,抛物线与x轴没有交点.
二次函数综合应用

二次函数综合应用二次函数是初中数学中的重要内容之一,是历年中考的一个必考知识点,并且也是综合代数与几何的一个重要载体,它往往以中考压轴题的形势出现。
此类问题考查知识点多,综合性强,难度较大,能较好地考查学生综合应用能力与灵活应变能力,在解题思路上注意渗透数形结合、函数与方程、分类讨论和转化与化归等数学思想的运用。
本文就综合问题的分类归纳解析,以供读者参考。
一、用待定系数法求函数解析式要确定函数解析式,就是要确定解析式中的待定系数(常数)。
由于二次函数的解析式有三种形式,即一般式:()20y ax bx c a =++≠,顶点式:()()20y a x h k a =-+≠,交点式:()()()120y a x x x x a =--≠,所以求二次函数解析式时,要根据已知条件的特点,选择适当形式,建立方程或方程组,简化计算过程。
例1.(北京市中考题)已知抛物线()20y ax bx c a =++≠与y 轴交于点A(0,3),与x 轴分别交于B(1,0)、C(5,0)两点,(1) 求抛物线的解析式;(2) 若点D 为线段OA 的一个三等分点,求直线DC 的解析式。
解:(1) 因为抛物线过A(0,3)、B(1,0)、C(5,0)三点,所以有 302550c a b c a b c =++=++= 解得 318,,355a b c ==-=.∴抛物线的解析式是2318355y x x =-+. (2) 依题知,OA 的三等分点分别为(0,1)、(0,2). 设直线DC 的解析式为y kx b =+当点D 的坐标为(0,1)时,有150b k b =+= 解得 1b =,15k =-∴直线DC 的解析式为115y x =-+ 当点D 的坐标为(0,2)时,有250b k b =+= 解得 2b =,25k =-∴直线DC 的解析式为225y x =-+二、从几何图形中建立函数关系从几何图形中确定或建立函数关系式是数形结合的新题型,已构成中考命题的热点,主要是运用相似的性质、勾股定理、面积关系(或公式)等建立量与量的函数关系,几何图形中要建立两个量之间的关系,一般的方法和步骤是:1、将题目中的几何量用含字母x 和y 的代数式表示,并将有关几何量通过添加辅助线等方法转化为我们熟悉的特殊图形中的量。
二次函数的综合运用

二次函数的综合运用二次函数是一种形式为 y = ax² + bx + c 的函数,其中 a、b、c 是常数且a ≠ 0。
二次函数在数学中有广泛的应用,涉及到诸如物理学、经济学和工程学等多个领域。
本文将探讨二次函数在各个领域中的综合运用,包括最值问题、图像分析、实际问题的建模等。
一、最值问题对于二次函数 y = ax² + bx + c,其中a ≠ 0,我们可以通过一些方法求得其最值。
为了简化讨论,我们以函数 y = x² + 2x - 3 为例。
1. 定义域和值域首先,我们需要确定该二次函数的定义域和值域。
对于二次函数 y= x² + 2x - 3,由于 x²的值始终大于等于 0,所以该函数的定义域为全体实数。
而二次函数在开口向上的情况下,其最小值即为函数的值域的下界。
根据二次函数的顶点公式,可以求得该函数的顶点为(-1, -4),因此该函数的最小值为 -4。
2. 求解极值点我们可以通过求导数的方法求得二次函数的极值点。
对于函数 y =x² + 2x - 3,将其对 x 求导后可得 y' = 2x + 2。
令 y' = 0,解得 x = -1。
将 x = -1 代入函数 y = x² + 2x - 3 中可得 y = -4,即函数在 x = -1 处取得极小值 -4。
同样,对于开口向下的二次函数,可以通过类似的方法求得其极大值。
二、图像分析二次函数的图像一般为抛物线,通过分析图像可以获得更多关于函数的信息。
下面以函数 y = x² + 2x - 3 为例进行具体分析。
1. 对称轴和顶点二次函数的对称轴是由函数的一阶导数确定的直线,其方程形式为x = -b/(2a)。
对于函数 y = x² + 2x - 3,对称轴的方程为 x = -1。
根据二次函数的顶点公式,可以求得该函数的顶点坐标为 (-1, -4)。
二次函数的综合应用

二次函数的综合应用㈠一、典例精析考点一:二次函数与方程1.已知抛物线与x轴没有交点.(1)求c的取值范围;(2)试确定直线y=cx+l经过的象限,并说明理由.2.已知函数y=mx2-6x+1(m是常数).⑴求证:不论m为何值,该函数的图象都经过y轴上的一个定点;⑵若该函数的图象与x轴只有一个交点,求m的值.考点二:二次函数与最大问题3、如图,二次函数的图像经过点,且与轴交于点. (1)试求此二次函数的解析式;(2)试证明:(其中是原点);(3)若是线段上的一个动点(不与、重合),过作轴的平行线,分别交此二次函数图像及轴于、两点,试问:是否存在这样的点,使?若存在,请求出点的坐标;若不存在,请说明理由。
5、如图,抛物线与x轴交与A(1,0),B(- 3,0)两点,(1)求该抛物线的解析式;(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.(3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?,若存在,求出点P的坐标及△PBC的面积最大值.若没有,请说明理由.考点三:二次函数与等腰三角形、直角三角形6.如图,直线交轴于A点,交轴于B点,过A、B两点的抛物线交轴于另一点C (3,0).⑴求抛物线的解析式;⑵在抛物线的对称轴上是否存在点Q,使△ABQ是等腰三角形?若存在,求出符合条件的Q 点坐标;若不存在,请说明理由.7、如图,在平面直角坐标系中,△ABC 是直角三角形,∠ACB=90,AC=BC ,OA=1,OC=4,抛物线y=x 2+bx+c 经过A ,B 两点,抛物线的顶点为D .(1)求b ,c 的值;(2)点E 是直角三角形ABC 斜边AB 上一动点(点A 、B 除外),过点E 作x 轴的垂线交抛物线于点F ,当线段EF 的长度最大时,求点E 的坐标;(3)在(2)的条件下:①求以点E 、B 、F 、D 为顶点的四边形的面积;②在抛物线上是否存在一点P ,使△EFP 是以EF 为直角边的直角三角形?若存在,求出所有点P 的坐标;若不存在,说明理由.8如图,抛物线y=21x 2+bx ﹣2与x 轴交于A ,B 两点,与y 轴交于C 点,且A (﹣1,0).(1)求抛物线的解析式及顶点D 的坐标;(2)判断△ABC 的形状,证明你的结论;(3)点M (m ,0)是x 轴上的一个动点,当MC+MD 的值最小时,求m 的值.9.如图所示,在平面直角坐标系Oxy 中,已知点A (-,0),点C (0,3),点B 是x 轴上一点(位于点A 的右侧),以AB 为直径的圆恰好经过点C .(1)求∠ACB 的度数;(2)已知抛物线y =ax 2+bx +3经过A 、B 两点,求抛物线的解析式;(3)线段BC 上是否存在点D ,使△BOD 为等腰三角形.若存在,则求出所有符合条件的点D 的坐标;若不存在,请说明理由.10如图,抛物线254y ax ax =-+经过ABC △的三个顶点,已知BC x ∥轴,点A 在x 轴上,点C 在y 轴上,且AC BC =.(1)求抛物线的对称轴;(2)写出A B C ,,三点的坐标并求抛物线的解析式;(3)探究:若点P 是抛物线对称轴上且在x 轴下方的动点,是否存在PAB △是等腰三角形.若存在,求出所有符合条件的点P 坐标;不存在,请说明理由.11在平面直角坐标系中,已知抛物线经过()40A -,,()04B -,,()20C ,三点. (1)求抛物线的解析式;(2)若点M 为第三象限内抛物线上一动点,点M 的横坐标为m ,AMB △的面积为S .求S 关于m 的函数关系式,并求出S 的最大值.(3)若点P 是抛物线上的动点,点Q 是直线y x =-上的动点,判断有几个位置能够使得点P Q B O ,,,为顶点的四边形为平行四边形,直接写出相应的点Q 的坐标.12如图,在平面直角坐标系中,直线y=x+2交x 轴于点P ,交y 轴于点A .抛物线y=x 2+bx+c 的图象过点E (﹣1,0),并与直线相交于A 、B 两点.(1)求抛物线的解析式(关系式);(2)过点A 作AC ⊥AB 交x 轴于点C ,求点C 的坐标;(3)除点C 外,在坐标轴上是否存在点M ,使得△MAB 是直角三角形?若存在,请求出点M 的坐标;若不存在,请说明理由.。
二次函数的综合应用

二次函数的综合应用二次函数的综合应用一、典例精析考点一:二次函数与方程1.已知抛物线与x轴没有交点。
1) 求$c$的取值范围;2) 确定直线$y=cx+l$经过的象限,并说明理由。
2.已知函数$y=mx-6x+1$($m$是常数)。
⑴证明:不论$m$为何值,该函数的图象都经过$y$轴上的一个定点;⑵若该函数的图象与$x$轴只有一个交点,求$m$的值。
考点二:二次函数与最大问题3、如图,二次函数$y=ax^2+bx+c$。
1)求此二次函数的解析式;2)证明:3)若是线段$AB$的图像经过点$C$,且与$x$轴交于点$D$(其中$D$是原点);二次函数图像及轴于$AB$两点,试问:是否存在这样的点,使$y$的坐标最大;若存在,请求出点$E$的坐标;若不存在,请说明理由。
5、如图,抛物线$y=ax^2+bx+c$与$x$轴交于$A(1,0)$,$B(-3,0)$两点。
1)求该抛物线的解析式;2)设(1)中的抛物线交$y$轴与$C$点,在该抛物线的对称轴上是否存在点$Q$,使得$\triangle QAC$的周长最小?若存在,求出$Q$点的坐标;若不存在,请说明理由。
3)在(1)中的抛物线上的第二象限上是否存在一点$P$,使$\triangle PBC$的面积最大。
若存在,求出点$P$的坐标及$\triangle PBC$的面积最大值。
若没有,请说明理由。
考点三:二次函数与等腰三角形、直角三角形6.如图,直线$y=x-3$与$x$轴交于$A$点,交$y$轴于$B$点,过$A$、$B$两点的抛物线交$x$轴于另一点$C$。
⑴求抛物线的解析式;⑵在抛物线的对称轴上是否存在点$Q$,使$\triangleABQ$是等腰三角形?若存在,求出符合条件的$Q$点坐标;若不存在,请说明理由。
7、如图,在平面直角坐标系中,$\triangle ABC$是直角三角形,$\angle ACB=90^\circ$,$AC=BC$,$OA=1$,$OC=4$,抛物线$y=x^2+bx+c$经过$A$,$B$两点,抛物线的顶点为$D$。
二次函数及函数的综合运用.docx

课时19二次函数的应用【课前热身】1. 二次函数y = 2x 2—4x + 5的对称轴方程是心—;当x=_时,y 冇最小值是.2. 有一个抛物线形桥拱,其最人高度为16米,跨度为40米,现在它的示意图放在平面直角坐标系屮(如右图),则此 抛物线的解析式为 ________________ .3. 某公司的生产利润原来是a 元,经过连续两年的增长达到了 y 万元,如果每年增氏的百分数都是x,那么y 与x 的函数关系是( )A. y = x 2+aB. y=a (x —1) 2 C. y=a(1 —x )2D. y=a (1 + x ) 24. 把一段长1.6米的铁丝围长方形ABCD,设宽为x,面积为y.则当y 最人时,x 所取的值是( )A. 0.5B. 0.4C. 0.3D. 0.6【考点链接】1. ______________________________________ 二次函数的解析式:(1)一般式: ; (2)顶点式: _____________________________________(3)交点式: ___________ .2. 顶点式的儿种特殊形式.3.二次函数y = tzx 2+bx + c 通过配方可得y = a (x + —)2 + 4aC ~1^,其抛物线关于直线兀=—对「 2a 4。
称,顶点坐标为( _______ , ________ ).(1) _________________________ 当。
>0时,抛物线开口向 ,冇最 (填“高"或“低”)点,当x= _______ 时,y 有戢 ____ ("大”或“小”)值是 _________ ;(2) _________________________ 当GV0时,抛物线开口向 ,有最 (填“高”或“低”)点,当x= _______ 时,y 有最 ____ (“人”或“小”)值是 ________ .⑴ ____________【典例精析】例1用铝合金型材做一个形状如图1所示的矩形窗框,设窗框的一边为xm,窗户的透光而积为y nA y与x的两数图象如图2所示.(1)观察图象,当x为何值时,窗户透光血积最大?⑵当窗户透光面积最人时,窗框的另一边长是多少?图2例2橘了洲头要建造一个圆形的喷水池,并在水池屮央垂肯安装一个柱了0P,柱了顶端P处装上喷头, 由p处向外喷出的水流(在各个方向上)沿形状相同的抛物线路径落卜-(如图所示).若□知0P =3米,喷出的水流的最高点A距水平面的高度是4米,离柱子0P的距离为1米.(1)求这条抛物线的解析式:(2)若不计其它因素,水池的半径至少要多少米,才能使喷出的水流不至于落在池外?【中考演练】1.(06浙江)二次函数y=分+0 — 5的最小值为_____________ .2.某飞机着陆生滑行的路程S米与时间t秒的关系式为:5 = 60r-1.5r2,试问飞机着陆后滑行米才能停止.3.矩形周长为16cm,它的一边长为xcm,面积为ycm ,则y与x之间函数关系为________ .1 °4.苹果熟了,从树上落下所经过的路程s与下落的时间t满足s = -^gt2(g是不为0的常数)则s与t5.(08恩施)将一张边长为30 cm的正方形纸片的四角分别剪去一个边长为x cm的小止方形,然后折叠成一个无盖的长方体•当x収下面哪个数值时,长方体的体积最大() A. 7 B. 6 C. 5 D. 46•下列甫数关系中,是二次函数的是()A.在弹性限度内,弹簧的长度y与所挂物体质量x Z间的关系B.当距离一定时,火车行驶的时间t与速度v之间的关系C.等边三角形的周长C与边长a Z间的关系D.圆心角为120。
二次函数实际问题中的综合运用

类型一:二次函数在实际问题中的综合应用在生活实际问题中,常常要解决最大、最小、最省、最合适等最值问题,如果这些问题与二次函数有关,那么一般解题步骤如下:①选择恰当的自变量,列出二次函数的解析式;②把这些实际问题转化为二次函数的最值问题;③对于给定区间上(即x有范围限制)的二次函数,不一定在时取得最值,针对不同的区间给予讨论,讨论的依据还是借助二次函数的图象,根据图像上函数值的大小直观得出最值,或通过配方直接得出。
【典型例题】1、某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系:(1)求出y与x之间的函数关系式;(2)写出每天的利润W与销售单价x之间的函数关系式;若你是商场负责人,会将售价定为多少,来保证每天获得的利润最大,最大利润是多少?2、某公司生产的一种健身产品在市场上受到普遍欢迎,每年可在国内、国外市场上全部售完.该公司的年产量为6千件,若在国内市场销售,平均每件产品的利润y1(元)与国内销售量x(千件)的关系为:若在国外销售,平均每件产品的利润y2(元)与国外的销售数量t(千件)的关系为(1)用x的代数式表示t为:t=________;当0<x≤4时,y2与x的函数关系为:y2=________;当________<x<________时,y2=100;(2)求每年该公司销售这种健身产品的总利润w(千元)与国内销售数量x(千件)的函数关系式,并指出x的取值范围;(3)该公司每年国内、国外的销售量各为多少时,可使公司每年的总利润最大?最大值为多少?【变式训练】1、科幻小说《实验室的故事》中,有这样一个情节:科学家把一种珍奇的植物分别放在不同温度的环境中,数、一次函数和二次函数中的一种.(1)请你选择一种适当的函数,求出它的函数关系式,并简要说明不选择另外两种函数的理由;(2)温度为多少时,这种植物每天高度增长量最大?(3)如果实验室温度保持不变,在10天内要使该植物高度增长量的总和超过250mm,那么实验室的温度x应该在哪个范围内选择?请直接写出结果.2、某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量yx应定为多少元.(3)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?3、某大学生利用暑假40天社会实践参与了一家网店经营,了解到一种成本为20元/件的新销售量p(件) P=50-x当1≤x≤20时,;当销售单价q(元/件)21≤x≤40时,(2)求该网店第x天获得的利润y关于x的函数关系式.(3)这40天中该网店第几天获得的利润最大?最大利润是多少?类型二:二次函数与几何综合的存在问题二次函数与几何综合的形式之一,就是以抛物线为载体,探讨是否存在一些点,使其构成特殊图形(特殊三角形、特殊平行四边形等),这类问题具有较强的综合性,需要综合运用各种相关知识及数形结合、分类讨论、转化化归思想等加以解决,解决此类问题的一般思路是:先假设结论存在,然后再特定的已知条件下,探索某种图形或数学关系是否存在。
二次函数与二次方程的综合应用

二次函数与二次方程的综合应用二次函数和二次方程都是数学中重要的概念,它们在现实生活中有着广泛的应用。
本文将通过几个实际问题的例子,来展示二次函数和二次方程的综合应用。
一、二次函数的应用二次函数是形如f(x) = ax^2 + bx + c的函数,其中a、b、c为常数,且a≠0。
它的图像是一个抛物线,有许多实际问题可以用二次函数来解决。
例1:抛物线的焦点和弦长已知抛物线y = ax^2 + bx + c的焦点为F(h, k),任意一点P(x, y)在该抛物线上。
求抛物线上的弦长FP的最小值。
解析:首先,我们知道抛物线的对称轴与焦点的横坐标相同,即x = h。
所以,P点的坐标可以表示为(x, ax^2 + bx + c)。
根据两点间距离公式,我们可以求出FP的长度:FP = √[(x - h)^2 + (ax^2 + bx + c - k)^2]为了求最小值,我们可以对FP进行微分,并令其导数为0:d(FP)/dx = 0通过求导并化简,得到一个关于x的二次方程,解这个方程可以得到最小值点的横坐标x。
再将x的值带入FP的表达式中,即可求出FP 的最小值。
例2:抛物线的最值问题一辆车以匀加速度行驶,已知车从静止开始行驶10秒后的速度为20m/s,行驶过程中的位移与时间的关系可以用抛物线y = ax^2 + bx + c 来描述。
求车的最大位移和此时的时间。
解析:首先,我们知道速度是位移对时间的导数,即v(x) = dy/dx = 2ax + b。
根据已知条件,当x = 10时,v(x) = 20。
这给出了两个方程:2a(10) + b = 20和a(10^2) + b(10) + c = 0。
解这个二元一次方程组,可以得到a、b的值,进而求得抛物线的函数表达式。
最大位移对应于抛物线的顶点,可以通过求导来解析求得。
最大位移发生的时间是x值,在已知函数表达式中求解即可。
二、二次方程的应用二次方程是形如ax^2 + bx + c = 0的方程,其中a、b、c为常数,且a≠0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第22课时 二次函数的综合运用 一、考点分析 1、抛物线形问题
2、二次函数与一次函数的综合
3、二次函数与存在性问题
4、二次函数与几何知识的的综合
二、典例解析
例1、(2008白银市)如图,在平面直角坐标系中,四边形OABC 是矩形,点B 的坐标为(4,3).平行于对角线AC 的直线m 从原点O 出发,沿x 轴正方向以每秒1个单位长度的速度运动,设直线m 与矩形OABC 的两边..分别交于点M 、N ,直线m 运动的时间为t (秒). (1) 点A 的坐标是__________,点C 的坐标是__________; (2) 当t = 秒或 秒时,MN =
2
1
AC ; (3) 设△OMN 的面积为S ,求S 与t 的函数关系式;
(4) 探求(3)中得到的函数S 有没有最大值?若有,求出最大值;若没有,要说明理由.
例2、一蔬菜基地种植的某种绿色蔬菜,根据今年的市场行情,预计从5月1•日起的50天内,它的市场售价y 1与上市时间x 的关系可用图(a )的一条线段表示;•它的种植成本y 2与上市时间x 的关系可用图(b )中的抛物线的一部分来表示.
(1)求出图(a )中表示的市场售价y 1与上市时间x 的函数关系式. (2)求出图(b )中表示的种植成本y 2与上市时间x 的函数关系式.
(3)假定市场售价减去种植成本为纯利润,问哪天上市的这种绿色蔬菜既不赔本也不赚钱?
(市场售价和种植成本的单位:元/千克,时间单位:天)
例3、(2008年西宁市) 28.如图14,已知半径为1的
1O 与x 轴交于A B ,两点,OM 为1
O 的切线,切点为M ,圆心1O 的坐标为(20),,二次函数2
y x bx c =-++的图象经过A B ,两点.
(1)求二次函数的解析式;
(2)求切线OM 的函数解析式;
(3)线段OM 上是否存在一点P ,使得以P O A ,,为顶点的三角形与1OO M △相似.若存在,请求出所有符合条件的点P 的坐标;若不存在,请说明理由.
三、考点精练
1.(2008年泰安市)在同一直角坐标系中,函数y mx m =+和2
22y mx x =-++(m 是常数,且0m ≠)的图象可能..
是( )
2、学校要建造一个圆形喷水池,在水池中央垂直于水面安装一个花形柱子OA .O 恰好在水面中心,安置在柱子顶端A 处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下.且在过OA 的任意平面上的抛物线如图l -2-36所示,建立平面直角坐标系(如图l -2-37),水流喷出的高度y (m)与水面距离x (m)之间的函数关系式是2532
2
y x x =-++,请回
答下列问题:
(1)花形柱子OA 的高度;
(2)若不计其它因素,水池的半径至少要多少米,才能使喷出的水不至于落在池外?
A.
B.
C.
D. 图14
3、(2006年旅顺口区)已知边长为4的正方形截去一个角后成为五边形ABCDE (如图),其中AF=2,BF=1.试在AB 上求一点P ,使矩形PNDM 有最大面积.
4、(08枣庄)如图,在直角坐标系中放入一个边长OC 为9的矩形纸片ABCO .将纸片翻折后,
点B 恰好落在x 轴上,记为B ′,折痕为CE ,已知tan ∠OB ′C =34
. (1)求B ′点的坐标;
(2)求折痕CE 所在直线的解析式.
5、如右图,抛物线n x x y ++-=52经过点)0,1(A ,与y 轴交于点B.
(1)求抛物线的解析式;
(2)P 是y 轴正半轴上一点,且△PAB 是等腰三角形,试求点P 的坐标.
6、(2008乌鲁木齐).如图9,在平面直角坐标系中,以点(11)
C ,为圆心,2为半径作圆,交x 轴于A B ,两点,开口向下的抛物线经过点A B ,,且其顶点P 在
C 上.
(1)求ACB ∠的大小;
(2)写出A B ,两点的坐标;
(3)试确定此抛物线的解析式;
(4)在该抛物线上是否存在一点D ,使线段OP 与CD 互相平分?若存在,求出点D 的坐
标;若不存在,请说明理由.
7、如图l -2-48,Rt △PMN 中,∠P =90○
,PM=PN ,MN=8cm ,矩形 ABCD 的长和宽分别为8cm 和2cm ,C 点和M 点重合,BC 和MN 在一条直线上,令 Rt △PMN 不动,矩形ABCD 沿MN 所在直线向右以每秒1cm 的速度移动(图l -2-49)直到C 点与N 点重合为止.设移动x 秒后,矩形ABCD 与△PMN 重叠部分的面积为y cm 2 ,求y 与x 之间的函数关系式.
8、如图11,在梯形ABCD 中,AD ∥BC ,AB=AD=DC=2cm ,BC=4cm ,在等腰△PQR 中,∠QPR=120°,底边QR=6cm ,点B 、C 、Q 、R 在同一直线l 上,且C 、Q 两点重合,如果等腰△PQR 以1cm/秒的速度沿直线l 箭头所示方向匀速运动,t 秒时梯形ABCD 与等腰△PQR 重合部分的面积记为S 平方厘米 (1)当t=4时,求S 的值
(2)当4t ≤≤10,求S 与t 的函数关系式,并求出S 的最大值
图
11。
