第3章--振动系统的运动微分方程题解
机械振动基础课后习题解答_第3章习题
m
0
0 m
u1 u2
3k k
k 3k
u1 u2
2ku0
sin 0
t
K
2M
3k
2m
k
k
3k 2m
H11 ( )
3k 2m ()
H 21 ( )
k ()
u1(t) u2 (t)
H11 ( ) H21()
2ku0
sin
t
3k 为反共振频率 m
P140,3-9: 图示系统初始静止,求左端基础产生阶跃位移u0后系统的响应。
ml2 1 0 M 3 0 7 /16
K
l2k 16
9 9
9
13
| K 2M | 0
1 0.65
k m
2 2.62
k m
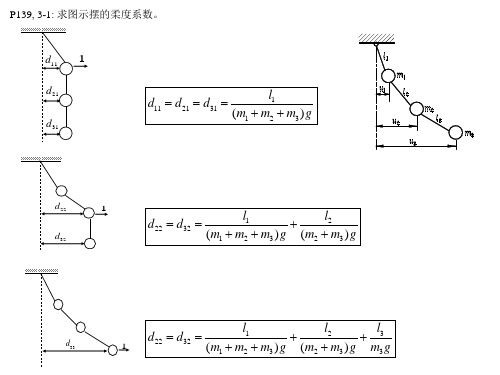
P139,3-3: 建立图示系统的运动微分方程,并求当ki k,i 1, 6, m1 m, m2 2m, m3 m时的固有 频率和固有振型。
m1
M
m2
u2
c
3c
2c
u2
k
3k
2k
u2
0
m u3 0 2c 2c u3 0 2k 2k u3 f0
1 0,2
k m
, 3
2k m
1 1 1
φ1
1 , φ2
0
, φ3
1
1
1/ 2
1
u1 1
u2
1
u3 1
1 0 1/ 2
1 q1
1
q2
1 q3
)d
u0 2
(1 cos1t)
q2
(t)
u0 2
(1
cos 2t )
第3章 振动系统的运动微分方程题解

45 / 2045习 题3-1 复摆重P ,对质心的回转半径为C ρ,质心距转动轴的距离为a ,复摆由水平位置无初速地释放,列写复摆的运动微分方程。
解:系统具有一个自由度,选复摆转角ϕ为广义坐标,原点及正方向如如题4-1图所示。
复摆在任意位置下,根据刚体绕定轴转动微分方程O O M J =ϕ其中)(22a gP J C O +=ρ 得到复摆运动微分方程为ϕϕρcos )(22Pa a gP C =+ 或0cos )(22=-+ϕϕρga a C3-2均质半圆柱体,质心为C ,与圆心O 1的距离为e ,柱体半径为固定R ,质量为m ,对质心的回转半径为C ρ,在平面上作无滑动滚动,如题3-2图所示,列写该系统的运动微分方程。
解:系统具有一个自由度,选θ为广义坐标。
半圆柱体在任意位置的动能为:222121ωC C J mv T +=题3-1图题3-2图46 / 2046用瞬心法求C v :2222*2)cos 2()(θθθ Re R e CC v C -+== θω = 2CC m J ρ= 故2222221)cos 2(21θρθθ Cm Re R e m T +-+=系统具有理想约束,重力的元功为 θθδd mge W sin -=应用动能定理的微分形式W dT δ=θθθρθθd mge m Re R e m d C sin 21)cos 2(2122222-=⎥⎦⎤⎢⎣⎡+-+ θθθθθθθθθθρd mge d mRe d mRe d R e m C sin sin cos 2)(2222-=+-++ 等式两边同除dt ,θθθθθθθθθθρ sin sin cos 2)(2222mge mRe mRe R e m C -=+-++ 0≠θ ,等式两边同除θ故微分方程为0sin sin )cos 2(2222=+++-+θθθθρθmge mRe Re R e m C ① 若为小摆动θθ≈sin ,1cos ≈θ,并略去二阶以上微量,上述非线性微分方程可线性化,系统微摆动的微分方程为0])[(22=++-θθρge r R C要点及讨论(1)本题也可以用平面运动微分方程求解。
自动控制原理第三章习题解答

tp =
1−ξ 2
= e −π 0.6 /
1−0.62
= e −π 0.6 /
1−0.62
= 9 .5 %
π
1 − ξ ωn
2
=
π
1.6
= 1.96( s )
ts =
3-5
3.5
ξω n
=
3.5 = 2.92( s ) 1.2
设单位反馈系统的开环传递函数为
G ( s) =
0.4 s + 1 s ( s + 0.6)
s5 s4 s3 s2 s1 s0
1 12 35 3 20 25 16 80 3 3 5 25 10 25
有一对虚根,系统不稳定 3-13 已知单位反馈系统的开环传递函数
G ( s) =
K (0.5s + 1) s ( s + 1)(0.5s 2 + s + 1)
试确定系统稳定时的 K 值范围。 解:系统特征方程为
ε 0 ,试问 k1 应满足什么条件?
见习题 3-20 解答 3-2 设系统的微分方程式如下: (1)
&(t ) = 2r (t ) 0.2c
&&(t ) + 0.24c &(t ) + c(t ) = r (t ) (2) 0.04c
试求系统的单位脉冲响应 k(t)和单位阶跃响应 h(t)。已知全部初始条件为零。 解: (1) 因为 0.2 sC ( s ) = 2 R ( s ) 单位脉冲响应: C ( s ) = 10 / s 单位阶跃响应 h(t)
试求系统的超调量σ%、峰值时间tp 和调节时间ts。 解: h(t ) = 1 −
机械系统动力学 第三章 机械系统运动微分方程的求解1

• 3-1机械系统运动方程求解方法-解析法 • 3-2机械系统的运动方程求解方法-数值法 • 3-3机械系统的运动方程求解方法-半解析数
值法
3-1机械系统运动方程求解方法-解析法
3-1-1 单自由度系统的振动
1.问题的提法 工程中大量的动力学问题都可以 归结于图3-1-1 单自由度振动系 统的力学模型,其动力学问题的数 学模型表示为常微分方程的初值 问题 控制方程:
n
3-1机械系统运动方程求解方法-解析法
3-1-1 单自由度系统的振动
在初始条件为 x(0) x0, x(0) x0 欠阻尼条件下,方程的定解
x(t)
ent ( x0
cos d t
x0
x0 d
sin dt)
[1
(
X st
)2 ]2 [2 (
)]2
sin(d t
)
n
n
上中的第一项为单自由度系统自由振动响应,当t
图3-1-1 单自由度振动系 统的力学模型
mx cx kx F(t)
满足初始条件:
x(0) x0, x(0) x0
3-1机械系统运动方程求解方法-解析法
3-1-1 单自由度系统的振动
2. 单自由度振动系统简谐激励作 用下的响应
运动微分方程:
mx cx kx F0 sin t
图3-1-1 单自由度振动系 统的力学模型
3-1机械系统运动方程求解方法-解析法
3-1-1 单自由度系统的振动 2)特解
特解的求法很多,有比较系数法、旋转矢量法、拉 氏变换法等,较简单快捷的方法是旋转矢量法
设特解: x2(t) X sin(t )
代入方程 mx cx kx F0 sin t
机械振动课后习题集和规范标准答案第三章习题集和标准答案
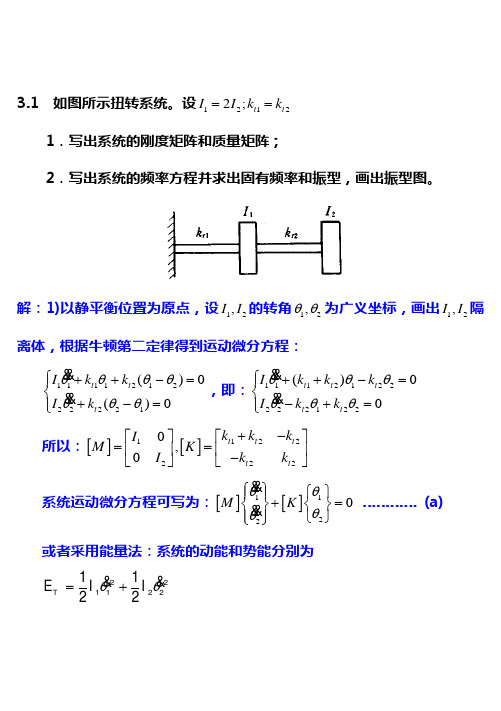
3.1 如图所示扭转系统。
设12122;t t I I k k ==1.写出系统的刚度矩阵和质量矩阵;2.写出系统的频率方程并求出固有频率和振型,画出振型图。
解:1)以静平衡位置为原点,设12,I I 的转角12,θθ为广义坐标,画出12,I I 隔离体,根据牛顿第二定律得到运动微分方程:111121222221()0()0t t t I k k I k θθθθθθθ⎧++-=⎪⎨+-=⎪⎩&&&&,即:1112122222122()00t t t t t I k k k I k k θθθθθθ⎧++-=⎪⎨-+=⎪⎩&&&&所以:[][]12212220,0t t t t t k k k IM K k k I +-⎡⎤⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦系统运动微分方程可写为:[][]11220M K θθθθ⎧⎫⎧⎫⎪⎪+=⎨⎬⎨⎬⎪⎪⎩⎭⎩⎭&&&& ………… (a)或者采用能量法:系统的动能和势能分别为θθ=+&&2211221122T E I Iθθθθθθθ=+-=++-222211212121221121111()()2222t t t t t t U k k k k k k 求偏导也可以得到[][],M K由于12122;t t I I k k ==,所以[][]212021,0111t M I K k -⎡⎤⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦2)设系统固有振动的解为: 1122cos u t u θωθ⎧⎫⎧⎫=⎨⎬⎨⎬⎩⎭⎩⎭,代入(a )可得:[][]122()0u K M u ω⎧⎫-=⎨⎬⎩⎭………… (b)得到频率方程:22121211222()0t t t t k I k k k I ωωω--==--V即:224222121()240t t I k I k ωωω=-+=V解得:211,222(22t k I ω±==所以:1ω=<2ω= ………… (c)将(c )代入(b )可得:112121211122(22220(22t t t t t t k k I k I u u k k k I I ⎡⎤±--⎢⎥⎧⎫⎢⎥=⎨⎬⎢⎥⎩⎭⎢⎥--⎢⎥⎣⎦g g g解得:11212u u =-;12222u u = 令21u =,得到系统的振型为:-0.70710.70713.2 求图所示系统的固有频率和振型。
振动理论课后答案

解:
模态函数的一般形式为:
题设边界条件为:
,
边界条件可化作:
,
导出C2= 0及频率方程:
,其中
解:
,
不计质量的梁上有三个集中质量,如图所示。用邓克利法计算横向振动的基频。
图
解:
当系统中三个集中质量分别单独存在时:
, ,
在图所示系统中,已知m和k。用瑞利法计算系统的基频。
图
解:
近似选取假设模态为:
系统的质量阵和刚度阵分别为:
,
由瑞利商公式:
在图所示系统中,已知k和J。用传递矩阵法计算系统的固有频率和模态。
解:
设该简谐振动的方程为 ; 二式平方和为
将数据代入上式:
;
联立求解得
A=10.69cm; 1/s;T= s
当 时, 取最大,即:
得:
答:振动周期为;振幅为10.69cm;最大速度为22.63m/s。
1-3一个机器内某零件的振动规律为 ,x的单位是cm, 1/s。这个振动是否为简谐振动试求它的振幅、最大速度及最大加速度,并用旋转矢量表示这三者之间的关系。
求图T 2-7中系统的固有频率,悬臂梁端点的刚度分别是 及 ,悬臂梁的质量忽略不计。
图T 2-7答案图T 2-7
解:
和 为串联,等效刚度为: 。(因为总变形为求和)
和 为并联(因为 的变形等于 的变形),则:
和 为串联(因为总变形为求和),故:
故:
由一对带偏心质量的等速反向旋转齿轮构成的振动机械安装在弹簧和阻尼器构成的支承上,如图所示。当齿轮转动角速度为 时,偏心质量惯性力在垂直方向大小为 。已知偏心重W=N,偏心距e=15.0cm,支承弹簧总刚度系数k=N/cm,测得垂直方向共振振幅 ,远离共振时垂直振幅趋近常值 。求支承阻尼器的阻尼比及在 运行时机器的垂直振幅。
振动力学(两自由度系统和多自由度系统)

2
振动理论及应用
第3章 多自由度系统的振动
3.1 两自由度系统的振动方程 ——刚度矩阵和质量矩阵
建立运动微分方程的方法和单自由度系统基本一样, 但难 度更大。
3.1.1 运动微分方程
标准的m-k-c系统,对每一质量利用牛顿定律得:
3
振动理论及应用
坐标原点仍取在静平衡位置
具体求解时,只假设j坐标处的位移为1,其它各坐标的位 移均为0。
7
振动理论及应用
5.2.3 惯性影响系数与质量矩阵
第3章 多自由度系统的振动
质量矩阵[M]中的元素称为惯性(质量)影响系数,其 mij的力学意义是:仅在j坐标处产生单位广义加速度,需在i坐 标处施加的广义力。
具体求解时,只假设j坐标处的加速度为1,其它各坐标的 加速度均为0。
2
x1 5 kx1 5 kx2
V x2
2 5
kx1
1 5
kx2
26
振动理论及应用
第3章 多自由度系统的振动
计算广义力,设只有x1处产生虚位移x1,则
Q1
cx1 x1 x1
cx1
同样设x2处产生虚位移x2,则
Q2
c 0
x2
0
代入拉格朗日方程即可。
27
振动理论及应用
第3章 多自由度系统的振动
5l 3
48EI
k12
l3 3EI
k22
1
求出各个刚度系数即组 成刚度矩阵[K]。
17
振动理论及应用
第3章 多自由度系统的振动
用拉格朗日方程 建立振动系统的运动微分方程
对于非标准的m-k-c多自由度振动系统,用传统的动力学 方法建立运动微分方程比较困难,更适合使用拉格郎日方程和 能量的方法。拉格郎日方程为:
振动系统的运动微分方程题解

习 题3-1 复摆重P ,对质心的回转半径为C ρ,质心距转动轴的距离为a ,复摆由水平位置无初速地释放,列写复摆的运动微分方程。
解:系统具有一个自由度,选复摆转角ϕ为广义坐标,原点及正方向如如题4-1图所示。
复摆在任意位置下,根据刚体绕定轴转动微分方程 O O M J =ϕ其中)(22a gP J C O +=ρ 得到复摆运动微分方程为 ϕϕρcos )(22Pa a gP C =+ 或0cos )(22=-+ϕϕρga a C3-2均质半圆柱体,质心为C ,与圆心O 1的距离为e ,柱体半径为R ,质量为m ,对质心的回转半径为C ρ,在固定平面上作无滑动滚动,如题3-2图所示,列写该系统的运动微分方程。
解:系统具有一个自由度,选θ为广义坐标。
半圆柱体在任意位置的动能为:222121ωC C J mv T +=用瞬心法求C v : 2222*2)cos 2()(θθθ Re R e CC v C -+== θω =2C C m J ρ=故2222221)cos 2(21θρθθ Cm Re R e m T +-+=系统具有理想约束,重力的元功为题3-1图题3-2图θθδd mge W sin -= 应用动能定理的微分形式W dT δ=θθθρθθd mge m Re R e m d C sin 21)cos 2(2122222-=⎥⎦⎤⎢⎣⎡+-+ θθθθθθθθθθρd mge d mRe d mRe d R e m C sin sin cos 2)(2222-=+-++ 等式两边同除dt ,θθθθθθθθθθρ sin sin cos 2)(2222mge mRe mRe R e m C -=+-++ 0≠θ ,等式两边同除θ故微分方程为0sin sin )cos 2(2222=+++-+θθθθρθmge mRe Re R e m C ①若为小摆动θθ≈sin ,1cos ≈θ,并略去二阶以上微量,上述非线性微分方程可线性化,系统微摆动的微分方程为0])[(22=++-θθρge r R C要点及讨论(1)本题也可以用平面运动微分方程求解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
将式(a)、式(b)与式(c)代入变分式
(d)
得到
(e)
对式(e)进行分部积分运算,得到
(f)
由于, 时,哈密顿原理要求w= 0,因而式(f)变为
(f)
因为,t1与t2区间的虚位移w不可能为零,由此,得到梁的边界条件
(h)
与运动方程
(i)
两端简支的梁,显然是满足边界条件式(h)的。
3-7应用拉格朗日方程导出题4-7图所示系统的运动微分方程。
(d)
展开上述频率方程,得
(e)
解得式(e)的两个根为
(f)
将式(f)代入式(c),可得两个自振频率
(g)
(3)振型分析
由振幅方程得
两个振型的大致形状如图3-13(a)、(b)所示。
解:系统具有一个自由度,选 为广义坐标。
半圆柱体在任意位置的动能为:
用瞬心法求 :
故
系统具有理想约束,重力的元功为
应用动能定理的微分形式
等式两边同除 ,
,等式两边同除
故微分方程为
①
若为小摆动 , ,并略去二阶以上微量,上述非线性微分方程可线性化,系统微摆动的微分方程为
要点及讨论
(1)本题也可以用平面运动微分方程求解。系统的受力图与运动分析图如图(b)所示。列写微分方程
另解:由动静法得,以整体为研究对象
以M为研究对象:
又忽略高阶小量 ,所以以上两式化简后得:
化成矩阵形式为:
3-6题3-6图所示两端简支的均匀梁,已知弯曲刚度为EI,单位长度的质量为m,分布载荷为F(y,t)。试用哈密顿原理求运动方程。
解:若梁的挠曲函数为w(y,t),则动能为
(a)
应变(势能)为
(b)
,
同理求出 , 。最后得到柔度矩阵为
另解:(1)求刚度矩阵[K]和质量矩阵[M]
在各楼层处附加水平链杆,并分别使各层产生一单位位移。由各层的剪力平衡条件,可求得各刚度影响系数,其数值分别如图3-13(b)、(c)所示。得刚度矩阵为
(a)
质量矩阵为
(b)
图3-13
(2)频率分析
引入符号
(c)
则由式(3-12)知
对于图(b),建立刚体的水平运动微分方程为
(1)
对于图(c):建立刚体在铅垂平面内的运动微分方程为
(2)
(3)
(4)
其中xC、yC及x均是对固定坐标系的坐标,同时考虑到微小运动的假说,于是有
(5)
(6)
由方程(1)、(2)消去未知力,FOx并考虑式(5)得
(7)
又由方程(2)、(3)和(4)消去未知力FOy、FOx,并考虑式(5)和(6),得
3-5题3-5图所示为刚性建筑模型。刚性基础质量为m,刚性建筑的质量为M,对质心C的转动惯量为IC。两刚体在O处铰接并附有刚度系数为k1的扭转弹簧。其他参数如图示。设地基有水平运动z(t),试建立系统微幅运动微分方程。图中 。
解:应用牛顿矢量力学建立刚体运动的微分方程时,首先要画出每个刚体的受力图,如题3-5图(b)、(c)所示。
解:运动的分离体图如图(b)所示。
地震中可设为微小角度,因此
因此运动方程为
如果 则
则频率方程为
即
或
另解:动静法得。
以刚体m为研究对象:
又忽略高阶小量 ,所以以上两式化简后得:
图中:kx、m 应反向。方程应为
3-9为了使结构隔离机器产生的振动,将机器安装在一很大的机座上,机座由弹簧支承,如题3-9图所示。试求机座在图示平面内的运动方程。
(2)本题也可用机械能守恒定律求解。
系统的动能
选半圆柱体中心O1所在平面为零势面,系统的势能
由
两边对时间 求导数,即可得到与式①相同的运动微分方程。
3-3均质杆AB,长l,质量为m,沿光滑墙面滑下,如题3-3图所示。设水平面也为光滑的。列写该系统的运动微分方程。
题3-3图
解:系统具有一个自由度,选 为广义坐标。系统在任一位置的动能为
(2)用动能定理建立系统运动微分方程的步骤为:
①分析系统受力,在理想约束的情况下只有主动力作功,所以一般在受力图上只画主动力。
②建立广义坐标,确定其原点和正方向;分析系统运动,重点是分析速度(角速度),将速度(角速度)用广义速度表示。
③计算系统在任意位置的动能,将动能表示为广义坐标、广义速度的函数。
解:由材料力学知,当悬臂梁自由端无转角时,其梁的等效刚度为 ,由此可将题3-12图等效为(a)图,其中
,
广义坐标如图(a)示。利用刚度影响系数法求刚度矩阵 。
设 ,画出受力图,并施加物体力 ,列平衡方程,可得到
,
同理可求得 。最后求得刚度矩阵为
=
由刚度矩阵求逆得到柔度矩阵为
得到系统的位移方程为
也可由柔度影响系数法求柔度矩阵。即,对图(a)中的 施加单位力,而 不受力,此时第一个弹簧变形为 ,第二个弹簧变形为零。由此可得位移为,
(8)
方程(7)和(8)为系统微幅运动微分方程,若令x和为确定系统位置的广义坐标,写为矩阵形式
那么,方程(7)和(8)改写为矩阵形式如下:
(9)
由此例题可以看出,应用牛顿矢量力学建立系统的运动微分方程,一定要画受力图,于是必然要涉及未知约束力,因此较为繁琐,特别是该例中的组合刚体系统更是如此。然而对于多自由度系统,应用拉格朗日方程建立运动微分方程较为简单。
上述方程包含 , , , , 五个未知量,必须补充运动学关系才能求解。建立质心坐标与广义坐标 之间的关系
,
所以
运动学方程式⑤⑥与方程②③④联立,消去未知约束力 , ,就可以得到与式①相同的系统运动微分方程。
因为在理想约束的情况下,未知约束力在动能定理的表达式中并不出现,所以用动能定理解决已知力求运动的问题更简便、直接。
,
系统的动能
主动力的元功
根据动能定理建立的方程为
所以
“—”号说明当 取正值时 为负,即反时针方向。
(3)本题也可用平面运动微分方程求解,读者试列出方程。
3-4如题3-4图所示,均质圆柱体质量为m,半径为r,沿倾斜角为 的三角块作无滑动滚动,质量为M的三角块置于光滑的水平面上。列写该系统的运动微分方程。
④计算力的功,若用积分形式动能定理,则计算主动力在有限路程上的功,若用微分形式的动能定理,则计算力的元功。
⑤应用动能定理建立系统的受力与运动间的关系。
(3)在理想约束、主动力又为势力的情况下,可用机械能守恒定律建立系统运动微分方程。
(4)对于多自由度系统,如两个自由度系统,动能定理只给出一个方程,必须与其他定理,如动量定理或动量矩定理联合应用,才能得到另外一个方程。
解:设 质心的水平位移与 相对于质心的转角为广义坐标。利用刚度影响系数法求刚度矩阵 。
设 ,画出受力图,并施加物体力与力偶 ,列平衡方程,
,
,
设 ,画出受力图,并施加物体力与力偶 ,列平衡方程,
,
,,Βιβλιοθήκη , , ,得作用力方程为
题3-12图
3-12题3-12图是两层楼建筑框架的示意图,假设梁是刚性的,框架中各根柱为棱柱形,下层弯曲刚度为EJ1,上层为EJ2,采用微小水平运动x1及x2为坐标,列出系统运动的位移方程。
题3-9图
解:选择坐标q1、q2、q3,这些坐标已能完全描述该系统的运动,并相互独立。设机器和机座的总质量为M,总质量对质心G点的惯性矩为IG,则
式中,V为贮存在弹簧中的势能。
有:
由拉格朗日方程得
则运动方程为
因此系统具有三坐标耦合的运动方程。假定 ,由频率方程可求出系统的各阶固有频率。
3-10题3-10图是一个带有附有质量m1和m2上的约束弹簧的双摆,采用质量的微小水平平动x1和x2为坐标,写出系统运动的作用力方程。
题3-7图
解:取各质量偏离其平衡位置的x1、x2、x3、x4为广义坐标。即
(1)
则系统的动能
(2)
系统的势能为
(3)
计算拉格朗日方程中的各项导数如下:
将以上各项导数代入拉格朗日方程得
(4)
写成矩阵形式
(5)
其中
质量矩阵
刚度矩阵
位移列阵
(a)(b)
题3-8图
3-8在地震研究中,建筑物可简化为支承在两弹簧上的质量为m的刚体,其中直线弹簧的弹性系数为k,扭转弹簧的弹性系数为kT,如题3-8图所示。设IG为建筑物相对质心G的转动惯量,试利用坐标x(相对于平衡位置的直线运动)及描述建筑物转动的坐标,求出运动方程。
由瞬心法求质心的速度
, ,
所以
系统的主动力图为图(a)所示。重力的元功为
由动能定理
所以
系统的运动微分方程为
要点及讨论
(1)平面运动刚体可用式 计算刚体动能,式中 为刚体对瞬心的转动惯量, 为质心与瞬心间的距离。
在本题中质心的速度 也可用式 计算。其中
(2)所谓广义坐标应包含坐标值(线位移或角位移)、坐标原点、坐标正方向。广义坐标的选择一般不是唯一的,例如在本题中也可选杆与水平线的夹角 为广义坐标,正方向如图(b)所示(顺时针),广义坐标选定后其它运动量(位移及位移的一阶、二阶导数)都根据广义坐标确定(包括大小与正方向)。如质心C的位移与速度,正方向应如图所示,大小分别为
解:利用刚度影响系数法求刚度矩阵 。
设 ,分别画出 与 的受力图,并施加二物块力 ,列平衡方程,
对 :
, 题3-10图
,
对 :
,
,
设 ,分别画出 与 的受力图,并施加二物块力 ,列
平衡方程,
对 : ,
,
对 : ,
,
由, , , , ,
,解得,
, , ,
得作用力方程为
3-11题3-11图为一刚性杆竖直支承于可移动的支座上,刚杆顶面和底面受水平弹簧的约束,质心C上受水平力PC和扭矩MC的作用。设刚杆长度、横截面积和质量密度分别为l、A及 ,以质心C的微小位移xC与 为坐标,列出系统运动的作用力方程。
