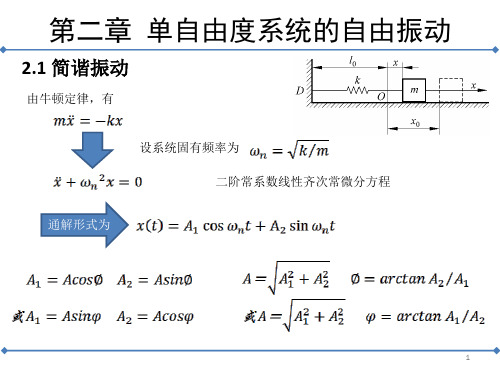
第二章-单自由度系统的自由振动-yyt

2.3 单自由度无阻尼自由振动—作业
水塔塔身的高度为300ft，材料为钢筋混凝土，内外径分 别为8ft和10ft，装满水时水塔的重量为6*105lbf。钢筋 混凝土的弹性模量为4*106lbf/in2 ，忽略塔身的质量。求 （1）水塔横向振动的固有频率； （2）若横向初始位移为10in，则由其引起的振动响应； （3）水塔的最大速度和加速度。
质量元件
平动：
力矩和周期已知
O l C mg
Fm mx
Tm J
力、质量和加速度的单位分别为N、kg和m / s 2。
转动：
图 用振动测量方法求
桨叶的转动惯量 力矩、转动惯量和角加速度的单位分别为Nm、kg m 2和rad / s 2 .
23
2.3 单自由度无阻尼自由振动—实例
解: 由动量矩定理得
力矩和周期已知
O l C mg
(t ) mgl sin (t ) J o
sin
(t ) mgl (t ) 0 J o
n
mgl Jo
Jo mgl
图 用振动测量方法求
桨叶的转动惯量
mgl 2 Jo T 2 n 4
Tn 2
24
（2）最大位移位置 T 0 ; V Vmax 机械能守恒
Tmax Vmax
2 2 max mx kxmax
即
max vmax k x n m xmax A
固有频率
28
能量方法：
例 一倒置的摆，杆质量不计，假设起转动惯量为I， 求做微幅振动时摆的固有频率。
机械能守恒
x(t ) A sin(nt )
振幅 频率 初相位
振幅：
A
x 0 x n
2 0
2
简谐运动的三要素
•
n x0 arctan 初相位： 0 x
在简谐运动三要素中，哪些参数是系统的固有参数？哪些参数是依赖于外部条件 的参数？ 无阻尼的质量弹簧系统受到初始扰动后，其自由振动是以 n 为振动频率的简谐振 动，并且永无休止； 初始条件是外界能量注入的一种方式，有初始位移即注入了弹性势能，有初始速 度即注入了动能。
kx 0 m x
振动微分方程
27
能量方法：
对无阻尼系统，即无能量损失，可以根据机械能守恒原理直接推导 出系统的振动微分方程或者直接求取系统的固有频率。
证明： 考虑两个特殊位置上系统能量
（1）静平衡位置 T Tmax
1 2 max ; V 0 mx 2 1 2 kx max 2
当F(t)≠0： 强迫振动
牛顿第二定律：物体动量的 微分方程

同学们试采用达朗贝尔原理、虚位移原理及能量 守恒原理推导一下图示振动系统的运动微分方程。
F(t)
10
2.2 微分方程齐次微分方程通解的求法—特征根法
(t ) bx(t ) 0 x(t ) ax
如将坐标原点设在卡住瞬时位置，则
则振动解： x ( t )
v
0 v x0 0 ; x
n
sin(n t ) 1.28sin(19.6t ) (cm )
绳中最大张力为静张力与最大动张力之和：
Tmax W kA 1.47105 0.74105 2.21105 ( N )
振动理论与声学原理
第二章 单自由度系统的自由振动
牛顿（1643年1月4日—1727年3月31日）是一 位英国物理学家、数学家、剑桥大学数学教授 、英国皇家学会主席。他在1687年发表的论文 《自然哲学与数学原理》里，对万有引力和三 大运动定律进行了描述。这些描述奠定了此后 三个世纪里物理世界的科学观点，并成为了现 代工程学的基础。
统的振动理论就可以得到满意的结果。
3. 单自由度系统的基本概念具有普遍意义。多自由度系统和无限自由 度系统的振动，在特殊的坐标系中考察时，显示出与单自由度系 统类似的性态。
k
弹簧－质量系统就是一个典型的单自由度系统
m x
8
2.2 运动微分方程
根据牛顿第二定律
(t ) F (t ) Fd (t ) Fs (t ) m x
2
max
1 m gl 2 2 2
ka2 m gl n I
30
等效质量和等效刚度法：
2l 3 l 3
当杆件顺时针转动角度θ时， 弹簧产生压缩变形，质量块上 升，而杆件发生了转动。
刚性连接
杆的质量为：m
M
k
转动时的动能计算公式为
2l 3
l 3
1 2 T J 0 2
其中J0为杆件的转动惯量。
2 n
k n m
固有频率
该二阶常系数齐次方程的通解为：
x(t ) X1 cosnt X 2 sin nt
初始条件
(0) x 0 x(0) x0 , x
X1 x0 , X 2
单位：rad/s
n
0 x
自由振动：
x(t ) x0 cos nt
n
0 x
m
25
2.4 求单自由度无阻尼系统固有频率的方法
① 微分方程法：
运动微分方程 ② 能量方法： 系统的固有频率
Tmax Vmax
③ 等效质量和等效刚度法：
系统的固有频率
T
V
④ 静变形法：
等效质量 meq 等效刚度 keq
n
keq meq
26
能量方法：
对无阻尼系统，即无能量损失，可以根据机械能守恒原理直接推导 出系统的振动微分方程或者直接求取系统的固有频率。
x(t ) A sin(nt )
A x 0 x n
2 0 2
k
m
振幅：
v0
k
v0
k0
固有频率
k n m
m
v0
19
2.3 单自由度无阻尼自由振动—实例
例1：升降机笼的质量为 m ，由钢丝绳牵挂以等速度 v0 向下运动。 钢丝 绳的刚度系数为 k ，质量可忽略不计。如果升降机运行中急刹车，钢丝绳上 端突然停止运动，求此时钢丝绳所受的最大张力。 v0 解: x0 0 k
15
•
•
2.3 单自由度无阻尼自由振动--谐波（简谐）振动
n :
A、 :
n
16
2.3 单自由度无阻尼自由振动--谐波（简谐）振动
17
上节课知识回顾
振动问题有哪几类，解决振动问题的方法
有哪些？ 单自由度无阻尼振动系统的特点是什么？
18
2.3 单自由度无阻尼自由振动—实例
例1：升降机笼的质量为 m ，由钢丝绳牵挂以等速度 v0 向下运动。 钢丝 绳的刚度系数为 k ，质量可忽略不计。如果升降机运行中急刹车，钢丝绳上 端突然停止运动，求此时钢丝绳所受的最大张力。 v0
x(t ) Cest
特解形式
(s as b)e 0
2 st
(s as b) 0
2
s1 , s2
特征值
特征方程
特征根 不相等实根 相等实根
s
s1 s2 s1 s2
通解形式
共轭复根
s1,2 i
x(t ) C1es1t C2es2t x(t ) es1t (C1 C2t ) x(t ) et (C1 cos t C2 sin t )
x(t ) A sin(nt )
振幅： A
arctan 初相位：
固有频率
x 0 x n n x0
2 0
2
x 0
n
k m
21
2.3 单自由度无阻尼自由振动—实例
例2 提升机系统。重物W=1.47x105N，钢丝刚度k=5.78x104N/cm。重物以 v=15m/min的速度匀速下降，求绳的上端突然卡住时， （1）重物的振动频率；（2）绳中最大张力。 gk 解：振动（自然）频率 n 19.6 rad / s W
Tmax Vmax
29
零平衡位置
能量方法：
解：广义坐标θ，平衡位置设置零坐标如图
显然，系统的振动方程为： (t ) cos(nt ) θ
(t ) sin( t ) 则，角速度为： n n
有 max 最大动能 Tmax
max n
n
m
（振幅）
0 v0 x
0 x
m k
k
m
k
A
2 x0 (
n
) 2 v0
v0
v0
(钢丝绳最大动张力)
Td kA v0 mk
（钢丝绳总张力的最大值）
k0
T mg v0 mk
m
v0
20
2.3 单自由度无阻尼自由振动—实例
例2 提升机系统。重物W=1.47x105N，钢丝刚度k=5.78x104N/cm。重物以 v=15m/min的速度匀速下降，求绳的上端突然卡住时， （1）重物的振动频率；（2）绳中最大张力。
刚性连接
杆的质量为：m
M
k
31
等效质量和等效刚度法：
1 V keq x 2 2
2
2l 3
l 3
1 2 T meq x 2
刚性连接
杆的质量为：m
1
2
授课内容
基本概念 微分方程求解方法回顾 单自由度无阻尼自由振动特性分析 求解无阻尼系统固有频率的方法 单自由度有阻尼自由振动 有阻尼自由运动微分方程的建立

3
2.1 基本概念

研究对象 单自由度系统