绘制根轨迹图示例(1)
合集下载
根轨迹示例之一:根轨迹规则

(2)若已知闭环系统的一个极点为
s1 1 ,试确定闭环传递函数。
解:闭环传递函数
( s )
K ( s 1)( s 5) ; ( s 2)2 ( s 5) 5K ( s 1)
K 值可根据给定的闭环极点 s1 1 应 用幅值条件求出:K=0.4 法二:直接在闭环特征方程中代入 s=-1
p 90 , p 90 , p 270 , p 270
1 2 3 4
根轨迹的分离点由前求得为
d 1 。
根轨迹与虚轴的交点为 s 0 , K * =10 作反馈极性为正时的根轨迹如图 5-2 所示。 由图 5-1 知,反馈极性为负时,使系统闭环稳定的 K * 范围为 0,16.25 ;由图 5-2 知,反馈极性为正时,使系统闭环稳定的 K * 范围为 0,10 。因此反馈极性未 知时,使系统闭环稳定的 K * 范围为 0,10 。
s d 2,3
故 d 2 , 为常规根轨迹的复分离点。 3
根轨迹与虚轴的交点 s1 , 2 j1 . 8 7 。概略绘制系统反馈极性为负时的根轨迹 1 如图 5-1 所示。 (2) 反馈极性为正时:作零度根轨迹, 实轴上的根轨迹区间为 (, ) , 根轨迹有四条渐近线,且 a 1 ; a 0 ,90 ,180 , 270 。 根轨迹的起始角为
根轨迹示例-1――由根轨迹规则画根轨迹
1. 系统的开环传递函数为
G( s) H ( 3)(s 2 2s 2)
并列出详细步骤。 (提示:分离点用试差法求近似值) 。 解:实轴上的根轨迹区间为[-3, 0]; 渐近线与实轴的交点与角度分别为:
p
p1,2 1 j 2,
Matlab实验三 绘制根轨迹

Matlab
for
Principles of Automatic Control
实验三 绘制根轨迹 1: 绘制根轨迹 2: 参量分析
① 绘制根轨迹 rlocus(sys)
Gk
(s)
K *(s 1) (s 2)(s 3)
rlocus(num, den)
rlocus(sys,k)
②参量分析(根轨迹图上一顿乱点即可)
K1
(s a )nm
1
根轨迹渐进线的方程是新的根轨迹方程。
Байду номын сангаас
• 例: 绘制根轨迹及其渐近线
G(s)
K1
s(s 1)(s 2)
⑥讨论增加零点对根轨迹的影响 试试-2至-4之间的零点
G(s)
K1
s(s 1)(s 2)
r=rlocus(sys)
Gk
(s)
K *(s 1) (s 2)(s 3)
r=rlocus(num, den)
[r,k]=rlocus(sys)
[r,k]=rlocus(num, den)
③测量出根轨迹增益和对应闭环极点坐标,
在窗口显示
Gk
(s)
K *(s 1) (s 2)(s 3)
[k,poles] = rlocfind(sys)
[k,poles] = rlocfind(sys,p) P为已知的要研究的闭环极点。
④绘制零、极点以及在窗口显示零极点
pzmap(sys)
Gk
(s)
K *(s 1) (s 2)(s 3)
[p,z]=pzmap(sys) 求解零极点的好方法
⑤绘制根轨迹渐近线
一般人我不告诉他:
当根轨迹渐进线与实轴的交点已求出后, 可得到方程,这是根轨迹渐进线的方程。
for
Principles of Automatic Control
实验三 绘制根轨迹 1: 绘制根轨迹 2: 参量分析
① 绘制根轨迹 rlocus(sys)
Gk
(s)
K *(s 1) (s 2)(s 3)
rlocus(num, den)
rlocus(sys,k)
②参量分析(根轨迹图上一顿乱点即可)
K1
(s a )nm
1
根轨迹渐进线的方程是新的根轨迹方程。
Байду номын сангаас
• 例: 绘制根轨迹及其渐近线
G(s)
K1
s(s 1)(s 2)
⑥讨论增加零点对根轨迹的影响 试试-2至-4之间的零点
G(s)
K1
s(s 1)(s 2)
r=rlocus(sys)
Gk
(s)
K *(s 1) (s 2)(s 3)
r=rlocus(num, den)
[r,k]=rlocus(sys)
[r,k]=rlocus(num, den)
③测量出根轨迹增益和对应闭环极点坐标,
在窗口显示
Gk
(s)
K *(s 1) (s 2)(s 3)
[k,poles] = rlocfind(sys)
[k,poles] = rlocfind(sys,p) P为已知的要研究的闭环极点。
④绘制零、极点以及在窗口显示零极点
pzmap(sys)
Gk
(s)
K *(s 1) (s 2)(s 3)
[p,z]=pzmap(sys) 求解零极点的好方法
⑤绘制根轨迹渐近线
一般人我不告诉他:
当根轨迹渐进线与实轴的交点已求出后, 可得到方程,这是根轨迹渐进线的方程。
第四章 根轨迹法(1)

第四章 根轨迹法
(1)当 K * = 0时,s1 = 0、s2 = -2, 此时闭环极点就是开环极点。 (2)当0< K * <1时, s1 、 s2 均为负 实数,且位于负实轴的(-2,0) 一 段上。 (3)当K * = 1时,s1 = s2 = -1,两 个负实数闭环极点重合在一起。 (4)当1< K * <∞时, s1, 1 1 k * 2 两个闭环极点变为一对共轭复数极点。 s1 、 s2 的实部不随K * 变化,其位于过 (-1,0)点且平行于虚轴的直线上。 (5)当K * =∞时, s1 = -1+ j∞、 s2 = -1-j∞,此时s1、s2将趋于无限 远处。
第四章 根轨迹法
② 位于s1左边的实数零、极 点: (S1 – P4 ) 、(S1 – Z1 ) 、 向量引起的相角为0°
∴ 判断 s1是否落在根轨迹 上,位于s1左边的零、极点不 考虑。
③ 位于s1右边的实数零、极点: 每个零、极点提供180°相 角,其代数和为奇数,则满足相角条件。
第四章 根轨迹法
a
(0) (1 j1) (1 j1) (4) (1) 5 4 1 3
60 180 2k 1 180 2k 1 a 180 nm 3 300
k 0 k 1 k 2
第四章 根轨迹法
五、法则五 根轨迹分离点和分离角
K G( s) H ( S )
* i 1 n j 1
(s z )
i
m
S (s p j )
-1
m个开环零点 n个开环极点 K *根轨迹增益
∴在s平面上凡是满足上式的任意一个点s1、s2、…、 s∞,都 是闭环特征根,即闭环极点。
第四章 根轨迹法
根轨迹绘制的基本法则

规则七、 根轨迹与虚轴的交点:交点和相应的Kr值 利用劳斯判据求出。 根轨迹与虚轴的交点对应于临界稳定状态,此时系统 出现虚根。 在例4-2-2中,系统闭环特征方程式为:
1 Kr ( s 5) s ( s 1)( s 2)
1 3 6 2K r 3 5K r
0,
s( s 1)( s 2) K r ( s 5) 0
同理可证明入射角。
例4-2-3
设系统开环零极点图如图4-7。p
0 0
j
3
确定根轨迹离开共轭复数根的出射角。
其中 ( p3 z1 ) 85 , ( p3 p1 ) 135
( p3 p2 ) 45 , ( p3 p4 ) 90
0 0
×●
P3
P2 × ●
n m j j 1 i 1
i
nm
对例4-2-2,渐近线与实轴夹角为:
l 180 n m
180 l 2
( l 1,3,) 90 , 90 ( 270 )
0
0 0
交点坐标为:
1 2 ( 5 ) 2
1 , 即(1,j0)。
j
●
× × ×
﹣2 ﹣1
P3
s0 点为从 p3 出发的根轨迹上一点。
z ( p1 p 2 p 3 p 4 ) 180 l
0
j
×●
z
P3
P1
p 3 180 l z ( p1 p 2 p 4 )
0
P2
×●
Z1
×
01 P
P2
P2 × ●
第四章课件根轨迹

经整理得: 2 s3 1s2 1 2s 0 8 0 s0.55
法则6 根轨迹的起始角和终止角:
根轨迹离开开环复数极点处的切线与正实轴的夹 角,称为起始角,以 p i 表示;
根轨迹进入开环复数零点处的切线与正实轴的夹 角,称为终止角,以 z i表示。
起始角、终止角可根据下式求出:
pi
(2k1)
m
j1 zj
法则3 根轨迹的渐近线:
当系统开环极点个数n大于开环零点个数m时, 有n-m条根轨迹分支沿着与实轴交角为 、交a 点为 的一组 a 渐近线趋向于无穷远处,且有
a
(2k1)
nm
n
m
pi zj
σa
i1
j1
nm
(k0,1,2,,nm1)
证明:根轨迹方程式可写成如下形式:
m
G(s)H(s) K*
(s zj )
设系统的开环传递函数为: G(s)H(s)K* P(s)
系统的特征方程式为:
Q(s)
D (s) 1 G (s)H (s) 1 K * P (s) Q (s) K * P (s) 0 Q (s)
对上式求导,得到: D ( s ) Q (s ) K * P ( s ) 0
由以上两式消去 K *得到
Q (s )P (s ) Q (s )P (s ) 0
点个数之和为奇数,则该区域必是根轨迹。 证明:
设s0为实轴上的某一测试点; j是各个开环零点到s0点向量的相角; i是各个开环极点到s0点向量的相角。
因为复数共轭零、极点到实轴上的任一点
的向量相角之和为2 ,因此在确定实轴上
的根轨迹时,可以不考虑它们的影响。
由图可见,s0点右边开 环实数零极点到s0点的向量 相角均为。
自动控制原理第四章根轨迹法

i 1
j 1
开环极点到此被测零点 (终点)的矢量相角
8. 根轨迹的平衡性(根之和) ( n-m 2)
特征方程 Qs KPs 0
sn an1sn1 a1s a0 K sm bm1sm1 b1s b0 0
n
Qs KPs s p j sn cn1sn1 c1s c0 0 j 1
i 1
j1
k 0,1,2,
s zoi i 开环有限零点到s的矢量的相角
s poj j 开环极点到s的矢量的相角
矢量的相角以逆时针方向为正。
幅值条件:
s
m
m
s zoi
li
A s
i 1 n
i 1 n
s poj
Lj
j 1
j1
li αi
-zoi
Lj βj
×
-poj
开 环 有 限 零 点 到s的 矢 量 长 度 之 积 开环极点到s的矢量长度之积
, 2 2
c 2k 11800 2
由此可推理得到出射角:
其余开环极点到被测极 点(起点)的矢量相角
n1
m
c 2k 1180o j i
j 1
i 1
有限零点到被测极点
(起点)的矢量相角
同理入射角:
其余开环有限零点到被测 零点(终点)的矢量相角
m1
n
r 2k 1180o i j
1 GsHs 0
m
GsHs
KPs Qs
K
i 1
n
s
s
zoi
poj
j 1
P s sm bm1sm1 b1s b0
Q s sn an1sn1 a1s a0
于是,特征方程
第四章根轨迹法

系统得闭环根轨迹图。
j
已知负反馈系统开环零极点 分布如图示。
2 p2
在s平面找一点s1 ,
1
画出各开环零、极点到 z1
s1
1
p1 0
s1点得向量。
3
检验s1就是否满足相角条件: p3
(s1 z1) [(s1 p1) + (s1 p2) + (s1 p3)]
= 1 1 2 3 = (2k+1) ??
点,称为根轨迹得分离点(会合点)。
Kg=0 p1
j
j1
Kg A
Kg z1
0
p2 Kg=0
分离点得性质:
1)分离点就是系统闭环重根; 2)由于根轨迹就是对称得,所以分离点或位于实轴上,或 以共轭形式成对出现在复平面上; 3)实轴上相邻两个开环零(极)点之间(其中之一可为无穷 零(极)点)若为根轨迹,则必有一个分离点;
n
m
(s p j ) K g (s zi ) 0
j 1
i 1
d
ds
n j 1
(s
pj)
Kg
d ds
m
(s zi ) 0
i 1
d n
ds j1
n
(s
pj)
dm
ds i1
m
(s zi )
(s pj ) (s zi )
j 1
i 1
(lnV ) V V
n
m
d ln (s pj ) d ln (s zi )
如果s1点满足相角条件,则就是根轨迹上得一点。寻找
大家学习辛苦了,还是要坚持
继续保持安静
在s 平面内满足相角条件得所有s1 点,将这些点连成光滑曲 线,即就是闭环系统根轨迹。
第四章 控制系统根轨迹分析法
i j 1 j
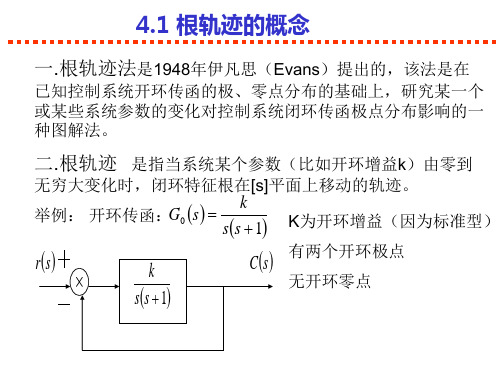
4.1 根轨迹的概念
模条件与角条件的作用: 1、角条件与k无关,即s平面上所有满足角条件的 点都属于根轨迹。(所以绘制根轨迹只要依据角条 件就足够了)。 2、模条件主要用来确定根轨迹上各点对应的根轨 I 迹增益k值。
m
k
j 1 m
n
s p
j
s Zi
args Z i
1
所以结论:实轴上线段右侧的零、极点数目之和为奇 数时,此区段为根轨迹。
jω
例
k G0 ( s ) Ts 1
1 T
×
×
×
×
σ
1 p T
j
1 1 T F 1 T 2k 1 1
k' G0 ( s ) s( s 0.5 )
j
p1 0 p2 0.5
k G0 s 举例: 开环传函: ss 1
K为开环增益(因为标准型) 有两个开环极点 无开环零点
rs
k ss 1
C s
k G s 2 闭环传函: s sk
2 D s s sk 0 则闭环特征方程为:
1 1 闭环特征根(即闭环传函的极点): s1 1 4k
0 0 .5 F 0.25 2 2k 1 3 , 2 2 2
-0.5 0
4.2 根轨迹的绘制规则
规则四:根轨迹的渐近线: (1)条数: (n-m)条 (2)与实轴所成角度 当
m n 2k 1
n m
s 时,认为所有开环零极点引向s的角相同
Z1 Z m p1 p n
G 0 s k
m
为m个开环零点
4.1 根轨迹的概念
模条件与角条件的作用: 1、角条件与k无关,即s平面上所有满足角条件的 点都属于根轨迹。(所以绘制根轨迹只要依据角条 件就足够了)。 2、模条件主要用来确定根轨迹上各点对应的根轨 I 迹增益k值。
m
k
j 1 m
n
s p
j
s Zi
args Z i
1
所以结论:实轴上线段右侧的零、极点数目之和为奇 数时,此区段为根轨迹。
jω
例
k G0 ( s ) Ts 1
1 T
×
×
×
×
σ
1 p T
j
1 1 T F 1 T 2k 1 1
k' G0 ( s ) s( s 0.5 )
j
p1 0 p2 0.5
k G0 s 举例: 开环传函: ss 1
K为开环增益(因为标准型) 有两个开环极点 无开环零点
rs
k ss 1
C s
k G s 2 闭环传函: s sk
2 D s s sk 0 则闭环特征方程为:
1 1 闭环特征根(即闭环传函的极点): s1 1 4k
0 0 .5 F 0.25 2 2k 1 3 , 2 2 2
-0.5 0
4.2 根轨迹的绘制规则
规则四:根轨迹的渐近线: (1)条数: (n-m)条 (2)与实轴所成角度 当
m n 2k 1
n m
s 时,认为所有开环零极点引向s的角相同
Z1 Z m p1 p n
G 0 s k
m
为m个开环零点
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
证明 已知系统的开环零点和极点分别为
z1 2 p1 1 j1 , p 2 1 j1,令s=u+jv为根轨迹的任一点, 由相角条件可得
(s z1 ) (s p1 ) (s p 2 ) 180 z1 、p1 和 p 2 代入得 将 s、
(u 2 jv) (u 1 j( v 1) (u 1 j( v 1)) 180
*
求导
(4)
观察(3)和(4),满足(3)的s值必满足(4),所以 分离点也可以由(4)得到。
j 1 j i
n
z j zi
z j p j zi ( j 代入闭环特征方程,令方程两 边实部和虚部分别相等,求出 。
以上七条规则是绘制根轨迹图所必须遵循的基 本规则。此外,尚须注意以下几点规范画法。 ⑴根轨迹的起点(开环极点 p) ”标 i 用符号“ z j ) 用符号“ o ” 标示。 示;根轨迹的终点 ( 开环零点 ⑵根轨迹由起点到终点是随系统开环根轨迹增益 值K* 的增加而运动的,要用箭头标示根轨迹运动的 方向。 ⑶ 要标出一些特殊点的 值,如起点( ), K* * 终点 ) ;K根 轨 K *( 0 迹在实轴上的分离点d * * * K * ) K ω K K ( ;与虚轴的交点 ( )。还有 c d c 一些要求标出的闭环极点 s 及其对应的开环根轨迹 1 增益 K ,也应在根轨迹图上标出,以便于进行系统 1 的分析与综合。
π 45 4
3π a 135 4
5π a 135 4 7π a 45 4
⑸由规则五可求出根轨迹与实轴的交点(分离点)。 分离点方程是
d [( s ( s 2)( s 2 2 s 2)] | s d 0 ds
即 d 3 3d 2 3d 1 0 解方程得到
d s2 2s 2 0 ds s 2 s d
d 2 4d 2 0
即
解方程可得
d1 3.414
d2 0.586
d2 0.586 不在实轴上的根轨迹上,舍去,实际
的分离点为 d1 。 ⑸由规则六,可求出开环复数极点(根轨迹的起 点)的起始角。
将上式等号两边取正切,则有
v 2 v(u 1) 0 2 2 u 2 (u 1) ( v 1)
u 2 4u 2 v 2 0
(u 2) 2 v 2 ( 2) 2
方程表示在S平面上的根轨迹是一个圆心位于点 (2, j0) 、半径 的圆弧。由此,可画出根轨迹的准确图形如图4-12所示。 2为
2 , 3 2
其中 1 0 是开环极点 p1 对应的坐标值,它是根轨 迹的起点之一。合理的交点应为 c 2,3 2 ,绘 制出该系统的根轨迹图如图4-11所示。
j
K*
[s]
j 2( K* c 6)
60°
* P 1 K 0
K*
P3 K* 0 P2 K* 0
(6)无复数开环极点和零点,不存在起始角和终止角。
(7)由规则七,可求出根轨迹与虚轴的交点 c,用s j 代入特征方程并令方程两边实部和虚部分别相等:
j 3 3 2 j 2 K * 0
K * 3 2 j (2 3 ) 0
解虚部方程得 1 0
(5)由规则5知,根轨迹与实轴的交点(分离点)是方程 d s(s 1)(s 2)sd 0 ds 3d 2 6d 2 0 解的合理值, 解得
d1 0.42
d 2 1.58
d 2 1.58 不在实轴的根轨迹上,舍去;实际的分离点 应为 d1 0.42 。
⑷由规则四知,可求出根轨迹三条渐近线的交点位置和 它们与实轴正方向的交角。
pi z j 1 2 a 1 nm 30
2k 1 a nm
当k=0时 当k=1时 当k=2时
a 60 3
a 180
5 a 60 3
s4 3 s s2 s1
1 4 5
20 4 K * 5
6 K* 4
K*
0 0
0
s
0
K*
令劳斯表中s1 行的首项系数为零,求得 K c* 5 , 2 * 2 由 s 行系数写出辅助方程为 5s K 0
* 5代 入 辅 助 方 程 可 求 令 s j , 并 将 K * K c 出 c 1 。系统的根轨迹如图4-13所示。
j
p1
d1 3.414
[s] 1
0
K*
-4
d1
P 1 ( K* 0) Z1 ( K* )
-3 -1 -2 P2 ( K * 0)
-1
p2
图4-12 例4-8系统的根轨迹图
由本例不难发现,由两个开环极点(实极
点或复数极点)和一个开环实零点组成的二阶系 统,只要实零点没有位于两个实极点之间,当开 环根轨迹增益 K r 由零变到无穷大时,复平面上 的闭环根轨迹,是以实零点为圆心,以实零点到 分离点的距离为半径的一个圆(当开环极点为两 个实极点时)或圆的一部分(当开环极点为一对 共轭复数极点时)。这个结论在数学上的严格证 明可参照本例进行。
i 1 i j 1
n
m
j
2 k 1 a n m
1 j1 d Z j
m n
nm
k 0,1,2,, n m 1
1 i 1 d Pi
2. 5 在实轴上的分离点
1.6 起始角和终止角
j 1
m j 1 j i
m
z j pi
p j pi pi (2k 1)
2 1.5 1 0.5
j
p3
K c* 5
0
0 –0.5 –1 –1.5 –2 –3 –2
p2 p4
p1
–1
0
1
2
图4-13 例4-9系统的根轨迹图
设开环传函
G (s) H (s) K *
B( s) A( s ) (1) (2) (3)
则特征方程
求导 两式相除 由特征方程得
A( s ) K * B ( s ) 0 A( s ) K * B( s ) 0 A( s ) B( s ) A( s ) B ( s ) 0 A( s ) K B( s) A( s ) B( s ) A( s ) B ( s ) * K B 2 (s)
例4-7 已知系统的开环传递函数为
K* G( s) H ( s) s( s 1)( s 2)
试绘制该系统完整的根轨迹图。
解:(1)根轨迹的起点是该系统的三个开环极点, 即 P1=0,P2=-1,P3=-2,由于没有开环零点( m=0) , 三条根轨迹的终点均在无穷远处。 3 2 * (2)该系统的特征方程为 s 3s 2s K 0 这是一个三阶系统,该系统有三条根轨迹在s平面 上。三条根轨迹连续且对称于实轴。 (3) 由规则三知,实轴上的根轨迹为实轴上 P1 到P2的线段和由P3至实轴上负无穷远线段。
d 1
⑹由规则六可求出复数极点 p 3 和 p 4 的起始角
180 (p 3 p1 ) (p 3 p 2 ) (p 3 p 4 ) p 3 180 135 45 90 90 p 4 p3 90
⑺ 该系统为4阶系统,用解析法求根轨迹与虚轴的 * 交点 c 和对应的开环根轨迹增益的临界值 K c 比较困 * 难。下面采用劳斯判据求出 c 和 K c 的值。 根据系统的特征方程列出劳斯表如下:
(4) 由规则四可求出 4 条根轨迹渐近线与实轴的交点 为 pi z j 2 1 j 1 j a 1 nm 40 渐近线与实轴正方向的交角为
2 k 1 a π n m
a
当k = 0时, 当k = 1时, 当k = 2时, 当k = 3时,
三、绘制根轨迹图示例
七条绘制规则:
1 起点与终点:起始于开环极点,终止于开 环零点; 2 分支数、连续性、对称性:分支数等于系 统特征方程的阶数,根轨迹连续且对称于实轴。 3 实轴上的根轨迹:实轴上某线段右侧的开 环零、极点的个数之和为奇数,则该线段是实轴 上的根轨迹;
1. 4 渐近线
a
p z
p1 180 (p1 z1 ) (p1 p 2 ) 180 45 90 135 p 2 p1 135
⑹为准确地画出 S平面上根轨迹的图形,运用相角条 件可证明本系统在S平面上的根轨迹是一个半径 为 2 ,圆心位于点 ( 2, j0) 的圆弧。
-2
-1
d1
0
60°
j 2( K* c 6)
K*
图4-11 例4-7系统根轨迹图
例4-8
已知系统的开环传递函数为
K * ( s 2) G( s) H ( s) 2 s 2s 2
试绘制该系统的根轨迹图。 解(1)由开环传递函数可知,该系统有一个开环实零点 z1 2 和一对开环共轭复数极点 p1,2 1 j ,根轨迹的 起点为 p1 ( K * 0) 和 p2 ( K * 0) ,其终点为 z1 ( K * ) 和无 穷远点 ( K * ) 。 (2)是一个二阶系统,在S平面上有两条连续且对称于实 轴的根轨迹。 (3)由规则三知,实轴上由-2至-∞的线段为实轴上的根 轨迹。 ⑷由规则五,可求出根轨迹与实轴的交点(分离点)。 分离点方程是
将上例与图例比较
例4-9 已知系统的开环传递函数为
K* G( s) H ( s) s( s 2)( s 2 2s 2)
试绘制该系统的根轨迹图。 解 ⑴由规则一知,根轨迹的起点分别是系统的4个开 环极点,即 p1 0 p2 2 , p3, 4 1 j1 。由于系 统无有限开环零点(m=0),根轨迹的终点均在S平面的无 穷远处(无穷零点)。 ⑵由已知系统的开环传递函数可得到它的特征方程为 s 4 4s 3 6s 2 4s K * 0 由规则二知,该系统的根轨迹共有4条分支(n=4),4条根 轨迹连续且对称于实轴。 ⑶由规则三知,实轴上的根轨迹是实轴上由0到-2的线 段。
z1 2 p1 1 j1 , p 2 1 j1,令s=u+jv为根轨迹的任一点, 由相角条件可得
(s z1 ) (s p1 ) (s p 2 ) 180 z1 、p1 和 p 2 代入得 将 s、
(u 2 jv) (u 1 j( v 1) (u 1 j( v 1)) 180
*
求导
(4)
观察(3)和(4),满足(3)的s值必满足(4),所以 分离点也可以由(4)得到。
j 1 j i
n
z j zi
z j p j zi ( j 代入闭环特征方程,令方程两 边实部和虚部分别相等,求出 。
以上七条规则是绘制根轨迹图所必须遵循的基 本规则。此外,尚须注意以下几点规范画法。 ⑴根轨迹的起点(开环极点 p) ”标 i 用符号“ z j ) 用符号“ o ” 标示。 示;根轨迹的终点 ( 开环零点 ⑵根轨迹由起点到终点是随系统开环根轨迹增益 值K* 的增加而运动的,要用箭头标示根轨迹运动的 方向。 ⑶ 要标出一些特殊点的 值,如起点( ), K* * 终点 ) ;K根 轨 K *( 0 迹在实轴上的分离点d * * * K * ) K ω K K ( ;与虚轴的交点 ( )。还有 c d c 一些要求标出的闭环极点 s 及其对应的开环根轨迹 1 增益 K ,也应在根轨迹图上标出,以便于进行系统 1 的分析与综合。
π 45 4
3π a 135 4
5π a 135 4 7π a 45 4
⑸由规则五可求出根轨迹与实轴的交点(分离点)。 分离点方程是
d [( s ( s 2)( s 2 2 s 2)] | s d 0 ds
即 d 3 3d 2 3d 1 0 解方程得到
d s2 2s 2 0 ds s 2 s d
d 2 4d 2 0
即
解方程可得
d1 3.414
d2 0.586
d2 0.586 不在实轴上的根轨迹上,舍去,实际
的分离点为 d1 。 ⑸由规则六,可求出开环复数极点(根轨迹的起 点)的起始角。
将上式等号两边取正切,则有
v 2 v(u 1) 0 2 2 u 2 (u 1) ( v 1)
u 2 4u 2 v 2 0
(u 2) 2 v 2 ( 2) 2
方程表示在S平面上的根轨迹是一个圆心位于点 (2, j0) 、半径 的圆弧。由此,可画出根轨迹的准确图形如图4-12所示。 2为
2 , 3 2
其中 1 0 是开环极点 p1 对应的坐标值,它是根轨 迹的起点之一。合理的交点应为 c 2,3 2 ,绘 制出该系统的根轨迹图如图4-11所示。
j
K*
[s]
j 2( K* c 6)
60°
* P 1 K 0
K*
P3 K* 0 P2 K* 0
(6)无复数开环极点和零点,不存在起始角和终止角。
(7)由规则七,可求出根轨迹与虚轴的交点 c,用s j 代入特征方程并令方程两边实部和虚部分别相等:
j 3 3 2 j 2 K * 0
K * 3 2 j (2 3 ) 0
解虚部方程得 1 0
(5)由规则5知,根轨迹与实轴的交点(分离点)是方程 d s(s 1)(s 2)sd 0 ds 3d 2 6d 2 0 解的合理值, 解得
d1 0.42
d 2 1.58
d 2 1.58 不在实轴的根轨迹上,舍去;实际的分离点 应为 d1 0.42 。
⑷由规则四知,可求出根轨迹三条渐近线的交点位置和 它们与实轴正方向的交角。
pi z j 1 2 a 1 nm 30
2k 1 a nm
当k=0时 当k=1时 当k=2时
a 60 3
a 180
5 a 60 3
s4 3 s s2 s1
1 4 5
20 4 K * 5
6 K* 4
K*
0 0
0
s
0
K*
令劳斯表中s1 行的首项系数为零,求得 K c* 5 , 2 * 2 由 s 行系数写出辅助方程为 5s K 0
* 5代 入 辅 助 方 程 可 求 令 s j , 并 将 K * K c 出 c 1 。系统的根轨迹如图4-13所示。
j
p1
d1 3.414
[s] 1
0
K*
-4
d1
P 1 ( K* 0) Z1 ( K* )
-3 -1 -2 P2 ( K * 0)
-1
p2
图4-12 例4-8系统的根轨迹图
由本例不难发现,由两个开环极点(实极
点或复数极点)和一个开环实零点组成的二阶系 统,只要实零点没有位于两个实极点之间,当开 环根轨迹增益 K r 由零变到无穷大时,复平面上 的闭环根轨迹,是以实零点为圆心,以实零点到 分离点的距离为半径的一个圆(当开环极点为两 个实极点时)或圆的一部分(当开环极点为一对 共轭复数极点时)。这个结论在数学上的严格证 明可参照本例进行。
i 1 i j 1
n
m
j
2 k 1 a n m
1 j1 d Z j
m n
nm
k 0,1,2,, n m 1
1 i 1 d Pi
2. 5 在实轴上的分离点
1.6 起始角和终止角
j 1
m j 1 j i
m
z j pi
p j pi pi (2k 1)
2 1.5 1 0.5
j
p3
K c* 5
0
0 –0.5 –1 –1.5 –2 –3 –2
p2 p4
p1
–1
0
1
2
图4-13 例4-9系统的根轨迹图
设开环传函
G (s) H (s) K *
B( s) A( s ) (1) (2) (3)
则特征方程
求导 两式相除 由特征方程得
A( s ) K * B ( s ) 0 A( s ) K * B( s ) 0 A( s ) B( s ) A( s ) B ( s ) 0 A( s ) K B( s) A( s ) B( s ) A( s ) B ( s ) * K B 2 (s)
例4-7 已知系统的开环传递函数为
K* G( s) H ( s) s( s 1)( s 2)
试绘制该系统完整的根轨迹图。
解:(1)根轨迹的起点是该系统的三个开环极点, 即 P1=0,P2=-1,P3=-2,由于没有开环零点( m=0) , 三条根轨迹的终点均在无穷远处。 3 2 * (2)该系统的特征方程为 s 3s 2s K 0 这是一个三阶系统,该系统有三条根轨迹在s平面 上。三条根轨迹连续且对称于实轴。 (3) 由规则三知,实轴上的根轨迹为实轴上 P1 到P2的线段和由P3至实轴上负无穷远线段。
d 1
⑹由规则六可求出复数极点 p 3 和 p 4 的起始角
180 (p 3 p1 ) (p 3 p 2 ) (p 3 p 4 ) p 3 180 135 45 90 90 p 4 p3 90
⑺ 该系统为4阶系统,用解析法求根轨迹与虚轴的 * 交点 c 和对应的开环根轨迹增益的临界值 K c 比较困 * 难。下面采用劳斯判据求出 c 和 K c 的值。 根据系统的特征方程列出劳斯表如下:
(4) 由规则四可求出 4 条根轨迹渐近线与实轴的交点 为 pi z j 2 1 j 1 j a 1 nm 40 渐近线与实轴正方向的交角为
2 k 1 a π n m
a
当k = 0时, 当k = 1时, 当k = 2时, 当k = 3时,
三、绘制根轨迹图示例
七条绘制规则:
1 起点与终点:起始于开环极点,终止于开 环零点; 2 分支数、连续性、对称性:分支数等于系 统特征方程的阶数,根轨迹连续且对称于实轴。 3 实轴上的根轨迹:实轴上某线段右侧的开 环零、极点的个数之和为奇数,则该线段是实轴 上的根轨迹;
1. 4 渐近线
a
p z
p1 180 (p1 z1 ) (p1 p 2 ) 180 45 90 135 p 2 p1 135
⑹为准确地画出 S平面上根轨迹的图形,运用相角条 件可证明本系统在S平面上的根轨迹是一个半径 为 2 ,圆心位于点 ( 2, j0) 的圆弧。
-2
-1
d1
0
60°
j 2( K* c 6)
K*
图4-11 例4-7系统根轨迹图
例4-8
已知系统的开环传递函数为
K * ( s 2) G( s) H ( s) 2 s 2s 2
试绘制该系统的根轨迹图。 解(1)由开环传递函数可知,该系统有一个开环实零点 z1 2 和一对开环共轭复数极点 p1,2 1 j ,根轨迹的 起点为 p1 ( K * 0) 和 p2 ( K * 0) ,其终点为 z1 ( K * ) 和无 穷远点 ( K * ) 。 (2)是一个二阶系统,在S平面上有两条连续且对称于实 轴的根轨迹。 (3)由规则三知,实轴上由-2至-∞的线段为实轴上的根 轨迹。 ⑷由规则五,可求出根轨迹与实轴的交点(分离点)。 分离点方程是
将上例与图例比较
例4-9 已知系统的开环传递函数为
K* G( s) H ( s) s( s 2)( s 2 2s 2)
试绘制该系统的根轨迹图。 解 ⑴由规则一知,根轨迹的起点分别是系统的4个开 环极点,即 p1 0 p2 2 , p3, 4 1 j1 。由于系 统无有限开环零点(m=0),根轨迹的终点均在S平面的无 穷远处(无穷零点)。 ⑵由已知系统的开环传递函数可得到它的特征方程为 s 4 4s 3 6s 2 4s K * 0 由规则二知,该系统的根轨迹共有4条分支(n=4),4条根 轨迹连续且对称于实轴。 ⑶由规则三知,实轴上的根轨迹是实轴上由0到-2的线 段。
