基于神经网络PID控制的电液位置伺服系统
基于BP神经网络的PID控制系统设计

基于BP神经网络的PID控制系统设计一、引言PID(Proportional-Integral-Derivative)控制器是一种常用的自动控制器,其通过测量系统的输出偏差,根据比例、积分和微分三个因素来控制系统的输出。
然而,传统的PID控制器难以适应复杂、非线性和时变的系统,对于这类系统的控制,神经网络已经被证明是一种有效的方法。
本文将介绍基于BP神经网络的PID控制系统设计。
二、BP神经网络简介BP神经网络(Backpropagation Neural Network)是一种常用的前向反馈型人工神经网络,其通过反向传播算法来训练网络参数,从而实现对输入数据的学习和预测。
BP神经网络拥有多层神经元,每个神经元都与下一层神经元相连,并通过权重和阈值来传递和处理输入信息。
三、PID控制器简介PID控制器由比例(Proportional)、积分(Integral)和微分(Derivative)三个部分组成,其控制输出的公式为:u(t) = Kp * e(t) + Ki * ∑e(t)dt + Kd * de(t)/dt其中,u(t)为控制器的输出,Kp、Ki、Kd为控制器的三个参数,e(t)为系统的输出偏差,∑e(t)dt为偏差的积分项,de(t)/dt为偏差的微分项。
1.数据采集和预处理:首先需要采集系统的输入和输出数据,并对其进行预处理,包括数据归一化和滤波处理等。
2.神经网络设计和训练:根据系统的输入和输出数据,设计BP神经网络的结构,并使用反向传播算法来训练网络参数。
在训练过程中,根据系统的输出偏差来调整比例、积分和微分三个参数。
3.PID控制器实现:根据训练得到的神经网络参数,实现PID控制器的功能。
在每个控制周期内,根据系统的输出偏差来计算PID控制器的输出,将其作为控制信号发送给被控制系统。
4.参数调优和性能评估:根据控制系统的实际情况,对PID控制器的参数进行调优,以提高系统的控制性能。
基于CMAC的PID控制在电液伺服系统中的应用

c n r l r ra i s fe b c o t 1 h wi r c i ga i t ft es s m si r v d sg i c nl o tol e z e d a k c n r .T e s f t kn b l y o y t i e l e o t a i h e mp o e in f a t i y,me n h l ,te aw i e h
e e to—Biblioteka d a l o i o ev y tms i gv n l cr y r u i p st n s r o s se s ie .B p l ig t e d sg e o t l l o t m t e s s m n l — c i y a p yn e in d c nr g r h o t y t a d ai h oa i h e a
ABS TRACT :I iw o eta k n o t l rb e o e ee t h d a l ev y tms h rc mig ft c i g n ve ft rc ig c nr o lm f h lcr y r u i s r o s se ,s ot o n so a kn h op t o c r d t ni n a e u u l x s d i h rd t n lc n r l t o s n od rt ov h sp o lm ,a e fC r b l r e e t r s al e it n t e ta i o a o t h d .I r e o s l e ti rb e o y e i o me n i a o e e el d a Mo e t c lt n C n r l ri ito u e y te p p rb s d o o v n in l I c n r 1 F rt o i e o ・ d l iu a i o t l s n rd c d b h a e a e n c n e t a D o to. i ,a c mb n d c n Ar o oe o P s
基于DSP和神经网络PID控制的交流数字伺服系统

定 的 自学 习 、 自适 应 、 线 性 映 射能 力 和 容 错 性 , 非 因此 , 具有 很 快
的信息处理速度, 这正是数字化交 流伺服系统所要求的。B P神经
网络 具 有 逼 近任 意 非 线 性 函 数 的能 力 , 而 且结 构 和 学 习算 法 简 单 明 确 。通 过 神 经 网络 自身 的学 习, 可 以找 到某 一 最 优 控 制 律 下 的 P ID参 数 。基 于 B 、、 P神 经 网络 的 PD控 制 系 统结 构 如 图 1 示 , I 所
闭 环 控制 , 且 ,/,/ 3个参 数 为 在线 整 定 ; 并 / / i o 神经 网络 N , N 根 据 系 统 的运 行 状 态 , 节 PD 控 制器 的参 数 , 调 I 以期 达 到 某 种 性 能 指
大改观。本文提 出了永磁 同步 电动机的速度控制中较 为有效 的控制方法即神经网络 PD和 D P在伺服系统控制中的应用。 I S 神经网络 PD D P 伺服 系统 I S 永磁 同步电动机
关键词: 电机控制
Absr t ThePM S ha n d a tg st tDC tr swih u .Thef c ft t ac : M sma y a v na e ha mo osi t o t a eo PMSM eWO c n r l n y tm a h ng d g e ty wh tv r he S l o tol g s se h sc a e r a l, i ae e
图 2 N B 网络 结 构 N-P
2 神经 网络 PD算法 I
神经网络 [ 是一种大规模并行 、 1 分布式信息处理 系统, 具有
一ห้องสมุดไป่ตู้
制规律。
基于PSO的神经网络PID在液位控制中的应用

( hn t eC nt co nr C .Ld,ehia C ne,e ig 1 10 ,hn ) C iaSa o su tn E gg o,t. cncl et B in 0 3 0 C ia t r i T r j
Ab ta t F c sn o h p o l m h t t wa df c l o o f m t e I p r mee s n h s o g s t ig i sr c : o u i g n t e r b e t a i s i ut c n i i t r h P D a a tr a d a ln e t n t l me
t e i i a au s o e r l n t o k i h s a e .An i t l g n o t l ag r h fr l ud l v lc n r lwa u h n t l v le f BP n u a ew r n t i i p p r n el e t c nr lo i m o i i e e o to s p t i o t q f r a d b s d o P n u a ew r p i z d b atce s r a g rtm.T e t o e ae n e u s n PC — I ow r ae n B e rl tok o t n mie y p r l wam lo i i h h n i p r ts a d d b g o T I p o e s c n r l s se r c s o t y t m.T e e p rme t r s h r v d t a h o to c e c mp r d wi t d t n l P D o t l o h x e i n e u p o e h t t e c n r l s h me o a e t r i o a I c nr h a i o
基于单神经元自适应PID电液伺服位置控制系统开发应用研究
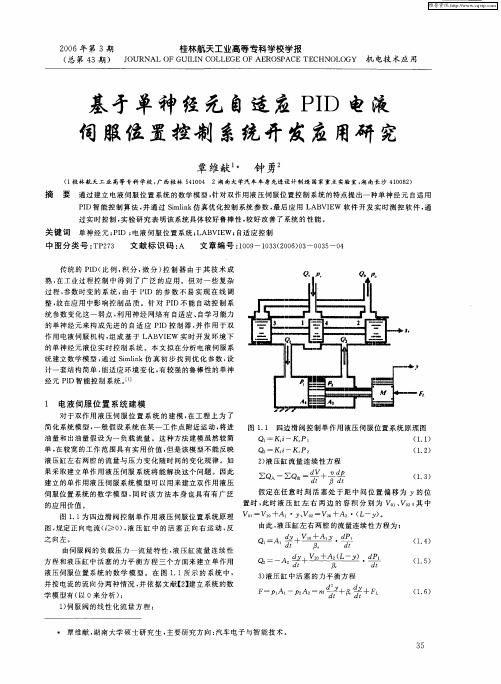
假 定 在 任 意 时 刻 活 塞 处 于距 中 间位 置 偏 移 为 Y的 位 置 时 , 时 液 压 缸 左 右 两 边 的 容 积 分 别 为 、 V 其 中 此 , 、 o; o
Vo 一 V1+ A1・Y、 2 V2 + A2・( 1 o Vo 一 o L— ) 。
由此 , 压 缸 左 右 两 腔 的 流 量连 续 性 方 程 为 ; 液
维普资讯
20 0 6年 第 3期
桂林 航天工 业高等 专科 学校学 报
( 总第 4 3期 ) J U N LO UII O L G FAE O P C E HN L G 机 电技 术应 用 O R A FG LN C L E EO R S A ET C O O Y
由伺 服 阀 的 负 载 压 力 一 流 量 特 性 , 压 缸 流 量 连续 性 液 方 程 和液 压 缸 中 活 塞 的 力 平 衡 方 程 三 个方 面来 建 立 单 作 用 液 压伺 服 位 置 系 统 的数 学 模 型 。 在 图 1 1所 示 的 系 统 中 , . 并 按 电流 的 流 向 分 两 种 情 况 , 依 据 文 献 [ 1 立 系 统 的 数 并 2建 学 模 型有 ( 0来 分 析 ) 以 : 1伺 服 阀 的 线 性 化 流 量 方 程 : )
Q1 K — K 1 = i P Q2 K — K 2 = i P ( .) 1 1 ( .) 1 2
油 量 和 出 油量 假 设 为一 负 载 流量 。这 种 方 法建 模 虽 然 较 简
单 , 较 宽 的 工作 范 围 具 有 实 用 价 值 , 是该 模 型不 能 反 映 在 但
关键词
单神经元 ;I ; PD 电液伺服位置系统 ;A V E ; 适应控制 L B IW 自
液压伺服系统智能PID控制

also with very strong interference moment.All these make the parameters of system
随着我国现代化建设的向前推动,随动系统在我国工农业生产、国防与科学 技术各个部门越来越得到广泛的运用。广泛采用随动系统,既节省人力,又提高 效率和工作质量。
液压传动与控制是以液体(油、高水基液压油、合成液体)作为介质来实现 各种机械量(力、位移或速度等)的传递。
液压传动与单纯的机械传动、电气传动和气压传动相比,具有传递功率大、 结构紧凑、体积小重量轻等特点.因而被广泛运用于各种机械设备及精密的自动 控制系统中。
首先,改进了PX.8电液伺服系统的硬件。主要工作是选用性能更加优异的信号 反馈元器件和电子元器件,重新设计了伺服放大器。伺服放大器的主要功能是将计算 机的控制信号按照系统需要的丌坏增益放大,具有足够的能力推动执行机构运行,还 能完成速度、加速度、角度位置反馈信号的检测和调整。同时,还设计完成了一些辅
本文改进了Px一8电液伺服系统,对伺服放大器进行了重新设计。考虑到系统在 工作中,常规PID控制方法难于获得始终良好的控制效果,本文尝试了一种基于遗传 算法和神经网络的智能PID控制方法,并进行了系统仿真和实验台实验研究。
仿真和实验结果表明,本文所提出的智能控制方法具有很好的自适应性和鲁棒 性,可以有效的抑制负载变化和外界干扰对系统的不利影响,具有较好的控制效果。
在控制理论方面,伺服系统的智能控制理论系统是一门跨学科、需要多学科提供 基础支持的技术科学,因而智能控制系统必然是一个综合集成智能系统。当前,国内 外智能控制技术研究领域主要分为以下几类:
基于模糊神经网络的电液伺服系统建模
( .c ol f caia E g er g N nn nvrt o SineadT cnl y N n n i gu20 9 , h a 1Sho hncl n i ei , aj gU i sy f c c n eho g , aj gJ ns 10 4 C i ; o Me n n i e i e o i a n 2 Mitr R peetieO ie fh eea A m m ns eat n hnAe , hnH bi 30 3 C i ) . la ersn t  ̄c eG nrl r a et D pr t nWu a ra Wua ue 4 07 , hn iy av ot me i a
法 相 比 效果 好 。 证 了 方 法 的有 效 性 。 验 关键 词 : 电液 伺 服 系统 ; 法 聚类 ; 糊 神 经 网络 减 模
中图分 类号 :P 7 T23
文献标识码 : B
M o ef g o e t o y r u i y t m s d o u z u a t r d l n fEler h d a l S se Ba e n F z y Ne r l i e Newo k
p id i d l n fee t h d a l y t m. h i l t n r s l n o aii n i t e d l n c nq e l n mo e l g o lcr y r u i s s e i o c e T e smu ai e u t a d c mp r o sw t oh rmo e l gt h i u s o s s h i e
el g o l to y r u i s se , ih i a tp c ln n ie rs s m. u t ci ecu trn g r h i u e ee- l n f e r h d a l y tm wh c s ia o l a y t i ec c y n e S br t l s i ga o t m s s d t d tr a v e l i o mie te i i a t cu eo z yn u a n t o k,i ep o e so an n f ewok,te r s l p r mee e t n h nt sr t r f u z e r ew r i l u f l n t rc s f e r ig o t r h e u t a a t r si n i h l n i d —
基于PID神经网络的电液比例速度控制系统的研究
Li Yu e C n di he Qi ng a
( 江西理工大学机 电工程学院,江西 赣州
G n h u 3 10 ) a z o 4 0 0
(o l g f M ca ia n l c rc lE g n e ig inx n v r i y o c ec n e ho o y in x C le e o eh n c l a d Ee t ia n ie r n ,Ja g iU i e st fS in ea d T c n l g ,J a g i
1 电液比例速度控制系统 电液比例速度控制系统 “按控 制方式可以分为开环速度 1 控 制与闭环速度控制,其原理框图如 图一所示。开环控制系
【D) Ⅲ 外 糸 瓢
统主要 用在工作过程巾需要快速而平稳地转换速度 的场合, 而 闭环 系统 则用在工作速度需要较精确地控制的地方。 我们主要分析其闭环速度控制系统,其工作原理是 :
K v rs E e t o t d a l c P o o t o a o t o y t m PI e r l N t o k;S s e i u a i n e wod : 1 c r -t r u i r p r i n l C n r l S s e ; D N u a e w r y y tm S m lt o
给定输入信号在经过电控 器 ( 比例放大器 )调整后,控 制 电液比例阀的开 口大小和方 向, 由此再控制液压执行器运动
图一
速度控制系统结构框图
2 P D神经元网络控制策略 I
P D N的结构 随着网络输出量的个数的增减而变化, IN 其基本形式为单输出的S 1N 结构如图二所示 。 PD N 它的输入层
CMAC-PID并行控制算法在电液伺服系统中的应用
() 4
式中 , x为一连续的输入空 间; S为其状态空间 ; C为
刍 eA。 ~Q ) 0= P ( Y ’ 。
() 5
式中: 为液体等效体积 弹性模量 ; 为活塞杆 的速
度 。由式 () () ( ) () 可得 液 压 缸 流 量 连续 方 2 、3 、4 和 5 ,
2 系统描述
起的许多不确定性 , 这些缺点给 电液伺服 系统 的控制 带来 了困难 。
在电液伺服系统 的控制策略上 , 常规的 P 控制 1 D 器已在实际中得到 了应用。其对相 当多 的控制对象 , 特别是线性定常系统是非常有效的, 调节过程 的品质 取决 于 P D控制 器各个参 数 的整定 。然而 , I 传统 的 PD控制算法是在某一特定条件下整定完成 的, 于 I 对 电液伺服系统而言 , 由于其 高度非线性和许 多不确定 性, 常规 PD控制器往往达不到设计要求 。事实上 , I 常规 PD算法结合现代先进 的其他控 制策略形成 复 I 合控制算法始终是一个热点。
小脑模 型神 经 网络 ( C 是 模 拟人 小 脑 的学 习 )
图1 所示为 电液伺服系统的简图 , 它由非对称缸 、 伺服阀和负载组成。假设供油压力 P 为常数 , 出油压
力 为零 。从液 压伺 服 系 统 的流 量方 程 、 力方 程 和 力 压 平衡 方 程 中可得 出它 的数学 表 达式 。在稳 态工 作点 附
C AC产生。数字仿真的结果证明了该并行算法有很 高的跟踪能力和抗干扰性 , M 并且响应速度非常快。 关键词 :MA - I C CPD并行控制算法; 前馈补偿 ; 电液伺服 系 统
中 图分 类 号 : P 7 文献 标识码 : 文章 编 号 :0 04 5 (0 61 —040 T 23 B 10 —88 20 )105 —4
基于神经网络的交流伺服控制系统设计
n t r o AC s ro s se e wok t e v y tm. Usn mprv d BP e r ln t r s t e c n rle o l k h ig i oe n u a ewo k a h o tol rc ud ma e te AC s r o s se r a h t e fx d p sto a i l n c u ae y T e s se smu ain r s l d mo ta e e v y tm e e h e o iin r p d y a d a c r tl . h y tm i lto e u t e nsr ts i BP n u a ewo k c n r le s a fv r b e pe fr n e o a i r c i g a d c n r lp e iin. e r ln t r o to lrha a o a l ro ma c fr p d ta k n n o to r c so Ke wo d y r s:Ne r lNewo k;S r o S se ;Po iin Co to u a t r e v y tm sto n r l
所示 。
网络 的学 习算法 由正 向传播 和反 向传播 两部 分组
成 。在 正 向传 播 的过程 中 , 入 信 息从 输 入 层 经过 隐 输
含层逐 层处 理 , 并传 向输 出层 , 每一层 神经元 的状 态 只
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
收稿日期:2004-03-02
作者简介:董增寿(1970-),男,太原重型机械学院电子分院讲师,研究方向为电子设计自动化和图像处理。
第25卷 第3期太原重型机械学院学报
Vol.25 №3
2004年9月
J OU RNAL OF TA IYUAN HEAV Y MACHIN ER Y INSTITU TE
Sep.2004
文章编号:1000-159X (2004)03-0213-03
基于神经网络PID 控制的电液位置伺服系统
董增寿
(太原重型机械学院,太原 030024)
摘 要:针对电液位置伺服系统,利用神经元的自学习、自适应特点,将神经网络与PID 控制方法相结合,对电液伺服系统在线边学习边控制,实现系统的快速实时控制。
仿
真研究表明,该电液伺服系统具有令人满意的静、动态性能。
关键词:位置伺服系统;神经网络;PID 控制
中图分类号:TP273+122 文献标识码:A
电液伺服系统在机械制造、船舶操纵和工业过程控制中得到了越来越广泛的应用.随着自动化技术的发展和自动化程度的不断提高,对电液伺服系统的稳定性、快速性、准确性、自适应性和鲁棒性等控制品质提出了更高的要求[1]。
为满足这些要求,一方面要提高液压系统本身的制造技术和品质特性;另一方面选择合适的控制器是关键。
一般情况下,控制器可分为两大类,一类是基于被控系统的精确数学模型的控制器,称为传统型控制器,它包括PID 控制器、超前和滞后校正控制器、最优化控制器和自适应控制器等;另一类为人工智能型控制器,这类控制器不依赖于被控系统的精确数学模型,而依赖于人的经验知识,或者依赖于系统的输入与输出之间的非线性映射模型,例如模糊逻辑控制器和人工神经网络控制器等。
由于电液伺服系统中伺服阀流量-压力非线性、伺服阀零偏、增益非线性以及滞环等非线性因素的影响,以及系统模型参数难以准确辨识等原因,基于系统严格数学模型的控制算法往往难以取
得令人满意的控制效果。
鲁棒性很强的PID 控制
算法也存在着参数难以调节等问题。
尤其对于电液速度伺服系统,当系统承受交变外负载时,系统的控制更为困难[2]。
近年来,人工神经网络在液压系统高精度控制方面已经有许多成功的应用。
人工神经网络具有很强的信息综合、学习记忆和自适应能力,能够逼近任意非线性函数,可以处理那些难以用模型和规则描述的过程,在一些不确定的控制中已成功应用。
人工神经网络在控制中的特点是算法简单,学习过程较长,参数收敛速度缓慢,存在局部极小点,不易达到最优控制点等,使其在工业控制中的广泛应用受到限制[3]。
本文将传统PID 控制与神经网络有机地结合起来,根据电液位置伺服系统的运行状态,调节PID 控制器的三个可调参数K P 、K I 和K D ,仿真结果表明该方法具有很好的控制效果。
1 基于BP 神经网络参数自学习的PID 控制器
BP 神经网络结构明确、学习算法简单,通过神
经网络自身的学习,可以找到某一最优控制律下的PID 参数。
基于BP 神经网络的PID 控制系统[4]如
图1所示.控制器由两部分组成
:
图1 神经网络参数自学习PID 控制
Fig.1 PID controller for improved neural netw ork self learning
PID 控制器直接对被控对象闭环控制,
根据系统的
运行状态,神经网络在线整定三个参数K P 、K I 和
K D ,调节PID 控制器的参数,以期达到某种性能指
标的最优化。
增量式数字PID 控制算式为:
u (k )=u (k -1)+k P [e (k )-e (k -1)] +k I e (k )+k D [e (k )-2e (k -1)+e (k -2)]
其中,K P 、K I 、K D 分别为比例、积分和微分系数。
设神经网络NN 是一个三层BP 网络,其结构如图2所示。
为反映PID 控制器三类信号的特性,BP 网络输入选为:
图2 BP 神经网络参数自学习的PID 控制器结构
Fig.2 The scheme of PID controller for BP neural netw ork self recognition
x 1(k )=e (k ),x 2(k )=
∑k
i =1
e (i ),
x 3(k )=e (k )-e (k -1)
网络输出为K P 、K I 、K D ,由于K P 、K I 、K D 不能为负,输出神经元的激活函数取非负的Sigmoid 函数:
g (x )=
1
2
[1+tanh (x )],隐含层一般取8个节点,激活函数取正负对称的Sigmoid 函数:f (x )=
tanh (x )。
取性能指标函数为E =1/2[r (k )-y (k )]2,依最速下降法修正网络的加权系数,即按目标函数
E 对加权系数的负梯度方向搜索,并引入惯性项,
即:
Δw (k +1)=-a
5E
5w (k )+η
Δw (k )其中,a 为学习率;η为惯性系数。
由(1)式可以求得:
5u (k )5K P (k )=e (k )-e (k -1),5u (k )
5K I (k )=e (k ),
5u (k )
K D (k )
=e (k )-2e (k -1)+e (k -2)
输出层加权系数的计算公式为:
Δw (k +1)=a δi y (k )+ηΔw li (k )δl =e (k )5y (k )5u (k )5u (k )5K I (k )
g[・]其中:
5y (k )5u (k )未知,用近似符号sgn 5y (k )
5u (k )
取代,
由此带来的计算误差可以通过学习速率η来调整。
隐含层加权系数的计算公式为:Δw ij (k +1)=a δi x j (k )+η
Δw ij (k )δi =f ′
[・]∑
3
l =1
δl
w li
(k )
其中,f ′[・]=[1-f 2
(x )]/2;g[・]=g (x )[1-g (x )],i =1~8(隐含层),j =1~3(隐含层),l =1~3(输出层)。
412 太原重型机械学院学报 2004年
2 仿真及结论
设电液位置伺服系统的近似模型的传递函数为:G (s )=
3
s (1+0.15)(1+0.5s )
,输入为阶跃
函数,分别用经典的PID 控制器以及神经网络参数自学习PID 控制器进行控制,结果见图3,图中,曲线2为神经网络参数自学习PID 控制结果,曲线1为经典的PID 控制控制结果,可以看出,当调整时间基本不变,超调量明显减少,得到了较好的控制效果。
图3 仿真结果
Fig.3 Simulation results
参考文献:
[1] 高翔,孔丽英,等1电液伺服系统的仿真与自校正PID 控制器的设计[J ]1海军工程大学学报,2001,13(5):332371[2] 何洪,孙薇,周恩涛,等1电液速度伺服系统的CMAC -1积分控制[J ]1机床与液压,1999,(1):122131[3] 郭前岗1一种新型神经网络结构的PID 控制器及其仿真研究[J ]1西北轻工业学报,1998,9(3):10821131[4] 施保华,黄敬尧1改进型神经网络参数自学习PID 控制器的实现[J ]1三峡大学学报,2002,24(3):24222441
Application of N eural N et work Control of Self 2adjusted PID Parameters for
Electro 2hydraulic Position Servo System
DONG Z eng 2shou
(Taiyuan Heavy Machinery Institute ,Taiyuan 030024,China )
Abstract :We used Neural Network Control of Self 2adjusted PID Parameters in Electro 2hydraulic Position Servo System.For artificial neural network having a lot of self 2learning ,self 2adjusting and such functions ,this con 2troller had better control effect for linear and non 2linear time 2fixedness systems than traditional PID controllers.The simulation results show that this system has good dynamic and static performance.K ey w ords :electro 2hydraulic position servo system ,neural network ,PID control
5
12第25卷第3期 董增寿:基于神经网络PID 控制的电液位置伺服系统 。
