数学实验习题
四年级湘教版下学期数学计算题实验学校习题

四年级湘教版下学期数学计算题实验学校习题班级:__________ 姓名:__________1. 解方程。
5X-1.5=13.5 45+2X=515 X-7.82=5.18 X÷6=245X+X=20 3X+3.6=7.89 4X-12=7.2 X÷1.2=0.62. 你发现了什么?你能直接写出下面各式的得数吗?123456789×45= 123456789×54= 123456789×81=123456789×63= 123456789×72= 123456789×36=123456789×9= 123456789×18= 123456789×27=3. 口算。
0.78-0.28= 0.8-0.3= 10-0.3=0.8-0.13= 6.4+6= 10+0.3=0.57+0.16= 1-0.7= 12-1.2=0.4+0.6= 3+1.7= 0.76-0.6=4. 直接写得数。
20×30= 60×120= 250×4=16×400= 80×50= 260×10=5. 口算。
2.51×10= 2.63×10= 0.645×1000=0.03×100= 4.03÷10= 7÷100=63.5÷1000= 5.63÷100= 0.1÷100=1.02×10=2.1÷1000= 0.56×1000=6. 你能简便地表示下列各式吗?a×8= b×4.7= a×4+b×5=3.6×m×n= b×b= c+c=4+b+b= 4×b×b= d+d+d=7. 解下列方程。
数学软件与数学实验习题(2)

一、选择题1、空间曲线绘图命令是:(B)。
(A) plot2 (B) plot3 (C) surf (D) plot2、在matlab中,命令hold off 表示是:(D)。
(A) 在图中消隐分隔线。
(B) 使系统处于可放大状态。
(C) 保留当前图形和它的轴,使其后图形放在当前图形上。
(D) 此后图形指令运作将抹掉当前窗口中的旧图形,然后画上新图形。
3、生成三维表面图的命令是:(A)。
(A) surf (B) meshc (C) mesh (D) meshz4、下面哪个命令的功能是是系统处于可放大状态(C)。
(A) grid on (B) hold on (C)zoom on (D) hidden on5、在MATLAB的若干通用操作指令中,清除内存中的变量的是(A)(A)clear (B)cla (C)clf (D)clc6、下列表示可以作为MATLAB的变量的是(DF)(A)abcd-2 (B)xyz_2# (C)@h(D)X_1_a (E)for (F)for17、运行下面的代码后,输入:1回车,2回车,1回车,则输出结果为(C)a=input('a=?');b=input('b=?');c=input('c=?');d=b*b-4*a*c;x=[(-b+sqrt(d))/(2*a),(-b-sqrt(d))/(2*a)];disp(['x1=',num2str(x(1)),',x2=',num2str(x(2))]);(A)x1=num2str(1) x2=num2str(1)(B)x1=num2str(-1) x2=num2str(1)(C)x1= -1 x2=-1(D)x1=1 x2=-1二、填空题1、命令clf的含义是清除图形窗口2、命令colormap的含义是图形颜色控制命令3、已知A=[096;130];B=[143;150];写出下列各指令运行的结果。
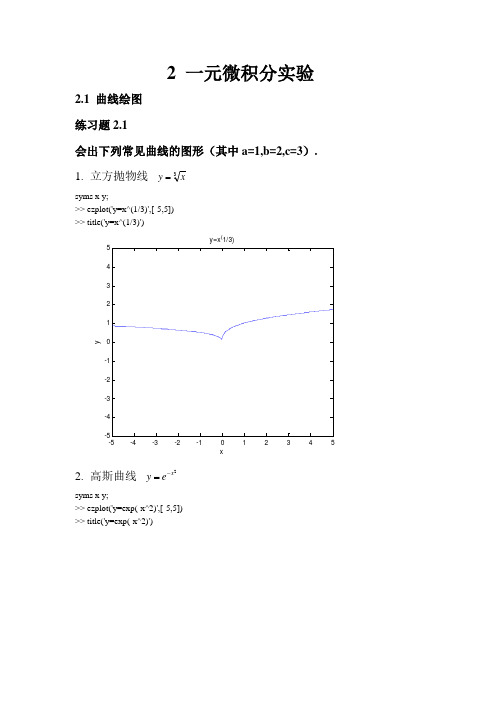
数学实验习题

数学实验习题实验1 MATLAB 基本特性与基本运算1. 求解方程02=++c bx ax的根。
其中(1)3,2,1===c b a (2)3,2,1-=-==c b a (提示:运用求根公式。
结果为(1)ix 212,1±-=,(2)3,12,1-=x )2. 已知圆的半径为15,求圆的周长和面积。
3. 输入例1-6中语句,计算三角形的面积并修改边长值重新计算三角形的面积。
4. 查询表1-4中部分常用函数的功能与用法。
5. 设⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡--=0220,2112B A ,求矩阵方程X B A AX -=-2的解。
6. 画出231xxy +=和22)1ln(xx z +=在区间[-5,5]上的图形(提示:用 .^ 和 ./ 运算)。
7. 画出x ex e x f xxsin cos )(cos 2sin 2-=在区间[-5,5]上的图形。
8. 设x ex ex f xxsin cos )(cos 2sin 2-=,试在[-5,5]上求出函数的零点及极大、极小值。
9. 求方程0d )cos 32( 03=--+⎰s t t e txt当=s 1、11、21时的根。
10. 已知⎰+=1214dxxπ(试证明),试用不同的积分命令求其近似值(pi=3.14159265358…)。
11.设||sin 12)(/1x ax ex f x-+=-,试求当)(lim 1x f x →存在时a 的大小以及极限值。
12.设)cos sin()(x x x x f ++=,求)(x f 在]4,0[π上的极值、拐点。
13.计算积分(1)⎰dxx x sin ;(2)dxxx ⎰++12)1ln(。
实验2 MATLAB 绘制二维、三维图形1. 在圆域122≤+yx上画出上半球面221yxz --=的图形。
2. 画出椭球面11241222=++zyx的图形。
3. 在矩形域[-2,2]×[-2,2]区域上画出函数)(22y x xez +-=的图形。
数学实验1-3章习题答案
ans =
18.3287
函数的单调区间为:
(1)单调递增区间:-2<x<-1.5326 -0.7315<x<0以及1.5951<x<2;
(2)单调递减区间:-1.5326<x<-0.7315以及0<x<1.5951.
(2)
函数的图形为:
clear
>> fplot('3*x^5-20*x^3+10',[-3,3])
ans =
-3
最值2:
x=1:0.1:3;
>> y=3.*x.^5-20.*x.^3+10;
>> [m k]=max(y)
m =
199
k =
21
>> x(k)
ans =
3
驻点1及相应的二阶导数值:
clear
>> syms x y
>> y=3*x^5-20*x^3+10;
>> yxx=diff(y,x,2);
>> grid on
f=inline('100*acos(1-1/200*(r^2))+r^2*acos(1/20*r)-10*sqrt(r^2-1/400*r^4)-50*pi','r');
>> y=fzero(f,12)
y =
11.5873
3.求解下列非线性方程组在远点附近的根:
clear
>> syms x y z
>> [x y z]=solve('9*x^2+36*y^2+4*z^2-36','x^2-2*y^2-20*z','16*x-x^3-2*y^2-16*z^2',x,y,z)
高中数学实验教材习题精选 必修4 练习5

高中数学实验教材习题精选 必修4 练习5一:选择题1.已知α为第三象限角,则2α所在的象限是 (A )第一或第二象限 (B )第二或第三象限(C )第一或第三象限 (D )第二或第四象限2.=+-)12sin 12)(cos 12sin 12(cos ππππ( )A .23-B .21-C .21D .23 3.函数)20,0,)(sin(πϕωϕω<≤>∈+=R x x y 的部分图象如图,则( ) A .4,2πϕπω== B .6,3πϕπω== C .4,4πϕπω== D .45,4πϕπω== 4.若||1,||2,a b c a b ===+ ,且c a ⊥ ,则向量a 与b 的夹角为( )(A )30° (B )60° (C )120° (D )150°二:填空题5.已知tan 2α=2,则tanα的值为________,tan ()4πα+的值为_______ 6.直角坐标平面xoy 中,若定点)2,1(A 与动点),(y x P 满足4=∙OA OP ,则点P 的轨迹方程是______________。
7.α是第二象限角,P (x ,5)为其终边上一点且cos α=42x ,则x 的值为________ 三:解答题:8. 已知tan2α=2,求 (I )tan()4πα+的值; (II )6sin cos 3sin 2cos αααα+-的值. 9.已知函数2()2sin sin 2,[0,2].f x x x x =+∈π求使()f x 为正值的x 的集合.10.已知函数f (x )=2sin x cos x +cos2x .(Ⅰ) 求f (4π)的值;(Ⅱ) 设α∈(0,π),f (2α)sin α的值.参考答案:一:选择题1-4 DDCC二:填空题5、-34,-71 6、x+2y-4=07、-3三:解答题:8、解:(I )∵ tan2α=2, ∴ 22tan 2242tan 1431tan 2ααα⨯===---; 所以tan tan tan 14tan()41tan 1tan tan 4παπααπαα+++==--=41134713-+=-+; (II )由(I), tan α=-34, 所以6sin cos 3sin 2cos αααα+-=6tan 13tan 2αα+-=46()173463()23-+=--. 9、解:∵()1cos 2sin 2f x x x =-+1)4x π=-()02s i n (2)04f x x π∴>⇔->s i n (2)42x π⇔->- 5222444k x k πππππ⇔-+<-<+ 34k x k πππ⇔<<+ 又[0,2].x π∈ ∴37(0,)(,)44x πππ∈⋃ 10、解:(Ⅰ)x x x f 2cos 2sin )(+=12cos 2sin )4(=π+π=π∴f (Ⅱ) 22cos sin )2(=α+α=αf 23)4cos(,21)4sin(±=π+α=π+α∴262)44s i n (s i n ±=π-π+α=α 0sin ),0(>α∴π∈α 8531sin +=∴a。
四年级苏教版数学上册应用题实验学校习题

四年级苏教版数学上册应用题实验学校习题班级:__________ 姓名:__________一、计算题。
1. 铺路队铺一条2400米长的水泥路,原计划30天完成,实际前6天就铺了600米,照这样计算,铺路队实际多少天就能铺完这条水泥路?2. 270名同学到公园游玩,每30名同学分成一组,由9名老师带队,成人票每张40元,学生票每张29元,他们购买门票要多少元?3. 新学期红星小学准备买50个篮球,其中有三家文体超市篮球的价格都是50元,但三家超市的优惠办法各不相同。
A店:买10个篮球免费赠送1个,不足10个不赠送。
B店:每个篮球优惠5元。
C店:购物每满200元,返还现金20元。
为了节省费用,红星小学应到哪家超市购买篮球?请计算说明。
4. 某电影院楼上楼下共有座位48排,每排能坐30名观众,其中楼上有座位15排,楼下可坐多少名观众?5. 两艘轮船同时从两个港口相对航行,甲轮船每小时航行28千米,乙轮船每小时航行35千米,经过12小时还相距30千米,两个港口之间的航程是多少千米?6. 王叔叔驾驶一辆小汽车,从甲地出发,平均每小时行80千米,行了15小时到达乙地,他原路返回时因天下雨多用了1小时。
问:返回时平均每小时行多少千米?7. 一辆汽车从甲地到乙地,去时的速度为80千米/时,用了5小时到达,返回时只用了4小时,返回时的速度是多少?8. 一列货车和一列客车同时在早晨6时从甲地开往乙地,货车平均每小时行45千米,客车平均每小时行60千米。
早晨8时,客车比货车多行多少千米?9. 同学们从学校到公园春游,每分钟行60米,出发15分后,同学们走了多长的路程?10. 小强和小敏同时从学校出发,向自己家走去,小强的速度是70米/分,小敏的速度是63米/分。
15分钟后,两人同时到家,小强回家的路程比小敏远多少米?11. 在第一次世界大战开始时,战斗机速度的最高记录是169千米/时,而现在的战斗机速度远远超过了当时的战斗机。
小学数学练习实验性
小学数学练习实验性数学练习试卷一、选择题(每题5分,共10小题)1. 小明有5支红色的铅笔,他又买了3支蓝色的铅笔。
那么小明一共有多少支铅笔?A. 5支B. 8支C. 3支D. 6支2. 海洋生物园里有14只海豚,其中10只是雌性的。
那么剩下的是雄性的海豚有几只?A. 4只B. 14只C. 20只D. 24只3. 小明有20元,他用了12元买了一本书,剩下的钱还够买多少支铅笔?A. 2支B. 8支C. 4支D. 10支4. 一辆公交车上有27个座位,其中已经有18个人坐下了。
那么还有多少人站着?A. 27人B. 9人C. 10人D. 18人5. 有一台计算器的屏幕上显示的数字是75,我们知道打开后它会显示2位数的加法题,那么下一道题的结果是多少?A. 152B. 42C. 37D. 666. 在植物园里,有10棵树上有花,其中有8棵是樱花树。
那么剩下的是其他种类的花树有几棵?A. 10棵B. 2棵C. 8棵D. 18棵7. 一包糖果里有25颗糖果,小明拿出5颗给小红吃了,那么剩下的糖果还有几颗?A. 30颗B. 5颗C. 25颗D. 20颗8. 课堂上有30个同学,其中2/3是女生,那么剩下的是男生有多少人?A. 10人B. 30人C. 20人D. 40人9. 一辆货车上有16吨货物,已经卸下6吨,那么剩下的货物还有多少吨?A. 10吨B. 12吨C. 16吨D. 6吨10. 小明的奶奶今年60岁,他的爷爷比奶奶大10岁。
那么小明的爷爷多少岁?A. 70岁B. 80岁C. 50岁D. 90岁二、填空题(每题10分,共5小题)1. 把4的3倍加上5,结果是_____。
2. 小明有30个绿苹果和20个红苹果,绿苹果的数量比红苹果多_____个。
3. 用12减去不小于5的任意一个数,结果最小是_____。
4. 如果上午8点半,那么离中午12点还有_____小时。
5. 用12除以3,结果是_____。
三、计算题(每题15分,共3题)1. 现在是下午3点,再过5小时是几点钟?2. 一盒糖果里有15颗,小明吃掉了1/3,小红吃掉了1/4,那么剩下的糖果还有几颗?3. 一辆货车上有48个箱子,每个箱子里有6本书,共有多少本书?四、解答题(每题30分,共2题)1. 小明得到了一张5元的零花钱,他买了一支2元的铅笔、一本10元的书和一块3元的巧克力。
四年级北师大上学期数学应用题实验学校习题
四年级北师大上学期数学应用题实验学校习题班级:__________ 姓名:__________一、计算题。
1. 一列火车以108千米/时的速度从甲地开往乙地,行驶了13小时,已知从甲地到乙地的铁路长1724千米。
(1)这时火车离甲地有多少千米?(2)这时火车离乙地有多少千米?2. 育才文具店进了250个魔方,进价是30元/个,文具店以45元/个销售,共卖出105个,后开始降价,以25元/个销售。
如果魔方全部卖掉,文具店是盈利了,还是亏损了?(请写出你的思考过程)3. 一列火车每小时行 120 千米,一架飞机的速度是它的 l5 倍,飞机每小时比火车多行多少千米?4. 整教部分是0,小数部分由1、2、3、4这四个数字组的四位小数有24个,把它们按从小到大的顺序排列第19个小数是多少?5. 在一个数的末尾添上一个“0”后,得到的数比原来的数多738,原来的数是多少?6. 奥斑马和小美各有钱若干元.若小美给奥斑马10元,则奥斑马比小美多的钱是小美余下来的钱数的5倍;若奥斑马给小美10元,则他们的钱数正好相等.奥斑马和小美原来各有多少钱?7. 先写出字母公式,再把数值代入公式计算出结果。
爷爷买回来8瓶椰岛鹿龟酒,共用去272元,则每瓶椰岛鹿龟酒是多少元。
8. 下面是鹏程小学为“希望工程”捐款统计表,根据统计表用计算器解决问题。
(1)全校一共捐款多少元?(2)平均每个年级捐款多少元?(3)五年级比一年级多捐款多少元?9. 小明8分钟能够打640个字,要打8800个字,需要几分钟?10. 一座大桥长3千米,一列火车通过大桥的速度是1200米/分,火车从车头开始上桥到车尾离开桥共需要3分钟。
这列火车的车身长多少米?11. 新学期红星小学准备买50个篮球,其中有三家文体超市篮球的价格都是50元,但三家超市的优惠办法各不相同。
A店:买10个篮球免费赠送1个,不足10个不赠送。
B店:每个篮球优惠5元。
C店:购物每满200元,返还现金20元。
通过操作实验探索规律 小学数学 练习题
一、选择题1. 放风筝比赛时,规定用40米长的线,风筝线与地面形成的角度是()时,风筝飞得最高。
A.75度B.30度C.60度D.45度2. 阿米巴原虫是用简单分裂方式繁殖的(一个分裂变两个这样不停地分裂)。
每分裂一次需要3分钟,一个阿米巴原虫18分钟后变成了()个阿米巴原虫。
A.128 B.63 C.643. 体重40千克的乐乐坐在绳长4米的秋千上,体重35千克的壮壮坐在绳长3米的秋千上,他们同时荡了1分钟。
他们荡的次数()。
A.乐乐多B.壮壮多C.一样多D.不确定4. 甲乙两个球完全相同,从不同的高度(如图),自由落下,两球的反弹高度相比较,()。
A.甲球大B.乙球大C.一样大D.无法比较5. 用1个70毫升和1个30毫升的容器盛取20毫升的水到水池A中,并盛取80毫升的水到水池B中,倒进或倒出某个容器都算一次操作,则最少需要经过()次操作。
A.15 B.16 C.17 D.18二、填空题6. 照下图这样,把6根短绳连在一起,要打______个结。
7. 沿着纸环的( )处剪就会使一个小纸环变成一个大纸环。
8. 河内塔问题是一个古老的益智游戏,游戏的规则是每次只能移动1个珠子大珠子不能放在小珠子上面.现在借助②号杆,把①号杆上的三颗珠子移到③号杆,而不改变珠子的上下顺序,最少移动______次.9. 一根绳子对折、对折、对折、再对折,从中间剪开,绳子分成______段.10. 在平面上画212条直线,这些直线最多能形成( )个交点。
三、解答题11. A4纸张长20cm,粘贴处宽2cm.(1)问10张这样贴在一起总长是多少?(2)若总长为362cm,则贴了几张纸?12. 三条直线相交,最多有多少个交点?四条直线相交,最多有多少个交点?你能自己寻找规律,发现10条直线相交最多有多少个交点吗?(提示:先认真画,数出交点数,再仔细观察,寻找规律.)13. 数一数图中共有三角形多少个?14. 将自然数排列如下,在这个数阵里,小明用正方形框出九个数。
三年级北师大版上册数学应用题实验学校习题
三年级北师大版上册数学应用题实验学校习题班级:__________ 姓名:__________1. 一列火车早上7:00从甲地出发,15:00到达乙地,这列火车共行驶了多长时间?2. 小红家有一个密码箱,其密码是由0至9中不同的四个数字组成的,由于疏忽,她只记住了后三位是365,那么小红要想打开箱子,最多需要试几次?3. 汤清杨和哥哥在开学时都买了一些作业本,如果哥哥给他3本的话,那么两个人的作业本数就一样多;如果汤清杨给哥哥1本的话,那么哥哥的本数就是他的3倍。
汤清杨和哥哥各买了多少本作业本?4. 修路队已经修路360米,还剩下未修的是已经修好的5倍。
这条路有多长?5. 兰兰读一本100页的故事书,每天读8页,她从8月11日开始读,能在8月21日读完这本故事书吗?6. 学校食堂王师傅买了 4 袋面粉,每袋面粉 118 元,他付给收银员一些钱后,收银员找给他 28 元,王师傅给的是多少钱?7. 明明和丽丽分别从相距220km的两地同时相向而行。
明明每小时行10km,丽丽每小时行12km,几小时后相遇?8. 一列火车每小时行驶125千米,早上8:00从昆明出发,中午11:00到丽江,昆明到丽江一共有多少千米?9. 某汽车厂计划全年生产汽车16800台,结果提前2个月就完成了全年的生产任务。
照这样的速度,全年可生产汽车多少台?10. 饲养场有黄牛和黑牛一共84头,黄牛卖掉20头后和黑牛同样多,饲养场原有黄牛和黑牛各多少头?11. 从甲地到乙地全长396千米,一辆汽车平均每小时行78千米,5小时能从甲地到达乙地吗?12. 每张成人票19元,买6张成人票大约要多少钱?13. 果园里今年收苹果728千克,收的梨是苹果的3倍,收梨多少千克?收苹果和梨一共多少千克?14. 图书馆购进一批少儿图书,其中《成语故事》72本,《寓言故事》比《成语故事》多18本。
《童话故事》的本数是《寓言故事》的3倍,购进《童话故事》多少本?15. 为庆祝“六·一”,学校大门旁边挂一排彩色气球,按照一个黄气球,两个红气球,三个绿气球的顺序排列。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1) 用Plot3D 命令作出函数cos 2sin3(33,33)z x y x y =--≤≤-≤≤的图形, 采用选
项PlotPoints->40.
Plot3D[z=-Cos[2x]Sin[3y],{x,-3,3},{y,-3,3},PlotPoints→{40}]
2) 作出函数sin(z π
=的图形.
Plot3D[z=Sin[Pi*x^2+y^2],{x,-4,4},{y,-4,4}]
3) 用Plot3D 命令作出函数22()/8
22(cos sin )x y z e
x y -+=+在,x y ππππ
-≤≤-≤≤上的图形, 采用选项PlotPoints->60.
Plot3D[z=Exp[-(x^2+y^2)8]*(Cos[x]^2+Sin[x]^2),{x,-Pi,Pi},{y,-Pi,Pi},PlotPoints→{60}]
4)
二元函数22
xy
z x y
=
+在点(0,0) 处不连续, 用Plot3D 命令作出在区域22,22x y -≤≤-≤≤上的图形(用选项PlotPoints->40). 观察曲面在(0,0)附近的变
化情况.
Plot3Dz=x*yx2+y2,x,-2,2,y,-2,2,PlotPoints→40
5)一个环面的参数方程为
(3cos )cos ,
(3cos )sin ,0,02.sin ,
x u v y u v u v z u ππ=+⎧⎪=+≤≤≤≤⎨=⎪⎩ 试用命令ParametricPlot3D 作出它的图形.
ParametricPlot3D[{(3+Cos[u])*Cos[v],(3+Cos[u])*Sin[v],Sin[u]},{u,0,Pi},{v,0,2Pi}]
6)一个称作正螺面的曲面的参数方程为
cos ,
sin ,11,08./3,
x u v y u v u v z v =⎧⎪=-≤≤≤≤⎨=⎪⎩ 试用命令ParametricPlot3D 作出它的图形.
ParametricPlot3D[{u*Cos[v],u*Sin[v],v3},{u,-1,1},{v,0,8}]
7)用命令Plot3D 作双曲抛物面22
14
x y z =-, 其中66,1414x y -≤≤-≤≤(用选项
BoxRatios->{1,1,1}, PlotPoints->30).
Plot3D[z=x^2-y^24,{x,-6,6},{y,-14,14},BoxRatios→{1,1,1},PlotPoints→{30}]
8)用命令ParametricPlot3D 作出圆柱面221x y +=和圆柱面2
2
1x z +=相交的图形.
g1=ParametricPlot3D[{Sin[u],Cos[u],v},{u,-Pi,Pi},{v,- 3,3}];
g2=ParametricPlot3D[{Sin[u],v,Cos[u]},{u,-Pi,Pi},{v,-3,3}];
Show[g1,g2,PlotRange →{{-3,3},{-3,3},{-3,3}}]
9)用命令ParametricPlot3D 作出抛物柱面2x y =和平面1x z +=相交的图形. g1 = ParametricPlot3D[{Sin[u], Sin[u]^2, v}, {u, -Pi, Pi}, {v, -3, 3}] g2 = ParametricPlot3D[{Sin[u], v, Sin[u] - 1}, {u, -Pi, Pi}, {v, -3, 3}] Show[g1, g2, PlotRange -> {{-3, 3}, {-3, 3}, {-3, 3}}]
10)用命令ParametricPlot3D 作出圆柱面221x y +=和圆柱面221x z +=相交所成的空间曲线在第一封内的图形.
g1=ParametricPlot3D[{Sin[u],Cos[u],v},{u,-Pi,Pi},{v,- 3,3}];
g2=ParametricPlot3D[{Sin[u],v,Cos[u]},{u,-Pi,Pi},{v,-3,3}];
Show[g1,g2,PlotRange →{{0,3},{0,3},{0,3}}]
11)用命令ParametricPlot3D 作出球面22222x y z ++=和柱面22(1)1x y -+=相交所成的空间曲线的图形
g3=ParametricPlot3D[{2*Sin[u]*Cos[v],2*Sin[u]*Cos[v],2*Cos[u]},{u,-Pi,Pi},{v,-Pi,Pi}];
g4=ParametricPlot3D[{1+Cos[u],v,Sin[u]},{u,-Pi,Pi},{v ,-Pi,Pi}]
Show[g3,g4,PlotRange →{{-3,3},{-3,3},{-3,3}}]
12)用动画演示由椭圆
22
1 (0)
49
y z
y
+=≥绕z轴旋转产生旋转椭圆面的过程.。
