锐角三角比的意义(一)
锐角三角比讲义..
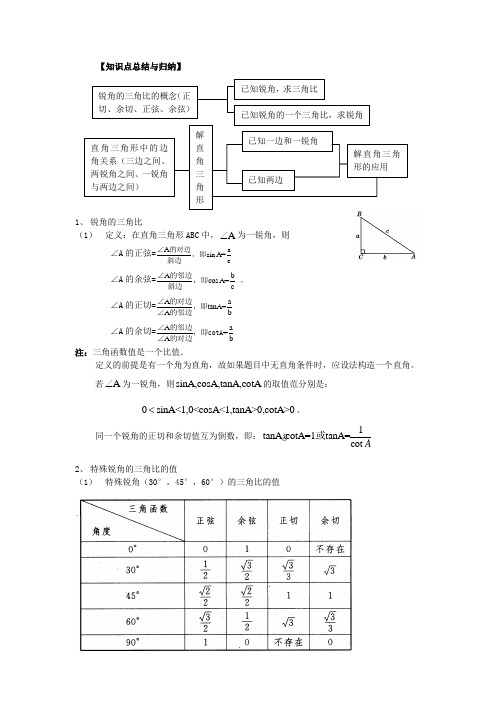
【知识点总结与归纳】1、 锐角的三角比(1) 定义:在直角三角形ABC 中,A ∠为一锐角,则∠A 的正弦=A a sin A=c∠的对边,即斜边∠A 的余弦=A b cos A=c∠的邻边,即斜边,∠A 的正切=A a tanA=A b∠的对边,即∠的邻边∠A 的余切=A a =A b∠的邻边,即cotA ∠的对边注:三角函数值是一个比值.定义的前提是有一个角为直角,故如果题目中无直角条件时,应设法构造一个直角。
若A ∠为一锐角,则sinA,cosA,tanA,cotA 的取值范分别是:0sinA<1,0<cosA<1,tanA>0,cotA>0<。
同一个锐角的正切和余切值互为倒数,即:1tanA cotA=1tanA=cot A或2、 特殊锐角的三角比的值(1) 特殊锐角(30°,45°,60°)的三角比的值锐角的三角比的概念(正切、余切、正弦、余弦)已知锐角,求三角比已知锐角的一个三角比,求锐角 直角三角形中的边角关系(三边之间、两锐角之间、一锐角与两边之间) 解直角三角形已知一边和一锐角已知两边解直角三角形的应用(2) 同角,互余的两角多的三角比之间的关系: 倒数关系:1tanA=cot A平方关系:22sin A+cos A=1 积商关系:sin cos tanA=,cot cos sin A AA A A= 余角和余函数的关系:如果090A B ∠+∠=,那么sinA=cosB, tanA=cotB (正弦和余弦,正切和余切被称为余函数关系)。
注意:求锐角三角比的值问题(1) 在直角三角形中,给定两边求锐角的三角比,关键是搞清某锐角的“对边”“邻边”,掌握三角比的定义。
(2) 给出锐角的度数,求这个锐角的三角比特殊锐角,一般情况下,使用精确值;在实际应用中,根据问题要求处理。
求非特殊锐角的三角比的值,使用计算器或查表求值。
锐角三角比的意义

B
BC 2
tan A
.
AC 3
tan B AC 3
C
A
BC 2
B
当直角三角形的一个锐角的大小
确定时,这个锐角的邻边与对边 a
c
的比值也是确定的。
C
b
A
我们把直角三角形中一个锐角的邻边与对边的比
叫做这个锐角的余切(cotangent)。
如图,锐角A的余切记作cotA,这时
cot
A
锐角A的邻边 锐角A的对边
在Rt△_____中,∠B的邻边是BD. (3) ∠ACD的邻边是___________,
∠BCD的对边是___________。 C
A
D
B
2、在RtABC中,C 90,如果将这个三角形的各边 扩大2倍后得到ABC,那么tan A与tan A的关系是()
(A)tan A 2 tan A (B)tan A 2 tan A (C)tan A tan A
B1C1 AC1 ,B1C1 AC1 B2C2 AC2 B3C3 AC3
C3 C2 C1
A
B1C1 B2C2 B3C3
AC1 AC2 AC3
结论1:如果给定直角三角形的一个锐角,那
么这个锐角的对边与邻边的长度的比值就是一
个确定的数。
锐角A的对边 锐角A的邻边
一个确定的值
问题2:当直角三角形中一个锐角的大小变化时,
鹿鸣学校 张仲炎
直角三角形
角的关系:有一个角是直角、两锐角互余
边的关系:两条直角边的平方和等于斜边的平方 (勾股定理)
A 边与角的关系:含30°角的直角三角形 含45°角的直角三角形
b
c
C
a
锐角三角比的意义

儒洋教育学科教师辅导讲解锐角A 的对边()及邻边()的比叫做锐角A 的正切,记作。
如图△中,∠900,baAC BC A A A ===的邻边锐角的对边锐角tan锐角A 的邻边()及对边()的比叫做锐角A 的余切,记作。
如图△中,∠900,abBC AC A A A ===的对边锐角的邻边锐角cot锐角A 的对边()及斜边()的比叫做锐角A 的正弦,记作。
如图△中,∠900,caAB BC A A A ===的斜边锐角的对边锐角sin 锐角A 的对边()及斜边()的比叫做锐角A 的余弦,记作。
如图△中,∠900,cb AB AC A A A ===的斜边锐角的邻边锐角cos在直角三角形中,锐角A 的正切()、余切()、正弦()、余弦()统称为锐角A 的三角比,简称三角比。
注意:定义中应该注意的几个问题:1、, 是在直角三角形中定义的,∠A 是锐角(注意数形结合,构造直角三角形).2、, 是一个完整的符号,表示∠A 的正切,习惯省去“∠”号.3、,是一个比值.注意比的顺序,且,均>0,无单位.4、, 的大小只及∠A 的大小有关,而及直角三角形的边长无关.5、角相等,则其三角函数值相等;两锐角的三角函数值相等,则这两个锐角相等.三、例题讲解:例1、(1)在△中,∠90°,178,求、、、?(2)在△中,∠90°,6,,求①的长;②、、? (3)若α为锐角,且,求α、α、α?相关练习:1、求出图6-4所示的△中的、和、的值.2、△中,∠900,12,5,求:,,,的值。
3、△中,∠900,9,7,求:,,,的值。
例2:在△中,∠90°,12,7,求:(1) 和的值(2)和的值结论:①同一锐角的正切及余切互为倒数,即:或tanA cotA1•=②两个互余的锐角中,一锐角的正切等于它的余角的余切。
即:若∠∠90°,那么,思考:∠A为锐角,则、、、的值的范围。
B锐角三角比的意义及概念

锐角 A的邻边 锐角A的对边
AC BC
b a
锐角 A 的对边(BC)与斜边(AB)的比叫做锐角 A 的正弦,记作 sinA。
如图
Rt⊿ABC
中,∠C=900, sin
A
锐角A的对边 锐角A的斜边
BC AB
a c
锐角 A 的对边(BC)与斜边(AB)的比叫做锐角 A 的余弦,记作 cosA。
如图 Rt⊿ABC 中,∠C=900, cos A
4.△ABC 中,∠C=90°,AB=c,AC=b,BC=a,则 cosA·tanA=______. 5.若三角形三边长的比为 5:12:13,则此三角形最小内角的正切值为______. 6.在△ABC 中,若∠C=90°,∠B=2∠A,则 cosA 等于( )
A. 3 2
B. 1 2
C. 3
D. 3 3
锐角A的邻边 锐角A的斜边
AC AB
b c
在直角三角形中,锐角 A 的正切(tanA)、余切(cotA)、正弦(sinA)、余弦(cosA)统称为锐角 A 的三角比,
简称三角比。明确:
(1) 0<sina<1,0<cosa<1.
(2)一般地,在 Rt△ABC 中, 当∠C=90°时,sinA=cosB,cosA=sinB,tanA·tanB=1
A
1题图 C
B
B 的正弦=___________=___________.
c a
2.ABC 中,C=90,设 A、B、C 的对边分别是 a、b、c,A 的三角比(用 a、b、c 表示): A
b
C
sinA=___________cosA=___________tgA=___________ctgA=_____
锐角三角比的意义

儒洋教育学科教师辅导讲义课 题 锐角三角比的意义教学目标1、理解锐角的正切、余切、正弦、余弦的概念;2、能正确使用锐角的正切、余切、正弦、余弦的符号语言;3、培养观察、归纳、总结数学问题的能力。
教学内容一、新课讲解:1、操作:(1)任作锐角∠。
(2)在上任取B 1、B 2、B 3,分别过B 1、B 2、B 3作的垂线。
垂足为C 1、C 2、C 3。
(3)量出B 1C 1和1,B 2C 2和2,B 3C 3和3的长度,并计算出111B C AC ,222B CAC ,333B C AC 的值。
2、探究:由以上操作可得到:△1C 1、△2C 2、△3C 3。
显然有1C 12C 23C 3,于是可得:331122123B C B C B CAC AC AC ==3、结论:在放大和缩小时,当锐角A 的大小固定不变后,无论△的边长怎么变化,两条直角边的比值总是不变的。
大写字母C 表示△的直角,小写字母a 表示∠A 的对边,b 表示∠B 的对边,c 表示斜边。
(如上图) 同理,通过分析可知在放大和缩小时,当锐角A 的大小固定不变后, 无论△的边长怎么变化,直角边与斜边的比值总是不变的。
二、知识要点:锐角A 的对边()与邻边()的比叫做锐角A 的正切,记作。
如图△中,∠900,baAC BC A A A ===的邻边锐角的对边锐角tan锐角A 的邻边()与对边()的比叫做锐角A 的余切,记作。
如图△中,∠900,abBC AC A A A ===的对边锐角的邻边锐角cot锐角A 的对边()与斜边()的比叫做锐角A 的正弦,记作。
如图△中,∠900,caAB BC A A A ===的斜边锐角的对边锐角sinCBC 1B 3B 2B 1C 3C 2AbacACB锐角A 的对边()与斜边()的比叫做锐角A 的余弦,记作。
如图△中,∠900,cbAB AC A A A ===的斜边锐角的邻边锐角cos在直角三角形中,锐角A 的正切()、余切()、正弦()、余弦()统称为锐角A 的三角比,简称三角比。
§25_1锐角三角比的意义(1)

25.1锐角三角比的意义(1)
普陀区课题组
教学目标:
1、经历锐角的正切、余切的概念的形成过程,感受该概念的建立是以相似三角形为基础的.
2、掌握锐角的正切和余切的定义,会根据直角三角形中两边的长求锐角的正切或余切的值.
教学重点和难点:
锐角的正切、余切的概念的形成过程及使用.
教学过程:
教师活动学生活动设计意图
一、复习引入
1、情境引入
小明站在离旗杆底部10米远处,目
测旗杆的顶部,视线与水平线的夹角为
34度,并已知目测高度为1米.然后他
很快就算出旗杆的高度了.你想知道小
明怎样算出的吗?
师:这是与锐角三角比相关的一个数
学问题,从这节课起我们就来学习锐角
三角比的相关知识.
2、复习
在Rt△ABC中,若∠C=90o,我们知道,
AB称作斜边,AC、BC称作直角边.
其中与∠A相对的直角边称为∠A的对
边,与∠A相邻的直角边称为∠A的邻
边.
C B
A
问1:∠B的对边是什么?∠B的邻边又是什么?
练一练(书本第63页1、2题)生答1:∠B的对边是AC,∠B的邻边
是BC.
学生完成
从学生的生
活实际出发,提出
问题,引出思考,
激发学习的积极
性.初步体会实际
问题数学化的过
程.。
第一讲 锐角三角比的意义

九年级上册数学教案锐角三角比的意义第一讲锐角三角比的意义知识框架1 .正切直角三角形中一个锐角的对边与邻边的比叫做这个锐角的正切(tangent).锐角A的正切记作tan A.tanA BC aAA AC b===锐角的对边锐角的邻边.2 . 余切直角三角形中一个锐角的邻边与对边的比叫做这个锐角的余切(cotangent).锐角A的余切记作cot A.cotA AC b AA BC a ===锐角的邻边锐角的对边3 . 正弦直角三角形中一个锐角的对边与斜边的比叫做这个锐角的正弦(sine).锐角A的正弦记作sin A.sinA BC aAAB c===锐角的对边斜边.4 .余弦直角三角形中一个锐角的邻边与斜边的比叫做这个锐角的余弦(cosine ).锐角A 的余弦记作cos A .cos A AC bA AB c===锐角的邻边斜边.5 .锐角的三角比一个锐角的正切、余切、正弦、余弦统称为这个锐角的三角比. 例题解析【例1】 在Rt ABC ∆中,90ACB ∠=︒,A ∠的对边是______,A ∠的邻边是______B ∠的对边是______,B ∠的邻边是______.【例2】 在Rt MNP ∆中,90MPN ∠=︒,PQ MN ⊥,垂足为点Q .(1) 在Rt MNP ∆中,M ∠的对边是______,M ∠的邻边是______;在Rt MPQ ∆中,M ∠的对边是______,M ∠的邻边是______.九年级上册数学教案锐角三角比的意义(2)在Rt∆____中,N∠的对边是MP;在Rt∆____中,N∠的邻边是NQ.(3)MPQ∠的邻边是______,NPQ∠的对边是______.【例3】在Rt MNP∆中,90MPN∠=︒,PQ MN⊥,垂足为点Q.(1)()() tanNPMMQ==.(2)PQQN=______,=MPPN______.(用正切或余切表示)【例4】在Rt ABC∆中,90C∠=︒,AC = 4,BC = 5,求tan A、cot A、tan B、cot B的值.【例5】在Rt ABC∆中,90C∠=︒,AC = 4,AB = 5,求tan A、cot A、tan B、cot B的值.【例6】矩形ABCD中,对角线AC、BD相交于点O,已知OA = 2,AB = 3,求tan OAD∠和cot ODC∠的值.【例7】已知正比例函数y=的图像上有一动点A,x轴上有一动点B,求tan AOB∠和cot AOB∠的值.【例8】已知,在Rt ABC∆中,90C∠=︒,BC = 9,tan A = 34.求:(1)AB的长;(2)tan B的值.【例9】在Rt MNP∆中,90MPN∠=︒,PQ MN⊥,垂足为点Q.(1)()() sinNPMMP==.(2)PQPN=______,=MQMP______.(用正弦或余弦表示)【例10】在Rt ABC∆中,90C∠=︒,AC = 4,AB = 5,求sin A,cos A,sin B,cos B的值.【例11】在直角坐标平面内有一点P(2,3).求OP与x轴正半轴的夹角α的正弦和余弦的值.【例12】已知,在Rt ABC∆中,90C∠=︒,BC = 9,sin A =34.求:(1)AB的长;(2)sin B的值.【例13】已知,在Rt ABC∆中,90C∠=︒,sin A =23,求sin B的值.【例14】在Rt ABC∆中,90C∠=︒,AB = 5,BC = 4,求A∠的四个三角比的值.九年级上册数学教案 锐角三角比的意义【例15】 在Rt ABC ∆中,90C ∠=︒,BC = 3,tan A =34,求B ∠的四个三角比的值.【例16】 在Rt ABC ∆中,90C ∠=︒,sin B =34,求sin A 、cos A 、tan A 和cot A . 【例17】在Rt ABC ∆中,90C ∠=︒,AB = 13,BC = 12,AC = 5,求sin A 、cos A 、tan A和cot A .【例18】 已知等腰ABC ∆中,底边BC = 20 cm ,面积为40 cm 2,求sin B 和tan C .【例19】在Rt ABC ∆中,90ABC ∠=︒,BD ⊥AC ,若AB = 9,BC = 12,求sin A 、cos α、tan β、cot C 的值.【例20】 在Rt ABC ∆中,90C ∠=︒,点D 在边BC 上,AD = BD = 5,4sin 5ADC ∠=, 求cos ABC ∠和tan ABC ∠的值.【例21】在直角坐标平面内有一点A(3,1),点A与原点O的连线与x轴正半轴的夹角为α,求sinα、cosα、tanα和cotα.【例22】已知一次函数y = 2x-1与x轴所夹的锐角为α,求tanα和sinα的值.【例23】在平面直角坐标系内,O为原点,点A的坐标为(10,0),点B在第一象限内,BO = 5,3sin5BOA∠=.求:(1)点B的坐标;(2)cos BAO∠的值.【例24】直角三角形纸片的两直角边长分别为6、8,现将ABC∆如图那样折叠,使点A 与点B重合,折痕为DE,求sin CBE∠的值.【例25】直角三角形纸片的两直角边长分别为6、8,现将ABC∆如图那样折叠,使点A 与点B重合,折痕为DE,求sin CBE∠的值.九年级上册数学教案 锐角三角比的意义【例26】 在平行四边形ABCD 中,AB = 10,B ∠为锐角,sin B =45,1tan 2ACB ∠=, 求AD 、AC 的长.【例27】 在ABC ∆中,AB = 20,BC = 21,AC = 13,求ACB ∠的四个三角比的值.【例28】 已知ABC ∆中,sin A =513,tan B = 2,且AB = 29.求ABC ∆的面积.【例29】 在梯形ABCD 中,AD // BC ,AB ⊥AD ,对角线AC 、BD 相交于点E ,BD ⊥CD ,AB = 12,4cot 3ADB ∠=,求:(1)DBC ∠的余弦值;(2)DE 的长.【例30】 在ABC ∆中,90ACB ∠=︒,CD ⊥AB 于点D ,DCB α∠=,若AD : BC = 16 : 15,求sin α、cot α的值.【例31】 在等腰Rt ABC ∆中,90BAC ∠=︒,已知A (1,0),B (0,3),M 为BC课堂练习题【习题1】已知,在Rt ABC∆中,90C∠=︒,AB = 5,AC = 4.则:(1)sin A = ______,cos A = ______,tan A = ______,cot A = ______;(2)sin B = ______,cos B = ______,tan B= ______,cot B = ______.【习题2】在Rt ABC∆中,90C∠=︒,BC = 3,cos A =25,则AB = ______.【习题3】已知90A B∠+∠=︒,则sin A – cos B的值为______.【习题4】在ABC∆中,AB = BC = 20,AC=sin A和tan A的值.【习题5】在Rt ABC∆中,90C∠=︒,CD⊥AB于D.已知AC = 8,BC = 15.求DCA∠的三角比.【习题6】在Rt ABC∆中,90ACB∠=︒,sin A = 23,点D、E分别在边AB、AC上,DE⊥AC,DE = 2,DB = 9,求DC的长.【习题7】已知,锐角α的顶点在坐标原点,一边与x轴正半轴重合,另一边经过点P(1).求α的三角比.九年级上册数学教案 锐角三角比的意义BDCABFE 【习题8】 已知一次函数y =43x – 4的图像分别与x 轴、y 轴交于A 、B 两点,P 是线段AB 的中点,求sin POB ∠的值.【习题9】 ABC ∆中,90ACB ∠=︒,CD ⊥AB 于点D ,DCA α∠=,AD : BC = 7 : 12,求sin α、 tan α的值.【习题10】 如图,在梯形ABCD 中,AD // BC ,AD = AB = CD = 4,1cos 4C ∠=. (1)求BC 的长; (2)求tan ADB ∠的值.课后作业【作业1】 在Rt ABC ∆中,90C ∠=︒,A ∠、B ∠的对边是a 、b ,则ba( )A .A ∠的正弦值B .B ∠的余弦值C .A ∠的余切值D .B ∠的余切值【作业2】 在Rt ABC ∆中,90C ∠=︒,AB = c ,AC = b ,BC = a ,则下列关系不成立的是()A .b = c ·cos AB .a = b ·tan BC .c =cos aBD .tan A ·tan B = 1【作业3】 已知,在Rt ABC ∆中,90C ∠=︒,AB = 16,cos A =34. 求:(1)AC 的长;(2)tan B 的值.【作业4】 已知ABC ∆的三边a 、b 、c 满足a : b : c = 5 : 12 : 13,则sin A + cos A =______.【作业5】 若α是锐角,且1cot 3α=,则()cos 90α︒-=______.【作业6】 已知ABC ∆中,BC = 10,cos C =18,AC = 8.求AB 的长和B ∠的正切值.九年级上册数学教案 锐角三角比的意义用心 细心 耐心 恒心 11【作业7】 如图,在ABC ∆中,AB = BC = 10,AC =sin B 和tan B 的值.【作业8】 在Rt ABC ∆中,90C ∠=︒,AC = 8,BC = 6,CD 是斜边AB 上的高.若点E 在线段DB 上,联结CE ,24sin 25AEC ∠=.求CE 的长.【作业9】 已知ABC ∆中,C ∠是锐角,BC = a ,AC = b .求证:1sin 2ABC S ab C ∆=.【作业10】 已知,在平面直角坐标系内有A 、B 、C 三点,点A 的坐标为(2,1),点B的坐标为(1,4),点C 的坐标为(8,3),求sin ACB ∠和tan ABC ∠的值.。
沪教版九年级上册数学25.1-25.2 锐角的三角比

25.1-25.2锐角三角比的意义及求值【学习目标】1、通过实验、观察、探究、交流、猜测等数学活动,探索锐角三角比的意义。
2、理解锐角三角比的意义,记住三角比的符号,会进行三角比的文字语言与符号语言的转化。
3、会求直角三角形中指定锐角的三角比。
4、应用锐角三角比的意义及运用特殊锐角三角比值进行计算。
【主要概念】【一】锐角的三角函数的意义【1】正切的概念在Rt△ABC中,∠C=90°,我们把锐角A的对边与邻边的比,叫做∠A的正切,记作tanA.【2】正弦和余弦的概念如图,在Rt△ABC中,∠C=90°,锐角A的对边与斜边的比叫做∠A的正弦,记作sinA,即锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA,即【3】三角函数的概念:在直角三角形中,锐角A 的正切(tanA)、正弦(sinA)、余弦(cosA),都叫做∠A 的三角函数.【二】同角的三角函数之间的关系 【1】平方关系:sin 2α+cos 2α=1【2】商数关系:【三】互余的两角的关系任意锐角的正弦值等于它的余角的余弦值,任意锐角的余弦值等于它的余角的正弦值,任意锐角的正切值与它的余角的正切值的积等于1.即若A+B=90°,则sinA=cosB ,cosA=sinB ,tanA·tanB=1.【四】特殊锐角的三角函数值0° 30°45°60°90° sinA1cosA 1tanA1—典型例题:例1、在Rt ⊿ABC 中,∠C=900,AC=3,BC=2,求tanA 和tanB 的值. 解:在Rt ⊿ABC 中,∵AC=3,BC=2∴tanA=32=AC BCtanB=23=BC AC .分析:(1)要求sinα与cosα的关系的值,而已知tanα的值,故可通过来求值.A B C(2)已知tanα的值,也可通过,把要求的式子的分子,分母同时除以cos 2α转化成关于tanα的关系,这样便可求出结论.点评:在进行三角函数有关计算时,常利用有关公式进行变换.例3、在Rt ⊿ABC 中,∠C=900,BC=4,AB=5,求cotA 和cotB 的值. 解:在Rt ⊿ABC 中,由勾股定理得 AB 2=AC 2+BC 2 ∵BC=4,AB=5, ∴AC=3452222=-=-BC AB .∴cotA=43=BC AC cotB=34=AC BC . 例4、在Rt △ABC 中,∠C=90°,若,求cosB ,tanB 的值.分析:本题主要考查锐角三角函数的定义,结合图形求解可化繁为简,迅速得解. 解:如图,设BC=3m ,则AB=5m ,AB C例5、如图所示,已知AB是⊙O的直径,CD是弦,且CD⊥AB,BC=6,AC=8,则sin∠ABD的值是()分析:因为AB是⊙O的直径,所以∠ACB=90°.因为BC=6,AC=8,所以AB=10.因为∠ABD=∠ACD=∠ABC,所以在Rt△ACB中,故正确答案为D.答案:D例6、计算分析:这是一组有关特殊角三角函数值的计算题,计算中最关键是将它们先化成具体的数值,同时还要应用其它一些知识帮助求值,如(1)注意分母有理化,(2)应掌握整数指数幂的意义.解:点评:学过锐角三角函数后,特殊角的三角函数的计算是常考不衰的内容,做这类题主要分两步:(一)代入;(二)计算.因此,特殊角的三角函数值必须牢记.例7、若α为锐角且sinα>sinβ,那么()A.tanα>tanβB.tanα<tanβC.tanα=tanβ D.tanα、tanβ大小关系不确定例8、求适合下列各式的锐角α.点拨:所有锐角三角函数值都是正数,而且正弦和余弦值都不大于1,不符合条件的三角函数值应舍去.例9、如图,在△ABC中,∠A=30°,∠B=45°,AC=4,求BC的长.分析:题中有30°,45°特殊角,想把它们放到直角三角形中,利用三角函数来解题.点评:(1)在作高线构造直角三角形时,一般不过特殊角的顶点作垂线,这样便于利用特殊角解题.(2)有些简单的几何图形可分解为几个直角三角形的组合,从而利用三角函数的定义求解.例10、如图所示.在四边形ABCD中,AB=2,CD=1,∠A=60°,∠D=∠B=90°,求此四边形ABCD的面积.分析:由已知∠B=90°,∠A=60°这两个条件想到延长BC,AD,使它们相交,构成直角三角形.例11、在矩形ABCD中DE⊥AC于E,设∠ADE=α,且,AB=4,求AD.分析:在矩形中AB=DC=4,可证∠α=∠1,于是条件转移到△DCE中来了,求出DE.解:在矩形中AB=DC=4,∠2+∠α=90°又DE⊥AC,∠1+∠2=90°∴∠1=∠α点评:注意把条件集中到一起.例12 、如图Rt △ABC 中,∠C =90°,AC =3,BC =4.求:sin A ,cos A ,tanB ,cotB 的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
锐角三角比的意义(一)
古松学校顾卫标教学设计说明
一、教材的地位与作用
本节课是学生在学习了直角三角形和相似三角形有关性质后,通过研究直角三角形中的边、角关系建立锐角三角比的概念。
锐角三角比是初三数学中的重要数学槪念,概念的形成不仅为研究直角三角形提供了有用的工具,而且在数学学习与生活生产实际中都有广泛应用。
二、教学内容的编排
1.概念的形成
由于本课时是锐角三角比概念形成的第一节课,主要教学目标是掌握锐角的正切、余切的槪念及相互关系,因此我把锐角正切、余切的概念形成作为本节课的重点及难点。
在问题解决过程中不断反馈和分析信息,做到适时点拨,引导学生自己从问题解决过程中提炼岀超越问题情景的思想,并在前一章“相似形”所学知识的基础上寻找岀新知识的生长点,即直角三角形一个锐角大小确泄后,其直角边的比值也确疋,从而建立起新的数学概念一角的正切、余切的概念,并让学生感知学习这两个概念的实际意义。
这样既能突出重点、难点,又能符合学生的普遍接受能力。
2.概念的应用
为了加强学生对锐角正、余切概念及相互关系的应用,本节课设计不同层次的例题和习题,并通过归纳和总结,帮助学生从知识到能力的迁移,进一步优化知识结构。
此外,从总体上这两组题目的内容是由注入深、循序渐进的。
三、教学方法
本节课的课堂教学主要采用问题解决教学的方法。
在槪念学习时并没有把知识宜接传授给学生,而是让学生从问题解决过程中去发现、去探求,并通过教师适当、必要的引导对结论进行归纳。
在教学过程中还运用各种手段,从各个方而来帮助学生理解,使形象思维与抽象思维充分地、有机地结合起来,旨在学生对新概念的现解更深入、更准确、更有效。
四、教学策略
1.以问题评价为主要形式,及时调控教学进程。
在教学过程的各环节中,通过设置富有开放性、挑战性且层层深入的问题来址壺学生思维进程,教师通过学生回答问题的积极性、主动性、正确性来灵活调控教学进程。
2.以多种训练形式为途径,增加教学反馈的层而。
通过多种训练形式,如口答、板演及学生间、师生间交流,可使不同层次的学生的学习情况反馈给教师,针对反馈情况教师作启发性指导。
一、教学目标:
1.知识目标:
(1)掌握锐角的正切、余切概念及相互关系。
(2)初步应用锐角的正切、余切概念求锐角的正切、余切值。
2.能力目标:
(1)在探究锐角正切、余切的概念中,培养学生发散性思维。
(2)帮助学生从数学知识向能力迁移,优化知识结构。
二、教学重点、难点:
锐角的正切、余切的概念、概念的形成过程及苴初步应用。
三、教学过程
教学内容
教师 学生
①任意两个等腰三角形是否一立相似? ② 任意两个直角三角形是否一立相似? ③ 任意两个等腰直角三角形是否一左相似?等腰直角三 角形中两直角边之比为多少?这与等腰直角三角形的大小 有关系吗? ④ 任意两个有一个锐角为30。
的直角三角形是否一泄相 似? 30。
角所对的直角边与另一直角边(即30。
角的邻边)之 比为多少?这与直角三角形的大小有关系吗? 二、新知讲解 初步形成概念:直角三角形中,一个锐角所对的宜 角边、所邻的直角边之比值与直角三角形的大小无关。
dG _ B 2C 2 _ AC }
AC 2 AC 3 锐角A 的正切和余切: 如图,RtAABC 中,ZC=90° , ZA 的对边(BC ) 与ZA 的邻边(AC )的比值叫做ZA 的正切,用tgA 表 一 nn 乙4的对边 BC a
依次提问
注:(1)锐 角A 的正切 必须在含 A
的直角三角 形中获得:
(2)tg A 是锐角A
的 正切表示, 它是一个整 体,绝不能 分开:
学生口答
学生自行 探究
口答
例 1・在 RtAABC 中,ZC=90°, AC=12, BC=7,
求 tgAx ctgA 、tgB 和 ctgB 的值。
三.巩固练习
1.如图:AABC 和APQR 都是直角三角形,ZC=ZR= 90°, AC=7, BC=5, PQ=5, PR=3
求(1) tgA, ctgB (2) tgP, ctgQ o
2.如图:AABC 是直角三角形,ZC = 90% D 、E 在BC
上,AC=4, BD=5, DE=2, EC=3, ZABC=a, ZADC=p,
教学内容 同样在直角三角形中,一个锐角A 确立后,此角的 邻边与其对边的比也是一个确左的值,我们称此比值为 锐角A 的余切,用ctgA 表示, 教师 学生 学生阅读 走义并识
即:d 憎二竺/ 上4
的对边
BC a 锐角A 的正切和余切的关系;
提问
记锐角的 正切和余
切的表示 方法
板书
口答
ZAEC=yo 求:
四.拓展训练
例2・如图,Z\ABC 中,AD丄BC 于D, AD=4, BD=6, CD=2,求ctgC, tgB 的值。
例3・在平而直角坐标系内有一点P(3, 4),求OP与x
五.回顾小结
1.本节课的主要知识内容:锐角A的正切和余切。
,
2.锐角A的正切和余切的应用。
六、布置作业
1・如图,在RtAABC 中,ZC = 90° , CD丄AB,教师归纳总学生自行
解决
口答
教学内容
教师学生
分析、归纳
计算求值
师生共同
小结。
