锐角的三角比
锐角三角比讲义..
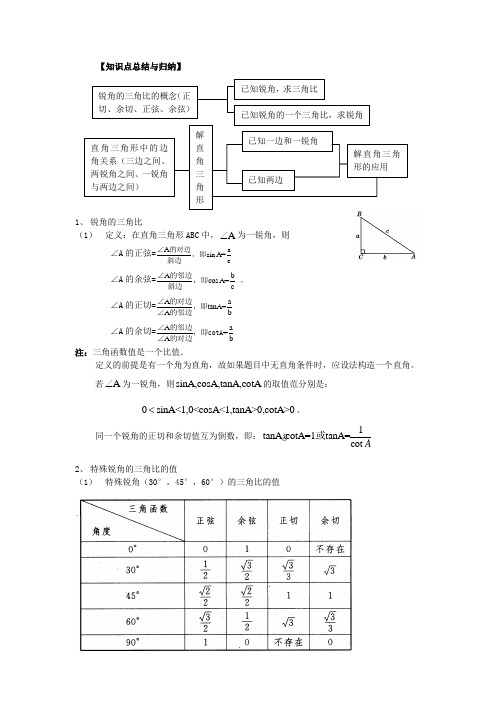
【知识点总结与归纳】1、 锐角的三角比(1) 定义:在直角三角形ABC 中,A ∠为一锐角,则∠A 的正弦=A a sin A=c∠的对边,即斜边∠A 的余弦=A b cos A=c∠的邻边,即斜边,∠A 的正切=A a tanA=A b∠的对边,即∠的邻边∠A 的余切=A a =A b∠的邻边,即cotA ∠的对边注:三角函数值是一个比值.定义的前提是有一个角为直角,故如果题目中无直角条件时,应设法构造一个直角。
若A ∠为一锐角,则sinA,cosA,tanA,cotA 的取值范分别是:0sinA<1,0<cosA<1,tanA>0,cotA>0<。
同一个锐角的正切和余切值互为倒数,即:1tanA cotA=1tanA=cot A或2、 特殊锐角的三角比的值(1) 特殊锐角(30°,45°,60°)的三角比的值锐角的三角比的概念(正切、余切、正弦、余弦)已知锐角,求三角比已知锐角的一个三角比,求锐角 直角三角形中的边角关系(三边之间、两锐角之间、一锐角与两边之间) 解直角三角形已知一边和一锐角已知两边解直角三角形的应用(2) 同角,互余的两角多的三角比之间的关系: 倒数关系:1tanA=cot A平方关系:22sin A+cos A=1 积商关系:sin cos tanA=,cot cos sin A AA A A= 余角和余函数的关系:如果090A B ∠+∠=,那么sinA=cosB, tanA=cotB (正弦和余弦,正切和余切被称为余函数关系)。
注意:求锐角三角比的值问题(1) 在直角三角形中,给定两边求锐角的三角比,关键是搞清某锐角的“对边”“邻边”,掌握三角比的定义。
(2) 给出锐角的度数,求这个锐角的三角比特殊锐角,一般情况下,使用精确值;在实际应用中,根据问题要求处理。
求非特殊锐角的三角比的值,使用计算器或查表求值。
《求锐角的三角比的值》 讲义

《求锐角的三角比的值》讲义一、锐角三角比的定义在直角三角形中,锐角的三角比包括正弦(sin)、余弦(cos)、正切(tan)。
正弦(sin)等于锐角的对边与斜边的比值;余弦(cos)等于锐角的邻边与斜边的比值;正切(tan)等于锐角的对边与邻边的比值。
例如,在一个直角三角形 ABC 中,∠C 为直角,∠A 为锐角,其对边为 a,邻边为 b,斜边为 c。
那么,sin A = a / c,cos A = b / c,tan A = a / b。
二、特殊锐角的三角比值我们先来了解一些特殊锐角(30°、45°、60°)的三角比值,这些是需要大家牢记的。
1、 30°角对于 30°角的直角三角形,假设斜边为 2,对边为 1,根据勾股定理可得邻边为√3。
所以,sin 30°= 1 / 2,cos 30°=√3 / 2,tan 30°=√3 / 3。
2、 45°角在等腰直角三角形中,两个直角边相等,假设直角边为 1,斜边为√2。
则 sin 45°= cos 45°=√2 / 2,tan 45°= 1。
3、 60°角与30°角相对应,60°角的直角三角形中,假设斜边为2,邻边为1,对边为√3。
所以,sin 60°=√3 / 2,cos 60°= 1 / 2,tan 60°=√3。
三、利用三角函数定义求三角比值当已知直角三角形的边长时,我们可以直接根据三角比的定义来求出相应锐角的三角比值。
例如,在直角三角形中,∠C 为直角,∠A 为锐角,已知∠A 的对边为 4,邻边为 3,斜边为 5。
则 sin A = 4 / 5,cos A = 3 / 5,tanA = 4 / 3。
再比如,一个直角三角形的斜边为 10,一个锐角的对边为 6,那么这个锐角的正弦值就是 6 / 10 = 3 / 5。
25.2 求锐角的三角比的值

第一节锐角的三角比§25.2求锐角的三角比的值教学目标(1)经历用几何方法探求特殊锐角的三角比的值的过程,掌握特殊锐角的三角比的值。
(2)会利用计算器求锐角的三角比的值,也能根据锐角的三角比的值求锐角的大小。
教学重点让学生经历用几何方法探求特殊锐角的三角比值的过程,掌握特殊锐角的三角比的值。
让学生学会利用计算器求锐角的三角比的值以及根据锐角的三角比的值求锐角的大小。
知识概要1.求特殊锐角的三角比的值,一般步骤是:(1)将直角三角形的某边长设为a,用a的代数式表示其他两边的长;(2)根据三角比的定义求值。
2.3.①如果两角互余,那么其中一个角的正切值(正弦值)与另一个角的余切值(余弦值)相等;②以030角、045角、060角为序,正切值和正弦值从小到大,余切值和余弦值则从大到小;③1=;④2为分母构成的数。
4.利用计算器求三角比的值时,先要选定“角度模式”(DEG)。
如果按MODE键一次屏幕未显示出“Deg Rad Gra”画面,那么反复按MODE键,直到显示为止。
然后按1键,计算器即进入了DEG 模式。
计算器的型号较多,应该参阅其使用说明书进行具体操作。
5.在DEG模式下,根据三角比函数名计算。
如:计算0sin25,按sin 2 5 =屏幕会显示结果。
如要计算余切,利用1cottanαα=求cotα。
如:计算0cot75,依次按1 ÷ tan 7 5 =即可;也可以依次按tan 7 5 =1x-=。
6.当角的大小涉及到“分”和(或)“秒”时,输入“度”“分”和“秒”后,必须按0’”键。
在求0sin2718''时,7.如果一个锐角的三角比的值,这个锐角就是确定的。
如果这个三角比的值不是特殊角的三角比的值,可以利用计算器计算锐角度数的近似值。
如:已知cot 1.3025α=,求锐角α。
可以依次按键: SHIFT tan -1 ( 1 ÷ 1.3025 ) = SHIFT 0’”经典题型解析(一)特殊锐角三角比例1.(1)计算:200020sin 45cos60tan 60cos 30-+⋅。
第六讲 锐角三角比(教师版)

第六讲 锐角的三角比知识要点:(一)锐角的三角比的定义:在Rt △ABC 中,若∠C =90o ,AB 称作斜边,AC 、BC 称作直角边.其中与∠A 相对的直角边称为∠A 的对边,与∠A 相邻的直角边称为∠A 的邻边. ∠A 、∠B 、∠C 所对的边分别记为a 、b 、c .邻边b对边aA①我们把锐角A 的对边与邻边的比叫做∠A 的正切(tangent ).记作tan A .tan A =ba=∠∠的邻边的对边A A②我们把锐角A 的邻边与对边的比叫做∠A 的余切(cotangent).记作cot A .cot A =的邻边的对边∠∠A A =ba③我们把锐角A 的对边与斜边的比叫做这个锐角的正弦(sine ).记作A sin .caA A A =∠∠=斜边的对边sin④我们把锐角A 的邻边与斜边的比叫做这个锐角的余弦(cosine ).记作A cos .cA A A bcos =∠∠=斜边的邻边(二)特殊角三角比的值:22sin cos 1,tan cot 1αααα+==(三)解直角三角形的定义:由直角三角形中除直角外的两个已知元素,求出所有未知元素的过程,叫做解直角三角形. 1.已知Rt △ABC 中,∠C =90°,∠A=45o ,设BC=a ,根据含45°角的直角三角形三边长之间的关系,求45°角的正切、余切、正弦、余弦值. 解:1, 1,22,222.在直角坐标平面中有一点P (3,4).求OP 与x 轴正半轴的夹角α的正切、正弦、和余弦的值.解:作PQ ⊥x 轴于点Q ,则∠OQP =900.由点P 的坐标为(3,4)得OQ =3,QP =4.则OP =5.∴tan α=43=PQ OQ ,sin α=45=PQ OP ,cos α=35=OQ OP . 3.计算:222sin 60cos60tan 604cos45--o oo o解:原式()2231222342⎛⎫⨯- ⎪⎝⎭=-⨯3122322322-==--322=+ 4.在Rt △ABC 中,∠C =90°,BC =6,3sin 4=A .求:(1)AB 的长 ;(2)sin B 的值.解:(1)在Rt △ABC 中,∠C =90°,∵sin =BC A AB ∴sin =BC AB A 又36,sin ,4==BC A ∴6834==AB(2)由勾股定理,得27=AC ∴277sin ===AC B AB 5. 如图,已知在∆ABC 中,点D 是BC 边上一点,⊥DA AB ,12=AC , 7=BD ,9=CD . (1)求证:∆ACD ∽∆BCA ;(2)求tan ∠CAD 的值.解:(1)证明:∵7BD =,9CD =,∴16BC =,∵12AC =,∴34CD AC =,34AC BC =,∴CD ACAC BC=,∵C C ∠=∠,∴ACD ∆∽BCA ∆.(2)∵ACD ∆∽BCA ∆,∴CAD B ∠=∠,34AD CD AB AC ==, ∵DA AB ⊥,∴3tan 4AD B AB ==,∴3tan 4CAD ∠=.6.已知:ABC ∆中,090=∠C ,030=∠A ,求015tan 的值。
25.1 锐角三角比的意义

第一节 锐角的三角比§25.1锐角的三角比的意义教学目标(1)经历锐角三角比的概念的形成过程,获得从实际的数学问题中抽象出数学概念的体验。
(2)掌握锐角的三角比的定义,会根据直角三角形中两边的长求锐角的三角比的值。
(3)了解锐角的三角比的范围。
教学重点让学生经历锐角的正切概念的形成过程,掌握正切、余切的定义。
引进锐角的正弦和余弦,帮助学生掌握正弦和余弦的定义,了解三角比的含义和符号表示。
知识概要1.直角三角形中,一个锐角的对边与邻边的长度的比值随着这个锐角大小的变化而变化。
锐角的大小确定,则对边与邻边的比值唯一确定。
2.我们把直角三角形中一个锐角的对边与邻边的比叫做这个锐角的正切。
锐角A 的正切记作tan A , tan =A BC a A A AC b==锐角的对边锐角的邻边。
注:在ABC ∆中,,,A B C ∠∠∠的对边通常分别用,,a b c 表示。
在Rt ABC ∆中,090C ∠=,直角边BC 和AC 分别叫做A ∠的对边和邻边。
3.我们把直角三角形中一个锐角的邻边与对边的比叫做这个锐角的余切。
锐角A 的余切记作cot A , cot =A AC b A A BC a ==锐角的邻边锐角的对边。
根据正切与余切的意义,可以得到 1tan cot A A =。
在Rt ABC ∆中,090C ∠=,可知090A B ∠+∠=,cot tan B A =。
4.如果直角三角形的一个锐角是确定的,那么它的对边或邻边与斜边的比也是确定的。
我们定义: 直角三角形中一个锐角的对边与斜边的比叫做这个锐角的正弦。
直角三角形中一个锐角的邻边与斜边的比叫做这个锐角的余弦。
在Rt ABC ∆中,090C ∠=,锐角A 的正弦记作sin A ,这时 sin =A BC a A A AB c ==锐角的对边锐角的邻边; 锐角A 的余弦记作cos A ,这时 cos =A AC b A A AB c ==锐角的邻边锐角的邻边。
锐角三角比

锐角三角比复习1.定义:①正弦(sin)等于对边比斜边;②余弦(cos)等于邻边比斜边;③正切(tan)等于对边比邻边;④余切(cot)等于邻边比对边。
•注意:若角的大小不变,无论角所对的边如何变化,角的三角比恒不变。
2.关系:①锐角三角比中,tanA>0,cotA>0,0<sinA<1,0<cosA<1②在同一个三角形中,∠C=90°,∠A+∠B=90°,tanA=cotB,sinA=cosB③tanA×cotA=1,sinA²+cosA²=1,tanA= sinA/cosA,cotA= cosA/sinA④tanA>sinA,cotA>cosA,(锐角)∠A=∠B→sinA=sinB⑤sin(90°-α)=cosα,cos(90°-α)=sinα;tan(90°-α)=cotα,cot(90°-α)=tanα3.特殊锐角三角比的值:4.锐角三角函数值的变化情况:①锐角三角函数值都是正值②当角度在0°~90°间变化时,正弦值随着角度的增大(或减小)而增大(或减小);余弦值随着角度的增大(或减小)而减小(或增大);正切值随着角度的增大(或减小)而增大(或减小);余切值随着角度的增大(或减小)而减小(或增大)。
③当角度在0°≤∠A≤90°间变化时,0≤sinα≤1, 1≥cosA≥0。
当角度在0°<∠A<90°间变化时,tanA>0, cotA>0。
5.解直角三角形:①直角三角形中六个元素:三角三边。
②直角三角形可解条件:⑴已知:一角一边(除直角以外)⑵已知:两边(除直角以外)③直角三角形中边的关系:a²+b²=c²·注意:若已知的一个三角形不是直角三角形,则通常由已知元素来构造直角三角形,把它划归为解直角三角形。
锐角三角比讲义
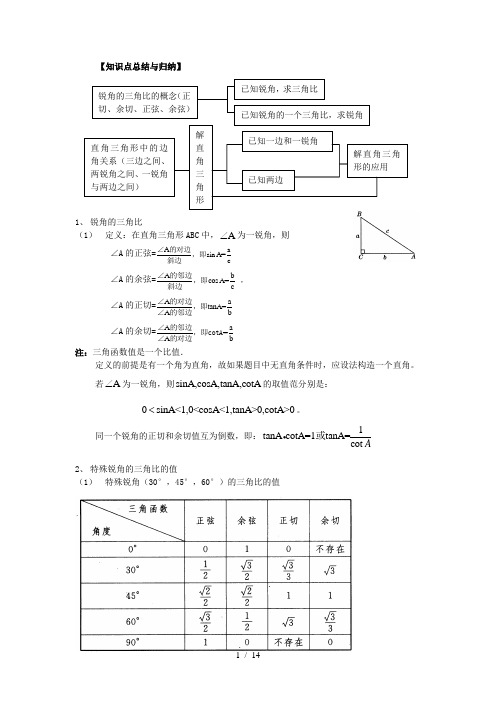
【知识点总结与归纳】1、锐角的三角比(1)定义:在直角三角形ABC中,A∠为一锐角,则∠A的正弦=A asin A=c∠的对边,即斜边∠A的余弦=A bcos A=c∠的邻边,即斜边,∠A的正切=A atanA=A b∠的对边,即∠的邻边∠A的余切=A a=A b∠的邻边,即cotA∠的对边注:三角函数值是一个比值.定义的前提是有一个角为直角,故如果题目中无直角条件时,应设法构造一个直角。
若A∠为一锐角,则sinA,cosA,tanA,cotA的取值范分别是:0sinA<1,0<cosA<1,tanA>0,cotA>0<。
同一个锐角的正切和余切值互为倒数,即:1tanA cotA=1tanA=cot A或2、特殊锐角的三角比的值(1)特殊锐角(30°,45°,60°)的三角比的值锐角的三角比的概念(正切、余切、正弦、余弦)已知锐角,求三角比已知锐角的一个三角比,求锐角直角三角形中的边角关系(三边之间、两锐角之间、一锐角与两边之间)解直角三角形已知一边和一锐角已知两边解直角三角形的应用(2) 同角,互余的两角多的三角比之间的关系: 倒数关系:1tanA=cot A平方关系:22sin A+cos A=1 积商关系:sin cos tanA=,cot cos sin A AA A A=余角和余函数的关系:如果090A B ∠+∠=,那么sinA=cosB, tanA=cotB (正弦和余弦,正切和余切被称为余函数关系)。
注意:求锐角三角比的值问题(1) 在直角三角形中,给定两边求锐角的三角比,关键是搞清某锐角的“对边”“邻边”,掌握三角比的定义。
(2) 给出锐角的度数,求这个锐角的三角比特殊锐角,一般情况下,使用精确值;在实际应用中,根据问题要求处理。
求非特殊锐角的三角比的值,使用计算器或查表求值。
(3) 当锐角不是直角三角形的内角,首先观察有否相等的锐角可代换,而且可代换的锐角含在某直角三角形中,如果没有可代换的相等的锐角,可作适当的垂线构建含有这个锐角的直角三角形。
锐角三角比公式

锐角三角比公式锐角三角比1. 什么是锐角三角比锐角三角比是三角函数中的一个概念,用于描述一个锐角的正弦、余弦和正切值。
在数学中,锐角是指小于90度的角。
锐角三角比可以帮助我们计算和描述锐角的各种属性。
2. 锐角三角比的相关公式下面是锐角三角比的几个常用公式:正弦(Sine)正弦值表示一个角度的对边与斜边的比值:sin(A) = 对边 / 斜边余弦(Cosine)余弦值表示一个角度的邻边与斜边的比值:cos(A) = 邻边 / 斜边正切(Tangent)正切值表示一个角度的对边与邻边的比值:tan(A) = 对边 / 邻边3. 示例解释为了更好地理解锐角三角比的概念和应用,我们来看几个示例。
示例 1假设有一个锐角三角形,其中角A的对边长度为5,邻边长度为12,斜边长度为13。
我们可以利用正弦、余弦和正切公式来计算角A 的锐角三角比值:sin(A) = 5 / 13 ≈cos(A) = 12 / 13 ≈tan(A) = 5 / 12 ≈示例 2现在假设有一个锐角三角形,其中角B的对边长度为7,邻边长度为24,斜边长度为25。
我们可以同样利用锐角三角比公式计算角B 的值:sin(B) = 7 / 25 =cos(B) = 24 / 25 =tan(B) = 7 / 24 ≈通过以上示例,我们可以看到锐角三角比可以帮助我们计算角度的各种属性,如角度的正弦、余弦和正切值。
这些值在许多数学和科学领域中都有广泛的应用,如物理、工程、地理等。
总结本文介绍了锐角三角比的概念和相关公式,并通过示例解释了如何计算锐角的正弦、余弦和正切值。
锐角三角比在数学中具有重要的应用价值,它可以帮助我们计算和描述锐角的各种属性。
在实际问题中,了解锐角三角比可以帮助我们更好地理解和解决各种角度相关的计算和测量问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
锐角的三角比
一、介绍
在数学中,三角比是指三角函数中的比值,用于描述三角
形的各个边与角之间的关系。
锐角是指小于90度的角,因此在本文中,我们将讨论关于锐角的三角比。
三角比一共有六个,分别是正弦(sin)、余弦(cos)、正切(tan)、余切(cot)、正割(sec)和余割(csc)。
这些三角比在数学
和物理等科学领域中都有广泛的应用,例如解决三角函数方程、测量角度和距离等。
二、正弦(sin)
在锐角三角形中,正弦表示三角形的对边与斜边之间的比值。
数学表达式如下:
sin(A) = 对边 / 斜边
其中,A表示锐角的大小。
正弦的取值范围是-1到1之间,当A接近0度时,正弦的值接近0;而当A接近90度时,正弦的值接近1。
三、余弦(cos)
余弦代表锐角三角形的邻边与斜边之间的比值。
数学表达式如下:
cos(A) = 邻边 / 斜边
同样地,余弦的取值范围也是-1到1之间。
在锐角三角形中,当A接近0度时,余弦的值接近1;当A接近90度时,余弦的值接近0。
四、正切(tan)
正切是锐角三角形中对边与邻边之间的比值。
数学表达式如下:
tan(A) = 对边 / 邻边
正切的取值范围是无穷,当A接近0度时,正切的值接近0;当A接近90度时,正切的值趋于无穷大。
五、余切(cot)
余切是锐角三角形中邻边与对边之间的比值。
数学表达式如下:
cot(A) = 邻边 / 对边
余切的取值范围也是无穷,当A接近0度时,余切的值趋
于无穷大;当A接近90度时,余切的值接近0。
六、正割(sec)
正割表示斜边与邻边之间的比值。
数学表达式如下:
sec(A) = 斜边 / 邻边
正割的取值范围是大于等于1的实数。
当A接近0度时,正割的值趋于无穷大;当A接近90度时,正割的值接近1。
七、余割(csc)
余割代表斜边与对边之间的比值。
数学表达式如下:
csc(A) = 斜边 / 对边
余割的取值范围也是大于等于1的实数。
当A接近0度时,余割的值接近无穷大;当A接近90度时,余割的值趋近于1。
八、总结
锐角的三角比是描述锐角三角形边和角之间关系的重要工具。
六个三角比都有其独特的特点,在不同的应用中起着重要作用。
正弦、余弦和正切是最常用的三角比,它们在三角函数方程的求解中特别重要。
对于同一个锐角,不同的三角比取值不同,这是因为它们对应的边长是不同的。
通过深入了解锐角的三角比,我们可以更好地理解三角形的性质和应用它们来解决各种数学和物理问题。
希望本文对于读者对锐角的三角比有了更清晰的认识。
