数学八年级下北师大版 2.5 一元一次不等式与一次函数课件2 (新版)北师大版
合集下载
北师大初中数学八年级下册一元一次不等式与一次函数PPT课件
甲商场的优惠条件是:第一台
按 原 报 价 收 费 , 其 余 每 台 优 惠 25
%。那么甲商场的收费y(元)
与所买电脑台数 x之间的关系式
是:
第4页/共8页
乙商场的优惠条件是:每台优惠20 %.那么乙商场的收费 y(元)与 买电脑台x数之间的关系式是:
(1)什么情况下到甲商场购 买更优惠?
(2)什么情况下到乙商场购 买更优惠?
归纳小结:
通过这节课得学习, 你有什么收获?
布置作业:
P23 习题1.7 (1、2)
第7页/共8页
感谢您的观看!
第8页/共8页
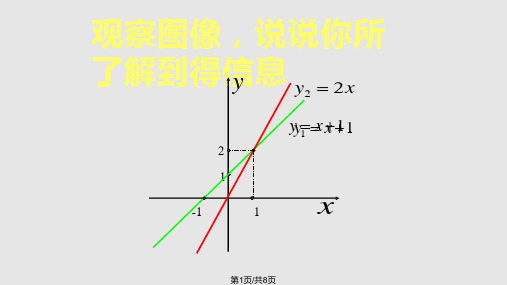
观察图像,说说你所 了解到得信y 息 y2 2x
yy1x x1 1
2
1
-1
1
x
第1页/共8页
1Байду номын сангаас某商品市场统一价为每件50 元,则所需费用 y (元)与所购商 品 x (件)之间的关系式为 2、甲商场打出“所有商品一律 优惠20%”,则所需费用 y (元) 与所购商品 x(件)之间的关系 式为
第2页/共8页
3、乙商场开展“买即赠”促销 活动:无论购买多少均送一件同 种商品(大件除外),则所需费 用y (元)与所购商品 x (件) 之间的关系式为 4、试想:在什么情况下,你会 选择甲商场?你能说明理由吗?
第3页/共8页
某学校计划购买若干台电脑,现 从两家商场了解到同一型号电脑 每台报价均为6000元,并且多买 有一定的优惠。
(3)什么情况下两家商场的 收费相同?
第5页/共8页
自编一体现一次函数、一元一 次不等式、一元一次方程联系的 应用题,由同伴解答。
关键词提示:1、移动公司;全球 通,月租20元,话费0.4元/分;神 州行,免月租,话费0.6元/分。 2、 拨号上网;甲种,信息费1.8元/时, 电话费1.2元/时;乙种,包月100 元,电话费1.2元第6页//共时8页
北师大版八年级下册数学2.5一元一次不等式与一次函数课件(共18张PPT)

如果图像是两条直线相交,那就看交点。
+ 习题2.6第51页第2,3,4题。
∴当y≤3时,x的取值范围为x≤1.
(解解(2方:2))程 当32kxxx=-x-27+-求常1=<b/1=20.0y数时.,=,也k,xy就=+k0是b≠的求0)当解k为(何k值,b时是,函数y=kx+b从的值“为函0. 数看图像”
-1 0 1 2 3 4 5 x
求y=kx+b的解(k,b是常数,k≠0)
(2)画出一次函数y=kx+b的图象。
解:当y=3求时,y=x=k1x+b的解(k,b (∴当3)y≤用3时函是,数x图常的象取数解值决,范以围k上为≠0三x≤)个1. 问题。
从“函数图像” 看
当函数y=kx+b的值等于0时,求 自变量x的值。
当函数y=kx+b的值大于或小于0 时,求自变量x的取值范围。
解x取:哪当些x=值-1时/2,时2,-x2-y5==01?
兄弟俩赛跑,哥-哥3先让弟弟跑9秒,A然(2后.5自,0己)才开始跑。 解∴不:等当式y=2-x3+时1≥,0的-x4=解2,集为x≥-1/2。
0 1 2 3 4-5 x
函数y=2x+1的图象如图所示,利用图象求:
x取哪些值时,2x-5=1?
+ 函数y=2x+1的图象如图所 示,利用图象求:
+ (2)不等式2x+1≥0的解 集;
+ 解:当x≥-1/2时,函数图 象在x轴的上方(包括x轴 上)
+ ∴不等式2x+1≥0的解集为 x≥-1/2。
y
3 2 1 -3 -2 -1 -10 -2 -3
八年级数学下册第2章一元一次不等式与一次函数pptx课件新版北师大版

(1)以 x(单位:元)表示标价总额, y(单位:元) 表示应支 付金额,分别就两家书店的优惠方式,求y 关于 x 的 函数表达式 .
感悟新知
解:甲书店应支付金额为 y 甲=0.8x.
知2-练
乙书店:当 x≤100 时,y 乙=x;
当 x>100 时,
y 乙=100+0.6(x-100)=0.6x+40.
2. 拓展
感悟新知
知1-讲
直线 y1=k1x+b1 与直线 y2=k2x+b2 的交点的横坐标即为 方程 k1x+b1=k2x+b2 的解; 不等式k1x+b1>k2x+b2(或 k1x+b1<k2x+b2)的解集就是直线 y1=k1x+b1 在直线 y2=k2x+b2 上(或下)方部分对应的 x 的取值范围 .
感悟新知
示例: 如图 2-5-1,直线 y1=k1x+b1 与 直线 y2=k2x+b2 交于点 P(a, b), 则方 程 k1x+b1=k2x+b2 的解为 x=a; 不等式 k1x+b1>k2x+b2 的 解集为 x>a ;不等式 k1x+b1<k2x+b2 的解集为 x<a.
知1-讲
感悟新知
感悟新知
解题秘方:紧扣两个函数的交点坐标和函数的图 象.根据函数图象直接确定不等式的 解集 .
知1-练
解:∵直线 y1=k1x 与直线 y2=k2x+b 交于点 A( 1, 2), ∴当 y1<y2 时, x 的取值范围是 x<1. 故不等式 k1x<k2x+b 的解集是 x<1.
感悟新知
解:甲书店应支付金额为 y 甲=0.8x.
知2-练
乙书店:当 x≤100 时,y 乙=x;
当 x>100 时,
y 乙=100+0.6(x-100)=0.6x+40.
2. 拓展
感悟新知
知1-讲
直线 y1=k1x+b1 与直线 y2=k2x+b2 的交点的横坐标即为 方程 k1x+b1=k2x+b2 的解; 不等式k1x+b1>k2x+b2(或 k1x+b1<k2x+b2)的解集就是直线 y1=k1x+b1 在直线 y2=k2x+b2 上(或下)方部分对应的 x 的取值范围 .
感悟新知
示例: 如图 2-5-1,直线 y1=k1x+b1 与 直线 y2=k2x+b2 交于点 P(a, b), 则方 程 k1x+b1=k2x+b2 的解为 x=a; 不等式 k1x+b1>k2x+b2 的 解集为 x>a ;不等式 k1x+b1<k2x+b2 的解集为 x<a.
知1-讲
感悟新知
感悟新知
解题秘方:紧扣两个函数的交点坐标和函数的图 象.根据函数图象直接确定不等式的 解集 .
知1-练
解:∵直线 y1=k1x 与直线 y2=k2x+b 交于点 A( 1, 2), ∴当 y1<y2 时, x 的取值范围是 x<1. 故不等式 k1x<k2x+b 的解集是 x<1.
北师大版数学八年级下学期一元一次不等式和一次函数教学课件2 共13页

y乙=4800x
1.什么情况下到甲店购买更优惠?
2.什么情况下到乙店购买更优惠?
3.什么情况下两店的收费相同? Nhomakorabea学而不思则罔●▂●思而不学则殆
9
华山两日游200元/人
甲旅行社
每人七五 折优惠
乙旅行社
一人免 费,其余 每人八折 优惠
我们有10~25人,该选
择哪家旅行社旅行社呢? 学而不思则罔●▂●思而不学则殆
10
每人七五
一人免费,其余每
折优惠
人八折优惠
解:设有x人参加旅游,甲旅行社收费y1 元,乙旅行社收费y2元,则
y1=200×0.75x, 即 y1=150x
y2=200×0.8(x-1) 即 y2=160x-160 由y1=y2,得150x=160x-160,解得x=16;
由y1>y2,得150x>160x-160,解得x<16;
陕西咸阳风轮中学 杨中平 7
新梦5300S电脑6000元/台
我店第一
台按原价受
只要买的
费,其余每
多,我店每台
台优惠25%
优惠20%
收买电费脑y甲台(元数)x与的购关
收费y乙(元)与购 买电脑台数x的关
系式是y甲=4500x学+而不1思5则罔0●0▂●思系而不学式则殆 是y乙=48008x
y甲=4500x+1500
y=2x-5 B(2.5,0)x
如果y=-2x-5,那
么当x取何值时, y>0?
A(0,-5) 学而不思则罔●▂●思而不学则殆
3
兄弟俩赛跑,哥哥让弟弟先
跑9米,自己才开始跑.已知每
秒跑4米,弟弟每秒跑3米.
北师大版数学八年级下册 《一元一次不等式与一次函数》课件

(2)取哪些值时,
− > ?
.
(3)取哪些值时, − < ?
(4)取哪些值时, − > ?
教学过程——新知探究
第二章 一元一次不等式与一元一次不等式组
知识点1 利用函数图像解一元一次不等式
图像法解一元一次不等式
我们先看问题(1),当取何值时,
− = ?
第二章 一元一次不等式与一元一次不等式组
知识点1 利用函数图像解一元一次不等式
图像法解一元一次不等式的应用
y
(3)−. + ≤
在函数图像上找到 = 的点,图像上纵坐标
为2 的点,其横坐标为1,
.
2
所以− + . ≤ 的解集是 ≥
(4)−
+ > 的解集是 <
.
对一元一次方程 − = 来说,解一元一次
方程可以看作当一次函数
= − 的函数值
.
等于0时,求出相应的自变量的值.
同样的对于 − > 来说,解一元一次不等式可
.
以看作当一次函数
= − 的值大于0时,求出
相应的自变量的取值范围.
教学过程——新知探究
第二章 一元一次不等式与一元一次不等式组
适.甲公司表示:快递物品不超过1kg的,收费12元;超过1kg,超过的
部分按单价2元/kg收费.
乙公司表示:快递物品不超过1kg的,收费10元;超过1kg,超过的部
分按单价4元/kg收费.
例如:小明要快递1.4kg的物品,选甲公司需付费12.8元,选乙公司需
付费11.6元.
设小明快递物品千克.
(1)请分别直接写出甲、乙两家快递公司快递该物品的费用y(元)
− > ?
.
(3)取哪些值时, − < ?
(4)取哪些值时, − > ?
教学过程——新知探究
第二章 一元一次不等式与一元一次不等式组
知识点1 利用函数图像解一元一次不等式
图像法解一元一次不等式
我们先看问题(1),当取何值时,
− = ?
第二章 一元一次不等式与一元一次不等式组
知识点1 利用函数图像解一元一次不等式
图像法解一元一次不等式的应用
y
(3)−. + ≤
在函数图像上找到 = 的点,图像上纵坐标
为2 的点,其横坐标为1,
.
2
所以− + . ≤ 的解集是 ≥
(4)−
+ > 的解集是 <
.
对一元一次方程 − = 来说,解一元一次
方程可以看作当一次函数
= − 的函数值
.
等于0时,求出相应的自变量的值.
同样的对于 − > 来说,解一元一次不等式可
.
以看作当一次函数
= − 的值大于0时,求出
相应的自变量的取值范围.
教学过程——新知探究
第二章 一元一次不等式与一元一次不等式组
适.甲公司表示:快递物品不超过1kg的,收费12元;超过1kg,超过的
部分按单价2元/kg收费.
乙公司表示:快递物品不超过1kg的,收费10元;超过1kg,超过的部
分按单价4元/kg收费.
例如:小明要快递1.4kg的物品,选甲公司需付费12.8元,选乙公司需
付费11.6元.
设小明快递物品千克.
(1)请分别直接写出甲、乙两家快递公司快递该物品的费用y(元)
北师大版八年级数学下册课件:2.5 一元一次不等式与一次函数 第1课时

x = 3,Leabharlann y = 2.∴点 C 的坐标为(3,2). (3)由图可知,当 x≥3 时,2x-4≥kx+b.
对于一次函数y=kx+b(k≠0): (1)当一次函数y>0时,自变量x的取值就是一元一次不等式 __k_x_+_b_>_0_的解集; (2)当一次函数y<0时,自变量x的取值就是一元一次不等式 __k_x_+_b_<_0_的解集; (3)当一次函数y=0时,自变量x的取值就是一元一次方程 __k_x_+_b_=_0_的解.
第二章
一元一次不等式与一元一次不等式组
2.5 一元一次不等式与一次函数
第1课时
1.能借助一次函数图象求一元一次不等式的解集. 2.通过一元一次不等式与一次函数的数形结合,解决实际问题.
我们学过一次函数y=kx+b与一元一次方程kx+b=0的关 系,那么一次函数y=kx+b与一元一次不等式kx+b>0或kx+b<0 又有什么关系呢?
解:画图略. (1)x>2. (2)x<4. (3)2<x<4.
(4)S=1×2×2=2.
2
2.如图,直线y=kx+b经过点A(5,0),B(1,4). (1)求直线AB的解析式; (2)若直线y=2x-4与直线AB相交于点C,求点C的坐标; (3)根据图象,写出关于x的不等式2x-4≥kx+b的解集.
1.作出函数y1=2x-4与y2=-2x+8的图象,并根据图象回答下列问题: (1)当x取何值时,2x-4>0? (2)当x取何值时,-2x+8>0? (3)当x取何值时,2x-4>0与-2x+8>0同时成立? (4)你能求出函数y1=2x-4,y2=-2x+8的图象与x轴所围成的三角 形的面积吗?
一元一次不等式与一次函数(第2课时)(课件)八年级数学下册(北师大版)
思考:10至25人的含义是什么?
探究新知
解:设该单位参加这次旅游的人数是 x 人,选择甲旅行 社时,所需的费用为 y 1 元,选择乙旅行社时,所需的费 用为 y 2 元,则 y 1 = 200 × 0.75 x, 即 y 1 = 150 x; y 2 = 200 × 0.8(x - 1),即 y 2 = 160 x - 160.
探究新知
例 3 : 为绿 化 校园 , 某校 计 划购 进 A, B两 种 树苗 , 共 21 棵.已知A种树苗每棵90元,B种树苗每棵70元.设购买B种 树苗x棵,购买两种树苗所需费用为y元. (1)y与x的函数关系式为________; (2)若购买B种树苗的数量少于A种树苗的数量,请给出一种
千米收取的费用比乙租赁公司多 D.除去月固定租赁费,甲租赁公司平均每
千米收取的费用比乙租赁公司少
随堂练习
4.某电信公司有甲、乙两种手机收费业务.甲种业务规定 月租费10元,每通话1 min收费0.3元;乙种业务不收月 租费,但每通话1 min收费0.4元.你认为何时选择甲种业 务对顾客更合算?何时选择乙种业务对顾客更合算?
情境导入
一次函数与一元一次不等式的关系是什么? 一次函数与一元一次不等式的关系: 任何一元一次不等式都可以化为ax+b>0或ax+b<0(a,b为 常数,a≠0)的形式,所以解一元一次不等式就可以看成当一次 函数的值大于或小于0时,求相应的自变量的取值范围. 从 图 象 上 看 , ax + b > 0 或 ax + b < 0 的 解 集 是 使 直 线 y = ax + b(a≠0)位于x轴的上方或下方的部分对应的x的取值范围.
探究新知
核心知识点一: 一元一次不等式与一次函数的综合应用
例1:某电信公司有甲、乙两种手机收费业务.甲种业务规 定月租费10元,每通话1min收费0.3 元;乙种业务不收月租 费,但每通话1min收费0.4 元. 你认为何时选择甲种业务对 顾客更合算?何时选择乙种业务对顾客更合算?
探究新知
解:设该单位参加这次旅游的人数是 x 人,选择甲旅行 社时,所需的费用为 y 1 元,选择乙旅行社时,所需的费 用为 y 2 元,则 y 1 = 200 × 0.75 x, 即 y 1 = 150 x; y 2 = 200 × 0.8(x - 1),即 y 2 = 160 x - 160.
探究新知
例 3 : 为绿 化 校园 , 某校 计 划购 进 A, B两 种 树苗 , 共 21 棵.已知A种树苗每棵90元,B种树苗每棵70元.设购买B种 树苗x棵,购买两种树苗所需费用为y元. (1)y与x的函数关系式为________; (2)若购买B种树苗的数量少于A种树苗的数量,请给出一种
千米收取的费用比乙租赁公司多 D.除去月固定租赁费,甲租赁公司平均每
千米收取的费用比乙租赁公司少
随堂练习
4.某电信公司有甲、乙两种手机收费业务.甲种业务规定 月租费10元,每通话1 min收费0.3元;乙种业务不收月 租费,但每通话1 min收费0.4元.你认为何时选择甲种业 务对顾客更合算?何时选择乙种业务对顾客更合算?
情境导入
一次函数与一元一次不等式的关系是什么? 一次函数与一元一次不等式的关系: 任何一元一次不等式都可以化为ax+b>0或ax+b<0(a,b为 常数,a≠0)的形式,所以解一元一次不等式就可以看成当一次 函数的值大于或小于0时,求相应的自变量的取值范围. 从 图 象 上 看 , ax + b > 0 或 ax + b < 0 的 解 集 是 使 直 线 y = ax + b(a≠0)位于x轴的上方或下方的部分对应的x的取值范围.
探究新知
核心知识点一: 一元一次不等式与一次函数的综合应用
例1:某电信公司有甲、乙两种手机收费业务.甲种业务规 定月租费10元,每通话1min收费0.3 元;乙种业务不收月租 费,但每通话1min收费0.4 元. 你认为何时选择甲种业务对 顾客更合算?何时选择乙种业务对顾客更合算?
北师大版数学八年级下册一元一次不等式与一次函数课件
100 m.
36
20
y2
9
y1
56789
新知探究
例.某单位计划在新年期间组织员工到某地旅游, 参加旅游人数估计为10至25人,甲、乙两家旅行社的 服务质量相同,且报价都是每人200元.经过协商,甲 旅行社表示可以给予每位游客七五折优惠;乙旅行社 表示可先免去一位游客的旅游费用,然后给予其余游 客八折优惠,该单位选择哪一家旅行社支付的旅游费 用较少?
第2章 一元一次不等式与 一元一次不等式组
2.5 一元一次不等式与一次函数
活动导入
一次函数的概念是什么? 如果y=kx+b(k、b是常数且k≠0),那么y就叫做x的 一次函数. 怎样求一次函数y=ax+b(a≠0)的图象与坐标轴交点 的坐标?
设ax+b=0,则 x = - b ,即一次函数y=ax+b的图 a
解:设该单位参加这次旅游的人数是x人,选择甲旅行社时, 所需费用为y1元,选择乙旅行社时,所需费用为y2元,则
y1=200×0.75x=150x, y2=200×0.8(x-1)=160x-160. 当y1=y2时,150x =160x-160,解得x =16; 当y1>y2时,150x >160x-160,解得x <16; 当y1<y2时,150x <160x-160,解得x >16. 因为参加旅游的人数为10至25人,所以当x =16时,甲乙旅行 社收费相同;当17≤x ≤25时,选择甲旅行社费用较少;当10≤x ≤15 时,选择乙旅行社费用较少.
y=2x-5相交于点(4,3),则当x>4时,
有2x-5>3.
新知探究
讨论: 一次函数y=ax+b(a≠0),一元一次方程ax+b=0,一 元一次不等式ax+b>0(或ax+b<0)三者之间的联系与区分.
36
20
y2
9
y1
56789
新知探究
例.某单位计划在新年期间组织员工到某地旅游, 参加旅游人数估计为10至25人,甲、乙两家旅行社的 服务质量相同,且报价都是每人200元.经过协商,甲 旅行社表示可以给予每位游客七五折优惠;乙旅行社 表示可先免去一位游客的旅游费用,然后给予其余游 客八折优惠,该单位选择哪一家旅行社支付的旅游费 用较少?
第2章 一元一次不等式与 一元一次不等式组
2.5 一元一次不等式与一次函数
活动导入
一次函数的概念是什么? 如果y=kx+b(k、b是常数且k≠0),那么y就叫做x的 一次函数. 怎样求一次函数y=ax+b(a≠0)的图象与坐标轴交点 的坐标?
设ax+b=0,则 x = - b ,即一次函数y=ax+b的图 a
解:设该单位参加这次旅游的人数是x人,选择甲旅行社时, 所需费用为y1元,选择乙旅行社时,所需费用为y2元,则
y1=200×0.75x=150x, y2=200×0.8(x-1)=160x-160. 当y1=y2时,150x =160x-160,解得x =16; 当y1>y2时,150x >160x-160,解得x <16; 当y1<y2时,150x <160x-160,解得x >16. 因为参加旅游的人数为10至25人,所以当x =16时,甲乙旅行 社收费相同;当17≤x ≤25时,选择甲旅行社费用较少;当10≤x ≤15 时,选择乙旅行社费用较少.
y=2x-5相交于点(4,3),则当x>4时,
有2x-5>3.
新知探究
讨论: 一次函数y=ax+b(a≠0),一元一次方程ax+b=0,一 元一次不等式ax+b>0(或ax+b<0)三者之间的联系与区分.
北师大版八年级下册2.5.2一元一次不等式与一次函数(共21张ppt)
北师大版 八年级下册
2.5 一元一次不等式与一次函数
一、温故知新
一元一次不等式与一次函数的联系
求ax+b>0 (或<0)的 数 函数y=ax+b(a ≠0)的函
解集(a ≠0,a,b为常数)
数值y大于0(或小于0)时, 对应的x的取值范围
求ax+b>0(或<0)的 形 直线y=ax+b(a ≠0)在y
优惠
方案一 方案一
优惠条件
每名员工票价打八折 男员工票价30元,女员工的票价打五折
解:设该公司有x名女员工,则男员工有(40-x)名,选择团
体票优惠时,所需费用为y1元,选择活动优惠时,所需的费用为 y2元,则
y1=40×30×0.8 =960 y2=30×(40-x)+30×0.5x=1200-15x
y1=200×0.75x =150x y2=200×0.8(x-1)=160x-160
①当y1=y2时, 150x =160x-160, 解得x =16; ②当y1>y2时, 150x >160x-160, 解得x<16; ③当y1<y2时, 150x <160x-160, 解得x>16.
因为参加旅游的人数为10~25人,
变量:旅游人数,旅游费用
一次函数
解:设该单位参加这次旅游的人数是x人, 选择甲旅行社时,所需费用为y1元, 选择乙旅行社时,所需的费用为y2元,则
y1=200×0.75x = 150x y2=200×0.8(x-1) =160x-160
解:设该单位参加这次旅游的人数是x人,选择甲旅行社时, 所需费用为y1元,选择乙旅行社时,所需的费用为y2元,则
O 低3
ly1:1y=1k=xk+x+bb
2.5 一元一次不等式与一次函数
一、温故知新
一元一次不等式与一次函数的联系
求ax+b>0 (或<0)的 数 函数y=ax+b(a ≠0)的函
解集(a ≠0,a,b为常数)
数值y大于0(或小于0)时, 对应的x的取值范围
求ax+b>0(或<0)的 形 直线y=ax+b(a ≠0)在y
优惠
方案一 方案一
优惠条件
每名员工票价打八折 男员工票价30元,女员工的票价打五折
解:设该公司有x名女员工,则男员工有(40-x)名,选择团
体票优惠时,所需费用为y1元,选择活动优惠时,所需的费用为 y2元,则
y1=40×30×0.8 =960 y2=30×(40-x)+30×0.5x=1200-15x
y1=200×0.75x =150x y2=200×0.8(x-1)=160x-160
①当y1=y2时, 150x =160x-160, 解得x =16; ②当y1>y2时, 150x >160x-160, 解得x<16; ③当y1<y2时, 150x <160x-160, 解得x>16.
因为参加旅游的人数为10~25人,
变量:旅游人数,旅游费用
一次函数
解:设该单位参加这次旅游的人数是x人, 选择甲旅行社时,所需费用为y1元, 选择乙旅行社时,所需的费用为y2元,则
y1=200×0.75x = 150x y2=200×0.8(x-1) =160x-160
解:设该单位参加这次旅游的人数是x人,选择甲旅行社时, 所需费用为y1元,选择乙旅行社时,所需的费用为y2元,则
O 低3
ly1:1y=1k=xk+x+bb
北师大版八年级下册一元一次不等式与一次函数课件(共27张)
yБайду номын сангаас4
3 2
1
x
-1
0 -1
12 3 4
-2
-3
-4
-5
➢一元一次不等式与一次函数在 决策型应用题中的应用
1.根据实际问题设求知数x, y1, y2 2.列出y1, y2与x的函数关系式 3. 分别讨论三种情况,解出方程和不等式 4.写出结论
C
B
x≤2
>1500千米
【例1】已知一次函数的图象过点A(1,4)、B(-1,0) 两点,求函数解析式并画出它的图象,并求:(1)x为何值 时,y>0,y=0,y<0;(2)当-3<x<0时,y的取值范 围;(3)当-2≤y≤2时,x的取值范围.
【例4】某校需要添置部分办公桌,现从两个家具店得到 信息:同样的办公桌每张标价均为225元,甲店的优惠条 件是购买办公桌不超过10张,按标价付费,超过10张,超 过的部分打8折;乙店的优惠条件是购买办公桌一律打9折, 若该校计划购买x张办公桌,在甲、乙两店购买所需费用 分别为y1、y2(元).(1)试分别写出y1、y2与x之间的 函数关系式;(2)请你帮助该校选择在哪个家具店购买 办公桌比较合算.解析:由题意知,费用的多少跟购买办公 室的数量有关,因此可根据题意设出的办公桌数量x张, 分别写出两个家具店所需费用的函数关系式,建立函数模 型,然后作比较,分y1>y2,y1=y2,y1<y2讨论.
如果y=-2x-5, 那么当x取何 值时,y>0?
你有哪些方法?
y 4 y=-2x-5 3 2 1
-3 -2 -1-01 -2 -3 -4 -5
x 12 3 4
如图是一次函数y=kx+b的 图象,
当x______时,kx+b=0; 当x______时,kx+b>0; 当x______时,kx+b<0; 当x______时,kx+b<4
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
合作探究1:先独立思考5分钟,再小组交流2分钟,展示、
评价和补充4分钟。
例题1:某单位计划在新年期间组织员 工到某地旅游,参加旅游的人数估计为 10~25人,甲、乙两家旅行社的服务质量相 同,且报价都是每人200元,经过协商,甲 旅行社表示可以给予每位游客七五折优惠; 乙旅行社表示可以先免去一位游客的旅游费 用,其余的游客八折优惠。该单位选择哪一 家旅行社支付的旅游费用较少?
与一次函数(二)
知识回顾:独立思考4分钟+展示2分钟
1、若y1= -2x-2,y2=3x+3,试确定当x取何值时,y1<y2 。你是怎样做的?
2、某商品原价60元,现优惠25%,则现价 是 元
3、某商品原价200元,现打七五折,则现价 是 元
阅读目标:1分钟
学习目标:
• 1、掌握一元一次不等式与一次函数的关系, 会运用不等式解决函数有关问题。 • 2、通过具体问题初步体会一次函数的变化 规律与一元一次不等式解集的联系。 • 3、感知不等式、函数、方程的不同作用与 内在联系,并渗透“数形结合”思想。
一元一次不等式与一次函数在决 策型应用题中的应用
画出图象 分析图象
实际问题
写出两个函数表达式
解决问题
不等式
解不等式
合作探究2:先独立思考4分钟,再小组交流2分钟,展示、
评价和补充4分钟。 例题2:某学校计划购买若干台电脑,现从两家商场了解到同一型 号电脑每台报价均为6000元,并且多买都有一定的优惠。 甲商场的优惠条件是:第一台按原报价收费,其余每台优惠 25% , 那 么 甲 商 场 的 收 费 y1 ( 元 ) 与 所 买 的 电 脑 台 数 x 之 间 的 关 系 是 。
(1)比买普通票总共便宜多少钱?
(2)不足20人时,多少人买20人的团体票 才比普通票便宜?
课堂小结:自由发言2分钟
通过本节课的学习,你有哪些收获?
作业:8分钟
习题2.7
1, 2
解:设该单位参加这次旅游的人数是x人,选择甲旅行社时,所需费用为y1元,选择乙旅行社时, 所需的费用为y2元,则 y1=200×0.75x=150x y2=200×0.8(x-1)=160x-160 当y1=y2时,150x=160x-160,解得x=16; 当y1>y2时,150x>160x-160,解得x<16; 当y1<y2时,150x<160x-160,解得x>16. 因为参加旅游的人数为10~25人, 所以当x=16时,甲乙两家旅行社的收费相同; 当17≤x≤25时,选择甲旅行社费用较少, 当10≤x≤15时,选择乙旅行社费用较少.
教学目标是:
1、掌握一元一次不等式与一次函数的关系,会运用不等式 解决函数有关问题。
2、通过具体问题初步体会一次函数的变化规律与一元一次 不等式解集的联系。 3、感知不等式、函数、方程的不同作用与内在联系,并渗 透“数形结合”思想。
第二章 一元一次不等式与 一元一次不等式组 2.5 一元一次不等式
乙商场的优惠条件是:每台优惠 20% ,那么乙商场的收费 y2 (元) 与所买的电脑台数x之间的关系是 。
(1) 什么情况下到甲商场购买更优惠? (2) 什么情况下到乙商场购买更优惠? (3) 什电脑所需费用y1元,购买乙商场的电脑所 需费用为y2元.则有 y1=6000+(1-25%)(x-1)×6000=4500x+1500 y2=80%×6000x=4800x (1)当y1<y2时,有4500x+1500<4800x 解得,x>5 即当所购买电脑超过5台时,到甲商场购买更优惠;
(2)当y1>y2时,有4500x+1500>4800x. 解得x<5. 即当所购买电脑少于5台时,到乙商场买更优惠; (3)当y1=y2时,即4500x+1500=4800x 解得x=5. 即当所购买电脑为5台时, 两家商场的收费相同.
巩固练习:先独立思考4分钟,展示、评价和补充2分钟。
红枫湖门票是每位45元,20人以上 (包含20人)的团体票七五折优惠,现在 有18位游客买20人的团体票
