第4章三角形证明 题型解读12 全等典型模型:“手拉手”模型-2020-2021学年北师大版七下数学
完整版)全等三角形之手拉手模型

完整版)全等三角形之手拉手模型
本文将介绍手拉手模型中的全等三角形。
所谓手拉手模型,是指有公共顶点的两个等腰三角形,顶角相等。
因为顶点相连的四条边,形象的可以看作两双手,所以通常称为手拉手模型。
基本模型如下:已知,△ABB'和△ACC'都是等腰三角形,AB=AB',AC=AC',且∠BAB'=∠CAC'。
可以得出三个结论:结论1:△ABC≌△AB'C'(SAS),BC=B'C';结论2:
∠BOB'=∠BAB';结论3:AO平分∠BOC'。
在共顶点的等腰直角三角形中,也可以应用手拉手模型。
例如,如下图所示,△ABC和△ADE是等腰直角三角形,且
∠BAC=∠DAE=90°。
可以证明:⑴BD=CE⑵BD⊥CE。
另外,在共顶点的等边三角形中,也可以使用手拉手模型。
如下图,点A为线段BD上一点,△ABC和△ADE均是等边
三角形。
可以求出:(1)CD=BE;(2)∠DAE+
∠BFD=180°;(3)∠BFA=∠DFA=60°。
总之,手拉手模型在全等三角形的证明中是一个非常有用的工具,能够帮助我们更好地理解和应用三角形的性质。
专题04 手拉手模型证全等(解析版)

专题04 手拉手模型证全等类型一等边手拉手1.图1、图2中,点C为线段AB上一点,△ACM与△CBN都是等边三角形.(1)如图1,线段AN与线段BM是否相等?证明你的结论;(2)线段AN与线段BM交于点O,求∠AOM的度数;(3)如图2,AN与MC交于点E,BM与CN交于点F,探究△CEF的形状,并证明你的结论.【答案】(1)AN=BM,见解析;(2)60°;(3)等边三角形,见解析【解析】【分析】(1)证△ACN≌△MCB(SAS),即可得出AN=BM;(2)由全等三角形的性质得∠ANC=∠MBC,则∠AOM=∠CAN+∠MBC=∠CAN+∠ANC =∠BCN=60°;(3)证△ACE≌△MCF(ASA),得CE=CF,即可得出结论.【详解】解:(1)AN=BM,理由如下:∵△ACM、△CBN都是等边三角形,∴AC=CM,CN=CB,∠ACM=∠BCN=60°,∴∠ACM +∠MCN =∠BCN +∠MCN ,∴∠ACN =∠BCM ,在△ACN 和△MCB 中,AC MC ACN MCB CN CB =⎧⎪∠=∠⎨⎪=⎩,∴△ACN ≌△MCB (SAS ),∴AN =BM ;(2)由(1)得:△ACN ≌△MCB ,∴∠ANC =∠MBC ,∴∠AOM =∠CAN +∠MBC =∠CAN +∠ANC =∠BCN =60°;(3)△CEF 是等边三角形,理由如下:∵△ACN ≌△MCB ,∴∠CAE =∠CMF ,∵∠MCF =180°﹣∠ACM ﹣∠BCN =60°,∴∠ACE =∠MCF ,在△ACE 和△MCF 中,CAE CMF AC MCACE MCF ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△ACE ≌△MCF (ASA ),∴CE =CF ,∵∠MCF =60°,∴△CEF 是等边三角形.【点睛】本题考查等边三角形的性质、全等三角形的判定与性质,是重要考点,难度较易,掌握相关知识是解题关键.2.如图,△ABD 和△BCE 都是等边三角形,∠ABC <105°,AE 与DC 交于点F . (1)求证:AE =DC ;(2)求∠BFE 的度数;(3)若AF =9.17cm ,BF =1.53cm ,CF =7.53cm ,求CD .【答案】(1)见解析;(2)60°;(3)18.23cm【解析】【分析】(1)由等边三角形的性质可知∠DBA=∠EBC=60°,BD=AB,BC=BE.从而可证∠DBC =∠ABE.即可利用“SAS”可证明△DBC≌△ABE,得出结论AE=DC.(2)过点B作BN⊥CD于N,BH⊥AE于H.由△DBC≌△ABE可知∠BEH=∠BCN,∠BDF =∠BAF.再结合等边三角形的性质可求出∠FDA+∠DAF=120°,进而求出∠DF A=180°-120°=60°,即求出∠DFE=180°-60°=120°.即可利用“AAS”证明△BEH≌△BCN,得出结论BH=BN,即得出BF平分∠DFE,即可求出∠BFE=60°.(3)延长BF至Q,使FQ=AF,连接AQ.根据所作辅助线可知∠AFQ=∠BFE=60°,即证明△AFQ是等边三角形,得出结论AF=AQ=BQ,∠F AQ=60°.又可证明∠DAF=∠BAQ.利用“SAS”可证明△DAF≌△BAQ,即得出DF=BQ=BF+FQ=BF+AF,最后即可求出CD=DF+CF=BF+AF+CF=1.53+9.17+7.53=18.23cm.【详解】(1)证明:∵△ABD和△BCE都是等边三角形,∴∠DBA=∠EBC=60°,BD=AB,BC=BE,∴∠DBA+∠ABC=∠EBC+∠ABC,即∠DBC=∠ABE,∵在△DBC和△ABE中,BD ABDBC ABE BC BE=⎧⎪∠=∠⎨⎪=⎩,∴△DBC≌△ABE(SAS),∴AE=DC;(2)解:如图,过点B作BN⊥CD于N,BH⊥AE于H.∵△DBC ≌△ABE ,∴∠BEH =∠BCN ,∠BDF =∠BAF ,∵△ABD 是等边三角形,∴∠BDA +∠BAD =120°,∴∠FDA +∠DAF =120°,∴∠DF A =180°-120°=60°,∴∠DFE =180°-60°=120°,在△BEH 和△BCN 中,90BEH BCN BHE BNC BE BC ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩,∴△BEH ≌△BCN (AAS ),∴BH =BN ,∴BF 平分∠DFE ,∴∠BFE =12∠DFE =12×120°=60°;(3)解:如图,延长BF 至Q ,使FQ =AF ,连接AQ .则∠AFQ =∠BFE =60°,∴△AFQ 是等边三角形,∴AF =AQ =BQ ,∠F AQ =60°,∵△ABD 是等边三角形,∴AD =AB ,∠DAB =60°,∴∠DAB +∠BAF =∠BAF +∠F AQ ,即∠DAF =∠BAQ ,在△DAF 和△BAQ 中,AD AB DAF BAQ AF AQ =⎧⎪∠=∠⎨⎪=⎩,∴△DAF ≌△BAQ (SAS ),∴DF =BQ =BF +FQ =BF +AF ,∴CD =DF +CF =BF +AF +CF =1.53+9.17+7.53=18.23cm .【点睛】本题为三角形综合题.考查等边三角形的判定和性质,全等三角形的判定和性质,三角形内角和定理以及角平分线的判定和性质.正确的作出辅助线也是解答本题的关键. 3.如图,点C 为线段BD 上一点,,ABC CDE △△都是等边三角形,AD 与CE 交于点,F BE 与AC 相交于点G .(1)求证:≌ACD BCE ;(2)求证:ACF BCG ≌(3)若8,25CF CG BD +==,求ACD △的面积.【答案】(1)见解析;(2)见解析;(3)【解析】【分析】(1)根据SAS 即可证明△BCE ≌△ACD ;(2)由△ACD ≌△BCE 可得∠CBG =∠CAF ,从而利用ASA 可证明△ACF ≌△BCG ;(3)求出CG =CF =4,过G 作GM ⊥BD 于M ,过点F 作FN ⊥BD 于N ,求出GM ,FN ,根据S △ACD =S △ACF +S △CDF =S △BCG +S △CDF 可求出答案.【详解】解:(1)证明:∵△ABC ,△CDE 是等边三角形,∴AC =BC ,CD =CE ,∠ACB =∠DCE =60°,∴∠ACB +∠ACE =∠DCE +∠ACE ,即∠BCE =∠DCA ,∴△ACD ≌△BCE (SAS ).(2)由(1)得△ACD ≌△BCE ,∴∠CBG =∠CAF ,又∵∠ACF =∠BCG =60°,BC =AC ,在△ACF 和△BCG 中,ACF BCG BC ACCAF CBG ∠=∠⎧⎪=⎨⎪∠=⎩, ∴△ACF ≌△BCG (ASA );(3)∵△ACF ≌△BCG ,∴S △ACF =S △BCG ,CG =CF ,而CF +CG =8,∴CG =CF =4,过G 作GM ⊥BD 于M ,过点F 作FN ⊥BD 于N ,又∵∠ACB =∠DCE =60°,∴GM=FN= ∴S △ACD =S △ACF +S △CDF=S △BCG +S △CDF =12BC •GM +12CD •FN=12⨯(BC +CD )=【点睛】本题考查了全等三角形的判定和性质以及等边三角形的判定和性质,利用全等三角形的性质得出CG =CF 是解答此题的关键.类型二 等直手拉手4.已知:两个等腰直角三角板△ACB 和△DCE (AC =BC ,DC =CE ,∠ACB =∠DCE =90°)如图所示摆放,连接AE 、BD 交于点O .AE 与DC 交于点M ,BD 与AC 交于点N .(1)如图1(两个等腰直角三角板大小不等),试判断AE 与BD 有何关系并说明理由; (2)如图2(两个等腰直角三角板大小相等,即AC =DC ),在不添加任何辅助线的情况,请直接写出图2中四对全等的直角三角形.【答案】(1)AE =BD 且AE ⊥BD .理由见解析;(2)△ACB ≌△DCE ,△EMC ≌△BCN ,△AON ≌△DOM ,△AOB ≌△DOE【解析】【分析】(1)证明△ACE ≌△BCD ,可得AE =BD ,∠CEA =∠BDC ,由∠CME =∠DMO ,根据三角形内角和定理即可得∠DOM =∠ECM =90°,进而可证AE ⊥BD .(2)根据三角形全等的判定找出相等边和角,进而找出全等三角形.【详解】解:(1)结论;AE =BD 且AE ⊥BD .理由如下:∵∠ACB =∠DCE ,∴∠ACB +∠DCA =∠DCE +∠DCA ,即∠DCB =∠ACE ,∵AC =BC ,CD =CE ,在△ACE 与△BCD 中,AC BC ACE DCB CD CE =⎧⎪∠=∠⎨⎪=⎩,∴△ACE ≌△BCD (SAS ),∴AE =BD ,∠CEA =∠BDC ,∵∠CME =∠DMO ,∴180()180()CEA CME DMO BDC ︒-∠+∠=︒-∠+∠,即∠DOM =∠ECM =90°,∴AE ⊥BD ,∴AE =BD 且AE ⊥BD ;(2)∵AC =DC ,∴AC =CD =EC =CB ,在△ACB 与△DCE 中,AC DC ACB DCE CB CE =⎧⎪∠=∠⎨⎪=⎩,∴△ACB ≌△DCE (SAS );由(1)可知:∠AEC =∠BDC ,∠EAC =∠DBC ,∴∠DOM =90°,∵∠AEC =∠CAE =∠CBD ,∴△EMC ≌△BCN (ASA ),∴CM =CN ,∴DM =AN ,∴△AON ≌△DOM (AAS ),∵DE =AB ,AO =DO ,∴△AOB ≌△DOE (HL ).【点睛】本题考查了三角形全等的性质与判定,掌握三角形全等的性质与判定是解题的关键. 5.已知Rt ABC △中,AB AC =,90BAC ∠=︒,点D 为直线BC 上的一动点(点D 不与点B 、C 重合),以AD 为边作Rt ADE △,AD AE =,连接CE .(1)发现问题:如图①,当点D 在边BC 上时,①请写出BD 和CE 之间的数量关系________,位置关系________;②线段CE 、CD 、BC 之间的关系是_________;(2)尝试探究:如图②,当点D 在边BC 的延长线上且其他条件不变时,(1)中CE 、CD 、BC 之间存在的数量关系是否成立?若成立,请证明;若不成立,请说明理由;(3)拓展延伸:如图③,当点D 在边CB 的延长线上且其他条件不变时,若6BC =,1CE =,则线段AD 的长为________.【答案】(1)①BD CE =,BD CE ⊥.②BC CE CD =+.(2)不成立,CE BC CD =+.(3)5【解析】【分析】(1)①根据全等三角形的判定定理证明△BAD ≌△CAE ,根据全等三角形的性质证明; ②根据全等三角形的对应边相等证明即可;(2)证明△BAD ≌△CAE ,根据全等三角形的性质解答即可;(3)根据△BAD ≌△CAE 得到BD =CE =1,再证明△DCE 是直角三角形,利用勾股定理求出DE ,即可求出AD 的长度;【详解】(1)①解:结论:BD =CE ,BD ⊥CE ,理由:∵∠ABC =∠ACB =45°,∠ADE =∠AED =45°,∴∠BAC =∠DAE =90°,∴∠BAD =∠CAE ,在△BAD 和△CAE 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,∴△BAD ≌△CAE ,∴BD =CE ,∠ACE =∠B =45°,∴∠BCE =90°,即BD ⊥CE ,故答案为:BD =CE ;BD ⊥CE ;②证明:∵BD =CE ,∴BC =BD +CD =CE +CD ;故答案为:BC CE CD =+.(2)解:(1)中BC 、CE 、CD 之间存在的数量关系不成立,新的数量关系是CE =BC +CD , 理由:∵∠BAC =∠DAE =90°,∴∠BAD =∠CAE ,在△BAD 和△CAE 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,∴△BAD ≌△CAE ,∴BD =CE ,∴CE =BC +CD ;(3)解:∵∠BAC =∠DAE =90°,∴∠BAD =∠CAE ,在△BAD 和△CAE 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,∴△BAD ≌△CAE ,∴BD =CE =1,∠ABD =∠ACE =135°,∵∠ACB =45°,∴∠DCE =90°,在Rt △DCE 中,CD =BD +BC =7,CE =1,∴DE=∴52AD ==; 故答案为:5.【点睛】本题考查三角形综合题,等腰直角三角形的性质、全等三角形的判定和性质、勾股定理等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.6.在△ABC 中,∠BAC =90°,AB =AC ,D 为BC 的中点.(1)如图1,E 、F 分别是AB 、AC 上的点,且BE =AF 、求证:△DEF 是等腰直角三角形经过分析已知条件AB =AC ,D 为BC 的中点.容易联想等腰三角形三线合一的性质,因此,连结AD (如图2),以下是某同学由己知条件开始,逐步按层次推出结论的流程图.请帮助该同学补充完整流程图.补全流程图:①___≅____,②∠EDF =___(2)如果E 、F 分别为AB 、CA 延长线上的点,仍有BE =AF ,其他条件不变,试猜想△DEF是否仍为等腰直角三角形?请在备用图中补全图形、先作出判断,然后给予证明.【答案】(1)△BDE ,△ADF ,90°;(2)△DEF 仍为等腰直角三角形,理由见解析【解析】【分析】(1)连接AD ,根据∠BAC =90°,AB =AC ,D 为BC 的中点,可以得到∠B =∠C =45°,AD ⊥BC ,1==452BAD CAD BAC =∠∠∠,12AD CD BD BC ===,从而可以证明△BDE ≌△ADF (SAS ),得到DE =DF ,∠BDE =∠ADF ,由∠ADE +∠BDE =∠BDA =90°,可得∠ADE +∠ADF =90°,即∠EDF =90°,即可证明;(2)连接AD ,同样证明△BDE ≌△ADF (SAS ),得到DE =DF ,∠BDE =∠ADF ,再由∠ADF +∠BDF =∠BDA =90°,即可得到∠BDE +∠BDF =90°,即∠EDF =90°,即可证明.【详解】解:(1)如图所示,连接AD ,∵∠BAC =90°,AB =AC ,D 为BC 的中点,∴∠B =∠C =45°,AD ⊥BC ,1==452BAD CAD BAC =∠∠∠,12AD CD BD BC ===, ∴∠B =∠BAD =∠CAD ,在△BDE 和△ADF 中,BD AD B DAF BE AF =⎧⎪∠=∠⎨⎪=⎩,∴△BDE ≌△ADF (SAS ),∴DE =DF ,∠BDE =∠ADF ,∵∠ADE +∠BDE =∠BDA =90°,∴∠ADE +∠ADF =90°,即∠EDF =90°,∴△DEF 是等腰直角三角形;故答案为:△BDE ,△ADF ,90°;(2)△DEF 仍为等腰直角三角形,理由如下:连接AD ,∵∠BAC =90°,AB =AC ,D 为BC 的中点,∴∠ABC =∠C =45°,AD ⊥BC ,1==452BAD CAD BAC =∠∠∠,12AD CD BD BC ===, ∴∠F AD =180°-∠CAD =135°,∠EBD =180°-∠ABC =135°,∴∠F AD =∠EBD ,在△BDE 和△ADF 中,BD AD EBD FAD BE AF =⎧⎪∠=∠⎨⎪=⎩,∴△BDE ≌△ADF (SAS ),∴∴DE =DF ,∠BDE =∠ADF ,∵∠ADF +∠BDF =∠BDA =90°,∴∠BDE +∠BDF =90°,即∠EDF =90°,∴△DEF 是等腰直角三角形.【点睛】本题主要考查了全等三角形的性质与判定,等腰直角三角形的性质与判定,解题的关键在于能够熟练掌握全等三角形的性质与判定条件.7.(1)问题发现:如图1,ACB △和DCE 均为等腰直角三角形,90ACB DCE ∠=∠=︒,连接AD ,BE ,点A 、D 、E 在同一条直线上,则AEB ∠的度数为__________,线段AD 、BE 之间的数量关系__________;(2)拓展探究:如图2,ACB △和DCE 均为等腰直角三角形,90ACB DCE ∠=∠=︒,连接AD ,BE ,点A 、D 、E 不在一条直线上,请判断线段AD 、BE 之间的数量关系和位置关系,并说明理由. (3)解决问题:如图3,ACB △和DCE 均为等腰三角形,ACB DCE α∠=∠=,则直线AD 和BE 的夹角为__________.(请用含α的式子表示)【答案】(1)90°,AD =BE ;(2)AD =BE ,AD ⊥BE ;(3)α【解析】【分析】(1)由已知条件可得AC BC =,CD CE =,进而根据∠ACB −∠DCB =∠DCE −∠DCB ,可得∠ACD =∠BCE ,证明△ACD ≌△BCE (SAS ),即可求得AD =BE ;∠BEC =∠CDA =135°;(2)延长AD 交BE 于点F ,同理可得△ACD ≌△BCE ,设∠F AB =α,则∠CAD =∠CBE =45°-α,根据∠ABE =45°+45°-α=90°-α,进而根据∠AFB =180°-∠F AB -∠ABE =180°-α-(90°-α)=90°,即可求解;(3)延长BE 交AD 于点G ,方法同(2)证明△ACD ≌△BCE ,进而根据三角形的内角和定理即可求得直线AD 和BE 的夹角.【详解】(1)∵ACB △和DCE 均为等腰直角三角形,90ACB DCE ∠=∠=︒,∴AC BC =,CD CE =,∠CDE =45°∴∠CDA =135°∵∠ACB −∠DCB =∠DCE −∠DCB ,∴∠ACD =∠BCE .在△ACD 和△BCE 中,AC BC ACD BCE CD CE ⎧⎪∠∠⎨⎪⎩===,∴△ACD ≌△BCE (SAS ),∴∠BEC =∠ADC =135°,AD =BE∴∠AEB =90°故答案为:90°,AD =BE(2)AD =BE ,AD ⊥BE ,理由如下,同理可得△ACD ≌△BCE ,则AD =BE ,延长AD 交BE 于点F ,设∠F AB =α,则∠CAD =∠CBE =45°-α∴∠ABE =45°+45°-α=90°-α∴∠AFB =180°-∠F AB -∠ABE =180°-α-(90°-α)=90°∴AD ⊥BE(3)如图,延长BE 交AD 于点G ,∵ACB △和DCE 均为等腰三角形,∴AC BC =,CD CE =,∵∠ACB =∠DCE =α,∵∠ACB +∠ACE =∠DCE +∠ACE ,∴∠ACD =∠BCE .在△ACD 和△BCE 中,AC BC ACD BCE CD CE ⎧⎪∠∠⎨⎪⎩===,∴△ACD ≌△BCE (SAS ),∴∠CBE =∠CAD∵ACB DCE α∠=∠=∴∠CBA =∠CAB =()11180=9022αα︒-︒- ∴∠GAB +∠GBA =()()CAD CAB ABC CBE ∠+∠+∠-∠,ABC CAB =∠+∠180α=︒-,∴∠AGB =180°-(∠GAB +∠GBA )α= ,即直线AD 和BE 的夹角为α.故答案为:α.【点睛】本题考查了等腰三角形的性质,三角形内角和定理,全等三角形的性质与判定,掌握旋转模型证明三角形全等是解题的关键.8.已知:等腰Rt ABC 和等腰Rt ADE △中,AB AC =,AE AD =,90BAC EAD ∠=∠=︒.(1)如图1,延长DE 交BC 于点F ,若68BAE ∠=︒,则DFC ∠的度数为;(2)如图2,连接EC 、BD ,延长EA 交BD 于点M ,若90AEC ∠=︒,求证:点M 为BD 中点;(3)如图3,连接EC 、BD ,点G 是CE 的中点,连接AG ,交BD 于点H ,9AG =,5HG =,直接写出AEC △的面积.【答案】(1)68︒;(2)见解析;(3)36【解析】【分析】(1)由已知条件可得45D C ∠=∠=︒,对顶角AQD CQF ∠=∠,则DAC DFC ∠=∠,根据DAE CAB ∠=∠即可的DFC BAE ∠=∠;(2)过点B 作ME 的垂线交EM 的延长线于N ,证明AEC BNA △≌△,得AE BN =,进而可得AD NB =,再证明DAM BNM △≌△即可得证点M 为BD 中点;(3)延长AG 至K ,使得9GK AG ==,连接CK ,设AE 交BC 于点P ,先证明ABE ACD △≌△,进而证明AEG KCG △≌△,根据角度的计算以及三角形内角和定理求得BAD KCA ∠=∠,进而证明ABD CAK △≌△,再根据,90CAG ABD BAC ∠=∠∠=︒,证明AH BD ⊥,根据已知条件求得ABD S最后证明AEC ABD S S =即可.【详解】 (1)设DF 交AC 于Q ,如图1,ABC 是等腰Rt ABC 和ADE 是等腰Rt ADE △AQD CQF ∠=∠180,180DAQ D AQD QFC C CQF ∠=-∠-∠∠=-∠-∠DAQ QFC ∴∠=∠90BAC EAD ∠=∠=︒即BAE EAQ EAQ QAD ∠+∠=∠+∠BAE QAD ∴∠=∠DFC BAE ∴∠=∠68BAE ∠=︒68DFC ∴∠=︒故答案为68︒(2)如图2,过点B 作ME 的垂线交EM 的延长线于N ,90N ∴∠=︒90AEC =︒∠N AEC ∴∠=∠90BAC ∠=︒90EAC NAB ∴∠+∠=︒90NAC ACE ∠+∠=︒NAB ECA ∴∠=∠ ABC 是等腰Rt ABC 和ADE 是等腰Rt ADE △,AB AC AD AE ∴== 又AC AB =∴AEC BNA △≌△NB AE ∴=AE AD =AD NB ∴=90DAE ∠=︒DAM N ∴∠=∠又DMA BMN ∠=∠DAM BNM ∴△≌△DM BM ∴=即M 是BD 的中点(3)延长AG 至K ,使得9GK AG ==,连接CK ,设AE 交BC 于点P ,如图90BAC EAD ∠=∠=︒即BAE EAC EAC CAD ∠+∠=∠+∠BAE CAD ∴∠=∠ABC 是等腰Rt ABC 和ADE 是等腰Rt ADE △,AB AC AE AD ∴==在ABE △与ACD △中,AE AD BAE CAD AB AC =⎧⎪∠=∠⎨⎪=⎩∴ABE △≌ACD △(SAS )ABE ABD S S ∴=△△,BE CD = G 点是EC 的中点EG GC ∴=AGE KGC ∠=∠,AG GK =AGE KGC ∴△≌△(SAS )∴,AE CK AEG KCG =∠=∠,AE KC AD ∴==ACK ACB BCE KCG ∠=∠+∠+∠45AEC BCE =︒+∠+∠45ABC BAP =︒+∠+∠90BAE =︒+∠BAD =∠AKC ABD ∴△≌△(SAS )18BD AK ∴==,CAK ABD ∠=∠90BAG CAG ∠+∠=︒90ABD BAG ∴∠+∠=︒即90AHB ∠=︒9AG =,5HG =954AH AG HG ∴=-=-=111843622ABD S BD AH ∴=⋅=⨯⨯=△ 36AEC AEG AGC GCK AGC ACK ABD S S S S S S S =+=+===△△△△△△△∴AEC S 36=【点睛】本题考查了三角形全等的性质与判定,等腰直角三角形的性质,三角形内角和定理,三角形外角性质,构造辅助线是解题的关键.类型三 等腰手拉手9.已知:如图,在△ABC 中,AB =AC ,在△ADE 中,AD =AE ,且∠BAC =∠DAE ,连接BD ,CE 交于点F ,连接AF .(1)求证:△ABD ≌△ACE ;(2)求证:F A 平分∠BFE .【答案】(1)见解析(2)见解析【解析】【分析】(1)根据SAS 证明结论即可;(2)作AM ⊥BD 于M ,作AN ⊥CE 于N .由(1)可得BD =CE ,S △BAD =S △CAE ,然后根据角平分线的性质即可解决问题.(1)证明:∵∠BAC =∠DAE ,∴∠BAC +∠CAD =∠DAE +∠CAD ,即∠BAD =∠CAE ,在△BAD 和△CAE 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,∴△BAD ≌△CAE (SAS );(2)证明:如图,作AM ⊥BD 于M ,作AN ⊥CE 于N .由△BAD ≌△CAE ,∴BD =CE ,S △BAD =S △CAE , ∵1122BD AM CE AN ⋅⋅=⋅⋅, ∴AM =AN ,∴点A 在∠BFE 平分线上,∴F A 平分∠BFE .【点睛】本题考查全等三角形的判定和性质、三角形的面积,解题的关键是熟练掌握全等三角形的判定和性质,学会转化的思想,巧用等积法进行证明.10.如图,在等腰△ABC 与等腰△ADE 中,AB =AC ,AD =AE ,∠BAC =∠DAE =α,连接BD 和CE 相交于点P ,交AC 于点M ,交AD 于点N .(1)求证:BD=CE.(2)求证:AP平分∠BPE.(3)若α=60°,试探寻线段PE、AP、PD之间的数量关系,并说明理由.【答案】(1)见解析(2)见解析(3)PE=AP+PD,见解析【解析】【分析】(1)由“SAS”可证△BAD≌△CAE,可得BD=CE;(2)由全等三角形的性质可得S△BAD=S△CAE,由三角形面积公式可得AH=AF,由角平分线的性质可得AP平分∠BPE;(3)由全等三角形的性质可得∠BDA=∠CEA,由“SAS”可证△AOE≌△APD,可得AO=AP,可证△APO是等边三角形,可得AP=PO,可得PE=AP+PD,即可求解.(1)证明:∵∠BAC=∠DAE=α,∴∠BAD=∠CAE,又∵AB=AC,AD=AE,∴△BAD≌△CAE(SAS),∴BD=CE;(2)证明:如图,过点A作AH⊥BD,AF⊥CE,∵△BAD≌△CAE,∴S△BAD=S△CAE,BD=CE,∴12BD×AH=12CE×AF,∴AH=AF,又∵AH⊥BD,AF⊥CE,∴AP平分∠BPE;(3)解:PE=AP+PD,理由如下:如图,在线段PE上截取OE=PD,连接AO,∵△BAD≌△CAE,∴∠BDA=∠CEA,又∵OE=PD,AE=AD,∴△AOE≌△APD(SAS),∴AP=AO,∵∠BDA=∠CEA,∠PND=∠ANE,∴∠NPD=∠DAE=α=60°,∴∠BPE=180°-∠NPD=180°-60°=120°,又∵AP平分∠BPE,∴∠APO=60°,又∵AP=AO,∴△APO是等边三角形,∴AP =PO ,∵PE =PO +OE ,∴PE =AP +PD .【点睛】本题是三角形综合题,考查了全等三角形的判定和性质,直角三角形的性质,等边三角形的判定和性质以及角之间的关系,证明△BAD ≌△CAE 是解本题的关键.11.如图,在△ABC 和△ADE 中,AB =AC ,AD =AE ,∠BAC =∠DAE ,连接BD ,CE ,BD 与CE 交于点O ,BD 与AC 交于点F .(1)求证:BD =CE .(2)若∠BAC =48°,求∠COD 的度数.(3)若G 为CE 上一点,GE =OD ,AG =OC ,且AG ∥BD ,求证:BD ⊥AC .【答案】(1)见解析;(2)132°;(3)见解析【解析】【分析】(1)根据∠BAC =∠DAE ,推出∠BAD =∠CAE ,从而结合“SAS ”证明△BAD ≌△CAE ,即可得出结论;(2)根据外角定理推出∠COD =∠OBC +∠BCA +∠ACE ,结合全等三角形的性质推出∠COD =∠ABC +∠BCA ,最后在△ABC 中利用内角和定理求解即可;(3)连接AO ,根据题意确定△ADO ≌△AEG ,得到∠OAD =∠GAE ,AO =AG ,再结合题干条件推出△AOC 为等腰三角形,以及∠BOA =∠BOC ,从而根据“三线合一”证明即可.【详解】(1)证:∵∠BAC =∠DAE ,∴∠BAC +∠CAD =∠DAE +∠CAD ,即:∠BAD =∠CAE ,在△BAD 和△CAE 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩∴△BAD ≌△CAE (SAS ),∴BD =CE ;(2)解:∵∠COD =∠OBC +∠BCO ,∠BCO =∠BCA +∠ACE ,∴∠COD =∠OBC +∠BCA +∠ACE ,∵△BAD ≌△CAE ,∴∠ABD =∠ACE ,∴∠COD =∠OBC +∠BCA +∠ABD =∠ABC +∠BCA ,∵∠BAC =48°,∴∠ABC +∠BCA =180°-48°=132°,∴∠COD =132°;(3)证:如图所示,连接AO ,∵△BAD ≌△CAE ,∴∠ADO =∠AEG ,在△ADO 和△AEG 中,E A ADO A G E E D G D A O =⎧⎪⎨⎪∠==⎩∠ ∴△ADO ≌△AEG (SAS ),∴∠OAD =∠GAE ,AO =AG ,∴∠AOG =∠AGO ,∴∠OAD +∠DAG =∠GAE +∠DAG ,即:∠OAG =∠DAE ,∵∠DAE =∠BAC ,∴∠BAC =∠OAG ,在△ABF 和△COF 中,∠BAC =180°-∠ABD -∠AFB ,∠BOC =180°-∠ACE -∠CFO , 由(2)知∠ABD =∠ACE ,∵∠AFB =∠CFO ,∴∠BAC =∠BOC ,∴∠BOC =∠OAG ,∵AG ∥BD ,∴∠BOA =∠OAG ,∴∠BOA =∠BOC ,∵AO =AG ,AG =CO ,∴AO =CO ,即:△AOC为等腰三角形,∵∠BOA=∠BOC,∴OF⊥AC,∴BD⊥AC.【点睛】本题考查全等三角形的判定与性质,等腰三角形的判定与性质等,掌握全等三角形的判定与性质,熟悉“手拉手”模型的证明是解题关键.类型四手拉手综合12.现有一块含30°角的直角三角板AOB,点N在其斜边AB上,点M在其最短直角边OA 所在直线上.以MN为边作如图所示的等边△MNP.(1)如图1,当M在线段OA上时,证明:AM﹣AN=AP;(2)如图2当M在射线OA上时,试探究AM、AN、AP三者之间的数量关系并给出证明.【答案】(1)见解析;(2)AM+AN=AP,理由见解析【解析】【分析】(1)在AB上取点C,使得AC=AM,则△ACM为等边三角形,结合“手拉手”模型证明△CMN≌△AMP,得到CN=AP,即可得证;(2)在射线AO上取点D,使得AN=AD,仿照(1)的过程证明△DNM≌△ANP,即可得到AP=DM,从而得出结论.【详解】证:(1)由题意可知,∠BAO =60°,如图所示,在AB 上取点C ,使得AC =AM ,则△ACM 为等边三角形,MC =MA ,∠CMA =60°,∵△NMP 为等边三角形,∴MN =MP ,∠NMP =60°,∴∠CMA =∠NMP ,∴∠CMA -∠NMA =∠NMP -∠NMA ,∴∠CMN =∠AMP ,在△CMN 和△AMP 中,M M CMN A P P A N M C M M =⎧⎪⎨⎪∠==⎩∠ ∴△CMN ≌△AMP (SAS ),∴CN =AP ,∴CN +AN =AP +AN =AC ,∵AC =AM ,∴AP +AN =AM ,∴AM -AN =AP ;(2)AM +AN =AP ,理由如下:如图所示,在射线AO 上取点D ,使得AN =AD ,∵∠BAO =60°,∴△AND 为等边三角形,ND =NA ,∠DNA =60°,∵△NMP 为等边三角形,∴NM =NP ,∠MNP =60°,∴∠DNA =∠MNP ,∴∠DNA +∠ANM =∠MNP +∠ANM ,∴∠DNM =∠ANP ,在△DNM 和△ANP 中,N N DNM A P P A M N D N N =⎧⎪⎨⎪∠==⎩∠ ∴△DNM ≌△ANP (SAS ),∴AP =DM ,∵AN =AD ,DA +AM =DM ,∴AN +AM =AP .【点睛】本题考查等边三角形的性质,全等三角形的判定与性质等,掌握双等边三角形中“手拉手”模型是解题关键.13.已知:△ABC 与△BDE 都是等腰三角形.BA =BC ,BD =BE (AB >BD )且有∠ABC =∠DBE .(1)如图1,如果A 、B 、D 在一直线上,且∠ABC =60°,求证:△BMN 是等边三角形; (2)在第(1)问的情况下,直线AE 和CD 的夹角是 °;(3)如图2,若A 、B 、D 不在一直线上,但∠ABC =60°的条件不变则直线AE 和CD 的夹角是 °;(4)如图3,若∠ACB =60°,直线AE 和CD 的夹角是 °.【答案】(1)证明见解析;(2)60;(3)60;(4)60;【解析】【分析】(1)根据题意,得∠ABC =∠DBE =60°,从而得ABE DBC ∠=∠;通过证明ABE CBD ≌,得BAE BCD ∠=∠;通过证明BAM BCN ≌,得BM BN =,根据等边三角形的性质分析,即可完成证明;(2)结合题意,通过证明ABC 为等边三角形,得60BAC BCA ∠=∠=︒;结合(1)的结论,根据三角形外角性质,推导得120AOD ∠=︒,从而完成求解;(3)同理,通过证明ABC 为等边三角形,得60BAC BCA ∠=∠=︒;通过证明ABE CBD ≌,得BAE BCD ∠=∠;根据三角形外角性质,推导得120AOD ∠=︒,从而完成求解; (4)根据题意,通过证明ABC 为等边三角形,推导得ABE CBD ∠=∠,通过证明ABE CBD ≌,得BAE BCD ∠=∠,结合三角形外角的性质计算,即可得到答案.【详解】(1)∵∠ABC =∠DBE =60°∴18060MBN ABC DBE ∠=︒-∠-∠=︒,ABE ABC MBN ∠=∠+∠,DBC DBE MBN ∠=∠+∠ ∴ABE DBC ∠=∠∵BA =BC ,BD =BEABE △和CBD 中BA BC ABE DBC BE BD =⎧⎪∠=∠⎨⎪=⎩∴ABE CBD ≌∴BAE BCD ∠=∠ BAM 和BCN △中 60BAE BCD AB BC ABC MBN ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩∴BAM BCN ≌∴BM BN =∴BMN △为等边三角形;(2)∵∠ABC =∠DBE =60°, BA =BC∴ABC 为等边三角形;∴60BAC BCA ∠=∠=︒根据题意,AE 和CD 相交于点O∵BAE BCD ∠=∠∴AOD OAC ACO OAC BCA BCD OAC BCA BAE ∠=∠+∠=∠+∠+∠=∠+∠+∠∵OAC BAE BAC ∠+∠=∠∴120AOD BAC BCA ∠=∠+∠=︒∴18060AOC AOD ∠=︒-∠=︒,即直线AE 和CD 的夹角是60︒故答案为:60;(3)∵∠ABC =∠DBE =60°, BA =BC∴ABC 为等边三角形;∴60BAC BCA ∠=∠=︒∵ABE ABC MBN ∠=∠+∠,DBC DBE MBN ∠=∠+∠,∠ABC =∠DBE =60°∴ABE DBC ∠=∠∵BA =BC ,BD =BEABE △和CBD 中BA BC ABE DBC BE BD =⎧⎪∠=∠⎨⎪=⎩∴ABE CBD ≌∴BAE BCD ∠=∠如图,延长AE ,交CD 于点O∴AOD OAC ACO OAC BCA BCD OAC BCA BAE ∠=∠+∠=∠+∠+∠=∠+∠+∠∵OAC BAE BAC ∠+∠=∠∴120AOD BAC BCA ∠=∠+∠=︒∴18060AOC AOD ∠=︒-∠=︒,即直线AE 和CD 的夹角是60︒故答案为:60;(4)∵BA =BC ,∴ACB CAB ∠=∠∵∠ACB =60°∴60ACB CAB ∠=∠=︒∴ABC 为等边三角形∵BD =BE ,∠ABC =∠DBE∴60DBE ∠=︒∵ABE ABC CBE ∠=∠-∠,CBD DBE CBE ∠=∠-∠∴ABE CBD ∠=∠ABE △和CBD 中BA BC ABE DBC BE BD =⎧⎪∠=∠⎨⎪=⎩∴ABE CBD ≌∴BAE BCD ∠=∠分别延长CD 、AE ,相较于点O ,如下图:∴AOF OAC ACO OAC BCA BCD OAC BCA BAE ∠=∠+∠=∠+∠+∠=∠+∠+∠∵OAC BAE BAC ∠+∠=∠∴120AOF BAC BCA ∠=∠+∠=︒∴18060AOC AOF ∠=︒-∠=︒,即直线AE 和CD 的夹角是60︒故答案为:60.【点睛】本题考查了等腰三角形、等边三角形、全等三角形、补角、三角形外角的知识;解题的关键是熟练掌握等边三角形、全等三角形、三角形外角的性质,从而完成求解.14.在ABC 中,AB =AC ,点D 是直线BC 上一点(不与B ,C 重合),以AD 为一边在AD 的右侧作ADE ,使AD =AE ,∠DAE =∠BAC ,连接CE .(1)(请直接写出你的结论)如图1,当点D 在线段BC 上:①如果∠BAC =90°,则∠BCE =°;②如果∠BAC =100°,则∠BCE =°;(2)设∠BAC =α,∠BCE =β.①如图2,当点D在线段BC上移动,则α、β之间有怎样的数量关系?请说明理由;②当点D在直线BC上移动,则α、β之间有怎样的数量关系?请画出图形,并直接写出你的结论.【答案】(1)①90;②80;(2)①α+β=180°,理由见解析;②图见解析,α+β=180°或α=β【解析】【分析】、(1)①由等腰直角三角形的性质可得∠ABC=∠ACB=45°,由“SAS”可证△BAD≌△CAE,可得∠ABC=∠ACE=45°,可求∠BCE的度数;②由等腰三角形的性质求出∠ABD=∠ACB=40°,由“SAS”可证△ABD≌△ACE得出∠ABD =∠ACE=40°,则可得出结论;(2)①由“SAS”可证△ABD≌△ACE得出∠ABD=∠ACE,再用三角形的内角和即可得出结论;②分两种情况画出图形,由“SAS”可证△ABD≌△ACE得出∠ABD=∠ACE,再用三角形的内角和即可得出结论.【详解】解:(1)①∵AB=AC,∠BAC=90°,∴∠ABC=∠ACB=45°,∵∠DAE=∠BAC,∴∠BAD=∠CAE,∵AB=AC,AD=AE,∴△BAD≌△CAE(SAS)∴∠ABC=∠ACE=45°,∴∠BCE=∠ACB+∠ACE=90°,故答案为:90;②∵∠BAC=100°,AB=AC,∴∠ABD=∠ACB=40°,∵∠BAC=∠DAE,∴∠BAD=∠CAE,在△ABD和△ACE中,∵∠BAD=∠CAE,∵AB=AC,AD=AE,∴△ABD≌△ACE(SAS),∴∠ABD=∠ACE=40°,∴∠BCE =∠ACE +∠ACB =40°+40°=80°,故答案为:80.(2)①α+β=180°,理由:∵∠BAC =∠DAE ,∴∠BAC ﹣∠DAC =∠DAE ﹣∠DAC .即∠BAD =∠CAE .在△ABD 与△ACE 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,∴△ABD ≌△ACE (SAS ),∴∠B =∠ACE .∴∠B +∠ACB =∠ACE +∠ACB .∵∠ACE +∠ACB =β,∴∠B +∠ACB =β,∵α+∠B +∠ACB =180°,∴α+β=180°.②如图1:当点D 在射线BC 上时,α+β=180°,连接CE ,∵∠BAC =∠DAE ,∴∠BAD =∠CAE ,在△ABD 和△ACE 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,∴△ABD ≌△ACE (SAS ),∴∠ABD =∠ACE ,在△ABC 中,∠BAC +∠B +∠ACB =180°,∴∠BAC +∠ACE +∠ACB =∠BAC +∠BCE =180°,即:∠BCE+∠BAC=180°,∴α+β=180°,如图2:当点D在射线BC的反向延长线上时,α=β.连接BE,∵∠BAC=∠DAE,∴∠BAD=∠CAE,又∵AB=AC,AD=AE,∴△ABD≌△ACE(SAS),∴∠ABD=∠ACE,∴∠ABD=∠ACE=∠ACB+∠BCE,∴∠ABD+∠ABC=∠ACE+∠ABC=∠ACB+∠BCE+∠ABC=180°,∵∠BAC=180°﹣∠ABC﹣∠ACB,∴∠BAC=∠BCE.∴α=β;综上所述:点D在直线BC上移动,α+β=180°或α=β.【点睛】本题主要考查全等三角形的判定及性质,等腰三角形的性质和三角形内角和定理,掌握全等三角形的判定方法及性质是关键.15.小明同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来则形成一组全等的三角形,小明把具有这个规律的图形称为“手拉手”图形.(1)问题发现:如图1,若△ABC和△ADE均是顶角为40°的等腰三角形,BC、DE分别是底边,求证:BD=CE;(2)拓展探究:如图2,若△ACB和△DCE均为等边三角形,点A、D、E在同一条直线上,连接BE,则∠AEB的度数为;线段BE与AD之间的数量关系是;(3)解决问题:如图3,若△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一条直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM、AE、BE之间的数量关系并说明理由.【答案】(1)见解析;(2)60°,BE=AD;(3)∠AEB=90°,AE=BE+2CM,理由见解析【解析】【分析】(1)先判断出∠BAD=∠CAE,进而利用SAS判断出△BAD≌△CAE,即可得出结论;(2)同(1)的方法判断出△BAD≌△CAE,得出AD=BE,∠ADC=∠BEC,最后用角的差,即可得出结论;(3)同(2)的方法,即可得出结论.【详解】解:(1)∵△ABC和△ADE均是顶角为40°的等腰三角形,∴AB=AC,AD=AE,∠BAC=∠DAE,∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,∴∠BAD=∠CAE,∴△BAD≌△CAE(SAS),∴BD=CE;(2)∵△ABC和△ADE均是等边三角形,∴CA=CB,CD=CE,∠ACB=∠DCE=∠CDE=∠CED=60°,∴∠ACB﹣∠BCD=∠DCE﹣∠BCD,∴∠ACD=∠BCE,∴△ACD≌△BCE(SAS),∴AD=BE,∠ADC=∠BEC,∵∠CDE=60°,∴∠BEC=∠ADC=180°﹣∠CDE=120°,∵∠CED=60°,∴∠AEB=∠BEC﹣∠CED=60°,故答案为:60°,BE=AD;(3)AE=BE+2CM,理由:同(1)(2)的方法得,△ACD≌△BCE(SAS),∴AD=BE,∠ADC=∠BEC,∵△CDE是等腰直角三角形,∴∠CDE=∠CED=45°,∴∠ADC=180°﹣∠CDE=45°,∴∠BEC=∠ADC=135°,∴∠AEB=∠BEC﹣∠CED=135°﹣45°=90°,∵CD=CE,CM⊥DE,∴DM=ME,∵∠DCE=90°,∴DM=ME=CM.∴AE=AD+DE=BE+2CM.。
人教版数学八年级上册 综合专题2—全等三角形手拉手模型

长线交 CE 于 F 点.
证明重要结论:
C
① △ABD≌△ACE;
FD
② BD = CE;
③ BD 的延长线 BF⊥CE;
EA
B
解:∵△ABC、△ADE 都是等腰直角三角形, ∴ AB = AC,AD = AE. 在△ABD 和△ACE 中,
∴ △ABD≌△ACE(SAS). ∴ BD = CE. ∴ ∠ABD = ∠ACE. ∵ ∠BDC = ∠ABD + ∠BAC
E
① △ABD≌△ACE
② BD = CE
③ ∠BFC = ∠BAC = ∠DAE B
F D G
C
解:∵△ABC、△ADE 都是等腰三角形,
∴ AB = AC,AD = AE.
又∵∠BAC = ∠DAE,
A
∴∠BAC + ∠CAD =∠DAE +∠CAD,
即∠BAD = ∠CAE.
在△ABD 和△ACE 中
BE 交于点 O,AD 与 BC 交于点 P,BE 与 CD 交于点
Q,连接 PQ,则有以下五个结论: B ① AD = BE; ② PQ∥AE;
③ AP = BQ; ④ DE = DP;
⑤∠AOB = 60°.
P
OD Q
其中正确的结论有__①__②__③__⑤___.
A
C
E
=∠ACE + ∠BFC, ∴ ∠BFC = ∠BAC = 90°. ∴ BF⊥CE.
C FD
EA
B
练一练
2. 如图,△ABC、△ADE 都是等腰直角三角形,
∠BAC = ∠DAE = 90°,连接 BD、CE 交于点 F.
(1) 求证:BD = CE; (2) 求证:BD⊥CE. C
专题12.19 三角形全等几何模型-“手拉手”模型(知识讲解)
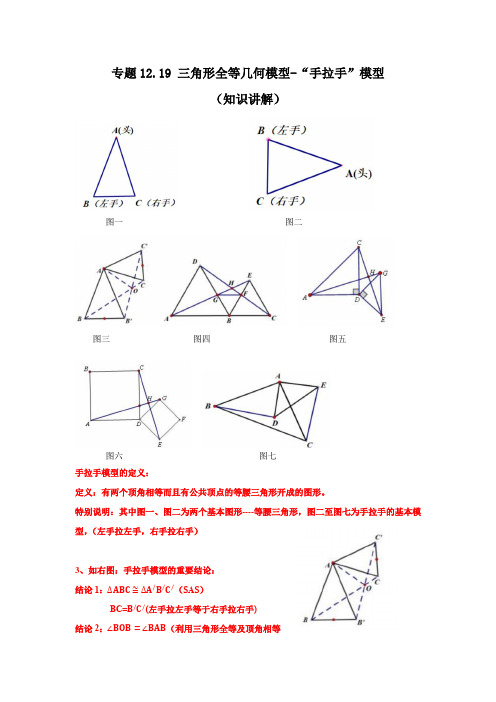
专题12.19 三角形全等几何模型-“手拉手”模型(知识讲解)图一图二图三图四图五图六图七手拉手模型的定义:定义:有两个顶角相等而且有公共顶点的等腰三角形开成的图形。
特别说明:其中图一、图二为两个基本图形----等腰三角形,图二至图七为手拉手的基本模型,(左手拉左手,右手拉右手)3、如右图:手拉手模型的重要结论:结论1:∆ABC≅∆A/B/C/(SAS)BC=B/C/(左手拉左手等于右手拉右手)结论2:∠BOB=∠BAB(利用三角形全等及顶角相等的等腰三角形底角相等)结论3:AO平分∠B O C/(利用三角形全等面积相等,再利用角平分线性质定理证明)典型例题讲练:在学习全等三角形知识时、教学兴趣小组发现这样一个模型:它是由两个共顶点且顶角相等的等腰三角形构成.在相对位置变化的同时,始终存在一对全等三角形.通过资料查询,他们得知这种模型称为“手拉手模型” 兴趣小组进行了如下操究:(1)如图1、两个等腰三角形△ABC和△ADE中,AB=AC,AE=AD,△BAC=△DAE,连接BD、CE、如果把小等腰三角形的腰长看作小手,大等腰三角形的腰长看作大手,两个等腰三角形有公共顶点,类似大手拉着小手,这个就是“手拉手模型”,在这个模型中,和△ADB 全等的三角形是,此线BD和CE的数量关系是(2)如图2、两个等腰直角三角形△ABC和△ADE中,AB=AC,AE=AD,△BAC=△DAE=90°,连接BD,CE,两线交于点P,请判断线段BD和CE的数量关系和位置关系,并说明理由:(3)如图3,已知△ABC、请完成作图:以AB、AC为边分别向△ABC外作等边△ABD和等边△ACE(等边三角形三条边相等,三个角都等于60°),连接BE,CD,两线交于点P,并直接写出线段BE和CD的数量关系及△PBC+△PCB的度数、【答案】(1)△AEC,BD=CE;(2)BD=CE且BD△CE,理由见解析;(3)作图见解析,BE=CD,△PBC+△PCB=60°.【分析】(1)根据SAS证明两个三角形全等即可证明;(2)通过条件证明△DAB△△EAC(SAS),得到△DBC+△ECB=90°,即可证明BD△CE,从而得到结果;≅即可得到证明;(3)根据已知条件证明DAC BAE解:(1)△AB=AC,AE=AD,△BAC=△DAE,∠+∠=∠+∠,△DAE EAB BAC EAB即DAB EAC ∠=∠,△()△△ADB AEC SAS ≅,△BD=CE ;(2)BD=CE 且BD△CE ;理由如下:因为△DAE=△BAC=90°,如图2.所以△DAE+△BAE=△BAC+△BAE .所以△DAB=△EAC .在△DAB 和△EAC 中,,,.AD AE DAB EAC AB AC =⎧⎪∠=∠⎨⎪=⎩所以△DAB△△EAC (SAS ).所以BD=CE ,△DBA=△ECA .因为△ECA+△ECB+△ABC=90°,所以△DBA+△ECB+△ABC=90°.即△DBC+△ECB=90°.所以△BPC=180°-(△DBC+△ECB )=90°.所以BD△CE .综上所述:BD=CE 且BD△CE .(3)如图3所示,BE=CD ,△PBC+△PCB=60°.由图可知60DAB EAC ∠=∠=︒,AD=AB ,AE=AC ,△+DAB BAC EAC BAC ∠∠=∠+∠,即DAC BAE ∠=∠,△()△DAE △BAE SAS ≅,△BE=CD ,ABE ADC ∠=∠,又△60BDA ∠=︒,△60ADC BDC ABE BDC ∠+∠=∠+∠=︒,△120BPC ABP BDC BDA ∠=∠+∠+∠=︒,△△PBC+△PCB=60°.【点拨】本题主要考查了全等三角形的知识点应用,准确分析图形是解题的关键. 举一反三变式1:如图,AC △BC ,DC △EC ,AC =BC ,DC =EC ,AE 与BD 交于点F .(1)求证:AE =BD ;(2)求△AFD 的度数.【答案】(1)详情见解析;(2)90AFD ∠=︒【分析】(1)利用角的等量代换求出ACE BCD ∠=∠,再判断ACE ≌BCD △即可求解; (2)利用全等三角形的性质得到E D ∠=∠,再通过角的等量代换求解即可.解:(1)△AC BC ⊥,DC EC ⊥△90ACB ECD ∠=∠=︒△ACB BCE ECD BCE ∠+∠=∠+∠△ACE BCD ∠=∠在ACE 和BCD △中AC BC ACE BCD DC EC =⎧⎪∠=∠⎨⎪=⎩△ACE ≌BCD △(SAS)△AE BD =(2)设BD 与CE 的交点为G ,如图所示:△ACE ≌BCD △△E D ∠=∠△180EFG FGE E ++=︒∠∠∠,180GCD CGD D ++=︒∠∠∠,且BGE CGD ∠=∠△90EFG GCD ==︒∠∠△90AFD ∠=︒【点拨】本题主要考查了全等三角形的性质和判定,灵活运用角的等量代换是解题的关键.例题2.已如:如图1,B ,C ,D 三点在一条直线上,△ABC 和△ECD 均为等边三角形,连接BE ,AD 交于点F ,BE 交AC 于点M ,AD 交CE 于点N .(1)以下结论正确的有 ;△AD =BE △△EFD =60° △MC =NC △△AMB =△END(2)探究:将图1中的△ECD 绕点C 顺时针旋转一个角度(旋转角小于60°),如图2所示. △问:(1)中的正确结论哪些还成立?若成立,请说明理由;△连接FC ,如图3所示,求证:FC 平分△BFD【答案】(1)△△△;(2)△ △△;△见解析.【分析】(1)△根据等边三角形的性质得CA =CB ,CD =CE ,△ACB =60°,△DCE =60°,则△ACE =60°,利用“SAS ”可判断△ACD △△BCE ,则AD =BE ;△根据三角形外角关系得△EFD =△EBC +△ADC =△DAC +△ADC =△ACB =60°,从而可得结论; △连接MN ,证明△MCN 是等边三角形即可得出结论;△60,60AMB EBC END NDC ∠=︒+∠∠=︒+∠,而AC ≠CD 得CAD CDA ∠≠∠,从而可得出结论;(2)△方法同(1),逐个结论进行证明即可;△作,CG BE CH AD ⊥⊥于点G ,H ,证明△BGC △△AHC ,△CGF △△CHF 可得△CFG CFH =∠,从而可得结论.解:(1)△△ABC ,△ECD 是等边三角形,△AC=BC ,CE=CD ,△ACB=△ECD=60°△△ACD=△BCE=△120°△△ACD△△BCE△AD=BE ,故△正确;△△FEN=△NDC又△△ENF=△CND△△EFD=△ECD=60°,故△正确;又△△ACE=△NCD=60°△MEC=△NDCEC=CD△△EMC△△DNC△MC=NC ,故△正确;又△△AMB=△ACB+△ECB=60°+△ECB ,△END=△ECD+△NDC=60°+△NDC而AC CD ≠△CAD CDA ∠≠∠△MBC NDC ∠≠∠△MBC END ∠≠∠,故△错误;故答案为:△△△;(2)△△ACB=△ECD=60°△△BCE=△ACD又AC=BC ,CE=CD△△ACD△△BCE△AD=BE,故△正确;△△ADC=△BEC又△ENF=△CND△△EFD=△ECD=60°,故△正确△△ACE≠60°=△ECD△△EMC 不全等于△DNC ,△MC≠NC ,故△错误(3),CG BE CH AD ⊥⊥于点G ,H ,如图,由(2)△知,△CBG=△CAHAC=BC△BGC=△AHC=90°△△BGC△△AHC△CG=CH又CF=CF ,△CGF=△CHF=90°△△CGF△△CHF△△CFG=△CFH△FC 平分△BFD【点拨】本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS ”、“SAS ”、“ASA ”、“AAS ”;全等三角形的对应边相等.也考查了等边三角形的判定与性质.举一反三变式:如图,在ABC∆中,分别以AC,BC为边作等边三角形ACD和等边三角形BCE,连接AE,BD交于点O,则AOB∠的度数为()A.100︒B.120︒C.130︒D.150︒【答案】B【分析】先证明△DCB△△ACE,求出△CAE=△CDB,再利用“8字型”证明△AOH=△DCH =60°即可解决问题.解:如图:AC与BD交于点H,△△ACD,△BCE都是等边三角形,△CD=CA,CB=CE,△ACD=△BCE=60°,△△DCB=△ACE,在△DCB和△ACE中,CD CADCB ACECB CE⎧⎪∠∠⎨⎪⎩===,△△DCB△△ACE,△△CAE=△CDB,△△DCH+△CHD+△BDC=180°,△AOH+△AHO+△CAE=180°,△DHC=△OHA,△△AOH=△DCH=60°,△△AOB=180°−△AOH=120°.故选:B.【点拨】本题考查全等三角形的判定和性质、等边三角形的性质等知识,解题的关键是正确寻找全等三角形,学会利用“8字型”证明角相等,属于中考常考题型.例题3.(阅读材料)小明同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的项角的顶点,并把它们的底角顶点连接起来则形成一组全等的三角形,小明把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小明发现若△BAC=△DAE,AB=AC,AD=AE,则△ABD△△ACE.(材料理解)(1)在图1中证明小明的发现.(深入探究)(2)如图2,△ABC和△AED是等边三角形,连接BD,EC交于点O,连接AO,下列结论:△BD=EC;△△BOC=60°;△△AOE=60°;△EO=CO,其中正确的有.(将所有正确的序号填在横线上).(延伸应用)(3)如图3,AB=BC,△ABC=△BDC=60°,试探究△A与△C的数量关系.【答案】(1)证明见解析;(2)△△△;(3)△A+△C=180°.【分析】(1)利用等式的性质得出△BAD=△CAE,即可得出结论;(2)同(1)的方法判断出△ABD△△ACE,得出BD=CE,再利用对顶角和三角形的内角和定理判断出△BOC=60°,再判断出△BCF△△ACO,得出△AOC=120°,进而得出△AOE=60°,再判断出BF<CF,进而判断出△OBC>30°,即可得出结论;(3)先判断出△BDP是等边三角形,得出BD=BP,△DBP=60°,进而判断出△ABD△△CBP(SAS ),即可得出结论.(1)证明:△△BAC=△DAE ,△△BAC+△CAD=△DAE+△CAD , △△BAD=△CAE ,在△ABD 和△ACE 中,AB AC BAD CAE AD AE ⎧⎪∠∠⎨⎪⎩=== ,△△ABD△△ACE ;(2)如图2,△△ABC 和△ADE 是等边三角形, △AB=AC ,AD=AE ,△BAC=△DAE=60°, △△BAD=△CAE ,在△ABD 和△ACE 中,AB AC BAD CAE AD AE ⎧⎪∠∠⎨⎪⎩=== ,△△ABD△△ACE ,△BD=CE ,△正确,△ADB=△AEC , 记AD 与CE 的交点为G ,△△AGE=△DGO ,△180°-△ADB -△DGO=180°-△AEC -△AGE , △△DOE=△DAE=60°,△△BOC=60°,△正确,在OB上取一点F,使OF=OC,△△OCF是等边三角形,△CF=OC,△OFC=△OCF=60°=△ACB,△△BCF=△ACO,△AB=AC,△△BCF△△ACO(SAS),△△AOC=△BFC=180°-△OFC=120°,△△AOE=180°-△AOC=60°,△正确,连接AF,要使OC=OE,则有OC=12 CE,△BD=CE,△CF=OF=12 BD,△OF=BF+OD,△BF<CF,△△OBC>△BCF,△△OBC+△BCF=△OFC=60°,△△OBC>30°,而没办法判断△OBC大于30度,所以,△不一定正确,即:正确的有△△△,故答案为△△△;(3)如图3,延长DC至P,使DP=DB,△△BDC=60°,△△BDP 是等边三角形,△BD=BP ,△DBP=60°,△△BAC=60°=△DBP ,△△ABD=△CBP ,△AB=CB ,△△ABD△△CBP (SAS ),△△BCP=△A ,△△BCD+△BCP=180°,△△A+△BCD=180°.【点拨】此题考查三角形综合题,等腰三角形的性质,等边三角形的性质,全等三角形的判定和性质,构造等边三角形是解题的关键.举一反三变式:如图,C 为线段AE 上一动点(不与点,A E 重合),在AE 同侧分别作等边三角形ABC 和等边三角形,CDE AD 与BE 交于点O ,AD 与BC 交于点P ,BE 与CD 交于点Q ,连结PQ .以下结论:①AD BE =;①//PQ AE ;①60AOB ∠=︒;①CPQ 是等边三角形,恒成立的是______.【答案】△△△△【分析】△由△ABC 和△CDE 都是等边三角形,可知AC=BC ,CD=CE ,△ACB=△DCE=60°,所以△ACD=△BCE=120°,所以△ACD△△BCE (SAS ),从而AD=BE ,故△正确;△△由△ACD△△BCE 得△CBE=△DAC ,加之AC=BC ,易得△ACB=△BCQ=60°,可证△CQB△△CPA (ASA ),从而CP=CQ ,再加之△PCQ=60°,可推出△PCQ 为等边三角形,易得△PQC=60°=△DCE ,根据内错角相等,两直线平行,可知△△正确;△结合△ACD△△BCE 和三角形的外角的性质,可得△AOB=60°,故△正确.解:△△等边△ABC 和等边△CDE ,△AC=BC ,CD=CE ,△ACB=△DCE=60°,△△ACB+△BCD=△DCE+△BCD ,即△ACD=△BCE ,△在△ACD 与△BCE 中,AC BC ACD BCE CD CE ⎧⎪∠∠⎨⎪⎩===△△ACD△△BCE (SAS ),△AD=BE ,故△正确;△△△△ACD△△BCE ,△△CBE=△DAC ,△由△ACB=△DCE=60°得△BCD=60°,△△ACP=△BCQ ,又△AC=BC ,△△CQB△△CPA (ASA ),△CP=CQ ,又△△PCQ=60°△△PCQ 为等边三角形,△△PQC=60°,△△PQC=60°=△DCE△PQ△AE故△△正确;△△△ACD△△BCE (SAS ),△△CAD=△CBE ,△△AOB=△CAD+△CEB=△CBE+△CEB ,又△△ACB=△CBE+△CEB=60°,△△AOB=△ACB=60°,故△正确.故答案为:△△△△.【点拨】本题考查了等边三角形的性质、全等三角形的判定与性质、三角形外角的性质,熟练应用三角形全等的判定是解题的关键.。
中考数学相似三角形中的重要模型手拉手模型

相似三角形中的重要模型-手拉手模型相似三角形是初中几何中的重要的内容,常常与其它知识点结合以综合题的形式呈现,其变化很多,是中考的常考题型。
手拉手模型相似是手拉手模型当中相对于手拉手全等模型较难的一种模型,在实际的应用和解题当中出现时,对于同学们来说,都比较困难。
而深入理解模型内涵,灵活运用相关结论可以显著提高解题效率,本专题重点讲解相似三角形的“手拉手”模型(旋转模型)。
手拉手相似证明题一般思路方法:①由线段乘积相等转化成线段比例式相等;②分子和分子组成一个三角形、分母和分母组成一个三角形;③第②步成立,直接从证这两个三角形相似,逆向证明到线段乘积相等; ④第②步不成立,则选择替换掉线段比例式中的个别线段,之后再重复第③步。
模型1.“手拉手”模型(旋转模型)【模型解读与图示】“手拉手”旋转型定义:如果将一个三角形绕着它的项点旋转并放大或缩小(这个顶点不变),我们称这样的图形变换为旋转相似变换,这个顶点称为旋转相似中心,所得的三角形称为原三角形的旋转相似三角形。
1)手拉手相似模型(任意三角形)条件:如图,∠BAC=∠DAE=α,A DA E kA BA C==; 结论:△ADE ∽△ABC ,△ABD ∽△ACE ;E CkB D=.2)手拉手相似模型(直角三角形)条件:如图,90A O BC OD ∠=∠=︒,O C O D kO AO B==(即△COD ∽△AOB );结论:△AOC ∽△BOD ;B DkA C=,AC ⊥BD ,12A B C DS A B C D=⨯.3)手拉手相似模型(等边三角形与等腰直角三角形)条件:M 为等边三角形ABC 和DEF 的中点; 结论:△BME ∽△CMF ;B EC F条件:△ABC 和ADE 是等腰直角三角形; 结论:△ABD ∽△ACE.例1.(2022·山西·寿阳县九年级期末)问题情境:如图1所示,在△ABC 中,D 、E 分别是AB 、AC 上的点,DE ∥BC ,在图1中将ADE 绕A 点顺时针旋转一定角度,得到图2,然后将BD 、CE 分别延长至M 、N ,使DM =12BD ,EN =12CE ,得到图3,请解答下列问题:(1)猜想证明:若AB =AC ,请探究下列数量关系:①在图2中,BD 与CE 的数量关系是_________. ②在图3中,猜想∠MAN 与∠BAC 的数量关系,并证明你的猜想;(2)拓展应用:其他条件不变,若AB ,按上述操作方法,得到图4,请你继续探究:∠MAN 与∠BAC的数量关系?AM 与AN 的数量关系?直接写出你的猜想.例2.(2022•新乡中考模拟)在△ABC中,CA=CB=m,在△AED中,DA=DE=m,请探索解答下列问题.【问题发现】(1)如图1,若∠ACB=∠ADE=90°,点D,E分别在CA,AB上,则CD与BE的数量关系是,直线CD与BE的夹角为;【类比探究】(2)如图2,若∠ACB=∠ADE=120°,将△AED绕点A旋转至如图2所示的位置,则CD 与BE之间是否满足(1)中的数量关系?说明理由.【拓展延伸】(3)在(1)的条件下,若m=2,将△AED绕点A旋转过程中,当B,E,D三点共线.请直接写出CD的长.例3.(2022·山东·九年级课时练习)【问题发现】如图1,在Rt△ABC中,∠BAC=90°,AB=AC,D为斜边BC上一点(不与点B,C重合),将线段AD绕点A顺时针旋转90°得到AE,连接EC,则线段BD与CE的数量关系是______,位置关系是______;【探究证明】如图2,在Rt△ABC和Rt△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,将△ADE绕点A旋转,当点C,D,E在同一条直线上时,BD与CE具有怎样的位置关系,说明理由;【拓展延伸】如图3,在Rt△BCD中,∠BCD=90°,BC=2CD=4,过点C作CA⊥BD于A.将△ACD绕点A顺时针旋转,点C的对应点为点E.设旋转角∠CAE为α(0°<α<360°),当C,D,E在同一条直线上时,画出图形,并求出线段BE的长度.例4.(2022·山东·东营市一模)【提出问题】(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.【类比探究】(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.【拓展延伸】(3)如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.例5.(2022•长垣市一模)在△AB=AC,点D为AB边上一动点,∠CDE=∠BAC=α,CD=ED,连接BE,EC.(1)问题发现:如图①,若α=60°,则∠EBA=,AD与EB的数量关系是;(2)类比探究:如图②,当α=90°时,请写出∠EBA的度数及AD与EB的数量关系并说明理由;(3)拓展应用:如图③,点E为正方形ABCD的边AB上的三等分点,以DE为边在DE上方作正方形DEFG,点O为正方形DEFG的中心,若OA=,请直接写出线段EF的长度.例6.(2022·成都市·九年级课时练习)一次小组合作探究课上,老师将两个正方形按如图所示的位置摆放(点E 、A 、D 在同一条直线上),发现B ED G=且B ED G⊥.小组讨论后,提出了下列三个问题,请你帮助解答:(1)将正方形A E F G 绕点A 按逆时针方向旋转(如图1),还能得到B E D G=吗?若能,请给出证明,请说明理由;(2)把背景中的正方形分别改成菱形A E F G 和菱形A B C D ,将菱形A E F G 绕点A 按顺时针方向旋转(如图2),试问当E A G ∠与B A D ∠的大小满足怎样的关系时,B ED G=;(3)把背景中的正方形分别改写成矩形A E F G 和矩形A B C D ,且23AE AB AGAD==,2A Ea=,2A Bb=(如图3),连接D E ,B G .试求22D E B G+的值(用a ,b 表示).课后专项训练1.如图,在△ABC与△ADE中,∠ACB=∠AED=90°,∠ABC=∠ADE,连接BD、CE,若AC:BC=3:4,则BD:CE为()A.5:3B.4:3C.√5:2D.2:√32.如图,△ABC∽△ADE,∠BAC=∠DAE=90°,AB与DE交于点O,AB=4,AC=3,F是DE的中点,连接BD,BF,若点E是射线CB上的动点,下列结论:①△AOD∽△FOB,②△BOD∽△EOA,③∠FDB+∠FBE=90°,④BF=56AE,其中正确的是()A.①②B.③④C.②③D.②③④3、如图,正方形A B C D的边长为8,线段C E绕着点C逆时针方向旋转,且3C E=,连接B E,以B E为边作正方形B E F G,M为A B边的中点,当线段F M的长最小时,ta n E C B∠=______.4.(2022•虹口区期中)如图,在△ABC和△ADE中,∠BAD=∠CAE,∠ABC=∠ADE.(1)求证:△ABC∽△ADE;(2)判断△ABD与△ACE是否相似?并证明.5.(2023·浙江·九年级课时练习)在△ABC中,AB=AC,∠BAC=α,点P为线段CA延长线上一动点,连接PB,将线段PB绕点P逆时针旋转,旋转角为α,得到线段PD,连接DB,DC.(1)如图1,当α=60°时,求证:P A=DC;(2)如图2,当α=120°时,猜想P A和DC的数量关系并说明理由.(3)当α=120°时,若AB=6,BP D到CP的距离.6.(2022·重庆·九年级课时练习)观察猜想(1)如图1,在等边A B C中,点M 是边B C 上任意一点(不含端点B 、C ),连接A M ,以A M 为边作等边A M N,连接C N ,则A B C ∠与A C N ∠的数量关系是______. (2)类比探究:如图2,在等边A B C中,点M 是B C 延长线上任意一点(不含端点C ),(1)中其它条件不变,(1)中结论还成立吗?请说明理由. (3)拓展延伸:如图3,在等腰A B C中,B AB C=,点M 是边B C 上任意一点(不含端点B 、C ),连接A M ,以A M 为边作等腰A M N,使顶角A M NA B C∠=∠.连按C N .试探究A B C ∠与A C N ∠的数量关系,并说明理由.7.(2022·江苏·九年级课时练习)【问题发现】如图1,在Rt △ABC 中,∠BAC =90°,AB =AC ,D 为斜边BC 上一点(不与点B ,C 重合),将线段AD 绕点A 顺时针旋转90°得到AE ,连接EC ,则线段BD 与CE 的数量关系是______,位置关系是______;【探究证明】如图2,在Rt △ABC 和Rt △ADE 中,∠BAC =∠DAE =90°,AB =AC ,AD =AE ,将△ADE 绕点A 旋转,当点C ,D ,E 在同一条直线上时,BD 与CE 具有怎样的位置关系,说明理由;【拓展延伸】如图3,在Rt △BCD 中,∠BCD =90°,BC =2CD =4,过点C 作CA ⊥BD 于A .将△ACD 绕点A 顺时针旋转,点C 的对应点为点E .设旋转角∠CAE 为α(0°<α<360°),当C ,D ,E 在同一条直线上时,画出图形,并求出线段BE 的长度.8.(2022·山东·九年级课时练习)如图,A B C和A D E是有公共顶点直角三角形,90B A C D A E ∠=∠=︒,点P 为射线B D ,C E 的交点.(1)如图1,若A B C和A D E是等腰直角三角形,求证:C PB D⊥;(2)如图2,若30A D EA B C ∠=∠=︒,问:(1)中的结论是否成立?请说明理由.(3)在(1)的条件下,4A B =,3A D =,若把A D E 绕点A 旋转,当90E A C ∠=︒时,请直接写出P B 的长度9.(2023·广东·深圳市九年级期中)(1)如图1,Rt △ABC 与Rt △ADE ,∠ADE =∠ABC =90°,12A BA DB CD E==,连接BD ,CE .求证:5B DC E=.(2)如图2,四边形ABCD ,∠BAD =∠BCD =90°,且12A B A D=,连接BC ,BC 、AC 、CD 之间有何数量关系?小明在完成本题中,如图3,使用了“旋转放缩”的技巧,即将△ABC 绕点A 逆时针旋转90°,并放大2倍,点B 对应点D .点C 落点为点E ,连接DE ,请你根据以上思路直接写出BC ,AC ,CD 之间的关系. (3)拓展:如图4,矩形ABCD ,E 为线段AD 上一点,以CE 为边,在其右侧作矩形CEFG ,且12A B C EB CE F==,AB=5,连接BE,BF.求BE的最小值.510.(2023·绵阳市·九年级专题练习)在△ABC中,AB=AC,∠BAC=α,点P是△ABC外一点,连接BP,将线段BP绕点P逆时针旋转α得到线段PD,连接BD,CD,AP.观察猜想:的值为,直线CD与AP所成的较小角的度数为°;(1)如图1,当α=60°时,C DA P的值及直线CD与AP所成的较小角的度数;类比探究:(2)如图2,当α=90°时,求出C DA P拓展应用:(3)如图3,当α=90°时,点E,F分别为AB,AC的中点,点P在线段FE的延长线上,点A,D,P三点在一条直线上,BD交PF于点G,CD交AB于点H. 若CD=2BD的长.11.(2023·湖北·九年级专题练习)在A B C和A D E中,B A B C∠=∠=,点=,D A D E=,且A B C A D EαE在A B C的内部,连接EC,EB,EA和BD,并且90∠+∠=︒.A C E AB Eα=︒时,线段BD与CE的数量关系为__________,线段EA,EB,EC的【观察猜想】(1)如图①,当60数量关系为__________.α=︒时,(1)中的结论是否依然成立?若成立,请给出证明,若不成立,【探究证明】(2)如图②,当90请说明理由;【拓展应用】(3)在(2)的条件下,当点E在线段CD上时,若B C=B D E的面积.12.(2023··广西一模)如图,A C B△和D C E均为等腰直角三角形,,.现将D C E绕点C旋转.∠=∠=︒==A CB DC E A C B CD CE C90,(1)如图1,若,,A D E三点共线,A D=B到直线C E的距离;(2)如图2,连接,A EB D,点F为线段B D的中点,连接C F,求证:A E C F⊥;(3)如图3,若点G在线段A B上,且8,==,在A C G内部有一点O,请直接写出A C A G22O C A G++的最小值.13.(2022•南山区校级一模)(1)【问题发现】如图①,正方形AEFG 的两边分别在正方形ABCD 的边AB 和AD 上,连接CF .填空:①线段CF 与DG 的数量关系为 ;②直线CF 与DG 所夹锐角的度数为 .(2)【拓展探究】如图②,将正方形AEFG 绕点A 逆时针旋转,在旋转的过程中,(1)中的结论是否仍然成立,请利用图②进行说明.(3)【解决问题】如图③,△ABC 和△ADE 都是等腰直角三角形,∠BAC =∠DAE =90°,AB =AC =10,O 为AC 的中点.若点D 在直线BC 上运动,连接OE ,则在点D 的运动过程中,线段OE 长的最小值为 (直接写出结果).14、某校数学活动小组在一次活动中,对一个数学问题作如下探究:(1)问题发现:如图1,在等边A B C 中,点P 是边B C 上任意一点,连接A P ,以A P 为边作等边A P Q,连接CQ ,BP 与CQ 的数量关系是________; (2)变式探究:如图2,在等腰A B C中,A BB C=,点P 是边B C 上任意一点,以A P 为腰作等腰A P Q,使A PP Q=,A P QA B C∠=∠,连接C Q ,判断A B C ∠和A C Q ∠的数量关系,并说明理由;(3)解决问题:如图3,在正方形A D B C 中,点P 是边B C 上一点,以A P 为边作正方形A P E F ,Q 是正方形A P E F 的中心,连接C Q .若正方形A P E F 的边长为5,2C Q =A DBC 的边长.15、如图,四边形ABCD 和四边形AEFG 都是正方形,C ,F ,G 三点在一直线上,连接AF 并延长交边CD 于点M .(1)求证:△MFC ∽△MCA ;(2)求证△ACF ∽△ABE ; (3)若DM =1,CM =2,求正方形AEFG 的边长.16、已知,ABC 中,AB =AC ,∠BAC =2α°,点D 为BC 边中点,连接AD ,点E 为线段AD 上一动点,把线段CE绕点E顺时针旋转2α°得到线段EF,连接FG,FD.(1)如图1,当∠BAC=60°时,请直接写出B F的值;(2)如图2,当∠BAC=90°时,(1)中的结论是A E否仍然成立?若成立,请给出证明;若不成立,请写出正确的结论,并说明理由;(3)如图3,当点E在AD上移动时,请直接写出点E运动到什么位置时D F的值最小.最小值是多少?(用含α的三角函数表示)D C。
2023年中考数学微专题复习课件5 手拉手模型

模型
模型说明
手拉 手相 似模 型
1.△AOB∽△CO D,OA=OB, ∠AOB=α; 2.将△COD绕点 O旋转,直线 AC,BD交于点 E,所夹锐角为β
图示
5
基ห้องสมุดไป่ตู้结论
1.△AOC≌△BOD (点A,O,C三点 不共线); 2.当α≤90°时,β =α,当α>90° 时,β=180°-α; 3.点E在△OAB的外 接圆上
第四章 三角形
微专题五 手拉手模型
1.说明:两个三角形的顶点重合,其中一个三角形不动,另一个三角形绕着重合的顶点 旋转,就好像手拉着手一样,所以称为“手拉手”模型. 2.判断方法:将初始图形的公共顶点放在上方,图形正对着我们,左边顶点称为“左 手”,右边顶点称为“右手”.
2
3.特点:(1)两条“拉手线”所在直线夹角与初始图形中公共顶点对应的角相等 或互补; (2)三角形顺时针或逆时针旋转,得到的结论相同; (3)“手拉手”模型中,若“手拉手”的两个三角形均是等腰三角形,且公共顶点是 顶角顶点,则对应边与“拉手线”组成的两个三角形全等;若两个三角形为非等腰三角 形,则对应边与“拉手线”组成的两个三角形相似.
26
▶类型2:手拉手相似模型 2.如图1,在Rt△ABC中,∠B=90°,AB=8,BC=6,D,E分别是BC,AC的中点,连 接DE,将△EDC绕点C按逆时针方向旋转,记旋转角为α.
(1)问题发现:
图1
27
(2)拓展探究: ②当△ACE为直角三角形时,直接写出线段BD的长.
图2
28
图2
29
(1)问题发现
图1
9
(2)如图2,当∠BAC=90°且AB≠AC时,(1)中的结论是否仍然成立?若成立,请 写出证明过程;若不成立,请说明理由;
什么是手拉手几何模型?12个常用结论你都能证明出来吗?怎么用?

什么是手拉手几何模型?12个常用结论你都能证明出来吗?怎么用?手拉手模型,是数学里最常见的一个几何图形,是属于共端点几何模型中的一个类别。
在平时的数学考试中,经常会遇到一类考题,它像旋转一样,它像两个人手拉住手一样。
所,民间称之为手拉手模型。
如上图,就是手拉手模型的基础图形。
当然考试的时候,也经常会出现变式题。
但不管怎么变,所有的题型都是从这几个基础图形,变式而来的。
所以必须先把上图,这基础的内容弄懂,理解透彻。
手拉手模型到底有什么用?在考试的时候,常常会出现在压轴题里,选择题填空题和简答题,都经常出现。
然后这个模型,基本都会推导出12个基本结论。
这12个基本结论,你熟练了。
如果,这12个结论你都知道是怎么推导出来的。
那么考试的时候,看起来特别复杂的几何题,自然都不在话下。
这就是学习方法。
上面的图,就是手拉手基础模型的12个结论。
你尝试这一个一个的推导出来。
(第11,12个结论是初三才学的内容,前面10个结论初二同学基本都能证明。
)方老师经常告诉同学们,数学要多思考,多练习,多总结归纳。
那么像这样子,一个图形,一道题目,涵盖了所有这一类题型的,所有结论和出题模式。
这就是总结和归纳。
第1题,手拉手模型的基础形式,这两个三角形全等,就是SAS,可以轻松证明出来。
第2题,第①小题,SAS证明△ABE≌△CBF就可以了。
第②,因为三角形全等,AB=CB,所以△ABC是等腰直角三角形。
结论就很简单了,自行推导。
第3题,第4题,一样的,根据手拉手模型的一般套路,根据题意找到两个三角形全等。
后面的结论,就非常简单。
总之一句话,手拉手模型的第一步,先找到手拉住手的两个三角形全等关系。
然后,对应角相等,对应边相等。
后面的结论,自然不难。
也请大家多总结,多归纳,多和同学交流,分享心得。
数学的学习,一通百通,所以一定要多钻研。
这才是提高数学成绩的法宝。
初中数学模型【讲义】全等“手拉手”模型(上)

全等“手拉手”模型一、模型背景全等“手拉手”模型:两个顶角相等的等腰三角形,若顶点重合,则构成全等“手拉手”模型,其中连接左、右对应的底角顶点所得线段,称为“拉手线”(如图中BE和CF)全等“手拉手”模型,主要是利用全等三角形的知识,判断拉手线之间的数量关系和位置关系(夹角度数)二、模型内容(一)等边三角形的“手拉手”模型1. 共线型(特例)如图,已知等边三角形ABC与等边三角形ADE,其中C、A、D三点共线,连接BD、CE交于点H.问题1. 判断BD与CE的数量关系;问题2. 求∠BHC的度数(BD与CE的夹角)【证明】2. 不共线型(一般情况)如图,已知等边三角形ABC与等边三角形ADE,连接BD、CE交于点H.问题1. 判断BD与CE的数量关系;问题2. 求∠BHC的度数(BD与CE的夹角)【证明】引申:(判断以下结论哪些依然满足,哪些不满足,无需证明)(1)全等关系:△ABD≌△ACE;△ACM≌△ABN;△AEM≌△ADN(2)线段相等:BD=CE;BN=CM;EM=DN(3)角度:∠BHC=60°;∠DHE=60°;∠MHN=120°(4)角平分线:AH平分∠CHD(5)等边三角形:△AMN是等边三角形(6)平行:MN∥CD(7)截长补短线段相等:CH=BH+AH;DH=EH+AH;MH+NH=AH(8)四点共圆:A、M、H、N四点共圆;A、C、B、H四点共圆;A、D、E、H四点共圆(二)等腰直角三角形的“手拉手”模型如图,已知等腰直角三角形ABC与等腰直角三角形ADE,连接BD、CE交于点H.问题1. 判断BD与CE的数量关系;问题2. 求∠BHC的度数(BD与CE的夹角)(三)正方形的“手拉手”模型如图,已知正方形ABCD与正方形AEFG,连接BE、DG交于点H,连接AH.(四)等腰三角形的“手拉手”模型(类型一、二、三的一般情况)如图,已知等腰三角形ABC与等腰三角形ADE,AB=AC,AD=AE,∠BAC=∠DAE=α,连接BD、CE.问题1. 判断BD与CE的数量关系;问题2. 延长BD和CE相交于点H,求∠BHC的度数(BD与CE的夹角)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《三角形证明》题型解读12 全等典型模型:“手拉手”模型【知识梳理】(一)“手拉手模型”的基本图形题型特征:△ABC 与△BDE 是等边三角形,A 、B 、D 三点在同一直线上。
解题方法:一定有以下六个结论(三组全等、一个60°、一个等边△、一组平行线) ①△ABE ≌△CBD证明过程:∵△ABC 与△BDE 是等边三角形,∴∠1=∠2=∠3=60°,∴∠ABE=∠CBD=120°,∵AB=BC ,BE=BD , ∴△ABE ≌△CBD (SAS ) ②△ABH ≌△CBF证明过程:∵△ABE ≌△CBD ,∴∠4=∠5,∵AB=BC ,∠1=∠2,∴△ABH ≌△CBF (SAS ) ③△BHE ≌△BFD证明过程:∵△ABE ≌△CBD ,∴∠6=∠7,∵BE=BD ,∠2=∠3,∴△BHE ≌△BFD (SAS ) ④∠AGC=60°证明过程:∵△ABE ≌△CBD ,∴∠6=∠7,在△GFE 和△BFD 中(“8”字模型),∠3=180°-∠BFD-∠7,∠EGF=180°-∠GFE-∠6,∵∠6=∠7,∠GFE=∠BFD ,∴∠3=∠EGF ,∵∠AGC=∠EGF ,∠3=60°,∴∠AGC=∠3=60° ⑤△BHF 是等边三角形证明过程:∵△BHE ≌△BFD (SAS ),∴BH=BF ,∵∠2=60°,∴△BHF 是等边三角形(有一个角是60°的等腰三角形是等边三角形) ⑥HF//AD证明过程:∵△BHF 是等边三角形,∴∠8=60°,∵∠3=60°,∴∠8=∠3,∴HF//AD (二)“手拉手模型”的变化图形题型特征:△ABC 与△BDE 是等边三角形,A 、B 、D 三点不在同一直线上。
图2M N 765431H GFEDCBA765431HG F ED CBA解题方法:一定有以下六个结论(一组全等,一个60°、一个角平分线) ①△ABE ≌△CBD证明过程:∵△ABC 与△BDE 是等边三角形,∴∠1=∠3=60°,∴∠ABE=∠CBD (共角模型),∵AB=BC ,BE=BD , ∴△ABE ≌△CBD (SAS ) ②∠AGC=60°证明过程:∵△ABE ≌△CBD ,∴∠6=∠7,在△GFE 和△BFD 中(“8”字模型),∠3=180°-∠BFD-∠7,∠EGF=180°-∠GFE-∠6,∵∠6=∠7,∠GFE=∠BFD ,∴∠3=∠EGF ,∵∠AGC=∠EGF ,∠3=60°,∴∠AGC=∠3=60° ③BG 平分∠HBF证明过程:作BM ⊥AE 于点M ,BN ⊥GD 于点N ,如图2,∵△ABE ≌△CBD ,∴∠4=∠5,∵AB=BC ,∠AMB=∠CNB=90°,∴△ABM ≌△CBN (AAS ),∴BM=BN ,∴BG 平分∠HBF (到角两边的距离相等的点,在这个角的角平分线上)(三)常见“手拉手”变化图形【典型例题】例1.如图,C 为线段AE 上一动点(不与A 、E 重合),在AE 同侧分别作等边△ABC 和等 边△CDE ,AD 与BE 交于点O ,AD 与BC 交于点P ,BE 与CD 交于点Q ,连接PQ ,以下五个结论: ①AD =BE ;②PQ ∥AE ;③CP =CQ ;④BO =OE ;⑤∠AOB =60°,恒成立的结论有( )。
A 、①③⑤ B 、①③④⑤ C 、①②③⑤ D 、①②③④⑤ 解析:由“手拉手模型”的基础图形的六个结论可直接判别,选CABC 、ADE 是等边三角形,则ABD ≅ACE ,CE=BD 其实质是ADE 绕点A 旋转EDE DE DEDABC ABCABC C BAABC 、ADE 是等腰直角三角形,则ABD ≅ACE ,CE=BD 其实质是ADE 绕点A 旋转E DEDEDEDABCAB CABCCBA例2.如图,△ABD 与△AEC 都是等边三角形,AB ≠AC ,下列结论中,正确的个数是( ) ①BE=CD ;②∠BOD=60°;③∠BDO=∠CEO ;④若∠BAC=90°,且DA//BC ,则BC ⊥CE. A. 1 B. 2 C. 3 D. 4 【思路分析】多结论题型、数学典型模型“手拉手模型”。
选C(1)证线段相等,首选三角形全等,找BE 、CD 所在三角形△ABE 、△ADC 全等。
由△ABD 、△AEC 是等边三角形,不难找到全等条件:已知条件AD=AB 、已知条件∠BAD=∠EAC=60°,由共角模型易得∠DAC=∠BAE,已知条件AC=AE,由SAS 易证△ADC ≌△ABE,∴BE=CD,①正确;(2)依解题思路的延续性,由(1)中△ADC ≌△ABE 可得∠ADC=∠ABE ,由三角形内角和公式可得:∠BOD=180°-(∠ODB+∠DBA+∠ABE)=180°-(∠ODB+∠DBA+∠ADC)= 180°-(∠ADB+∠DBA)=180-(60°+60°)=60°,②正确; (3)可用反证法解题。
假设③成立,由于△ODB 与△OEC 组成的“8字模型”易得∠OBD=∠OCE ,即60°+∠ABO=60°+∠ACO ,∴∠ABO=∠ACO ,∵∠ACO=∠AEB,∴∠ABO=∠AEB,∴AB=AE ,即AB=AC,与AB ≠AC 矛盾,故假设不成立,即③错误;(4)若BC ⊥CE ,即∠ACE+∠ACB=90°,且∠ACE=60°,由于∠ABC+∠ACB=90°,所以只需证∠ABC=60°即可,由AD//BC ,由两直线平行内错角相等可得∠ABC=∠DAB=60°,∴∠BCE=90°,即BC ⊥CE ,④正确.例3. 如图,四边形ABCD 中,F 是CD 上一点,E 是BF 上一点,连接AE 、AC 、DE ,若AB=AC ,AD=AE ,∠BAC=∠DAE=70°,AE 平分∠BAC ,则下列结论中:①△ABE ≌△ACD ;②BE=EF ;③∠BFD=110°;④AC 垂直平分DE ,正确的结论是____解析:(1)由“共角模型”可得∠BAE=∠CAD ,由AB=AC,AE=AD,可证△ABE ≌△ACD ,①正确;(2)由△ABE ≌△ACD 可得∠AEB=∠ADC ,∵∠AEB+∠AEF=180°,∴∠ADC+∠AEF=180°,∵∠DAE=70°,,由四边形内角和定理可得:∠EFD=360°-∠AED-∠ADF-∠EAD=360°-180°-70°=110°,③正确;(3)由∠BAC=∠DAE=70°,AE 平分∠BAC ,可得∠BAE=∠EAG=∠DAG=35°,则由AE=AD,AG=AG ,可证△EAG ≌△DAG ,G F EDCBAD oECBA OEDCB A∴EG=GD,∠AGE=∠AGD=90°,④正确;(4)题目已知条件无法判定BE=EF ,故③与题目无关;故选C例4. △ABC 与△BDE 是等边三角形,求证:AE=BD解析:由“共角模型”可得∠BCD=∠ACE ,由BC=AC,DC=CE,可证△BCD ≌△ACE ,∴BD=AE.例5.如图,四边形ABCD 、DEFG 都是正方形,求证:AE=CG解析:由“共角模型”可得∠CDG=∠ADE ,由CD=AD,DG=DE,可证△CDG ≌△ADE ,∴CG=AD.例6.如图,∠BAD=∠CAE=90°,AB=AD ,AE=AC. (1)求证:BC=DE ;(2)若AC=12,求四边形ABCD 的面积.解析:(1)由“共角模型”可得∠BAC=∠DAE ,由AB=AD,AC=AE,可证△BAC ≌△DAE ,∴BC=DE. (2)由△BAC ≌△DAE 可得S ∆BAC =S ∆DAE ,∴S 四边形ABCD =S ∆ABC +S ∆ACD =S ∆ADE +S ∆ACD =S ∆ACE =12×12×12=72例6.如图,△ABC 和△EBD 中,∠ABC=∠DBE=90°,AB=CB ,BE=BD ,连接AE ,CD ,AE 与CD 交于点M ,AE 与BC 相交于点N.EDCBAE DCBAFGEDCBA(1)求证:AE=CD ; (2)求证:AE ⊥CD ;(3)连接BM ,有以下结论:①BM 平分∠CBE ;②MB 平分∠AMD.其中正确的有______(请写序号)解析:(1)由“共角模型”可得∠ABE=∠CBD ,由AB=BC,BE=BD,可证△ABE ≌△CBD ,∴AE=CD. (2)由△ABE ≌△CBD 可得∠BAE=∠BCD ,△ABN 与△CNM 恰好组成“8字模型”, 则易得∠ABN=∠CMN=90°, 即AE ⊥CD ;(3)结论②正确,理由是:过点B 分别作BF ⊥AE 于点F ,BG ⊥CD 于点G , 由(1)中△ABE ≌△CBD 可得S ∆ABE =S ∆CBD , ∵AE=CD ,则△ABE 与△CBD 面积相等底也相等, ∴BF=BG ,由角平分线的判定定理可得②正确;MN EDC BAMN G F DCBA。
