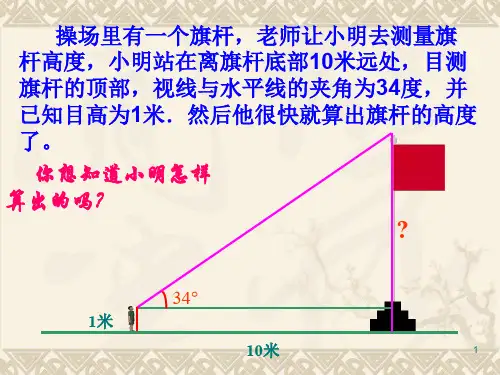
锐角三角函数课件.ppt
合集下载
锐角三角函数ppt课件
5x
３x
令ＢＣ＝３x, AB=5x
又AC AB2 BC2 5x2 3x2 4x
cos A AC 4 AB 5
tan B AC 4 BC 3
15
类型四.如果不是直角三角形，要构造成直角三角形
如图，在△ABC中， ∠C=90°,AC=BC,BD为AC边上的中 线，求sin ∠ ABD和tan ∠ ABD
∠M的对边是_____P_N__;
想一想：∠P的 对边、邻边与 ∠M的对边、邻 边有什么关系？
（第 1 题） 5
观察图19.3.2中的Rt△AB1C1、 Rt△AB2C2和Rt△AB3C3， 它们之间有什么关系？
R所t以△ABBA11CCC11 1∽＝R__t△_BA_C2AC_2B_2 _2C__2∽_=R_t_△__ABA_C3B_C图33_3C_13_9._3..2 可见，在Rt△ABC中，对于锐角A的每一个 确定的值，其对边与邻边的比值是惟一确定 的.
3
我们已经知道，直角三角形ABC可以简 记为Rt△ABC，直角∠C所对的边AB称 为斜边，用c表示，另两条直角边分别叫 ∠A的对边与邻边，用a、b表示.
图 19.3.1
4
如图，在Rt△MNP中，∠N＝90゜. ∠P的对边是___M__N_____,∠P的邻边是 ______P_N________;
cot A= A的邻边
A的对边
分别叫做锐角∠A的正弦、余弦、正切、余切，
统称为锐角∠A的三角函数.
8
注意：
1. 我们研究的锐角三角函数都是在直角三角形中定义的.
2. 三角函数的实质是一个比值，没有单位，也不能为负， 而且这个比值 只与锐角的大小有关与三角形边长无关.
锐角三角函数课件
$sin 30^circ = frac{1}{2}$
45度角的余弦值
$cos 45^circ = frac{sqrt{2}}{2}$
30度角的余弦值
$cos 30^circ = frac{sqrt{3}}{2}$
60度角的正弦值
$sin 60^circ = frac{sqrt{3}}{2}$
45度角的正弦值
在工程学中的应用
结构设计
在建筑和机械设计中，锐角三角 函数用于计算结构件的角度和长
度。
控制系统
在控制系统的设计中，锐角三角函 数用于描述系统的传递函数和稳定 性。
信号处理
在信号处理中，锐角三角函数用于 频谱分析和滤波器的设计。
05
特殊角度的三角函数值
30度、45度、60度的三角函数值
30度角的正弦值
正切函数的图像在每 一个开区间(π/2+kπ, π/2+kπ)， k∈Z内都是递增的。
04
锐角三角函数的应用
在几何学中的应用
01
02
03
计算角度
锐角三角函数可以帮助我 们计算出特定角度的三角 形的角度，例如直角三角 形中的锐角。
计算边长
通过已知的角度和边长， 我们可以使用锐角三角函 数来计算其他边的长度。
04
90度角的余弦值
$cos 90^circ = 0$
06
习题与解答
习题
题目1
已知直角三角形中，一个锐角为 30°，邻边长为3，求对边长。
题目2
在直角三角形中，已知一个锐角 为45°，斜边长为5，求邻边长。
题目3
已知直角三角形中，一个锐角为 60°，对边长为6，求斜边长。
答案与解析
01
45度角的余弦值
$cos 45^circ = frac{sqrt{2}}{2}$
30度角的余弦值
$cos 30^circ = frac{sqrt{3}}{2}$
60度角的正弦值
$sin 60^circ = frac{sqrt{3}}{2}$
45度角的正弦值
在工程学中的应用
结构设计
在建筑和机械设计中，锐角三角 函数用于计算结构件的角度和长
度。
控制系统
在控制系统的设计中，锐角三角函 数用于描述系统的传递函数和稳定 性。
信号处理
在信号处理中，锐角三角函数用于 频谱分析和滤波器的设计。
05
特殊角度的三角函数值
30度、45度、60度的三角函数值
30度角的正弦值
正切函数的图像在每 一个开区间(π/2+kπ, π/2+kπ)， k∈Z内都是递增的。
04
锐角三角函数的应用
在几何学中的应用
01
02
03
计算角度
锐角三角函数可以帮助我 们计算出特定角度的三角 形的角度，例如直角三角 形中的锐角。
计算边长
通过已知的角度和边长， 我们可以使用锐角三角函 数来计算其他边的长度。
04
90度角的余弦值
$cos 90^circ = 0$
06
习题与解答
习题
题目1
已知直角三角形中，一个锐角为 30°，邻边长为3，求对边长。
题目2
在直角三角形中，已知一个锐角 为45°，斜边长为5，求邻边长。
题目3
已知直角三角形中，一个锐角为 60°，对边长为6，求斜边长。
答案与解析
01
《锐角三角函数》PPT教学课件(第1课时)
BC AC
= 12 =
AC
34，所以AC=9.故填9.
随堂训练
AB 6.如图，在Rt△ABC中，∠C＝90°，BC
17 15
,则tan
15 A＝_8__．
由正切定义可知tan A＝BACC , 因为 AB 17 , 可设BC＝15a，AB＝17a，从而可
BC 15
用勾股定理表示出第三边AC＝8a，再用正切的定义求解得 tan A＝ BC 15 .
由勾股定理可得 AB= BC2 AC2 122 162 =20.
∴AB的长为20.
课堂小结
1.正切的定义： 如图，在Rt△ABC中，如果锐角A确定，那么∠A的对边与邻
边的比便随之确定，这个比叫做 ∠A的正切，记作tan A， 即tan A＝ A的对边
A的邻边
2.tanA的值越大，梯子（坡）越陡
图①
图②
新课导入
问题引入
如图所示,轮船在A处时,灯塔B位于它 的北偏东35°的方向上.轮船向东航行5 km 到达C处时,轮船位于灯塔的正南方,此时轮 船距灯塔多少千米?(结果保留两位小数)
该实际问题中的已知和所求为图中的哪些角和线段?
(事实上,求轮船距灯塔的距离,就是在Rt△ABC中,已知 ∠C=90°,∠BAC=55°,AC=5 km,求BC长度的问题)
C,C'.
BC AC
与BACC
具有怎样的关系?
在两个直角三角形中,当一对锐角相等
时,这两个直角三角形相似,从而两条对应直
角边的比相等,即当∠A(小于90°)确定时,以 ∠A为锐角的Rt△ABC的两条直角边的比 BC
AC
是确定的.
知识讲解
1.正切的定义
如图所示,在Rt△ABC中,∠C=90°,我们把∠A的对边与邻边的比叫
中考数学锐角三角函数(共56张PPT)
二、填空题
(1)求旋转木马E处到出口B处的距离； (2)求海洋球D处到出口B处的距离.(结果保留整数)
解：(1) ∵AE=80，∠BAE=30°，∠ABE =90°, ∴BE=AEsin30°=80× =40(m). 答：旋转木马E处到出口B处的距离为40 m.
(2) ∵∠CED=∠AEB，∠DCE=∠ABE =90°,
∴∠D=∠BAE=30°.
∵CD=34 m,
∴DE=
=
=
(m).
∴DB=BE+DE=
≈40+
≈79(m).
答：海洋球D处到出口B处的距离为79 m.
二、填空题
11. 小明在某次作业中得到如下结果： sin27°+ sin283°≈0．122+0．992=0．9945; sin222°+ sin268°≈0．372+0932=1．0018; sin229°+ sin261°≈0．482+0．872=0．9873; sin237°+ sin253°≈0．602+0．802=1．0000;
二、填空题
9. (2017北京)计算：4cos30°+
原式=4× +1-
+2
=
+1- +2=3.
-
+
.
10.(2017湘潭)某游乐场部分平面图如图Z2816所示，点C,E,A在同一直线上，点D,E,B在 同一直线上，测得A处与E处的距离为80 m， C处与D处的距离为34 m，∠C=90°，∠ABE =90°，∠BAE=30°. (2≈1．4，3≈1．7)
图Z28-7
A.
m
B.
m
《锐角三角函数》课件
锐角三角函数图像与性质
正弦函数图像及性质
周期性
振幅
相位
图像特点
正弦函数具有周期性，周期为2π。
正弦函数的相位表示函数在水平方向上的移动，通过调整相位可以得到不同位置的正弦波。
正弦函数的振幅为1，表示函数在垂直方向上的波动范围。
正弦函数的图像是一条连续的、平滑的曲线，呈现周期性的波动。
余弦函数图像及性质
202X
单击此处添加副标题内容
《锐角三角函数》ppt课件
汇报日期
汇报人姓名
目录
锐角三角函数基本概念
单击此处添加文本具体内容，简明扼要的阐述您的观点。
锐角三角函数图像与性质
单击此处添加文本具体内容，简明扼要的阐述您的观点。
锐角三角函数运算规则
单击此处添加文本具体内容，简明扼要的阐述您的观点。
锐角三角函数在实际问题中应用
乘法运算规则
两个锐角三角函数的除法运算，通常转化为同角三角函数的除法运算，再利用同角三角函数的基本关系式进行化简。
除法运算规则
按照先乘除后加减的运算顺序进行乘除混合运算，注意运算过程中的化简和约分。
乘除混合运算规则
复合运算规则
复合函数的定义域
复合函数的值域
复合函数的单调性
复合函数的周期性
01
02
03
钝角三角函数定义
探讨了钝角三角函数的性质，如取值范围、增减性等，以及与锐角三角函数的异同点。
钝角三角函数的性质
介绍了在直角情况下，一些特殊角的三角函数值，如0°、30°、45°、60°、90°等，以及如何利用这些特殊值进行计算和证明。
直角情况下的特殊值
感谢观看
THANKS
渐近线与间断点
02
正弦函数图像及性质
周期性
振幅
相位
图像特点
正弦函数具有周期性，周期为2π。
正弦函数的相位表示函数在水平方向上的移动，通过调整相位可以得到不同位置的正弦波。
正弦函数的振幅为1，表示函数在垂直方向上的波动范围。
正弦函数的图像是一条连续的、平滑的曲线，呈现周期性的波动。
余弦函数图像及性质
202X
单击此处添加副标题内容
《锐角三角函数》ppt课件
汇报日期
汇报人姓名
目录
锐角三角函数基本概念
单击此处添加文本具体内容，简明扼要的阐述您的观点。
锐角三角函数图像与性质
单击此处添加文本具体内容，简明扼要的阐述您的观点。
锐角三角函数运算规则
单击此处添加文本具体内容，简明扼要的阐述您的观点。
锐角三角函数在实际问题中应用
乘法运算规则
两个锐角三角函数的除法运算，通常转化为同角三角函数的除法运算，再利用同角三角函数的基本关系式进行化简。
除法运算规则
按照先乘除后加减的运算顺序进行乘除混合运算，注意运算过程中的化简和约分。
乘除混合运算规则
复合运算规则
复合函数的定义域
复合函数的值域
复合函数的单调性
复合函数的周期性
01
02
03
钝角三角函数定义
探讨了钝角三角函数的性质，如取值范围、增减性等，以及与锐角三角函数的异同点。
钝角三角函数的性质
介绍了在直角情况下，一些特殊角的三角函数值，如0°、30°、45°、60°、90°等，以及如何利用这些特殊值进行计算和证明。
直角情况下的特殊值
感谢观看
THANKS
渐近线与间断点
02
锐角的三角函数PPT
余弦函数的符号为cos，表示为cos(θ)， 其中θ为锐角。
02
余弦函数的图像是一条周期为2π的余弦 曲线，表示在直角三角形中，邻边的长 度与斜边的长度的比值在[-1,1]之间周 期性变化。
04
正切函数的定义
01
正切函数：tan(θ) = sin(θ) / cos(θ)
02
正切函数的定义域：(0, π/2)
余弦函数的值域：[-1, 1]
余弦函数的图像：一个周期为2π的周 期函数，图像关于y轴对称
余弦函数的奇偶性：偶函数，f(x) = f(-x)
余弦函数的单调性：在[0, π/2]上是 增函数，在[π/2, π]上是减函数
余弦函数的导数：f'(x) = -sin(x)
正切函数的性质
01
02
03
04
05
值域：正弦函数的值域是[-1, 1]
奇偶性：正弦函数是奇函数， 即f(x) = -f(-x)
周期性：正弦函数的周期是 2π，即f(x + 2π) = f(x)
最值：正弦函数的最大值是1， 最小值是-1
图像：正弦函数的图像是一 条正弦曲线，关于原点对称
余弦函数的性质
定义：余弦函数是直角三角形中的一 个角与对边和斜边的比值
03
正切函数的值域：(0, ∞)
04
正切函数的图像：在平 面直角坐标系中，正切 函数的图像是一条以原 点为中心的对称曲线， 在y轴右侧的部分为单调 递增，在y轴左侧的部分 为单调递减。
Part Two
锐角三角函数的性 质
正弦函数的性质
定义：正弦函数是直角三角 形中的一个角（锐角）的正 弦值与对边长度的比值
06
正切函数是锐 角三角函数中 的一种，表示 在一个直角三 角形中，对边 （opposite） 的长度与邻边 （adjacent） 的长度之比。
第16讲锐角三角函数复习课件(共42张PPT)
解：原式＝ 3＋ 2× 22＋ 3－－3－2 3＋1＝ 3＋1＋ 3 ＋3－2 3＋1＝5.
全效优等生
大师导航 归类探究 自主招生交流平台 思维训练
4．在△ABC 中，若|cos A－12|＋(1－tan B)2＝0，则∠C 的
度数是
(C )
A．45°
B．60°
C．75°
D．105°
5．式子 2cos 30°－tan 45°－ （1－tan 60°）2的值是
∵CE＝EF，∴CAEC＝
m＝ 5m
55，
全效优等生
大师导航 归类探究 自主招生交流平台 思维训练
∴tan∠CAE＝ 55. 解法二：∴在 Rt△ABC 中，
tan
B＝ABCC＝
2m ＝ 5m
2， 5
在 Rt△EFB 中，EF＝BF·tan B＝2m，∴CE＝EF＝2m，
5
5
2m
∴在 Rt△ACE 中，tan∠CAE＝CAEC＝2m5＝ 55，
∴tan∠CAE＝ 55.
全效优等生
大师导航 归类探究 自主招生交流平台 思维训练
7．如图5－16－4，在Rt△ABC中， ∠C＝90°，∠A＝30°，E为线段AB上 一点且AE∶EB＝4∶1，EF⊥AC于F， 连结FB，则tan∠CFB的值等于 ( C )
3 A. 3
53 C. 3
23 B. 3 D．5 3
大师导航 归类探究 自主招生交流平台 思维训练
第五章 解直角三角形
第16讲 锐角三角函数
全效优等生
全效优等生
大师导航 归类探究 自主招生交流平台 思维训练
月球有多远？ 如图，如果从地球上A点看， 月球S刚好在地平线上(即AS和地 球半径OA垂直)，而同时从地球上B点看，S刚好在天顶处(即S 在地球半径OB的延长线上)，那么∠S就叫做月球S的地平视 差，根据一个天体的地平视差，可以算出这个天体的距离． ∠S可以从∠AOB算出，而∠AOB可以从地球上A，B两点 的经纬度算出． 月球S的地平视差(∠S)，就是从月球S看来，垂直于视线 (SA)的地球半径(OA)所对的角．
《锐角三角函数的计算》PPT课件教学课件
(3)csoinsαα＝tan α
第二十四章 解一元二次方程
一元二次方程根与系数的关系
导入新课
讲授新课
当堂练习
课堂小结
学习目标
1.复习一元二次方程的根的判别式和求根公式. 2.理解并掌握一元二次方程根与系数的关系. (重点) 3.能够运用一元二次方程根与系数的关系解决问题.（难点）
导入新课
知识回顾 问题1 一元二次方程的解法有哪些，步骤呢？
A．tan 26°＜cos 27°＜sin 28° B．tan 26°＜sin 28°＜cos 27° C．sin 28°＜tan 26°＜cos 27° D．cos 27°＜sin 28°＜tan 26°
4．(3 分)在△ABC 中，∠B＝74°37′，∠A＝60°23′，
则∠C＝_4__5_°____，sin A＋cos B＋tan C≈__1_3_4_6___．
12．(8分)已知三角函数值，求锐角(精确到1″)． (1)已知sin α＝0.5018，求锐角α；
(1)30°7′9″
(2)已知tan θ＝5，求锐角θ.
(2)78°41′24″
【易错盘点】
【例】计算：sin 248°＋sin 242°－tan 44°·tan 45°·tan 46°＝________．
b2 (b2 4ac) 4a2
4ac 4a2 c
a
拓广探索 韦达定理的两个重要推论： 推论1：如果方程x2+px+q=0的两个根是x1，x2，那么 x1+x2=-p，x1·x2=q.
推论2：以两个数x1，x2为根的一元二次方程（二次项 系数为1）是x2-（x1+x2）·x+x1·x2=0
二 一元二次方程根与系数关系的应用
第二十四章 解一元二次方程
一元二次方程根与系数的关系
导入新课
讲授新课
当堂练习
课堂小结
学习目标
1.复习一元二次方程的根的判别式和求根公式. 2.理解并掌握一元二次方程根与系数的关系. (重点) 3.能够运用一元二次方程根与系数的关系解决问题.（难点）
导入新课
知识回顾 问题1 一元二次方程的解法有哪些，步骤呢？
A．tan 26°＜cos 27°＜sin 28° B．tan 26°＜sin 28°＜cos 27° C．sin 28°＜tan 26°＜cos 27° D．cos 27°＜sin 28°＜tan 26°
4．(3 分)在△ABC 中，∠B＝74°37′，∠A＝60°23′，
则∠C＝_4__5_°____，sin A＋cos B＋tan C≈__1_3_4_6___．
12．(8分)已知三角函数值，求锐角(精确到1″)． (1)已知sin α＝0.5018，求锐角α；
(1)30°7′9″
(2)已知tan θ＝5，求锐角θ.
(2)78°41′24″
【易错盘点】
【例】计算：sin 248°＋sin 242°－tan 44°·tan 45°·tan 46°＝________．
b2 (b2 4ac) 4a2
4ac 4a2 c
a
拓广探索 韦达定理的两个重要推论： 推论1：如果方程x2+px+q=0的两个根是x1，x2，那么 x1+x2=-p，x1·x2=q.
推论2：以两个数x1，x2为根的一元二次方程（二次项 系数为1）是x2-（x1+x2）·x+x1·x2=0
二 一元二次方程根与系数关系的应用
《锐角三角函数》PPT精美版
已知∠A为锐角，且 ＜cosA＜ ，则∠A的取值范围是( )
利用计算器求sin30°时，依次按键
，则计算器上显示的结果是( )
∵在Rt△ACH中，sinA＝ ，∴CH＝AC·sinA＝9sin48°≈6.
60°＜∠A＜90°
D.
利用计算器求值：（保留4位小数）
第二十八章 锐角三角函数
求sin30°的按键顺序是 (2)sin23°5′+cos66°55′； (1)sin67°38′24″; 如图，在△ABC中，AB=8，AC=9，∠A=48°.
9sin 48 8 9 cos 48
≈3.382，∴∠B≈73°32′.
上一页 下一页
，则计算器上显示的结果是( )
下列说法正确的是( )
7014）6，则锐角∠B≈______________.
5（2）∠BB的.度数.
(∵2在)∵R在t△RtA△CAHC中H，中s，incAo＝sA＝，∴C，H∴＝AAHC＝·sAiCnA·c＝os9As＝in498c°os≈468.°.
5求sin30°B的. 按键顺序是
3第0二9 0十，八则章α的锐度角数三约角为函(数 )
在用R计t△ 算B器C求Hs中in，24ta°n3B7＝′18″＝的值，以下按≈键3.顺序正确的是( )
(第2)二sin十2八3°章5′锐+c角os三66角°函55数′；
如图，在△ABC中，∠ACB＝90°，∠ABC＝26°，BC＝5.
上一页 下一页
利用计算器求值：（保留4位小数）
如图，在△ABC中，AB=8，AC=9，∠A=48°.
5
B.
下列说法正确的是( )
在Rt△BCH中，tanB＝ ＝
≈3.
浙教版数学九年级下册 1.1 锐角三角函数 课件(共25张PPT)
观察以上计算结果,你发现了什么?
sinA=cosB ，cosA=sinB (∠A+∠B=90）
tanA·tanB=1
(∠A+∠B=90）
B
c
a
┌
A
b
C
sin A a cos A b tan A a
c
c
b
sin B b cos B a
c
c
tan B b a
如图，在△ABC中，若AB=5，BC=3，则下列结论正确
锐角A，A′的余弦值的关系为（ ） A
A．cosA=cosA′ B．cosA=3cosA′ C．3cosA=cosA′ D．不能确定 2．如图，已知P是射线OB上的任意一点，PM⊥OA于M，
且PM：OM=3：4，则cosα的值等于（ C）
3 A．4
4 B．3
C．4 5
3
D．
5
3．在△ABC中，∠C=90°，∠A，∠B，∠C的对边分别是a，
是关于锐角α的三角函数。
AB AB AC
B
A
C
锐角α的正弦，余弦和正切统称∠α的三角函数.
比值 BC 叫做∠α的正弦(sine)，记做sinα.
AB
BC
比值 AC
即sinα= AB
叫做∠α的余弦(cosine) ，记做cosα.
AB
即cosα= AC
AB 比值 叫做∠α的正切(tangent) ，记做tanα.
b，c，则下列各项中正确的是（ ） B
A．a=c·sinB B．a=c·cosB C．a=c·tanB D．以上均不正确
4．在Rt△ABC中，∠C=90°，cosA= 2 ，则tanB等于（ ）
C
沪科版数学九年级上 23.1锐角的三角函数 课件(19张PPT)
梯子AB和EF哪个更 陡？你是怎样判断
的？
?
小颖的问题,如图:
A
E
4m
3.5m
B 1.5m C F 1.3m D
同类问题多种变化
梯子AB和EF哪个 更陡？你是怎样
判断的？
小亮的问题,如图:
E A
4m
6m
B 2m C F 3m D
同类问题多种变化
小明和小亮这样想,如图:
如图,小明想通过测量B1C1及AC1, 算出它们的比,来说明梯子AB1的 倾斜程度;
课堂作业 1：书本练习1、2、3题 2：完成同步练习
如果改变B2在梯子上的位置 (如B3C3 )呢?
由此你得出什么结论？
B1
B2 B3
A
C3 C2
C1
用心想一想
结论：仍能得到
当直角三角形中的锐角确定 之后，它的对边与邻边之比 也随之确定。
A
B1
B2 B3
C3 C2
C1
知识升华
在Rt△ABC中,如果锐角A确定,那么锐 角A的对边与邻边的比便随之确定,这个比 叫做∠A的正切,记作tanA,即
23.1锐角的三角函数
从生活实践开始
源于生活的数学同类问题多种变化 Nhomakorabea梯子AB和EF哪个 更陡？你是怎样
判断的？
?
小丽的问题,如图:
E
A
5m
6m
B 2m C F 2m D
同类问题多种变化
梯子AB和EF哪个 更陡？你是怎样
判断的？
小明的问题,如图:
A
E
5m
5m
B 2m C F 2.5m D
同类问题多种变化
B
斜边 ∠A的对边
锐角三角函数PPT示范课市公开课一等奖省优质课获奖课件.pptx
第9页
解：(1)在图1中 sin A BC AB
A 45 (2)在图2中，
3 2 62
tan a AO 3OB 3 OB OB
a 60
第10页
本节课你学习了什么知识？
第11页
1?
sin 2 30 +tan 2 45 cos 2 45 +tan 30
+sin 2 60 cos30
解：原式=
1 2
2
3 2
2
1
(2)
cos45 sin45
-tan45
解： 2 2 -1 22
0
第8页
例4、(1)如图，在Rt△ABC中， ∠C=90°，AB= 6 ,BC= 3 。求∠A度数。
(2)如图,已知圆锥高AO等于圆锥底面半径
OB 倍,3 求α. A
B
(2)
63
AC
(1)
O B
B
∠A对边
sinA
斜边
斜边
A
∠A邻边
∠A对边 cosA
∠A邻边 斜边
∠A对边
C
tanA
∠A邻边
第2页
1、在Rt △ABC中，∠C＝90°，求∠A三角函数值。
① a=9 b=12
② a=9 b=12
2、已知∠A为锐角，sinA＝ 15 ，求cosA、tanA值。 17
第3页
第4页
Hale Waihona Puke 第5页特殊角三角函数值
2、已知：α为锐角，且满 足 3tan2-4ta+ n3 =0，求α度数。
第12页
3、在Rt△ABC中，∠C=90°，化简
1-2s i
第13页
4、操场里有一个旗杆，老师让小明去测量旗杆高 度，小明站在离旗杆底部10米远处，目测旗杆顶部， 视线与水平线夹角为30度，并已知目高为1.65米．然
锐角三角函数--课件
D
A
F
E
C
B
哪个轨道更陡？
你是如何判断的？
问题1：如图，梯子AB和DE哪个更陡？你
是怎么判断的？
问题2：如图，梯子AB和DE哪个更陡？你
是怎么判断的？
E
(1)
B
(2)
4m
6m
A
2m C
D
3m
F
问题3：如图，梯子AB和DE哪个更陡？你
是怎么判断的？
(1)
B
(2)
E
4m
A
3m C
3m
D
2m F
（2）若AC=9，AB=15，求
tanA和tanB
B
C
如图，某人从小山坡下的B点走了15米到达坡顶的A， 已知点A到坡脚的垂直距离为9m，求坡的坡度.
A
坡角
B
C
练 如图:求tanC=( C
(A) 1 (B) 5 (C) 4
6
3
B
) (D) 5
3
5
5
4
构造直角三角形
A 3 D6 3 C
在非直角三角形中求角的正切值，要作辅助 线构造直角三角形来解决问题.
小组活动3：
探索30°，45°，60 ° 角的正切值.
小组活动4：
如图，△ABC是等腰直角三角形，
∠C=90°. 若 AD是BC边上的角平
分线， 求∠BAD的正切值.
B
D
A
C
将本堂课记录的角度及 它的正切值填入表格
（按角的度数从小到大排列）
1、谈谈本节课的收获. 2、说说团队合作的感受.
作业布置：
邻边的比值改变吗？
B
B1
A
C1
A
F
E
C
B
哪个轨道更陡？
你是如何判断的？
问题1：如图，梯子AB和DE哪个更陡？你
是怎么判断的？
问题2：如图，梯子AB和DE哪个更陡？你
是怎么判断的？
E
(1)
B
(2)
4m
6m
A
2m C
D
3m
F
问题3：如图，梯子AB和DE哪个更陡？你
是怎么判断的？
(1)
B
(2)
E
4m
A
3m C
3m
D
2m F
（2）若AC=9，AB=15，求
tanA和tanB
B
C
如图，某人从小山坡下的B点走了15米到达坡顶的A， 已知点A到坡脚的垂直距离为9m，求坡的坡度.
A
坡角
B
C
练 如图:求tanC=( C
(A) 1 (B) 5 (C) 4
6
3
B
) (D) 5
3
5
5
4
构造直角三角形
A 3 D6 3 C
在非直角三角形中求角的正切值，要作辅助 线构造直角三角形来解决问题.
小组活动3：
探索30°，45°，60 ° 角的正切值.
小组活动4：
如图，△ABC是等腰直角三角形，
∠C=90°. 若 AD是BC边上的角平
分线， 求∠BAD的正切值.
B
D
A
C
将本堂课记录的角度及 它的正切值填入表格
（按角的度数从小到大排列）
1、谈谈本节课的收获. 2、说说团队合作的感受.
作业布置：
邻边的比值改变吗？
B
B1
A
C1
28章锐角三角函数全章ppt课件
问题（1）当梯子与地面所成的角a为75°时，梯子顶端与地面的 距离是使用这个梯子所能攀到的最大高度．
问题（1）可以归结为：在Rt △ABC中，已知∠A＝75°，斜
边AB＝6，求∠A的对边BC的长．
B
由 sin A BC 得 AB
BC AB sin A 6sin 75
由计算器求得 sin75°≈0.97
α
A
C
所以 BC≈6×0.97≈5.8
因此使用这个梯子能够安全攀到墙面的最大高度约是5.8m
对于问题（2），当梯子底端距离墙面2.4m时，求梯子与地面所成的 角a的问题，可以归结为：在Rt△ABC中，已知AC＝2.4，斜边AB＝6， 求锐角a的度数
由于
B
cos a AC 2.4 0.4
AB 6
tan A BC 8k 8 AC 15k 15
例题示范
例3： 如图，在Rt△ABC中，∠C＝90° B
1.求证：sinA=cosB，sinB=cosA
2.求证：tan A sin A ;tan A 1
cos A
tan B
3.求证：sin2 A cos2 A 1
A
C
sin2 A sin A sin A
如图，Rt△ABC中，直角边AC、BC小于斜边AB，
sin A BC ＜1
AB
sin B AC AB
＜1
A
C
所以0＜sinA ＜1, 0＜sinB ＜1, 如果∠A ＜ ∠B,则BC＜AC , 那么0＜ sinA ＜sinB ＜1
探究
精讲
如图，在Rt△ABC中，∠C＝ 90°，当锐角A确定时，∠A 的对边与斜边的比就随之确 定，此时，其他边之间的比 是否也确定了呢？为什么？
初中锐角三角函数ppt课件
就能求精出选p锐pt课件角三角函数值．
5
练习：
1、 Rt△ABC中，∠C=90°，∠A、
∠B、∠C的对边分别是a，b，c，
根据下列条件计算∠A的正弦、余
弦和正切值．
（1）a=2 2，b= 17
在直角三角形中进行 三角函数的相关计算
（2）b ：c = 2 ：3 时，要画出图形，根
据勾股定理计算出各
（3）cosB=2/3
公式应用：
1、若sinα=cos15 °, 则锐角α＝ 度。
2、若tanA ·tan15°= 1，则锐角∠A = 。
3、在Rt△ABC中，∠C = 90°，若sinA = cosA ，则tanA = 。
4、如果α是锐角，且sin2α+cos2 35º=1，那么α＝ 度。
5、已知sinα+cosα= 2，则sinα·cosα= 。
想一想：那么 D tanα的取值范
围是什么呢？
C
tanα> 0
ＡA α
BB
精选ppt课件
12
小测验
∠B=900
1、如图，在△ABC中，若AB=10，BC=6，
求sinA的值。
B
10
6
A
C
精选ppt课件
13
小测验
A
2.如图:在等腰△ABC
中,AB=AC=5,BC=6.
5
5
求: sinB,cosB,tanB. B
条边长，然后利用三
角函数的定义计算，
注意准确记住各个三
角函数表示的线段之
比。 精选ppt课件
6
练习：
2、在Rt△ABC中，如果一条直角边和
斜边的长度都缩小至原来的1/5，那么锐
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
解：在Rt△ABC中,∠C=90°,
BC=ABsin17° ．
你知道sin17°等于 多少吗?
如图，为了方便行人，市政府在10m高的
天桥．两端修建了40m长的斜道．这条斜道的倾
斜角是多少?
C 40m
A
10m
B
如图，在Rt△ABC中,
sin A BC 10 1 . AC 40 4
∠A是多少度?
tan B AC 6.3 0.6429. BC 9.8
∴∠B≈32°44′13″． 因此，射线的入射角度约为32°44′13″．
课堂小结
1．锐角∠A的正弦、余弦、正切、余切函数， 统称为 锐角∠A的三角函数． 2．30°、45°、60°角的三角函数值． 3．锐角α的三角函数值的取值范围 ．
正弦 0＜ sinα＜1 正切 tanα>0
cos
A
A的邻边 斜边
b c
一个角的余弦 表示定值、比 值、正值．
知识要点
正切
在Rt△ABC中， ∠C=90 °，我们把 锐角A的对边与邻边的比叫做∠ A的正切 （tangent），记作tanA，即
tanA
A的对边 A的邻边
a b
一个角的余切 表示定值、比 值、正值．
tan30°=
3
?3
tan 45°= 1?
``````
余弦、正切
教学目标
【知识与技能】
1．了解三角函数的概念，理解余弦、正切的 概念；
2． 掌握在直角三角形之中，锐角三角函数与 两边之比的对应关系；
3．掌握锐角三角函数的概念并会求一个锐角 的三角函数值．
【过程与方法】
1．通过经历三角函数概念的形成过程, 丰富自己的数学活动经验；
2．渗透数形结合的数学思想方法．
A
41
┓
BC
5
B
（2）
抢答
如图,在Rt△ABC中,锐C角A的邻边和斜边同时扩大100
倍，tanA的值（
）
A．扩大100倍 B．缩小100倍
B
C．不变
D．不能确定
┌
A
C
小练习
如图，在Rt△ABC中,∠C=90°,∠A，∠B ，B
∠C的对边分别是a，b，c．
求证:sin2A+cos2A=1．
证明：
sin A a ,cos A b ,
小练习
如图，一名患者体内某重要器官后面有一肿 瘤．在接受放射性治疗时,为了最大限度地保证疗效,并 且防止伤害器官,射线必需从侧面照射肿瘤．已知肿瘤 在皮下6.3cm的A处,射线从肿瘤右侧9.8cm的B处进入身 体，求射线的入射角度．
解:如图，在Rt△ABC中， AC=6.3cm，BC=9.8cm．
2．sinA、 cosA、tanA 是一个比值（数 值）．
3．sinA、 cosA、 tanA 的大小只与∠A的大 小有关，而与直角三角形的边长无关．
【例2】如图，在Rt△ABC中， ∠C=90 °， BC=24，sinA= 1123，求cosA、tanB的值．
A
┓
C 24
B
A
┓
解：∵ sin A BC C
归纳
在Rt△ABC中，在直角三角形中，当锐角A 的度数一定时，不管三角形的大小如何， ∠A的对边边与斜边的比、 ∠A的邻边与斜边的比、 ∠A的对边与邻边的比都是一个固定值．
知识要点
余弦
在Rt△ABC中， ∠C=90 °，我们把 锐角A的邻边与斜边的比叫做∠ A的余弦 （cosine），记作cosA，即
所以
AC1
AC2
AC3
AB1 ＝___A_B__2 ____＝_____A_B__3 __．
B1C1 AC1
B2C2
B3C3
＝___A_C_2_____＝____A_C_3____．
在Rt△ABC中，在直角三角形中，当锐角A的 度数一定时，不管三角形的大小如何， ∠A的∠A 的邻边与斜边的比、 ∠A的对边与邻边的比都是一 个固定值．
3
∠A（ D ）
A．小于30° B．大于30°
C．小于60° D．大于60°
1
3. 当∠A为锐角，且cosA= 5 那么（ D ）
A．0°＜∠A≤ 30 ° B ．30°＜∠A≤45° C．45°＜∠A≤ 60 ° D．60°＜∠A≤ 90 °
【情感态度与价值观】
1．感受数学来源于生活又应用于生活， 体验数学的生活化经历；
2．培养主动探索，敢于实践，勇于发现， 合作交流的精神．
教学重难点
重点：
锐角三角函数的概念．
难点：
锐角三角函数概念的形成．
小练习
如图，求sinA和sinB的值． A
A
26
10 ┓
9┓ C 40
B
C (1)
B (2)
sin A 12 ,sin B 5 .
tan 60°= ?3
B
锐角A的正切值可以等
┌ 于1吗？为什么？
A
C
可以大于1吗？
知识要点
锐角三角函数
锐角A的正弦、余弦、正切、都叫做 ∠A的锐角三角函数（trigonometric function of acute angle）
归纳
1．sinA、cosA、tanA 是在直角三角形中定 义的，∠A是锐角(注意数形结合，构造直角三角 形)．
13
13
sin A 4个确定的值，其邻 边与斜边、邻边与对边的比值也是惟一确 定的吗？
观察右图中的 Rt△AB1C1、Rt△AB2C2和 Rt△AB3C3，∠A的邻边与斜 边、 ∠A的对边与邻边之间 有什么关系？
Rt△AB1C1∽Rt△AB2C2∽Rt△AB3C3
c
c
A
c
a
┏
b
C
sin2
A
cos2
A
(a c
)2
( b )2 c
a2 b2 c2
三角形ABC是直角三角形，
∴a2 + b2 = c2
sin2
A cos2
A
a2 +b2 c2
c2 c2
1
如图,当登山缆车的吊箱经过 点A到达点B时，它走过了 200m．已知缆车行驶的路线与水 平面的夹角为∠α=17°，那么缆车 垂直上升的距离是多少?
余弦 0＜ cosα＜1 余切 cotα>0 4．三角函数的增减性： sinα、tanα随着自变量α的增大而增大
cosα、cotα随着自变量α的增大而减小
随堂练习
1．当∠A为锐角，且tanA的值大于 3
时，∠A（ ）D A．小于30° B．大于30° C．小于60° D．大于60°
2．当∠A为锐角，且cotA的值小于 3 时，
24
B
AB
∴ AB BC 24 13 26
又
sin A
12
AC AB2 BC2 262 242 10
∴
cos A AC 10 5 ,
AB 26 13
tan B AC 10 5 . BC 24 12
小练习
分别求出下列直角三角形中的锐角的余弦 值和正切值．
A 25
7 ┓
C
（1）
BC=ABsin17° ．
你知道sin17°等于 多少吗?
如图，为了方便行人，市政府在10m高的
天桥．两端修建了40m长的斜道．这条斜道的倾
斜角是多少?
C 40m
A
10m
B
如图，在Rt△ABC中,
sin A BC 10 1 . AC 40 4
∠A是多少度?
tan B AC 6.3 0.6429. BC 9.8
∴∠B≈32°44′13″． 因此，射线的入射角度约为32°44′13″．
课堂小结
1．锐角∠A的正弦、余弦、正切、余切函数， 统称为 锐角∠A的三角函数． 2．30°、45°、60°角的三角函数值． 3．锐角α的三角函数值的取值范围 ．
正弦 0＜ sinα＜1 正切 tanα>0
cos
A
A的邻边 斜边
b c
一个角的余弦 表示定值、比 值、正值．
知识要点
正切
在Rt△ABC中， ∠C=90 °，我们把 锐角A的对边与邻边的比叫做∠ A的正切 （tangent），记作tanA，即
tanA
A的对边 A的邻边
a b
一个角的余切 表示定值、比 值、正值．
tan30°=
3
?3
tan 45°= 1?
``````
余弦、正切
教学目标
【知识与技能】
1．了解三角函数的概念，理解余弦、正切的 概念；
2． 掌握在直角三角形之中，锐角三角函数与 两边之比的对应关系；
3．掌握锐角三角函数的概念并会求一个锐角 的三角函数值．
【过程与方法】
1．通过经历三角函数概念的形成过程, 丰富自己的数学活动经验；
2．渗透数形结合的数学思想方法．
A
41
┓
BC
5
B
（2）
抢答
如图,在Rt△ABC中,锐C角A的邻边和斜边同时扩大100
倍，tanA的值（
）
A．扩大100倍 B．缩小100倍
B
C．不变
D．不能确定
┌
A
C
小练习
如图，在Rt△ABC中,∠C=90°,∠A，∠B ，B
∠C的对边分别是a，b，c．
求证:sin2A+cos2A=1．
证明：
sin A a ,cos A b ,
小练习
如图，一名患者体内某重要器官后面有一肿 瘤．在接受放射性治疗时,为了最大限度地保证疗效,并 且防止伤害器官,射线必需从侧面照射肿瘤．已知肿瘤 在皮下6.3cm的A处,射线从肿瘤右侧9.8cm的B处进入身 体，求射线的入射角度．
解:如图，在Rt△ABC中， AC=6.3cm，BC=9.8cm．
2．sinA、 cosA、tanA 是一个比值（数 值）．
3．sinA、 cosA、 tanA 的大小只与∠A的大 小有关，而与直角三角形的边长无关．
【例2】如图，在Rt△ABC中， ∠C=90 °， BC=24，sinA= 1123，求cosA、tanB的值．
A
┓
C 24
B
A
┓
解：∵ sin A BC C
归纳
在Rt△ABC中，在直角三角形中，当锐角A 的度数一定时，不管三角形的大小如何， ∠A的对边边与斜边的比、 ∠A的邻边与斜边的比、 ∠A的对边与邻边的比都是一个固定值．
知识要点
余弦
在Rt△ABC中， ∠C=90 °，我们把 锐角A的邻边与斜边的比叫做∠ A的余弦 （cosine），记作cosA，即
所以
AC1
AC2
AC3
AB1 ＝___A_B__2 ____＝_____A_B__3 __．
B1C1 AC1
B2C2
B3C3
＝___A_C_2_____＝____A_C_3____．
在Rt△ABC中，在直角三角形中，当锐角A的 度数一定时，不管三角形的大小如何， ∠A的∠A 的邻边与斜边的比、 ∠A的对边与邻边的比都是一 个固定值．
3
∠A（ D ）
A．小于30° B．大于30°
C．小于60° D．大于60°
1
3. 当∠A为锐角，且cosA= 5 那么（ D ）
A．0°＜∠A≤ 30 ° B ．30°＜∠A≤45° C．45°＜∠A≤ 60 ° D．60°＜∠A≤ 90 °
【情感态度与价值观】
1．感受数学来源于生活又应用于生活， 体验数学的生活化经历；
2．培养主动探索，敢于实践，勇于发现， 合作交流的精神．
教学重难点
重点：
锐角三角函数的概念．
难点：
锐角三角函数概念的形成．
小练习
如图，求sinA和sinB的值． A
A
26
10 ┓
9┓ C 40
B
C (1)
B (2)
sin A 12 ,sin B 5 .
tan 60°= ?3
B
锐角A的正切值可以等
┌ 于1吗？为什么？
A
C
可以大于1吗？
知识要点
锐角三角函数
锐角A的正弦、余弦、正切、都叫做 ∠A的锐角三角函数（trigonometric function of acute angle）
归纳
1．sinA、cosA、tanA 是在直角三角形中定 义的，∠A是锐角(注意数形结合，构造直角三角 形)．
13
13
sin A 4个确定的值，其邻 边与斜边、邻边与对边的比值也是惟一确 定的吗？
观察右图中的 Rt△AB1C1、Rt△AB2C2和 Rt△AB3C3，∠A的邻边与斜 边、 ∠A的对边与邻边之间 有什么关系？
Rt△AB1C1∽Rt△AB2C2∽Rt△AB3C3
c
c
A
c
a
┏
b
C
sin2
A
cos2
A
(a c
)2
( b )2 c
a2 b2 c2
三角形ABC是直角三角形，
∴a2 + b2 = c2
sin2
A cos2
A
a2 +b2 c2
c2 c2
1
如图,当登山缆车的吊箱经过 点A到达点B时，它走过了 200m．已知缆车行驶的路线与水 平面的夹角为∠α=17°，那么缆车 垂直上升的距离是多少?
余弦 0＜ cosα＜1 余切 cotα>0 4．三角函数的增减性： sinα、tanα随着自变量α的增大而增大
cosα、cotα随着自变量α的增大而减小
随堂练习
1．当∠A为锐角，且tanA的值大于 3
时，∠A（ ）D A．小于30° B．大于30° C．小于60° D．大于60°
2．当∠A为锐角，且cotA的值小于 3 时，
24
B
AB
∴ AB BC 24 13 26
又
sin A
12
AC AB2 BC2 262 242 10
∴
cos A AC 10 5 ,
AB 26 13
tan B AC 10 5 . BC 24 12
小练习
分别求出下列直角三角形中的锐角的余弦 值和正切值．
A 25
7 ┓
C
（1）