SNN算法总结

合集下载

脉冲神经网络研究进展综述

脉冲神经网络研究进展综述一、本文概述随着和机器学习的飞速发展，神经网络作为其中的核心组件，已经得到了广泛的研究和应用。

然而，传统的神经网络模型在处理复杂、动态和实时的任务时，由于其计算复杂度高、能耗大等问题，面临着巨大的挑战。

脉冲神经网络（Spiking Neural Networks，SNNs）作为一种新型的神经网络模型，以其独特的脉冲编码和传输机制，为解决这些问题提供了新的思路。

本文旨在全面综述脉冲神经网络的研究进展，包括其基本原理、模型设计、训练方法以及应用领域等方面。

我们将详细介绍脉冲神经网络的基本概念和脉冲编码机制，阐述其与传统神经网络的主要区别和优势。

然后，我们将回顾脉冲神经网络模型的发展历程，分析各种模型的特点和应用场景。

接着，我们将探讨脉冲神经网络的训练方法和学习机制，包括监督学习、无监督学习和强化学习等。

我们将展示脉冲神经网络在各个领域的应用实例，如图像识别、语音识别、机器人控制等，并展望其未来的发展方向。

通过本文的综述，我们希望能够为研究者提供一个清晰、全面的脉络，以了解脉冲神经网络的研究现状和发展趋势，为未来的研究提供有益的参考和启示。

我们也期望能够激发更多研究者对脉冲神经网络的兴趣和热情，共同推动这一领域的发展。

二、脉冲神经网络的基本原理脉冲神经网络（Spiking Neural Networks，SNNs）是一种模拟生物神经网络中神经元脉冲发放行为的计算模型。

与传统的人工神经网络（Artificial Neural Networks，ANNs）不同，SNNs的神经元通过产生和传递脉冲（或称为动作电位）来进行信息的编码和传输。

这种模型更接近生物神经元的实际运作机制，因此具有更强的生物可解释性和更高的计算效率。

在SNNs中，神经元的状态通常由膜电位（Membrane Potential）来表示。

当膜电位达到某个阈值时，神经元会发放一个脉冲，并将膜电位重置为静息状态。

脉冲的发放时间和频率都可以作为信息的编码方式。

各种聚类算法的比较

各种聚类算法的比较聚类的目标是使同一类对象的相似度尽可能地小；不同类对象之间的相似度尽可能地大。

目前聚类的方法很多，根据基本思想的不同，大致可以将聚类算法分为五大类：层次聚类算法、分割聚类算法、基于约束的聚类算法、机器学习中的聚类算法和用于高维度的聚类算法。

摘自数据挖掘中的聚类分析研究综述这篇论文。

1、层次聚类算法1.1聚合聚类1.1.1相似度依据距离不同：Single-Link:最近距离、Complete-Link：最远距离、Average-Link：平均距离1.1.2最具代表性算法1）CURE算法特点：固定数目有代表性的点共同代表类优点：识别形状复杂，大小不一的聚类，过滤孤立点2）ROCK算法特点：对CURE算法的改进优点：同上，并适用于类别属性的数据3）CHAMELEON算法特点：利用了动态建模技术1.2分解聚类1.3优缺点优点：适用于任意形状和任意属性的数据集；灵活控制不同层次的聚类粒度，强聚类能力缺点：大大延长了算法的执行时间，不能回溯处理2、分割聚类算法2.1基于密度的聚类2.1.1特点将密度足够大的相邻区域连接，能有效处理异常数据，主要用于对空间数据的聚类1）DBSCAN：不断生长足够高密度的区域2）DENCLUE：根据数据点在属性空间中的密度进行聚类，密度和网格与处理的结合3）OPTICS、DBCLASD、CURD：均针对数据在空间中呈现的不同密度分不对DBSCAN作了改进2.2基于网格的聚类2.2.1特点利用属性空间的多维网格数据结构，将空间划分为有限数目的单元以构成网格结构；1）优点：处理时间与数据对象的数目无关，与数据的输入顺序无关，可以处理任意类型的数据2）缺点：处理时间与每维空间所划分的单元数相关，一定程度上降低了聚类的质量和准确性2.2.2典型算法1）STING：基于网格多分辨率，将空间划分为方形单元，对应不同分辨率2）STING+：改进STING，用于处理动态进化的空间数据3）ＣＬＩＱＵＥ：结合网格和密度聚类的思想，能处理大规模高维度数据4）WaveCluster：以信号处理思想为基础2.3基于图论的聚类2.3.1特点转换为组合优化问题，并利用图论和相关启发式算法来解决，构造数据集的最小生成数，再逐步删除最长边1）优点：不需要进行相似度的计算2.3.2两个主要的应用形式1）基于超图的划分2）基于光谱的图划分2.4基于平方误差的迭代重分配聚类2.4.1思想逐步对聚类结果进行优化、不断将目标数据集向各个聚类中心进行重新分配以获最优解1）概率聚类算法期望最大化、能够处理异构数据、能够处理具有复杂结构的记录、能够连续处理成批的数据、具有在线处理能力、产生的聚类结果易于解释2）最近邻聚类算法——共享最近邻算法SNN特点：结合基于密度方法和ROCK思想，保留K最近邻简化相似矩阵和个数不足：时间复杂度提高到了O(N^2)3）K-Medioids算法特点：用类中的某个点来代表该聚类优点：能处理任意类型的属性；对异常数据不敏感4）K-Means算法1》特点：聚类中心用各类别中所有数据的平均值表示2》原始K-Means算法的缺陷：结果好坏依赖于对初始聚类中心的选择、容易陷入局部最优解、对K值的选择没有准则可依循、对异常数据较为敏感、只能处理数值属性的数据、聚类结构可能不平衡3》K-Means的变体Bradley和Fayyad等：降低对中心的依赖，能适用于大规模数据集Dhillon等：调整迭代过程中重新计算中心方法，提高性能Zhang等：权值软分配调整迭代优化过程Sarafis：将遗传算法应用于目标函数构建中Berkh in等：应用扩展到了分布式聚类还有：采用图论的划分思想，平衡聚类结果，将原始算法中的目标函数对应于一个各向同性的高斯混合模型5）优缺点优点：应用最为广泛；收敛速度快；能扩展以用于大规模的数据集缺点：倾向于识别凸形分布、大小相近、密度相近的聚类；中心选择和噪声聚类对结果影响大3、基于约束的聚类算法3.1约束对个体对象的约束、对聚类参数的约束；均来自相关领域的经验知识3.2重要应用对存在障碍数据的二维空间按数据进行聚类,如COD(Clustering with Obstructed Distance)：用两点之间的障碍距离取代了一般的欧式距离3.3不足通常只能处理特定应用领域中的特定需求4、用于高维数据的聚类算法4.1困难来源因素1）无关属性的出现使数据失去了聚类的趋势2)区分界限变得模糊4.2解决方法1)对原始数据降维2)子空间聚类CACTUS：对原始空间在二维平面上的投影CLIQUE：结合基于密度和网格的聚类思想，借鉴Apriori算法3)联合聚类技术特点：对数据点和属性同时进行聚类文本：基于双向划分图及其最小分割的代数学方法4.3不足：不可避免地带来了原始数据信息的损失和聚类准确性的降低5、机器学习中的聚类算法5.1两个方法1)人工神经网络方法自组织映射：向量化方法，递增逐一处理；映射至二维平面，实现可视化基于投影自适应谐振理论的人工神经网络聚类2)基于进化理论的方法缺陷：依赖于一些经验参数的选取，并具有较高的计算复杂度模拟退火：微扰因子；遗传算法（选择、交叉、变异）5.2优缺点优点：利用相应的启发式算法获得较高质量的聚类结果缺点：计算复杂度较高，结果依赖于对某些经验参数的选择。

军事情报智能推荐算法综述

第12卷第2期2021年4月指挥信息系统与技术Command Information System and TechnologyVol.12No.2Apr.2021军事情报智能推荐算法综述王适之黄志良申远赵博（空军预警学院4系武汉430019）摘要：面对现代战场上复杂环境和海量情报信息，综述了军事情报推荐系统中应用的各种推荐算法的研究现状。

首先，阐述了目前在军事情报智能推送中应用的协同过滤推荐、基于内容的推荐和组合推荐3种推荐算法，介绍了各个算法的研究思路、算法模型和处理流程，分析了各个算法在军事情报智能推送中存在的问题；然后，探讨了深度学习在该类系统上的多种应用思路和不足；最后，在分析已有研究基础上，对未来的研究趋势进行了展望。

关键词：情报服务；推荐系统；协同过滤；基于内容；混合推荐中图分类号：TN957.51文献标志码：A文章编号：1674‑909X(2021)02‑0007‑09Review of Intelligent Recommendation Algorithm for Military Intelligence WANG Shizhi HUANG Zhiliang SHEN Yuan ZHAO Bo（The4th Department，Air Force Early Warning Academy，Wuhan430019，China）Abstract：Oriented to the complex environment of the modern battlefield and the massive informa‑tion，the research status of types of recommendation algorithms applied in the recommendation system for the military intelligence is summarized.Firstly，three kinds of present recommendation algorithms applied in the intelligent push of the military intelligence are expounded，including the collaborative fil‑tering recommendation，the content-based recommendation，and the hybrid recommendation.The re‑search idea，the model of the algorithm and the processing flow of each type of the algorithm are intro‑duced，and the problems of each type of the algorithm in the intelligent push of the military intelli‑gence are analyzed.Then，types of the application ideas and the deficiencies of the deep learning in the systems are discussed.Finally，based on the above analysis on the present research，the future devel‑op trend is expected.Key words：information service；recommendation system；collaborative filtering；content-based；hy‑brid recommendation0引言在情报服务过程中，情报分发位于情报收集和情报处理之后，属于情报服务流程的最末端，负责将生成好的情报送到情报用户手中。

基于随机森林和投票机制的大数据样例选择算法

2021⁃01⁃10计算机应用,Journal of Computer Applications 2021,41(1):74-80ISSN 1001⁃9081CODEN JYIIDU http ：//基于随机森林和投票机制的大数据样例选择算法周翔1，2，翟俊海1，2*，黄雅婕1，2，申瑞彩1，2，侯璎真1，2（1.河北大学数学与信息科学学院，河北保定071002；2.河北省机器学习与计算智能重点实验室（河北大学），河北保定071002）（∗通信作者电子邮箱mczjh@ ）摘要：针对大数据样例选择问题，提出了一种基于随机森林（RF ）和投票机制的大数据样例选择算法。

首先，将大数据集划分成两个子集，要求第一个子集是大型的，第二个子集是中小型的。

然后，将第一个大型子集划分成q 个规模较小的子集，并将这些子集部署到q 个云计算节点，并将第二个中小型子集广播到q 个云计算节点。

接下来，在各个节点用本地数据子集训练随机森林，并用随机森林从第二个中小型子集中选择样例，之后合并在各个节点选择的样例以得到这一次所选样例的子集。

重复上述过程p 次，得到p 个样例子集。

最后，用这p 个子集进行投票，得到最终选择的样例子集。

在Hadoop 和Spark 两种大数据平台上实现了提出的算法，比较了两种大数据平台的实现机制。

此外，在6个大数据集上将所提算法与压缩最近邻（CNN ）算法和约简最近邻（RNN ）算法进行了比较，实验结果显示数据集的规模越大时，与这两个算法相比，提出的算法测试精度更高且时间消耗更短。

证明了提出的算法在大数据处理上具有良好的泛化能力和较高的运行效率，可以有效地解决大数据的样例选择问题。

关键词：大数据；样例选择；决策树；随机森林；投票机制中图分类号：TP181文献标志码：AInstance selection algorithm for big data based onrandom forest and voting mechanismZHOU Xiang 1，2，ZHAI Junhai 1，2*，HUANG Yajie 1，2，SHEN Ruicai 1，2，HOU Yingzhen 1，2（1.College of Mathematics and Information Science ，Hebei University ，Baoding Hebei 071002，China ；2.Hebei Key Laboratory of Machine Learning and Computational Intelligence （Hebei University ），Baoding Hebei 071002，China ）Abstract:To deal with the problem of instance selection for big data ，an instance selection algorithm based on RandomForest （RF ）and voting mechanism was proposed for big data.Firstly ，a dataset of big data was divided into two subsets ：the first subset is large and the second subset is small or medium.Then ，the first large subset was divided into q smaller subsets ，and these subsets were deployed to q cloud computing nodes ，and the second small or medium subset was broadcast to q cloud computing nodes.Next ，the local data subsets at different nodes were used to train the random forest ，and the random forest was used to select instances from the second small or medium subset.The selected instances at different nodes were merged to obtain the subset of selected instances of this time.The above process was repeated p times ，and p subsets of selected instances were obtained.Finally ，these p subsets were used for voting to obtain the final selected instance set.The proposed algorithm was implemented on two big data platforms Hadoop and Spark ，and the implementation mechanisms of these two big data platforms were compared.In addition ，the comparison between the proposed algorithm with the Condensed Nearest Neighbor （CNN ）algorithm and the Reduced Nearest Neighbor （RNN ）algorithm was performed on 6large datasets.Experimental results show that compared with these two algorithms ，the proposed algorithm has higher test accuracy and smaller time consumption when the dataset is larger.It is proved that the proposed algorithm has good generalization ability and high operational efficiency in big data processing ，and can effectively solve the problem of big data instance selection.Key words:big data;instance selection;decision tree;Random Forest (RF);voting mechanism0引言在信息技术飞速发展的时代，不仅技术在快速发展，数据也在呈指数型上升。

基本算法2-递推法实例

一般地，设原来的符合题意的n-1条直线把这平面分成个区域，再增加一条直线l，就变成n条直线，按题设条件，这l必须与原有的n-1条直线各有一个交点, 且这n-1个交点及原有的交点互不重合。这n-1个交点把l划分成n个区间，每个区间把所在的原来区域一分为二，所以就相应比原来另增了n个区域，即：
const max=100; var
f1,f2,s:array[1..max] of longint; i,j,k,l,n:longint; begin readln(n); f1[max]:=0 ; f1[max-1]:=1; {F0=10} for i:= 1 to n do
begin f2:=f1; k:=0; { ×7 } for j:= max downto 1 do begin k:=k+f1[j]*7; f1[j]:=k mod 10; k:=k div 10; end;
end.
var a,b:array[1..100] of longint; i,j,n:longint;
begin readln(n); a[100]:=4 ; b[100]:=1; for i:= 2 to n do begin for j:= 100 downto 1 do b[j]:=b[j]*2; for j:= 100 downto 2 do if b[j]>=10 then begin b[j-1]:=b[j-1]+b[j] div 10 ; b[j]:=b[j] mod 10; end; for j:= 100 downto 1 do begin a[j]:=a[j]+b[j]; if a[j]>=10 then begin a[j-1]:=a[j-1]+a[j] div 10 ; a[j]:=a[j] mod 10; end; end; end; j:=1; while a[j]=0 do j:=j+1; for i:= j to 100 do write(a[i]) ;

基于局部密度和相似度的自适应SNN算法

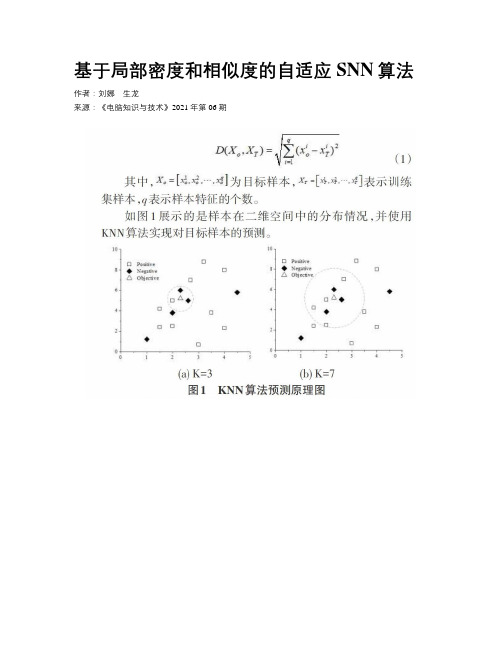
基于局部密度和相似度的自适应SNN算法作者：刘娜生龙来源：《电脑知识与技术》2021年第06期摘要：在近邻算法中，近邻样本和目标样本之间的绝对距离和相似性为目标样本类别的判断提供重要的决策依据，K值的大小也会直接决定了近邻算法的预测效果。

然而，SNN算法在预测过程中，使用固定的经验K值来预测不同局部密度的目标样本，具有一定的片面性。

因此，为实现SNN算法中K值的合理调节，提高算法的预测准确度和稳定性，提出一种基于局部密度和相似度的自适应SNN算法（AK-SNN）。

算法的性能在UCI数据集上进行验证，结果显示该算法取得优于KNN和SNN的预测效果和鲁棒性。

关键词：KNN;SNN;相似度计算;局部密度;自适应;AK-SNN中图分类号： TP301 文献标识码：A文章编号：1009-3044（2021）06-0006-04Abstract：In the nearest-neighbor algorithm， the absolute distance and similarity between the nearest-neighbor samples and the object sample provide significant decision basis for judging class of the object sample， and the size of K directly determines the prediction effect of the nearest-neighbor algorithm. However， in prediction process of SNN algorithm， it uses empirical K value selection topredict target samples with different local densities， which has some one-sidedness. Therefore， an adaptive SNN algorithm （AK-SNN） based on local density and similarity is proposed to realize reasonable adjustment of K in the SNN algorithm and improve the prediction accuracy and stability of the algorithm. The performance of the algorithm is verified on the UCI dataset， and the results show that the proposed algorithm achieves better prediction effect and robustness than KNN and SNN.Key words：KNN; SNN; similarity calculation; local density; AK-SNN引言近邻算法具有容易实现、训练时间短等特点，是一种高效实用的分类算法。

共享最近邻聚类算法流程

共享最近邻聚类算法流程
共享最近邻（Shared Nearest Neighbor, SNN）聚类算法是一种基于密度的聚类方法，其流程概要如下：
1. 计算样本间的距离，构建邻近矩阵，统计每个样本与其他样本的共享最近邻数目。

2. 根据预先设定的阈值，判断样本间的共享最近邻数量，若超过阈值则认为两者属于同一密度相连区域。

3. 逐步扩展密度相连区域，将紧密相连的样本聚为一类，形成聚类簇。

4. 在这个过程中不断更新邻近信息，直至所有样本都被分配至相应的聚类簇中。

该算法利用样本间的共享最近邻关系来发现数据集中的自然聚类结构，适用于发现任意形状和大小的聚类，但因其时间复杂度较高，不太适合大规模数据集。

脉冲强化学习总结（持续更新）

脉冲强化学习总结（持续更新）引⾔要将脉冲强化学习进⾏分类，⾸先要了解SNN学习算法以及强化学习本⾝的类别。

现代RL中⼀种⾮详尽但有⽤的算法分类法。

图⽚源⾃：OpenAI Spinning Up ()强化学习算法：参考⽂献：Model-Free vs Model-Based RL RL算法中最重要的分⽀点之⼀是智能体是否能够访问(或学习)环境模型的问题。

我们所说的环境模型是指预测状态转换和奖励的函数。

拥有⼀个模型的主要好处是，它允许智能体通过提前思考、看到⼀系列可能的选择会发⽣什么，并明确地在其选项之间做出决定来进⾏规划。

然后，智能体可以将预先规划的结果提取到⼀个学到的策略中。

这种⽅法的⼀个特别著名的例⼦是AlphaZero。

当这种⽅法起作⽤时，与没有模型的⽅法相⽐，它可以⼤⼤提⾼样本效率。

主要的缺点是，智能体通常⽆法使⽤环境的真实模型。

如果⼀个智能体想要在这种情况下使⽤⼀个模型，它必须完全从经验中学习模型，这会带来⼀些挑战。

最⼤的挑战是，模型中的偏差可以被智能体利⽤，从⽽导致智能体在学习模型⽅⾯表现良好，但在真实环境中表现得次优(或超级糟糕)。

模型学习从根本上说是很难的，所以即使是愿意投⼊⼤量时间和计算的巨⼤努⼒也可能没有回报。

使⽤模型的算法称为基于模型(model-based)的⽅法，不使⽤模型的算法称为⽆模型(model-free)⽅法。

虽然⽆模型⽅法放弃了使⽤模型在样本效率⽅⾯的潜在收益，但它们往往更易于实现和调整。

截⾄⽬前，与基于模型的⽅法相⽐，⽆模型⽅法更受欢迎，并且得到了更⼴泛的开发和测试。

What to Learn RL算法的另⼀个关键分⽀点是学习什么的问题。

通常的候选名单包括：策略，⽆论是随机的还是确定性的，动作-价值函数(Q函数)，价值函数，和/或环境模型。

What to Learn in Model-Free RL 本⽂主要考虑⽆模型RL，使⽤⽆模型RL表⽰和训练智能体有两种主要⽅法：Policy Optimization. 这个族中的⽅法将策略显式表⽰为πθ(a|s)。

上交snn与目标检测的中文综述

上交SNN与目标检测的中文综述一、简介1.1 SNN(Spiking Neural Network)简介SNN是一种脉冲神经网络，与传统的神经网络模型不同，它采用了神经元的脉冲输出形式，模拟大脑中神经元的工作方式。

由于其良好的生物学实现性质和低功耗特性，SNN近年来受到了广泛关注。

1.2 目标检测简介目标检测是计算机视觉领域的一项重要任务，其目标是在图像或视频中识别并定位出特定物体的位置和类别。

目标检测技术在自动驾驶、智能视频监控、智能机器人等领域有着重要的应用价值。

二、 SNN在目标检测中的应用2.1 SNN与传统卷积神经网络(CNN)的比较传统的目标检测算法多基于CNN模型，而SNN作为一种新型的神经网络模型在目标检测任务中也有着独特的优势。

SNN具有较低的计算复杂度和功耗，更适合在嵌入式设备上部署，这使得SNN在移动端目标检测应用中具有巨大的潜力。

2.2 SNN在目标检测中的性能近年来，研究者们针对SNN在目标检测任务中展开了大量的实验与研究。

通过针对SNN架构的优化和改进，其在目标检测性能上取得了显著的提升，并逐渐逼近甚至超越了传统CNN模型在目标检测任务中的表现。

三、 SNN与目标检测的挑战与未来3.1 挑战尽管SNN在目标检测任务中取得了一定的进展，但其在精度、鲁棒性等方面仍然存在一定的挑战。

如何进一步优化SNN模型，提高其在目标检测中的性能，仍然是当前研究的重要课题。

3.2 未来随着人工智能和深度学习技术的不断发展，SNN作为一种新兴的神经网络模型必将迎来更多的关注和应用。

未来，SNN在目标检测领域的研究将会更加深入，相信其在该领域的应用潜力将会得到更好的发挥。

结语作为新兴的脉冲神经网络模型，SNN在目标检测任务中展现出了巨大的潜力。

随着研究者们对SNN模型的不断优化和改进，相信它将会在目标检测领域发挥重要的作用，为该领域的发展带来全新的机遇与挑战。

希望本篇综述能够对读者了解SNN与目标检测的相关内容有所帮助。

snn训练方法

snn训练方法SNN训练方法简介SNN（Spiking Neural Network）是一种仿真神经网络模型，模拟了生物神经元的放电过程。

它在神经科学研究以及人工智能领域具有广泛的应用。

本文将介绍一些常见的SNN训练方法。

方法一：Spike Time Dependent Plasticity (STDP)•STDP是一种基于突触前后神经元的活跃性时间差异调整突触连接权重的方法。

•当突触前神经元在突触后神经元放电之前激活时，突触的连接权重增加；反之则减少。

•STDP模型可以在模拟真实生物神经网络的时空特性的同时，提高SNN的学习能力。

方法二：Surrogate Gradient Learning (SGL)•SGL通过定义激活函数的形式，将SNN的离散时间信号转化为连续时间信号，从而使得可以使用基于梯度的训练算法。

•常用的激活函数包括Sigmoid、ReLU等。

•SGL让SNN可以借助常见的优化算法（例如梯度下降）进行训练，大大提高了训练效率。

方法三：Recurrent Spiking Network (RSNN)•RSNN是一种具有反馈连接的SNN模型，允许神经元之间的状态信息传递。

•通过引入反馈连接，RSNN可以处理序列数据以及非线性动力学任务。

•RSNN在时间序列预测、图像处理等领域有着广泛的应用前景。

方法四：Deep Spiking Neural Network (DSNN)•DSNN是一种深度结构的SNN模型，通过堆叠多个SNN层实现高级特征的抽取和多级的决策过程。

•DSNN可以通过逐层预训练和微调的方式进行训练，从而有效地解决梯度消失问题。

•DSNN在图像识别、自然语言处理等领域取得了令人瞩目的成果。

方法五：Liquid State Machine (LSM)•LSM是一种基于SNN的结构，模拟了大脑中的液态神经网络。

•LSM通过选择性地启用一部分神经元，并将输出通过一组固定的突触连接传递到下一层，来处理信息流。

神经网络算法原理详解

神经网络算法原理详解随着人工智能技术的飞速发展，越来越多的企业开始将这一技术应用到实际生产生活中。

其中，神经网络算法作为人工智能技术的一种，已经逐渐被人们所重视。

那么，什么是神经网络算法？其原理是如何实现的呢？一、神经网络算法概述神经网络算法是一种通过一系列的数学计算、类比人类神经网络结构来实现智能预测、自适应控制、图像识别等计算机技术。

与传统的算法不同，神经网络算法更加注重数据对于计算结果的影响，能够对训练数据进行有效学习和归纳。

该算法在大数据分析和机器学习的场景中起到了非常重要的作用，因此备受业界广泛关注。

二、1. 神经元神经元是神经网络的基本单元，类比于生物学上的神经元。

它由输入部分、细胞体和输出部分组成。

输入部分接受到其他神经元传递过来的信息，将信号进行计算，然后将计算结果传递到细胞体。

细胞体根据计算结果产生一个量，并将量传递到输出部分。

输出部分再将该量传递给其他神经元。

2. 神经网络结构神经网络通常由三层结构组成，即输入层、隐藏层和输出层。

其中：输入层接受到外部输入信息，将信息传递到隐藏层；隐藏层根据输入信息计算并产生一个新的量，将该量传递到输出层；最终，输出层将神经网络计算结果输出，实现预测和分类等功能。

3. 神经网络算法的工作流程（1）初始化权重参数：神经网络中的每个神经元都有一个权重向量，神经网络算法在初始时需要为每个权重向量赋予一个随机的初始值。

（2）前馈计算：神经网络在接受输入信息之后，开始进行前馈计算。

首先，输入信息被输入到输入层，然后根据输入层原始数据和权重参数进行计算，得到隐藏层的输出；接着，隐藏层的输出作为下一层的输入，进一步计算并得到输出层的输出。

（3）误差计算：神经网络通过与期望输出对比、计算误差，以便调整权重参数。

误差可以使用常见的均方误差或交叉熵等方式计算。

（4）反向传播：神经网络通过反向传播进行权重参数的优化。

具体来说，它根据误差计算结果，从输出层向反向传播，通过链式求导方法计算出每个权重向量的梯度；然后，基于梯度下降算法，对权重向量进行调整，逐步将神经网络调整到最佳状态。

snn在目标检测方面的综述 -回复

snn在目标检测方面的综述-回复SNN在目标检测方面的综述引言目标检测是计算机视觉领域的一个重要任务，其目标是在图像或视频中自动识别和定位特定对象。

目标检测在许多应用中都扮演着关键角色，例如智能监控、自动驾驶、人脸识别等。

近年来，神经网络的发展为目标检测带来了重大突破，其中SNN（脉冲神经网络）在目标检测方面的应用也逐渐受到关注和研究。

本文将对SNN在目标检测方面的研究进行综述。

1. SNN简介1.1 SNN概述脉冲神经网络（Spiking Neural Network，SNN）是一种模拟神经脉冲传输的神经网络模型，其模拟神经元之间的离散信号传递和突触间的时域关系，更接近于生物神经网络的工作方式。

1.2 SNN的特点与传统的神经网络相比，SNN有以下几个特点：- 稀疏编码：SNN使用离散的脉冲来传递和编码信息，相比传统神经网络的连续值传递，具有更高效的能量传输和处理能力。

- 时序关系：SNN考虑了神经元之间的时序关系，即神经元发放脉冲的顺序和时间间隔，将时间作为信息的一部分。

- 事件驱动：SNN采用事件驱动的方式进行计算，仅在需要时进行处理，降低了计算和能量开销。

- 动态可塑性：SNN的连接权重和神经元的动力学特性可以通过学习进行调整和改变，具有更强的自适应性。

2. SNN在目标检测中的应用2.1 SNN目标检测框架SNN应用于目标检测时，通常采用类似于传统目标检测方法的框架，包括特征提取、目标定位和分类等步骤。

不同点在于，SNN使用离散的脉冲信号进行计算和传递，并采用时序关系进行信息处理。

2.2 特征提取传统的目标检测方法通常使用基于深度神经网络的特征提取器，例如基于卷积神经网络（CNN）的提取器。

在SNN中，可以使用类似的方法，但需要对网络结构进行调整，以适应脉冲信号的处理。

2.3 目标定位目标定位是目标检测中的一个核心问题，其目标是在图像或视频中准确地确定目标的位置。

在SNN中，可以使用传统的定位算法，例如边界框回归、锚点等方法。

脉冲神经网络的监督学习算法研究综述

脉冲神经网络的监督学习算法研究综述一、本文概述随着的快速发展，脉冲神经网络（Spiking Neural Networks，SNNs）作为一种更接近生物神经系统的计算模型，正逐渐引起研究者的广泛关注。

脉冲神经网络以脉冲序列作为信息编码和传递的基本方式，不仅具有生物神经元的动态特性和时间编码机制，而且能够在硬件实现上更高效地模拟和处理大规模神经网络。

近年来，脉冲神经网络的监督学习算法研究取得了显著的进展，这些算法在模式识别、图像处理、语音识别等领域的应用中展现出了独特的优势。

本文旨在全面综述脉冲神经网络的监督学习算法的研究现状和发展趋势。

我们将首先介绍脉冲神经网络的基本原理和模型，包括神经元的脉冲发放模型、网络的拓扑结构和学习机制等。

接着，我们将重点综述几种典型的脉冲神经网络监督学习算法，包括基于脉冲时间依赖性的学习算法、基于突触权重的学习算法以及混合学习算法等。

我们还将讨论这些算法在不同应用场景中的性能表现，以及它们各自的优势和局限性。

我们将对脉冲神经网络的监督学习算法的未来发展方向进行展望，包括算法的优化和改进、新型脉冲神经网络模型的设计、以及与其他计算模型的融合等。

通过本文的综述，我们希望能够为脉冲神经网络的研究者提供一个清晰的研究脉络和有价值的参考，同时也为脉冲神经网络在实际应用中的推广和发展提供有力的支持。

二、脉冲神经网络基础知识脉冲神经网络（Spiking Neural Networks, SNNs）是一种模拟生物神经系统中脉冲信号传递方式的计算模型。

与传统的人工神经网络（Artificial Neural Networks, ANNs）不同，SNNs中的神经元通过发放脉冲（或称为动作电位）来进行信息的传递和处理，而不是通过连续的激活函数。

这种脉冲传递方式使得SNNs在模拟生物神经系统时具有更高的生物真实性。

在SNNs中，神经元通常被抽象为脉冲发生器模型，如Hodgkin-Huxley模型、Leaky Integrate-and-Fire（LIF）模型等。

深度学习算法的核心知识点

深度学习算法的核心知识点深度学习算法是一种基于人工神经网络的机器学习方法，它通过模仿人脑神经网络的结构和功能来实现智能的目的。

在计算机科学和人工智能领域，深度学习算法是近年来备受关注的热门技术。

本文将介绍深度学习算法的核心知识点，包括神经网络、激活函数、损失函数和优化方法等。

一、神经网络神经网络是深度学习算法的基础，它模拟了人脑神经系统的网络结构和功能。

神经网络由神经元和它们之间的连接组成。

每个神经元接收来自其他神经元的输入信号，并通过激活函数对这些输入信号进行处理，最后生成输出信号。

深度学习中的神经网络一般包括输入层、若干隐藏层和输出层。

二、激活函数激活函数是神经网络中非常重要的组件，它决定了神经元输出的结果。

常用的激活函数有sigmoid、ReLU和tanh等。

Sigmoid函数将输入的值映射到0到1之间，常用于二分类问题。

ReLU函数当输入大于0时输出为输入值，否则为0，它在深度学习中得到了广泛应用。

Tanh 函数将输入映射到-1到1之间，常用于多分类问题。

三、损失函数损失函数用于衡量模型的预测结果与实际值之间的差异。

常用的损失函数有均方差损失函数和交叉熵损失函数。

均方差损失函数适用于回归问题，它计算预测值与实际值之间的平均误差。

交叉熵损失函数适用于分类问题，它衡量模型输出的概率分布与真实标签之间的差异。

四、优化方法优化方法用于更新神经网络中的参数，使得模型的预测结果更加准确。

常用的优化方法有梯度下降法、随机梯度下降法和Adam优化算法等。

梯度下降法通过计算损失函数对参数的梯度来更新参数。

随机梯度下降法是梯度下降法的改进版，它在每次更新时随机选取一部分样本进行计算，降低了计算量。

Adam优化算法综合了动量法和RMSProp算法的优点，能够自适应地调整学习率。

五、数据预处理数据预处理是深度学习中一个重要的步骤，它对原始数据进行清洗和转换，以提高模型的准确性和鲁棒性。

数据预处理包括数据清洗、特征选择、数据转换和数据归一化等。

snn速率编码

SNN速率编码一、SNN速率编码概述SNN（Spiking Neural Network）速率编码是一种模拟生物神经网络的计算模型，它通过模拟神经元之间的脉冲传递和编码信息，实现了一种高效、低功耗的神经网络计算方式。

SNN速率编码的发展源于对生物神经网络的研究，其基本思想是将神经元之间的脉冲传递和编码信息作为基本单元，构建出一种能够模拟生物神经网络计算能力的神经网络模型。

二、SNN速率编码的发展历程SNN速率编码的发展历程可以追溯到上世纪90年代，当时科学家们开始对生物神经网络进行深入研究，发现了神经元之间的脉冲传递和编码信息的方式。

随后，一些科学家开始尝试将这种计算方式应用于计算机科学领域，从而诞生了SNN速率编码的概念。

随着计算机科学技术的不断发展，SNN速率编码的理论和技术也在不断得到完善和发展。

三、SNN速率编码的原理SNN速率编码的原理主要包括以下几个方面：1.神经元模型：SNN速率编码中的神经元模型是一种能够模拟生物神经元行为的计算模型，它通过接收其他神经元的脉冲信号，并根据一定的规则进行脉冲发放，从而实现信息的传递和编码。

2.SNN编码方式：SNN速率编码中的编码方式主要采用脉冲频率编码，即将输入信号转换为脉冲频率信号，然后通过神经元之间的脉冲传递和编码信息，实现信息的传递和处理。

3.SNN编码算法：SNN速率编码中的算法主要包括脉冲发放算法、脉冲传递算法和信息解码算法等，这些算法能够实现神经元之间的脉冲传递和编码信息的处理。

四、SNN速率编码的应用场景SNN速率编码在多个领域具有广泛的应用场景，例如：1.模式识别：通过训练SNN模型，可以对输入信号进行分类和识别，例如在语音识别、图像识别等领域具有广泛的应用。

2.信号处理：SNN速率编码可以用于处理和分析各种信号，例如在音频处理、图像处理等领域具有广泛的应用。

3.自然语言处理：通过训练SNN模型，可以对自然语言进行理解和生成，例如在机器翻译、文本生成等领域具有广泛的应用。

snn激活函数

snn激活函数SNN激活函数深度学习中的激活函数是神经网络中的重要组成部分，它在神经元中引入非线性因素，使得神经网络能够拟合非线性函数。

近年来，随着神经网络的发展，不断有新的激活函数被提出。

其中，SNN （Spiking Neural Network）激活函数作为一种新型的激活函数，受到了广泛的关注。

SNN激活函数是一种模拟脉冲神经元的激活函数，它模拟了神经元的脉冲放电过程。

与传统的激活函数相比，SNN激活函数更加接近生物神经元的工作原理，能够更好地描述神经元的兴奋和抑制过程。

SNN激活函数通过将输入信号转化为脉冲信号，来模拟神经元的放电过程。

当输入信号超过神经元的阈值时，神经元会发出一个脉冲信号，否则神经元保持静止。

这种脉冲信号的传递方式，使得神经网络可以更加精确地处理时间相关的信息。

SNN激活函数的引入，为神经网络的应用带来了新的可能性。

首先，SNN激活函数能够减少神经网络的计算量，提高计算效率。

由于SNN 激活函数模拟了神经元的脉冲放电过程，它能够将输入信号转化为脉冲信号，从而减少了神经网络的计算量。

这种计算方式使得神经网络在处理大规模数据时更加高效，能够更好地应用于实际场景。

SNN激活函数能够提高神经网络的稳定性和鲁棒性。

SNN激活函数的脉冲信号传递方式能够使得神经网络对噪声和干扰具有较强的抵抗能力。

由于脉冲信号的传递方式是离散的，它对输入信号的波动具有较强的稳定性，能够有效地抑制噪声和干扰信号的影响。

这种特性使得SNN激活函数在处理复杂任务时具有更好的鲁棒性，能够更好地应对实际应用中的各种干扰。

SNN激活函数还能够提高神经网络的泛化能力。

SNN激活函数能够更好地拟合非线性函数，使得神经网络能够更好地适应不同的数据分布。

由于SNN激活函数模拟了神经元的放电过程，它能够更好地捕捉数据中的非线性特征，从而提高了神经网络的泛化能力。

这种泛化能力使得神经网络能够更好地适应不同的任务和数据集，具有更强的适应性和灵活性。

基于脉冲神经网络的指挥智能体技术

基于脉冲神经网络的指挥智能体技术
王栋;赵彦东;陈希飞
【期刊名称】《火力与指挥控制》
【年(卷),期】2024(49)5
【摘要】针对现有智能体技术应用于军事指挥控制领域中时存在计算资源需求高、奖励值稀疏、收敛速度慢、推理效果差的问题,提出了一种基于脉冲神经网络(spiking neural network,SNN)和分层强化学习的指挥智能体技术。

基于分层强
化学习思想对军事指挥智能体进行建模,利用SNN构建智能体决策模型;通过
ANN-SNN转换的学习算法获得基于SNN的指挥智能体;基于“墨子”兵棋推演
软件开展对比试验,与现有智能体技术相比,提出方法对计算资源的需求较低,且具有较高的博弈对抗胜率。

【总页数】9页(P36-43)
【作者】王栋;赵彦东;陈希飞
【作者单位】北方自动控制技术研究所
【正文语种】中文
【中图分类】TP273;TP183
【相关文献】
1.一种基于神经网络的多智能体建模技术
2.基于脉冲神经网络的智能小车的自动避障系统研究
3.指挥控制系统中的自然智能和人工智能——人工智能技术在指挥控
制系统中面临的挑战4.基于人工脉冲神经网络的门诊静脉采血智能预约平台设计5.基于人工智能技术的配网智能化监控指挥技术研究
因版权原因，仅展示原文概要，查看原文内容请购买。

snntorch snn.leaky原理-概述说明以及解释

snntorch snn.leaky原理-概述说明以及解释1.引言1.1 概述在这个部分，你可以介绍什么是snntorch和SNN.Leaky，并简要说明它们在神经网络领域中的重要性和应用。

可以提到snntorch是一个基于PyTorch的神经网络库，专注于实现脉冲神经网络（SNN）模型，并介绍SNN.Leaky作为SNN中的一种重要神经元模型。

同时，也可以简要提及SNN.Leaky的特点和优势，引发读者对其进一步了解和关注。

分的内容1.2 文章结构文章结构是指文章整体的组织架构和各部分之间的逻辑关系。

本文的结构主要包括引言、正文和结论三个部分。

在引言部分，我们首先会对整篇文章进行概述，介绍snntorch和SNN.Leaky的背景和基本概念。

接着会介绍文章的结构，即各部分的内容组成和安排。

最后说明本文的目的，即探讨和分析snntorch和SNN.Leaky 的重要性和应用。

正文部分主要分为三个小节。

首先是介绍snntorch，讲解其特点和功能，以及在神经网络建模中的应用。

其次是解释SNN.Leaky的原理，包括其工作原理、优势和特点。

最后是讨论SNN.Leaky在实际应用中的情况和潜在发展空间。

结论部分将总结snntorch和SNN.Leaky在神经网络领域的重要性和价值，强调它们对于神经科学和人工智能研究的意义。

展望未来的发展趋势和方向，探讨可能的研究方向和挑战。

最后，通过结束语对全文进行总结和概括，强调文章的主要观点和亮点。

1.3 目的本文旨在介绍snntorch和SNN.Leaky的原理、特点和应用。

通过深入探讨这两个概念，我们希望读者能够更加全面地了解神经网络中的概念与机制，并掌握它们在实际应用中的意义与作用。

同时，我们也希望通过此文的阐述，能够引发读者对未来神经网络发展的思考与展望，促进相关领域的研究与探索。

通过本文的阐述，我们希望能够为读者提供有益的知识和启发，促进神经网络技术的进步与发展。