热力学模型
热力学方程模型
应用WILSON NRTL UNIQUAC模型计算乙醇-水体系汽液平衡摘要:利用已知的乙醇-水混合体系在常压下的汽液相平衡数据。
选用Aspen plus 模拟软件系统自带的活度系数数学模型关联相平衡数据,并和实验测定值相比较。
关键词:汽液相平衡, Aspen plus流体相平衡数据是化工过程中重要的基础数据,在热力学方面,新的热力学模型的开发,各种热力学模型的比较筛选。
特别是在分析和解决传质分离设备的设计、操作、控制过程中,开发新的传质分离过程,往往离不开平衡数据的测定,关联和推算【1】。
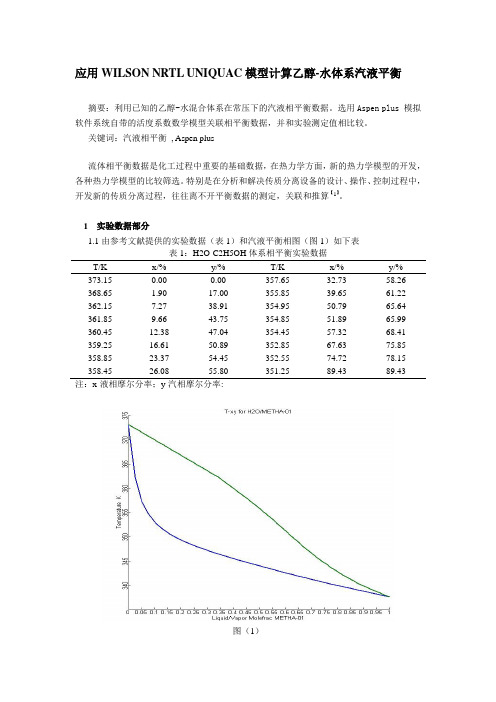
1 实验数据部分1.1由参考文献提供的实验数据(表1)和汽液平衡相图(图1)如下表表1:H2O-C2H5OH体系相平衡实验数据T/K x/% y/% T/K x/% y/% 373.15 0.00 0.00 357.65 32.73 58.26 368.65 1.90 17.00 355.85 39.65 61.22 362.15 7.27 38.91 354.95 50.79 65.64 361.85 9.66 43.75 354.85 51.89 65.99 360.45 12.38 47.04 354.45 57.32 68.41 359.25 16.61 50.89 352.85 67.63 75.85 358.85 23.37 54.45 352.55 74.72 78.15 358.45 26.08 55.80 351.25 89.43 89.43注:x-液相摩尔分率;y-汽相摩尔分率:图(1)2 计算原理2.1汽液相平衡的计算在热力学汽液相平衡的计算中,对于真实体系,采用逸度来表示汽液相平衡,即:Li Vf f =i(1)通常的计算方法有活度系数法和状态方程法2种,UNIQUAC 、WILSON 、NRTL 的相平衡计算称为活度系数法,是将液相组分i 的逸度与混合溶液中组分i 的活度系数建立联系。
高等工程热力学-第一章、热力学基本原理及定义

⑵试写出终态温度T2及排出质量me的表达式。
§1-3 热力学第二定律
一、热力学第二定律的实质及说法
1、热力学第一定律的局限性及热力学第二定律的实质
◆热力学第一定律的实质是能量转换及守恒定律。.
◆任何一个已经完成或正在进行的过程都遵循热力学第一定律。
◆热过程是有方向性的,过程的进行是有条件的, 并有一定的限度。
◆热力学第一定律具有局限性。
热力学第二定律的实质----能质衰贬原理
◆热力学第二定律揭示了不同形式的能量,在转换成功 量的能力上是有“质”的差别的;
◆即使同一种形式的能量,其存在状态不同时,它的转 换能力也是不同的。
◆正是因为各种不同存在形式或不同存在状态的能量, 在传递及转换能力上存在着“质”的差别,所以,在能 量传递及转换过程中,就呈现出一定的方向、条件及限 度的特征。
①能量的存在形式。 有序能>无序能 ②周围环境----定义能质高低的共同基准。
“不能脱离周围环境来进行能质分析!” ③能量的存在状态,即系统所处的状态。
2、寂态(dead state)
当系统与周围环境达到热力学平衡时,系统的状态称为寂态。 此系统中的能量就完全丧失了转换的能力,其能质为零。因此, 寂态可以作为度量任何系统能量品位高低的统一基准。 系统的状态偏离寂态越远,系统能量的品位越高。
∴ 而
则
忽略动、位能变化,则
一种流体的焓增加等于另一种流体的焓减。 即一种流体的吸收的热量等于另一种放出的热量。
例3、喷管
0
0
0
则 对1kg流动工质
∵ ∴ ∴
例4、绝热节流
0
0
第3讲-流程模拟中热力学模型的选择和使用

热力学模型重要性
热力学模型在流程模拟中的作用
在流程模拟中,热力学模型用于描述流体和固体的性质,以及能量和物质的 传递过程。
热力学模型对于模拟结果的影响
热力学模型的准确性直接影响了流程模拟结果的准确性和精度。不同的热力 学模型会有不同的预测结果,因此选择合适的热力学模型非常重要。
02
热力学模型种类及特点
根据实际需求选择
根据实际需求,选择精度高、计算速度快、稳定性好的热力学模型。
参数拟合与校准
参数拟合
根据实验数据,采用合适的方法拟合模型参数。例如,最小二乘法、梯度下 降法等。
校准
对模型进行校准,以减小模型预测结果与实际实验数据的误差。可以采取交 叉验证等方法进行校准。
模型验证与误差分析
模型验证
使用未参与参数拟合的实验数据验证模型的准确性。可以选择若干个具有代表性 的实验数据进行验证。
艺优化提供依据。
案例二:合成氨工业流程模拟
合成氨工业是重要的基础化工产业之一,其生产过程需要高温、高压条件和高精 度的工艺控制。
通过流程模拟,可以优化生产过程,提高合成氨的产量和生产效率,降低能源消 耗和生产成本。
在合成氨工业流程模拟中,热力学模型可以用来预测和模拟各种化学反应和传递 过程,为工艺优化提供依据。
工艺过程的特性
不同的工艺过程需要选用不同的热力学模 型。例如,对于化学反应过程,可能需要 选用化学反应动力学模型;对于传递过程 ,可能需要选用传热、传质相关的模型。
VS
物质的特性
不同物质的热力学性质往往存在较大差异 ,需要根据物质的特性选择合适的模型。 例如,对于高分子材料,可能需要选用分 子热力学模型。
装置规模
装置规模的大小会影响热力学模型的选择。对于大型装置, 热力学模型的选择应该更加严格和精确,以避免误差的放大 。
热力学系统定量化研究之一:模型及基本概念

系 ; 新 的热 力学 系统 中 , 出 将 “ 息 ” 为与 物 质 和 能 量 等 同的 物 理 量 , 力 学 系 统 与 外 界 传 递 和交 换 的 物 量 包 括 物 在 提 信 作 热
质 、 量 和信 息 . 能 以热 力 学 系 统 物 质 流 交换 过 程 为 例 , 导 系 统稳 定 条件 判 据 ( 界 开 放 度 判 据 ) 该 成 果 对 经 典 热 力 学 理 推 边 . 论 有 所 完 善 和补 充 , 精 确 分 析 热 力学 系统 热 质 传 递 过 程 提 供理 论 依 据 . 为 关 键 词 : 力学 系 统 ; 量 化 模 型 ; 放 度 ;交 换率 ;稳 定 性 判 据 热 定 开 文献标识码 : A 文章 编 号 : 0 0—1 9 ( 0 1 0 0 9 一O 10 8 1 2 1 ) 1— 0 6 4
过程 已不适 用 , 为此 不可 逆热力 学理 论将宏 观 系统 划分 成 一些 小 的元 胞 ( 系统 ) “ . 些元 胞 具有 宏 子 l ]这 I 观足够 小 、 观足够 大 ( 微 属于介 观尺度 )距 离平 衡态 不太 远 , , 即具 有局 域平 衡 的特点 . 于元 胞 和局域 平衡 基 概念 , 些热力 学量 在非平 衡 态的情 况下 , 以定 义 为空 间和时 间 的函数 . 一 可
学 系 统 . 力 学 系 统 定 量 模 型 见 图 1 热 .
( E)
其 中 , 界 ( 壳 ) 界 壁 和 界 门 组 成 . 壁 是 “ 缘 ” , 止 物 边 界 由 界 绝 的 禁 质、 能量 和信 息 ( 息与 物质 、 信 能量具 有 同等重要 作用 ) 通过 . 门具 界
图1 热力学系统定量化模型
作 者 简 介 : 志 国( 9 6 ) 男 , 士 后 , 授 , 要 从事 热 力学 基 础 及 油 气 开采 交 叉科 学 方 面 的研 究 . 王 16一 , 博 教 主
热力学知识:热力学中的热力学模型和热力学峰值

热力学知识:热力学中的热力学模型和热力学峰值热力学是一门研究热和能量转移的学科,它是物理学中的一个重要分支领域。
随着科技的不断发展,热力学的理论和应用也在不断地完善和拓展。
在热力学的研究中,热力学模型和热力学峰值是常见的概念,那么,接下来本文就来详细介绍这两个概念。
一、热力学模型热力学模型是指对于某个物质体系的热力学性质,用一组数值模型进行描述的方式。
这些模型可以用来预测物质体系在不同条件下的热力学行为和性质。
热力学模型的基本原理是基于物质体系之间的相互作用力和热力学函数的关系。
其中,最基本的热力学函数包括熵、能量和热容等。
对于理想气体,其热力学模型可以用状态方程来描述。
状态方程可以给出气体的压力、温度和体积之间的关系。
最常见的状态方程包括理想气体状态方程和范德瓦尔斯状态方程。
而对于其他复杂的物质体系,热力学模型的建立需要更加复杂的理论和实验验证。
例如,在分子动力学模拟中,可以使用势函数来描述分子之间的相互作用,进而推导出热力学性质,如热容和热传导等。
值得注意的是,不同的热力学模型适用于不同的物质体系,因此建立热力学模型需要考虑到物质的特殊性质。
同时,模型的可靠性和可行性也需要通过实验数据的验证来证实。
二、热力学峰值热力学峰值是指在某一温度下,热力学性质随某一参数的变化呈现单峰或双峰形状的曲线。
例如,对于某个材料,热导率在一定的温度区间内随晶粒尺寸或缺陷浓度的变化呈现出单峰或双峰形状。
热力学峰值的出现是由于在某一温度下,相互作用力和热力学函数之间的平衡关系发生变化。
换言之,在某一温度下,物质体系中存在一个平衡点,使得热力学性质呈现出峰值状态。
热力学峰值在实际应用中有着广泛的应用。
例如,在材料科学中,热力学峰值可以用来评估材料的热导率。
对于制备材料的过程,通过调整材料的晶粒尺寸或添加适量的缺陷,可以控制材料的热导率和电导率,以适应特定的应用需求。
总而言之,热力学模型和热力学峰值是热力学中的两个基本概念。
物理学中的重要数学模型

物理学中的重要数学模型物理学是研究物质和能量以及它们之间相互作用的科学。
在物理学中,数学模型是解决问题和描述物理现象的重要工具。
物理学中的数学模型可以帮助我们理解自然界的规律和现象,并推导出各种重要的物理定律。
本文将介绍物理学中的几个重要的数学模型,并讨论它们在解决实际问题中的应用。
一、牛顿运动定律牛顿运动定律是经典力学的基础,描述了物体在外力作用下的运动规律。
它以数学方程的形式表达,其中最著名的就是牛顿第二定律:F=ma。
该方程说明了物体的加速度与其受到的力和质量的关系。
通过牛顿运动定律,我们能够计算出运动物体的位置、速度和加速度等参数,从而预测物体的运动轨迹和行为。
二、电磁场理论电磁场理论是描述电磁现象的基本理论,由马克斯韦尔方程组构成。
这些方程组包含了电场和磁场之间的相互关系,以及它们与电荷和电流的关系。
通过求解马克斯韦尔方程组,我们可以得到电磁波的传播速度、电磁感应的规律等重要结论。
电磁场理论的数学模型在电磁学、光学和电子学等领域具有广泛的应用。
三、量子力学量子力学是描述微观世界中粒子行为的理论,其核心是薛定谔方程。
薛定谔方程描述了量子系统的波函数演化规律,通过对波函数的求解,我们可以计算出粒子的能量、位置和动量等性质。
量子力学的数学模型为我们理解原子、分子和量子力学系统提供了重要的工具,对于研究材料科学、原子物理学和量子计算等领域具有关键的意义。
四、热力学热力学是研究热现象和能量传递的学科,基于宏观系统的平衡态和不可逆过程。
热力学的核心是热力学定律,其中最基本的是热力学第一定律和热力学第二定律。
热力学模型通过数学方程描述了能量的转移和转换过程,帮助我们理解热力学系统的特性和行为。
热力学的数学模型应用广泛,例如在热机效率计算、热传导问题和相变等方面。
五、流体力学流体力学研究流体的运动和力学性质,涵盖了气体和液体的运动行为。
流体力学的数学模型基于连续介质假设,通过质量守恒方程、动量守恒方程和能量守恒方程等方程描述了流体的运动规律和流动特性。
热学中常见的四个物理模型

热学中常见的四个物理模型作者:张海峰来源:《数理化学习·高一二版》2013年第06期高考物理在考查知识的同时,注重能力考查,并把对学生能力的考查放在首位.建立好物理模型是学好物理的重要一环,它需要学生具有一定的空间想象能力和应用数学知识处理物理问题的能力.本文列举几例热学中常见的物理模型供大家参考.一、球体模型二、立方体模型例2标准状态下气体的摩尔体积是V0=22.4 L/mol,试估算教室内空气分子间的平均距离.设教室内温度为0 ℃,阿伏伽德罗常数NA=6×1023 mol-1(计算结果保留1位有效数字).解析:气体分子间距离比较大,分子间的作用力很微弱,气体体积和气体分子的体积指的是它们占据的空间体积,可以看成是立方体模型.V0=NA×a3,代入数据得空气分子间的平均距离为a=3×10-9 m.三、理想气体模型例3如图1所示,带有活塞的气缸中封闭一定质量的理想气体,将一个半导体NTC热敏电阻R置于气缸中,热敏电阻与气缸外的电源E和电流表A组成闭合回路,气缸和活塞具有良好的绝热(与外界无热交换)性能,若发现电流表的读数增大,以下判断正确的是(不考虑电阻散热)(A)气体一定对外做功(B)气体体积一定增大(C)气体内能一定增大(D)气体压强一定增大解析:理想气体的特点:气体分子的体积与气体体积相比较可以忽略不计;气体分子之间的相互作用力很小,可以忽略不计;分子之间及分子与器壁之间发生的碰撞无动能损失;理想气体的分子势能可以忽略不计,所以理想气体的内能由物质的量和温度决定.电流增大,电阻减小,温度T升高,内能U增大.气体的内能U=EK+Ep,而理想气体的分子势能可以认为等于零,所以U增大,选项(C)正确.由热力学第一定律,ΔU=W+Q,ΔU>0,由于系统与外界无热交换,所以Q=0,可知ΔU=W>0,外界对气体做功,气体的体积V减小,选项(A)、(B)错误.由理想气体的状态方程PVT=恒量,得到气体的压强p应增大,选项(D)正确.答案:(C)、(D)四、圆柱体模型例4风能是一种环保型能源.目前全球风力发电的总功率已达7000 MW,我国约为100 MW.据勘测我国的风力资源至少有2.53×105 MW.所以风力发电是很有前途的一种能源.风力发电时将风的动能转化为电能.设空气的密度为ρ,水平风速为v,风力发电机每个叶片长为L,风能转化为电能的效率为η,那么该风力发电机发出的电功率P是多大?从以上几例可以看出,建立物理模型相当重要,所以,教师在平时的教学过程中要重视对学生建模能力的培养.[江苏省常熟市浒浦高级中学(215513) ]。
7热力学模型热力学与动力学

idGB RT ln xB
由一对aa原子和一对bb原子混合后形成两个ab对结合能变化因此形成一个ab对的结合能变化为若1摩尔混合物中有naa摩尔的aa原子对nbb摩尔的bb原子对nab摩尔的ab原子对和nba摩尔的ba原子对这样混合物的内能为形成aa对的数目等于相邻位置对的数目与出现aa对的几率的乘积而某一原子位置出现a原子的几率就等于溶体中a或b原子分数aa原子对数目a原子数2因此有其中n0nanb分别为1摩尔混合物中原子总数阿佛加德罗数a原子数和b原子数xa和xb分别为a和b原子分数z为配位数
M m x1 M 1 x2 M 2
Gm x1 1 x2 2
推广到多元体系 对于二元系,摩尔自由焓的微分 推广到多元体系
依吉布斯-杜亥姆公式,对二元系有
G m xi i
dGm 1dx1 2 dx2
dGm
dx
i
i
x1d1 x2 d 2 0
0 0
pi 0pi xi
(xi1)
i 0i RT ln pi
i 0i RT ln0pi RT ln xi
i i RT ln xi
i i标 RT ln ai
偏离拉乌尔定律溶体
i i标 RT ln xi
ai i xi
形成溶体时自由焓的变化
二元系中两相平衡条件为
β α A A
β α B B
亨利定律与乌拉尔定律 亨利定律
当一种溶质溶解在溶剂内,若溶体足够稀时,则溶质从溶体中逸出的能力 正比于它的摩尔分数,即 (xi0) pi kxi
拉乌尔定律 溶体的活度
混合气体中对每一组元i有
溶体服从拉乌尔定律 设
