有效值和峰值及相电压和线电压的关系
qd计算三相电压峰值

qd计算三相电压峰值
三相电压的峰值指的是每个相位的电压波形的峰值大小。
在三相交流系统中,有三个相位:A、B、C。
每个相位的电压波形是正弦波形,因此峰值可以通过以下公式计算:
峰值电压(Vp)= 电压有效值(Vrms)* √2
其中,电压有效值可以通过以下公式计算:
电压有效值(Vrms)= 电压峰值(Vp)/√2
因此,如果已知电压有效值,可以通过上述公式计算出电压峰值。
另外,三相电压峰值还可以通过以下方法计算:
1.如果已知线电压(VL),则每个相位的电压峰值为线电压的峰值的一半。
峰值电压(Vp)=线电压(VL)/2
2. 如果已知相电压(Vph),则每个相位的电压峰值等于相电压的峰值。
峰值电压(Vp)= 相电压(Vph)
在三相系统中,每个相位的电压波形相互间隔120度(⅔π),因此当一相波形达到峰值时,其他两相的波形正处于向上升的过程中。
这种相位差可确保三相电压波形的均匀分布和平衡。
因此,在三相系统中,三个相位的电压峰值大小是相等的。
总结起来,计算三相电压峰值的方法如下:
1. 已知电压有效值(Vrms)时,使用公式:
峰值电压(Vp)= 电压有效值(Vrms)* √2
2.已知线电压(VL)时,使用公式:
峰值电压(Vp)=线电压(VL)/2
3. 已知相电压(Vph)时,使用公式:
峰值电压(Vp)= 相电压(Vph)
以上是关于三相电压峰值的计算方法的简要介绍。
实际应用中,需要考虑到电压的频率和波形形状等因素,以获得更准确的峰值值。
峰值与有效值之间的关系

通常我们说峰值(PK)是有效值(RMS)的 1.414 倍,这个值就是所谓的峰值因子(CF)。 但它其实不是常数。否则误差就可能很大。 本特利先定义如下:(注意:不同公司的仪器,这个定义不是必然一样的) PP 值:一个完整周期内最大的正峰值和最大的负峰值之间的距离。(如何定义完整周期?) PK 值:PP 值的一半。也称“真峰值” 有效值:“真有效值”
RMS = 0.578
‐1
CF = 1.732 通过 √2 x RMS 计算的峰值 = 0.817(同样通过峰值算有效值的话)
误差= 18.30% 例 3 – 50% 方波
+1 峰峰值 = 2.0 单位 正峰值 = 1.0 单位 RMS = 1.0
‐1 CF = 1.00 通过 √2 x RMS 计算的峰值 = 1.414(同样通过峰值算有效值的话)
例 1 – 正弦波
峰峰值 = 2.0 单位 正峰值 = 1.0 单位 RMS = 0.707 CF = 1.414
T 就是上面的同一完整周期。 +1 ‐1
通过 √2 x RMS 计算的峰值 = 1.00 (同样通过峰值算有效值的话)
误差 = 0% 例 2 – 三角波
+1 峰峰值 = 2.0 单位 正峰值 = 1.0 单位
误差 = 41.4%
例 4 – 2% 脉冲
峰峰值 = 2.0 单位 正峰值 = 2.0 单位 RMS = 0.283 CF = 7.071 通过 √2 x RMS 计算的峰值 = 0.400(同 样通过峰值算有效值的话) 误差 = 60.0%
+2 0
波形
正弦波 (例 1) 三角波 (例 2) 方波 (例 3) 脉冲波 (例 4)
各种波峰峰值和有效值的关系

各种波峰峰值和有效值的关系
波峰是所测量波形的最高点,峰-峰值是波形的峰值和谷值之间的差值,有效值是波形的均方根值。
它们的关系如下:
对于正弦波而言,波峰值等于有效值乘以√2,峰-峰值等于有效值乘以2√2。
对于方波而言,波峰值等于峰-峰值的一半,而有效值需要按照其频率来计算。
对于三角波而言,波峰和波谷的值相等,峰-峰值就是两个峰值的差值,有效值同样需要按照其频率来计算。
因此不同类型的波形,它们的波峰峰值和有效值的关系都略有不同,需要根据具体情况进行计算。
三相电压幅值和有效值

三相电压幅值和有效值
三相电压是指由三个不同的正弦交流电组成的电源,它们之间的相位差为120度。
三相电压的幅值和有效值是两个重要的电气参数,下面将对其进行详细介绍。
幅值是指正弦波的最大绝对值,也就是波形的峰值。
对于三相电压,其幅值是指每个相位上的电压最大值。
通常情况下,幅值是以伏特(V)为单位。
有效值是指正弦波的平均值,即一个等效的直流电压值。
对于三相电压,其有效值是指三个不同相位上的电压平均值相等的情况下的平均电压值。
有效值通常以安培(A)为单位。
需要注意的是,三相电压的有效值与幅值之间存在一定的关系。
根据欧姆定律,在相同的电阻上,直流电压和交流电压的有效值是相等的。
因此,三相电压的有效值可以通过以下公式计算:
有效值 = 幅值 / √2
其中,√2是指根号2,即1.414。
因此,如果三相电压的幅值为380V,则其有效值为:
有效值 = 380V / √2 ≈ 220V
这个结果也被称为“线电压”,因为它指的是每根电线上的电压值。
同时,三相电压的“相电压”有效值等于幅值的√3倍,即:
相电压有效值≈√3 ×幅值≈ 220V × 1.732 ≈ 381V
这个结果指的是每相电压的有效值,也就是每相负载所承受的电压值。
电压的有效值、平均值与峰值
电压的有效值、平均值与峰值
1 电压的有效值
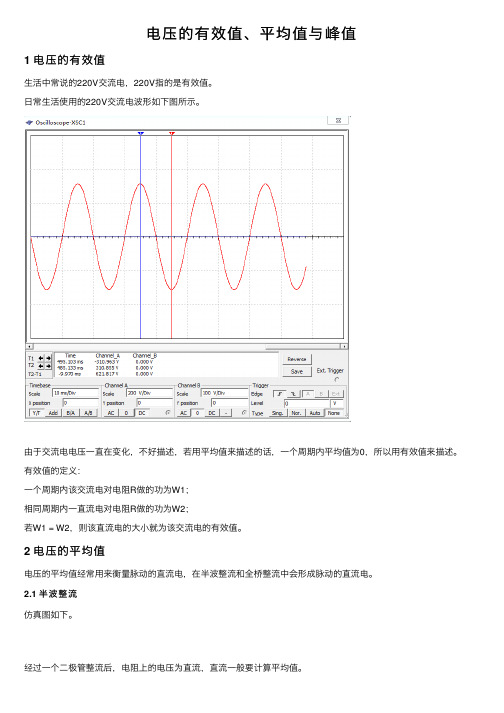
⽣活中常说的220V交流电,220V指的是有效值。
⽇常⽣活使⽤的220V交流电波形如下图所⽰。
由于交流电电压⼀直在变化,不好描述,若⽤平均值来描述的话,⼀个周期内平均值为0,所以⽤有效值来描述。
有效值的定义:
⼀个周期内该交流电对电阻R做的功为W1;
相同周期内⼀直流电对电阻R做的功为W2;
若W1 = W2,则该直流电的⼤⼩就为该交流电的有效值。
2 电压的平均值
电压的平均值经常⽤来衡量脉动的直流电,在半波整流和全桥整流中会形成脉动的直流电。
2.1 半波整流
仿真图如下。
经过⼀个⼆极管整流后,电阻上的电压为直流,直流⼀般要计算平均值。
V直流平均 = 周期内电压与时间积的积分/周期T
经过计算 V直流平均 = 0.45 * V1有效
2.2 全桥整流
仿真图如下图所⽰。
V直流平均 = 周期内电压与时间积的积分/周期T 经过计算 V直流平均 = 0.9 * V1有效
3 电压的峰值
在正弦信号中,电压的最⼤值就是峰值。
正弦信号中:峰值 = 根号2倍的有效值
4 参考
半波整流电路有什么特点,电压平均值和有效值有什么不同。
有效值、平均值、峰峰值

有效值、平均值、峰峰值
平均值很简单,就是各个时刻的值累加,然后求平均
有效值的计算公式为:根号(电压平方在一个周期内对时间的积分/周期)
假设一个方波,高电平电压为U1,低电平电压为U0(换成电流是一样的道理),它的占空比为n(即高电平U1所占一个周期的比例为n):
那么峰峰值当然就是U1-U0了。
平均值就是 U1*n+U0*(1-n)。
有效值就是根号(U1*U1*n+U0*U0*(1-n))。
所以有效值(效值作功的当量均值)就是求i*i或v*v的平均值,然后开方(还原量纲)。
至于平均值就是简单的对i或v求均值。
正弦交流电的有效值等于最大值被根2除,即I=0.707Im;正弦波的平均值Iav=0.637Im。
对图2所示的方波而说,由定义显然可得有效值与最大值相等。
对图3所示的三角波和图4所示的锯齿波。
由定义可得有效值等于最大值被根3除I≈0.577Im。
方波电压的有效值,峰值,平均值之间的关系
方波电压的有效值,峰值,平均值之间的关系方波电压的有效值、峰值和平均值是电学中常见的三种参数,它们之间的关系如下:
首先,方波电压是一种周期性的电压信号,它的形状类似于一个矩形波形,其峰值为正/负最大值。
方波电压的有效值(也称为有效电压),是指该方波电压在一个周期内所产生的热或功率效果与相同值的正弦波电压所产生的热或功率效果相同的电压大小。
而方波电压的平均值则是指该方波电压在一个周期内的电压平均值。
根据方波电压的定义,可以得到以下三个参数之间的关系:
1. 方波电压的峰值等于其有效值的倍数。
即Vp = Vrms × 根号2
2. 方波电压的平均值等于其峰值与零点电压之间的中点值。
即 Vavg = (Vp + 0) / 2
3. 方波电压的有效值等于其峰值与平均值之间的均方根值。
即 Vrms = 根号(Vp^2 + Vavg^2)
综上所述,方波电压的峰值、平均值和有效值之间有着明确的数学关系,这些参数在电学工程设计和实际应用中都有着重要的作用。
- 1 -。
电路原理电压的有效值 峰峰值 与平均值
电路原理电压的有效值峰峰值与平均值电路原理中的电压是一个重要的概念,我们可以从有效值、峰峰值和平均值三个方面对其进行全面的讲解。
首先,电压的有效值是指交流电压的大小,它是为了与直流电压相比较而引入的概念。
对于正弦波形的交流电压而言,它的有效值等于其峰值的0.707倍。
有效值的概念十分重要,因为它代表了交流电压中所包含的能量与直流电压相等时的大小。
在电路设计和分析中,我们经常使用有效值来计算电流、功率等参数,因此理解和准确地计算电压的有效值对于工程师来说至关重要。
其次,峰峰值是交流电压波形的峰值之间的差值,即波形从最高点到最低点的距离。
对于正弦波形的交流电压而言,它的峰峰值等于其峰值的两倍。
峰峰值的概念在测量和比较不同电压信号的幅度时非常有用。
例如,当我们需要了解一台设备或电路在工作时所能承受的最大电压范围时,我们可以利用峰峰值来进行评估。
此外,峰峰值还可以用于测量电压信号的纹波和噪声。
最后,平均值是交流电压波形在一个周期内所有时间的平均值。
在正弦波形的情况下,它的平均值为零,因为正负半周期的平均值互相抵消。
然而,在其他非正弦波形信号中,平均值可以有非零的值。
平均值的概念对于了解交流电压的整体趋势非常有用。
例如,在电源设计中,我们通常需要确保输出电压的平均值稳定,并且与设计要求一致。
综上所述,了解电压的有效值、峰峰值和平均值是电路原理中的基础知识。
它们在电路设计、分析和测量中起着重要的作用。
了解这些概念不仅有助于我们正确评估电压信号的幅度和能量,还能帮助我们更好地理解和解决电路故障和设计问题。
因此,在电路原理的学习和工程实践中,我们应该充分理解和应用这些概念,以确保电路的正常运行和性能优化。
单相、三相整流的输入电流、平均电流、电流有效值、峰值电流与输出电流的关系
单相、三相整流的输入电流与输出电流的关系简要分析单相和三相电容滤波不可控整流的输入电流、母线电流、输出电流之间的关系,最后给出简单的估算公式。
1、单相输入整流单相输入整流如下图1,δ为二极管的起始导电角,θ为导通角。
图1 电容滤波单相桥不控整流电路及波形(图形出处:《电力电子学---电力电子变换和控制技术》--陈坚)图中()2*sin()s v t Vs t ωδ=+,电流计算式如下:可以得到:变频器使用条件下,负载R 需要通过折算直流母线电流来确定。
sin δ约为母线电压最小值与额定值的比。
起始导电角、导通角、负载、电容间的关系如下表:sin()in t ωδ+。
(1)单相输入电流有效值忽略效率,假设输入功率等于输出功率,则Pin=Pout 。
Pin=Uin*Iin ,(电流电压均为有效值)。
*Uo*Io ,(Uo 为输出的线电压,Io 为输出电流)。
可得到*Io ,即单相输入的变频器,倍。
考虑功率因数时,Iin= *Io/cos γ。
(2)单相母线电流平均值in ,根据母线提供的功率等于输出功率,则**in d o o I I =,(S2变频器,Uin 为220V ,Uo 为220V ),2d o I I =,( 1.22d o I I =) 单个二极管承受的电流平均值为母线电流平均值的一半。
(3)单相输入电流峰值输入电流类似与正弦波,只是导通角度减小,但周期和输入电压一致。
将输入电流的方向电流变为正后即为母线电流,所以输入电流峰值即为母线电流峰值。
输入电流峰值与负载和滤波电容有关,它们决定了导通角θ。
当负载在有感性负载如电机或直流电抗器的情况下,输入电流的波形类似于正弦半波。
函数y=Asin(wt),通过积分计算可得到正弦半波的最大值与平均值的关系为2AV Ay π=,2AV MAX y y π=单相整流的输出电流周期为π,最大导通角为π,当导通角为θ时,2*AV MAXy y θππ=输出功率逆推得到母线电流平均值与波形计算值相等,d AV I y =,则输入电流最大值:()*in MAX o I I ππθ=考虑功率因数,则()**4cos o in MAX I I ππθλ=,(()*1.92*cos o in MAX I I πθλ=)根据经验,输入电流峰值为输出电流有效值的4-6倍左右,当有直流电抗器时,导通角度会增加,峰值会稍微降低。
电路基础原理交流电的有效值与峰值
电路基础原理交流电的有效值与峰值电路基础原理:交流电的有效值与峰值电路是电力工程中最基础的部分之一,也是我们日常生活中不可或缺的组成部分。
而要理解电路的工作原理,我们首先需要了解交流电的有效值和峰值。
交流电是一种频率变化的电流,其波形可以用正弦函数来描述。
正弦波形是一种周期性的波形,具有连续且无限次重复的特点。
在交流电中,有两个重要的参数需要我们关注,即有效值和峰值。
有效值是指交流电在相同功率下所产生的热效应与直流电相同的电压或电流值。
在数学上,有效值也被称为交流电的均方根值,记作Irms。
有效值是交流电中最常用的参数之一,它可以描述交流电的大小。
峰值是指交流电波形中的最大正或负值,也就是波形的最高点或最低点。
峰值一般用峰值电压或峰值电流来表示,记作Um或Im。
峰值能够帮助我们了解交流电的峰值大小。
例如,当我们说一台电视机能够承受10A的峰值电流时,说明电视机的电路必须能够承受由交流电产生的最大电流值。
在电路中,交流电的有效值和峰值之间存在一定的关系。
根据数学公式,有效值等于峰值除以根号二,即Irms=Im/√2。
这种关系对于电路设计和分析非常重要。
通过计算交流电的有效值,我们可以估计电路中的能量损耗、功率消耗以及各个元器件所需的承受能力。
因此,在电路设计过程中,我们通常将有效值作为一个重要参考指标。
除了理论计算,我们还可以通过仪器来测量交流电的有效值和峰值。
示波器是一种常用的测量交流电波形的仪器,它可以显示出交流电的实时波形,并且也可以通过测量来计算出交流电的有效值和峰值。
总结起来,电路基础原理中的交流电有效值和峰值是我们理解电路工作原理和性能的关键参数。
了解这两个参数可以帮助我们选择适当的元器件,以及预测电路的性能、功耗和能耗。
通过测量和计算,我们能够准确地确定交流电的有效值和峰值,从而更好地应用于实际电路设计中。
通过对交流电有效值和峰值的了解,我们能更好地理解电路中的电流和电压的变化规律,为电路的设计、维护和故障排除提供了坚实的基础。
