如何将一个大正方形分割成不等于2个_3个_5个的任意数量的小正方形
高思奥数一年级下册含答案第15讲图形剪拼

例题 2
把下面的正方形分成形状相同、大小相等的 示)
4 个图形,可以怎么分?(用虚线表
【提示】把正方形折一折.
练习 2 把一张形状为“ L”的纸,剪成 4 个形状相同、大小相等的图形.你有几种剪法?(用虚线表
【提示】紧挨着的相同的动物一定是要隔开的.
例题 6
请把下面的正方形分割成 4 个形状相同、 大小相等的图形, 使每个图形中都含有一只小鸟和一 条小鱼.
【提示】 4 个形状相同、大小相等的图形可以是
这样的吗?
课外阅读
四巧板
四巧板由下图中的四块拼板组成.
拼一拼,看看下面的图形是不是由这四块板拼成的?
☆ ☆
☆
☆
5. 把下面的正方形分割成 4 个形状相同、大小相等的图形,使每个图形中都含有一个☆和一个★.
★☆ ★
☆☆ ★★☆
★
★
★
★
4. 请把下面的正方形分割成 4 个形状相同、大小相等的图形,使每个图形中都含有一个☆.Βιβλιοθήκη ☆ ☆☆☆
5. 把下面的正方形分割成 4 个形状相同、大小相等的图形,使每个图形中都含有一个☆和一个★.
例题 4 请把下面的长方形分割成 4 个形状相同、大小相等的图形,使每个图形中都含有 一只小青蛙.
【提示】一共有 12 个格子,分割成 4 个形状相同、大小相等的图形,每个图形应该有几个格 子呢?
练习 4 请把下面图形分割成 4 个形状相同、大小相等的图形,使每个图形中都含有一只小老虎.
例题 5 请把下面的正方形分割成 4 个形状相同、大小相等的图形,使每个图形中都含有 一只小猫.
高思奥数导引小学四年级含详解答案第11讲 几何图形剪拼

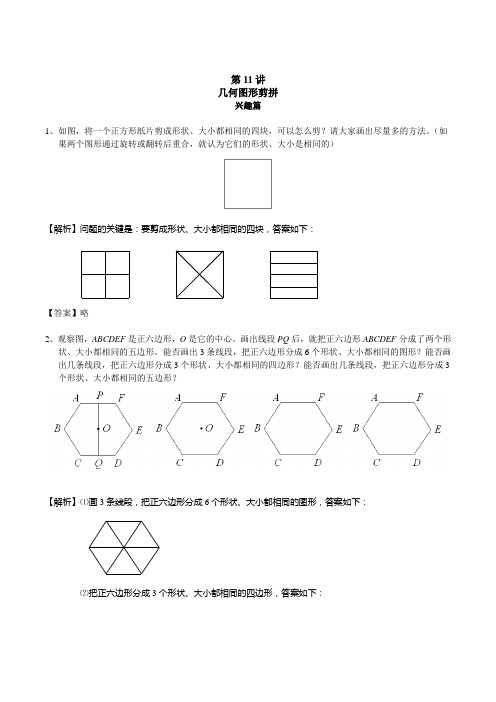
第11讲几何图形剪拼兴趣篇1、如图,将一个正方形纸片剪成形状、大小都相同的四块,可以怎么剪?请大家画出尽量多的方法。
(如果两个图形通过旋转或翻转后重合,就认为它们的形状、大小是相同的)2、观察图,ABCDEF是正六边形,O是它的中心。
画出线段PQ后,就把正六边形ABCDEF分成了两个形状、大小都相同的五边形。
能否画出3条线段,把正六边形分成6个形状、大小都相同的图形?能否画出几条线段,把正六边形分成3个形状、大小都相同的四边形?能否画出几条线段,把正六边形分成3 个形状、大小都相同的五边形?3、如图,在一块正方形纸片中有一个正方形的空洞。
现在要求用一条经过大正方形中心点的线段,把纸片分成面积相等的两部分,应该怎么分?4、请把图中的两个图形分别沿格线剪成四个形状、大小都相同的图形。
5、请把图沿格线分成形状、大小都相同的三部分,使得每部分都恰好含有一个“○”。
6、如图,三角形和六角星的每条边长都相等,那么用多少个三角形可以拼成六角星?请在图中表示出来。
7、如图,左图是由五个相同大小的小正方形拼成的,右图是由一个正方形和一个等腰直角三角形拼成的。
请把这两个图形分别剪成四个形状、大小都相同的图形。
8、如图,请把一个大正方形分割为两种面积不同的小正方形。
(1)如果要求两种小正方形一共有6个,应该怎么分?(2)如果要求两种小正方形一共有7个,应该怎么分?9、如图,有两个面积相等的正方形纸片,现在想把它们剪拼成一个更大的正方形,要求如下:(1)如果分别剪开这两个正方形,再拼接成一个大正方形,应该怎么办?(2)如果只允许剪开一个正方形,再拼接成一个大正方形,应该怎么办?10、图是由若干个小正方形组成的图形,你能将其剪成两块,然后拼成一个大正方形吗?拓展篇1、请在图中标出分割线,把下图沿格线分成形状、大小都相同的四个部分。
(如果两个图形通过旋转或反转后重合,就认为它们的形状、大小事相同的)2、把图沿格线分割成形状、大小都相同的四个部分,请在图中画出具体的分割办法。
第 4讲 正三角形

四边形 ADOF 为矩形,OF AD ,同理: OD BE , OE CF ,
AD BE CF OD OE OF 3 a 2
【独立尝试】
1. 一艘轮船由海平面上 A 地出发向南偏西 40°的方向行驶 40 海里到达 B 地,再
由 B 地向北偏西 20°的方向行驶 40 海里到达 C 地,则 A、C 两地相距( )
()
A.3
B.4
C.5
D.6
6. 如图所示,已知等边△ABC 的边长为 a,P 是△ABC 内一点,PD∥AB,
PE∥BC,PF∥AC,点 D、E、F 分别在 BC、AC、AB 上,则
PE
B
MFC B
MF C B
①1
①2
MF E C
P
①3
解析:由图
1, 连 结
AP, 得
SAPB
SAPC
SABC
,可得
1 2
1
DP•AB+
2
PE•AC=
1 2
AM•BC,化简得 DP+PE=AM,此时 h3 0 ,即 h1 h2 h3 h ;同理在图 2 中,连结 AP,
BP,CP,由 SABC SAPB SAPC SPBC ,化简得 h1 h2 h3 h . 同样道理在图 3 中,可
A.30 海里
B.40 海里
C.50 海里
D.60 海里
北 C
A
C
A
北
P
B
A
第 1 题图
E
D
第 2 题图
B
BR
C
第 3 题图
2. 如 图 ,CD 是 Rt△ABC 斜 边 AB 上 的 高 ,将 △BCD 沿 CD 折 叠 ,B 点 恰 好 落 在 AB
2014年中考数学高分冲刺17-图形的分割与剪拼

关键点十七 图形的分割与剪拼纵观近年来全国各地的中考试卷,图形操作型的问题渐多,而这些题又可分为两大类:一类是围绕“图形变换”展开的(我们已有专题论及),另一类是围绕图形的分割与剪拼展开的。
我们现在要研究的,就是这后边的一类,分割与剪拼的形式与依据主要有:Ⅰ、原图形基础上进行分割,而分割的要求又分为: (1)借助于“边、角”计算的分割; (2)依“面积等分”为要求的分割;Ⅱ、将原图形等面积地变化成新图形的“剪与拼”。
一、图形的分割1、借助于“边、角”计算的分割例1 (1)已知ABC ∆中,︒=∠︒=∠5.67,90B A ,请画一条直线,把这个三角形分割成两个等腰三角形。
(2)已知ABC ∆中,C ∠是其最小的内角,过顶点B 的一条直线把这个三角形分割成了两个等腰三角形,请探求ABC ∠与C ∠之间的关系。
【观察与思考】对于(1)只需“构造等角”;对于(2), (1) 可从“等边”推演角之间的关系。
解:(1)如图①,图②,有两种不同的分割法。
(2)设ABC ∠y =,C ∠x =,过顶点B 的直线 ① 交边AC 于D 。
在等腰三角形DBC 中,①若C ∠是顶角,如图③,则︒>∠90ADB ,,2190)180(21x x CDB CBD -︒=-︒=∠=∠ y x A --︒=∠180。
②此时只能有ABD A ∠=∠,即)2190(180x y y x -︒-=--︒, ︒=+∴54043y x ,即ABC ∠与C ∠的关系是:C ABC ∠-︒=∠43135。
②若C∠是底角,则有两种情况。
③AC A BC︒5.67 ︒5.67 ︒5.22︒5.22AB C︒45 ︒5.22︒5.22︒45 ABC DABD ∆中,x y ABD x ADB -=∠=∠,2。
Ⅰ、由AD AB =,得x y x -=2,此时有x y 3=,即有关系C ABC ∠=∠3。
④ Ⅱ、由BD AB =,得x yx 2180=--︒,此时 ︒=+1803y x ,即C ABC ∠-︒=∠3180。
第11讲 几何图形剪拼
第11讲几何图形剪拼兴趣篇1、如图,将一个正方形纸片剪成形状、大小都相同的四块,可以怎么剪?请大家画出尽量多的方法。
(如果两个图形通过旋转或翻转后重合,就认为它们的形状、大小是相同的)【解析】问题的关键是:要剪成形状、大小都相同的四块,答案如下:【答案】略2、观察图,ABCDEF是正六边形,O是它的中心。
画出线段PQ后,就把正六边形ABCDEF分成了两个形状、大小都相同的五边形。
能否画出3条线段,把正六边形分成6个形状、大小都相同的图形?能否画出几条线段,把正六边形分成3个形状、大小都相同的四边形?能否画出几条线段,把正六边形分成3 个形状、大小都相同的五边形?【解析】⑴画3条线段,把正六边形分成6个形状、大小都相同的图形,答案如下:⑵把正六边形分成3个形状、大小都相同的四边形,答案如下:⑶把正六边形分成3个形状、大小都相同的五边形,答案如下:【答案】3、如图,在一块正方形纸片中有一个正方形的空洞。
现在要求用一条经过大正方形中心点的线段,把纸片分成面积相等的两部分,应该怎么分?【解析】过中心点的直线分面积相等,只要作出正方形空洞的中心,连结此中心与大正方形即可。
如下图:【答案】4、请把图中的两个图形分别沿格线剪成四个形状、大小都相同的图形。
【解析】⑴图中共有12个方格,要分成四个形状、大小都相同的图形,则每个图形有:12÷4=3(个)方格。
分法如图:⑵图中共有12个小三解形,分成的4个形状、大小都相同的图形,每个图形有12÷4=3(个)小三解形。
分法如下图:【答案】5、请把图沿格线分成形状、大小都相同的三部分,使得每部分都恰好含有一个“○”。
【解析】图中共有12个小正方形,分成形状、大小都相同的三部分,每部分:12÷3=4(个)小正方形。
分法如下:【答案】6、如图,三角形和六角星的每条边长都相等,那么用多少个三角形可以拼成六角星?请在图中表示出来。
【解析】采用分割法知共需12个三解形,分法如下图:【答案】12个,7、如图,左图是由五个相同大小的小正方形拼成的,右图是由一个正方形和一个等腰直角三角形拼成的。
祖暅原理及其分析(1)

祖暅原理及其分析摘要:刘徽在发现《九章算术》球体积公式错误的基础上,构造了"牟合方盖",正确指出了解决该问题的思路。
祖氏父子间接求出了"牟合方盖"的体积,从而彻底解决了球体积计算公式的难题,并提出了祖暅原理。
本文回顾了中国古代数学取得的巨大成就,激发大家的民族自豪感和学习数学史的热情,然后用高等数学的知识证明了祖暅原理,强调高等数学对中学数学教学的指导作用,增强大家学习高等数学的自觉性。
一、刘徽对球体积公式的探索刘徽一生不仅成就卓越,而且品格高尚。
在学术研究中,他既不迷信古人,也不自命不凡,而是坚持实事求是,以理服人。
如少广章的“开立圆术”给出的球体积计算方法相当于公式V=9/16D³(这里的D为球的直径),刘徽对这一公式的正确性产生怀疑,他娴熟的使用界面法进行验证,发现内切圆的体积与正方形的体积之比为π/4,在《九章算术》取π=3的情况下,只有在内切球与圆柱的体积之比也是π/4时,上述近似公式才成立,而实际上后者是不成立的,为了说明这一点,刘徽又引入了一种新的立体:以正方体相邻的两个侧面为底分别做两次内切圆柱切割,剔除外部,剩下的内核部分刘徽称之为“牟合方盖”。
他用截面法证明内切球与“牟合方盖”的体积之比为π/4,而明显可以看出,“牟合方盖”的体积比圆柱要小,故上述公式是错误的,显然,如果能求牟合方盖的体积,球的体积就自然可以求出了。
但对于牟合方盖的体积如何求出,刘徽百思不得其解,故最后不得不“付之缺疑,以俟能言者”。
刘徽没有成功,但他的思路正确,为后人解决这一问题打下基础。
二、祖暅原理祖氏父子在研究《九章算术》及刘徽注时发现了刘徽遗留下来的关于如何计算“牟合方盖”的问题,并且开始沿着刘徽的道路继续探索,经父子俩不懈的努力,终于由祖暅解决了牟合方盖体积的计算,得到牟合方盖与其外切正方形的体积之比是2/3,祖暅还将其推导过程中所用的、事实上也是刘徽已经使用过得不可分割原理,总结提炼成一般的命题:“幂势相同,则积不容异”,即夹在两个平行平面间的两个几何体,被平行于这两个平面的任意平面所截,若所的截面总相等,则此二几何体体积相等。
费马定理

费马大定理费马大定理在数论领域,费马的名字因“费马大定理”而特别响亮。
费马大定理亦称“费马猜想”,最先由费马在阅读巴歇(CBachet)校订的丢番图《算术》时作为卷2命题8的一条页边批注而提出。
1670年费马之子萨缪尔(Samue1)连同其父的批注一起出版了巴歇的书的第二版,此后三个多世纪,费马大定理成为世界上最著名的数学问题,吸引历代数学家为它的证明付出了巨大的努力,有力地推动了数论乃至整个数学的进步;1994年,这一旷世难题被英国数学家威尔斯(A。
Wi1es)解决以下就是费马的页边批注,原文为法文,把一个数的立方分成另两个数的立方和,把一个数的四次方分成另两个数四次方的和,或一般地,把一个数的高于2的任何次方分成两个数的同次方的和是不可能的。
我确信已找到了一个极佳的证明,但书的空白大窄,写不下。
费马小定理费马经常把他的一些研究结果写信告诉其他数学家。
在1640年10月18日致德·贝西(RRdeBessy)的一封信中包含了后以" 费马小定理”著称的如下结果:如果p 是素数,a与p 互素,则被p 整除。
费马曾对欧凡里得《几何原本的定理》,36很感兴趣,该定理是说:如果2”一1是素数,则形如2~’(2”一1)的数是完全数,即它等于其所有因子的和。
这种像2一‘的数费马叫做完全数的根。
在1640年6月写给梅森神父(M。
Mersenne的信中费马有如下结论:如果n 非素,贝2”一 1非素;如果”是素数,则2”一2可被门整除;如果”是素数,贝:J 2、一:只能被形士口2kn+i的素数整除。
同年8月在给贝西的信中,费马讨论了2、+1型的数(当”一2’时, 22t+1型数后被称为“费马数”。
)费马在10月18日写给贝西的信中首先回顾了上述诸信的结果,然后转向“费马小定理”。
以下摘录该信有关部分,转译自趴J.Struik:A、 Source BOok in Math. pp。
28~29。
小学奥数讲义4年级-5- 图形的剪拼-难版

第5讲图形的剪拼知识梳理把一个几何图形按某种要求分成几个图形,就叫做图形的分割.将一个或者多个图形先分割开,再拼成一种指定的图形,则叫做图形的剪拼.我们在图形的分割、拼合和剪拼的过程中,都要结合所提供的图形特点来思考.如果把一个图形分割成若干个大小、形状相等的部分,那么就要想办法找图形的对称点,把图形先分少,再分多.如果是要把几个图形拼合成一个大图形,要特别注意每条边的长度,把相等的边长拼合在一起,先拼少的,再拼多的.如果是剪拼图形,要抓住“剪、拼前后图形的面积相等”这个关键,根据已知条件和图形的特点,通过分析推理和必要的计算,确定剪拼的方法.典型例题【例1】★请将一个任意三角形分成四个面积相等的三角形。
【解析】本题要求分成面积相等的三角形,因此可以利用“同底等高的三角形面积相等”这一性质来分割。
方法一:将某一边等分成四份,连结各分点与顶点(见左下图)。
方法二:画出某一边的中线,然后将中线二等分,连结分点与另两个顶点(见右上图)。
【小试牛刀】试将一个等边三角形分割成8个全等的直角三角形。
【解析】如图【例2】★将右图分割成五个大小相等的图形。
【解析】因为图中共有15个小正方形,所以分割成的图形的面积应该等于15÷5=3(个)小正方形的面积。
3个小正方形有和两种形式,于是可得到很多种分割方法,下图是其中的三种。
【小试牛刀】下图是一个直角梯形,请你画一条线段,把它分成两个形状相同并且面积相等的四边形.321D C B A 1FE221D C BA【解析】直角梯形的上底为1,下底为2,要分成两个相同的四边形,需要一条边可以分成1和2,AD 边长正好为3,所以AD 边分成两段,找到AD 的三等分点E ,现在,CD AE =,DE AB =,BF EF =,所以还要找到BC 的中点F ,连接EF ,就把梯形ABCD 分成完全相同的两部分.如右上图.【例3】★★右图是一个4×4的方格纸,请在保持每个小方格完整的情况下,将它分割成大小、形状完全相同的两部分。
