八年级下册人教版数学《反比例函数》基础练习题
初二数学人教版(下册)反比例函数典型例题汇总(附答案)

例 下面函数中,哪些是反比例函数?(1);(2);(3);(4);(5)3x y -=x y 8-=54-=x y 15-=x y .81=xy 解:其中反比例函数有(2),(4),(5).说明:判断函数是反比例函数,依据反比例函数定义,,它也可变形为xky =)0(≠k 及的形式,(4),(5)就是这两种形式.1-=kx y k xy =反比例函数的典型例题二例 在以下各小题后面的括号里填写正确的记号.若这个小题成正比例关系,填(正);若成反比例关系,填(反);若既不成正比例关系又不成反比例关系,填(非).(1)周长为定值的长方形的长与宽的关系 ( );(2)面积为定值时长方形的长与宽的关系 ( );(3)圆面积与半径的关系 ( );(4)圆面积与半径平方的关系 ( );(5)三角形底边一定时,面积与高的关系 ( );(6)三角形面积一定时,底边与高的关系 ( );(7)三角形面积一定且一条边长一定,另两边的关系 ( );(8)在圆中弦长与弦心距的关系 ( );(9)x 越来越大时,y 越来越小,y 与x 的关系 ( );(10)在圆中弧长与此弧所对的圆心角的关系 ( ).答:说明:本题考查了正比例函数和反比例函数的定义,关键是一定要弄清出二者的定义.例 已知反比例函数,y 随x 增大而减小,求a 的值及解析式.62)2(--=a xa y 分析 根据反比例函数的定义及性质来解此题.解 因为是反比例函数,且y 随x 的增大而减小,62)2(--=a xa y 所以 解得⎩⎨⎧>--=-.02,162a a ⎩⎨⎧>±=.2,5a a 所以,解析式为.5=a xy 25-=反比例函数的典型例题四例 (1)若函数是反比例函数,则m 的值等于( )22)1(--=m xm y A .±1B .1C .D .-13(2)如图所示正比例函数)与反比例函数的0(>=k kx y xy 1=图像相交于A 、C 两点,过A 作x 轴的垂线交x 轴于B ,连结BC .若的面积为S ,则:ABC ∆A . B .C .D .S 的值不确定1=S 2=S 3=S 解:(1)依题意,得 解得.⎩⎨⎧-=-≠-,12,012m m 1-=m 故应选D .(2)由双曲线关于O 点的中心对称性,可知:.x y 1=OBC OBA S S ∆∆=∴.12122=⋅=⨯⨯==∆AB OB AB OB S S OBA 故应选A .例已知,与x 成正比例,与x 成反比例,当时,;当21y y y +=1y 2y 1=x 4=y 时,,求时,y 的值.3=x 5=y 1-=x 分析 先求出y 与x 之间的关系式,再求时,y 的值.1-=x 解 因为与x 成正比例,与x 成反比例,1y 2y 所以.)0(,212211≠==k k xk y x k y 所以.xkx k y y y 2121+=+=将,;,代入,得1=x 4=y 3=x 5=y 解得 ⎪⎩⎪⎨⎧=+=+.5313,42121k k k k ⎪⎪⎩⎪⎪⎨⎧==.821,81121k k 所以.xx y 821811+=所以当时,.1-=x 4821811-=--=y 说明不可草率地将都写成k 而导致错误,题中给出了两对数值,决定了21k k 、的值.21k k 、反比例函数的典型例题六例 根据下列表格x 与y 的对应数值.x ……123456…y …632 1.5 1.21…(1)在直角坐标系中,描点画出图像;(2)试求所得图像的函数解析式,并写出自变量x 的取值范围.解:(1)图像如右图所示.(2)根据图像,设,取代入,得)0(≠=k xky 6,1==y x . ∴.16k=6=k ∴函数解析式为.)0(6>=x xy 说明:本例考查了函数的三种表示法之间的变换能力,即先由列表法通过描点画图转化为图像法,再由图像法通过待定系数法转化为解析法,题目新颖别致,有较强的趣味性.反比例函数的典型例题七例(1)一次函数与反比例函数在同一坐标系中的图像大致是如图中1+-=x y xy 3=的( )(2)一次函数与反比例函数在同一直角坐标系内的图像的大致12--=k kx y xky =位置是图中的( )解:的图像经过第一、二、四象限,故排除B 、C ;又的图像两支1+-=x y xy 3=在第一、三象限,故排除D .∴答案应选A .(2)若,则直线经过第一、三、四象限,双曲线的图0>k )1(2+-=k kx y xky =像两支在第一、三象限,而选择支A 、B 、C 、D 中没有一个相符;若,则直线0<k 经过第二、三、四象限,而双曲线的两支在第二、四象限,故只有C 正)1(2+-=k kx y 确.应选C .例已知函数是反比例函数,且其函数图像在每一个象限内,随24231-⎪⎭⎫ ⎝⎛+=mx m y y 的增大而减小,求反比例函数的解析式.x 解:因为是的反比例函数,y x 所以,所以或1242-=-m 21=m .21-=m 因为此函数图像在每一象限内,随的增大而减小,y x 所以,所以,所以,031>+m 31->m 21=m 所以反比例函数的解析式为.65xy =说明:此题根据反比例函数的定义与性质来解反比例函数 ,当时,xky =)0(≠k 0>k 随增大而减小,当时,随增大而增大.y x 0<k y x例 一个长方体的体积是100立方厘米,它的长是y 厘米,宽是5厘米,高是x 厘米.(1)写出用高表示长的函数关系式;(2)写出自变量x 的取值范围;(3)当厘米时,求y 的值;3=x (4)画出函数的图像.分析 本题依据长方体的体积公式列出方程,然后变形求出长关于高的函数关系式.解 (1)因为长方体的长为y 厘米,宽为5厘米,高为x 厘米,所以,所以.1005=xy xy 20=(2)因为x 是长方体的高.所以.即自变量x 的取值范围是.0>x 0>x (3)当时,(厘米)3=x 326320==y (4)用描点法画函数图像,列表如下:x…0.5251015…y…401042311…描点画图如图所示.例 已知力F 所作用的功是15焦,则力F 与物体在力的方向通过的距离S 的图象大致是( ).说明 本题涉及力学中作功问题,主要考查在力的作用下物体作功情况,由此,识别正、反比例函数,一次函数的图象位置关系.解 据,得15=,即,所以F 与S 之间是反比例函数关系,故S F W ⋅=S F ⋅SF 15=选(B ).例 一个圆台形物体的上底面积是下底面积的如果如下图所示放在桌上,对桌面的.32压强是,翻过来放,对桌面的压强是多少?Pa 200解:由物理知识可知,压力,压强与受力面积之间的关系是因为是同F p S .SFp =一物体,的数值不变,所以与成反比例.F p S 设下底面是,则由上底面积是,0S 032S 由,且时,,SFp =0S S =200=p 有.20020000S S pS F =⨯==因为是同一物体,所以是定值.0200S F =所以当时,032S S =).Pa (3003220000===S S S F p 因此,当圆台翻过来时,对桌面的压强是300帕.说明:本题与物理知识结合考查了反比例函数,关键是清楚对于同一个物体,它对桌面的压力是一定的.例如图,P 是反比例函数上一点,若图中阴影部分的矩形面积是2,求这个xky =反比例函数的解析式.分析 求反比例函数的解析式,就是求k 的值.此题可根据矩形的面积公式及坐标与线段长度的转化来解.解 设P 点坐标为.),(y x 因为P 点在第二象限,所以.0,0><y x 所以图中阴影部分矩形的长、宽分别为.y x ,-又,所以.因为,所以.2=-xy 2-=xy xy k =2-=k 所以这个反比例函数的解析式为.xy 2-=说明 过反比例函数图像上的一点作两条坐标轴的垂线,可得到一个矩形,这个矩形的面积等于中的.xky =k例 当n 取什么值时,是反比例函数?它的图像在第几象限内?122)2(-++=n n xn n y 在每个象限内,y 随x 增大而增大还是减小?分析 根据反比例函数的定义可知,是反比例函数,)0(≠=k xky 122)2(-++=n n x n n y 必须且只需且.022≠+n n 112-=-+n n 解 是反比例函数,则122)2(-++=n n xn n y ⎪⎩⎪⎨⎧-=-+≠+,11,0222n n n n ∴⎩⎨⎧-==-≠≠.10,20n n n n 或且即 .1-=n 故当时,表示反比例函数:.1-=n 122)2(-++=n n xn n y xy 1-=,01<-=k ∴双曲线两支分别在二、四象限内,并且在每个象限内,y 随x 的增大而增大.。
17.1反比例函数复习测试题(人教版初中数学八年级下册)

第十七章 反比例函数测试题(B )一、选择题(每小题4分,共40分)1、下列关系式中,哪个等式表示y 是x 的反比例函数( )A :23y x =B : 2x y =C :12y x =+D :1y x=- 2、反比例函数y=2x的图象位于( )A :第一、二象限B :第一、三象限C :第二、三象限D :第二、四象限3、函数y=1x与函数y=x 的图象在同一平面直角坐标系内的交点个数是( ). A :1个 B :2个 C :3个 D :0个4、已知点A (-1,5)在反比例函数(0)ky k x=≠的图象上,则该函数的解析式为( ) A :1y x = B :25y x = C :5y x=- D :5y x =5、若反比例函数(0)ky k x=≠经过(-2,3),则这个反比例函数一定经过( )A :(-2,-3)B :(3,2)C :(3,-2)D :(-3,-2) 6、某村的粮食总产量为a (a 为常数)吨,设该村的人均粮食产量为y 吨,人口数为x ,则y 与x 之间的函数关系式的大致图像应为( )7、如图,过反比例函数xy 2009=(x >0)的图象上任意两点A 、B 分别作x 轴的垂线,垂足分别为C 、D ,连接OA 、OB ,设△AOC 和△BOD 的面积分别是S 1、S 2,比较它们的大小,可得( )A :S 1>S 2B :S 1=S 2C :S 1<S 2D :大小关系不能确定 8、已知反比例函数(0)ky k x=<的图象上有两点1122(,)(,)A x y B x y ,且12x x <则12y y -的值是( )A :正数B :负数C :非正数D :不能确定姓名班级A F 1y kx =+ 9、若y 与-3x 成反比例,x 与z4成反比例,则y 是z 的( ) A :正比例函数 B :反比例函数 C :一次函数 D :不能确定10、函数与ky x=在同一坐标系内的大致图象是( )A :B :C :D : 二、填空题(每小题4分,共40分) 11、反比例函数35y x=-中,比例系数k= ; 12、如果函数25(2)ky k x -=-是反比例函数,那么k= ;13、如图:在反比例函数(0)ky k x=≠图象上取一点A 分别作AC ⊥x 轴,AB ⊥y 轴, 且S 矩形ABOC = 12,那么这个函数解析式为 ;14、已知函数(0)k y k x=≠,当12x =-时,6y =,则函数的解析式为 ; 15、反比例函数k y x =的图象经过3(,5)2-和(a ,-3),则a= ;16、已知正比例函数y kx =和反比例函数3y x=的图象都过A (m ,1),则m= ;正比例函数的解析式为 ;17、函数2y x=- 的图象,在每一象限内,y 随x 的增大而 (填“增大”或“减小”);18、如果反比例函数ky x=的图象经过点(-3,-4),那么这个函数的图象应分别分布在 象限;19、已知y -2与x 成反比例,当x=3时,y=1,则y 与x 的函数关系式为 ; 20、反比例函数3k y x+=的图象在二、四象限,则k 的取值范围是 。
八年级数学反比例函数练习题

第一课时[A 组]1、下列函数中,哪些是反比例函数?( )(1)y=-3x ; (2)y=2x+1; (3) y=-x 2;(4)y=3(x-1)2+1; 2、下列函数中,哪些是反比例函数(x 为自变量)?说出反比例函数的比例系数:(1) x y 1-= ;(2)xy=12 ;(3) xy=-13 (4)y=3x3、列出下列函数关系式,并指出它们是分别什么函数.说出比例系数①火车从安庆驶往约200千米的合肥,若火车的平均速度为60千米/时,求火车距离安庆的距离S(千米)与行驶的时间t(时)之间的函数关系式 ②某中学现有存煤20吨,如果平均每天烧煤x 吨,共烧了y 天,求y 与x 之间的函数关系式. 4、.已知一个长方体的体积是100立方厘米,它的长是ycm ,宽是5cm ,高是xcm . (1) 写出用高表示长的函数式; (2) 写出自变量x 的取值范围; (3) 当x =3cm 时,求y 的值5、已知y 与x 成反比例,并且x =3时y =7,求: (1)y 和x 之间的函数关系式;(2)当13x =时,求y 的值; (3)y =3时,x 的值。
7、写出一个经过点(-3,6)的反比例函数 你还能写出另外一个也经过点(-3,6)的双曲线吗?8、当m 为何值时,函数224-=m x y 是反比例函数,并求出其函数解析式.9、已知y 成反比例,且当4b =时,1y =-。
求当10b =时,y 的值。
10:画出下列函数双曲线,y=-x 2的图象,已知点A (-3,a )、B (-2,b ),C(4,c)在双曲线,y=-x 2的图象令上,请把[B 组]11、已知函数221()m y m m x -=+,当m 取何值时(1)是正比例函数;(2)是反比例函数。
12、(1)已知y =y1+y2,y1与x 成正比例,y2与x 成反比例, 并且x =2和x =3时,y 的值都等于 19.求y 和x 之间的函数关系式(2)若y 与2x -2成反比例,且当x=2时,y=1,则y 与x 之间的关系式为13、(03广东)如图1,某个反比例函数的图像经过点P .则它的解析式( )(A )xy 1=(x >0) (B )x y 1-= (x >0)(C )xy 1=(x <0) (D )x y 1-= (x <0)第二课时[A 组]1、xy 3-=的图像叫 ,图像位于 象限,在每一象限内,当x 增大时,则y ;函数4y x=图象在第象限,在每个象限内y 随x 的减少而 2:、根据下列表格中x 与y 的对应值:(1)在直角坐标系中,描点画出图象;(2)试求式。
数学:《反比例函数》同步练习2(人教版八年级下)

数学:《反比例函数》同步练习2(人教版八年级下)一、选择题:1.函数①x y 2=,②x y =,③1-=xy ,④xy 8=中,是反比例函数的个数有( ) A .0个 B .1个 C .2个 D .3个2. 下列函数中y 既不是x 的正比例函数,也不是反比例函数的是( )A. y x=-19B.x y -=10C. 152xy =- D . 214x y =3. 函数y kx b =+与y kxkb =≠()0的图象可能是( )A. B. C. D.4.函数922)2(--+=m mx m y 是反比例函数,则m 的值是 ( )A. m =4或m =-2B. m =4C. m =-2D. m =-15.在第三象限中,下列函数,y 随x 的增大而减小的有( )①3x y -= ②xy 8= ③52+-=x y ④65--=x y A .1个 B .2个 C .3个 D .4个6. 函数xy 2=与函数x y =的图象在同一平面直角坐标系内的交点个数是( ) A . 0个 B .1个 C .2个 D .3个7.某气球充满一定质量的气体后,当温度不变时,气球内的气体的气压P (kPa )是气体体积V (m 3)的反比例函数,其图象如图所示,当气球内的气压大于140kPa 时,•气球将爆炸,为了安全起见,气体体积应( )A .不大于2435m 3 B .不小于2435m 3 C .不大于2437m 3 D .不小于2437m 3第7题图 第8题图8. 如图所示,A 、B 是函数xy 1=的图像上关于原点对称的任意两点,AC ∥y 轴,BC ∥x 轴,△ABC 的面积记为S ,则( )A.1=SB. 21<<SC. 2=SD.2>S9. 函数xy 1-=第四象限的图象上有两点),(11y x A 、),(22y x B 且21x x <,那么下列结论正确的是( ) A.21y y < B.21y y > C.21y y = D.1y 与2y 的大小关系不能确定10. 若点(3,4)是反比例函数xm m y 122++=图象上一点,则此函数图象必经过点( )A.(3,-4)B.(2,-6)C.(4,-3)D. (2,6)二、填空题:11. 给出下列x 与y 的函数关系式:①,②,③,④,⑤,⑥13=xy ,其中是反比例函数的有 。
初二八年级下册数学反比例函数测试题及试卷答案

数学反比例函数测试题及试卷答案(时间90分钟 满分100分)班级 学号 姓名 得分一、选择题(每小题3分,共24分)1.如果x 、y 之间的关系是10(0)ax y a -+=≠,那么y 是x 的 ( ) A .正比例函数 B .反比例函数 C .一次函数D .二次函数2.函数y =-4x的图象与x 轴的交点的个数是 ( )A .零个B .一个C .两个D .不能确定3.反比例函数y =-4x的图象在 ( )A .第一、三象限B .第二、四象限C .第一、二象限D .第三、四象限 4.已知关于x 的函数y =k (x +1)和y =-kx(k ≠0)它们在同一坐标系中的大致图象是(• )5.已知反比例函数y =xk的图象经过点(m ,3m ),则此反比例函数的图象在 ( ) A .第一、二象限 B .第一、三象限 C .第二、四象限 D .第三、四象限6.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P ( kPa ) 是气体体积V ( m 3) 的反比例函数,其图象如图所示.当气球内的气压大于120 kPa 时,气球发将爆炸.为了安全起见,气球的体积应 ( ) A .不小于54m 3B .小于54m 3C .不小于45m 3D .小于45m 33)第6题7.如果点P 为反比例函数xy 4=的图象上一点,PQ ⊥x 轴,垂足为Q ,那么△POQ 的面 积为 ( ) A .2 B . 4 C .6 D . 8 8.已知:反比例函数xmy 21-=的图象上两点A (x 1,y 1),B (x 2, y 2)当x 1<0<x 2时, y 1<y 2,则m 的取值范围 ( )A .m <0B .m >0C .m <21 D .m >21二、填空题(每小题2分,共20分)9.有m 台完全相同的机器一起工作,需m 小时完成一项工作,当由x 台机器(x 为不大于m 的正整数)完成同一项工作时,所需的时间y 与机器台数x 的函数关系式是____. 10.已知y 与x 成反比例,且当x 32=-时,y =5,则y 与x 的函数关系式为__________. 11.反比例函数xy 3=的图象在第一象限与第 象限. 12.某食堂现有煤炭500吨,这些煤炭能烧的天数y 与平均每天烧煤的吨数x 之间的函数关系式是 . 13.若nxm y ++=2)5(是反比例函数,则m 、n 的取值是 .14.两位同学在描述同一反比例函数的图象时,甲同学说:这个反比例函数图象上任意一点到两坐标轴的距离的积都是3;乙同学说:这个反比例函数的图象与直线y =x 有两 个交点,你认为这两位同学所描述的反比例函数的解析式是 . 15.在ABC △的三个顶点A (2,-3)、B (-4,-5)、C (-3,2)中,可能在反比例函数(0)ky k x=>的图象上的点是 . 16.如果反比例函数4ny x-=的图象位于第二、四象限,则n 的取值范围是_______;如果图象在每个象限内,y 随x 的增大而减小,则n 的取值范围是 . 17.如图,△P 1OA 1、△P 2A 1 A 2是等腰直角三角形,点P 1、P 2在函数4(0)y x x=>的图象上,斜边OA 1、A 1 A 2都在x 轴上,则点A 2的坐标是 . 18.两个反比例函数k y x =和1y x=在第一象限内的图象如图所示,点P 在k y x =的图象上,PC ⊥x 轴于点C ,交1y x =的图象于点A ,PD ⊥y 轴于点D ,交1y x =的图象于点B ,当点P 在k y x =的图象上运动时,以下结论: ①△ODB 与△OCA 的面积相等;②四边形PAOB 的面积不会发生变化;③PA 与PB 始终相等;O 12 第17题④当点A 是PC 的中点时,点B 一定是PD 的中点.其中一定正确的是 (把你认为正确结论的序号都填上,少填或错填不给分). 三、解答题(共56分) 19.(4分)反比例函数xky =的图象经过点A (2 ,3). (1)求这个函数的解析式;(2)请判断点B (1 ,6)是否在这个反比例函数的图象上,并说明理由.20.(4分)已知三角形的一边为x ,这条边上的高为y ,三角形的面积为3,写出y 与x的函数表达式,并画出函数的图象.21.(4分)如图,一次函数y =kx +b 的图像与反比例函数xmy =的图像相交于A 、B 两点, (1)利用图中条件,求反比例函数和一次函数的解析式(2)根据图像写出使一次函数的值大于反比例函数的值的x 的取值范围.22.(6分)某蓄水池的排水管每时排水8 m 3,6h 可将满池水全部排空. (1)蓄水池的容积是多少?(2)如果增加排水管,使每时排水量达到Q (m 3),那么将满池水排空所需的时间t (h )将如何变化?(3)写出t 与Q 之间的函数关系式.(4)如果准备在5小时之内将满水池排空,那么每时的排水量至少为多少? (5)已知排水管的最大排水量为每时12m 3,那么最少多长时间可将满池水全部排空?23.(6分)双曲线5y x在第一象限的一支上有一点C (1,5),过点C 的直线y =kx +b (k >0)与x 轴交于点A (a ,0).(1)求点A 的横坐标a 与k 之间的函数关系式;(2)当该直线与双曲线在第一象限内的另一交点D 的横坐标是9时,求△COA 的面积.第21题图24.(6分)已知反比例函数xmy 3-=和一次函数1-=kx y 的图象都经过点m P (,)3m - (1)求点P 的坐标和这个一次函数的解析式;(2)若点M (a ,1y )和点N (1+a ,2y )都在这个一次函数的图象上.试通过计算或利用一次函数的性质,说明1y 大于2y25.(6分)近视眼镜的度数y (度)与镜片焦距x (米)成反比例,已知800度近视眼镜镜片的焦距为0.125米, (1)求y 与x 的函数关系;(2)若张华同学近视眼镜镜片的焦距为0.25米,你知道他的眼睛近视多少度吗?26.(6分)对于取消市场上使用的杆秤的呼声越来越高,原因在于一些不法商贩在卖货时将秤砣挖空,或更换较小称砣,使砣较轻,从而欺骗顾客.(1)如图,对于同一物体,哪个图用的是标准秤砣,哪个用的是较轻的秤砣? (2)在称同一物体时,所称得的物体质量y (千克)与所用秤砣质量x (千克)之间满足关系.(3)当砣较轻时,称得的物体变重,这正好符合哪个函数的哪些性质?27.(6分)联想电脑公司新春期间搞活动,规定每台电脑0.7万元,交首付后剩余的钱数y 与时间t 的关系如图所示:(1)根据图象写出y 与t 的函数关系式. (2)求出首付的钱数.(3)如果要求每月支付的钱数不少于400元,那么还至少几个才能将所有的钱全部还清?图1图2月)y ()28.(8分)如图,直线b kx y +=与反比例函数xk y '=(x <0)的图象相交于点A 、点B ,与x 轴交于点C ,其中点A 的坐标为(-2,4),点B 的横坐标为-4. (1)试确定反比例函数的关系式;(2)求△AOC 的面积.新人教八年级(下)第17章《反比例函数》答案一、选择题1.B;2. A;3. B;4. A ;5. B ;6. C ;7.A ;8. C.二、填空题9.y =x m 210.152y x=- 11.三 12.y =x 500 13.m ≠-5 n =-3 14.y =x 3 15.B16.n >4,n <4 17.(0) 18.①②④ 三、解答题 19.(1)y =x 6;(2)在 20. y =6x ,图像略 21.(1)2y x=-,1y x =--;(2) 2x <-或0x <<1 22.(1)348m ;(2)t 将减小;(3)48t Q=;(4)4859.6Q Q==,;(5)48412t ==23.(1)51a k =-+, (2) 25 24.(1)12--=x y ;(2)略 25.(1)100y x=,(2)400度 26.(1)图②是用与秤配套的秤砣,图①则使用较轻的秤砣.(2)反比例. (3)函数y =x k(k >0),当x 变小时,y 增大 27.(1)y =t6000 ;(2)7000-6000=1000(元);(3)400=t6000,t =15 28.(1)8xy =-;(2)126。
数学:《反比例函数》同步练习1(人教版八年级下)
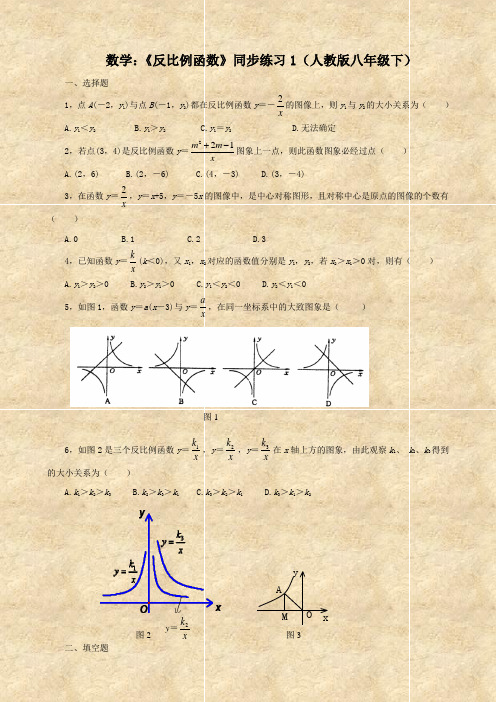
数学:《反比例函数》同步练习1(人教版八年级下)一、选择题1,点A (-2,y 1)与点B (-1,y 2)都在反比例函数y =-x 2的图像上,则y 1与y2的大小关系为( ) A.y 1<y 2 B.y 1>y 2 C.y 1=y 2 D.无法确定2,若点(3,4)是反比例函数y =221m m x+-图象上一点,则此函数图象必经过点( ) A.(2,6) B.(2,-6) C.(4,-3) D.(3,-4)3,在函数y =x 2,y =x +5,y =-5x 的图像中,是中心对称图形,且对称中心是原点的图像的个数有( )A.0B.1C.2D.34,已知函数y =k x(k <0),又x 1,x 2对应的函数值分别是y 1,y 2,若x 2>x 1>0对,则有( ) A.y 1>y 2>0 B.y 2>y 1>0 C.y 1<y 2<0 D.y 2<y 1<0 5,如图1,函数y =a (x -3)与y =a x ,在同一坐标系中的大致图象是( )6,如图2是三个反比例函数y =1k x ,y =2k x ,y =3k x 在x 轴上方的图象,由此观察k 1、 k 2、k 3得到的大小关系为( )A.k 1>k 2>k 3B.k 2>k 3>k 1C.k 3>k 2>k 1D.k 3>k 1>k 2二、填空题 y =2k x 图2 图1图3 O A M xy7,已知反比例函数y =k x(k ≠0)与一次函数y =x 的图象有交点,则k 的范围是______. 8,已知反比例函数y =32m x -,当m ___时,其图象的两个分支在第二、四象限内;当m ___时,其图象在每个象限内y 随x 的增大而减小.9,若反比例函数y =3k x -的图象位于一、三象限内,正比例函数y =(2k -9)x 过二、四象限,则k 的整数值是______.10,已知点P (1,a )在反比例函数y =k x (k ≠0)的图象上,其中a =m 2+2m +3(m 为实数),则这个函数的图象在第______象限.11,写出一个反比例函数,使它的图象在第二、 四象限,这个函数的解析式是_____.12,已知反比例函数y =xk (k ≠0),当x >0时,y 随x 的增大而增大,那么一次函数y =kx -k 的图像过 象限. 三、解答题13,反比例函数的图象过点(2,-2),求函数y 与自变量x 之间的关系式,它的图象在第几象限内?y 随x 的减小如何变化?请画出函数图象,并判断点(-3,0),(-3,-3)是否在图象上?14,若反比例函数y =24212-+m x m 的图象经过第二、四象限,求函数的解析式.15,如图3所示,一个反比例函数的图象在第二象限内,点A 是图象上的任意一点,AM ⊥x 轴于M ,O 是原点,若S △AOM =3,求该反比例函数的解析式,并写出自变量的取值范围.16,点P ,Q 在y =-3x的图象上. (1)若P (1,a ),Q (2,b ),比较a ,b 的大小;(2)若P (-1,a ),Q (-2,b ),比较a ,b 的大小;(3)你能从中发现y 随x 增大时的变化规律吗?(4)若P (x 1,y 1),Q (x 2,y 2),x 1<x 2,你能比较y 1与y 2的大小吗?17,(08达州市)平行于直线y x =的直线l 不经过第四象限,且与函数3(0)y x x=>和图象交于点A ,过点A 作AB y ⊥轴于点B ,AC x ⊥轴于点C ,四边形ABOC 的周长为8.求直线l 的解析式.18,已知变量y 与x 成反比例,并且当x =2时,y =-3.(1)求y 与x 的函数关系式;(2)求当y =2时x 的值;(3)在直角坐标系内画出(1)小题中函数图象的草图.答案:一、1,A ;2,A ;3,C ;4,C ;5,D ;6,C .二、7,k >0;8,<23、>23;9,4;0,在一、三象限.提示:因为m 2+2m +3>0,则a >0,点P (1,a )在图象上,则k >0;11,答案不唯一,比例系数小于0;12,一、二、四.三、13,y =-4x,二、四,在每一象限内y 随x 的减小而减小,略,点(-3,0),(-3,-3)都不在图象上;14,y =-9x ;15,y =-6x (x <0);16,(1)b >a ,(2)a >b ,(3)在每个象限内,y 随x 的增大而增大,(4)当位于同一分支上时,y 1<y 2,当位于不同分支上时,y 1>y 2;17,【答案】设A 点的坐标为(x,y ),由题意得2x+2y=8,整理得y= 4-x 即A 的坐标为(x,4-x ),把A 点代入3(0)y x x=>中,解得x=1或x=3 由此得到A 点的坐标是(1,3)或(3,1)又由题意可设定直线l 的解析式为y=x+b (b ≥0)把(1,3)点代入y=x+b ,解得 b =2把(3,1)点代入y=x+b ,解得 b=-2,不合要求,舍去所以直线l 的解析式为y=x+218,y =-6x ,(2)x =-3,(3)略. A B OCyx 3(0)y x x=> l。
八年级下册人教版数学《反比例函数》基础练习题
反比例函数基础训练题一、填空题:1、形如)0(≠=k xky 的函数称为反比例函数,基中自变量x 的取值范围是 ; 2、反比例函数xy 23-=中,相应的k= ;3、三角形面积为6,它的底边a 与这条底边上的高h 的函数关系式是 ;4、反比例函数经过点(2,-3),则这个反比例函数关系式是 ;5、下列函数中:①xy 2=,②11+=x y ,③2x y =④x y 23-=⑤11+=x y其中是y 关于x 的反比例函数有: ;(填写序号)6、已知变量y 、x 成反比例,且当x =2时y=6,则这个函数关系式是 ;7、反比例函数xy 3-=的图像在第 象限,在它的图像上y 随x 的减小而 ; 反比例函数xy 2=的图像在第 象限,在它的图像上y 随x 的增大而 ;8、写出一个反比例函数,使得这个反比例函数的图像在第一、三象限,这个函数是 ; 且写出这个函数上一个点的坐标是 ;9、已知反比例函数经过点A (2,1)和B (m ,-1),则m = ;10、正比例函数x y 3=与反比例函数xy 2=有 个交点;11、如图(1):则这个函数的表达式是 ;如图(2):则这个函数的表达式是 ;12、若反比例函数x ky =图像的一支在第二象限,则k 的取值范围是 ; 13、若反比例函数x k y 1-=图像的一支在第三象限,则k 的取值范围是 ;14、若反比例函数x ky -=2的图像在第一、三象限,则k 的取值范围是 ;15、对于函数x y 1=的图像关于 对称;16、对于函数x y 3=,当x >0时y 0,这部分图像在第 象限;17、对于函数xy 3-=,当x <0时y 0,这部分图像在第 象限;18、正比例函数与反比例函数经过点(1,2),则这个正比例函数是 ,反比例函数是 ; 19、若函数12)1(-+=m xm y 是反比例函数,则m = ,它的图像在第 象限;20、已知22)1(--=a xa y 是反比例函数,则a =____ ;21、两点),1(),,1(21y Q y P -在函数xy 2-=图像上,则1y 2y (选填“<””>”) 22、函数xy 32=图像上的点)3,(),1,(),2,(321x C x B x A --,则321,,x x x 之间的大小关系是 ;(用大于号连接)二、选择题: 23、下列各点中,在函数xy 2-=的图像上的是( ) A 、(2,1) B 、(-2,1) C 、(2,-2) D 、(1,2) 24、函数xy 1-=与x y =的图像在同一直角坐标系中交点的个数是( ) A 、0个 B 、1个 C 、2个 D 、3个25、某村的粮食总产量为a (a 为常数)吨,设该村的人均粮食产量为y 吨,人口数为x ,则y 与x 之间的函数关系式的大致图像应为( )26、如图(3):点A 为双曲线上一点A B ⊥x 轴,2=∆aABO S ,则双曲线的解析式是( ) A 、x y 2=B 、4x y -=C 、x y 4=D 、xy 4-=27、在同一直角坐标系中,函数y=kx-k 与(0)ky k x=≠的图像大致是( )28、在同一直角坐标平面内,若直线1y x k =与双曲线2k y x=无交点,则( ) (A) 1k 、2k 异号 (B) 1k 、2k 同号 (C) 1k >0, 2k <0 (D) 1k <0, 2k >0反比例函数基础练习1. 双曲线ky x=经过点(2-,3),则_____=k ;2. 已知y 与x 成反比例,当1=y 时,4=x ,则当2=x 时,_____=y ;3. 反比例函数和正比例函数的图象都经过点A(1-,2-),则这两个函数的解析式分别是_________和_________;4. 某厂有煤1500吨,求这些煤能用的天数y 与每天用煤的吨数x 之间的函数关系式为_________;5. 若点(3,6)在反比例函数xky = (k ≠0)的图象上,那么下列各点在此图象上的是( )(A )(3-,6) (B ) (2,9) (C )(2,9-) (D )(3,6-)6. 已知反比例函数的图象过(2,-2)和(-1,n ),则n 等于 ( ) (A )3 (B )4(C )6(D )127. 反比例函数x k y =的图像经过(-23,5)点、(a ,-3)及(10,b )点,则k = ,a = ,b = ; 8. 已知2-y 与x 成反比例,当x =3时,y =1,则y 与x 间的函数关系式为 ; 9. 如果函数22(1)m y m x -=-是反比例函数,那么m 的值是_________ ;10. 反比例函数xky =(k ≠0)的图象是__________,当k >0时,图象的两个分支分别在第__________、__________象限内,在每个象限内,y 随x 的增大而__________;当k <0时,图象的两个分支分别在第__________、__________象限内,在每个象限内,y 随x 的增大而__________; 11. 已知函数1k y x+=的图象两支分布在第二、四象限内,则k 的范围是_________ 12. 反比例函数 2k y x= (0≠k )的图象的两个分支分别位于 ( )(A ) 第一、二象限 (B ) 第一、三象限 (C ) 第二、四象限 (D ) 第一、四象限 13. 若反比列函数1232)12(---=k k xk y 的图像经过二、四象限,则k = _______14. 已知反比例函数的图像经过点(a ,b ),则它的图像一定也经过 ( ) (A ) (a -,b -) (B ) (a ,b -) (C ) (a -,b ) (D ) (0,0) 15. 反比例函数422)1(---=m mx m y ,当x <0时,y 随x 的增大而增大,则m 的值是( )(A ) 1- (B ) 3(C ) 1-或3 (D ) 216. 若A (x 1,y 1),B (x 2,y 2),C (x 3,y 3)都是反比例函数xy 1-=的图象上的点,且 x 1<0<x 2<x 3,则y 1,y 2,y 3由小到大的顺序是 ;17. 设有反比例函数y k x=+1,(,)x y 11、(,)x y 22为其图象上的两点,若x x 120<<时,y y 12>,则k 的取值范围是___________18. 点A 为反比例函数图象上一点,它到原点的距离为5,到x 轴的距离为3,若点A 在第二象限内.则这个反比例函数的解析式为 ( )(A ) 12y x =(B ) 12y x =- (C ) 112y x = (D ) 112y x =- 19. 反比例函数()0>=k xky 在第一象限内的图象如图,点M 是图像上一点,MP 垂直x 轴于点P ,如果△MOP 的面积为1,那么k 的值是 ;20. 如图2所示,A 、B 是函数xy 1-=的图象上关于原点O 对称 的任意两点,AC ∥x 轴,BC ∥y 轴,△ABC 的面积为S ,则 ( ) (A ) S =1 (B ) S =2(C ) 1<S <2(D ) S <221. 已知12y y y =+,其中1y 与1x成反比例且比例系数为1k ,2y 与2x 成正比例且比例系数为2k ,若1-=x 时,0=y ,则1k 与2k 的关系为 ( )(A ) 12k k =- (B ) 12k k ≠ (C ) 121k k =- (D ) 12k k = 22. 若ab <0,则函数ax y =与xby =在同一坐标系内的图象大致可能是下图中的 ( )(A ) (B ) (C ) (D )23. 函数2x y -=和函数x y 2=的图像有 个交点;24. 已知正比例函数kx y =与反比例函数3y x=的图象都过A (m ,1),则m = ,正比例函数与反比例函数的解析式分别是 、 ; 25. 直线x y 2=与双曲线xy 1=的交点为_________;yxO PM。
初二数学人教版(下册)反比例函数综合练习(附答案)
反比例函数综合练习一、选择题1.反比例函数y= -2/x的图象位于()A.第一、二象限 B.第一、三象限 C.第二、三象限 D.第二、四象限2.已知矩形的面积为10,则它的长y与宽x之间的关系用图象大致可表示为()、. 若双曲线y=6/x 经过点A(m,3),则m的值为()A.2 B.-2 C.3 D.-33. 如图,过原点的一条直线与反比例函数y=k/x(k<0)的图像分别交于A、B两点,若A、、点的坐标为(a,b),则B点的坐标为()A.(a,b) B.(b,a) C.(-b,-a) D.(-a,-b)4、下列关系中,两个量之间为反比例函数关系的是()A 、 正方形的面积S 与边长a 的关系B 、 正方形的周长L 与边长a 的关系C 、 长方形的长为a ,宽为20,其面积S 与a 的关系D 、 长方形的面积为40,长为a ,宽为b ,a 与b 之间的关系 5、在同一直角坐标系中,函数x y 3=与xy 1-=的图象大致是( )6、设()()2211,,,y x B y x A 是反比例函数xy 2-=图象上和两点,若1x <2x <0则1y 与2y 之间的关系是( )A 、2y <1y <0B 、1y <2y <0C 、2y >1y >0D 、1y >2y >0 7、函数k kx y +=与xky =在同一坐标系中的图象如图所示,则k 的取值范围为( ) A 、k >0 B 、k <0 C 、-1<k <0 D 、k <-18、(2006年兰州市)如图1所示,P 1、P 2、P 3是双曲线上的三点,过这三点分别作y 轴的垂线,得到三个三角形△P 1A 1O 、△P 2A 2O 、△P 3A 2O ,设它们的面积分别是S 1、S 2、S 3,则( ) A 、S 1<S 2<S 3 B 、S 2<S 1<S 3 C 、S 1<S 3<S 2 D 、S 1=S 2=S 3yOxyOxyOxO xyx二、填空题9.在函数xky =中,当2=x 时,3-=y 。
(完整word版)反比例函数基础练习题及答案
反比例函数练习一.选择题(共22小题)1.下列函数中,y是x的反比例函数的为()A.y=2x+1 B.C.D.2y=x2.)函数y=k是反比例函数,则k的值是()A.﹣1 B.2 C.±2D.±3.若y=(m﹣1)x|m|﹣2是反比例函数,则m的值为()A.m=2 B.m=﹣1 C.m=1 D.m=04.若y与x成反比例,x与z成反比例,则y是z的()A.正比例函数B.反比例函数C.一次函数D.不能确定5.反比例函数(m为常数)当x<0时,y随x的增大而增大,则m的取值范围是()A.m<0 B.C.D.m≥6.已知k1<0<k2,则函数y=和y=k2x﹣1的图象大致是()A.B.C.D.7.在同一直角坐标系中,函数y=kx+k与y=(k≠0)的图象大致为()A. B.C.D.8.下列函数的图象中,与坐标轴没有公共点的是()A.B.y=2x+1 C.y=﹣x D.y=﹣x2+19.若ab>0,则函数y=ax+b与函数在同一坐标系中的大致图象可能是()A.B.C.D.10.若方程=x+1的解x0满足1<x0<2,则k可能是()A.1 B.2 C.3 D.611.如图,有反比例函数y=,y=﹣的图象和一个圆,则图中阴影部分的面积是()第11题图第12题图A.πB.2πC.4πD.条件不足,无法求12.如图所示,点P(3a,a)是反比例函数y=(k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为()A.y=B.y=C.y=D.y=13.关于反比例函数y=的图象,下列说法正确的是()A.图象经过点(1,1)B.两个分支分布在第二、四象限C.两个分支关于x轴成轴对称D.当x<0时,y随x的增大而减小14.如图是反比例函数y=(k为常数,k≠0)的图象,则一次函数y=kx﹣k的图象大致是()A B C D15.已知函数y=的图象如图,以下结论:①m<0;分支上y随x的增大而增大;③若点A(﹣1,a)、点B(2,b)在图象上,则a<b;④若点P(x,y)在图象上,则点P1(﹣x,﹣y)也在图象上.其中正确的个数是()A.4个 B.3个C.2个D.1个16.函数的自变量x满足≤x≤2时,函数值y满足≤y≤1,则这个函数可以是()A.y=B.y=C.y=D.y=17.反比例函数y=在每个象限内的函数值y随x的增大而增大,则m的取值范围是()A.m<0 B.m>0 C.m>﹣1 D.m<﹣118.以正方形ABCD两条对角线的交点O为坐标原点,建立如图所示的平面直角坐标系,双曲线y=经过点D,则正方形ABCD的面积是()第18题图第19题图A.10 B.11 C.12 D.1319.如图,A、B是双曲线y=上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C.若△ADO的面积为1,D为OB的中点,则k的值为()A.B.C.3 D.420.如图,过点O作直线与双曲线y=(k≠0)交于A、B两点,过点B作BC⊥x轴于点C,作BD⊥y轴于点D.在x轴上分别取点E、F,使点A、E、F在同一条直线上,且AE=AF.设图中矩形ODBC的面积为S1,△EOF的面积为S2,则S1、S2的数量关系是()第20题图第21题图A.S1=S2B.2S1=S2C.3S1=S2D.4S1=S221.如图,在平面直角坐标系中,点A是x轴正半轴上的一个定点,点P是双曲线y=(x>0)上的一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会()A.逐渐增大B.不变C.逐渐减小D.先增大后减小22.如图,反比例函数y=﹣在第二象限的图象上有两点A、B,它们的横坐标分别为﹣1,﹣3,直线AB 与x轴交于点C,则△AOC的面积为()A.8 B.10 C.12 D.24二.填空题(共4小题)23.已知y=(a﹣1)是反比例函数,则a= .24.已知反比例函数的解析式为y=,则最小整数k= .25.函数y=,当y≥﹣2时,x的取值范围是(可结合图象求解).26.若反比例函数的图象在其每个象限内,y随x的增大而增大,则k的值可以是.(写出一个符合条件的值即可)三.解答题(共4小题)27.已知反比例函数y=﹣(1)说出这个函数的比例系数;(2)求当x=﹣10时函数y的值;(3)求当y=6时自变量x的值.28.已知函数y=(5m﹣3)x2﹣n+(n+m),(1)当m,n为何值时是一次函数?(2)当m,n为何值时,为正比例函数?(3)当m,n为何值时,为反比例函数?29.如图,是反比例函数y=的图象的一支.根据给出的图象回答下列问题:(1)该函数的图象位于哪几个象限?请确定m的取值范围;(2)在这个函数图象的某一支上取点A(x1,y1)、B(x2,y2).如果y1<y2,那么x1与x2有怎样的大小关系?30.如图,已知函数y=(x>0)的图象经过点A、B,点A的坐标为(1,2),过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC、OD.(1)求△OCD的面积;(2)当BE=AC时,求CE的长.答案:一.选择题(共22小题)1.C 2.D 3.B 4.A 5.C 6.C 7.B 8.A 9.C 10.C 11.B 12.D 13.D 14.B 15.B 16.A 17.D 18.C 19.B 20.B 21.C 22.C二.填空题(共4小题)23.-1 24.1 25.x≤-2或x>0 26.-1(答案不唯一)三.解答题(共4小题)27. 28. 29. 30.。
初中数学人教版反比例函数练习题
初二下人教版反比例函数一.选择题(共14小题)1.(2016•富顺县校级一模)若函数为反比例函数,则m的值为()A.±1 B.1 C.D.﹣12.(2016•东丽区一模)在反比例函数的每一条曲线上,y都随着x的增大而减小,则k的值可以是()A.﹣1 B.1 C.2 D.33.(2016•太仓市模拟)对反比例函数,下列说法不正确的是()A.它的图象在第一、三象限B.点(﹣1,﹣4)在它的图象上C.当x<0时,y随x的增大而减小D.当x>0时,y随x的增大而增大4.(2016•深圳校级模拟)函数y=ax﹣a与y=(a≠0)在同一直角坐标系中的图象可能是()A.B.C.D.5.(2016•玄武区一模)如图,正方形OABC的边长为6,A,C分别位于x轴、y轴上,点P在AB上,CP交OB于点Q,函数y=的图象经过点Q,若S△BPQ=S△OQC,则k的值为()A.﹣12 B.12 C.16 D.186.(2016•邯郸校级自主招生)如图,A、B是双曲线上的点,A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C,若S△AOC=9.则k的值是()A.9 B.6 C.5 D.47.(2016•端州区一模)函数是反比例函数,则m的值是()A.m=±1 B.m=1 C.m=±D.m=﹣18.(2016•锦江区模拟)已知函数y=(m+2)是反比例函数,且图象在第二、四象限内,则m的值是()A.3 B.﹣3 C.±3 D.﹣9.(2016•如皋市一模)求一元二次方程x2+3x﹣1=0的解,除了课本的方法外,我们也可以采用图象的方法:在平面直角坐标系中,画出直线y=x+3和双曲线y=的图象,则两图象交点的横坐标即该方程的解.类似地,我们可以判断方程x3﹣x﹣1=0的解的个数有()A.0个B.1个C.2个D.3个10.(2015•长乐市一模)函数y=的图象是()A.B.C.D.11.(2016春•重庆校级月考)如图,函数y=(x<0)的图象与直线y=x+m相交于点A 和点B.过点A作AE⊥x轴于点E,过点B作BF⊥y轴于点F,P为线段AB上的一点,连接PE、PF.若△PAE和△PBF的面积相等,且x P=﹣,x A﹣x B=﹣3,则k的值是()A.﹣5 B. C.﹣2 D.﹣112.(2015•朝阳)如图,在直角坐标系中,直线y1=2x﹣2与坐标轴交于A、B两点,与双曲线y2=(x>0)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:①S△ADB=S△ADC;②当0<x<3时,y1<y2;③如图,当x=3时,EF=;④当x>0时,y1随x的增大而增大,y2随x的增大而减小.其中正确结论的个数是()A.1 B.2 C.3 D.413.(2015•大庆)已知点A(﹣2,0),B为直线x=﹣1上一个动点,P为直线AB与双曲线y=的交点,且AP=2AB,则满足条件的点P的个数是()A.0个B.1个C.2个D.3个14.(2014•南宁)已知点A在双曲线y=﹣上,点B在直线y=x﹣4上,且A,B两点关于y轴对称.设点A的坐标为(m,n),则+的值是()A.﹣10 B.﹣8 C.6 D.4二.填空题(共8小题)15.(2015•宁德)如图,在平面直角坐标系中,反比例函数y=(x>0)的图象交矩形OABC的边AB于点D,交边BC于点E,且BE=2EC.若四边形ODBE的面积为6,则k=.16.(2015•甘南州)如图,点A在双曲线上,点B在双曲线y=上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为.17.(2015•贵港)如图,已知点A1,A2,…,A n均在直线y=x﹣1上,点B1,B2,…,B n 均在双曲线y=﹣上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,A nB n⊥x轴,B n A n+1⊥y轴,…,记点A n的横坐标为a n(n为正整数).若a1=﹣1,则a2015=.18.(2016•抚顺县一模)反比例函数,在每个象限内,y随x的增大而增大,则m 的取值范围是.19.(2016•句容市一模)如果反比例函数y=的图象在第二、四象限,那么k的取值范围是.20.(2016•无锡一模)如图:已知点A、B是反比例函数y=﹣上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为.21.(2016•丹东一模)如图,正比例函数y=ax的图象与反比例函数y=的图象相交于点A,B,若点A的坐标为(﹣2,3),则点B的坐标为.22.(2016•张家界模拟)如图,如果曲线l1是反比例函数y=在第一象限内的图象,且过点A(2,1),那么l1关于x轴对称的曲线l2的解析式为.三.解答题(共8小题)23.(2016•罗定市一模)如果函数y=m是一个经过二、四象限的反比例函数,则求m的值和反比例函数的解析式.24.(2016•嘉定区二模)如图,在平面直角坐标系xOy中,过点A(﹣4,2)向x轴作垂线,垂足为B,联结AO得到△AOB,过边AO中点C的反比例函数的图象与边AB交于点D.求:(1)反比例函数的解析式;(2)求直线CD与x轴的交点坐标.25.(2016•鱼峰区一模)如图.直线y=ax+b与双曲线相交于两点A(1,2),B(m,﹣4).(1)求直线与双曲线的解析式;(2)求不等式ax+b>的解集(直接写出答案)26.(2016•乐亭县一模)如图,在平面直角坐标系中直线y=x﹣2与y轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).(1)求反比例函数的关系式;(2)若将直线y=x﹣2向上平移4个单位后与反比例函数图象在第一象限内交于点C,求△ABC的面积;(3)若将直线y=x﹣2向上平移后与反比例函数图象在第一象限内交于点C,且△ABC的面积为18,求平移后的直线的函数关系式.27.(2016•呼和浩特一模)如图,在平面直角坐标系中,一次函数y=kx+b的图象分別交x 轴、y轴于A、B两点.与反比例函数y=﹣的图象交于C,D两点,DE⊥x轴于点E.已知DE=3,AE=6.(1)求一次函数的解析式;(2)直接写出不等式kx+b+>0的解集.28.(2016•南皮县模拟)如图,在直角坐标系中,Rt△ABC位于第一象限,两条直角边AC、AB分别平行于x轴、y轴,点A的坐标为(1,1),AB=2,AC=3.(1)求BC边所在直线的解析式;(2)若反比例函数y=的图象经过点A,求m的值;(3)若反比例函数y=的图象与△ABC有公共点,请直接写出n的取值范围.29.(2016•广州模拟)如图,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函数y=在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4.(1)求直线AO的解析式;(2)求反比例函数解析式;(3)求点C的坐标.30.(2016•云南模拟)如图,已知反比例函数y=(k≠0)的图象过点A(﹣3,2).(1)求这个反比例函数的解析式;(2)若B(x1,y1),C(x2,y2),D(x3,y3)是这个反比例函数图象上的三个点,若x1>x2>0>x3,请比较y1,y2,y3的大小,并说明理由.初二下人教版反比例函数参考答案一.选择题(共14小题)1.D;2.A;3.D;4.D;5.C;6.B;7.D;8.B;9.B;10.C;11.C; 12.C; 13.B; 14.A;二.填空题(共8小题)15.3;16.2;17.2;18.m<1;19.k>1;20.2;21.(2,-3);22.y=-;三.解答题(共8小题)23.;24.;25.;26.;27.;28.;29.;30.;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
反比例函数基础训练题
一、填空题:
1、形如)0(≠=
k x
k
y 的函数称为反比例函数,基中自变量x 的取值范围是 ; 2、反比例函数x
y 23
-=中,相应的k= ;
3、三角形面积为6,它的底边a 与这条底边上的高h 的函数关系式是 ;
4、反比例函数经过点(2,-3),则这个反比例函数关系式是 ;
5、下列函数中:①x y 2=
,②11+=x y ,③2x y =④x y 23-=⑤1
1+=x y 其中是y 关于x 的反比例函数有: ;(填写序号)
6、已知变量y 、x 成反比例,且当x =2时y=6,则这个函数关系式是 ;
7、反比例函数x
y 3
-=的图像在第 象限,在它的图像上y 随x 的减小而 ; 反比例函数x
y 2
=
的图像在第 象限,在它的图像上y 随x 的增大而 ;
8、写出一个反比例函数,使得这个反比例函数的图像在第一、三象限,这个函数是 ; 且写出这个函数上一个点的坐标是 ;
9、已知反比例函数经过点A (2,1)和B (m ,-1),则m = ;
10、正比例函数x y 3=与反比例函数x
y 2
=有 个交点;
11、如图(1):则这个函数的表达式是 ;
如图(2):则这个函数的表达式是 ;
12、若反比例函数x k
y =
图像的一支在第二象限,则k 的取值范围是 ; 13、若反比例函数x k y 1
-=图像的一支在第三象限,则k 的取值范围是 ;
14、若反比例函数x k
y -=2的图像在第一、三象限,则k 的取值范围是 ;
15、对于函数x y 1
=的图像关于 对称;
16、对于函数x y 3
=,当x >0时y 0,这部分图像在第 象限;
17、对于函数x
y 3
-=,当x <0时y 0,这部分图像在第 象限;
18、正比例函数与反比例函数经过点(1,2),则这个正比例函数是 ,反比例函数是 ; 19、若函数1
2)1(-+=m x
m y 是反比例函数,则m = ,它的图像在第 象限;
20、已知
2
2)1(--=a x
a y 是反比例函数,则a =____ ;
21、两点),1(),,1(21y Q y P -在函数x
y 2
-=图像上,则1y 2y (选填“<””>”) 22、函数x
y 32
=图像上的点)3,(),1,(),2,(321x C x B x A --,则321,,x x x 之间的大小关系是 ;(用大于号连接)
二、选择题: 23、下列各点中,在函数x
y 2
-
=的图像上的是( ) A 、(2,1) B 、(-2,1) C 、(2,-2) D 、(1,2) 24、函数x
y 1
-
=与x y =的图像在同一直角坐标系中交点的个数是( ) A 、0个 B 、1个 C 、2个 D 、3个
25、某村的粮食总产量为a (a 为常数)吨,设该村的人均粮食产量为y 吨,人口数为x ,则y 与x 之间的函数关系式的大致图像应为( )
26、如图(3):点A 为双曲线上一点A B ⊥x 轴,2=∆aABO S ,则双曲线的解析式是( ) A 、x y 2=
B 、4x y -=
C 、x y 4=
D 、x
y 4
-=
27、在同一直角坐标系中,函数y=kx-k 与(0)k
y k x
=
≠的图像大致是( )
28、在同一直角坐标平面内,若直线1y x k =与双曲线2
k y x
=
无交点,则( ) (A) 1k 、2k 异号 (B) 1k 、2k 同号 (C) 1k >0, 2k <0 (D) 1k <0, 2k >0
反比例函数基础练习
1. 双曲线k
y x
=经过点(2-,3),则_____=k ;
2. 已知y 与x 成反比例,当1=y 时,4=x ,则当2=x 时,_____=y ;
3. 反比例函数和正比例函数的图象都经过点A(1-,2-),则这两个函数的解析式分别是_________和_________;
4. 某厂有煤1500吨,求这些煤能用的天数y 与每天用煤的吨数x 之间的函数关系式为_________;
5. 若点(3,6)在反比例函数x
k
y = (k ≠0)的图象上,那么下列各点在此图象上的是( )
(A )(3-,6) (B ) (2,9) (C )(2,9-) (D )(3,6-)
6. 已知反比例函数的图象过(2,-2)和(-1,n ),则n 等于 ( ) (A )3 (B )4
(C )6
(D )12
7. 反比例函数x
k
y =
的图像经过(-23,5)点、(a ,-3)及(10,b )点,则k = ,a = ,b = ;
8. 已知2-y 与x 成反比例,当x =3时,y =1,则y 与x 间的函数关系式为 ; 9. 如果函数2
2
(1)m y m x -=-是反比例函数,那么m 的值是_________ ;
10. 反比例函数x
k
y =
(k ≠0)的图象是__________,当k >0时,图象的两个分支分别在第__________、__________象限内,在每个象限内,y 随x 的增大而__________;当k <0时,图象的两个分支分别在第__________、__________象限内,在每个象限内,y 随x 的增大而__________; 11. 已知函数1
k y x
+=
的图象两支分布在第二、四象限内,则k 的范围是_________ 12. 反比例函数 2
k y x
= (0≠k )的图象的两个分支分别位于 ( )
(A ) 第一、二象限 (B ) 第一、三象限 (C ) 第二、四象限 (D ) 第一、四象限 13. 若反比列函数1
232)12(---=k k x
k y 的图像经过二、四象限,则k = _______
14. 已知反比例函数的图像经过点(a ,b ),则它的图像一定也经过 ( ) (A ) (a -,b -) (B ) (a ,b -) (C ) (a -,b ) (D ) (0,0) 15. 反比例函数4
22
)1(---=m m
x m y ,当x <0时,y 随x 的增大而增大,则m 的值是( )
(A ) 1- (B ) 3
(C ) 1-或3 (D ) 2
16. 若A (x 1,y 1),B (x 2,y 2),C (x 3,y 3)都是反比例函数x
y 1
-
=的图象上的点,且 x 1<0<x 2<x 3,则y 1,y 2,y 3由小到大的顺序是 ;
17. 设有反比例函数y k x
=
+1
,(,)x y 11、(,)x y 22为其图象上的两点,若x x 120<<时,y y 12>,则k 的取值范围是___________
18. 点A 为反比例函数图象上一点,它到原点的距离为5,到x 轴的距离为3,若点A 在第二象限内.则这个反比例函数的解析式为 ( )
(A ) 12y x =
(B ) 12y x =- (C ) 112y x = (D ) 112y x =- 19. 反比例函数()0>=k x
k
y 在第一象限内的图象如图,点M 是图像上一点,MP 垂直x 轴于点P ,
如果△MOP 的面积为1,那么k 的值是 ;
20. 如图2所示,A 、B 是函数x
y 1
-=
的图象上关于原点O 对称 的任意两点,AC ∥x 轴,BC ∥y 轴,△ABC 的面积为S ,则 ( ) (A ) S =1 (B ) S =2
(C ) 1<S <2
(D ) S <2
21. 已知12y y y =+,其中1y 与
1x
成反比例且比例系数为1k ,2y 与2
x 成正比例且比例系数为2k ,若1-=x 时,0=y ,则1k 与2k 的关系为 ( )
(A ) 12k k =- (B ) 12k k ≠ (C ) 12
1
k k =- (D ) 12k k = 22. 若ab <0,则函数ax y =与x
b
y =在同一坐标系内的图象大致可能是下图中的 ( )
(A ) (B ) (C ) (D )
23. 函数2
x y -
=和函数x y 2
=的图像有 个交点;
24. 已知正比例函数kx y =与反比例函数3
y x
=的图象都过A (m ,1),则m = ,正比例函数与反比例函
数的解析式分别是 、 ; 25. 直线x y 2=与双曲线x
y 1
=的交点为_________;
y
O P
M。
