BP人工神经网络的基本原理模型与实例
（完整版）BP神经网络原理及应用
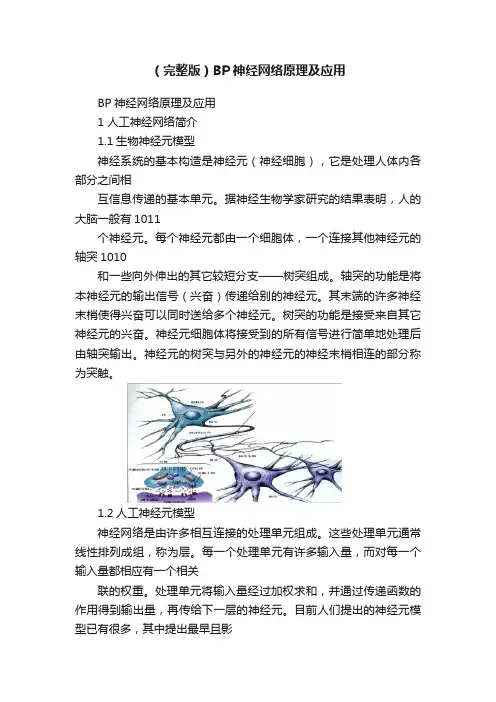
（完整版）BP神经网络原理及应用BP神经网络原理及应用1 人工神经网络简介1.1生物神经元模型神经系统的基本构造是神经元（神经细胞），它是处理人体内各部分之间相互信息传递的基本单元。
据神经生物学家研究的结果表明，人的大脑一般有1011个神经元。
每个神经元都由一个细胞体，一个连接其他神经元的轴突1010和一些向外伸出的其它较短分支——树突组成。
轴突的功能是将本神经元的输出信号（兴奋）传递给别的神经元。
其末端的许多神经末梢使得兴奋可以同时送给多个神经元。
树突的功能是接受来自其它神经元的兴奋。
神经元细胞体将接受到的所有信号进行简单地处理后由轴突输出。
神经元的树突与另外的神经元的神经末梢相连的部分称为突触。
1.2人工神经元模型神经网络是由许多相互连接的处理单元组成。
这些处理单元通常线性排列成组，称为层。
每一个处理单元有许多输入量，而对每一个输入量都相应有一个相关联的权重。
处理单元将输入量经过加权求和，并通过传递函数的作用得到输出量，再传给下一层的神经元。
目前人们提出的神经元模型已有很多，其中提出最早且影响最大的是1943年心理学家McCulloch和数学家Pitts在分析总结神经元基本特性的基础上首先提出的M-P 模型，它是大多数神经网络模型的基础。
)()(1∑=-=ni j i ji j x w f t Y θ （1.1）式(1.1)中,j 为神经元单元的偏置（阈值），ji w 为连接权系数（对于激发状态，ji w 取正值，对于抑制状态，ji w 取负值），n 为输入信号数目，j Y 为神经元输出，t 为时间，f()为输出变换函数，有时叫做激发或激励函数，往往采用0和1二值函数或Ｓ形函数。
1.3人工神经网络的基本特性人工神经网络由神经元模型构成；这种由许多神经元组成的信息处理网络具有并行分布结构。
每个神经元具有单一输出，并且能够与其它神经元连接；存在许多（多重）输出连接方法，每种连接方法对应一个连接权系数。
BP神经网络模型应用实例
BP神经网络模型第1节基本原理简介近年来全球性的神经网络研究热潮的再度兴起，不仅仅是因为神经科学本身取得了巨大的进展．更主要的原因在于发展新型计算机和人工智能新途径的迫切需要．迄今为止在需要人工智能解决的许多问题中，人脑远比计算机聪明的多，要开创具有智能的新一代计算机，就必须了解人脑，研究人脑神经网络系统信息处理的机制．另一方面，基于神经科学研究成果基础上发展出来的人工神经网络模型，反映了人脑功能的若干基本特性，开拓了神经网络用于计算机的新途径．它对传统的计算机结构和人工智能是一个有力的挑战，引起了各方面专家的极大关注．目前，已发展了几十种神经网络，例如Hopficld模型，Feldmann等的连接型网络模型，Hinton等的玻尔茨曼机模型，以及Rumelhart等的多层感知机模型和Kohonen的自组织网络模型等等。
在这众多神经网络模型中，应用最广泛的是多层感知机神经网络。
多层感知机神经网络的研究始于50年代，但一直进展不大。
直到1985年，Rumelhart等人提出了误差反向传递学习算法（即BP算），实现了Minsky的多层网络设想，如图34-1所示。
BP 算法不仅有输入层节点、输出层节点，还可有1个或多个隐含层节点。
对于输入信号，要先向前传播到隐含层节点，经作用函数后，再把隐节点的输出信号传播到输出节点，最后给出输出结果。
节点的作用的激励函数通常选取S 型函数，如Qx e x f /11)(-+=式中Q 为调整激励函数形式的Sigmoid 参数。
该算法的学习过程由正向传播和反向传播组成。
在正向传播过程中，输入信息从输入层经隐含层逐层处理，并传向输出层。
每一层神经元的状态只影响下一层神经输入层 中间层 输出层 图34-1 BP 神经网络模型元的状态。
如果输出层得不到期望的输出，则转入反向传播，将误差信号沿原来的连接通道返回，通过修改各层神经元的权值，使得误差信号最小。
社含有n 个节点的任意网络，各节点之特性为Sigmoid 型。
BP神经网络实验报告
BP神经网络实验报告一、引言BP神经网络是一种常见的人工神经网络模型，其基本原理是通过将输入数据通过多层神经元进行加权计算并经过非线性激活函数的作用，输出结果达到预测或分类的目标。
本实验旨在探究BP神经网络的基本原理和应用，以及对其进行实验验证。
二、实验方法1.数据集准备本次实验选取了一个包含1000个样本的分类数据集，每个样本有12个特征。
将数据集进行标准化处理，以提高神经网络的收敛速度和精度。
2.神经网络的搭建3.参数的初始化对神经网络的权重和偏置进行初始化，常用的初始化方法有随机初始化和Xavier初始化。
本实验采用Xavier初始化方法。
4.前向传播将标准化后的数据输入到神经网络中，在神经网络的每一层进行加权计算和激活函数的作用，传递给下一层进行计算。
5.反向传播根据预测结果与实际结果的差异，通过计算损失函数对神经网络的权重和偏置进行调整。
使用梯度下降算法对参数进行优化，减小损失函数的值。
6.模型评估与验证将训练好的模型应用于测试集，计算准确率、精确率、召回率和F1-score等指标进行模型评估。
三、实验结果与分析将数据集按照7:3的比例划分为训练集和测试集，分别进行模型训练和验证。
经过10次训练迭代后，模型在测试集上的准确率稳定在90%以上，证明了BP神经网络在本实验中的有效性和鲁棒性。
通过调整隐藏层结点个数和迭代次数进行模型性能优化实验，可以发现隐藏层结点个数对模型性能的影响较大。
随着隐藏层结点个数的增加，模型在训练集上的拟合效果逐渐提升，但过多的结点数会导致模型的复杂度过高，容易出现过拟合现象。
因此，选择合适的隐藏层结点个数是模型性能优化的关键。
此外，迭代次数对模型性能也有影响。
随着迭代次数的增加，模型在训练集上的拟合效果逐渐提高，但过多的迭代次数也会导致模型过度拟合。
因此，需要选择合适的迭代次数，使模型在训练集上有好的拟合效果的同时，避免过度拟合。
四、实验总结本实验通过搭建BP神经网络模型，对分类数据集进行预测和分类。
BP神经网络的基本原理_一看就懂
BP神经网络的基本原理_一看就懂BP神经网络（Back Propagation Neural Network）是一种常用的人工神经网络模型，用于解决分类、回归和模式识别问题。
它的基本原理是通过反向传播算法来训练和调整网络中的权重和偏置，以使网络能够逐渐逼近目标输出。
1.前向传播：在训练之前，需要对网络进行初始化，包括随机初始化权重和偏置。
输入数据通过输入层传递到隐藏层，在隐藏层中进行线性加权和非线性激活运算，然后传递给输出层。
线性加权运算指的是将输入数据与对应的权重相乘，然后将结果进行求和。
非线性激活指的是对线性加权和的结果应用一个激活函数，常见的激活函数有sigmoid函数、ReLU函数等。
激活函数的作用是将线性运算的结果映射到一个非线性的范围内，增加模型的非线性表达能力。
2.计算损失：将网络输出的结果与真实值进行比较，计算损失函数。
常用的损失函数有均方误差（Mean Squared Error）和交叉熵（Cross Entropy）等，用于衡量模型的输出与真实值之间的差异程度。
3.反向传播：通过反向传播算法，将损失函数的梯度从输出层传播回隐藏层和输入层，以便调整网络的权重和偏置。
反向传播算法的核心思想是使用链式法则。
首先计算输出层的梯度，即损失函数对输出层输出的导数。
然后将该梯度传递回隐藏层，更新隐藏层的权重和偏置。
接着继续向输入层传播，直到更新输入层的权重和偏置。
在传播过程中，需要选择一个优化算法来更新网络参数，常用的优化算法有梯度下降（Gradient Descent）和随机梯度下降（Stochastic Gradient Descent）等。
4.权重和偏置更新：根据反向传播计算得到的梯度，使用优化算法更新网络中的权重和偏置，逐步减小损失函数的值。
权重的更新通常按照以下公式进行：新权重=旧权重-学习率×梯度其中，学习率是一个超参数，控制更新的步长大小。
梯度是损失函数对权重的导数，表示了损失函数关于权重的变化率。
BP神经网络数学原理及推导过程
BP神经网络数学原理及推导过程BP神经网络（Backpropagation Neural Network），也称为反向传播神经网络，是一种常见的人工神经网络模型，主要用于解决回归和分类问题。
它在数学上涉及到多元微积分、线性代数和概率论等方面的知识。
本文将从数学原理和推导过程两个方面进行阐述。
一、数学原理：1. 激活函数（Activation Function）：激活函数是神经网络中非线性变换的数学函数，用于引入非线性因素，增加神经网络的表达能力。
常见的激活函数有Sigmoid函数、ReLU函数等。
2. 前向传播（Forward Propagation）：神经网络的前向传播是指将输入数据从输入层依次传递到输出层的过程。
在前向传播中，每个神经元接收上一层神经元传递过来的激活值和权重，计算出当前神经元的输出值，并将输出值传递给下一层神经元。
3. 反向传播（Backward Propagation）：神经网络的反向传播是指根据损失函数的值，从输出层开始，沿着网络的反方向不断调整神经元的权重，以达到最小化损失函数的目的。
在反向传播中，通过链式法则计算每个神经元对损失函数的导数，进而利用梯度下降算法更新权重。
4. 误差函数（Error Function）：误差函数用于衡量神经网络输出结果和真实值之间的差异，常见的误差函数有均方差（Mean Squared Error）函数和交叉熵（Cross Entropy）函数。
5.权重更新规则：反向传播算法中的核心部分就是权重的更新。
权重更新通常采用梯度下降算法，通过计算损失函数对权重的偏导数，按照负梯度方向更新权重值，使得损失函数逐渐减小。
二、推导过程：下面将以一个简单的多层感知机为例，推导BP神经网络的权重更新规则。
假设我们有一个三层的神经网络，第一层为输入层，第二层为隐藏层，第三层为输出层，隐藏层和输出层都使用Sigmoid激活函数。
1.前向传播：首先，我们根据输入层的输入值X和权重W1，计算隐藏层的输入值H1：H1=X*W1然后，将隐藏层的输入值H1带入到Sigmoid函数中，得到隐藏层的输出值A1：A1=σ(H1)接下来，根据隐藏层的输出值A1和权重W2，计算输出层的输入值H2：H2=A1*W2最后，将输出层的输入值H2带入到Sigmoid函数中，得到输出层的输出值A2：A2=σ(H2)2.反向传播：设输出层的输出值为Y，隐藏层的输出值为A1，损失函数为L。
bp算法分类实例
bp算法分类实例一、BP算法基本原理BP算法，即反向传播算法（Back Propagation），是一种常用的人工神经网络训练算法。
它通过不断调整网络中各个连接权值，使得网络能够学习到输入与输出之间的映射关系。
BP算法基于梯度下降法的思想，通过计算误差的梯度来更新权值，从而逐步减小网络的预测误差。
BP算法的基本原理可以简述为以下几个步骤：1. 初始化网络的权值和阈值。
2. 输入样本，并通过前向传播计算网络的输出。
3. 计算输出误差，并根据误差计算每个权值需要调整的量。
4. 通过反向传播，将误差从输出层向输入层逐层传播，并根据误差梯度更新各层的权值和阈值。
5. 重复步骤2~4，直到网络的输出接近或达到预期输出。
6. 对于分类问题，可以使用交叉熵损失函数来计算误差，并使用softmax函数作为输出层的激活函数。
二、BP算法应用实例为了更好地理解BP算法的应用，我们以一个简单的手写数字识别问题为例进行说明。
假设我们有一组手写数字的图像数据集，每个图像都是28x28像素的灰度图像，且标注了对应的数字。
我们的目标是通过BP算法训练一个神经网络模型，使其能够自动识别输入图像中的数字。
我们需要将每个图像展开成一个向量，并将像素值归一化到0~1的范围内。
然后，我们构建一个多层感知机（MLP）神经网络，其中包含输入层、隐藏层和输出层。
输入层的节点数与图像的像素数相同，输出层的节点数与数字的类别数相同，隐藏层的节点数可以根据需要进行设置。
接下来，我们使用BP算法对神经网络进行训练。
训练过程中，我们将数据集分为训练集和验证集，用训练集进行权值的更新和调整，用验证集评估网络的性能。
我们通过计算交叉熵损失函数来度量网络的预测误差，并使用梯度下降法来更新权值和阈值。
训练完成后，我们可以使用测试集来评估网络的泛化能力。
将测试集中的图像输入到网络中，通过前向传播得到网络的输出，并与标注的数字进行比较，即可得到分类结果。
我们可以计算分类准确率来评估网络的性能。
BP网络的原理与应用
BP网络的原理与应用1. 简介BP神经网络，即反向传播神经网络（Back Propagation Neural Network），是一种常见的人工神经网络模型，广泛应用于模式识别、分类、预测等领域。
它通过训练数据进行反向传播的方式来调整神经网络的权重和偏置，从而实现对输入数据的学习和预测。
2. 原理BP神经网络由输入层、隐藏层和输出层构成，每层由多个神经元组成。
其中，输入层接收外界输入的数据，隐藏层进行信号的处理和转换，最终输出层给出模型的预测结果。
BP网络的训练过程主要由两个阶段组成：前向传播和反向传播。
2.1 前向传播在前向传播阶段，输入数据经过一次性的计算和传递，从输入层逐层向前，最终记录到输出层的神经元中。
具体步骤如下： 1. 将输入数据传递给输入层神经元，每个神经元计算输入数据与其对应权重和偏置的乘积之和。
2. 将计算结果经过激活函数（如Sigmoid函数）进行处理，得到隐藏层神经元的输出。
3. 重复以上步骤，将隐藏层的输出作为下一层的输入，直到传递到输出层。
2.2 反向传播在反向传播阶段，根据训练数据与实际输出之间的差距，计算输出误差，并根据误差大小调整权重和偏置，以达到提高网络性能的目的。
具体步骤如下： 1. 计算输出层的误差，即实际输出与训练数据的差值。
2. 通过链式法则逐层计算隐藏层的误差，以及权重和偏置的调整值。
3. 更新每个神经元的权重和偏置，通过选择合适的优化算法（如梯度下降法）进行调整。
4. 重复以上步骤，通过多次迭代，不断减小预测误差和损失函数，提高网络的精确度和泛化能力。
3. 应用BP神经网络广泛应用于许多领域，如图像识别、语音识别、文本分类、金融预测等。
下面列举一些常见的应用场景：•图像识别：通过训练大量图像数据，可以实现对不同物体、人脸等的自动识别和分类。
•语音识别：通过训练大量语音数据，可以实现对语音信号的识别和转换，用于语音助手、智能家居等。
•文本分类：通过训练大量文本数据，可以实现对文本内容的分类和情感分析，用于垃圾邮件过滤、情感识别等。
神经网络原理及BP网络应用实例
神经网络原理及BP网络应用实例摘要：本文主要对神经网络原理进行系统地概述,再列举BP网络在曲线逼近中的应用。
神经网络是一门发展十分迅速的交叉学科，它是由大量的处理单元组成非线性的大规模自适应动力系统。
神经网络具有分布式存储、并行处理、高容错能力以及良好的自学习、自适应、联想等特点。
随着计算机的发展，目前已经提出了多种训练算法和网络模型，其中应用最广泛的是前馈型神经网络。
本文将介绍人工神经网络的基本概念、基本原理、BP神经网络、自适应竞争神经网络以及神经网络的应用改进方法。
关键字：神经网络；收敛速度；BP网络；改进方法The principle of neural network and the applicationexamples of BP networkAbstract：Neural network is a cross discipline which now developing very rapidly, it is the nonlinearity adaptive power system which made up by abundant of the processing units . The neural network has features such as distributed storage, parallel processing, high tolerance and good self-learning, adaptive, associate, etc. Currently various training algorithm and network model have been proposed , which the most widely used type is Feedforward neural network model. Feedforward neural network training type used in most of the method is back-propagation (BP) algorithm. This paper will introduces the basic concepts, basic principles, BP neural network, adaptive competitive neural network and the application of artificial neural network.Keywords：neural network，convergence speed，BP neural network，improving method1 神经网络概述1.1 生物神经元模型人脑是由大量的神经细胞组合而成的，它们之间相互连接。
BP神经网络原理及应用
BP神经网络原理及应用BP神经网络，即反向传播神经网络（Backpropagation Neural Network），是一种基于梯度下降算法的多层前馈神经网络，常用于分类与回归等问题的解决。
BP神经网络通过反向传播算法，将误差从输出层往回传播，更新网络权值，直至达到误差最小化的目标，从而实现对输入模式的分类和预测。
BP神经网络的结构包括输入层、隐藏层和输出层。
输入层接收外部输入的特征向量，隐藏层负责将输入特征映射到合适的高维空间，输出层负责输出网络的预测结果。
每个神经元与其前后的神经元相连，每个连接都有一个权值，用于调整输入信号的重要性。
BP神经网络利用激活函数（如sigmoid函数）对神经元的输出进行非线性变换，增加网络的非线性表达能力。
1.前向传播：将输入信号传递给网络，逐层计算每个神经元的输出，直至得到网络的输出结果。
2.计算误差：将网络输出与期望输出比较，计算误差。
常用的误差函数包括平方误差和交叉熵误差等。
3.反向传播：根据误差，逆向计算每个神经元的误差贡献，从输出层往回传播到隐藏层和输入层。
根据误差贡献，调整网络的权值和阈值。
4.更新权值和阈值：根据调整规则（如梯度下降法），根据误差贡献的梯度方向，更新网络的权值和阈值。
1.模式识别与分类：BP神经网络可以通过训练学习不同模式的特征，从而实现模式的自动分类与识别。
例如，人脸识别、文本分类等。
2.预测与回归：BP神经网络可以通过历史数据的训练，学习到输入与输出之间的映射关系，从而实现对未知数据的预测与回归分析。
例如，股票价格预测、天气预测等。
3.控制系统：BP神经网络可以用于建模和控制非线性系统，实现自适应、自学习的控制策略。
例如，机器人控制、工业过程优化等。
4.信号处理与图像处理：BP神经网络可以通过学习复杂的非线性映射关系，实现信号的去噪、压缩和图像的识别、处理等。
例如，语音识别、图像分割等。
5.数据挖掘与决策支持：BP神经网络可以根据历史数据学习到数据之间的相关关系，从而帮助决策者进行数据挖掘和决策支持。
BP人工神经网络的基本原理模型与实例培训课件
BP人工神经网络的基本原理模型与实例
2
8.1人工神经网络的基本概念
人工神经网络在本质上是由许多小的非线性函数组成 的大的非线性函数，反映的是输入变量到输出变量间的复 杂映射关系。先给出单个人工神经网络的一般模型描述：
1/7/2021
BP人工神经网络的基本原理模型与实例
3
8.1人工神经网络的基本概念
本讲大纲：
人工神经网络的基本概念 误差反向传播(BP)神经网络
1/7/2021
BP人工神经网络的基本原理模型与实例
1
8.1人工神经网络的基本概念
从数学和物理方法以及信息处理的角度，对人脑神经 网络进行抽象，并建立某种简化模型，称为人工神经网络。
应用领域： 模式识别 系统辨识 预测预估 数据挖掘 经济学 ……
1/7/2021
x1
x2
w1
w2
θ
1
0
0.2
0.4
0.4
BP人工神经网络的基本原理模型与实例
9
8.1人工神经网络的基本概念
x1 w1 x2 w2
f (·) wm xm
-1
...... ......
1/7/2021
BP人工神经网络的基本原理模型与实例
10
8.1人工神经网络的基本概念
当多个神经元组合起来时，人工神经网络的总体结构如下：
5 θ5
w46 -0.1842
0.5459
6
w56
θ6
净输入和输出的计算
单元 j
净输入 Ij
净输出 Oj
4
0.192+0-0.306-0.408=-0.522
1/(1+e-0.522)=0.6276
BP神经网络模型及实例
(1)由动量的梯度下降法
在神经网络工具箱中， traingdm函数采用了由动量的梯度下降法，提高 了学习速度并增加了算法的可靠性。
x x1, x2,
hi hi1, hi2,
ho ho1, ho2,
yi yi1, yi2,
yo yo1, yo2,
do d1, d2,
, xn
, hip
, hop
, yiq
, yoq
, dq
2.4.2 BP网络的标准学习算法
– 输入层与中间层的连接权值:
wih
– 隐含层与输出层的连接权值:
2.4.1 BP神经网络模型
• 三层BP网络
2.4.1 BP神经网络模型
• 激活函数
– 必须处处可导
• 一般都使用S型函数
• 使用S型激活函数时BP网络输入与输出关 系
– 输入 net x1w1 x2w2 ... xnwn
– 输出
y
f
(net)
1
1 enet
2.4.1 BP神经网络模型
2.4 BP神经网络模型与学习算法
概述
• Rumelhart，McClelland于1985年提出了BP网络的误差 反向后传BP(Back Propagation)学习算法
David Rumelhart
J. McClelland
• BP算法基本原理
– 利用输出后的误差来估计输出层的直接前导层的误差，再用这个 误差估计更前一层的误差，如此一层一层的反传下去，就获得了 所有其他各层的误差估计。
阐述bp神经网络的原理
阐述bp神经网络的原理
BP神经网络全称为反向传播神经网络，是一种常用的人工神经网络模型。
其原理基于两个基本思想：前向传播和反向误差传播。
前向传播：BP神经网络是一个多层感知器，由输入层、隐藏层和输出层组成。
输入层接收外部输入的数据，隐藏层负责处理输入，并传递给输出层，输出层根据处理结果生成输出。
隐藏层和输出层的每个神经元都有一个权重向量，用于对输入数据进行线性组合。
然后，通过激活函数对线性组合结果进行非线性变换，得到该神经元的输出。
隐藏层和输出层的每个神经元的输出都会作为下一层神经元的输入。
反向误差传播：当神经网络的输出与期望输出之间存在差异时，需要通过反向传播算法来调整权重，以减小这个误差。
算法的基本思想是将误差从输出层向隐藏层逐层传递，通过调整每个神经元的权重，最终使得网络的输出与期望输出尽可能接近。
具体实现时，首先计算输出层的误差，然后根据误差调整输出层的权重。
接下来，将误差反向传播到隐藏层，再根据误差调整隐藏层的权重。
这个过程会不断迭代，直到网络的输出与期望输出的误差足够小。
通过反向误差传播算法，BP神经网络可以学习到输入-输出的映射关系，从而能
够对未知输入进行预测或分类。
然而，BP神经网络也存在一些问题，例如容易陷入局部极小值、对初始权重较敏感等，因此在实际应用中需要进行一定的调优和训练策略。
bp神经网络的基本原理
bp神经网络的基本原理
BP神经网络是一种常用的人工神经网络模型，用于解决分类和回归问题。
它的基本原理是通过反向传播算法来调整网络的权重和偏置，从而使网络能够学习和逼近输入输出之间的非线性关系。
BP神经网络由输入层、隐藏层和输出层组成。
输入层接收外部输入的数据，隐藏层是网络中间的处理层，输出层给出最终的结果。
每个神经元都与前一层的神经元以及后一层的神经元相连接，每个连接都有一个权重值。
BP神经网络的学习过程首先需要给定一个训练数据集，并设置好网络的结构和参数。
然后，通过前向传播将输入数据从输入层传递到隐藏层和输出层，计算网络的输出结果。
接着，根据输出结果与实际输出之间的差异，使用误差函数来评估网络的性能。
在反向传播阶段，根据误差函数的值，利用链式法则计算每个连接的权重和偏置的梯度。
然后，根据梯度下降法更新连接的权重和偏置，使误差不断减小。
这个过程反复进行，直到网络输出的误差达到了可接受的范围或者训练次数达到了预设的最大值。
通过不断地调整权重和偏置，BP神经网络可以逐渐学习到输入输出之间的映射关系，从而在面对新的输入数据时能够给出合理的输出。
同时，BP神经网络还具有一定的容错性和鲁棒性，可以处理一些噪声和不完整的数据。
总的来说，BP神经网络的基本原理是通过反向传播算法来训练网络，将输入数据从输入层传递到输出层，并且根据实际输出与期望输出之间的差异来优化网络的权重和偏置，以达到学习和逼近输入输出之间关系的目的。
BP人工神经网络的基本原理模型与实例
w14
0.2+(0.9) (-0.0087)(1)=0.192
w15
-0.3+(0.9) (-0.0065)(1)=-0.306
w24
0.4+(0.9) (-0.0087)(0)=0.4
w25
0.1+(0.9) (-0.0065)(0)=0.1
w34
-0.5+(0.9) (-0.0087)(1)=-0.508
8.1人工神经网络旳基本概念
人工神经网络在本质上是由许多小旳非线性函数构成 旳大旳非线性函数，反应旳是输入变量到输出变量间旳复 杂映射关系。先给出单个人工神经网络旳一般模型描述：
8.1人工神经网络旳基本概念
先来看一种单一输入旳神经元模型 输入变量：x1 连接权重：w1 激活函数：f (·)
x1 w1
w1x1 f (·)
8.1人工神经网络旳基本概念
8.1人工神经网络旳基本概念
单极sigmoid函数
8.1人工神经网络旳基本概念
双曲函数
8.1人工神经网络旳基本概念
增长激活阈值后旳神经元模型 输入变量：x1 连接权重：w1 激活函数：f (·)
x1 w1
w1x1-θ f (·)
-1
小练习：请你算一算，当初始输入、权重和激活阈值为如下数值时，该神 经元旳净输入和输出分别是多少？
2．反向传播 反向传播时，把误差信号按原来正向传播旳通路反向
传回，并对每个隐层旳各个神经元旳权系数进行修改，以 望误差信号趋向最小。
8.2 误差反向传播(BP)神经网 络
8.2 误差反向传播(BP)神经网 络
x1 x2
x3
单元 j 6
1 w14
Err4=
BP神经网络的基本原理_一看就懂
BP神经网络的基本原理_一看就懂BP神经网络（Back propagation neural network）是一种常用的人工神经网络模型，也是一种有监督的学习算法。
它基于错误的反向传播来调整网络权重，以逐渐减小输出误差，从而实现对模型的训练和优化。
1.初始化网络参数首先，需要设置网络的结构和连接权重。
BP神经网络通常由输入层、隐藏层和输出层组成。
每个神经元与上下层之间的节点通过连接权重相互连接。
2.传递信号3.计算误差实际输出值与期望输出值之间存在误差。
BP神经网络通过计算误差来评估模型的性能。
常用的误差计算方法是均方误差（Mean Squared Error，MSE），即将输出误差的平方求和后取平均。
4.反向传播误差通过误差反向传播算法，将误差从输出层向隐藏层传播，并根据误差调整连接权重。
具体来说，根据误差对权重的偏导数进行计算，然后通过梯度下降法来更新权重值。
5.权重更新在反向传播过程中，通过梯度下降法来更新权重值，以最小化误差。
梯度下降法的基本思想是沿着误差曲面的负梯度方向逐步调整权重值，使误差不断减小。
6.迭代训练重复上述步骤，反复迭代更新权重值，直到达到一定的停止条件，如达到预设的训练轮数、误差小于一些阈值等。
迭代训练的目的是不断优化模型，使其能够更好地拟合训练数据。
7.模型应用经过训练后的BP神经网络可以应用于新数据的预测和分类。
将新的输入数据经过前向传播，可以得到相应的输出结果。
需要注意的是，BP神经网络对于大规模、复杂的问题，容易陷入局部最优解，并且容易出现过拟合的情况。
针对这些问题，可以采用各种改进的方法，如加入正则化项、使用更复杂的网络结构等。
综上所述，BP神经网络通过前向传播和反向传播的方式，不断调整权重值来最小化误差，实现对模型的训练和优化。
它是一种灵活、强大的机器学习算法，具有广泛的应用领域，包括图像识别、语音识别、自然语言处理等。
BP人工神经网络的基本原理、模型与实例
BP人工神经网络的实例
BP人工神经网络可以应用于多个领域，如图像识别、语音处理、预测分析等，为解决复杂问题提供了有效的神经网络的输入是具体问题的相关数据，比如图像数据、声音数据等。 输出是经过神经网络计算后得出的结果。
神经元和连接权重
神经元是BP人工神经网络的基本单元，通过调整连接权重来不断优化神经网 络的表现和学习能力。
前向传播和反向传播
前向传播是指输入数据从输入层经过隐藏层到达输出层的过程。反向传播是指根据误差计算，通过调整连接权 重来优化神经网络的过程。
训练和优化算法
BP人工神经网络的训练过程是通过不断调整连接权重使得神经网络的输出结 果接近于期望结果的过程。优化算法如梯度下降算法等可以加速训练的过程。
BP人工神经网络的基本 原理、模型与实例
人工神经网络（Artificial Neural Network）以人类大脑神经网络的的运作方式 为模型，用于模拟智能行为和解决复杂问题。
BP人工神经网络的基本原理
BP人工神经网络通过多层神经元和连接权重的组合，实现输入数据到输出结 果的计算和转换过程。
BP人工神经网络的模型
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
BP人工神经网络的基本原理模型与实例BP（Back Propagation）人工神经网络是一种常见的人工神经网络模型，其基本原理是模拟人脑神经元之间的连接和信息传递过程，通过学习
和调整权重，来实现输入和输出之间的映射关系。
BP神经网络模型基本上由三层神经元组成：输入层、隐藏层和输出层。
每个神经元都与下一层的所有神经元连接，并通过带有权重的连接传
递信息。
BP神经网络的训练基于误差的反向传播，即首先通过前向传播
计算输出值，然后通过计算输出误差来更新连接权重，最后通过反向传播
调整隐藏层和输入层的权重。
具体来说，BP神经网络的训练过程包括以下步骤：
1.初始化连接权重：随机初始化输入层与隐藏层、隐藏层与输出层之
间的连接权重。
2.前向传播：将输入向量喂给输入层，通过带有权重的连接传递到隐
藏层和输出层，计算得到输出值。
3.计算输出误差：将期望输出值与实际输出值进行比较，计算得到输
出误差。
4.反向传播：从输出层开始，将输出误差逆向传播到隐藏层和输入层，根据误差的贡献程度，调整连接权重。
5.更新权重：根据反向传播得到的误差梯度，使用梯度下降法或其他
优化算法更新连接权重。
6.重复步骤2-5直到达到停止条件，如达到最大迭代次数或误差小于
一些阈值。
BP神经网络的训练过程是一个迭代的过程，通过不断调整连接权重，逐渐减小输出误差，使网络能够更好地拟合输入与输出之间的映射关系。
下面以一个简单的实例来说明BP神经网络的应用：
假设我们要建立一个三层BP神经网络来预测房价，输入为房屋面积
和房间数，输出为价格。
我们训练集中包含一些房屋信息和对应的价格。
1.初始化连接权重：随机初始化输入层与隐藏层、隐藏层与输出层之
间的连接权重。
2.前向传播：将输入的房屋面积和房间数喂给输入层，通过带有权重
的连接传递到隐藏层和输出层，计算得到价格的预测值。
3.计算输出误差：将预测的价格与实际价格进行比较，计算得到输出
误差。
4.反向传播：从输出层开始，将输出误差逆向传播到隐藏层和输入层，根据误差的贡献程度，调整连接权重。
5.更新权重：根据反向传播得到的误差梯度，使用梯度下降法或其他
优化算法更新连接权重。
6.重复步骤2-5直到达到停止条件，如达到最大迭代次数或误差小于
一些阈值。
通过训练，我们可以得到一个训练好的BP神经网络模型，然后可以
使用该模型来对新的房屋数据进行价格预测。
总之，BP人工神经网络是一种常见的人工神经网络模型，通过模拟
神经元之间的连接和信息传递过程，通过学习和调整权重，来实现输入和
输出之间的映射关系。
通过反向传播算法，BP神经网络可以训练出一个能够逐渐减小输出误差的模型，用于解决各种预测、分类和回归等问题。