力学中自激振荡的公式
振动分析中常用的计算公式

振动台在使用中经常运用的公式1、 求推力(F )的公式F=(m 0+m 1+m 2+ ……)A …………………………公式(1) 式中:F —推力(激振力)(N )m 0—振动台运动部分有效质量(kg ) m 1—辅助台面质量(kg )m 2—试件(包括夹具、安装螺钉)质量(kg )A — 试验加速度(m/s 2)2、 加速度(A )、速度(V )、位移(D )三个振动参数的互换运算公式 2.1 A=ωv ……………………………………………………公式(2) 式中:A —试验加速度(m/s 2)V —试验速度(m/s ) ω=2πf (角速度) 其中f 为试验频率(Hz )2.2 V=ωD ×10-3………………………………………………公式(3) 式中:V 和ω与“2.1”中同义D —位移(mm 0-p )单峰值2.3 A=ω2D ×10-3 ………………………………………………公式(4) 式中:A 、D 和ω与“2.1”,“2.2”中同义 公式(4)亦可简化为:A=D f ⨯2502式中:A 和D 与“2.3”中同义,但A 的单位为g1g=9.8m/s 2所以: A ≈D f ⨯252,这时A 的单位为m/s 2 定振级扫频试验平滑交越点频率的计算公式 3.1 加速度与速度平滑交越点频率的计算公式f A-V =VA28.6 ………………………………………公式(5)式中:f A-V —加速度与速度平滑交越点频率(Hz )(A 和V 与前面同义)。
3.2 速度与位移平滑交越点频率的计算公式DV f DV 28.6103⨯=- …………………………………公式(6) 式中:D V f -—加速度与速度平滑交越点频率(Hz )(V 和D 与前面同义)。
3.3 加速度与位移平滑交越点频率的计算公式f A-D =DA ⨯⨯23)2(10π ……………………………………公式(7) 式中:f A-D — 加速度与位移平滑交越点频率(Hz ),(A 和D 与前面同义)。
振动分析中常用的计算公式

振动台在使用中经常运用的公式1、 求推力(F )的公式F=(m 0+m 1+m 2+ ……)A …………………………公式(1) 式中:F —推力(激振力)(N )m 0—振动台运动部分有效质量(kg ) m 1—辅助台面质量(kg )m 2—试件(包括夹具、安装螺钉)质量(kg )A — 试验加速度(m/s 2)2、 加速度(A )、速度(V )、位移(D )三个振动参数的互换运算公式 2.1 A=ωv ……………………………………………………公式(2) 式中:A —试验加速度(m/s 2)V —试验速度(m/s ) ω=2πf (角速度) 其中f 为试验频率(Hz )2.2 V=ωD ×10-3………………………………………………公式(3) 式中:V 和ω与“2.1”中同义D —位移(mm 0-p )单峰值2.3 A=ω2D ×10-3 ………………………………………………公式(4) 式中:A 、D 和ω与“2.1”,“2.2”中同义 公式(4)亦可简化为:A=D f ⨯2502式中:A 和D 与“2.3”中同义,但A 的单位为g1g=9.8m/s 2所以: A ≈D f ⨯252,这时A 的单位为m/s 2 定振级扫频试验平滑交越点频率的计算公式 3.1 加速度与速度平滑交越点频率的计算公式f A-V =VA28.6 ………………………………………公式(5)式中:f A-V —加速度与速度平滑交越点频率(Hz )(A 和V 与前面同义)。
3.2 速度与位移平滑交越点频率的计算公式DV f DV 28.6103⨯=- …………………………………公式(6) 式中:D V f -—加速度与速度平滑交越点频率(Hz )(V 和D 与前面同义)。
3.3 加速度与位移平滑交越点频率的计算公式f A-D =DA ⨯⨯23)2(10π ……………………………………公式(7) 式中:f A-D — 加速度与位移平滑交越点频率(Hz ),(A 和D 与前面同义)。
振动理论11(3)-自激振动
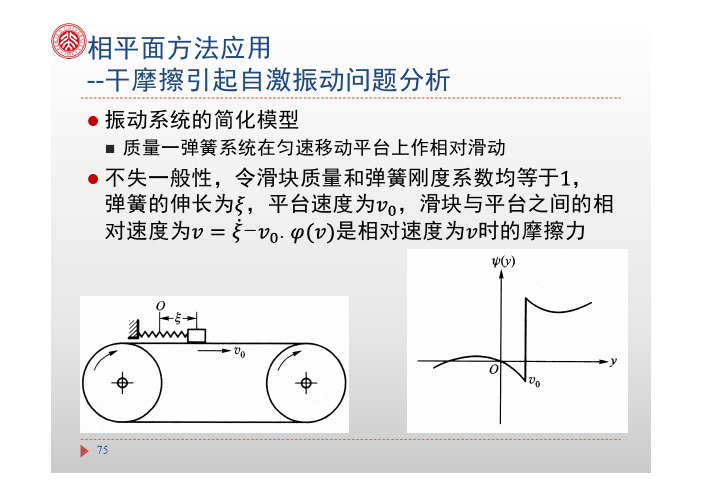
●振动系统的简化模型⏹质量一弹簧系统在匀速移动平台上作相对滑动●不失一般性,令滑块质量和弹簧刚度系数均等于,弹簧的伸长为,平台速度为,滑块与平台之间的相对速度为−. 是相对速度为时的摩擦力相平面方法应用--干摩擦引起自激振动问题分析75●受干摩擦力和弹簧恢复力作用的滑块运动方程为●弹簧伸长稳定时刻作为滑块平衡位置,即令●将平衡位置作为新的坐标原点,引入新的变量76则方程化作+其中的阻尼项为77●一阶自治方程●其对应的相轨迹如下⏹虚线为零斜率等倾线,在原点附近位于第一、三象限,类似于负阻尼情形78●在原点附近,相当于负阻尼情形:原点处的奇点为不稳定焦点,对应于不稳定的滑块平衡位置●当滑块因扰动偏离平衡位置时,相点沿螺线向外运动,振幅不断增大●一旦相点到达辅助曲线的水平段,即沿此线段移动到达右边,然后环绕原点一周后再与线段相遇,并再次重复此过程●过点的相轨迹自然成为相平面内的极限环。
●以上分析说明了干摩擦自激振动的产生原因。
79●当相点沿线段运动时,滑块相对平台的相对速度为零,这时平台咬住滑块以速度一同匀速运动●待弹簧恢复力随弹簧变形增长得足以克服静摩擦力时,滑块开始相对平台向后滑动,并在摩擦力作用下不断减速●滑动直到相对速度减至零,平台再次咬住滑块时上述过程重复发生对应的物理描述80●在此系统中,等速移动的平台为恒定能源,通过滑块与平台之间干摩擦特性调节能量的输入和输出●平台咬住滑块时对滑块作正功,释放后对滑块作负功,使滑块维持稳定的自激振动●各种实际的干摩擦自振现象都可从以上简单模型的分析得到解释●在工程中,滑块与平台之间时而粘住时而滑动的不连续爬行现象可在机械传动系统中发生。
利用润滑剂使干摩擦转化为黏性摩擦,干摩擦自振现象即自然消失。
对应的物理描述81输电线舞动82●高压输电线路在某些天气条件下会发生低频大振幅的振动⏹输电线通常为圆形截面,用相距300英尺的线塔牵拉⏹输电线在跨长内做半波振动,跨中振幅可达10英尺,频率大约每秒1周,或者更低●由于这一特征,这一现象通常被称为舞动而不是振动●在温暖气候的国家,很少会发生此类现象。
6.2.1-自激振荡的原理

课题:§ 6.2.1 自激振荡的原理
教学目的、要求: 1、熟记自激振荡的条件
2、理解自激振荡的工作原理教学重点:自激振荡的条件
教学难点:自激振荡的原理及判别
授课方法:讲授法练习法
教学参考及教具(含电教设备):多媒体黑板板书设计:
.阻尼振荡:电容上电压每经一次振荡都
将减小,最后停振。
.等幅振荡:正弦振荡器的工作原理。
.阻尼振荡:电容上电压每经一次振荡都将减小,最后停振。
.等幅振荡:正弦振荡器的工作原理。
LC
f 2π1
0=
注:电流与电压是按正弦规律变化的。
振荡器
用反馈信号代替原有的外加信号源V S 。
.自激:没有外部输入信号,由于电路内部正反馈作用而自动维持.相位平衡条件指放大器的反馈信号与输入信号必须同相位,即相)的偶数倍 ϕ = 2n π(n 是整数,相位差。
.振幅平衡条件,指放大器的反馈信号必须达到一定的幅度。
> 原输入端信号。
振荡建立好:反馈信号 = 原输入端信号。
分析:
(1)V处于截止状态,振幅条件不满足(2)用瞬时极性法判别为负反馈。
(3)不能产生自激振荡
教学过程
学生活动
学时分配
小结:
1.LC 回路的自由振荡
2.自激振荡产生的条件 作业:
2。
自激振荡分析与解决

如果放大器工作在通频带以外,由于相移增大,就有可能使负反馈变成正反馈, 以至产生自激振荡。
1 自激振荡的条件[1]自激振荡的条件为AF=-1,即|AF|= 1和arg(AF)=φA+φF=±(2n+1)π(n=0,1,2,…)上述公式是在负反馈的基础上推导出来的,相应条件是在-180°的基础上(中频时U0与Ui反相)所产生的附加相移Δφ。
2 检查电路是否稳定工作的方法(1) 方法一:根据AF的幅频和相频波特图来判断。
设LAF=20lg|AF|(dB)1) 当Δφ=-180°时(满足相位条件):若LAF<0,则电路稳定;若LAF≥0 (满足幅度条件),则自激。
2) 当|AF|=1,即LAF=0dB时(满足幅度条件):若|Δφ|<180,移相不足,不能自激;若|Δφ|≥180°,满足相位条件,能自激。
3)LAF=0时的频率为f0,Δφ=180°时的频率为fc,当f0 用上述三个判据中任何一个判断均可,需要注意的是,当反馈网络为纯电阻时,反馈系数F为实数,AF的波特图与A的波特图成为相似形。
为简便起见,通常只画出A的波特图进行研究。
因为F为已知(或可求),20lg(1/F)是一条水平线,它与A的幅频波特图相交于一点,这交点满足|A|=1/F,即|AF|=1(对应于20lg|AF|=0),根据交点处的相位小于-180°就能判断稳定与否。
(2)方法二:只根据幅频特性,无需相频特性的判别法。
因为20lg|AF|=0时,Δφ=-180°产生自激。
幅度条件改写成:20lg|A|+20lg|F| =0即:20lg|A|-20lg1/|F|=0,20lg|A|= 20lg1/|AF|≈20lg|Af|。
因此,自激条件又可描述为,当Δφ=-180°时,如果开环增益近似等于闭环增益将自激。
而开环增益的-20dB/dec段,对应于Δφ=-45°~- 135,-40dB/dec段对应于Δφ=-135°~- 225°。
第003章 自激振动

I A= 2B
(3.14)
《振动力学》讲义 第3章 自激振动 极限环
从极限环外 趋近极限环
α
从极限环内 趋近极限环
图3.10
《振动力学》讲义 第3章 自激振动 下面来研究极限环的稳定性。由(3.12)、(3.13)可得函 数关系 xT = xT [η (ξ )] (3.15)
(3.15)式的含义是:相点从 x = ξ 出发运动一周,将到达 x = xT 点,参见图3.10。因为 ξ = A 时,有 xT = A 、η = A, 因此,当 ξ = A + ∆ξ,∆ξ → 0 时
εω A3
由谐波平衡得 方程的解为
ω = ω0 ,
4 A=2
) sinψ + L = 0
x = 2 cos(ω0 t − θ )
注意,以上近似解只有当 ε 为小参数时才成立,图 3.5也是针对ε 为小参数的情况画出的。对于ε 为大参数 的情况将在§3.4节中研究。
《振动力学》讲义 第3章 自激振动
(3.12) (3.13)
xT = (η − B) 2 + 2 I − B
如果能使 xT = ξ ,则相轨迹封闭而成为极限环,由(3.12)、 (3.13)可求出实现这一结果应满足的条件为 I I ξ= ; 同时可得 η = 2B 2B 这意味着,对于给定的B、I 值,当相点从点(I / 2B, 0 )出 发,将沿极限环运动。马上将证明,这个极限环是稳定的, 因此系统能实现自激振动,极限环如图3.10;其振幅 A为
图3.1
图3.2
《振动力学》讲义 第3章 自激振动 电能,一部分转化为铃锤的动能和弹性势能,另一部分由于 材料阻尼、敲击等因素而耗散。接下来的过程是,弹性势能 使铃锤恢复形状,使电源再次接通,完成一次振动,并开始 下一次振动。 可见,自激振动的形成过程和机理是:振系在某些初始 激励下能作往复运动,同时振系内有一个固有的自动调节环 节起作用,它能自动感知振系状态,根据振系状态自动调节 能量的吸收,并能使振系 在每个往复运动中吸收的 能源 调节器 振动系统 能量逐渐等于耗散的能量, 从而使振系的能量和状态 状态反馈 周期性变化,即形成自激 振动。自激振动的形成机 理,可用框图表示,如图 图3.3 3.3。
高中物理振动和波公式总结

高中物理振动和波公式总结高中物理振动和波公式总结高中物理振动和波公式1.简谐振动F=-kx {F:回复力,k:比例系数,x:位移,负号表示F的方向与x始终反向}2.单摆周期T=2π(l/g)1/2 {l:摆长(m),g:当地重力加速度值,成立条件:摆角θ<100;l>>r}3.受迫振动频率特点:f=f驱动力4.发生共振条件:f驱动力=f固,A=max,共振的防止和应用5.机械波、横波、纵波:波就是振动的传播,通过介质传播。
在同种均匀介质中,振动的传播是匀速直线运动,这种运动,用波速V 表征。
对于匀速直线运动,波速V不变(大小不变,方向不变),所以波速V是一个不变的量。
介质分子并没有随着波的传播而迁移,介质分子的永不停息的无规则的运动,是热运动,其平均速度为零。
6.波速v=s/t=λf=λ/T{波传播过程中,一个周期向前传播一个波长;波速大小由介质本身所决定}7.声波的波速(在空气中)0℃332m/s;20℃:344m/s;30℃:349m/s;(声波是纵波)8.波发生明显衍射(波绕过障碍物或孔继续传播)条件:障碍物或孔的尺寸比波长小,或者相差不大9.波的干涉条件:两列波频率相同(相差恒定、振幅相近、振动方向相同)10.多普勒效应:由于波源与观测者间的相互运动,导致波源发射频率与接收频率不同{相互接近,接收频率增大,反之,减小}高中物理振动和波知识点1.简谐运动(1)定义:物体在跟偏离平衡位置的位移大小成正比,并且总是指向平衡位置的回复力的作用下的振动,叫做简谐运动.(2)简谐运动的特征:回复力F=-kx,加速度a=-kx/m,方向与位移方向相反,总指向平衡位置.简谐运动是一种变加速运动,在平衡位置时,速度最大,加速度为零;在最大位移处,速度为零,加速度最大.(3)描述简谐运动的物理量①位移x:由平衡位置指向振动质点所在位置的有向线段,是矢量,其最大值等于振幅.②振幅A:振动物体离开平衡位置的最大距离,是标量,表示振动的强弱.③周期T和频率f:表示振动快慢的物理量,二者互为倒数关系,即T=1/f.(4)简谐运动的图像①意义:表示振动物体位移随时间变化的规律,注意振动图像不是质点的运动轨迹.②特点:简谐运动的图像是正弦(或余弦)曲线.③应用:可直观地读取振幅A、周期T以及各时刻的位移x,判定回复力、加速度方向,判定某段时间内位移、回复力、加速度、速度、动能、势能的变化情况.2.弹簧振子:周期和频率只取决于弹簧的劲度系数和振子的质量,与其放置的环境和放置的方式无任何关系.如某一弹簧振子做简谐运动时的周期为T,不管把它放在地球上、月球上还是卫星中;是水平放置、倾斜放置还是竖直放置;振幅是大还是小,它的周期就都是T.3.单摆:摆线的质量不计且不可伸长,摆球的直径比摆线的长度小得多,摆球可视为质点.单摆是一种理想化模型.(1)单摆的振动可看作简谐运动的条件是:最大摆角α<5°.(2)单摆的回复力是重力沿圆弧切线方向并且指向平衡位置的分力.(3)作简谐运动的单摆的周期公式为:①在振幅很小的条件下,单摆的振动周期跟振幅无关.②单摆的振动周期跟摆球的质量无关,只与摆长L和当地的重力加速度g有关.③摆长L是指悬点到摆球重心间的距离,在某些变形单摆中,摆长L应理解为等效摆长,重力加速度应理解为等效重力加速度(一般情况下,等效重力加速度g'等于摆球静止在平衡位置时摆线的张力与摆球质量的比值).4.受迫振动(1)受迫振动:振动系统在周期性驱动力作用下的振动叫受迫振动.(2)受迫振动的特点:受迫振动稳定时,系统振动的频率等于驱动力的频率,跟系统的固有频率无关.(3)共振:当驱动力的频率等于振动系统的固有频率时,振动物体的振幅最大,这种现象叫做共振.共振的条件:驱动力的频率等于振动系统的固有频率. .5.机械波:机械振动在介质中的传播形成机械波.(1)机械波产生的条件:①波源;②介质(2)机械波的分类①横波:质点振动方向与波的传播方向垂直的波叫横波.横波有凸部(波峰)和凹部(波谷).②纵波:质点振动方向与波的传播方向在同一直线上的波叫纵波.纵波有密部和疏部.[注意]气体、液体、固体都能传播纵波,但气体、液体不能传播横波.(3)机械波的特点①机械波传播的是振动形式和能量.质点只在各自的平衡位置附近振动,并不随波迁移.②介质中各质点的振动周期和频率都与波源的振动周期和频率相同.③离波源近的质点带动离波源远的质点依次振动.6.波长、波速和频率及其关系(1)波长:两个相邻的且在振动过程中对平衡位置的位移总是相等的质点间的距离叫波长.振动在一个周期里在介质中传播的距离等于一个波长.(2)波速:波的传播速率.机械波的传播速率由介质决定,与波源无关.(3)频率:波的频率始终等于波源的振动频率,与介质无关.(4)三者关系:v=λf7. ★波动图像:表示波的传播方向上,介质中的各个质点在同一时刻相对平衡位置的位移.当波源作简谐运动时,它在介质中形成简谐波,其波动图像为正弦或余弦曲线.由波的图像可获取的信息①从图像可以直接读出振幅(注意单位)②从图像可以直接读出波长(注意单位).③可求任一点在该时刻相对平衡位置的位移(包括大小和方向)④在波速方向已知(或已知波源方位)时可确定各质点在该时刻的振动方向.⑤可以确定各质点振动的加速度方向(加速度总是指向平衡位置)高中物理学习方法听得懂高中生要积极主动地去听讲,把老师所说的每一句话都用心来听,熟记高中物理概念定义,这是“知其然”,老师讲解的过程就是“知其所以然”,听懂,才会运用。
振动理论11(2)-自激振动

相平面●不显含时间变量的系统称为自治系统,即时间不出现在运动微分方程中,只有时间的微分出现在形如下面的方程中⏹其中函数表示单位质量物体上恢复力与阻尼力的合力●把上面的方程用两个一阶方程来表示如果和为笛卡尔坐标,平面称为相平面. 系统的状态就可以用坐标和来描述,表示为相平面上的一个点随系统的改变,相平面内的点移动,在相平面内产生一个曲线,称为相轨迹(trajectory).●状态速度定义为●当状态速度为零时即达到平衡态:速度和加速度均为零●利用第一个方程,用第二个方程除第一个方程,●对于相平面上的每个点,如果是可确定的,迹的斜率是唯一的:●相轨迹的走向总是顺时针方向,与轴正交。
●如果(即迹点在轴上)并且, 迹的斜率无限大, 所有跟这个点相关的迹均垂直于轴51●如果,, 斜率不确定.这时的相点定义为奇异点.奇异点与平衡状态相关,在该平衡状态里,速度和力均为零关于奇异点表征的平衡是稳定的还是不稳定的,还需要进一步的讨论例题●确定单自由度振动的相平面:●解由, 写成两个一阶方程:二式相除,●分离变量并积分●这是一族椭圆,大小由确定。
●这个方程是一个保守体系:●奇异相点为保守系统的自由振动首先用相平面法研究最简单的机械系统,即保守系统。
其动力学方程为对应的相轨迹微分方程为分离变量并积分●为保守系统的势能●积分常数⏹系统的总机械能,取决于初始条件●上述相轨迹方程表示了系统的机械能守恒,即保守系统的能量积分●也可写作●对应于实际发生的运动,必须有(否则只是想像的)56●相轨迹曲线相对横坐标轴对称●与交点(动能为零)的●势能曲线的驻点对应横坐标轴上的奇点●在势能取极小值的⏹(有动能,有非零值),在相平面上对应奇点的封闭相轨迹⏹当(没有非零的值)时,不存在对应的相轨迹⏹这种类型的奇点是稳定的,称为中心。
它对应于系统的稳定平衡状态57●在势能取极大值的⏹,在区间内没有对应的相轨迹⏹在时,及处处相接触⏹当时,这两个分支则演变为分布在轴的上方和下方的两支曲线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
力学中自激振荡的公式
Self-excited oscillation, also known as self-sustained oscillation, is a phenomenon in mechanics where a system oscillates without the need for an external force to drive the motion. 这种现象通常出现在机械、电气或流体系统中,其中能量的回馈机制导致系统对于微小的扰动产生持续的振荡。
Self-excited oscillations are fascinating and complex, often requiring a deep understanding of the system's dynamics and feedback mechanisms to analyze and control. 例如,在机械系统中,自激振荡可能导致零件的磨损或甚至系统的崩溃,因此深入了解这一现象对于系统的稳定性和性能至关重要。
了解自激振荡的机制有助于我们改进设计和控制方法,从而避免潜在的危险和不稳定性。
One of the most well-known examples of self-excited oscillation is the Tacoma Narrows Bridge collapse in 1940, where the bridge began to oscillate violently and eventually collapsed due to aeroelastic flutter. 在这种情况下,风的作用引起了桥梁的自激振荡,最终导致了桥梁的毁坏。
这种现象引起了人们对结构动力学和流体力学相互作用的深入探讨,以避免类似事件的再次发生。
自激振荡的研究还广泛应用于振荡器、电路和混沌系统等领域,为我们理解和控制复杂系统的动力学性质
提供了重要参考。
通过研究自激振荡现象,我们可以深入了解系统的稳定性、频率响应和模态分析,从而更好地设计和优化系统。
The mathematical formulation of self-excited oscillation typically involves solving differential equations that describe the dynamic behavior of the system under consideration. 通过分析系统的惯性、阻
尼和弹性特性,我们可以建立合适的数学模型,并通过求解这些微分方程来预测系统的振动行为。
这种建模方法在工程实践中经常被使用,以评估系统的稳定性和动态性能。
除了传统的数学建模方法,现代仿真工具和计算技
术也为我们研究自激振荡提供了强大的工具。
通过使用计算机模拟和虚拟实验,我们可以更快地获取系统的动态特性和相应参数,从而优化设计和控制策略。
In the field of mechanical engineering, self-excited oscillation is a critical issue in the design and analysis of rotating machinery, such as turbines, compressors, and pumps. 自激振荡可能导致旋转机械系统的不稳定性和振动,进而影响系统的性能和寿命。
通过对系统进行振动分析和模态测试,工程师可以识别潜在的自激振荡问题,并采取相应的控制措施来避免系统的失效。
工程实践中的成功故事表明,通过深入了解自激振荡的机制和动态特性,我们可以设计出更稳定、更可靠的机械系统,为各种应用场景提供优质的解决方案。
From a control engineering perspective, self-excited oscillation poses a challenging problem in the design of control systems that can effectively suppress or mitigate the oscillations. 控制系统的设计与调整对于遏制自激振荡至关重要,通过合适的控制策略和反馈机制,我们可以调节系统的动态响应,降低振动幅度,提高系统的稳定性。
在实际应用中,控制系统的设计必须考虑系统的动力学性质和自激振荡的特点,以确保系统能够在各种工作条件下都能保持稳定。
控制工程师通过模拟、实验和优化方法,不断改进控制系统的性能,为工程领域的发展和创新提供技术支持。
In conclusion, self-excited oscillation is a complex and intriguing phenomenon that occurs in various mechanical, electrical, and fluid systems. 了解自激振荡的机理和数学建模方法对我们设计和控制系统具有
重要意义,有助于避免系统的不稳定和失效。
通过深入研究自激振荡的特性,我们可以优化系统的性能,降低系统的振动幅度,提高系统的稳定性和可靠性。
借助先进的仿真工具和计算技术,我们可以更好地理解和预测系统的动态行为,为工程实践和科学研究提供有力支持。
通过跨学科的合作和不懈的努力,我们可以更好地理解自激振荡现象的本质,为创新和发展提供更广阔的空间。
