离散系统稳态误差计算
合集下载
则可用z变换的终值定理求出采样瞬时的稳态误差
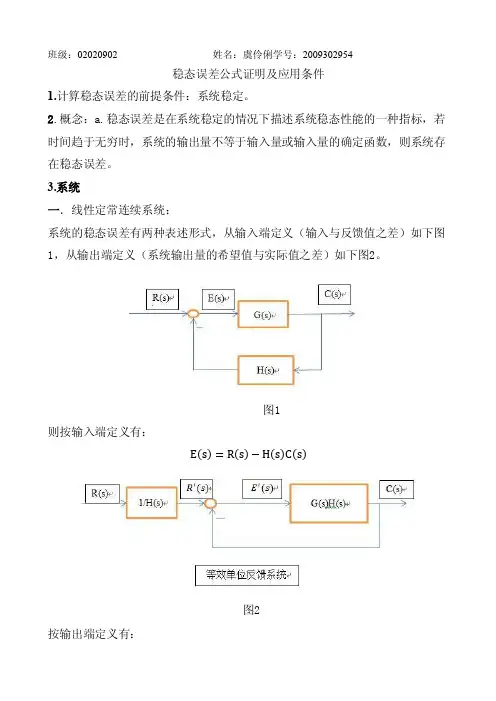
班级：02020902 姓名：虞伶俐学号：2009302954稳态误差公式证明及应用条件1.计算稳态误差的前提条件：系统稳定。
2.概念：a.稳态误差是在系统稳定的情况下描述系统稳态性能的一种指标，若时间趋于无穷时，系统的输出量不等于输入量或输入量的确定函数，则系统存在稳态误差。
3.系统一．线性定常连续系统：系统的稳态误差有两种表述形式，从输入端定义（输入与反馈值之差）如下图1，从输出端定义（系统输出量的希望值与实际值之差）如下图2。
图1则按输入端定义有：E s=R s−H s C s图2按输出端定义有：E,s=R′s−C s=E(s) H(s)由于按输入端与按输出端定义存在：E,s=E(s) H(s)因此下面仅讨论按输入端定义的误差。
证明过程：误差的时域表达式为：e t=L−1E s=L−1Φe(s)R s 系统误差传递函数为：Φe s=E sR s=11+G s H s误差信号e t包含瞬时分量e ts(t)和稳态分量e ss(t)两部分。
由于系统必须稳定，故当时间趋于无穷时，必有e ts(t)趋于零。
因而控制系统的稳态误差定义为误差信号e t的稳态分量e ss(∞)。
针对不同的输入有如下两种情况：a)在线性定常连续系统中对于在阶跃函数、斜坡函数或加速度函数或者它们的组合函数作用下的系统，如果有理函数s E s除在原点处有唯一的极点外，在s 右半平面及虚轴上解析，则可用拉氏变换的终值定理得：e ss∞=lims→0sE s=lims→0sR(s)1+G s H s在一般情况下设分子阶次为m，分母阶次为n的开环传递函数可表示为：G s H s=Kτi s+1mi=1s v T j s+1n−vj=1令G0s H0s=τi s+1 mi=1T j s+1 n−vj=1则G s H s=Ks vG0s H0s又e ss∞=lims→0sE s 所以e ss∞=lims→0sE s=lims→0s v+1R sK+lims→0s v当R s=R se ss∞=R1+lims→0G(s)H(s)=R1+K p当R s=R s2e ss∞=Rlims→0sG(s)H(s)=RK v当R s=R s3e ss∞=Rlims→0s2G(s)H(s)=RK a综上得表1（其稳态误差可用静态误差系数来表示）。
7-5离散系统的稳定性和稳态误差
(T − 1 + e − T ) z + (1 − e − T − Te − T ) = K ( z − 1)( z − e −T )
T =1
=
0.368 K ( z + 0.718 ) ( z − 1)( z − 0.368 )
Φ( z ) =
G( z ) 0.368 K ( z + 0.718 ) = 2 1 + G ( z ) z + ( 0.368 K − 1.368 ) z + ( 0.264 K + 0.368 )
例.设有零阶保持器的离散系统如下图所示，试求： 设有零阶保持器的离散系统如下图所示，试求： 1)当采样周期 分别为1s 0.5s时 1s和 1)当采样周期 T 分别为1s和0.5s时，系统的临界开环增益 K c 2)当 2)当 r (t ) = 1( t ) ，K = 1 ，T 分别为 0.1s,1s,2 s,4 s 时，系 统的输出响应 c (kT ) 。
1 = (1 − z ) K ⋅ Z 2 s ( s + 1) ( z − 1) K 1 1 1 ( z − 1) K = ⋅ Z 2 − + = z s s + 1 z s
−1
Tz z z ⋅ − + ( z − 1) 2 z − 1 z − e −T
1 ( z − 1)( z − 0.368) Φ e ( z) = = 2 1 + G ( z ) z − 0.736 z + 0.368
z1 = 0.368 + j 0.482 z2 = 0.368 − j 0.382
系统稳定，应用终值定理 系统稳定， 求稳态误差
自动控制原理胡寿松第七章解析
1、线性定理 齐次性 Z [ae (t)] aE(z ) Z[e1 (t) e 2 (t)] E1 (z ) E 2 (z ) 叠加性 2、实数位移定理
Z[e(t- kT )] z -k E(z)
Z [e(t kT)] z k [E(z)- e(nT)z -n ]
n 0
k -1
z变换实际上是采样函数拉氏变换的变形，
因此又称为采样拉氏变换
z变换只适用于离散函数，或者说只能表征
连续函数在采样时刻的特性，而不能反映其 在采样时刻之间的特性。
24
成都信息工程学院控制工程系
第七章 线性离散系统的分析与校正
25
成都信息工程学院控制工程系
第七章 线性离散系统的分析与校正
二、Z变换的性质
0T
*
采样器可以用一个周期性闭合的采样开关S来表示。
理想采样开关S： T (t ) (t nT )
n 0
11
成都信息工程学院控制工程系
第七章 线性离散系统的分析与校正
理想单位脉冲序列 采样过程可以看成是一个幅值调制过程。
12
成都信息工程学院控制工程系
第七章 线性离散系统的分析与校正
1 jns t T ( t ) e T n -
1 jns t * 代入采样信号表达式：e ( t ) e( t ) T (t ) e( t )e T n
对采样信号表达式取拉氏变换： 1 E* (s) E(s jns ) T n 采样信号的付氏变换： 1 E* ( j ) E[j( ns )] T n
T (t)的付氏级数形式：
T (t)
n -
(t - nT) C e
稳态误差计算(普通解法)
⎡ K ⎤ 1 ⎤ ⎡1 G( z) = Z ⎢ = KZ ⎢ − ⎥ ⎣ s s + 1⎥ ⎦ ⎣ s ( s + 1) ⎦
z ⎛ z =K⎜ − −T ⎝ z −1 z − e
系统特征方程为
图 6-21 离散系统结构图
K (1 − e−T ) z ⎞ = ⎟ −T ⎠ ( z − 1)( z − e )
D( z ) = ( z − 1)( z − e −T ) + K (1 − e −T ) z = z 2 + [(1 − e −T ) K − 1 − e −T ]z + e −T = 0
利用朱利稳定判据
⎧ D(1) = K (1 − e −T ) > 0 ⎪ ⎨ −T −T ⎪ ⎩ D(−1) = 2(1 + e ) − K (1 − e ) > 0
e(∞) = lim
z →1
( z − 1)( z − 0.368) =0 z 2 − 0.736 z + 0.368
2
当 r (t ) = t ，相应 r (nT ) = nT 时， R ( z ) = T z ( z − 1) ，于是由式(6-59)求得
e(∞) = lim
z →1
T ( z − 0.368) = T =1 z − 0.736 z + 0.368
G( z) =
e − T z + 1 − 2e − T 0.368 z + 0.264 = 2 −T ( z − 1)( z − e ) T =1 z − 1.368 z + 0.368
2
0.368 z + 0.264 →∞ z − 1.368 z + 0.368 0.368 z + 0.264 =1 K v = lim( z − 1) 2 z →1 z − 1.368 z + 0.368 K p = lim
培训_75离散系统的稳定性和稳态误差
数
m
1.单位阶跃输入时r(t) 1(t)
K(z zj)
R(z) z z 1
G(z)
j 1 nv
(z 1)v (z pi )
z 1 R(z)
z 1 1
z
ess
lim
z 1
z
lim
1 G(z) z1
z
1 G(z) z 1
i 1
对0型系统：K p
lim[1 G(z)],
z 1
对Ⅰ型系统：K p , ess 0
1 ess K p
对Ⅱ型及以上系统：K p , ess 0
0型系统在单位阶跃信号作用下存在位置 误差，I型及以上系统在单位阶跃信号作用下 不存在稳态误差。
2.单位斜坡输入时 r(t) t
R(z)
Tz (z 1)2
| z | eT , z T
j
ω sT/2 0
z平面
ω 1T -ω 1T
s平面上的等ω垂线，映射到z平面上的
轨迹是以原点出发的射线，相角z为 T
3. 等 线映射
j
j
β 2ω s
ωs 4
s tan j
ωs 0
ωs 2
ωs
ω s=0
0
3ω s
z esT e( tan j)T
0
加速度误 差
∞
∞ 1 Ka 0
m
K(z zj)
G(z)
j 1 nv
(z 1)v (z pi )
i 1
ess
lim
z 1
z
1 R(z) z 1 G(z)
第七节 离散系统的稳定性分析
离散系统如上图所示，则
E(z) R(z) 1 Go (z)
若闭环系统稳定，则由终值定理
ess
lim e(k)
k
lim (z
z 1
1) E ( z )
lim (z
z 1
1) R(z) 1 Go (z)
将离散系统仿照连续系统分为0、1、2型：
若系统开环脉冲传递函数G0 (z)中含有 i(i=0,1,2)个|z|=1的极点，则系统称为i型
第七节 离散系统的稳定性分析
如上节所讲，采样会破坏系统的稳定性，所 以在设计采样系统时最先考虑的是稳定性。 对采样系统稳定性分析主要建立在Z变换的 基础上。
连续系统的稳定性
连续系统稳定
所有特征根均具有负实部
方法：劳斯判据,Hurwitz判据及奈氏判据。
在分析采样系统时，可以利用Z变换与拉氏变 换数学上的关系，找到Z平面与S平面之间的周 期映射关系，从而利用原有的各种判据来分析
0
2型
0
2 r(t)=t*1(t)时
静态速度误差系数
R(z)
Tz (z 1)2
, ess
lim [(z
z1
1) 1 1 Go(z)
Tz (z 1)2
]
T
lim z1 (z
1 1)Go ( z)
若定义KV
1 T
lim (z 1)Go (z)
z 1
，则ess
1 Kv
Kv
ess
0型
0
1型 2型
Bode Diagrams
50 40 30 20 10
Phase (deg); Magnitude (dB)
-100 -120 -140 -160
自动控制原理 第七章 第二讲 离散系统的稳定性分析
R(s)
—
1 − e −Ts s
K s( s + 1)
C(s)
解：系统的开环传递函数为 Tz 1 (1 − e−T )z G(z) = (1 − z −1 )Z 2 = (1 − z −1 ) − 2 s (s + 1) (z − 1) (z − 1)(z − e−T ) 把T=0.1代入化简得 代入化简得
整理后可得 Routh表为 表为 0.158Kω2+1.264ω+(2.736-0.158K)=0 w2 0.158K 2.736-0.158K w1 1.264 w0 2.736-0.158K
要使系统稳定, 必须使劳斯表中第一列各项大于零, 要使系统稳定 必须使劳斯表中第一列各项大于零 即 0.158K＞0 和 2.736-0.158K＞0 ＞ ＞ 所以使系统稳定的K值范围是 ＜ ＜ 所以使系统稳定的 值范围是0＜K＜17.3。 值范围是 。 结论2： 一定 一定， 越大 系统的稳定性就越差 越大, 稳定性就越差。 结论 ：T一定，K越大 系统的稳定性就越差。
(1) 单位阶跃输入时 r(t)=1(t) (2) 单位斜坡输入时 r(t)=t (3) 单位加速度输入时 r(t)=t2/2
z R( z ) = z −1
z →1
K p = lim[1 + G ( z )]
Tz R( z ) = ( z − 1) 2
K v = lim( z − 1)G ( z )
π T π ω =− 0 T
Im z平平
π j T
ω=
0
σ
π
－1
ω ＝0 1 Re
－jT
2 、离散系统稳定的充要条件： 离散系统稳定的充要条件 稳定的充要条件：
—
1 − e −Ts s
K s( s + 1)
C(s)
解：系统的开环传递函数为 Tz 1 (1 − e−T )z G(z) = (1 − z −1 )Z 2 = (1 − z −1 ) − 2 s (s + 1) (z − 1) (z − 1)(z − e−T ) 把T=0.1代入化简得 代入化简得
整理后可得 Routh表为 表为 0.158Kω2+1.264ω+(2.736-0.158K)=0 w2 0.158K 2.736-0.158K w1 1.264 w0 2.736-0.158K
要使系统稳定, 必须使劳斯表中第一列各项大于零, 要使系统稳定 必须使劳斯表中第一列各项大于零 即 0.158K＞0 和 2.736-0.158K＞0 ＞ ＞ 所以使系统稳定的K值范围是 ＜ ＜ 所以使系统稳定的 值范围是0＜K＜17.3。 值范围是 。 结论2： 一定 一定， 越大 系统的稳定性就越差 越大, 稳定性就越差。 结论 ：T一定，K越大 系统的稳定性就越差。
(1) 单位阶跃输入时 r(t)=1(t) (2) 单位斜坡输入时 r(t)=t (3) 单位加速度输入时 r(t)=t2/2
z R( z ) = z −1
z →1
K p = lim[1 + G ( z )]
Tz R( z ) = ( z − 1) 2
K v = lim( z − 1)G ( z )
π T π ω =− 0 T
Im z平平
π j T
ω=
0
σ
π
－1
ω ＝0 1 Re
－jT
2 、离散系统稳定的充要条件： 离散系统稳定的充要条件 稳定的充要条件：
§7.5离散系统的稳定性与稳态误差)
z eT
z T
图参见P348
§7.5.2 离散系统稳定的充要条件是 z i 1
—— F(z)的全部极点均位于z平面的单位圆内
m
证明：
Φ(z)M(z) D(z)
(zi) n
i1 n
(zj) j1
Cjz
zj
K(z)
j1
n
k
c(k) Cjjk 0
j1
j 1
— 必要性
c*(t)k 0jn 1Cjjk(tkT )
静态加速度误差系数 Kalz i1m (z1)2GH (z)
r(t) t
Tz z (z 1 ) T1 e 2 ( T ) lz 1 i(z m 1 )(z 1 )2z 2 0 .8 z 0 .2 0 .4 2
r(t)t2 2
T 2 z(z 1 ) z(z 1 ) e 3 ( T ) lz i1( m z 1 )2 (z 1 )3z2 0 .8 z 0 .2
2. 静态误差系数法 —— r(t) 作用时e(∞)的计算规律
( 适用于系统稳定, r(t)作用,对误差采样的线性离散系统 )
设 G(H z)ZG (s)H (s)(z 11)vG0H (z)
lz im 1GH 0(z)K
Fe(z)E R((zz))1G1H (z)
e ( ) lz i1(m z 1 )F e(z)R (z)
x1jy
(x1)2y2
ujv
[w] 虚轴
x2 y2 1 u0(x1)2y2 0
x2y2 1 [z] 单位圆
z平面单位圆
内 外
的点
x2
y
2
1 1
u 0
对应w平面
u
0
例１ 已知离散系统特征方程 ，判定系统稳定性。
z T
图参见P348
§7.5.2 离散系统稳定的充要条件是 z i 1
—— F(z)的全部极点均位于z平面的单位圆内
m
证明：
Φ(z)M(z) D(z)
(zi) n
i1 n
(zj) j1
Cjz
zj
K(z)
j1
n
k
c(k) Cjjk 0
j1
j 1
— 必要性
c*(t)k 0jn 1Cjjk(tkT )
静态加速度误差系数 Kalz i1m (z1)2GH (z)
r(t) t
Tz z (z 1 ) T1 e 2 ( T ) lz 1 i(z m 1 )(z 1 )2z 2 0 .8 z 0 .2 0 .4 2
r(t)t2 2
T 2 z(z 1 ) z(z 1 ) e 3 ( T ) lz i1( m z 1 )2 (z 1 )3z2 0 .8 z 0 .2
2. 静态误差系数法 —— r(t) 作用时e(∞)的计算规律
( 适用于系统稳定, r(t)作用,对误差采样的线性离散系统 )
设 G(H z)ZG (s)H (s)(z 11)vG0H (z)
lz im 1GH 0(z)K
Fe(z)E R((zz))1G1H (z)
e ( ) lz i1(m z 1 )F e(z)R (z)
x1jy
(x1)2y2
ujv
[w] 虚轴
x2 y2 1 u0(x1)2y2 0
x2y2 1 [z] 单位圆
z平面单位圆
内 外
的点
x2
y
2
1 1
u 0
对应w平面
u
0
例１ 已知离散系统特征方程 ，判定系统稳定性。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
§6.6.1
一般方法（利用终值定理）（2）
K s 1
例１ 已知离散系统, K=2, T=1; 分别求 r(t)=1(t), t, t2/2 时的e (∞)。 解． Ts
1 1 e G( z ) Z Z s s
K (1 e T ) z ( z 1)( z e T ) v 1 1 ( z 1)( z e T ) Fe ( z ) T K (1 e ) z ( z 1)( z e T ) K (1 e T ) z 1 ( z 1)( z e T )
z 1
设
Fe ( z )
E( z) 1 R( z ) 1 GH ( z )
z 1
e( ) lim ( z 1) F e ( z ) R( z )
lim( z 1) R( z )
z 1
1 1 GH ( z )
§6.6.2
静态误差系数法（2）
e(T ) lim( z 1) F e ( z ) R( z ) lim( z 1) R( z )
§6.6.1
解．
一般方法（利用终值定理）（3）
例１ 已知离散系统, K=2, T=1; 分别求 r(t)=1(t), t, t2/2 时的e (∞)。
0 K 4.33
z 1
e( ) lim( z 1) R( z )F e ( z )
( z 1)( z e T ) Fe ( z ) ( z 1)( z e T ) K (1 e T )z
1 K 2T 2 KT
K 2T 2 KT 1 0
1.618 KT 0.618 6.427 K 2.427
§6.6.2
静态误差系数法（６）
例3 已知采样系统, T=0.25, r(t)=2· 1(t)+t, 使e(∞)<0.5, 求K范围。 解. K 的稳定范围为：
c0 c1 s c2 s 2
cm s m
ci s i
i 0
ess (kT ) c0r(kT ) c1r(kT ) c2r (kT )
cmr ( m ) (kT )
§6.6.3
动态误差系数法（2）
e T z (1 2e T ) 例4 单位反馈离散系统的开环脉冲传递函数 G( z ) ( z 1)( z e T )
(3) z域中的根轨迹法
自动控制原理
（第 34 讲）
§6 线性离散系统的分析与校正
§6.1 §6.2 §6.3 §6.4 §6.5 §6.6 §6.7 §6.8 §6.9 离散系统 信号采样与保持 Z 变换 离散系统的数学模型 稳定性分析 稳态误差计算 动态性能分析 离散系统的模拟化校正 离散系统的数字校正
* F* ( s ) F e e ( z ) z eTs
Φe (0)
1 1 2 Φ (0) s Φ (0) s e e 1! 2!
( m 0, 1, 2,
1 (m) Φe (0) s m m!
) （动态误差系数）
1 d m F* e ( s) cm m ! ds m s 0
e( )
AT 2T Kv K
— 与 T 有关
有ZOH时
(T 1 e T ) z (1 e T TeT ) K ( z 1)(z e T )
v 1
K (T Te T ) K v lim( z 1)G( z ) lim KT z 1 z 1 z e T
T 1
es (20) 20.5
§6.7
动态性能分析（1）
(z z ) (z p )
k 1 k i 1 n i m
6.7.1 闭环极点分布与动态响应
M ( z ) bm F( z ) D( z ) a n
C ( z ) F( z ) R( z )
mn
M (z) z D( z ) z 1 n c z M (1) z k D(1) z 1 k 1 z pk
z 1
r (t ) A t
AT ATz 1 AT e(T ) lim ( z 1) z 1 ( z 1) 2 1 GH ( z ) lim( z 1) GH ( z ) Kv z 1
静态速度误差系数
2
K v lim ( z 1) GH ( z )
AT A 2 e( ) Kv K K
— 与 T 无关
§6.6.2
静态误差系数法（5）
例3 已知采样系统, T=0.25, r(t)=2· 1(t)+t, 使e(∞)<0.5, 求K范围。 解. 系统稳定条件：
1 e Ts Ke 2Ts G( z ) Z s s 0 0 K D(1) KT KT Tz 2 z 1 1 2 1 2 2.472 D(1) K 2 KT 0 Z K 22 T Kz 8 (1 z )z 2 K 0 z ( z 1) z ( z 1) s KT 1 3 K0 1 T 4 D ( z ) z z 2 KT
G( z ) Z v 1 T s ( s 1 ) ( z 1 )( z e ) 无ZOH时 K (1 e T ) z K v lim ( z 1)G( z ) lim K T z 1 z 1 (z e )
1 e Ts K z 1 1 G( z ) Z Z 2 K s s ( s 1 ) z s ( s 1)
采样周期T=1, r(t)=t2/2, 求t=20时的动态误差es(20)=?
1 ( z 1)( z e T ) 解. F e ( z ) 1 G( z ) ( z 1)( z e T ) e T z (1 2e T )
z 2 1.386z 0.386 e 2 s 1.386e s 0.386 2 e 2 s e s 0.632 z z 0.632 2 * t c0 Fe (0) 0 r (t ) 2 d * c1 Fe ( s) s0 1 r ( t ) t ds 1 d2 * 1 c2 Fe ( s) s0 r ( t ) 1 2 2! ds 2 es (kT ) c0r (kT ) c1r (kT ) c2r (kT ) t 1 2
自动控制原理
自动控制原理
本次课程作业
(34)
6 — 14, 15, 16 6 — 17（选做）
课程回顾 §6.5 离散系统的稳定性分析
§6.5.1 s →z →w 映射
§6.5.2 离散系统稳定的充要条件
— F(z)的全部极点均位于z平面的单位圆内
§6.5.3 离散系统的稳定判据
(1) w域中的劳斯(Routh)稳定判据 (2) z域中的朱利 (Jurry) 稳定判据
z ( z 1)( z e T ) z 1) 0 r1 ( t ) 1(t ) e1 () lim( T T z 1 z 1 ( z 1)( z e ) K (1 e )z
r2 (t ) t
t2 r3 ( t ) 2
Tz ( z 1)( z e T ) T e2 () lim( z 1) 2 T T z 1 ( z 1) ( z 1)( z e ) K (1 e )z K Tz( z 1) ( z 1)( z e T ) e3 () lim( z 1) 3 T T z 1 2( z 1) ( z 1)( z e ) K (1 e )z
0 K 2.472
1 e Ts Ke 2Ts G( z ) Z s s Tz KT 2 z 1 1 2 1 2 K (1 z ) z Z 2 Kz 2 z ( z 1) z ( z 1) s KT K v lim ( z 1)G( z ) lim ( z 1) 2 KT z 1 z 1 z ( z 1) r1 (t ) 2 1(t ) e1 () 0
z 1
2
1 AT A 2 e(T ) lim( z 1) AT z( z 1) r (t ) t 3 2 z 1 2 ( z 1 ) 1 GH ( z ) lim ( z 1 ) GH ( z ) 2 z 1
AT 2 Ka
静态加速度误差系数 K a lim ( z 1)2 GH ( z )
z 1 z 1
1 1 GH ( z )
( z 1) r ( t ) A 1( t ) e(T ) lim z 1
静态位置误差系数
Az 1 A z 1 1 GH ( z ) 1 lim GH ( z )
z 1
A 1 K p
K p lim GH ( z )
z 1
§6.6.2
1 GH ( z ) ( z 1)v GH 0 ( z ) lim 静态误差系数法（ 3 ）GH 0 ( z ) K 1 z
§6.6.2
静态误差系数法（4）
例2 稳定离散系统的结构图如图 所示，已知r(t)=2t, 试讨论 有或没有ZOH 时的e(∞)。 解． K K (1 e T )z
自动控制原理
（第 34 讲）
§6 线性离散系统的分析与校正
§6.6 稳态误差计算 §6.7 动态性能分析
§6.6.1
一般方法（利用终值定理）（1）
§6.6.1 一般方法（利用终值定理）
设
1 GH ( z ) Z G( s ) H ( s ) GH0 ( z ) v ( z 1) lim GH 0 ( z ) K