6.内模控制
第1章过程控制系统概述习题与思考题

第1章 过程控制系统概述习题与思考题1.1 什么是过程控制系统,它有那些特点?1.2 过程控制的目的有那些?1.3 过程控制系统由哪些环节组成的,各有什么作用?过程控制系统有那些分类方法?1.4 图1.11是一反应器温度控制系统示意图。
A 、B 两种物料进入反应器进行反应,通过改变进入夹套的冷却水流量来控制反应器的温度保持不变。
试画出该温度控制系统的方框图,并指出该控制系统中的被控过程、被控参数、控制参数及可能影响被控参数变化的扰动有哪些?1.5 锅炉是化工、炼油等企业中常见的主要设备。
汽包水位是影响蒸汽质量及锅炉安全的一个十分重要的参数。
水位过高,会使蒸汽带液,降低了蒸汽的质量和产量,甚至会损坏后续设备;而水位过低,轻则影响汽液平衡,重则烧干锅炉甚至引起爆炸。
因此,必须对汽包水位进行严格控制。
图1.12是一类简单锅炉汽包水位控制示意图,要求:1)画出该控制系统方框图。
2)指出该控制系统中的被控过程、被控参数、控制参数和扰动参数各是什么。
3)当蒸汽负荷突然增加,试分析该系统是如何实现自动控制的。
V-1图1.12 锅炉汽包水位控制示意图1.6 评价过程控制系统的衰减振荡过渡过程的品质指标有那些?有那些因素影响这些指标?1.7 为什么说研究过程控制系统的动态特性比研究其静态特性更意义?1.8 某反应器工艺规定操作温度为800 10℃。
为确保生产安全,控制中温度最高不得超过850℃。
现运行的温度控制系统在最大阶跃扰动下的过渡过程曲线如图1.13所示。
1)分别求出稳态误差、衰减比和过渡过程时间。
2)说明此温度控制系统是否已满足工艺要求。
T/℃图1.13 某反应器温度控制系统过渡过程曲线1.9 简述过程控制技术的发展。
1.10 过程控制系统与运动控制系统有何区别?过程控制的任务是什么?设计过程 控制系统时应注意哪些问题?第3章 过程执行器习题与思考题3.1 试简述气动和电动执行机构的特点。
3.2 调节阀的结构形式有哪些?3.3 阀门定位器有何作用?3.4 调节阀的理想流量特性有哪些?实际工作时特性有何变化?3.5 已知阀的最大流量min v q =50m 3,可调范围R=30。
神经网络与模糊控制考试题及答案

一、填空题1、模糊控制器由模糊化接口、解模糊接口、知识库和模糊推理机组成2、一个单神经元的输入是1.0 ,其权值是1。
5,阀值是—2,则其激活函数的净输入是-0。
5 ,当激活函数是阶跃函数,则神经元的输出是 13、神经网络的学习方式有导师监督学习、无导师监督学习和灌输式学习4、清晰化化的方法有三种:平均最大隶属度法、最大隶属度取最小/最大值法和中位数法,加权平均法5、模糊控制规则的建立有多种方法,是:基于专家经验和控制知识、基于操作人员的实际控制过程和基于过程的模糊模型,基于学习6、神经网络控制的结构归结为神经网络监督控制、神经网络直接逆动态控制、神网自适应控制、神网自适应评判控制、神网内模控制、神网预测控制六类7.傅京逊首次提出智能控制的概念,并归纳出的3种类型智能控制系统是、和.7、人作为控制器的控制系统、人机结合作为控制器的控制系统、无人参与的自主控制系统8、智能控制主要解决传统控制难以解决的复杂系统的控制问题,其研究的对象具备的3个特点为、和。
8、不确定性、高度的非线性、复杂的任务要求9.智能控制系统的主要类型有、、、、和。
9、分级递阶控制系统,专家控制系统,神经控制系统,模糊控制系统,学习控制系统,集成或者(复合)混合控制系统10.智能控制的不确定性的模型包括两类:(1);(2) 。
10、(1)模型未知或知之甚少;(2)模型的结构和参数可能在很大范围内变化。
11.控制论的三要素是:信息、反馈和控制。
12.建立一个实用的专家系统的步骤包括三个方面的设计,它们分别是、和。
知识库的设计推理机的设计人机接口的设计13.专家系统的核心组成部分为和.知识库、推理机14.专家系统中的知识库包括了3类知识,它们分别为、、和。
判断性规则控制性规则数据15.专家系统的推理机可采用的3种推理方式为推理、和推理。
15、正向推理、反向推理和双向推理16.根据专家控制器在控制系统中的功能,其可分为和。
16、直接型专家控制器、间接型专家控制器17.普通集合可用函数表示,模糊集合可用函数表示。
过程控制工程名词解释

过程控制工程名词解释过程控制:针对温度、压力(差压)、流量、液位(物位)、成分和物性等过程参数的控制。
(P13)系统:实现某一目标的完整体系,将环境对它的影响和它对环境的影响分离出来。
被控对象(过程):被控制的生产设备或装置。
被控过程既包括运行中的设备与生产关系,也反映其输入输出动态关系。
(P3)测量变送器:用于测量被控变量,并按一定的规律将其转换为标准信号作为输出。
执行器:常用的是控制阀。
它接受来自控制器的命令信号u,用于自动改变控制阀的开度。
控制器(调节器):它将被控变量的测量值与设定值进行比较,得出偏差信号e(t),并按一定的规律给出控制信号u(t)。
被控变量(受控变量、过程变量):被控对象需要维持在其理想值的工艺变量。
(P4)等于工艺介质加工艺部位加工艺参数。
设定值(给定值):被控变量要求达到的期望值。
控制变量:控制器的输出电信号。
操作变量(操纵变量):通常是指由执行器控制的某一工艺变量。
扰动变量:任何导致被控变量偏离其设定值的输入变量。
广义对象:为了简化控制系统的分析和设计,常把执行机构、被控对象和测量变送环节合并起来考虑,作为一个广义对象。
(P38)正反作用:当被控变量的测量值增大时,控制器的输出也增大,则该控制器为“正作用”;否则,当测量值增大时,控制器输出反而减少,则该控制器为“反作用”。
串级控制:一个控制器的输出用来改变另一个控制器的设定值。
(P86)主控制器:接受主变量的误差,输出到副控制器设定值的控制器。
副控制器:接受副变量的误差,输出到执行机构的控制器。
(液位)均匀控制(平均液位控制):控制目标是使操作变量(如储罐输出流量)尽可能平缓,以减少对下游装置的干扰,而允许贮罐液位在上下限之间波动。
积分饱和:当调节能力不足时,控制器内部状态超出正常工作范围。
而当主要干扰消除后,控制器内部状态首先需要返回至正常工作范围,然后控制器才真正开始起调节作用。
不完全微分PID:由于微分对高频噪声有放大作用,所以在具体实现时一般不用理想微分,而是在PID算式中加一个一阶低通滤波器(惯性环节)。
内模控制
然后在反馈和输人通道上增加反馈滤波器
和输人滤波器
,通过调整滤波器的结构和参数,使系统获得所期望的性能。 下面就对开环稳定过程进行离散内模控制器设计。
考虑一般情况,令被控对象为有纯滞后的非最小相位过程,则过
程模型可分解为两部分:
控制器取为: 设计时为保持闭环系统零稳态偏差特性,需满足:
可实现因子可取为:
经输人滤波器
后再送至控制器。
经柔化后的输人参考轨迹的一般形式为:
即
第4章 内模控制 4.6 简化模型预测控制(SMPC) 内模控制是一种极具理论价值的基于模型的控制策略,但其工程实
现因涉及模型求逆和滤波器合理设计等问题,设计过程较为复杂,尤
其是对于多输人多输出过程,实施难度更大。 1987年以后,Arulalan等人提出了一种简化模型预测控制(SMPC),其
对象输入为:
闭环系统输出为:
闭环系统误差为:
其中:
第4章 内模控制
对于模型无差,即 em (s) 的 0特殊情况,上式可简化为:
以上两式表明:对于无模型失配的情形,闭环传递函数
除了
中必须包含所有的滞后和右半
平面零点,且 必须有足够的阶次来避免物理上的不可实
现外,其他都是可以任意选择的。因此,闭环响应可以直接设
第4章 内模控制 4.3.3 设计示例
4.3.3.1 一阶加纯滞后过程
4.3.3.2 高阶过程
情形A.无右半平面(RHP)零点
情形B.具有右半平面(RHP)零点
第4章 内模控制
4.4 内模控制器设计——离散过程
当过程模型采用离散脉冲传递函数形式时,内模控制系统的性质仍
然成立。在离散时间条件下,设计内模控制器也仍然分为两步进行: 首先是设计一个稳定的理想控制器;
内模控制

第二章 基本概念............................................................................................................. 4
2.1、 鲁棒性与鲁棒控制 .......................................................................................... 4
3.2、前馈控制器 Q 的设计 ....................................................................................... 9
3.3、反馈滤波器 F................................................................................................... 10
1.2、发展现状
经过十多年的发展,IMC 方法不仅已扩展到了多变量和非线性系统,还产生了 多种设计方法,较典型的有零极点对消法、预测控制法、针对 PID 控制器设计的 IMC 法、有限拍法等。IMC 与其他控制方法的结合也是很容易的,如自适应 IMC,采用 模糊决策、仿人控制、神经网络的智能型 IMC 等.值得注意的是,目前已经证明,已 成功应用于大量工业过程的各类预测控制算法本质上都属于 IMC 类,在其等效的 IMC 结构中特殊之处只是其给定输入采用了未来的超前值(预检控制系统),这不仅 可以从结构上说明预测控制为何具有良好的性能,而且为其进一步的深入分析和改 进提供了有力的工具。
内模控制器设计 : 摘 要 将内模控制器和传统的 Smith 控制器进行比较对照,总体论述内模控
小转动惯量永磁同步电机电流环内模控制

0000 ; 0000 收稿日期: 2009收修定稿日期: 2009基金项目: 国家 985 工程资助项目( 0000 - 07204 ) ; 福建省自然科学基金计划资助项目( 2010J05141 ) ), ), 作者简介: 蒋学程( 1979男, 福建长乐人, 博士, 主要研究方向为永磁同步电机伺服系统运动控制等; 彭侠夫( 1963男, 教授, 博士生 导师。
1 ) s + ( s + B / J) ( KP s + KI ) Tm
Fig. 2
图 2 转矩电流环模型 Model of torque current loop
本文讨论的永磁同步电机为面装式永磁同步电 机,模型为 理 想 情 况 下 同 步 旋 转 坐 标 Park 模 型, 坐标变换约束条件为功率不变性 。 图中,B 为粘滞系数, R 为绕组电阻, L 为交 直轴电感,i d 为励磁电流, i q 电磁转矩电流, J 为 转动惯量,ω r 为转子电角速度,ω Ω 为机械角速度, ψ f 为转子磁链, P n 为极对数, T PWM 为逆变器时间 常数。 一般永磁同步电机系统采用 i d = 0 的矢量解耦 控制方法,在 i d = 0 下,电机转矩电流为 uq - ωr ψf iq = R + Ls 电机机械运动方程为 Pn ψf iq - TL ωr = Pn Js + B
2011 年5 月 第18 卷第3 期
7848 ( 2011 ) 03033104 文章编号: 1671-
控 制 工 程 Control Engineering of China
May 2 0 1 1 Vol. 18 , No. 3
小转动惯量永磁同步电机电流环内模控制
1, 2 1 蒋学程 ,彭侠夫
过程控制工程智慧树知到答案章节测试2023年中国石油大学(华东)

第一章测试1.广义对象包括()。
A:被控对象B:检测元件C:执行器D:控制器答案:ABC2.先进控制有()。
A:时滞补偿B:故障诊断C:预测控制D:解耦控制答案:ABCD3.过程控制系统中,代替人眼睛的是()。
A:执行器B:控制器C:检测装置D:被控对象答案:C4.控制系统组成中具有大脑功能的是()。
A:控制装置B:检测装置C:执行机构D:被控对象答案:A5.控制目标中不需要考虑环保因素。
A:对B:错答案:B6.随动控制系统的设定值是随时间变化的。
A:对B:错答案:A第二章测试1.被控对象的动态特性是描述被控对象输入输出关系动态特征的。
A:错B:对答案:B2.稳态指的是被控量不再随时间变化时,系统处于平衡状态。
A:对B:错答案:A3.误差绝对值积分(IAE)准则可避免正负积分面积相消现象。
A:对B:错答案:A4.灰箱模型是基于过程动态学的机理建模。
A:对B:错答案:B5.调节通道对象特性的T0小对控制系统有利。
A:错B:对答案:B6.比例积分作用为系统增加了一个开环零点,使系统相角超前,增加了稳定性。
A:错B:对答案:B7.调节系统在纯比作用下已整定好,加入积分作用后,为保证原稳定度,此时应将比例度()A:减小B:不变C:增大D:先增大后减小答案:C8.对于气动执行机构,当信号压力增加,推杆下移的,称该气动执行机构为A:可调式B:反作用式C:正作用式D:移动式答案:C9.在控制系统中,工艺变量需要控制的生产过程、设备或机械等,称为()A:反馈B:控制器C:被控过程D:设定值答案:C10.下面对过程的控制质量没有影响的是()A:扰动通道放大倍数B:扰动通道时间常数C:控制通道放大倍数D:扰动通道纯滞后时间答案:D11.过渡过程品质指标中,余差表示()A:新稳态值与给定值之差B:测量值与给定值之差C:超调量与给定值之差D:调节参数与被调参数之差答案:A12.下列哪个参数不是描述对象特性的参数()A:tB:TC:KD:τ答案:A13.受控制器的操纵,使被控变量保持在设定值的物理量是()A:操纵变量B:被控对象C:设定值D:测量值答案:A14.在阶跃扰动作用下,过程控制系统的过渡过程出现的形式如下,()是一种稳定控制系统A:非振荡发散过程B:衰减振荡过程C:发散振荡过程D:等幅振荡过程答案:B15.以下哪个传递函数可以表示积分环节()A:TsB:KC:K/(Ts)D:K/(Ts+1)答案:C16.PID参数整定方法有()A:响应曲线法B:临界比例度法C:继电器型PID自整定法D:经验法答案:ABCD第三章测试1.下列哪种不属于复杂控制系统?A:流量控制系统B:前馈控制系统C:串级控制系统D:解耦控制系统答案:A2.串级控制对所有的干扰都有很强的克服能力A:对B:错答案:B3.串级控制副参数的选择需要注意的问题有()?A:副参数必须可测B:调节阀与副参数之间具有因果关系C:尽可能将带有非线性或时变特性的环节包含于副回路中D:副参数的选择应使副对象的时间常数比主对象的时间常数小答案:ABCD4.串级控制多用于()场合?A:用于所有的控制场合;B:用于时滞较大的对象;C:用于对象具有较大的非线性特性,且负荷变化较大;D:用于克服变化剧烈和幅值大的干扰;答案:BCD5.均匀控制有()两种形式?A:前馈均匀控制B:单回路均匀控制C:串级均匀控制D:比值均匀控制答案:BC6.前馈控制的基本原理是()?A:可变性原理B:等价原理C:不变性原理D:抗干扰原理答案:C7.动态前馈的效果一定比静态前馈的效果好。
内模控制.ppt

内模控制的主要性质
2.理想控制器特性
当模型是准确的,且模型稳定,若设计控制器
使
GIMC
(s)
1 Gp (s)
,且 1 存在并可实现
Gp (s)
则,控制器具有理想控制器特性,即在所有时间 内和任何干扰作用下,系统输出都等于输入设定 值,保证对参考输入的无偏差跟踪。
内模控制的主要性质
3.零稳态偏差特性
Gˆ p Gˆ pGˆ p-
式中,Gˆ p 包含了所有的纯滞后和右半平面的零点,并 规定其静态增益为1。Gˆ p 为过程模型的最小相位部分。
步骤2 设计控制器
1 GIMC(s) Gˆ p (s) f (s)
这里 f 为IMC滤波器。选择滤波器的形式,以保证
内模控制器为真分式。
对于阶跃输入信号,可以确定Ⅰ型IMC滤波器的形式
其反馈信号
Dˆ (s) [Gp(s) Gˆp(s)]U(s) D(s) 0 ——内模控制系统具有开环结构。
内模控制的主要性质
1.对偶稳定性 若模型是准确的,则IMC系统内部稳定的充要
条件是过程与控制器都是稳定的。 所以,IMC系统闭环稳定性只取决于前向通
道的各环节自身的稳定性。 结论:对于开环不稳定系统,在使用IMC之
R(s)
GIMC(s) U(s)
Dˆ (s)
Gp (s)
D(s)
Y (s)
Gˆ p ( s)
Ym (s)
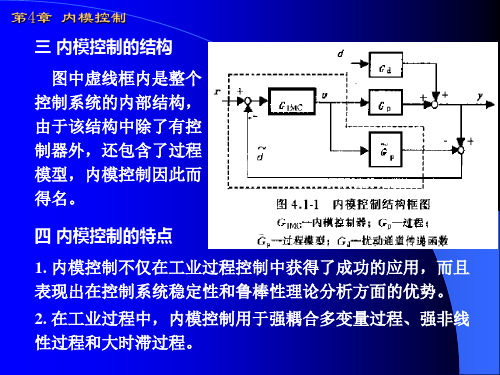
图6-1 内模控制结构框图
Gp (s) ——实际对象; Gˆ p(s) ——对象模型;
R(s) ——给定值;
Y (s) ——系统输出;
内模控制器的设计思路是从 理想控制器出发,然后考虑 了某些实际存在的约束,再 回到实际控制器的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
这里 f 为IMC滤波器。选择滤波器的形式,以保证 内模控制器为真分式。
对于阶跃输入信号,可以确定Ⅰ型IMC滤波器的形式
1 f ( s) (Tf s 1)r
对于斜坡输入信号,可以确定Ⅱ型IMC滤波器的形式为
rTf s 1 f ( s) (Tf s 1)r
Tf ——滤波器时间常数。
4.采用理想控制器构成的系统,对模型误差极为敏感,鲁棒性、 稳定性变差。
2. 内模控制器的设计
步骤1 因式分解过程模型
ˆ G ˆ G ˆ G p p pˆ 包含了所有的纯滞后和右半平面的零点,并 式中,G p ˆ 为过程模型的最小相位部分。 规定其静态增益为1。G p
步骤2 设计控制器
GIMC ( s ) 1 ˆ ( s) G p f ( s)
过程无扰动Leabharlann 图6-3过程有扰动
例3-2 考虑实际过程为
R( s)
D( s)
10s 1 5s 1
1 G( s) e 10 s 10s 1
1 10 s 1
e
10 s
Y (s)
1 e 8s 10s 1
内部模型为
ˆ ( s) G 1 e8 s 10s 1
讨论(1)当 K 1 , T 2 , 1 时,滤波时间常数取不同值 时,系统的输出情况。(2)当 K 1 , T 2 ,由于外界干扰 使 由1变为1.3,取 Tf 不同值时,系统的输出情况。
1~4曲线分别为 Tf 取0.1、0.5、1.2、2.5时,系统的输 出曲线。
图6-2
2.若对象含有s平面右半平面( RHP)零点,
ˆ 1 ( s) 中含有RHP极点,控制器本身不稳定,闭 则 GIMC (s) G p 环系统不稳定。
3.若对象模型严格有理,
ˆ 1 ( s) 非有理,即 lim GIMC (s) 则 GIMC (s) G p s 0 GIMC (s) 中将出现N阶微分器,对过程测量信号中的噪声极 为敏感,不切实际。
Gc ( s )
GIMC ( s )
Gp ( s )
Y (s)
ˆ (s) G p
图中虚线方 框为等效的 一般反馈控 制器结构
图3-2内模控制的等效变换
反馈系统控制器 Gc ( s) 为
即
1 f ( s) ˆ Gp ( s ) Gc ( s ) ˆ ( s) G p 1 f ( s) ˆ Gp ( s )
ˆ ( s) G ( s) G P p
ˆ ( s) 0 又因为 D ( s) 0 ,则 D
表明控制器是Y ( s ) 跟踪 R( s ) 变化的 理想控制器。
Y ( s) GIMC ( s)Gp ( s) R ( s)
1 ˆ ( s) G p
Gp ( s) R ( s) R ( s)
假若“模型可倒”,即 ˆ 则令 可得
GIMC ( s ) 1 ˆ ( s) G p
1 Gp ( s )
可以实现
Y ( s) 0
不管 D( s ) 如何变化,对 Y ( s )的 影响为零。表明控制器是克服 外界扰动的理想控制器。
(2)当 D ( s) 0, R ( s) 0 时: 假若模型准确,即
s Ke ˆ ( s) G ( s) G p p Ts 1
ˆ ( s) 0 D
则
ˆ 1 ( s ) Ts 1 e s G P K
在单位阶跃信号作用下,设计IMC控制器为
Ts 1 1 ˆ GIMC ( s ) G p ( s ) f ( s) K (Tf 1)
ˆ ˆ 1 ( s ) f ( s ) GIMC ( s ) G ( s ) f ( s ) G IMC p 1 K s1 ˆ G ( s ) G IMC IMC ( s ) f ( s ) 由: Gc ( s ) ˆ ˆ ( s )G ˆ 1 Gp ( s )GIMC ( s ) 1 G p IMC ( s ) f ( s )
r ——整数,选择原则是使 G
IMC
( s)成为有理传递函数。
因此,假设模型没有误差,可得
ˆ ( s ) f ( s ) R ( s ) [1 f ( s )G ˆ ( s)]D ( s ) Y ( s) G p p
设 D ( s) 0 时
Y ( s) ˆ Gp ( s ) f ( s ) R ( s)
可以将 Gc ( s) 写为
Gc ( s) 1 f (s) s
1 ˆ ( s) G p f (s) ˆ ( s)] / s [(T f s 1) r G p
当模型已知时,将上式和实际的PID算式,对应系
数相等,求解即可得基于内模控制原理的PID控制器 各参数 。
对上式中含有的滞后项进行近似——Pade近似和 Taylor近似。
D(s)
R(s)
GIMC( s)
U ( s)
Gp ( s )
Y (s)
ˆ ( s) G p
ˆ ( s) D
Ym (s)
图6-1 内模控制结构框图
Gp ( s) ——实际对象; ˆ ( s) G ——对象模型; p
R( s ) ——给定值;
Y ( s ) ——系统输出;
内模控制器的设计思路是从 理想控制器出发,然后考虑 了某些实际存在的约束,再 回到实际控制器的。
(a) (a)不存在模型误差仿真输出
(b) 存在模型误差时IMC仿真
(c) 存在模型误差时Smish预估控制 仿真
(c)
3 内模PID控制
(1) PID控制器的基本形式
Gc ( s) K p (1 1 Td s) Ti s
理想形式
对于模拟元件实现的工业PID
Td s 1 Gc ( s) K p (1 ) Ti s Td s 1 1 1 Gc ( s) K p (1 Td s) Ti s Td s 1 1 1 Gc ( s) K p (1 )(Td s 1) Ti s Td s 1
GIMC ( s) Gc ( s ) ˆ ( s) 1 GIMC (s)G p
可以看到控制器 Gc ( s) 的
因为在 s 0 时,
f ( s) 1 ˆ ( s) G ˆ ( s) G p p
得: Gc ( s) | s 0
零频增益为无穷大。因此 可以消除由外界阶跃扰动 引起的余差。这表明尽管 内模控制器 GIMC ( s) 本身 没有积分功能,但由内模 控制的结构保证了整个内 模控制可以消除余差。
G p ( s) G p (s)
则,控制器具有理想控制器特性,即在所有时间 内和任何干扰作用下,系统输出都等于输入设定 值,保证对参考输入的无偏差跟踪。
内模控制的主要性质
3.零稳态偏差特性
I型系统(模型存在偏差,闭环系统稳定,只要设 ˆ 1 (0) 即控制器的稳态增益等于 计控制器满足 GIMC (0) G p 模型稳态增益的倒数。)对于阶跃输入和常值干扰均 不存在稳态误差。
R( s)
(a)IMC系统结构
D( s)
1 101 2s
1 10 s 1
e
10 s
Y (s)
比较IMC和Smith预 估控制两种控制策 略。
1 e 8 s
1 10 s 1
(b)Smith预估控制系统结构 图6-4 存在模型误差时的系统结构图
(b)
第六章 内模控制
内模控制(Internal Model Control——IMC) 是一种基于过程数学模型进行控制器设计的新型
控制策略。
它与史密斯预估控制很相似,有一个被称为
内部模型的过程模型,控制器设计可由过程模型
直接求取。设计简单、控制性能好、鲁棒性强, 并且便于系统分析。
1.什么是内模控制?
表明:滤波器 f ( s ) 与闭环性能有非常直接的关系。 滤波器中的时间常数 Tf 是个可调整的参数。时间 常数越小,Y ( s ) 对 R( s ) 的跟踪滞后越小。 事实上,滤波器在内模控制中还有另一重要作
用,即利用它可以调整系统的鲁棒性。其规律
是,时间常数 Tf 越大,系统鲁棒性越好。
二、内模控制器对闭环 系统的影响:
Y ( s) GIMC ( s)Gp ( s)R ( s) [1 GIMC ( s)Gp ( s)]D ( s)
当模型没有误差,且没有外界扰动时 其反馈信号
ˆ ( s )]U ( s) D( s) 0 ˆ ( s ) [G ( s) G D p p
——内模控制系统具有开环结构。
D( s ) ——在控制对象输出上叠加的扰动。
讨论两种不同输入情况下,系统的输出情况:
(1)当 R ( s) 0, D ( s) 0 时:
ˆ ( s) G ( s) 假若模型准确,即 G P p ˆ ( s) D ( s) 由图可见 D
ˆ ( s)] Y ( s) D ( s)[1 GIMC ( s)Gp ( s)] D ( s)[1 GIMC ( s)G p
II型系统(模型存在偏差,闭环系统稳定,只要设 d ˆ 1 ˆ 计控制器满足 GIMC (0) Gp (0) ,且 [G p (s)GIMC (s)] 0 )
ds
对于所有斜坡输入和常值干扰均不存在稳态误差。
s 0
IMC系统本身具有偏差积分作用。
内模控制的实现问题
1.若对象含有滞后特性
ˆ 1 ( s中含有纯超前项,物理上难以实现。 ) 则 GIMC (s) G p
