第4章 内模控制

控制器传递函数为:
模型匹配时
思考:SMPC的缺陷？
第4章 内模控制 4.7 内模控制的工业应用
4.7.2 热交换器温度控制
右图所示是一个蒸汽加热器实 验装置，加热介质为蒸汽，冷流 体为水。控制目标是通过调节加 热蒸汽流量来保证热交换器出口 热水温度平稳。 图中温度控制器采用微机实现。
(一) 对象建模
热交换器出口温度与蒸汽流量 的关系可由开环阶跃响应的实验获得:
第4章 内模控制 (二) 内模控制器设计
(i)对象模型分解: (ii)滤波器设计（即IMC控制器设计）:
(三) 算法实现
第4章 内模控制
4.3.2 滤波器设计
f (s) p(s) q(s) 取如下形式：
满足上式的滤波器最简单形式为：
滤波器可以采取其他形式，甚至可获得更快的响应。 例如r＝2，滤波器可取为：
第4章 内模控制
4.3.3 设计示例
4.3.3.1 一阶加纯滞后过程
4.3.3.2 高阶过程
情形A.无右半平面(RHP)零点
结构和参数，可以有效地抑制输出振荡，且可获得所期望的动态特性 和鲁棒性。
通常，反馈滤波器可选较为简单的一阶形式:
第4章 内模控制
在反馈通道中插人滤波器，可使原来不稳定的闭环系统镇定下来， 同时还有另外一个作用：就是可抑制干扰的作用。 模型匹配时，由于干扰引起的输出为: 举例:
若已知输出端的干扰为指数上升形式，即
2. 类型2系统 若闭环系统稳定，即使模型与过程失配，即 , 只要控制器满足 ，且 则此系统属于类型2。该系统对于所有斜坡输入和干扰均不存 在稳态误差。
第4章 内模控制 4.2.3 内模控制的实现问题 对于IMC系统，在模型准确情况下，只要令 即可获得理想的设定值跟踪和完全的干扰抑制效果。 然而，理想控制器性质常难以获得，其原因在于: 1. 若对象含有时滞特性； 2. 若对象模型含有右半平面(RHP)零点； 3. 若对象模型严格有理； 4. 采用理想控制器构成的系统，对于模型误差极为敏感，若 模型不准确，则无法确保闭环系统的鲁棒稳定性。 为了解决上述问题，在设计内模控制器时应分为两步进行: 1. 设计一个稳定的理想控制器，而不考虑系统的鲁棒性和约束; 2. 引人滤波器，通过调整滤波器的结构和参数来获得期望的动 态品质和鲁棒性。
若取
，
若取
若取
，
,
第4章 内模控制
为了减少突加设定值时的冲击，柔化控制动作，通常将设定值 经输人滤波器 后再送至控制器。 经柔化后的输人参考轨迹的一般形式为:
即
第4章 内模控制 4.6 简化模型预测控制（SMPC）
内模控制是一种极具理论价值的基于模型的控制策略，但其工程实 现因涉及模型求逆和滤波器合理设计等问题，设计过程较为复杂，尤 其是对于多输人多输出过程，实施难度更大。 1987年以后，Arulalan等人提出了一种简化模型预测控制(SMPC)，其 基本思想是“系统的闭环响应至少能达到其开环响应的性能”，由此导 出 控制算法后，引入一个整定参数，使响应加快到比较满意的程度。
第4章 内模控制 一、内模控制器设计应分两步进行：
步骤1：过程模型 G p (s ) 的分解
～
步骤2：IMC控制器设计 控制器设为：
低通 滤波器
第4章 内模控制 二、内模控制器对闭环 系统的影响：
对象输入为:
闭环系统输出为:
闭环系统误差为:
其中:
第4章 内模控制
对于模型无差，即 em ( s) 0 的特殊情况，上式可简化为：
控制器取为： 设计时为保持闭环系统零稳态偏差特性，需满足：
可实现因子可取为:
第4章 内模控制
下面将验证一下闭环系统输出方程是否具有零稳态偏差特性：
模型匹配时，系统闭环响应为:
第4章 内模控制
若模型失配或有干扰存在时，则闭环系统不一定能获得所期望的动 态性能，甚至会出现闭环系统不稳定的情况。
解决方法：在反馈通道中插人一个反馈滤波器，适当选取波器的
第4章 内模控制 4.3 内模控制器设计——连续过程 基本内模控制结构
• IMC→常规控制器：
GIMC ( s) Gc ( s) 1 GIMC ( s)Gm ( s)
第4章 内模控制 常规的反馈控制系统
• 常规控制器→IMC：
Gc ( s) GIMC ( s) 1 Gc ( s)Gm ( s)
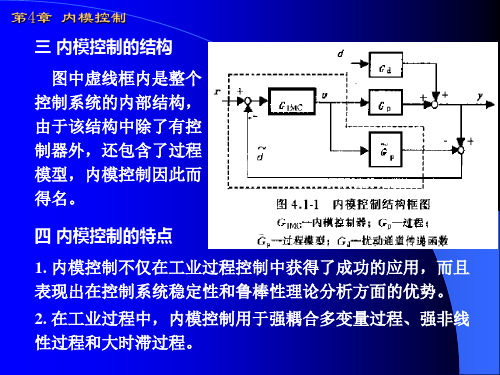
第4章 内模控制 三 内模控制的结构 图中虚线框内是整个 控制系统的内部结构， 由于该结构中除了有控 制器外，还包含了过程 模型，内模控制因此而 得名。 四 内模控制的特点 1. 内模控制不仅在工业过程控制中获得了成功的应用，而且 表现出在控制系统稳定性和鲁棒性理论分析方面的优势。 2. 在工业过程中，内模控制用于强耦合多变量过程、强非线 性过程和大时滞过程。
第4章 内模控制
4.6.2.1 SMPC的稳定性
特征方程: 举例:
则等效内模控制器特征方程为:
4.6.2.2 SMPC的零稳态偏差特性 (i)对于设定值的对于干扰的阶跃响应:
结论:SMPC控制对于设定值变化和干扰变化，无论模型误差存在与否,
均无稳态误差。 4.6.2.3 SMPC的鲁棒性 ——即“模型失配对系统稳定性的影响”
第4章 内模控制
4.6.2.4 SMPC不能实现对时滞的完全补偿
考虑如右对象: 对象的模型为: 闭环系统的特征方程为:
模型匹配时，闭环系统的特征方程可简化为:
第4章 内模控制
4.6.3 改进的SMPC算法
对算法改进，即是改进算法的控制率。
问题：即使模型匹配，也存
在稳态偏差。
第4章 内模控制
为保证系统稳定性，进一步将算法改进。
情形B.具有右半平面(RHP)零点
第4章 内模控制 4.4 内模控制器设计——离散过程
当过程模型采用离散脉冲传递函数形式时，内模控制系统的性质仍 然成立。在离散时间条件下，设计内模控制器也仍然分为两步进行： 首先是设计一个稳定的理想控制器； 然后在反馈和输人通道上增加反馈滤波器 和输人滤波器 ，通过调整滤波器的结构和参数，使系统获得所期望的性能。 下面就对开环稳定过程进行离散内模控制器设计。 考虑一般情况，令被控对象为有纯滞后的非最小相位过程，则过 程模型可分解为两部分：
第4章 内模控制
4.1 引言
一 内模控制 内模控制(Internal Model Control, 简称IMC)是一种基于过 程数学模型进行控制器设计的新型控制策略。由于其设计简 单、控制性能好和在系统分析方面的优越性，内模控制不仅是 一种实用的先进控制算法，而且是研究预测控制等基于模型的 控制策略的重要理论基础，以及提高常规控制系统设计水平的 有力工具。 二 内模控制的发展 1. 自20世纪50年代后期起，开始采用类似内模控制的概念来 设计最优反馈控制器。 2. 1982年，完整地提出了内模控制结构，并得到工程化实现。
第4章 内模控制 二 理想控制器特性
在理想情况下，IMC能实现对参考输人的无偏差跟踪. 然而: 1. 由于对象中常见的时滞和惯性环节， 中将出现纯超前 和纯微分环节，因此，理想控制器很难实现。 2. 对于具有反向特性，即包含不稳定零点的过程, 会含有不稳定极点。 中将
第4章 内模控制 三 零稳态偏差特性 1. 类型1系统 若闭环系统稳定，即使模型与过程失配，即 , 只要控制器设计满足 ，即控制器的稳态增益等 于模型稳态增益的倒数，则此系统属于类型1，且对于阶跃输 入和常值干扰均不存在稳态偏差。
4.6.1 常规SMPC算法
对象开环正规化阶跃响应为:
闭环系统的设定值单位阶跃 响应为:
第4章 内模控制
令上述两个响应相等，即
对被控对象施加上述控制作用时，由推导过程可知， 闭环系统的单 位设定值阶跃响应将与正规化开环阶跃响应完全等价。
常规 SMPC
第4章 内模控制
4.6.2 SMPC的性能分析（利用内模控制结构）
以上两式表明：对于无模型失配的情形，闭环传递函数 除了 中必须包含所有的滞后和右半 平面零点，且 必须有足够的阶次来避免物理上的不可实 现外，其他都是可以任意选择的。因此，闭环响应可以直接设 计，且设计步骤比常规反馈控制器要清楚很多。
第4章 内模控制 4.3.1
～
G p (s )
的分解
(i): (ii): 对于最小相位系统：
第4章 内模控制 4.2 内模控制基本原理 4.2.1 内模控制的结 构及其等价形式
则系统的闭环响应为：
第4章 内模控制 内模控制系统的反馈信号为：
4.2.2 内模控制的主要性质 一 对偶稳定性 当模型匹配时，IMC系统的闭环稳定性只取决于前向通道 各环节的自身的开环稳定性。
内模控制稳定性条件比起经典控制理论中常用的劳斯判 据、根轨迹判据和频率特性等稳定性分析方法要简单得多。 与内模控制相比，传统的反馈控制结构在如何选择控制器 类型和控制器参数以保证闭环系统的稳定性等间题上则显得 不够清晰。