第六章 数理统计基本概念
合集下载
第六章-数理统计的基本概念

而X(k)是将X1, X 2, , X n的取值从小到大排列后第k位的值。
(6)样本中位数
X
X
(
n1) 2
1 2
(
X
(
n 2
)
X ( n 1) ) 2
n为奇数 n为偶数
R软件用函数median(x)计算样本中位数。
(7)样本极差 RnX X (n) X (1) R软件用max(x) min(x)计算样本极差。
x2, … , xn),称为样本观测值。称 ( X1, X2, …, Xn )为
样本,n为样本容量.
概率论与数理统计
第六章 数理统计的基本概念
第9页
个体的二重性:
从总体X中抽取一个个体(但抽取个体的试验未结束,或理解
为试验是形式上的),该个体的值是不确定的,此时抽取的个体
仍用随机变量Xi 表示,它和总体X同分布;
第六章 数理统计的基本概念
第10页
根据随机变量独立性定义及独立随机变量的分布函数 和密度函数的定理,有 命题6.1.1 设总体X~F( ·,θ), (X1 , X2 , … , Xn)为其样本, 则
FX1 ,X2 , , Xn (x1, x2, , xn; θ) FX1 (x1, θ)FX2 (x2, θ) FXn (xn, θ)
概率论与数理统计
第六章 数理统计的基本概念
第3页
用局部推断整体,这就使得数理统计所作 推断的结论不可避免地存在偏差或错误,而刻 画或把握这种偏差的有效方法就是概率论。概 率论通过给出各种各样的统计量所服从的分布 或数字特征,来演绎地评价各种统计方法的优 劣或置信程度。
概率论与数理统计
第六章 数理统计的基本概念
数理统计基本概念

n1 Γ( ) 2 n 1 x 2 fT ( x ) (1 ) 2 , n n n Γ ( ) 2
P{6.262 χ 2 24.996}
2 2
P{χ 6.262} P{χ 24.996}
0.975 0.05 0.925
注意 应注意分布表的定义与查法!
#
数理统计基本概念
3.自由度为 n的 t 分布 作笔名发表文章.
T~t(n)
又称学生氏分布--第一个研究者以Student
( X 1 , X 2 , , X n ) ~ ( 2 ) e
n 2 2
i 1
( xi )2 2 2
n
数理统计基本概念
四、统计量 定义6.1.2 设X1 , X2 , ·, Xn是总体X的样本, · · T为n元实值函数,若样本的函数 T=T(X1 , X2 , ·, Xn) · · 是随机变量且不含未知参数,称 T为统计量. 对相应的样本值( x1 , x2 , … , xn ) ,称 t =T( x1 , x2 , … , xn )
理
统
计
的
引
入
数理统计基本概念
某厂生产的一批产品中次品率为 p 。从中 抽取10件产品装箱。 概
1)没有次品的概率 2)平均有几件次品
率
3)为以 0.95的概率保证箱中 有10件正品,箱中至少要装多 少件产品。
数
理
统
计
的
引
入
数理统计基本概念
所有这些问题的关键是 p 是已知的! 如何获取 p ? 这就是数理统计的任务了!
定的α(0<α<1),数uα满足
P{ X u } ,
(C ) u1 ;
P{6.262 χ 2 24.996}
2 2
P{χ 6.262} P{χ 24.996}
0.975 0.05 0.925
注意 应注意分布表的定义与查法!
#
数理统计基本概念
3.自由度为 n的 t 分布 作笔名发表文章.
T~t(n)
又称学生氏分布--第一个研究者以Student
( X 1 , X 2 , , X n ) ~ ( 2 ) e
n 2 2
i 1
( xi )2 2 2
n
数理统计基本概念
四、统计量 定义6.1.2 设X1 , X2 , ·, Xn是总体X的样本, · · T为n元实值函数,若样本的函数 T=T(X1 , X2 , ·, Xn) · · 是随机变量且不含未知参数,称 T为统计量. 对相应的样本值( x1 , x2 , … , xn ) ,称 t =T( x1 , x2 , … , xn )
理
统
计
的
引
入
数理统计基本概念
某厂生产的一批产品中次品率为 p 。从中 抽取10件产品装箱。 概
1)没有次品的概率 2)平均有几件次品
率
3)为以 0.95的概率保证箱中 有10件正品,箱中至少要装多 少件产品。
数
理
统
计
的
引
入
数理统计基本概念
所有这些问题的关键是 p 是已知的! 如何获取 p ? 这就是数理统计的任务了!
定的α(0<α<1),数uα满足
P{ X u } ,
(C ) u1 ;
数理统计的基本概念

(n 2) n n
n 1 2
, x .
t 分布的概率密度图形
图形关于 x 0 对称, lim f ( x; n) 0 , 且 x 当 n 充分大时,f (x; n) 趋近于标准正态 分布的概率密度。
定理 4: X 1, 2, , n 是抽自正态总体 设 X X
若总体 X 是离散型的,其分布律为:
则样本的联合分布为
§6.2 抽样分布
6.2.1 统计量的概念 由样本推断总体的某些情况时,需要对样本进行“ 加工”,构造出若干个样本的已知 (确定)的函数, 其作用是把样本中所含的某一方面的信息集中起来 。 这种不含任何未知参数的样本的函数称为统计量。 它是完全由样本所决定的量。 定义2:设 X 1 , X 2 , , X n 是来自总体X的样本, g( X 1 , X 2 , , X n ) 是样本 X 1 , X 2 , , X n 的函数,如果 g( X 1 , X 2 , , X n ) 中不包含任何未知参数,则称它 是一个统计量。
1 (0.82)
1 0.7939 0.2061
X ~ N (0, 22 ), X1 , X 2 , X3 , X 4 为其样本,求a,b 例2:总体
(2). (n 1)S / ~ (n 1)
2
X (1). X ~ N ( , / n), 或 ~ N (0,) ; 1 / n 2 2 2
2
X (3). X 与 S 相互独立; (4). ~ t(n 1). S/ n
定理5:设X1, X2, …, Xm 与Y1, Y2, …, Yn分别来自总体 2 两样本独立, X ~ N ( 1 , 12 )和Y ~ N ( 2 , 2 )的样本, 2 S12 / S2 则有 F 2 ~ F ( m 1, n 1). 2 1 / 2 定理6*:设X1, X2, …, Xm 与Y1, Y2, …, Yn分别来自
n 1 2
, x .
t 分布的概率密度图形
图形关于 x 0 对称, lim f ( x; n) 0 , 且 x 当 n 充分大时,f (x; n) 趋近于标准正态 分布的概率密度。
定理 4: X 1, 2, , n 是抽自正态总体 设 X X
若总体 X 是离散型的,其分布律为:
则样本的联合分布为
§6.2 抽样分布
6.2.1 统计量的概念 由样本推断总体的某些情况时,需要对样本进行“ 加工”,构造出若干个样本的已知 (确定)的函数, 其作用是把样本中所含的某一方面的信息集中起来 。 这种不含任何未知参数的样本的函数称为统计量。 它是完全由样本所决定的量。 定义2:设 X 1 , X 2 , , X n 是来自总体X的样本, g( X 1 , X 2 , , X n ) 是样本 X 1 , X 2 , , X n 的函数,如果 g( X 1 , X 2 , , X n ) 中不包含任何未知参数,则称它 是一个统计量。
1 (0.82)
1 0.7939 0.2061
X ~ N (0, 22 ), X1 , X 2 , X3 , X 4 为其样本,求a,b 例2:总体
(2). (n 1)S / ~ (n 1)
2
X (1). X ~ N ( , / n), 或 ~ N (0,) ; 1 / n 2 2 2
2
X (3). X 与 S 相互独立; (4). ~ t(n 1). S/ n
定理5:设X1, X2, …, Xm 与Y1, Y2, …, Yn分别来自总体 2 两样本独立, X ~ N ( 1 , 12 )和Y ~ N ( 2 , 2 )的样本, 2 S12 / S2 则有 F 2 ~ F ( m 1, n 1). 2 1 / 2 定理6*:设X1, X2, …, Xm 与Y1, Y2, …, Yn分别来自
概率论与数理统计 第六章--数理统计的基本概念

F分布性质2 若X ~t(n),则X2~F(1,n)
例4.设X1,X2, …,Xn是来自正态总体N(0,1) 的样本,试问c=( )统计量
c
2 X i 3 i 1 n
X
i 4
2 i
服从F分布?
抽样分布的分位点
设α为给定的常数,且0<α<1.若存在χα2(n)使
P ( n)
分位点的性质
(1) u1 u (2)
t1 (n) t (n)
1 (3) F (m, n) F1 (n, m)
回顾1. 设X1 ,X2 ,X3, X4是来自总体N(0,4)的简单 随机样本,X=a(X1-2 X2)2+b(3X3 -4X4)2,问当 a,b为何值时,统计量X服从 2分布 .
Max=1572, Min=738, 组数=6 组距=(Max-Min)/6=139140 取a0=735, 则分组区间及相关数据如下
组序 1 2 分区区间 (735,875] (875,1015] 频数 6 8 频率 0.2 0.27 累计频率 0.2 0.47
3
4 5 6 合计
(1015,1155]
2
所服从的分布为自由度为 n 的 分布 记为
2
~ (n)
2 2
分布的密度函数为
2
n x 1 1 n2 x2 e 2 f ( x; n ) 2 ( n 2 ) 0
x0 x0
其中伽玛函数 ( x )通过积分
( x ) e t dt, x 0 0 来定义.
(1155,1295] (1295,1435] (1435,1575]
9
4 2 1 30
0.3
概率论与数理统计 数理统计的基本概念

记为 x1, x2 ,, xn ,称它为一组样本观察 值,简称样本值.
6
定义 3 设 X1, X 2 ,, X n 为总体 X 的一个 样本,若 X1, X 2 ,, X n 相互独立且与总体 X 同分布,则称 X1, X 2 ,, X n 为来自总体 X 的 一个简单随机样本,简称样本.
8
常见统计量
设 X1, X 2,, X n 是来自总体 X 的样本, x1 , x2 ,, xn 是 样本的观察值,定义
样本均值 样本方差 样本标准差
X
1 n
n i 1
Xi
S 2
1 n 1
n i 1
(Xi
X )2
1n (
n 1 i1
X
2 i
nX
2)
S
S2
今后不作特殊说明,本书所指的样本 均为简单随机样本.
7
定义 4 设 X1, X 2 ,, X n 是来自总体 X 的样本, x1 , x2 ,, xn 为样本观察值,T (X1, X 2 ,, X n ) 是关于 X1, X 2 ,, X n 的样本函数.若T 中不含任何未知参 数,则称T (X1, X 2 ,, X n ) 是统计量,称T (x1, x2 ,, xn ) 是 统计量的观察值.
第六章 数理统计的基本概念
1
什ห้องสมุดไป่ตู้是数理统计学?
数理统计学是这样一门数学分支,它运用概率论 与数学的方法,研究如何有效地收集、整理和分析带 有随机性影响的数据,并由此对所研究的问题作出尽 可能合理的推断和预测,从而为相关决策提供参考和 建议.
2
数理统计和概率论的关系
●数理统计学和概率论是随机数学的姊妹篇 ●有密切的联系却又不是同一学科 ●概率论是数理统计学的理论基础 ●数理统计学是概率论的重要应用.
6
定义 3 设 X1, X 2 ,, X n 为总体 X 的一个 样本,若 X1, X 2 ,, X n 相互独立且与总体 X 同分布,则称 X1, X 2 ,, X n 为来自总体 X 的 一个简单随机样本,简称样本.
8
常见统计量
设 X1, X 2,, X n 是来自总体 X 的样本, x1 , x2 ,, xn 是 样本的观察值,定义
样本均值 样本方差 样本标准差
X
1 n
n i 1
Xi
S 2
1 n 1
n i 1
(Xi
X )2
1n (
n 1 i1
X
2 i
nX
2)
S
S2
今后不作特殊说明,本书所指的样本 均为简单随机样本.
7
定义 4 设 X1, X 2 ,, X n 是来自总体 X 的样本, x1 , x2 ,, xn 为样本观察值,T (X1, X 2 ,, X n ) 是关于 X1, X 2 ,, X n 的样本函数.若T 中不含任何未知参 数,则称T (X1, X 2 ,, X n ) 是统计量,称T (x1, x2 ,, xn ) 是 统计量的观察值.
第六章 数理统计的基本概念
1
什ห้องสมุดไป่ตู้是数理统计学?
数理统计学是这样一门数学分支,它运用概率论 与数学的方法,研究如何有效地收集、整理和分析带 有随机性影响的数据,并由此对所研究的问题作出尽 可能合理的推断和预测,从而为相关决策提供参考和 建议.
2
数理统计和概率论的关系
●数理统计学和概率论是随机数学的姊妹篇 ●有密切的联系却又不是同一学科 ●概率论是数理统计学的理论基础 ●数理统计学是概率论的重要应用.
第六章 数理统计的基本概念

1 n 2 S S ( X X ) i n 1 i 1
2
(4) 样本k阶(原点)矩
1 n k Ak X i n i 1
k 1, 2,
k 2,3,
(5) 样本k阶中心矩
1 n Bk ( X i X )k n i 1
§2
常用统计量的分布
统计量的分布称为抽样分布.下面介绍三种由 正态总体演化而来的统计量的分布:
• 从二战后到现在,是统计学发展的第三个时期,这是一个在 前一段发展的基础上,随着生产和科技的普遍进步,而使这 个学科得到飞速发展的一个时期,同时,也出现了不少有待 解决的大问题.
学科奠基者
数理统计作为一个进一步完善的数学学科的奠基者是英国人费歇尔。他1909 年入剑桥大学,攻读数学物理专业,三年后毕业。毕业后,他曾去投资办工 厂,又到加拿大农场管过杂务,也当过中学教员。1919年,他开始对生物统 计学产生了浓厚的兴趣,参加罗萨姆斯泰德试验站的工作,致力于数理统计 在农业科学和遗传学中(费歇尔1890—1962)的应用研究。 年轻的费歇尔主要的研究工作是用数学将样本的分布给以严格的确定。 在一般人看来枯燥乏味的数学,常能带给研究者极大的慰藉,费歇尔热衷于 数理统计的研究工作,后来的理论研究成果有:数据信息的测量、压缩数据 而不减少信息、对一个模型的参数估计等。 最使科学家称赞的工作则是试验设计,它将一切科学试验从某一个侧面 “科学化”了,不知节省了多少人力和物力,提高了若干倍的工效。 费歇尔培养了一个学派,其中有专长纯数学的,有专长应用数学的。在30- 50年代费歇尔是统计学的中心人物。1959年费歇尔退休后在澳大利亚度过了 最后三年。
若 x1 , x2 , , xn 是样本的观察值, 则 g ( x1 , x2 , xn ) 是 g ( X 1 , X 2 , X n )
概率论与数理统计(叶慈南 刘锡平 科学出版社)第6章 数理统计的基本概念教程
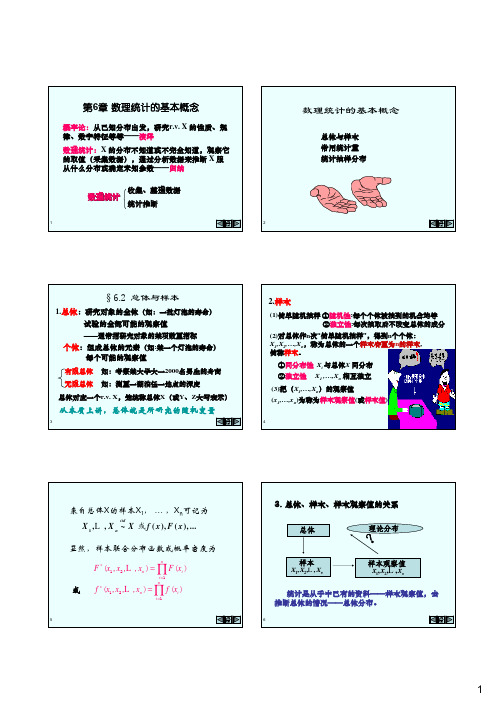
3.样本k阶(原点)矩 Ak = 样本k阶中心矩
Bk =
1 n k ∑ X i 反映总体k阶矩E(Xk)的信息 n i =1 P E ( X k ) = k , k = 1, 2, L →
反映总体k
9
1 n P → ∑ ( X i X )k E {[ X E ( X )]k } = mk n i =1 k=1,2,…
1o
X ~ N ( ,
σ2 ) n
即
X ~ N (0,1) σ/ n
2o 3o
(n 1) S 2 ~ χ 2 ( n 1) σ2 X 与 S 2 相互独立 4o X ~ t ( n 1) S/ n
23
24
4
1o
X ~ N ( , X=
σ2 ) n
即
X ~ N ( 0, 1) σ/ n
4o
正态总体的抽样分布定理
例 设 X1,…,X10 是取自N(0,0.32)的样本,求
P{∑ X i > 1.44}
2 i =1 10
定理一,二,三
2 2 设 X 1 ,..., X n 是来总体 N ( , σ ) 的样本, X , S 分别为样
本均值和样本方差,则
例 设 X 1 , X 2 , L , X 15 是来自总体 N (0,1)的一个简单随 2 2 X 12 + X 2 + L + X 10 机样本, Y= 则 服从 分布. 2 2 2 2( X 11 + X 12 + L + X 15 )
4
个体:组成总体的元素(如:某一个灯泡的寿命)
每个可能的观察值
有限总体 无限总体 如:考察某大学大一2000名男生的身高 如:考察某大学大一2000名男生的身高 如:测量一湖泊任一地点的深度
数理统计的基本概念ppt课件

体。 灯泡的寿命检验是一个破坏性试验,即当得知一个灯
泡寿命时,该灯泡的使用价值也就消失了.因此,不可能抽 检每个灯泡!
可以逐一测量每个工大男生的身高,但工作量大.而我 们仅需对工大男生身高情况有个大致了解,因此,不必要抽 测每个工大男生!
河南理工大学精品课程
.
概率论与数理统计
做法 从总体中随机地抽取若干个体(灯泡、工大男 生),测试其所需数据(寿命、身高),最后对所得数据通过 整理加工和分析来推断总体(这批灯泡寿命、工大男生身 高)的分布情况,从而了解整体情况.
x)2
ak
1 n ni1
xik(k1,2,)
bk 1 ni n1(xi x)k(k1,2,)
.
河南理工大学精品课程
概率论与数理统计
重要结论:样本矩(的连续函数)依概率收敛
于总体矩(的连续函数)[矩估计的理论基础]。
一般,我们所研究的总体的某项数量指标X是一个随 机变量,其取值在客观上有一定的分布.因此,对总体的研 究,就是对相应的随机变量X的研究。
今后,我们称X的分布函数和数字特征分别为总体的
分布函数和数字特征,并不再区分总体与相应的随机变量
X.对总体的称呼:总体,总体X与总体F.
河南理工大学精品课程
.
概率论与数理统计
数理统计的基本任务就是通过对样本的研究来对总 体的未知参数或分布类型作出估计,对有关总体的假设 作出推断。
后面介绍的内容仅限于有关总体参数的估计与推断, 称为参数估计与参数假设检验。
河南理工大学精品课程
.
概率论与数理统计
总体X
随机抽样 获得样本
样本X1,X2,…,Xn
完成试验 获得数据
样本值x1,x2,…,xn
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Note:简单随机样本:X1,X2…Xn 具有同一一分布且相互独立立的随机变量量
同一一分布:EX,DX,F均一一样
相互独立立:标准差cov(Xi,Xj)=0,cov(Xi,Xi)=DXi
2.样本的联合分布
1)联合分布函数(由于独立立)连乘
2)联合概率密度(由于独立立)连乘
3.统计量量与抽样分布
第六章数理理统计基本概念
引言言
概率论——偏理理论,主要是分布,数字特征(其是分布的量量化)
数理理统计——应用用,主要是估计,检验,最重要的是抽样分布!
知识点:一一 基本概念 二二 常用用的统计量量 三 常用用统计量量的抽样分布 四 正太总体的抽样分布
一一 基本概念
1.总体,个体,总体容量量 ,简单随机样本
Note:1)定义:1.服从标准正态分布;2.独立立 3.标准正态平方方和才服从X2分布
2)性质:1.叠加性(自自由度叠加)2.X2的期望,方方差
3)图像(注意上分位点)
要注意单位化!
2.t(n)分布(定义,性质,图像)
Note:1.定义:1.X服从标准正态,2.Y服从X2,3.X,Y相互独立立4.t的表达式
1)统计量量:简单随机样本的函数
2)抽样分布:统计量量的分布——灵魂(只有四个,N,X2,t,F)
二二 常用用(基本)的统计量量(注意样本均值,样本方方差,样本标准差都是随机变量量,可以求E D)
1.样本均值(公式,三个推论)
1)期望,方方差,若服从正态,则其也服从正态,具体形式
2.样本方方差(公式,注意两点)
2.性质:图像(对称)(类似标准正态分布图像)(分位点表达式)
3.F(m.n)分布(定义,性质,图像)
Note:1.定义:X服从X2(m)2.Y服从X2(n)3.X,Y独立立;4F表达式
2.性质:倒数
3.图像(类似于X2的图像)
四 正态分布的抽样分布(重点)
一一个正态分布
1.X1....Xn来自自正态总体的样本,已知样本均值和样本方方差
1)注意:1.分⺟母是n-1(遇⻅见Xbar自自由度就减1)
2.⻅见到S2想到kai2
3.样本标准差
4.样本k阶原点矩
5.样本k阶中心心矩
6.数字特征:(无无论何种)样本均值的期望,方方差;样本方方差的期望方方差(注意kai件三个)
1.X2(n)分布(定义,性质(2个),图像(注意上分位点))
有五个结论(必考)
1.五个结论的推导
2.分成两组:无无平方方 和 有 平方方的
同一一分布:EX,DX,F均一一样
相互独立立:标准差cov(Xi,Xj)=0,cov(Xi,Xi)=DXi
2.样本的联合分布
1)联合分布函数(由于独立立)连乘
2)联合概率密度(由于独立立)连乘
3.统计量量与抽样分布
第六章数理理统计基本概念
引言言
概率论——偏理理论,主要是分布,数字特征(其是分布的量量化)
数理理统计——应用用,主要是估计,检验,最重要的是抽样分布!
知识点:一一 基本概念 二二 常用用的统计量量 三 常用用统计量量的抽样分布 四 正太总体的抽样分布
一一 基本概念
1.总体,个体,总体容量量 ,简单随机样本
Note:1)定义:1.服从标准正态分布;2.独立立 3.标准正态平方方和才服从X2分布
2)性质:1.叠加性(自自由度叠加)2.X2的期望,方方差
3)图像(注意上分位点)
要注意单位化!
2.t(n)分布(定义,性质,图像)
Note:1.定义:1.X服从标准正态,2.Y服从X2,3.X,Y相互独立立4.t的表达式
1)统计量量:简单随机样本的函数
2)抽样分布:统计量量的分布——灵魂(只有四个,N,X2,t,F)
二二 常用用(基本)的统计量量(注意样本均值,样本方方差,样本标准差都是随机变量量,可以求E D)
1.样本均值(公式,三个推论)
1)期望,方方差,若服从正态,则其也服从正态,具体形式
2.样本方方差(公式,注意两点)
2.性质:图像(对称)(类似标准正态分布图像)(分位点表达式)
3.F(m.n)分布(定义,性质,图像)
Note:1.定义:X服从X2(m)2.Y服从X2(n)3.X,Y独立立;4F表达式
2.性质:倒数
3.图像(类似于X2的图像)
四 正态分布的抽样分布(重点)
一一个正态分布
1.X1....Xn来自自正态总体的样本,已知样本均值和样本方方差
1)注意:1.分⺟母是n-1(遇⻅见Xbar自自由度就减1)
2.⻅见到S2想到kai2
3.样本标准差
4.样本k阶原点矩
5.样本k阶中心心矩
6.数字特征:(无无论何种)样本均值的期望,方方差;样本方方差的期望方方差(注意kai件三个)
1.X2(n)分布(定义,性质(2个),图像(注意上分位点))
有五个结论(必考)
1.五个结论的推导
2.分成两组:无无平方方 和 有 平方方的
