您的位置：360文档中心› 二次函数系数abc与图像的关系精选练习题

二次函数系数abc与图像的关系精选练习题

合集下载

二次函数中各项系数abc与图像的关系

二次函数中各项系数abc与图像的关系

二次函数中各项系数a ，b ，c 与图像的关系一、首先就y=ax 2+bx+c （a≠0）中的a ，b ，c 对图像的作用归纳如下：1 a 的作用：决定开口方向：a > 0开口向上；a < 0开口向下；决定张口的大小：∣a ∣越大，抛物线的张口越小．2 b 的作用：b 和a 与抛物线图像的对称轴、顶点横坐标有关．b 与a 同号，说明02<-a b ，则对称轴在y 轴的左边； b 与a 异号，说明−b 2a >0，则对称轴在y 轴的右边；特别的，b = 0，对称轴为y 轴．3 c 的作用：c 决定了抛物线与y 轴的交点纵坐标．抛物线与y 轴的交点（0，c ）c > 0 抛物线与y 轴的交点在y 轴的正半轴；c < 0 抛物线与y 轴的交点在y 轴的负半轴；特别的，c = 0，抛物线过原点．4 a,b,c 共同决定判别式?=b 2−4ac 的符号进而决定图象与x 轴的交点b 2−4ac >0 与x 轴两个交点b 2−4ac =0 与x 轴一个交点b 2−4ac <0 与x 轴没有交点5 几种特殊情况：x=1时，y=a + b + c ；x= -1时，y=a - b + c ．当x = 1时，① 若y > 0，则a + b + c >0；② 若y < 时0，则a + b + c < 0当x = -1时，① 若y > 0，则a - b + c >0；② 若y < 0，则a - b + c < 0．扩：x=2, y=4a + 2b + c ；x= -2, y=4a -2b + c ； x=3, y=9a +3 b + c ；x= -3, y=9a -3b + c 。

一．选择题（共8小题）1．已知二次函数y=ax 2+bx +c 的图象大致如图所示，则下列关系式中成立的是（ ）A ．a ＞0B ．b ＜0C ．c ＜0D ．b +2a ＞02．如果二次函数y=ax 2+bx +c （a ≠0）的图象如图所示，那么下列不等式成立的是（ ）A ．a ＞0B ．b ＜0C ．ac ＜0D ．bc ＜0．3．已知二次函数y=ax 2+bx +c （a ≠0）的图象如图所示，有下列4个结论：①abc ＞0；②b ＜a +c ；③4a +2b +c ＞0；④b 2﹣4ac ＞0；其中正确的结论有（ ）A ．1个B ．2个C ．3个D ．4个4．二次函数y=ax 2+bx +c （a ≠0）的图象如图所示，对于下列结论：①a ＜0；②b ＜0；③c ＞0；④2a +b=0；⑤a ﹣b +c ＜0，其中正确的个数是（ ）A ．4个B ．3个C ．2个D ．1个第3题图 第4题图 第5题图 第6题图5．二次函数y=ax 2+bx +c （a ≠0）的图象如图，给出下列四个结论：：①a ＜0；②b ＞0；③b 2﹣4ac ＞0；④a +b +c ＜0；其中结论正确的个数有（ ）A ．1个B ．2个C ．3个D ．4个6．如图所示，抛物线y=ax 2+bx +c 的顶点为（﹣1，3），以下结论：①b 2﹣4ac ＜0；②4a ﹣2b +c ＜0；③2c﹣b=3；④a+3=c，其中正确的个数（）A．1 B．2 C．3 D．47．如图是二次函数y=ax2+bx+c图象的一部分，图象过点A（﹣3，0），对称轴为直线x=﹣1，下列给出四个结论中，正确结论的个数是（）个①c＞0；②若点B（﹣，y1）、C（﹣，y2）为函数图象上的两点，则y1＜y2；③2a﹣b=0；④＜0；⑤4a﹣2b+c＞0．A．2 B．3 C．4 D．58．二次函数y=ax2+bx+c的图象如图所示，以下结论：①abc＞0；②4ac＜b2；③2a+b＞0；④当x＜时，y随x的增大而减小；⑤a+b+c＞0．其中正确的有（）A．5个 B．4个 C．3个 D．2个二．填空题（共4小题）9．如图，抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=1，与x轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：①4ac＜b2；②方程ax2+bx+c=0的两个根是x1=﹣1，x2=3；③3a+c＞0；④当y＞0时，x的取值范围是﹣1≤x＜3；⑤当x＜0时，y随x增大而增大；其中结论正确有．10．一抛物线和抛物线y=﹣2x2的形状、开口方向完全相同，顶点坐标是（﹣1，3），则该抛物线的解析式为．11．抛物线y=ax2+12x﹣19顶点横坐标是3，则a=．12．将二次函数y=x2+6x+5化为y=a（x﹣h）2+k的形式为．三．解答题（共7小题）13．已知：抛物线y=﹣x2+bx+c经过点B（﹣1，0）和点C（2，3）．（1）求此抛物线的表达式；（2）如果此抛物线沿y轴平移一次后过点（﹣2，1），试确定这次平移的方向和距离．14．函数y=（m+2）是关于x的二次函数，求：（1）满足条件的m值；（2）m为何值时，抛物线有最低点？求出这个最低点．这时，当x为何值时，y随x的增大而增大？（3）m为何值时，函数有最大值？最大值是多少？这时，当x为何值时，y随x的增大而减小．15．已知二次函数的图象经过（0，0）（﹣1，﹣1），（1，9）三点．（1）求这个函数的解析式；（2）求这个函数图象的顶点坐标．16．已知抛物线的顶点坐标是（1，﹣4），且经过点（0，﹣3），求与该抛物线相应的二次函数表达式．17．已知二次函数y=x2﹣4x+5．（1）将y=x2﹣4x+5化成y=a （x﹣h）2+k的形式；（2）指出该二次函数图象的对称轴和顶点坐标；（3）当x取何值时，y随x的增大而增大？18．如图，二次函数的图象的顶点坐标为（1，），现将等腰直角三角板直角顶点放在原点O，一个锐角顶点A在此二次函数的图象上，而另一个锐角顶点B在第二象限，且点A的坐标为（2，1）．（1）求该二次函数的表达式；（2）判断点B是否在此二次函数的图象上，并说明理由．19．已知二次函数y=a（x﹣h）2，当x=4时有最大值，且此函数的图象经过点（1，﹣3）．（1）求此二次函数的解析式；（2）当x为何值时，y随x的增大而增大？。

二次函数系数abc与图像的关系

二次函数系数abc与图像的关系

二次函数系数a、b、c与图象的关系知识归纳：1.a的作用：决定开口方向和开口大小2.a与b的作用：左同右异（对称轴的位置）3.c的作用：与y轴交点的位置。

4.b2-4ac的作用：与x轴交点的个数。

5.几个特殊点：顶点，与x轴交点，与y轴交点，（1，a+b+c),(-1,a-b+c) （2，4a+2b+c), （-2，4a-2b+c)。

针对训练：1.判断下列各图中的a、b、c及△的符号。

(1)a___0；b___0；c___0；△__0.(2)a___0； b___0； c___0；△__0.(3)a___0； b___0； c___0；△__0.(4)a___0； b___0； c___0；△__0.(5)a___0； b___0； c___0；△__0.2.二次函数y=ax2+bx+c的图象如图，用（＞，＜，=）填空：a___0； b___0； c___0； a+b+c__0； a-b+c__0.3.二次函数y=ax 2+bx+c 的图象如图1所示，则下列关于a 、b 、c 间的关系判断正确的是（ ）A.ab<0B.bc<0C.a+b+c>0D.a －b+c<04.二次函数y=ax 2+bx+c 图象如图，则点 A （b 2-4ac ，-b a）在第 象限．5．已知a ＜0，b＞0，c ＞0，那么抛物线y=ax 2+bx+c 的顶点在（ ）A.第一象限B.第二象限C.第三象限D.第四象限6.已知二次函数y=ax 2+bx+c 的图像如图所示，判断下列各式的符号： (1)a ； (2)b ； (3)c ； (4)a+b+c ； (5)a-b+c ；(6)b 2-4ac ； (7)4ac-b 2； (8)2a+b ； (9)2a-b7.练习：填空（1）函数y=ax 2+bx+c （a≠0）的函数值恒为正的条件： ，恒为负的条件： .（2）已知抛物线y=ax 2+bx+c 的图象在x 轴的下方，则方程ax 2+bx+c=0的解得情况为： .（3）二次函数y=ax 2+bx+c 中，ac ＜0，则抛物线与x 轴有 交点。

中考数学总复习《二次函数图像与系数的关系》练习题及答案

中考数学总复习《二次函数图像与系数的关系》练习题及答案

中考数学总复习《二次函数图像与系数的关系》练习题及答案班级:___________姓名：___________考号：_____________一、单选题1．已知二次函数y=ax2+bx+c的图象如图所示，有以下结论：①a+b+c＜0；②a-b+c＞1；③abc＞0；④4a-2b+c＜0；⑤c-a＞1其中所有正确结论的序号是()A．①②B．①③④C．①②③⑤D．①②③④⑤2．已知二次函数y＝ax2+bx+c的图象如图所示，那么下列结论中正确的是（）A．ac＞0B．b＞0C．a+c＜0D．a+b+c＝03．如图，抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1，与x轴的一个交点坐标为(﹣1，0)，其部分图象如图所示．下列结论：①abc＜0；②3a+c=0；③当y＞0时，x的取值范围是﹣1≤x＜3；④方程ax2+bx+c﹣3=0有两个不相等的实数根；⑤点(﹣2，y1)，(2，y2)都在抛物线上，则有y1＜0＜y2．其中结论正确的个数是()．A．1个B．2个C．3个D．4个4．在平面直角坐标系xOy中，开口向下的抛物线y＝ax2＋bx＋c的一部分图象如图所示，它与x轴交于A(1，0)，与y轴交于点B(0，3)，则a的取值范围是（）A．a＜0B．－3＜a＜0C．a<−32D．−92<a<−325．在同一坐标系内，一次函数y=ax+b与二次函数y=ax2+8x+b的图象可能是A．B．C．D．6．已知b＜0时，二次函数y=ax2+bx+a2-1的图象如下列四个图之一所示．根据图象分析，a的值等于()A．－2B．－1C．1D．27．对于二次函数y=﹣（x+1）2﹣3，下列结论正确的是（）A．函数图象的顶点坐标是（﹣1，﹣3）B．当x＞﹣1时，y随x的增大而增大C．当x=﹣1时，y有最小值为﹣3D．图象的对称轴是直线x=18．二次函数y=ax2+bx+c，自变量x与函数y的对应值如表：x…-5-4-3-2-10…y…40-2-204…A．抛物线的开口向下B．当时，y随x的增大而增大C．二次函数的最小值是D．抛物线的对称轴是直线9．二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论中正确的是（）A．a＞0B．当x≥1时，y随x的增大而增大C．c＜0D．当﹣1＜x＜3时，y＞010．如图，在同一平面直角坐标系中，函数y=ax+2(a≠0)与y=−ax2−2x(a≠0)的图象可能是（）．A．B．C．D．11．已知二次函数y=﹣（x+k）2+h，当x＞﹣2时，y随x的增大而减小，则函数中k的取值范围是（）A．k≥﹣2B．k≤﹣2C．k≥2D．k≤212．已知：二次函数y＝ax2+bx+c的图象如图，则下列答案正确的是（）A．a＞0，b＞0，c＞0，△＜0B．a＜0，b＞0，c＜0，△＞0C．a＞0，b＜0，c＜0，△＞0D．a＜0，b＜0，c＞0，△＜0二、填空题13．二次函数y=ax2+bx+c（a≠0）的图象如图（虚线部分为对称轴），给出以下6个结论：①abc＞0；②a﹣b+c＞0；③4a+2b+c＞0；④2a＜3b；⑤x＜1时，y随x的增大而增大；⑥a+b＜m（am+b）（m为实数且m≠1）其中正确的结论有（填上所有正确结论的序号）14．已知二次函数y=ax2+bx+c的图象如图所示，则由此可得a0，b0，c 0.（填“<”或“>”）15．老师给出一个二次函数，甲，乙，丙三位同学各指出这个函数的一个性质：甲：函数的图象经过第一、二、四象限；乙：当x＜2时，y随x的增大而减小．丙：函数的图象与坐标轴只有两个交点．已知这三位同学叙述都正确，请构造出满足上述所有性质的一个函数．16．如果抛物线y＝（m﹣1）x2有最低点，那么m的取值范围为．17．已知二次函数y=ax2+bx+c的图象如图所示，它与x轴的两个交点分别为（-1，0），（3，0）．对于下列命题：①b-2a=0；②abc＜0；③a-2b+4c＜0；④8a+c＞0．其中正确的有。

二次函数系数a、b、c与图像的关系填空题专题练习(含答案).doc

二次函数系数a、b、c与图像的关系填空题专题练习(含答案).doc

二次函数系数a 、b 、c 与图像的关系填空题专题练习1、二次函数y=-x2+bx+c 的图象如图所示，试确定b 、c 的符号；b ____________ 0, c ________ 0.(填不等号)5、已知函数y 二ax"+bx+c 的图象如图所示，则下列结论中:®abc>0；②b 二2。

；③a+b+c<0；④a-b+c>0.正 确的是 _________ •0； (4) b 2-4ac_ 0.如图，已知抛物线y 二ax'+bx+c(aH0)经过原点和点(-2, 0),则2a -3b0.(填 >、V 或二) 象限.0； (3)c则直线y=abx+c 不过第6、已知如图，抛物线y=ax2+bx+c与x轴交于点A（—1, 0）和点B,化简：如夕★如护的结杲为：①c;②b;③b—a;④a —b + 2c.其中正确的有________________ .7、二次函数y=-x2+bx + c的图象如图，则一次函数y=bx+c的图象不经过第_______________ 象限.8、若二次函数x2+bx+c的图象如图，则ac 0 （“V” “>”或“二”）9、已知二次函数y二ax'+bx+c（aH0）的图象如图所示，则在下列代数式：①ac；②a+b+c；③4a-2b+c；④2a+b；⑤圧-4ac中，值大于0的序号为__________________10、如图是二次函数y=ax2 + bx + c（a^0）的图象的一部分，给出下列命题：①a+b + c二0；②b>2a；③ax2+bx+c=0 的两根分别为一3 和1:④a—2b+c>0.其中正确的命题是 ______________ ・（只要求填写正确命题的序号）有以下结论：①abc>0；②a - b+c<0；③2d二b；④4a+2b+c>0；⑤若点（・2, y（）和（・3, y2）在该图象上，则yi>y2.其中正确的结论是 ______________ （填入正确结论的序号）.12、如图是二次函数ypx'+bx+c 的部分图像,在下列四个结论中正确的是 _________________① 不等式 ax 2+bx+c>0 的解集是-l<x<5；②a-b+c>0；③b 2-4ac>0；④4a+b<0.下列结论：①4a+b 二0；②9a+c>3b ；③8a+7b+2c>0；④当x>・1时，y 的值随x 值的增大而增大.其中正确的结论有 ______________________ （填序号）14>二次函数y=ax^+bx+c （aHO ）的图象如图所示，下列结论：①2a+b 二0；②a+c>b ；③抛物线与 x 轴的另一个交点为（3, 0）；④abc>0.其中正确的结论是 _____________________ （填写序号）.15、如图是二次函数y=ax 2+bx+c 图彖的一部分，图彖过点A （ - 3, 0）,对称轴为直线X 二・1,给 出四个结论:①b 2>4ac ；②2a+b 二0；③a+b+c>0；④若点B （ - 2. 5, yj , C （ - 0. 5, y 2）为函数图象上的两 点，则yi<y2.其中正确结论是 __________________ ・图象过点（-1, 0）,对称轴为直线x=2,16、如图，是二次函数y=ax2+bx+c (aHO)的图象的一部分，给出下列命题：①abc<0；②b>2a；③a+b+c二0④ax'+bx+c二0的两根分别为・3和1；⑤8a+c>0. 其中正确的命题是____________________________ ・17>二次函数y=ax2+bx+c (aHO)的图象如图所示，下列结论:①2a+b>0；②abc<0；③b2 - 4ac>0；④a+b+c<0；⑤la・2b+c<0,其中正确的个数是______________________ .y八18、如图，抛物线y=ax2+bx+c的对称轴是x=-l.且过点(0.5, 0),有下列结论：①abc>0；②a-2b+4c=0；③25a・ 10b+4c=0；④3b+2c>0；⑤a - b^m (am - b)；其中所有正确的结论是___________________ .(填写正确结论的序号)19、己知二次函数y=ax2+bx+c (aHO)的图象如图所示，纟合出以下结论: ®b2>4ac；②abc>0③2a-b=0；④8a+c<0；⑤9a+3b+c<0.其中结论正确的是___________ .(填正确结论的序号)x=l20、在二次函数y=ax2+bx+c的图彖如图所示，下列说法中：①b‘・4ac<0；②2占>0；③abc>0；®a-b-c>0,说法正确的是(填序号).21>已知二次函数y=ax2+bx+c (aHO)的图象如图所示，有下列5个结论：①c二0；②该抛物线的对称轴是直线x二・1；③当x=l时，y=2a；④am2+bm+a>0 (mH - 1)；⑤设A (100, yi) , B (・100, y2)在该抛物线上，则yi>y2.其中正确的结论有・(写出所有正确结论的序号)22、已知二次函数y=ax2+bx+c (aHO)的图象如图所示，则下列结论：①a+b+c<0；②a - b+c<0；③b+2a<0；④abc>0,其屮正确的是_________________ (填编号)23、如图是二次函数y=ax2+bx+c (aHO)图彖的一部分，现有下列结论：①abc<0；②b?・4ac+5> 0；③2a+b<0；④a-b+c<0；⑤抛物线y=ax2+bx+c (a^O)与x轴的另一个点坐标为(・1, 0), 其屮正确的是(把所有正确结论的序号都填在横线上)y八24、己知实数m, n满足m - n2=l,则代数式n/+2n2+4ni - 1的最小值等于_____________ •25、如图所示，己知二次函数y二ax'+bx+c的图象经过（-1, 0）和（0, -1）两点，则化简代数式_ 乎 + 4 + + 乎 _ 4 二 _______________ .\26如图，抛物线y二ax'+bx+c与x轴交于点A （・1, 0）,顶点坐标为（1, n）,与y轴的交点在（0, 2）、（0, 3）之间（包含端点），则下列结论：①当x>3时，y<0；②3a+b>0；③_2④3WnW4中，正确的是_______________27、已知二次函数y二ax'+bx+c的图象如图所示，有以下结论：①a+b+cVO；②a - b+c> 1；③abc>0；④4a - 2b+c<0；其中正确的结论是 ______________28、已知二次函数ypx'+bx+c的图象如图所示，它与x轴的两个交点分别为（-1, 0） , （3, 0）.对于下列命题：①b-2a=0；②abc<0；③a-2b+4c<0；④8a+c>0.其中正确的有___________________________ .29、已知二次函数y=ax2+bx+c (aHO)的图象如图所示，下列结论:①bV0；②4a+2b+c<0； (3)a・b+c>0；④(a+c) 2<b2.其中正确的是___________________ (把所有正确结论的序号都填在横线上).30^己知二次函数y二ax'+bx + c的图象如图所示，则下列结论：①c二2；②b2—4ac<0；③当x=l时，y的最小值为a+b+c中，正确的有___________________31、已知二次函数y=ax'+bx+c(a^O)的图像如图所示，(1)给出三个结论：①『-4眈>0；②c>0；③b>0,其中正确结论的序号是： ___________ ・(2)给出三个结论：①9a+3b+c〈0：②2c>3b；③8a+c>0，其中正确结论的序号是：________________32、已知抛物线y=ax2+bx+c(a^0)经过点(一1, 0),且顶点在第一象限.有下•列三个结论：①a<0；②a+b+c>0；③一2a >0.其中止确的结论有______________ .丄33>如图，抛物线yi=a (x+2) 2 - 3与2 (x・3) ?+1交于点A(l, 3),过点A作x轴的平行线, 分别交两条抛物线于点B, C.则以下结论：①无论x取何值，y2的值总是正数；②沪1；③当x=0 时，y2 - yi=4④2AB=3AC.34、如图，抛物线"曲"窈-3与卩飞“耳+1交于点八（］,3）,过点A作x轴的平行_2线，分别交两条抛物线于点B，C.则以下结论：①无论x収何值，乃的值总是正数；②■亍；③当x二0时，y2-yi二6；④AB+AC二10；⑤刃时乃°,其中正确结论的个数是： ________________ .35>函数y二x'+bx+c与y二x的图象如图所示，有以下结论：①b'-4c>0；②3b+c+6=0；③当lVx< 3时，x2+ （b - 1） x+c<0；④JQ+C? = 3迥.其屮正确的有 _______________ .36、如图抛物线y=ax2+bx+c与只轴的一个交点A在点（-2, 0）和（-1, 0）之间（包括这两个点）, 定点C是矩形DEFG上（包括边界和内部）的一个动点，贝9：（1）_____________ abc 0（填或“〉”；（2）___________________________ 8的取值范围是.1、答案为：V >;2、答案为：(1)> (2)< (3)> (4)>；3、答案为：>；4、答案为：四;5、答案为：①③④.6、答案为：①③④;7、答案为：四；8、答案为：<；9、答案为:10、答案为11、答案为12、答案为13、答案为14、答案为15、答案为16、答案为17、答案为18、答案为19、答案为20、答案为21、答案为22、答案为23、答案为24、答案为25、答案为26、答案为27、答案为28、答案为29、答案为30、答案为31、答案为32、答案为33、答案为34、答案为35、答案为①②⑤；①③；②④.①③；①③；①④.①④.①③④⑤.3.①③⑤.①②⑤；②③④.①②④⑤.②③.②、④.2a；①③.①③.©:①③④.①③；①；①③①②③；①④.①②④⑤,②③④；参考答案36、答案为：<。

二次函数系数a、b、c与图像的关系

二次函数系数a、b、c与图像的关系

二次函数系数a 、b 、c 与图像的关系一、首先就y=ax 2+bx+c （a≠0）中的a ，b ，c 对图像的作用归纳如下：1 a 的作用：决定开口方向：a > 0开口向上；a < 0开口向下；决定张口的大小：∣a ∣越大，抛物线的张口越小．2 b 的作用：b 和a 与抛物线图像的对称轴、顶点横坐标有关．b 与a 同号，说明02<-a b ，则对称轴在y 轴的左边；b 与a 异号，说明−b 2a >0，则对称轴在y 轴的右边；特别的，b = 0，对称轴为y 轴．3 c 的作用：c 决定了抛物线与y 轴的交点纵坐标．抛物线与y 轴的交点（0，c ） c > 0 抛物线与y 轴的交点在y 轴的正半轴；c < 0 抛物线与y 轴的交点在y 轴的负半轴；特别的，c = 0，抛物线过原点．4 a,b,c 共同决定判别式∆=b 2−4ac 的符号进而决定图象与x 轴的交点b 2−4ac >0 与x 轴两个交点b 2−4ac =0 与x 轴一个交点b 2−4ac <0 与x 轴没有交点5 几种特殊情况：x=1时，y=a + b + c ；x= -1时，y=a - b + c ．当x = 1时，∣ 若y > 0，则a + b + c >0；∣ 若y < 时0，则a + b + c < 0当x = -1时，∣ 若y > 0，则a - b + c >0；∣ 若y < 0，则a - b + c < 0．扩：x=2, y=4a + 2b + c ；x= -2, y=4a -2b + c ； x=3, y=9a +3 b + c ；x= -3, y=9a -3b + c 。

反之，给我们相应的二次函数图象，我们可以得到其系数a,b,c 以及它们组合成的一些关系结构（例如对称轴−b 2a ; 判别式b 2−4ac ; y =a +b +c ……等等）的符号二、经典例题讲解例1 已知二次函数()02≠++=a c b a χχγ的图像如图，则a 、b 、c 满足（ ） A ．a < 0，b < 0，c > 0 ；B ．a < 0，b < 0，c < 0 ；C ． a < 0，b > 0，c > 0 ；D ．a > 0，b < 0，c > 0 ；例2（2015呼和浩特）如图，四个二次函数的图像中分别对应的是： ∣2χγa =∣2χγb =∣2χγc =∣2χγd =，则a ， b ， c ， d 的大小关系是 ．A ．a > b > c > dB ．a > b > d > cC ．b > a > c > dD ．b > a > d > c例3已知二次函数y=ax 2+bx+c 的图象如图，其对称轴x=-1，给出下列结果①b 2＞4ac ；②abc ＞0；③2a+b=0；④a+b+c ＞0；⑤4a-2b+c ＜0，则正确的结论是（ ）A 、①②③④B 、②④⑤C 、②③④D 、①④⑤y xO x y O ① ② ④ ③练习1. （2015•重庆）已知抛物线y=ax 2+bx+c （a ≠0）在平面直角坐标系中的位置如图所示，则下列结论中，正确的是（ ）A 、a ＞0B 、b ＜0C 、c ＜0D 、a+b+c ＞02.（2015•文山州）已知二次函数y=ax 2+bx+c 的图象如图所示，则a ，b ，c 满足（ ）A 、a ＜0，b ＜0，c ＞0，b 2- 4ac ＞0B 、a ＜0，b ＜0，c ＜0，b 2- 4ac ＞0C 、a ＜0，b ＞0，c ＞0，b 2- 4ac ＞0D 、a ＞0，b ＜0，c ＞0，b 2- 4ac ＞03.（2015•泸州）已知二次函数y=ax 2+bx+c （a ，b ，c 为常数，a ≠0）的图象如图所示，有下列结论：①abc ＜0，②b 2- 4ac ＞0，③a-b+c=0，④a+b+c ＞0，其中正确结论的个数是（ ）A 、1B 、2C 、3D 、44.（2015•仙游县二模）已知二次函数y=ax 2+bx+c （a ≠0）的图象如图所示，给出以下结论： ①a+b+c ＜0； ②a ﹣b+c ＜0； ③b+2a ＜0； ④abc ＞0．\其中所有正确结论的序号是（ ）A ． ③④B ． ②③C ． ①④D ． ①②③y x O5.（2011•雅安）已知二次函数y=ax2+bx+c的图象如图，其对称轴x=-1，给出下列结果①b2＞4ac；②abc＞0；③2a+b=0；④a+b+c＞0；⑤a-b+c＜0，则正确的结论是（）A、①②③④B、②④⑤C、②③④D、①④⑤6.（2015•黔南州）如图所示为二次函数y=ax2+bx+c（a≠0）的图象，在下列选项中错误的是（）A、ac＜0B、x＞1时，y随x的增大而增大C、a+b+c＞0D、方程ax2+bx+c=0的根是x1=-1，x2=3能力提升1.已知二次函数y=ax2+bx+c（a≠0）的图象如下图所示，有下列5个结论：①abc＜0；②a-b+c＞0；③2a+b=0；④b2- 4ac＞0；⑤a+b+c＞m（am+b）+c（m＞1的实数），其中正确的结论有（）A．1个B．2个C．3个D．4个2.（2014•玉林一模）如图是二次函数y=ax2+bx+c图象的一部分，图象过点A（﹣3，0），对称轴为x=﹣1．给出四个结论：①b2＞4ac；②2a+b=0；③3a+c=0；④a+b+c=0．其中正确结论的个数是（）A．1个B．2个C．3个D．4个3.（2015•天津）已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有下列结论：①b2- 4ac＞0；②abc＞0；③8a+c＞0；④9a+3b+c＜0其中，正确结论的个数是（）A、1B、2C、3D、44. 如图所示，二次函数y=ax2+bx+c（a≠0）的图象经过点（-1，2），且与x轴交点的横坐标为x1、x2，其中-2＜x1＜-1，0＜x2＜1，下列结论：①abc＞0；②4a-2b+c＜0；③2a-b＞0；④b2+8a＞4ac，正确的结论是。

二次函数系数abc与图像的关系精选练习题

二次函数系数abc与图像的关系精选练习题

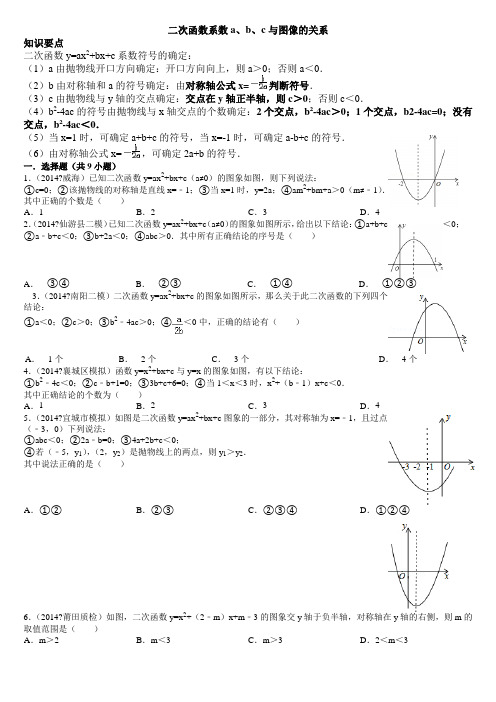
二次函数系数a、b、c与图像的关系知识要点二次函数y=ax2+bx+c系数符号的确定：（1）a由抛物线开口方向确定：开口方向向上，则a＞0；否则a＜0．（2）b由对称轴和a的符号确定：由对称轴公式x=判断符号．（3）c由抛物线与y轴的交点确定：交点在y轴正半轴，则c＞0；否则c＜0．（4）b2-4ac的符号由抛物线与x轴交点的个数确定：2个交点，b2-4ac＞0；1个交点，b2-4ac=0；没有交点，b2-4ac＜0．（5）当x=1时，可确定a+b+c的符号，当x=-1时，可确定a-b+c的符号．（6）由对称轴公式x=，可确定2a+b的符号．一．选择题（共9小题）1．（2014?威海）已知二次函数y=ax2+bx+c（a≠0）的图象如图，则下列说法：①c=0；②该抛物线的对称轴是直线x=﹣1；③当x=1时，y=2a；④am2+bm+a＞0（m≠﹣1）．其中正确的个数是（）A．1B．2C．3D．42．（2014?仙游县二模）已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，给出以下结论：①a+b+c＜0；②a﹣b+c＜0；③b+2a＜0；④abc＞0．其中所有正确结论的序号是（）A．③④B．②③C．①④D．①②③3．（2014?南阳二模）二次函数y=ax2+bx+c的图象如图所示，那么关于此二次函数的下列四个结论：①a＜0；②c＞0；③b2﹣4ac＞0；④＜0中，正确的结论有（）A．1个B．2个C．3个D．4个4．（2014?襄城区模拟）函数y=x2+bx+c与y=x的图象如图，有以下结论：①b2﹣4c＜0；②c﹣b+1=0；③3b+c+6=0；④当1＜x＜3时，x2+（b﹣1）x+c＜0．其中正确结论的个数为（）A．1B．2C．3D．45．（2014?宜城市模拟）如图是二次函数y=ax2+bx+c图象的一部分，其对称轴为x=﹣1，且过点（﹣3，0）下列说法：①abc＜0；②2a﹣b=0；③4a+2b+c＜0；④若（﹣5，y1），（2，y2）是抛物线上的两点，则y1＞y2．其中说法正确的是（）A．①②B．②③C．②③④D．①②④6．（2014?莆田质检）如图，二次函数y=x2+（2﹣m）x+m﹣3的图象交y轴于负半轴，对称轴在y轴的右侧，则m的取值范围是（）A．m＞2 B．m＜3 C．m＞3 D．2＜m＜37．（2014?玉林一模）如图是二次函数y=ax2+bx+c图象的一部分，图象过点A（﹣3，0），对称轴为x=﹣1．给出四个结论：①b2＞4ac；②2a+b=0；③3a+c=0；④a+b+c=0．其中正确结论的个数是（）A．1个B．2个C．3个D．4个8．（2014?乐山市中区模拟）如图，抛物线y=ax2+bx+c与x轴交于点A（﹣1，0），顶点坐标为（1，n），与y轴的交点在（0，2）、（0，3）之间（包含端点）．有下列结论：①当x＞3时，y＜0；②3a+b＞0；③﹣1≤a≤﹣；④≤n≤4．其中正确的是（）A．①②B．③④C．①③D．①③④9．（2014?齐齐哈尔二模）已知二次函数y=ax2+bx+c（a＞0）的图象与x轴交于点（﹣1，0），（x1，0），且1＜x1＜2，下列结论正确的个数为（）①b＜0；②c＜0；③a+c＜0；④4a﹣2b+c＞0．A．1个B．2个C．3个D．4个10、（2011?重庆）已知抛物线y=ax2+bx+c（a≠0）在平面直角坐标系中的位置如图所示，则下列结论中，正确的是（）A、a＞0B、b＜0C、c＜0D、a+b+c＞011、（2011?雅安）已知二次函数y=ax2+bx+c的图象如图，其对称轴x=-1，给出下列结果①b2＞4ac；②abc＞0；③2a+b=0；④a+b+c＞0；⑤a-b+c＜0，则正确的结论是（）A、①②③④B、②④⑤C、②③④D、①④⑤12、（2011?孝感）如图，二次函数y=ax2+bx+c的图象与y轴正半轴相交，其顶点坐标为（12，1），下列结论：①ac＜0；②a+b=0；③4ac-b2=4a；④a+b+c＜0．其中正确结论的个数是（）A、1B、2C、3D、4答案一．选择题（共9小题）1．（2014?威海）已知二次函数y=ax2+bx+c（a≠0）的图象如图，则下列说法：①c=0；②该抛物线的对称轴是直线x=﹣1；③当x=1时，y=2a；④am2+bm+a＞0（m≠﹣1）．其中正确的个数是（）A．1B．2C．3D．4考点：二次函数图象与系数的关系．分析：由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．解答：解：抛物线与y轴交于原点，c=0，（故①正确）；该抛物线的对称轴是：，直线x=﹣1，（故②正确）；当x=1时，y=a+b+c∵对称轴是直线x=﹣1，∴﹣b/2a=﹣1，b=2a，又∵c=0，∴y=3a，（故③错误）；x=m对应的函数值为y=am2+bm+c，x=﹣1对应的函数值为y=a﹣b+c，又∵x=﹣1时函数取得最小值，∴a﹣b+c＜am2+bm+c，即a﹣b＜am2+bm，∵b=2a，∴am2+bm+a＞0（m≠﹣1）．（故④正确）．故选：C．点评：本题考查了二次函数图象与系数的关系．二次函数y=ax2+bx+c（a≠0）系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点、抛物线与x轴交点的个数确定．2．（2014?仙游县二模）已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，给出以下结论：①a+b+c＜0；②a﹣b+c ＜0；③b+2a＜0；④abc＞0．其中所有正确结论的序号是（）A．③④B．②③C．①④D．①②③考点：二次函数图象与系数的关系．专题：数形结合．分析：由抛物线的开口方向判断a的符号，由抛物线与y轴的交点判断c的符号，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．解答：解：①当x=1时，y=a+b+c=0，故①错误；②当x=﹣1时，图象与x轴交点负半轴明显大于﹣1，∴y=a﹣b+c＜0，故②正确；③由抛物线的开口向下知a＜0，∵对称轴为0＜x=﹣＜1，∴2a+b＜0，故③正确；④对称轴为x=﹣＞0，a＜0∴a、b异号，即b＞0，由图知抛物线与y轴交于正半轴，∴c＞0∴abc＜0，故④错误；∴正确结论的序号为②③．故选：B．点评：二次函数y=ax2+bx+c系数符号的确定：（1）a由抛物线开口方向确定：开口方向向上，则a＞0；否则a＜0；（2）b由对称轴和a的符号确定：由对称轴公式x=﹣判断符号；（3）c由抛物线与y轴的交点确定：交点在y轴正半轴，则c＞0；否则c＜0；（4）当x=1时，可以确定y=a+b+c的值；当x=﹣1时，可以确定y=a﹣b+c的值．3．（2014?南阳二模）二次函数y=ax2+bx+c的图象如图所示，那么关于此二次函数的下列四个结论：①a＜0；②c＞0；③b2﹣4ac＞0；④＜0中，正确的结论有（）A．1个B．2个C．3个D．4个考点：二次函数图象与系数的关系．专题：数形结合．分析：由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．解答：解：①∵图象开口向下，∴a＜0；故本选项正确；②∵该二次函数的图象与y轴交于正半轴，∴c＞0；故本选项正确；③∵二次函数y=ax2+bx+c的图象与x轴有两个不相同交点，∴根的判别式△=b2﹣4ac＞0；故本选项正确；④∵对称轴x=﹣＞0，∴＜0；故本选项正确；综上所述，正确的结论有4个．故选D．点评：本题主要考查了二次函数的图象和性质，解答本题关键是掌握二次函数y=ax2+bx+c系数符号的确定，做题时要注意数形结合思想的运用，同学们加强训练即可掌握，属于基础题．4．（2014?襄城区模拟）函数y=x2+bx+c与y=x的图象如图，有以下结论：①b2﹣4c＜0；②c﹣b+1=0；③3b+c+6=0；④当1＜x＜3时，x2+（b﹣1）x+c＜0．其中正确结论的个数为（）A．1B．2C．3D．4考点：二次函数图象与系数的关系．分析：由函数y=x2+bx+c与x轴无交点，可得b2﹣4c＜0；当x=﹣1时，y=1﹣b+c＞0；当x=3时，y=9+3b+c=3；当1＜x＜3时，二次函数值小于一次函数值，可得x2+bx+c＜x，继而可求得答案．解答：解：∵函数y=x2+bx+c与x轴无交点，∴b2﹣4ac＜0；故①正确；当x=﹣1时，y=1﹣b+c＞0，故②错误；∵当x=3时，y=9+3b+c=3，∴3b+c+6=0；③正确；∵当1＜x＜3时，二次函数值小于一次函数值，∴x2+bx+c＜x，∴x2+（b﹣1）x+c＜0．故④正确．故选C．点评：主要考查图象与二次函数系数之间的关系．此题难度适中，注意掌握数形结合思想的应用．5．（2014?宜城市模拟）如图是二次函数y=ax2+bx+c图象的一部分，其对称轴为x=﹣1，且过点（﹣3，0）下列说法：①abc＜0；②2a﹣b=0；③4a+2b+c＜0；④若（﹣5，y1），（2，y2）是抛物线上的两点，则y1＞y2．其中说法正确的是（）A．①②B．②③C．②③④D．①②④考点：二次函数图象与系数的关系．分析：根据抛物线开口方向得到a＞0，根据抛物线的对称轴得b=2a＞0，则2a﹣b=0，则可对②进行判断；根据抛物线与y轴的交点在x轴下方得到c＜0，则abc＜0，于是可对①进行判断；由于x=﹣2时，y＜0，则得到4a﹣2b+c ＜0，则可对③进行判断；通过点（﹣5，y1）和点（2，y2）离对称轴的远近对④进行判断．解答：解：∵抛物线开口向上，∴a＞0，∵抛物线对称轴为直线x=﹣=﹣1，∴b=2a＞0，则2a﹣b=0，所以②正确；∵抛物线与y轴的交点在x轴下方，∴c＜0，∴abc＜0，所以①正确；∵x=2时，y＞0，∴4a+2b+c＞0，所以③错误；∵点（﹣5，y1）离对称轴要比点（2，y2）离对称轴要远，∴y1＞y2，所以④正确．故选D．点评：本题考查了二次函数图象与系数的关系：二次函数y=ax2+bx+c（a≠0），二次项系数a决定抛物线的开口方向和大小，当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口；一次项系数b和二次项系数a共同决定对称轴的位置：当a与b同号时（即ab＞0），对称轴在y轴左；当a与b异号时（即ab＜0），对称轴在y轴右．（简称：左同右异）．抛物线与y轴交于（0，c）．抛物线与x轴交点个数：△=b2﹣4ac＞0时，抛物线与x轴有2个交点；△=b2﹣4ac=0时，抛物线与x轴有1个交点；△=b2﹣4ac＜0时，抛物线与x轴没有交点．6．（2014?莆田质检）如图，二次函数y=x2+（2﹣m）x+m﹣3的图象交y轴于负半轴，对称轴在y轴的右侧，则m的取值范围是（）A．m＞2 B．m＜3 C．m＞3 D．2＜m＜3考点：二次函数图象与系数的关系．分析：由于二次函数的对称轴在y轴右侧，根据对称轴的公式即可得到关于m的不等式，由图象交y轴于负半轴也可得到关于m的不等式，再求两个不等式的公共部分即可得解．解答：解：∵二次函数y=x2+（2﹣m）x+m﹣3的图象交y轴于负半轴，∴m﹣3＜0，解得m＜3，∵对称轴在y轴的右侧，∴x=，解得m＞2，∴2＜m＜3．故选：D．点评：此题主要考查了二次函数的性质，解题的关键是利用对称轴的公式以及图象与y轴的交点解决问题．7．（2014?玉林一模）如图是二次函数y=ax2+bx+c图象的一部分，图象过点A（﹣3，0），对称轴为x=﹣1．给出四个结论：①b2＞4ac；②2a+b=0；③3a+c=0；④a+b+c=0．其中正确结论的个数是（）A．1个B．2个C．3个D．4个考点：二次函数图象与系数的关系．分析：由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．解答：解：∵抛物线的开口方向向下，∴a＜0；∵抛物线与x轴有两个交点，∴b2﹣4ac＞0，即b2＞4ac，①正确；由图象可知：对称轴x==﹣1，∴2a=b，2a+b=4a，∵a≠0，∴2a+b≠0，②错误；∵图象过点A（﹣3，0），∴9a﹣3b+c=0，2a=b，所以9a﹣6a+c=0，c=﹣3a，③正确；∵抛物线与y轴的交点在y轴的正半轴上，∴c＞0由图象可知：当x=1时y=0，∴a+b+c=0，④正确．故选C．点评：考查了二次函数图象与系数的关系，解答本题关键是掌握二次函数y=ax2+bx+c（a≠0）系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点、抛物线与x轴交点的个数确定．8．（2014?乐山市中区模拟）如图，抛物线y=ax2+bx+c与x轴交于点A（﹣1，0），顶点坐标为（1，n），与y轴的交点在（0，2）、（0，3）之间（包含端点）．有下列结论：①当x＞3时，y＜0；②3a+b＞0；③﹣1≤a≤﹣；④≤n≤4．其中正确的是（）A．①②B．③④C．①③D．①③④考点：二次函数图象与系数的关系．分析：①由抛物线的对称轴为直线x=1，一个交点A（﹣1，0），得到另一个交点坐标，利用图象即可对于选项①作出判断；②根据抛物线开口方向判定a的符号，由对称轴方程求得b与a的关系是b=﹣2a，将其代入（3a+b），并判定其符号；③根据两根之积=﹣3，得到a=，然后根据c的取值范围利用不等式的性质来求a的取值范围；④把顶点坐标代入函数解析式得到n=a+b+c=c，利用c的取值范围可以求得n的取值范围．解答：解：①∵抛物线y=ax2+bx+c与x轴交于点A（﹣1，0），对称轴直线是x=1，∴该抛物线与x轴的另一个交点的坐标是（3，0），∴根据图示知，当x＞3时，y＜0．故①正确；②根据图示知，抛物线开口方向向下，则a＜0．∵对称轴x==1，∴b=﹣2a，∴3a+b=3a﹣2a=a＜0，即3a+b＜0．故②错误；③∵抛物线与x轴的两个交点坐标分别是（﹣1，0），（3，0），∴﹣1×3=﹣3，=﹣3，则a=．∵抛物线与y轴的交点在（0，2）、（0，3）之间（包含端点），∴2≤c≤3，∴﹣1≤≤，即﹣1≤a≤．故③正确；④根据题意知，a=，=1，∴b=﹣2a=，∴n=a+b+c=c．∵2≤c≤3，≤≤4，≤n≤4．故④正确．综上所述，正确的说法有①③④．故选D．点评：本题考查了二次函数图象与系数的关系．二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定．9．（2014?齐齐哈尔二模）已知二次函数y=ax2+bx+c（a＞0）的图象与x轴交于点（﹣1，0），（x1，0），且1＜x1＜2，下列结论正确的个数为（）①b＜0；②c＜0；③a+c＜0；④4a﹣2b+c＞0．A．1个B．2个C．3个D．4个考点：二次函数图象与系数的关系．分析：由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．解答：解：①∵y=ax2+bx+c（a＞0）的图象与x轴交于点（﹣1，0），（x1，0），且1＜x1＜2，∴对称轴在y轴的右侧，即：﹣＞0，∵a＞0∴b＜0，故①正确；②显然函数图象与y轴交于负半轴，∴c＜0正确；③∵二次函数y=ax2+bx+c（a＞0）的图象与x轴交于点（﹣1，0），∴a﹣b+c=0，即a+c=b，∵b＜0，∴a+c＜0正确；④∵二次函数y=ax2+bx+c（a＞0）的图象与x轴交于点（﹣1，0），且a＞0，∴当x=﹣2时，y=4a﹣2b+c＞0，故④正确，故选D．点评：主要考查图象与二次函数系数之间的关系，会利用对称轴的范围求2a与b的关系，以及二次函数与方程之间的转换，根的判别式的熟练运用．。

二次函数的图像与系数a、b、c的关系经典习题

二次函数的图像与系数a、b、c的关系经典习题

A B CD yOx yO x yO x yO x yO x 一、二次函数图像与系数a 、b 、c 、关系1、二次函数y =ax 2+bx +c （a ≠０）的图象如图2所示，则点c M b a ⎛⎫⎪⎝⎭，在（ ）A 、第一象限B 、第二象限C 、第三象限D 、第四象限 2、如图，若a ＜0，b ＞0，c ＜0，则抛物线y=ax 2＋bx ＋c 的大致图象为（ ）3、二次函数2(0)y ax bx c a =++≠的图象如图所示，则下列说法不正确的是（ ）A 、240b ac ->B 、0a >C 、0c >D 、02ba-< 4、二次函数y =ax 2+bx +c 的图象如图3所示，则下列关于a ，b ，c 间关系的判断正确的是（ ） A 、ab ＜0 B 、bc ＜0 C 、a +b +c ＞0 D 、a -b +c ＜05、 二次函数c bx ax y ++=2，图象如图所示，则反比例函数xab y =的图象的两个分支分别在第 象限。

6、已知反比例函数xky =的图象如图所示，则二次函数222k x kx y +-=的图象大致为( )7、二次函数y=ax 2与一次函数y=ax ＋a 在同一坐标系中的图象大致为（ ）8、函数y=ax 2＋bx ＋c 和y=ax ＋b 在同一坐标系中，如图所示，则正确的是（ ）9、在同一直角坐标系内，二次函数y=ax 2＋（a ＋c ）x ＋c 与一次函数y=ax ＋c 的大致图象，有且只有一个是正确的，正确的是（ ）10、二次函数y=ax 2＋bx ＋c 与一次函数y=ax ＋c 在同一坐标系中的图象大致是图中的（ ）11、在同一坐标系中，函数y=ax 2＋bx 与y=xb的图象大致是图中的（ ）12、已知a ＜0，b ＞0，c ＞0，那么抛物线y =ax 2+bx +c 的顶点在（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限 13、已知二次函数y =ax 2+bx +c 的图象如图1所示，则a ，b ，c 满足（ ）A ．a ＜0，b ＜0，c ＞0B ．a ＜0，b ＜0，c ＜0C ．a ＜0，b ＞0，c ＞0D ．a ＞0，b ＜0，c ＞014、二次函数y =ax 2+bx +c （a ≠０）的图象如图2所示，则点c M b a ⎛⎫⎪⎝⎭，在（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限15、已知二次函数2y ax bx c =++（其中000a b c >><，，），关于这个二次函数的图象有如下说法：①图象的开口一定向上；②图象的顶点一定在第四象限；③图象与x 轴的交点至少有一个在y 轴的右侧．以上说法正确的个数为（ ）A ．0 B ．1 C ．2 D ．3二、⊿的符号的判定例1、下图中⊿0<的是（ ）（A ） （B ） （C ） （D ） （图3）练习：不论x 为何值,函数y=ax 2+bx+c(a ≠0)的值恒大于0的条件是( )A.a>0,△>0;B.a>0, △<0;C.a<0, △<0;D.a<0, △<0 三、含a 、b 的代数式符号的判定例1、抛物线y=x 2+2x-4的对称轴是直线（ ）.A.x=-2B.x=2C.x=-1D.x=1Oy x Oy x y x O y x O ..C A y xOy–1 3 3O xP1 -1O x =1yxy–1 3 3O xP 1 练习：二次函数)1)(3(2-+-=x x y 的图象的对称轴是直线________________．例2、二次函数2(0)y ax bx c a =++≠的图象如图3所示，则①20a b +>②20a b +<③02ba-<④20a b -<⑤20a b ->中正确的有________________________.(请写出序号即可)图4 图5练习：1、二次函数2(0)y ax bx c a =++≠的图象如图4所示，则下列说法不正确的是（ ） A ．240b ac ->B ．0a >C ．0c >D ．02ba-< 例1、如图5，抛物线)0(2>++=a c bx ax y 的对称轴是直线1=x ，且经过点P （3，0），则cb a +-的值为 （ ）A. 0 B. －1 C. 1 D. 2练习：已知a －b ＋c=0 9a ＋3b ＋c=0,则二次函数y=ax 2＋bx ＋c 的图像的顶点可能在（ ） （A ）第一或第二象限； （B ）第三或第四象限；（C ）第一或第四象限； （D ）第二或第三象限例2已知二次函数c bx ax y ++=2的图象如图所示，那么下列判断正确的是（ ）(A)abc ＞0 （B ）ac b 42-＞0(C)2a+b ＞0 （D ）c b a +-24＜0练习：1、已知二次函数2y ax bx c =++（0a ≠）的图象如图所示，有下列4个结论：①0abc >；②b a c <+；③420a b c ++>；④240b ac ->；其中正确的结论有（ ）A ．1个 B ．2个 C ．3个 D ．4个2、抛物线y=ax 2+bx+c 的图象如图6，OA=OC ，则（ ）（A ） ac+1=b; （B ） ab+1=c; （C ）bc+1=a; （D ）以上都不是图4 图5 图6图2y 0 1x-1 图1O xy-11作业：1、若二次函数c bx ax y ++=2中，a ＜0，b ＞0，c ＜0，042>-ac b ，则此二次函数图像不经过（ ） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限2、当a>0, b<0,c>0时,下列图象有可能是抛物线y=ax 2+bx+c 的是（ ）3、二次函数c bx ax y ++=2的图象如图1所示，则下列结论中，正确的个数是（ ）①0<++c b a ；②0>+-c b a ；③0>abc ；④a b 2= （A ）4（B ）3（C ）2 （D ）14、已知二次函数c bx ax y ++=2的图象如图2所示，那么下列判断不正确的是（ ） (A)abc ＞0； （B ）ac b 42-＞0；(C)2a+b ＞0； （D ）c b a +-24＜05、二次函数c bx ax y ++=2的图象如图所示，则 abc ，ac b 42-，b a +2，c b a ++这四个式子中， 值为正数的有（ ）A ．4个 B ．3个 C ．2个 D ．1个6、二次函数y =ax 2+bx +c 的图象如图3所示，则下列关于a ，b ，c 间关系的判断正确的是（ ） A ．ab ＜0 B ．bc ＜0 C ．a +b +c ＞0 D ．a -b +c ＜07、(2008年安徽省)如图为二次函数y=ax 2＋bx ＋c 的图象，在下列说法中：① ac ＜0； ②方程ax 2＋bx ＋c=0的根是x 1= －1, x 2= 3 ② a ＋b ＋c ＞0 ④当x ＞1时，y 随x 的增大而增大。

二次函数中各项系数abc与图像的关系

二次函数中各项系数abc与图像的关系

二次函数中各项系数a ;b ;c 与图像的关系一、首先就y=ax 2+bx+ca≠0中的a ;b ;c 对图像的作用归纳如下：1 a 的作用：决定开口方向：a > 0开口向上；a < 0开口向下；决定张口的大小：∣a ∣越大;抛物线的张口越小．2 b 的作用：b 和a 与抛物线图像的对称轴、顶点横坐标有关．b 与a 同号;说明02<-ab ;则对称轴在y 轴的左边； b 与a 异号;说明−b 2b >0;则对称轴在y 轴的右边；特别的;b = 0;对称轴为y 轴．3 c 的作用：c 决定了抛物线与y 轴的交点纵坐标．抛物线与y 轴的交点0;cc > 0 抛物线与y 轴的交点在y 轴的正半轴；c < 0 抛物线与y 轴的交点在y 轴的负半轴；特别的;c = 0;抛物线过原点．4 a;b;c 共同决定判别式?=b 2−4bb 的符号进而决定图象与x 轴的交点b 2−4bb >0 与x 轴两个交点b 2−4bb =0 与x 轴一个交点b 2−4bb <0 与x 轴没有交点5 几种特殊情况：x=1时;y=a + b + c ；x= -1时;y=a - b + c ．当x = 1时;① 若y > 0;则a + b + c >0；② 若y < 时0;则a + b + c < 0当x = -1时;① 若y > 0;则a - b + c >0；② 若y < 0;则a - b + c < 0．扩：x=2; y=4a + 2b + c ；x= -2; y=4a -2b + c ； x=3; y=9a +3 b + c ；x= -3; y=9a -3b + c ..一．选择题共8小题1．已知二次函数y=ax 2+bx+c 的图象大致如图所示;则下列关系式中成立的是A ．a ＞0B ．b ＜0C ．c ＜0D ．b+2a ＞02．如果二次函数y=ax 2+bx+ca ≠0的图象如图所示;那么下列不等式成立的是A ．a ＞0B ．b ＜0C ．ac ＜0D ．bc ＜0．3．已知二次函数y=ax 2+bx+ca ≠0的图象如图所示;有下列4个结论：①abc ＞0；②b ＜a+c ；③4a+2b+c ＞0；④b 2﹣4ac ＞0；其中正确的结论有A ．1个B ．2个C ．3个D ．4个4．二次函数y=ax 2+bx+ca ≠0的图象如图所示;对于下列结论：①a ＜0；②b ＜0；③c ＞0；④2a+b=0；⑤a ﹣b+c ＜0;其中正确的个数是A ．4个B ．3个C ．2个D ．1个第3题图 第4题图 第5题图 第6题图5．二次函数y=ax 2+bx+ca ≠0的图象如图;给出下列四个结论：：①a ＜0；②b ＞0；③b 2﹣4ac＞0；④a+b+c ＜0；其中结论正确的个数有A ．1个B ．2个C ．3个D ．4个6．如图所示;抛物线y=ax 2+bx+c 的顶点为﹣1;3;以下结论：①b 2﹣4ac ＜0；②4a ﹣2b+c ＜0；③2c ﹣b=3；④a+3=c;其中正确的个数A ．1B ．2C ．3D ．47．如图是二次函数y=ax 2+bx+c 图象的一部分;图象过点A ﹣3;0;对称轴为直线x=﹣1;下列给出四个结论中;正确结论的个数是 个①c ＞0；②若点B ﹣;y 1、C ﹣;y 2为函数图象上的两点;则y 1＜y 2；③2a ﹣b=0； ④＜0；⑤4a ﹣2b+c ＞0．A ．2B ．3C ．4D ．58．二次函数y=ax 2+bx+c 的图象如图所示;以下结论：①abc ＞0；②4ac ＜b 2；③2a+b ＞0；④当x ＜时;y 随x 的增大而减小；⑤a+b+c ＞0．其中正确的有A ．5个B ．4个C ．3个D ．2个二．填空题共4小题9．如图;抛物线y=ax 2+bx+ca ≠0的对称轴为直线x=1;与x 轴的一个交点坐标为﹣1;0;其部分图象如图所示;下列结论：①4ac ＜b 2；②方程ax 2+bx+c=0的两个根是x 1=﹣1;x 2=3；③3a+c ＞0；④当y ＞0时;x 的取值范围是﹣1≤x ＜3；⑤当x ＜0时;y 随x 增大而增大； 其中结论正确有 ．10．一抛物线和抛物线y=﹣2x 2的形状、开口方向完全相同;顶点坐标是﹣1;3;则该抛物线的解析式为 ．11．抛物线y=ax 2+12x ﹣19顶点横坐标是3;则a= ．12．将二次函数y=x 2+6x+5化为y=ax ﹣h 2+k 的形式为 ．三．解答题共7小题13．已知：抛物线y=﹣x 2+bx+c 经过点B ﹣1;0和点C2;3．1求此抛物线的表达式；2如果此抛物线沿y 轴平移一次后过点﹣2;1;试确定这次平移的方向和距离．14．函数y=m+2是关于x 的二次函数;求：1满足条件的m 值；2m 为何值时;抛物线有最低点 求出这个最低点．这时;当x 为何值时;y 随x的增大而增大3m 为何值时;函数有最大值 最大值是多少 这时;当x 为何值时;y 随x 的增大而减小．15．已知二次函数的图象经过0;0﹣1;﹣1;1;9三点．1求这个函数的解析式；2求这个函数图象的顶点坐标．16．已知抛物线的顶点坐标是1;﹣4;且经过点0;﹣3;求与该抛物线相应的二次函数表达式．17．已知二次函数y=x2﹣4x+5．1将y=x2﹣4x+5化成y=a x﹣h2+k的形式；2指出该二次函数图象的对称轴和顶点坐标；3当x取何值时;y随x的增大而增大18．如图;二次函数的图象的顶点坐标为1;;现将等腰直角三角板直角顶点放在原点O;一个锐角顶点A在此二次函数的图象上;而另一个锐角顶点B在第二象限;且点A的坐标为2;1．1求该二次函数的表达式；2判断点B是否在此二次函数的图象上;并说明理由．19．已知二次函数y=ax﹣h2;当x=4时有最大值;且此函数的图象经过点1;﹣3．1求此二次函数的解析式；2当x为何值时;y随x的增大而增大。

二次函数系数a、b、c与图像的关系专项练习

二次函数系数a、b、c与图像的关系专项练习

二次函数系数a 、b 、c 与图像的关系专项练习知识要点二次函数y=ax 2+bx+c 系数符号的确定：（1）a 由抛物线开口方向确定：开口方向向上，则a ＞0；否则a ＜0．（2）b 由对称轴和a 的符号确定：由对称轴公式x=判断符号．（3）c 由抛物线与y 轴的交点确定：交点在y 轴正半轴，则c ＞0；否则c ＜0．（4）b 2-4ac 的符号由抛物线与x 轴交点的个数确定：2个交点，b 2-4ac ＞0；1个交点，b2-4ac=0；没有交点，b 2-4ac ＜0．（5）当x=1时，可确定a+b+c 的符号，当x=-1时，可确定a-b+c 的符号．（6）由对称轴公式x=，可确定2a+b 的符号．一．选择题（共9小题）1．已知二次函数y=ax 2+bx+c （a ≠0）的图象如图，则下列说法：①c=0；②该抛物线的对称轴是直线x=﹣1；③当x=1时，y=2a ；④am 2+bm+a ＞0（m ≠﹣1）．其中正确的个数是（）A ．1B ．2C ．3D ．42．已知二次函数y=ax 2+bx+c （a ≠0）的图象如图所示，给出以下结论：①a+b+c ＜0；②a ﹣b+c ＜0；③b+2a ＜0；④abc ＞0．其中所有正确结论的序号是（）A ．③④B ．②③C ．①④D ．①②③3．二次函数y=ax 2+bx+c 的图象如图所示，那么关于此二次函数的下列四个结论：①a ＜0；②c ＞0；③b 2﹣4ac ＞0；④＜0中，正确的结论有（）A ．1个B ．2个C ．3个D ．4个4．函数y=x 2+bx+c 与y=x 的图象如图，有以下结论：①b 2﹣4c ＜0；②c ﹣b+1=0；③3b+c+6=0；④当1＜x ＜3时，x 2+（b ﹣1）x+c ＜0．其中正确结论的个数为（）A ．1B ．2C ．3D ．45．如图是二次函数y=ax 2+bx+c 图象的一部分，其对称轴为x=﹣1，且过点（﹣3，0）下列说法：①abc ＜0；②2a ﹣b=0；③4a+2b+c ＜0；④若（﹣5，y 1），（2，y 2）是抛物线上的两点，则y 1＞y 2．其中说法正确的是（）A ．①②B ．②③C ．②③④D ．①②④6．如图，二次函数y=x 2+（2﹣m ）x+m ﹣3的图象交y 轴于负半轴，对称轴在y 轴的右侧，则m 的取值范围是（）A ．m ＞2B ．m ＜3C ．m ＞3D ．2＜m ＜37．如图是二次函数y=ax 2+bx+c 图象的一部分，图象过点A （﹣3，0），对称轴为x=﹣1．给出四个结论：①b 2＞4ac ；②2a+b=0；③3a+c=0；④a+b+c=0．其中正确结论的个数是（）A ．1个B ．2个C ．3个D ．4个8．如图，抛物线y=ax 2+bx+c 与x 轴交于点A （﹣1，0），顶点坐标为（1，n ），与y 轴的交点在（0，2）、（0，3）之间（包含端点）．有下列结论：①当x ＞3时，y ＜0；②3a+b ＞0；③﹣1≤a ≤﹣；④≤n ≤4．其中正确的是（）A ．①②B ．③④C ．①③D ．①③④9．已知二次函数y=ax 2+bx+c （a ＞0）的图象与x 轴交于点（﹣1，0），（x 1，0），且1＜x 1＜2，下列结论正确的个数为（）①b ＜0；②c ＜0；③a+c ＜0；④4a ﹣2b+c ＞0．A ．1个B ．2个C ．3个D ．4个10、已知抛物线y=ax 2+bx+c （a ≠0）在平面直角坐标系中的位置如图所示，则下列结论中，正确的是（）A 、a ＞0 B 、b ＜0 C 、c ＜0 D 、a+b+c ＞011、已知二次函数y=ax 2+bx+c 的图象如图，其对称轴x=-1，给出下列结果①b 2＞4ac ；②abc ＞0；③2a+b=0；④a+b+c ＞0；⑤a-b+c ＜0，则正确的结论是（）A 、①②③④B 、②④⑤C 、②③④D 、①④⑤12、如图，二次函数y=ax 2+bx+c 的图象与y 轴正半轴相交，其顶点坐标为（12，1），下列结论：①ac ＜0；②a+b=0；③4ac-b 2=4a ；④a+b+c ＜0．其中正确结论的个数是（）A 、1B 、2C 、3D 、4答案一．选择题（共9小题）1．已知二次函数y=ax 2+bx+c （a ≠0）的图象如图，则下列说法：①c=0；②该抛物线的对称轴是直线x=﹣1；③当x=1时，y=2a ；④am 2+bm+a＞0（m ≠﹣1）．其中正确的个数是（）A ．1B ．2C ．3D ．4考点：二次函数图象与系数的关系．分析：由抛物线与y 轴的交点判断c 与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．解答：解：抛物线与y 轴交于原点，c=0，（故①正确）；该抛物线的对称轴是：，直线x=﹣1，（故②正确）；当x=1时，y=a+b+c∵对称轴是直线x=﹣1，∴﹣b/2a=﹣1，b=2a ，又∵c=0，∴y=3a ，（故③错误）；x=m 对应的函数值为y=am 2+bm+c ，x=﹣1对应的函数值为y=a ﹣b+c ，又∵x=﹣1时函数取得最小值，∴a ﹣b+c ＜am 2+bm+c ，即a ﹣b ＜am 2+bm ，∵b=2a ，∴am 2+bm+a ＞0（m ≠﹣1）．（故④正确）．故选：C ．点评：本题考查了二次函数图象与系数的关系．二次函数y=ax 2+bx+c （a ≠0）系数符号由抛物线开口方向、对称轴、抛物线与y 轴的交点、抛物线与x轴交点的个数确定．2．已知二次函数y=ax 2+bx+c （a ≠0）的图象如图所示，给出以下结论：①a+b+c ＜0；②a ﹣b+c ＜0；③b+2a ＜0；④abc ＞0．其中所有正确结论的序号是（）A ．③④B ．②③C ．①④D ．①②③考点：二次函数图象与系数的关系．专题：数形结合．分析：由抛物线的开口方向判断a 的符号，由抛物线与y 轴的交点判断c 的符号，然后根据对称轴及抛物线与x 轴交点情况进行推理，进而对所得结论进行判断．解答：解：①当x=1时，y=a+b+c=0，故①错误；②当x=﹣1时，图象与x 轴交点负半轴明显大于﹣1，∴y=a ﹣b+c ＜0，故②正确；③由抛物线的开口向下知a ＜0，∵对称轴为0＜x=﹣＜1，∴2a+b ＜0，故③正确；④对称轴为x=﹣＞0，a＜0∴a、b异号，即b＞0，由图知抛物线与y轴交于正半轴，∴c＞0 ∴abc＜0，故④错误；∴正确结论的序号为②③．故选：B．点评：二次函数y=ax2+bx+c系数符号的确定：（1）a由抛物线开口方向确定：开口方向向上，则a＞0；否则a＜0；（2）b由对称轴和a的符号确定：由对称轴公式x=﹣判断符号；（3）c由抛物线与y轴的交点确定：交点在y轴正半轴，则c＞0；否则c＜0；（4）当x=1时，可以确定y=a+b+c的值；当x=﹣1时，可以确定y=a﹣b+c的值．3．二次函数y=ax 2+bx+c的图象如图所示，那么关于此二次函数的下列四个结论：①a＜0；②c＞0；③b2﹣4ac＞0；④＜0中，正确的结论有（）A．1个B．2个C．3个D．4个考点：二次函数图象与系数的关系．专题：数形结合．分析：由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c 与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．解解：①∵图象开口向下，∴a＜0；故本选项正确；答：②∵该二次函数的图象与y轴交于正半轴，∴c＞0；故本选项正确；③∵二次函数y=ax2+bx+c的图象与x轴有两个不相同交点，∴根的判别式△=b2﹣4ac＞0；故本选项正确；④∵对称轴x=﹣＞0，∴＜0；故本选项正确；综上所述，正确的结论有4个．故选D．点评：本题主要考查了二次函数的图象和性质，解答本题关键是掌握二次函数y=ax2+bx+c系数符号的确定，做题时要注意数形结合思想的运用，同学们加强训练即可掌握，属于基础题．4．函数y=x2+bx+c与y=x的图象如图，有以下结论：①b2﹣4c＜0；②c﹣b+1=0；③3b+c+6=0；④当1＜x＜3时，x2+（b﹣1）x+c＜0．其中正确结论的个数为（）A．1B．2C．3D．4考点：二次函数图象与系数的关系．分析：由函数y=x2+bx+c与x轴无交点，可得b2﹣4c＜0；当x=﹣1时，y=1﹣b+c＞0；当x=3时，y=9+3b+c=3；当1＜x＜3时，二次函数值小于一次函数值，可得x2+bx+c＜x，继而可求得答案．解答：解：∵函数y=x2+bx+c与x轴无交点，∴b2﹣4ac＜0；故①正确；当x=﹣1时，y=1﹣b+c＞0，故②错误；∵当x=3时，y=9+3b+c=3，∴3b+c+6=0；。

专题训练(二) 二次函数系数a,b,c与图象的关系

专题训练(二) 二次函数系数a,b,c与图象的关系

专题训练(二)二次函数y=ax2+bx+c(a≠0)的系数a,b,c与图象的关系知识储备二次函数y=ax2+bx+c的图象与字母系数a,b,c 之间的关系:项目字母字母的符号图象的特征a a>0 开口向上a<0 开口向下bb=0 对称轴为y轴ab>0(b与a同号) 对称轴在y轴左侧ab<0(b与a异号) 对称轴在y轴右侧c c=0 经过原点c>0 与y轴正半轴相交c<0 与y轴负半轴相交b2-4ac b2-4ac=0与x轴有一个交点(顶点)b2-4ac>0 与x轴有两个交点b2-4ac<0 与x轴没有交点特殊关系当x=1时,y=a+b+c;当x=-1时,y=a-b+c当x=2时,y=4a+2b+c;当x=-2时,y=4a-2b+c若a+b+c>0,则当x=1时,y>0若a-b+c>0,则当x=-1时,y>0当对称轴为直线x=1时,2a+b=0;当对称轴为直线x=-1时,2a-b=0;判断2a+b的值大于还是小于0,看对称轴与直线x=1的位置关系;判断2a-b的值大于还是小于0,看对称轴与直线x=-1的位置关系▶类型一利用二次函数图象考查以上表格中的问题1.[2020·宁波江北区期末]二次函数y=ax2+bx+c(a≠0)的图象如图1所示,则下列关系式错误的是()A.a<0B.b>0C.b2-4ac>0D.a+b+c<0图 1 图22.[2020·宁波]如图2,二次函数y=ax2+bx+c(a>0)的图象与x轴交于A,B两点,与y轴正半轴交于点C,它的对称轴为直线x=-1.则下列选项中正确的是A.abc<0 B.4ac-b2>0C.c-a>0D.当x=-n2-2(n为实数)时,y≥c3.在同一平面直角坐标系内,二次函数y=ax2+bx+b(a≠0)与一次函数y=ax+b的图象可能是()图 3▶类型二利用二次函数图象考查ma+nc或mb+nc(m,n为非零整数)与0的关系4.如图4,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1.给出下列结论:①ac<0;②b2-4ac>0;③2a-b=0;④a-b+c=0.其中,正确的结论有()图4A.1个B.2个C.3个D.4个5.[2020·遵义改编]抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=-2,抛物线与x轴的一个交点在点(-4, 0)和点(-3,0)之间,其部分图象如图5所示,下列结论中正确的有()①4a-b=0;②c≤3a;③关于x的方程ax2+bx+c=2有两个不相等的实数根;④b2+2b>4ac.图5A.1个B.2个C.3个D.4个▶类型三利用二次函数图象考查am2+bm+c(a≠0,a,b,c为常数)与a+b+c的关系6.已知二次函数y=ax2+bx+c(a≠0)图象的对称轴为直线x=1,其图象如图6所示,现有下列结论:①abc>0,②b-2a<0,③a-b+c>0,④a+b>n(an+b)(n ≠1),⑤2c<3b.其中正确的是()A.①③B.②⑤C.③④D.④⑤图6 图77.抛物线y=ax2+bx+c(a≠0)的一部分如图7所示,与x轴的一个交点坐标为(4,0),抛物线的对称轴是直线x=1,有下列结论:①abc>0;②2a+b=0;③方程ax2+bx+c=3有两个不相等的实数根;④抛物线与x 轴的另一个交点坐标为(-2,0);⑤若点A(m,n)在该抛物线上,则am2+bm+c≤a+b+c.其中正确的有() A.5个B.4个C.3个D.2个▶类型四利用二次函数图象解一元二次方程或不等式8.若二次函数y=x2+bx的图象的对称轴是经过点(2,0)且平行于y轴的直线,则关于x的方程x2+bx=5的解为()A.x1=0,x2=4B.x1=1,x2=5C.x1=1,x2=-5D.x1=-1,x2=59.二次函数y=ax2+bx+c(a≠0)的图象如图8所示,则关于x的不等式ax2+bx+c>0的解是()图8A.x<-1B.x>3C.-1<x<3D.x<-1或x>3▶类型五利用一次函数、二次函数的图象解一元二次方程或不等式10.如图9所示,一次函数y1=kx+n(k≠0)与二次函数y2=ax2+bx+c(a≠0)的图象相交于A(-1,5),B(9,2)两点,则关于x的不等式kx+n≥ax2+bx+c的解为()图9A.-1≤x≤9B.-1≤x<9C.-1<x≤9D.x≤-1或x≥911.二次函数y=ax2+bx+c(a≠0)和正比例函数y=23x的图象如图10所示,则方程ax2+（32b x+c=0的两根之和()图10A.大于0B.等于0C.小于0D.不能确定专题二教师详解详析1.D[解析] 抛物线开口向下,则a<0,所以A选项的关系式正确;抛物线的对称轴在y轴的右侧,a,b异号,则b>0,所以B选项的关系式正确;抛物线与x轴有2个交点,则b2-4ac>0,所以C选项的关系式正确;当x=1时,y>0,则a+b+c>0,所以D选项的关系式错误.故选D.2.D[解析] ∵二次函数图象的对称轴为直线x=-1,∴-b2a=-1,∴b=2a.又∵a>0,∴b>0.∵抛物线与y轴正半轴交于点C,∴c>0,∴abc>0,故A错误;∵抛物线与x轴有两个不同的交点,∴b2-4ac>0,∴4ac-b2<0,故B错误;∵b=2a,∴当x=-1时,y=a-b+c=c-a<0,故C 错误;当x=-n2-2(n为实数)时,y=a(-n2-2)2+b(-n2-2)+c=a(-n2-2)2+2a(-n2-2)+c=a( n2+1)2-a+c.∵n为实数,∴n2≥0,(n2+1)2≥1.又∵a>0,∴a(n2+1)2-a≥0,∴y≥c,故D正确,因此本题选D.3.C4.C[解析] ∵抛物线开口向下,∴a<0.∵抛物线交y轴于正半轴,∴c>0,∴ac<0,故①正确;∵抛物线与x轴有两个交点,∴b2-4ac>0,故②正确;∵抛物线的对称轴为直线x=1,∴-b2a=1,∴-b=2a,∴2a+b=0,故③错误;∵抛物线与x轴的两个交点关于对称轴对称,∴点(3,0)关于直线x=1的对称点为(-1,0),即抛物线经过点(-1,0),∴a-b+c=0,故④正确.综上可知,正确的结论有①②④,共3个.5.C[解析] 由-b2a=-2,得4a-b=0,故①正确;由抛物线与x轴的一个交点在点(-4,0)和点(-3,0)之间,当x≤-2时,y随x的增大而增大,可知当x=-3时,y>0,由抛物线的对称性可知,当x=-1时,y>0,即a-b+c>0.又4a=b,∴a-4a+c>0,即c>3a.故②错误; 由图象得,关于x的方程ax2+bx+c=2有两个不相等的实数根正确; 由4ac-b24a=3,得4ac-b2=12a,∴4ac=12a+b2=3b+b2.易知a<0,b<0,c<0,∴4ac<2b+b2 ,故④正确.故选C.6.D[解析] ①由图象可知:a<0,b>0,c>0,∴abc<0,故此选项错误;②当x=-2时,y=4a-2b+c<0,即b-2a>c2>0,故此选项错误;③当x=-1时,y=a-b+c<0,故此选项错误;④当x=1时,y的值最大,此时,y=a+b+c,而当x=n 时,y=an2+bn+c,所以a+b+c>an2+bn+c(n≠1),故a+b>an2+bn,即a+b>n(an+b)(n≠1),故此选项正确.⑤由抛物线的对称性可知当x=3时函数值小于0,即y=9a+3b+c<0.∵抛物线的对称轴为直线x=-b2a=1,∴a=-b2,代入9a+3b+c<0,得9-b2 +3b+c<0,得2c<3b,故此选项正确;故④⑤正确.因此本题选D.7.B8.D9.D[解析] 根据图象可知,当y=0时,对应的x的值分别为x1=-1,x2=3.当y>0时,函数的图象在x轴的上方,由左边一段图象可知x<-1,由右边一段图象可知x>3.因此,当函数值y>0时,x的取值范围是x<-1或x>3.故选D.10.A[解析] 由图象可以看出:二次函数y2=ax2+bx+c(a≠0)和一次函数y1=kx+n(k≠0)的图象的交点的横坐标分别为-1,9.而当y1≥y2时,对应的图象正好在两交点之间,所以-1≤x≤9.故选A.11.A。

专题：二次函数系数abc与图象的关系(压轴题)

专题：二次函数系数abc与图象的关系(压轴题)

专题 二次函数的图象与系数a 、b 、c 的关系1．（2019·黑龙江省中考模拟）如图，二次函数y=ax 2+bx+c （a≠0）的图象与x 轴正半轴相交于A 、B 两点，与y 轴相交于点C ，对称轴为直线x=2，且OA=OC ，则下列结论：①abc ＞0；①9a+3b+c ＜0；①c ＞﹣1；①关于x 的方程ax 2+bx+c=0（a≠0）有一个根为1a-，其中正确结论的个数为（ ） A ．1 B ．2C ．3D ．4【答案】C【解析】解：由图象开口向下，可知a<0，与y 轴的交点在x 轴的下方，可知c<0，又对称轴方程为x=2，所以02ba->，所以b>0，故①正确； 由图象可知当x=3时，y>0，①9a+3b+c>0，故①错误；由图象可知OA<1，①OA=OC ，①OC<1，即-c<1，c>-1，故①正确： 假设方程的一个根为x=1a -，把x=1a -代入方程可得10bc a a-+= ，整理可得ac-b+1=0， 两边同时乘c 可得ac 2-bc+c=0，即方程有一个根为x=-c ，由①可知-c=OA ，而x=OA 是方程的根， ①x=-c 是方程的根，即假设成立，故①正确；综上可知正确的结论有三个；故答案为C.2．（2019·山东省初三二模）二次函数 y ＝ax 2+bx +c （a ≠0）的图象如图所示，对称轴是直线 x ＝1，下列结论：①ab ＜0；①b 2＞4ac ；①a +b +2c ＜0；①3a +c ＜0． 其中正确的是（ ） A ．①① B ．①①C ．①①①D ．①①①①【答案】C【解析】①抛物线开口向上，①a>0，①抛物线与y 轴的交点在x 轴下方，①c<0，①ab<0，所以①正确； ①抛物线与x 轴有2个交点，①①=b 2-4ac>0，所以①正确； ①x=1时，y<0，①a+b+c<0，而c<0，①a+b+2c<0，所以①正确； ①抛物线的对称轴为直线x=-b2a=1，①b=-2a ，而x=-1时，y>0，即a-b+c>0，①a+2a+c>0，所以①错误．3．（2019·合肥市第四十八中学初三月考）如图，已知二次函数y=ax 2+bx+c （a≠0）的图象与x 轴交于点A （﹣1，0），与y 轴的交点B 在（0，﹣2）和（0，﹣1）之间（不包括这两点），对称轴为直线x=1．下列结论：①abc ＞0 ①4a+2b+c ＞0 ①4ac ﹣b 2＜8a ①13＜a ＜23①b ＞c ．其中含所有正确结论的选项是（ ） A ．①① B ．①①① C ．①①①D ．①①①①【答案】D 【解析】①①函数开口方向向上，①a ＞0；①对称轴在y 轴右侧，①ab 异号，①抛物线与y 轴交点在y 轴负半轴，①c ＜0，①abc ＞0，故①正确；①①图象与x 轴交于点A （﹣1，0），对称轴为直线x=1，①图象与x 轴的另一个交点为（3，0），①当x=2时，y ＜0，①4a+2b+c ＜0，故①错误；①①图象与x 轴交于点A （﹣1，0），①当x=﹣1时，y=()()211a b c -+⨯-+=0，①a ﹣b+c=0，即a=b ﹣c ，c=b ﹣a ，①对称轴为直线x=1，①2ba-=1，即b=﹣2a ，①c=b ﹣a=（﹣2a ）﹣a=﹣3a ，①4ac ﹣2b =4•a•（﹣3a ）﹣()22a -=216a -＜0，①8a ＞0，①4ac ﹣2b ＜8a ，故①正确；①①图象与y 轴的交点B 在（0，﹣2）和（0，﹣1）之间，①﹣2＜c ＜﹣1，①﹣2＜﹣3a ＜﹣1，①23＞a ＞13，故①正确；①①a ＞0，①b ﹣c ＞0，即b ＞c ，故①正确4．（2019·安徽省初三期末）抛物线y=ax 2+bx+c 的顶点为D （﹣1，2），与x 轴的一个交点A 在点（﹣3，0）和（﹣2，0）之间，其部分图象如图，则以下结论：①b 2﹣4ac ＜0；①当x ＞﹣1时，y 随x 增大而减小；①a+b+c ＜0；①若方程ax 2+bx+c ﹣m=0没有实数根，则m ＞2； ①3a+c ＜0．其中正确结论的个数是（ ） A ．2个 B ．3个C ．4个D ．5个【答案】C 【解析】（1）①抛物线与x 轴有两个交点，①b 2−4ac >0，①结论①不正确．（2）抛物线的对称轴x =−1，①当x >−1时，y 随x 增大而减小，①结论①正确．（3）①抛物线与x 轴的一个交点A 在点(−3,0)和(−2,0)之间，①抛物线与x 轴的另一个交点在点(0,0)和(1,0)之间，①当x =1时，y <0，①a +b +c <0，①结论①正确． （4）①y =ax 2+bx +c 的最大值是2，①方程ax 2+bx +c −m =0没有实数根，则m >2，①结论①正确． （5）①抛物线的对称轴x =2ba-=−1，①b =2a ， ①a +b +c <0，①a +2a +c <0，①3a +c <0，①结论①正确． 综上，可得正确结论的序号是：①①①①,正确的结论有4个.5．（2019·山东省中考模拟）如图，已知二次函数y ＝ax 2+bx +c （a ≠0）的图象如图所示，对称轴为直线x ＝1．有下列4个结论：①abc ＞0；①4a +2b +c ＞0；①2c ＜3b ；①a +b ＞m （am +b ）（m 是不等于1的实数）．其中正确的结论个数有（ ） A ．1个 B ．2个C ．3个D ．4个【答案】C【解析】解：①由图象可知：a ＜0，c ＞0， ①﹣2ba＞0，①b ＞0，①abc ＜0，故①错误； ①由对称知，当x ＝2时，函数值大于0，即y ＝4a+2b+c ＞0，故①正确； ①当x ＝3时函数值小于0，y ＝9a+3b+c ＜0，且x ＝2ba-＝1， 即a ＝2b -，代入得9（2b-）+3b+c ＜0，得2c ＜3b ，故①正确； ①当x ＝1时，y 的值最大．此时，y ＝a+b+c ，而当x ＝m 时，y ＝am 2+bm+c ， 所以a+b+c ＞am 2+bm+c ，故a+b ＞am 2+bm ，即a+b ＞m （am+b ），故①正确．6．（2019·山东省中考模拟）如图是二次函数2(0)y ax bx c a =++≠图象的一部分，对称轴为12x =，且经过点（2，0）下列说法：①abc<0；①-2b+c=0；①4a+2b+c<0；①若(-52，y 1)，(52，y 2)是抛物线上的两点，则y 1<y 2；①1142a b +>m(am+b)其中(m≠12)其中说法正确的是A ．①①①①B ．①①C ．①①D ．①①①【答案】A【解析】解：①由抛物线的开口可知：a ＜0，又抛物线与y 轴的交点可知：c ＞0， 对称轴−2ba>0，①b ＞0，①abc ＜0，故①正确； ①将（2，0）代入y=ax 2+bx+c （a≠0），①4a+2b+c=0， ①−221b a =，①a=-b ，①-4b+2b+c=0，①-2b+c=0，故①正确； ①由①可知：4a+2b+c=0，故①错误； ①由于抛物线的对称轴为x=12，①（−52，y 1）与（72，y 1）关于x=12对称， 由于x ＞12时，y 随着x 的增大而减小， ①72＞52，①y 1＜y 2，故①正确； ①由图象可知：x=12时，y 可取得最大值，且最大值为14a+12b ，①m≠12①14a+12b+c ＞am 2+bm+c ，①14a+12b ＞m(am+b)，故①正确； 7．（2019·山东省中考模拟）如图，抛物线()20y ax bx c a =++≠的对称轴为1x =-，与x 轴的一个交点在()3,0-和()2,0-之间，其部分图象如图所示，则下列结论：()2140b ac ->；()22a b =；()3点17,2y ⎛⎫- ⎪⎝⎭、23,2y ⎛⎫- ⎪⎝⎭、35,4y ⎛⎫ ⎪⎝⎭是该抛物线上的点，则123y y y <<；()4320b c +<；()()5t at b a b +≤-（t 为任意实数）．其中正确结论的个数是（ ） A ．2 B ．3C ．4D ．5【答案】C 【解析】（1）抛物线与x 轴有两个交点，所以方程ax 2+bx +c =0（a ≠0）有两个不相等的实数根，所以b 2﹣4ac ＞0，此结论正确；（2）对称轴为x =﹣1=﹣2ba，即b =2a ，此结论正确； （3）由二次函数的对称性可得，x =54与x =﹣134的函数值相等，当x ＜﹣1时，y 随着x 的增大而增大，所以y 1＜y 3＜y 2，此结论错误；（4）由图像得，x =﹣3时，y ＜0，即9a ﹣3b +c ＜0，因为b =2a ，所以2b×9﹣3b +c ＜0，即3b +2c ＜0，此结论正确；（5）要证明t (at +b )≤a ﹣b ，即要证明at 2+bt +c ≤a ﹣b +c ，即要证明抛物线在x =﹣1时取最大值，由图像可得当x =﹣1时，y 最大，此结论正确. 正确结论的个数是4.8．（2018·江苏省中考模拟）二次函数y=ax 2+bx+c （a≠0）的图象如图，下列四个结论：①4a+c ＜0；①m （am+b ）+b ＞a （m≠﹣1）；①关于x 的一元二次方程ax 2+（b ﹣1）x+c=0没有实数根；①ak 4+bk 2＜a （k 2+1）2+b （k 2+1）（k 为常数）．其中正确结论的个数是（ ） A ．4个 B ．3个C ．2个D ．1个【答案】D 【解析】①因为二次函数的对称轴是直线x=﹣1，由图象可得左交点的横坐标大于﹣3，小于﹣2， 所以﹣2ba=﹣1，可得b=2a ，当x=﹣3时，y ＜0，即9a ﹣3b+c ＜0，9a ﹣6a+c ＜0，3a+c ＜0， ①a ＜0，①4a+c ＜0，所以①选项结论正确；①①抛物线的对称轴是直线x=﹣1，①y=a ﹣b+c 的值最大，即把x=m （m≠﹣1）代入得：y=am 2+bm+c ＜a ﹣b+c ，①am 2+bm ＜a ﹣b ，m （am+b ）+b ＜a ，所以此选项结论不正确； ①ax 2+（b ﹣1）x+c=0，①=（b ﹣1）2﹣4ac ， ①a ＜0，c ＞0，①ac ＜0，①﹣4ac ＞0，①（b ﹣1）2≥0，①①＞0，①关于x 的一元二次方程ax 2+（b ﹣1）x+c=0有实数根； ①由图象得：当x ＞﹣1时，y 随x 的增大而减小，①当k 为常数时，0≤k 2≤k 2+1，①当x=k 2的值大于x=k 2+1的函数值，即ak4+bk2+c＞a（k2+1）2+b（k2+1）+c，ak4+bk2＞a（k2+1）2+b（k2+1），所以此选项结论不正确；。

二次函数系数abc与图像关系练习题

二次函数系数abc与图像关系练习题

二次函数系数a、b、c与图像的关系知识要点二次函数y=ax2+bx+c系数符号的确定：（1）a由抛物线开口方向确定：开口方向向上，则a＞0；否则a＜0．（2）b由对称轴和a的符号确定：由对称轴公式x=判断符号．（3）c由抛物线与y轴的交点确定：交点在y轴正半轴，则c＞0；否则c＜0．（4）b2-4ac的符号由抛物线与x轴交点的个数确定：2个交点，b2-4ac＞0；1个交点，b2-4ac=0；没有交点，b2-4ac＜0．（5）当x=1时，可确定a+b+c的符号，当x=-1时，可确定a-b+c 的符号．（6）由对称轴公式x=，可确定2a+b的符号．一．选择题（共9小题）1．（2014?威海）已知二次函数y=ax2+bx+c（a≠0）的图象如图，则下列说法：①c=0；②该抛物线的对称轴是直线x=﹣1；③当x=1时，y=2a；④am2+bm+a＞0（m≠﹣1）．其中正确的个数是（）A．1B．2C．3D．42．（2014?仙游县二模）已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，给出以下结论：①a+b+c＜0；②a﹣b+c＜0；③b+2a＜0；④abc＞0．其中所有正确结论的序号是（）A．③④B．②③C．①④D．①②③3．（2014?南阳二模）二次函数y=ax2+bx+c的图象如图所示，那么关于此二次函数的下列四个结论：①a＜0；②c＞0；③b2﹣4ac＞0；④＜0中，正确的结论有（）A．1个B2个C3个D．4个．．4．（2014?襄城区模拟）函数y=x2+bx+c与y=x的图象如图，有以下结论：①b2﹣4c＜0；②c﹣b+1=0；③3b+c+6=0；④当1＜x＜3时，x2+（b﹣1）x+c＜0．其中正确结论的个数为（）A．1B．2C．3D．45．（2014?宜城市模拟）如图是二次函数y=ax2+bx+c图象的一部分，其对称轴为x=﹣1，且过点（﹣3，0）下列说法：①abc＜0；②2a﹣b=0；③4a+2b+c＜0；④若（﹣5，y1），（2，y2）是抛物线上的两点，则y1＞y2．其中说法正确的是（）A．①②B．②③C．②③④D．①②④6．（2014?莆田质检）如图，二次函数y=x2+（2﹣m）x+m﹣3的图象交y轴于负半轴，对称轴在y轴的右侧，则m的取值范围是（）A．m＞2B．m＜3C．m＞3D．2＜m＜37．（2014?玉林一模）如图是二次函数y=ax2+bx+c图象的一部分，图象过点A（﹣3，0），对称轴为x=﹣1．给出四个结论：①b2＞4ac；②2a+b=0；③3a+c=0；④a+b+c=0．其中正确结论的个数是（）A．1个B．2个C．3个D．4个8．（2014?乐山市中区模拟）如图，抛物线y=ax2+bx+c与x轴交于点A（﹣1，0），顶点坐标为（1，n），与y轴的交点在（0，2）、（0，3）之间（包含端点）．有下列结论：①当x＞3时，y＜0；②3a+b＞0；③﹣1≤a≤﹣；④≤n≤4．其中正确的是（）A．①②B．③④C．①③D．①③④9．（2014?齐齐哈尔二模）已知二次函数y=ax2+bx+c（a＞0）的图象与x轴交于点（﹣1，0），（x1，0），且1＜x1＜2，下列结论正确的个数为（）①b＜0；②c＜0；③a+c＜0；④4a﹣2b+c＞0．A．1个B．2个C．3个D．4个10、（2011?重庆）已知抛物线y=ax2+bx+c（a≠0）在平面直角坐标系中的位置如图所示，则下列结论中，正确的是（）A、a＞0B、b＜0C、c＜0D、a+b+c＞011、（2011?雅安）已知二次函数y=ax2+bx+c的图象如图，其对称轴x=-1，给出下列结果①b2＞4ac；②abc＞0；③2a+b=0；④a+b+c＞0；⑤a-b+c＜0，则正确的结论是（）A、①②③④B、②④⑤C、②③④D、①④⑤12、（2011?孝感）如图，二次函数y=ax2+bx+c的图象与y轴正半轴相交，其顶点坐标为（ 12，1），下列结论：①ac＜0；②a+b=0；③4ac-b2=4a；④a+b+c＜0．其中正确结论的个数是（）A、1B、2C、3D、4答案一．选择题（共9小题）1．（2014?威海）已知二次函数y=ax2+bx+c（a≠0）的图象如图，则下列说法：①c=0；②该抛物线的对称轴是直线x=﹣1；③当x=1时，y=2a；④am2+bm+a＞0（m≠﹣1）．其中正确的个数是（）A．1B．2C．3D．4考点：二次函数图象与系数的关系．分由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及析：抛物线与x轴交点情况进行推理，进而对所得结论进行判断．解答：解：抛物线与y轴交于原点，c=0，（故①正确）；该抛物线的对称轴是：，直线x=﹣1，（故②正确）；当x=1时，y=a+b+c∵对称轴是直线x=﹣1，∴﹣b/2a=﹣1，b=2a，又∵c=0，∴y=3a，（故③错误）；x=m对应的函数值为y=am2+bm+c，x=﹣1对应的函数值为y=a﹣b+c，又∵x=﹣1时函数取得最小值，∴a﹣b+c＜am2+bm+c，即a﹣b＜am2+bm，∵b=2a，∴am2+bm+a＞0（m≠﹣1）．（故④正确）．故选：C．点评：本题考查了二次函数图象与系数的关系．二次函数y=ax2+bx+c （a≠0）系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点、抛物线与x轴交点的个数确定．2．（2014?仙游县二模）已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，给出以下结论：①a+b+c＜0；②a﹣b+c＜0；③b+2a＜0；④abc＞0．其中所有正确结论的序号是（）A．③④B．②③C．①④D．①②③考点：二次函数图象与系数的关系．专题：数形结合．分析：由抛物线的开口方向判断a的符号，由抛物线与y轴的交点判断c的符号，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．解答：解：①当x=1时，y=a+b+c=0，故①错误；②当x=﹣1时，图象与x轴交点负半轴明显大于﹣1，∴y=a﹣b+c＜0，故②正确；③由抛物线的开口向下知a＜0，∵对称轴为0＜x=﹣＜1，∴2a+b＜0，故③正确；④对称轴为x=﹣＞0，a＜0∴a、b异号，即b＞0，由图知抛物线与y轴交于正半轴，∴c＞0∴abc＜0，故④错误；∴正确结论的序号为②③．故选：B．点评：二次函数y=ax2+bx+c系数符号的确定：（1）a由抛物线开口方向确定：开口方向向上，则a＞0；否则a＜0；（2）b由对称轴和a的符号确定：由对称轴公式x=﹣判断符号；（3）c由抛物线与y轴的交点确定：交点在y轴正半轴，则c ＞0；否则c＜0；（4）当x=1时，可以确定y=a+b+c的值；当x=﹣1时，可以确定y=a﹣b+c的值．3．（2014?南阳二模）二次函数y=ax2+bx+c的图象如图所示，那么关于此二次函数的下列四个结论：①a＜0；②c＞0；③b2﹣4ac＞0；④＜0中，正确的结论有（）A．1个B．2个C．3个D．4个考点：二次函数图象与系数的关系．专题：数形结合．分析：由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．解答：解：①∵图象开口向下，∴a＜0；故本选项正确；②∵该二次函数的图象与y轴交于正半轴，∴c＞0；故本选项正确；③∵二次函数y=ax2+bx+c的图象与x轴有两个不相同交点，∴根的判别式△=b2﹣4ac＞0；故本选项正确；④∵对称轴x=﹣＞0，∴＜0；故本选项正确；综上所述，正确的结论有4个．故选D．点本题主要考查了二次函数的图象和性质，解答本题关键是掌握评：二次函数y=ax2+bx+c系数符号的确定，做题时要注意数形结合思想的运用，同学们加强训练即可掌握，属于基础题．4．（2014?襄城区模拟）函数y=x2+bx+c与y=x的图象如图，有以下结论：①b2﹣4c＜0；②c﹣b+1=0；③3b+c+6=0；④当1＜x＜3时，x2+（b ﹣1）x+c＜0．其中正确结论的个数为（）A．1B．2C．3D．4考二次函数图象与系数的关系．点：分析：由函数y=x2+bx+c与x轴无交点，可得b2﹣4c＜0；当x=﹣1时，y=1﹣b+c＞0；当x=3时，y=9+3b+c=3；当1＜x＜3时，二次函数值小于一次函数值，可得x2+bx+c＜x，继而可求得答案．解答：解：∵函数y=x2+bx+c与x轴无交点，∴b2﹣4ac＜0；故①正确；当x=﹣1时，y=1﹣b+c＞0，故②错误；∵当x=3时，y=9+3b+c=3，∴3b+c+6=0；③正确；∵当1＜x＜3时，二次函数值小于一次函数值，∴x2+bx+c＜x，∴x2+（b﹣1）x+c＜0．故④正确．故选C．点评：主要考查图象与二次函数系数之间的关系．此题难度适中，注意掌握数形结合思想的应用．5．（2014?宜城市模拟）如图是二次函数y=ax2+bx+c图象的一部分，其对称轴为x=﹣1，且过点（﹣3，0）下列说法：①abc＜0；②2a﹣b=0；③4a+2b+c＜0；④若（﹣5，y1），（2，y2）是抛物线上的两点，则y1＞y2．其中说法正确的是（）A．①②B．②③C．②③④D．①②④考点：二次函数图象与系数的关系．分根据抛物线开口方向得到a＞0，根据抛物线的对称轴得b=2a＞0，则2a﹣b=0，则可对②进行判断；根据抛物线与y轴的交点析：在x轴下方得到c＜0，则abc＜0，于是可对①进行判断；由于x=﹣2时，y＜0，则得到4a﹣2b+c＜0，则可对③进行判断；通过点（﹣5，y1）和点（2，y2）离对称轴的远近对④进行判断．解答：解：∵抛物线开口向上，∴a＞0，∵抛物线对称轴为直线x=﹣=﹣1，∴b=2a＞0，则2a﹣b=0，所以②正确；∵抛物线与y轴的交点在x轴下方，∴c＜0，∴abc＜0，所以①正确；∵x=2时，y＞0，∴4a+2b+c＞0，所以③错误；∵点（﹣5，y1）离对称轴要比点（2，y2）离对称轴要远，∴y1＞y2，所以④正确．故选D．点评：本题考查了二次函数图象与系数的关系：二次函数y=ax2+bx+c （a≠0），二次项系数a决定抛物线的开口方向和大小，当a ＞0时，抛物线向上开口；当a＜0时，抛物线向下开口；一次项系数b和二次项系数a共同决定对称轴的位置：当a与b同号时（即ab＞0），对称轴在y轴左；当a与b异号时（即ab ＜0），对称轴在y轴右．（简称：左同右异）．抛物线与y轴交于（0，c）．抛物线与x轴交点个数：△=b2﹣4ac＞0时，抛物线与x轴有2个交点；△=b2﹣4ac=0时，抛物线与x轴有1个交点；△=b2﹣4ac＜0时，抛物线与x轴没有交点．6．（2014?莆田质检）如图，二次函数y=x2+（2﹣m）x+m﹣3的图象交y轴于负半轴，对称轴在y轴的右侧，则m的取值范围是（）A．m＞2B．m＜3C．m＞3D．2＜m＜3考点：二次函数图象与系数的关系．分由于二次函数的对称轴在y轴右侧，根据对称轴的公式即可得到关于m的不等式，由图象交y轴于负半轴也可得到关于m的析：不等式，再求两个不等式的公共部分即可得解．解答：解：∵二次函数y=x2+（2﹣m）x+m﹣3的图象交y轴于负半轴，∴m﹣3＜0，解得m＜3，∵对称轴在y轴的右侧，∴x=，解得m＞2，∴2＜m＜3．故选：D．点评：此题主要考查了二次函数的性质，解题的关键是利用对称轴的公式以及图象与y轴的交点解决问题．7．（2014?玉林一模）如图是二次函数y=ax2+bx+c图象的一部分，图象过点A（﹣3，0），对称轴为x=﹣1．给出四个结论：①b2＞4ac；②2a+b=0；③3a+c=0；④a+b+c=0．其中正确结论的个数是（）A．1个B．2个C．3个D．4个考点：二次函数图象与系数的关系．分析：由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．解答：解：∵抛物线的开口方向向下，∴a＜0；∵抛物线与x轴有两个交点，∴b2﹣4ac＞0，即b2＞4ac，①正确；由图象可知：对称轴x==﹣1，∴2a=b，2a+b=4a，∵a≠0，∴2a+b≠0，②错误；∵图象过点A（﹣3，0），∴9a﹣3b+c=0，2a=b，所以9a﹣6a+c=0，c=﹣3a，③正确；∵抛物线与y轴的交点在y轴的正半轴上，∴c＞0由图象可知：当x=1时y=0，∴a+b+c=0，④正确．故选C．点评：考查了二次函数图象与系数的关系，解答本题关键是掌握二次函数y=ax2+bx+c（a≠0）系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点、抛物线与x轴交点的个数确定．8．（2014?乐山市中区模拟）如图，抛物线y=ax2+bx+c与x轴交于点A（﹣1，0），顶点坐标为（1，n），与y轴的交点在（0，2）、（0，3）之间（包含端点）．有下列结论：①当x＞3时，y＜0；②3a+b＞0；③﹣1≤a≤﹣；④≤n≤4．其中正确的是（）A．①②B．③④C．①③D．①③④考点：二次函数图象与系数的关系．分析：①由抛物线的对称轴为直线x=1，一个交点A（﹣1，0），得到另一个交点坐标，利用图象即可对于选项①作出判断；②根据抛物线开口方向判定a的符号，由对称轴方程求得b与a的关系是b=﹣2a，将其代入（3a+b），并判定其符号；③根据两根之积=﹣3，得到a=，然后根据c的取值范围利用不等式的性质来求a的取值范围；④把顶点坐标代入函数解析式得到n=a+b+c=c，利用c的取值范围可以求得n的取值范围．解答：解：①∵抛物线y=ax2+bx+c与x轴交于点A（﹣1，0），对称轴直线是x=1，∴该抛物线与x轴的另一个交点的坐标是（3，0），∴根据图示知，当x＞3时，y＜0．故①正确；②根据图示知，抛物线开口方向向下，则a＜0．∵对称轴x==1，∴b=﹣2a，∴3a+b=3a﹣2a=a＜0，即3a+b＜0．故②错误；③∵抛物线与x轴的两个交点坐标分别是（﹣1，0），（3，0），∴﹣1×3=﹣3，=﹣3，则a=．∵抛物线与y轴的交点在（0，2）、（0，3）之间（包含端点），∴2≤c≤3，∴﹣1≤≤，即﹣1≤a≤．故③正确；④根据题意知，a=，=1，∴b=﹣2a=，∴n=a+b+c=c．∵2≤c≤3，≤≤4，≤n≤4．故④正确．综上所述，正确的说法有①③④．故选D．点评：本题考查了二次函数图象与系数的关系．二次函数y=ax2+bx+c 系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定．9．（2014?齐齐哈尔二模）已知二次函数y=ax2+bx+c（a＞0）的图象与x轴交于点（﹣1，0），（x1，0），且1＜x1＜2，下列结论正确的个数为（）①b＜0；②c＜0；③a+c＜0；④4a﹣2b+c＞0．A．1个B．2个C．3个D．4个考点：二次函数图象与系数的关系．分由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交析：点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．解答：解：①∵y=ax2+bx+c（a＞0）的图象与x轴交于点（﹣1，0），（x1，0），且1＜x1＜2，∴对称轴在y轴的右侧，即：﹣＞0，∵a＞0∴b＜0，故①正确；②显然函数图象与y轴交于负半轴，∴c＜0正确；③∵二次函数y=ax2+bx+c（a＞0）的图象与x轴交于点（﹣1，0），∴a﹣b+c=0，即a+c=b，∵b＜0，∴a+c＜0正确；④∵二次函数y=ax2+bx+c（a＞0）的图象与x轴交于点（﹣1，0），且a＞0，∴当x=﹣2时，y=4a﹣2b+c＞0，故④正确，故选D．点评：主要考查图象与二次函数系数之间的关系，会利用对称轴的范围求2a与b的关系，以及二次函数与方程之间的转换，根的判别式的熟练运用．。

二次函数系数abc与图像的关系

二次函数系数abc与图像的关系

确的是（ ）
•y
A）ab<0
•O
•x
B）bc<0
C）a+b+c>0
D）a－b+c<0
•（图1）
例4(青海二次函数 ，
则点
图象如图2所示
在第 象限．
•y
•O •x
•图2
例6．已知 那么抛物线
， 的顶点在（ ）
（A）第一象限 （B）第二象限 （C）第三象限 （D）第四象限
•7.已知二次函数y=ax2+bx+c的图像如图所 示，判断下列各式的符号：
•(1)a_•_>_0; b_•_>_0; c_•_<_0; • △ _•_>_0 •(2)a_•_>_0; b_•_<_0; c_•_=_0; • △ __•>_0
•(3)a_•_>_0; b_•_<_0; c_•_>_0; • △ _•_<_0
•(1) •y
•(2) •y
•O •x
•O
•x
•(3) •y
二次函数系数abc与图像的 关系
1.a的作用： •决定开口方向和开口大小 •2.a与b的作用：•左同右异（对称轴的位置） •3.c的作用： •与y轴交点的位置。
•4.
的作用：•与x轴交点的个数。
•5.几个特殊点：•顶点，与x轴交点，与y轴交点， •（1，a+b+c),(-1,a-b+c)
•1、判断下列各图中的a、b、c及△的符号
•(4) •y •O •x
•(4)a_•_<_0; b_•_>_0; c_•_<_0; •O
•x
• △ _•_=_0

二次函数图像与系数关系70题-含答案

二次函数图像与系数关系70题-含答案

二次函数图像与系数关系70题1．（2020·湖南茶陵·初三零模）如图是二次函数y=ax 2+bx+c （a≠0）图象的一部分，直线x=-1是对称轴，有下列判断：①b-2a=0；②4a-2b+c ＜0；③a-b+c=-9a ；④若（-3，y 1），（32，y 2）是抛物线上两点，则y 1＞y 2，其中正确的个数是（ ）A ．1个B ．2个C ．3个D ．4个2．（2020·浙江杭州外国语学校初三月考）如图，直线1y kx =与抛物线22y ax bx c =++交于A 、B 两点，则2()y ax b k x c =+-+的图象可能是（ ）A ．B ．C ．D ．3．（2020·浙江杭州外国语学校初三月考）如图，二次函数y ＝ax 2+bx +c （a ≠0）图象与x 轴交于A ，B 两点，与y 轴交于C 点，且对称轴为x ＝1，点B 坐标为（﹣1，0）．则下面的四个结论：①2a +b ＝0；②4a ﹣2b +c ＜0；③b 2﹣4ac ＞0；④当y ＜0时，x ＜﹣1或x ＞2．其中正确的有（ ）A．4个B．3个C．2个D．1个4．（2020·福建省连江第三中学初三月考）在同一坐标系内，函数y＝kx2和y＝kx＋2（k≠0）的图象大致如图（）A．B．C． D．5．（2020·福建省连江第三中学初三月考）已知二次函数y＝ax2＋bx＋c（a≠0）的图象如图所示，则下列结论：①3a＋b＜0；②a﹣b＋c＜0；③c＞0；④a＋b＞0．其中正确的结论有（）A．仅①②③B．仅②③④C．仅①②④D．①②③④6．（2020·辽宁新宾·初三其他）抛物线y＝ax2+bx+c的图象如图所示，那么一次函数y＝bx+b2﹣4ac与反比例函数y＝()()a b c a b cx++-+在同一坐标系内的图象大致是（）A．B．C．D．7．（2020·湖南茶陵·初三期末）反比例函数kyx=-与二次函数2y kx k=-(0)k≠在同一直角坐标系的图像可能是（）A．B．C．D．8．（2020·兰西县红星乡第一中学校初二月考）在同一直角坐标系中，函数y mx m=+和函数222y mx x=-++(m是常数，且0m≠)的图象可能是( )A．B．C．D．9．（2020·福建省福州第十九中学初三其他）二次函数y＝ax2+bx+c的图象如图所示，则下列命题中：①b＝﹣2a；②此抛物线向下移动c个单位后过点（2，0）；③﹣1＜a＜﹣12；④方程x2﹣2x+1c＝0有实数根，结论正确的个数（）A ．1个B ．2个C ．3个D ．4个10．（2020·内蒙古海勃湾·初三期末）已知二次函数y ＝ax 2+bx +c （a ≠0）的图象如图所示，有下列5个结论： ①abc ＞0；②b ＜a +c ；③4a +2b +c ＞0；④2c ＜3b ；⑤a +b ＞m （am +b ）（m ≠1的实数）．其中正确的结论有（ ）A ．2个B ．3个C ．4个D ．5个11．（2020·湖北武汉·初三月考）如图，抛物线2y ax bx c =++与x 轴正半轴交于A ，B 两点，与y 轴负半轴交于点C ．若点(4,0)B ，则下列结论中：①0abc >；②40a b +>；③()11,M x y 与()22,N x y 是抛物线上两点，若120x x <<，则12y y >；④若抛物线的对称轴是直线3x =，m 为任意实数，则(3)(3)(3)a m m b m -+-；⑤若3AB ≥，则430b c +>，正确的个数是（ ）A ．5B ．4C ．3D ．212．（2020·陕西师大附中初三一模）已知抛物线y ＝a （x ﹣h ）2＋k （a ≠0）经过A （m ﹣4，0），B （m ﹣2，3），C （4﹣m ，3）三点，其中m ＜3，则下列说法正确的是（ ）A ．a ＞0B ．h ＜0C ．k ≥3D ．当x ＜0时，y 随x 的增大而增大 13．（2019·四川邛崃·初三三模）如图，是二次函数y ＝ax 2+bx +c （a ≠0）的图象的一部分，给出下列命题：①a +b +c ＝0；②b ＞2a ；③ax 2+bx +c ＝0的两根分别为﹣3和1；④a ﹣2b +c ＞0．其中正确的命题是（ ）A ．①②B ．②③C ．①③D ．①②③④14．（2019·陕西渭滨·初三二模）如图为二次函数y=ax 2+bx+c 的图象，在下列说法中：①ac ＜0；②a+b+c ＞0；③方程ax 2+bx+c=0的根是x 1=﹣1，x 2=3； ④b 2﹣4ac ＞0；⑤当x ＞1时，y 随x 的增大而增大；正确的说法有（ ）A ．4个B ．3个C ．2个D ．1个15．（2020·长沙市长郡梅溪湖中学初二期末）二次函数y ＝ax 2+bx+c （a≠0）的图象如图所示，下列结论：①2a+b ＝0；②若m 为任意实数，则a+b≥am 2+bm ；③a ﹣b+c ＞0；④3a+c ＜0；⑤若ax 12+bx 1＝ax 22+bx 2，且x 1≠x 2，则x 1+x 2＝2．其中正确的个数为（ ）A ．2B ．3C ．4D ．516．（2020·四川阿坝·初三期末）如图为二次函数2y ax bx c =++的图象，在下列说法中:①0ac <；②方程20ax bx c ++=的根是121,3x x =-=③ 0a b c ++>；④当1x >时，y 随x 的增大而增大；⑤20a b -=；⑥240b ac ->，正确的说法有（ ）A ．1B ．2C ．3D ．417．（2020·湖南雨花·初二期末）如图，已知二次函数y=ax 2+bx+c （a≠0）的图象如图所示，给出以下四个结论：①abc=0，②a+b+c＞0，③a＞b ，④4ac﹣b 2＜0；其中正确的结论有（ ）A ．1个B ．2个C ．3个D ．4个18．（2020·湖南雨花·初二期末）同一平面直角坐标系中，抛物线y ＝(x －a )2与直线y ＝ax +a 的图象可能是（ ）A ．B ．C ．D ．19．（2020·陕西碑林·西北工业大学附属中学初三一模）已知二次函数 y ＝ax 2＋bx ＋c ，其中 y 与 x 的部分对应值如表：下列结论正确的是（ ）A ．abc ＜0B ．4a ＋2b ＋c ＞0C ．若 x ＜－1 或 x ＞3 时，y ＞0D ．方程 ax 2＋bx ＋c ＝5 的解为 x 1＝－2，x 2＝3 20．（2020·湖南湘潭·初三期末）如图，二次函数2(0)y ax bx c a =++≠的图象，则下列结论正确的是（ ）①0b <；②240b ac ->；③a c b +<；④0c >A ．①②③B ．②③④C ．①③④D ．①②③④21．（2020·甘肃肃州·初三期末）已知二次函数y=2ax bx c ++（a≠0）的图像如图所示，对称轴为x= -1，则下列式子正确的个数是（ ）（1）abc ＞0（2）2a+b=0（3）4a+2b+c ＜0（4）b 2-4ac ＜0A ．1个B ．2个C ．3个D ．4个22．（2019·黑龙江甘南·初三期末）如图，已知抛物线y ＝ax 2+bx +c 经过点（﹣1，0），对称轴是x ＝1，现有结论：①abc ＞0 ②9a ﹣3b +c ＝0 ③b ＝﹣2a ④﹣1）b +c ＜0，其中正确的有（ ）A ．1个B ．2个C ．3个D ．4个23．（2020·湖南天心·长郡中学初二期末）二次函数2y ax bx c =++的图象如图所示，则下列结论正确的是（ ）A ．0abc >B ．0a b c ++=C ．420a b c -+<D ．240b ac -<24．（2020·全国初三课时练习）在同一平面直角坐标系中，函数y ＝ax 2＋b 与y ＝ax ＋b （ab ≠0）的大致图象可能是（ ）A ．B ．C ．D ．25．（2020·陕西旬阳·初三期末）已知二次函数2y ax bx c =++（a≠0）的图象如图所示，则下列结论：①b＜0，c ＞0；②a+b+c ＜0；③方程的两根之和大于0；④a ﹣b+c ＜0，其中正确的个数是（ ）A ．4个B ．3个C ．2个D ．1个26．（2019·无锡市南长实验中学初三月考）在同一平面直角坐标系中，函数2y ax bx =-与y bx a =+的图象可能是（ ）A ．B ．C ．D ．27．（2020·长沙麓山国际实验学校初三期末）如图为二次函数()20y ax bx c a =++≠的图象，则下列说法：①0a >；②20a b +=；③0a b c ++>；④0>；⑤420a b c -+<，其中正确的个数为（ ）A ．1B ．2C ．3D ．428．（2020·全国初三课时练习）如图，抛物线2(0)y ax bx c a =++≠与x 轴交于点(1,0)A -和B ，与y 轴交于点C ．下列结论：①0abc <；②20a b +<；③420a b c -+>；④30a c +>，其中正确的结论个数为（ ）A ．1个B ．2个C ．3个D ．4个29．（2020·云南昆明三中初二期末）下列图像中，当0ab >时，函数2y ax =与y ax b =+的图象时（ ）A ．B ．C ．D ．30．（2021·全国初三专题练习）已知二次函数y=ax 2+bx+c （a ，b ，c 是常数，且a≠0）的图象如图所示，则一次函数2b y cx a =+与反比例函数ab y x=在同一坐标系内的大致图象是（ ）A ．B ．C ．D ．31．（2020·全国初三单元测试）如图，抛物线2(0)y ax bx c a =++≠交x 轴于点A ，B ，交y 轴于点C ．若点A 坐标为(4,0)-，对称轴为直线1x =-，则下列结论错误的是（ ）A ．二次函数的最大值为a b c -+B ．0a b c ++>C ．240b ac ->D ．20a b +=32．（2020·甘肃兰州·中考真题）如图，已知二次函数()2y ax bx c a 0=++≠的图象如图所示，有下列5个结论 abc 0>①；b a c ->②；4a 2b c 0++>③；3a c >-④；()a b m am b (m 1+>+≠⑤的实数).其中正确结论的有( )A ．①②③B ．②③⑤C ．②③④D ．③④⑤33．（2019·四川雁江·初三其他）如图中实线所示，函数y=|a （x ﹣1）2﹣1|的图象经过原点，小明同学研究得出下面结论：①a=1；②若函数y 随x 的增大而减小，则x 的取值范围一定是x ＜0；③若方程|a （x ﹣1）2﹣1|=k 有两个实数解，则k 的取值范围是k ＞1；④若M （m 1，n ），N （m 2，n ），P （m 3，n ），Q （m 4，n ）（n ＞0）是上述函数图象的四个不同点，且m 1＜m 2＜m 3＜m 4，则有m 2+m 3﹣m 1=m 4．其中正确的结论有（ ）A ．4个B ．3个C ．2个D ．1个34．（2020·安徽初三其他）如图，已知函数y ＝﹣3x 与y ＝ax 2+bx （a ＞0，b ＞0）的图象交于点P ，点P 的纵坐标为1，则关于x 的方程ax 2+bx +3x＝0的解为（ ）A．x＝3 B．x＝1 C．x＝﹣3 D．无解35．（2020·广东福田·深圳实验学校初三三模）如图，二次函数y＝ax2+bx+c(a≠0)的图象经过点(﹣1，2)，且与x轴交点的横坐标分别为x1，x2，其中﹣2＜x1＜﹣1，0＜x2＜1，下列结论：①4a﹣2b+c＜0；②2a﹣b＜0；③a＜0；④b2+8a＞4ac，其中正确的有( )A．1个B．2个C．3个D．4个36．（2020·黑龙江甘南·初三期末）在同一平面直角坐标系中，一次函数y＝ax+b和二次函数y＝ax2+bx+c的图象可能为（）A．B．C．D．37．（2020·山西浑源·初三期末）在平面直角坐标系中，开口向下的抛物线y＝ax2+bx+c的一部分图象如图所示，它与x轴交于A（1，0），与y轴交于点B（0，3），对称轴是直线x= -1．则下列结论正确的是（）A ．ac ＞0B ．b 2－4ac ＝0C ．a －b ＋c ＜0D ．当-3＜x ＜1时，y ＞038．（2020·四川广安二中初三期末）抛物线y ＝ax 2＋bx ＋c(a≠0)的对称轴为直线x ＝－1，与x 轴的一个交点在(－3，0)和(－2，0)之间，其部分图象如图，则下列结论：①4ac －b 2＜0；②2a －b ＝0；③a ＋b ＋c ＜0；④点(x 1，y 1)，(x 2，y 2)在抛物线上，若x 1＜x 2，则y 1＜y 2 .正确结论的个数是( )A ．1B ．2C ．3D ．439．（2020·福建闽侯·初三一模）抛物线y ＝ax 2+bx+c 与直线y ＝ax+c （a≠0）在同一直角坐标系中的图象可能是（ ）A ．B ．C ．D ．40．（2020·宁夏金凤·初三其他）已知二次函数214y x bx c =-++的图象如下，则一次函数124y x b =--与反比例函数c y x=在同一平面直角坐标系中的图象大致是（ ）A ．B ．C ．D ．41．（2020·安徽铜陵·）抛物线2(0)y ax bx c a =++≠的对称轴为直线1x =，与x 轴的一个交点坐标为()4,0A ，其部分图象如图所示．下列叙述中：①24b ac <；②关于x 的方程20ax bx c ++=的两个根是122,4x x =-=；③20a b +=；④0a b c ++<；⑤当04x <<时，y 随x 增大而增大．正确的个数是（ ）A ．4B ．3C ．2D ．142．（2020·全国初三课时练习）如图，是二次函数2y ax bx c =++图象的一部分，下列结论中：①0abc >；②0a b c -+<；③210ax bx c +++=有两个相等．．的实数根；④4a 2a b -<<-.其中正确结论的序号为（ ）A ．①②B ．①③C ．②③D ．①④ 43．（2020·全国初三课时练习）如图是抛物线()210y ax bx c a =++≠图象的一部分，抛物线的顶点坐标()1,3A ，与x 轴的一个交点()4,0B ，直线()20y mx n m =+≠与抛物线交于A ，B 两点，下列结论： ①20a b +=；②0abc >；③方程23ax bx c ++=有两个相等的实数根；④抛物线与x 轴的另一个交点是()1,0-；⑤当14x <<时，有21y y <．其中正确结论的个数是（ ）A ．5B ．4C ．3D ．244．（2020·广东初三一模）如图是二次函数2y ax bx c =++图象的一部分，图象过点()5,0A -，对称轴为直线2x =-，给出四个结论：①0c >；②抛物线与轴的另一个交点坐标为()3,0；③40a b -=；④若()13,M y -与21,2N y ⎛⎫ ⎪⎝⎭是抛物线上两点，则12y y <．其中，正确结论的个数是（ ）A．1 B．2 C．3 D．445．（2020·北京八中初三月考）a≠0，函数y＝ax与y＝﹣ax2+a在同一直角坐标系中的大致图象可能是（）A．B．C．D．46．（2020·山东菏泽·初三月考）如图，抛物线y＝ax2＋bx＋c(a≠0)的对称轴为直线x＝1，与x轴的一个交点坐标为(－1，0)，其部分图象如图所示，下列结论：①4ac＜b2；②方程ax2＋bx＋c＝0的两个根是x1＝－1，x2＝3；③3a＋c＞0；④当y＞0时，x的取值范围是－1≤x＜3；⑤当x＜0时，y随x增大而增大．其中结论正确的个数是( )A．4个B．3个C．2个D．1个47．（2020·内蒙古扎鲁特旗·初三月考）如图，已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有下列5个结论：①abc＜0；②b＜a+c；③4a+2b +c＞0；④2c＜3b；⑤a+b＜m （am+b）（m≠1的实数）．其中正确结论的有（）A ．①②③B ．①③④C ．③④⑤D ．②③⑤ 48．（2020·全国初三课时练习）已知，二次函数y ＝ax 2+bx+c 满足以下三个条件：①2b a＞4c ，②a ﹣b+c ＜0，③b ＜c ，则它的图象可能是（ ）A ．B ．C ．D ．49．（2020·全国初三课时练习）已知二次函数2(0)y ax bx c a =++≠的图象如图所示，现给出下列结论：①0abc >；②930a b c ++=；③248b ac a -<；④50a b c ++>．其中正确结论的个数是（ ）A ．1B ．2C ．3D ．450．（2020·全国初三课时练习）已知二次函数y ＝ax 2+bx+c 的图象如图所示，下列结论：①ac ＜0，②b ﹣2a ＜0，③b 2﹣4ac ＜0，④a ﹣b+c ＜0，正确的是( )A ．①②B ．①④C ．②③D ．②④51．（2020·全国初三课时练习）抛物线2y ax bx c =++的对称轴是直线1x =-，且过点（1，0）.顶点位于第二象限，其部分图像如图所示，给出以下判断：①0ab >且0c <；②420a b c -+>；③8>0+a c ；④33c a b =-；⑤直线22y x =+与抛物线2y ax bx c =++两个交点的横坐标分别为12x x 、，则12125x x x x ++⋅=-.其中正确的个数有( )A ．5个B ．4个C ．3个D ．2个52．（2020·全国初三课时练习）已知：二次函数2(0)y ax bx c a =++≠的图象如图所示，下列结论中：①0abc >；②20a b +<；③()a b m am b +>+（1m ≠的实数）；④22()a c b +<；⑤1a >，其中正确的是（ ）A ．2个B ．3个C ．4个D ．1个53．（2020·全国初三课时练习）已知二次函数2(0)y ax bx c a =++≠的图象如下图，有下列5个结论：①0abc >；②b a c >+；③420a b c ++>；④23c b >；⑤()a b m am b +>+（1m ≠的实数）．其中正确结论的有（ ）A ．①②③B ．②③④C ．③④⑤D ．②③⑤54．（2020·广西南宁·三美学校初三学业考试）如图是抛物线()20y ax bx c a =++≠，其顶点为()1,n ，且与x轴的个交点在点()3,0和()4,0之间，则下列结论正确的个数是（ ）个①若抛物线与x 轴的另一个交点为(),0k ，则21k -<<-；②c a n -=；③若x m <-时，y 随x 的增大而增大，则1m ≥-．A ．0B ．1C ．2D ．355．（2020·辽宁铁岭·初三月考）如图，二次函数2(0)y ax bx c a =++≠的图象与x 轴交于点()1,0A -，其对称轴为直线1x =，下面结论中正确的是（ ）A ．0abc ＞B ．20a b -=C ．420a b c ++＜D ．930a b c ++=56．（2020·山东枣庄·初三其他）二次函数2y ax bx c =++的图象如图所示，对称轴是直线1x =．下列结论：①0abc <；②30a c +>；③()220a c b +-<；④()a b m am b +≤+(m 为实数)．其中结论正确的个数为( )A ．1个B ．2个C ．3个D ．4个57．（2019·黑龙江铁锋·初三三模）已知二次函数2y ax bx c =++的图象如图所示，则以下结论：①0abc >，②230b a +=，③0a b c -+<，④520a c +<．其中正确的有（ ）A ．1个B ．2个C ．3个D ．4个58．（2020·广东潮南·初三其他）平面直角坐标系中，二次函数()20y ax bx c a =++≠的图象如图所示，现给出下列结论：①0abc <；②20c a +>；③930a b c -+=；④2a b am bm -≤+（m 为实数）；⑤240ac b -<．其中正确的结论的个数是（ ）A ．2B ．3C ．4D ．559．（2020·山东历下·初三三模）如图是二次函数y ＝ax 2+bx+c （a≠0）的图象，下列结论正确的个数是（ ） ①对称轴为直线x ＝﹣1；②b 2﹣4ac ＞0；③方程ax 2+bx+c ＝0的解是x 1＝﹣3，x 2＝1；④不等式ax 2+bx+c ＞3的解为﹣2＜x ＜0．A ．4B ．3C ．2D ．160．（2020·全国初三课时练习）如图是二次函数y=ax 2+bx+c （a ，b ，c 是常数，a≠0）图象的一部分，与x 轴的交点A 在点（2，0）和（3，0）之间，对称轴是x=1．对于下列说法：①ab ＜0；②2a+b=0；③3a+c ＞0；④a+b≥m （am+b ）（m 为实数）；⑤当﹣1＜x ＜3时，y ＞0，其中正确的是（ ）A ．①②④B ．①②⑤C ．②③④D ．③④⑤61．（2020·全国初三课时练习）在同一坐标系内，一次函数y ax b =+与二次函数2y ax 8x b =++的图象可能是A ．B ．C ．D ．62．（2020·全国初三课时练习）已知抛物线y=ax 2+bx+c （a≠0）的对称轴为直线x=2，与x 轴的一个交点坐标为（4，0），其部分图象如图所示，下列结论：①抛物线过原点；②4a+b+c=0；③a ﹣b+c ＜0；④抛物线的顶点坐标为（2，b ）；⑤当x ＜2时，y 随x 增大而增大．其中结论正确的是（ ）A．①②③B．③④⑤C．①②④D．①④⑤63．（2020·全国初三课时练习）抛物线y＝ax2+bx+c的顶点为(﹣1，3)，与x轴的交点A在点(﹣3，0)和(﹣2，0)之间，其部分图象如图，则以下结论，其中正确结论的个数为()①若点P(﹣3，m)，Q(3，n)在抛物线上，则m＜n；②c＝a+3；③a+b+c＜0；④方程ax2+bx+c＝3有两个相等的实数根．A．1个B．2个C．3个D．4个64．（2020·湖北广水·初三期末）如图，二次函数y=ax2+bx+c的图象与x轴交于点A（﹣1，0），与y轴的交点B在（0，2）与（0，3）之间（不包括这两点），对称轴为直线x=2．下列结论：①abc＜0；②9a+3b+c＞0；③若点M（12，y1），点N（52，y2）是函数图象上的两点，则y1＜y2；④﹣35＜a＜﹣25；⑤c-3a＞0其中正确结论有（）A．2个B．3个C．4个D．5个65．（2020·河南太康·初三期末）如图，抛物线y ＝2ax ＋bx ＋c(a≠0)与x 轴交于点A(1，0)和B ，与y 轴的正半轴交于点C ．下列结论：①abc ＞0；②4a －2b ＋c ＞0；③2a －b ＞0；④3a ＋c ＞0.其中正确结论的个数为（ ）A ．1个B ．2个C ．3个D ．4个66．（2020·湖北广水·初三其他）二次函数y ＝2ax bx c ++（a ≠0）图象如图所示，下列结论：①abc ＞0；②2a b +＝0；③当m ≠1时，+a b ＞2am bm +；④a b c -+＞0；⑤若211ax bx +＝222ax bx +，且1x ≠2x ，则12x x +＝2．其中正确的有（ ）A ．①②③B ．②④C ．②⑤D ．②③⑤67．（2020·甘肃张掖·初三其他）小明从图所示的二次函数2y ax bx c =++的图象中，观察得出了下面四条信息：①230a b +=；②24b ac -＜0；③0a b c -+>；④方程20ax bx c ++=必有一个根在－1到0之间．你认为其中正确信息的个数有( )A ．1个B ．2个C ．3个D ．4个68．（2020·湖北广水·初三其他）如图，抛物线2y ax bx c =++的图象交x 轴于()2,0A -和点B ，交y 轴负半轴于点C ，且OB OC =，下列结论：①0a b c +<；②40a c +>；③12a =；④1acb +=； 其中正确的结论个数有（ ）A ．1个B ．2个C ．3个D ．4个69．（2020·重庆市荣昌区宝城初级中学初三其他）如图，抛物线2y ax bx c =++与x 轴交于点A(-1，0)，B(3，0)，交y 轴的正半轴于点C ，对称轴交抛物线于点D ，交x 轴与点E ，则下列结论：①2a+b=0；②b+2c>0；③a+b>am 2+bm （m 为任意实数）；④一元二次方程220ax bx c +++=有两个不相等的实数根；⑤当△BCD为直角三角形时，a 的值有2个；⑥若点P 为对称轴上的动点，则PB PC -有最大值，．其中正确的有（ ）A ．2个B ．3个C ．4个D ．5个70．（2020·内蒙古呼伦贝尔·初三二模）如图所示的抛物线y ＝ax 2+bx +c 的对称轴为直线x ＝1，则下列结论中错误的是（ ）A．ac＜0 B．b2﹣4ac＞0 C．2a﹣b＝0 D．9a+3b+c＝0参考答案1．C【解析】【分析】①根据直线x=-1是对称轴，确定b-2a 的值；②根据x=-2时，y ＞0确定4a-2b+c 的符号；③根据x=-4时，y=0，比较a-b+c 与-9a 的大小；④根据抛物线的对称性，得到x=-3与x=1时的函数值相等判断即可．【详解】解：①∵直线x=-1是对称轴，∴-2b a=-1，即b-2a=0，①正确； ②x=-2时，y ＞0，∴4a-2b+c ＞0，②错误；∵x=-4时，y=0，∴16a-4b+c=0，又b=2a ，∴a-b+c=-9a ，③正确；④根据抛物线的对称性，得到x=-3与x=1时的函数值相等，∴y 1＞y 2，④正确，故选C ．【点睛】本题考查二次函数图象与系数的关系．2．B【解析】【分析】根据题目所给的图像，首先判断1y kx =中k ＞0，其次判断22y ax bx c =++中a ＜0，b ＜0，c ＜0，再根据k 、b 、的符号判断2()y ax b k x c =+-+中b-k ＜0，又a ＜0，c ＜0可判断出图像．【详解】解：由题图像得1y kx =中k ＞0，22y ax bx c =++中a ＜0，b ＜0，c ＜0，∴b -k ＜0，∴函数2()y ax b k x c =+-+对称轴x=2b k a --＜0，交x 轴于负半轴， ∴当12y y =时，即2kx ax bx c =++，移项得方程2()0ax b k x c +-+=，∵直线1y kx =与抛物线22y ax bx c =++有两个交点， ∴方程2()0ax b k x c +-+=有两个不等的解，即2()y ax b k x c =+-+与x 轴有两个交点，根据函数2()y ax b k x c =+-+对称轴交x 轴负半轴且函数图像与x 轴有两个交点， ∴可判断B 正确．故选：B【点睛】本题考查二次函数与一次函数的图象与性质，解题的关键是根据图像判断k 、a 、b 、c 的正负号，再根据二次函数与一元二次方程的关系判断出正确图像．3．B【解析】【分析】根据二次函数的图象和二次函数的性质，可以判断各个小题中的结论是否成立，从而可以解答本题．【详解】∵二次函数y ＝ax 2+bx+c （a≠0）的对称轴为x ＝1， ∴﹣2b a＝1，得2a+b ＝0，故①正确； 当x ＝﹣2时，y ＝4a ﹣2b+c ＜0，故②正确；该函数图象与x 轴有两个交点，则b 2﹣4ac ＞0，故③正确；∵二次函数y ＝ax 2+bx+c （a≠0）的对称轴为x ＝1，点B 坐标为（﹣1，0），∴点A （3，0），∴当y ＜0时，x ＜﹣1或x ＞3，故④错误；故选B ．【点睛】本题考查二次函数图象与系数的关系、抛物线与x 轴的交点，解答本题的关键是明确题意，利用二次函数的性质和数形结合的思想解答．4．D【解析】【分析】分别利用函数解析式分析图象得出答案．【详解】解：由一次函数解析式为：y=kx+2可知，图象应该与y 轴交于正半轴上，故A 、B 、C 错误；D 符合题意；故选：D ．【点睛】此题主要考查了二次函数的图象以及一次函数的图象，得出直线交y 轴的正半轴是解题关键． 5．D【解析】【分析】由抛物线的开口方向判断a 与0的关系，由抛物线与y 轴的交点判断c 与0的关系，然后根据对称轴进行推理，进而对所得结论进行判断．【详解】解：抛物线开口方向向下，则a ＜0，∵对称轴是直线x=2b a=1，则b=-2a ， ∴3a+b=3a-2a=a ＜0，故①正确；当x=-1时，y ＜0，即a-b+c ＜0，故②正确；抛物线与y 轴交于正半轴，则c ＞0，故③正确；∵b=-2a ，∴a+b=a-2a=-a ，∵a ＜0，∴-a ＞0，∴a+b ＞0，故④正确．综上所述，正确的结论是：①②③④．故选：D ．【点睛】本题主要考查图象与二次函数系数之间的关系，会利用对称轴的范围求2a 与b 的关系，掌握“数形结合”数学思想的应用．6．D【解析】【分析】根据二次函数开口方向，可以判断出a 的正负，根据对称轴的位置和a 的正负，可以判断出b 的正负，再根抛物线与y 轴的交点，可以判断出c 的正负，然后根据a 、b 、c 的正负去判断一次函数和二次函数在坐标系中的位置即可.【详解】∵二次函数图象开口向上，∴a ＞0，∵对称轴为直线x ＝﹣2b a＞0， ∴b ＜0，当x ＝﹣1时，a ﹣b +c ＞0，当x ＝1时，a ﹣b +c ＜0，∴（a +b +c ）（a ﹣b +c ）＜0，∵抛物线与x 轴有两个交点，∴b 2﹣4ac ＞0，∴一次函数图象经过第一、二、四象限，反比例函数图象经过第二四象限．故选：D ．【点睛】本题考查了一次函数、二次函数、反比例函数的图像与系数的关系，根据二次函数抛物线求出a 、b 、c 的正负是解决本题的管家.7．C【解析】【分析】先根据反比例函数图象确定k 的值，再分析二次函数图象是否符合，逐一判断即可【详解】A 、由反比例函数图象知：k ＞0，因此二次函数图象应开口向上，且与y 轴交于负半轴，故此选项错误；B 、由反比例函数图象知：k ＜0，因此二次函数图象应开口向下，故此选项错误；C 、由反比例函数图象知：k ＜0，因此二次函数图象应开口向下，且与y 轴交于正半轴，故此选项正确；D 、由反比例函数图象知：k ＞0，因此二次函数图象应开口向上，故此选项错误； 故选Ｃ．【点睛】本题考查反比例函数、二次函数的图象与性质，比较基础．8．D【解析】【分析】先根据一次函数图像确定m 的符号，在依据二次函数y=ax 2+bx+c 图像性质进行判断，当a ＞0时，开口向上；当a ＜0时，开口向下．对称轴为x=2b a -，与y 轴的交点坐标为（0，c ）． 【详解】解：A 、由函数y ＝mx+m 的图象可知m ＜0，即函数y ＝﹣mx 2+2x+2开口方向朝上，与图象不符，故A 选项错误；B 、由函数y ＝mx+m 的图象可知m ＜0，对称轴为x ＝2b a -＝212m m -=＜0，则对称轴应在y 轴左侧，与图象不符，故B 选项错误；C 、由函数y ＝mx+m 的图象可知m ＞0，即函数y ＝﹣mx 2+2x+2开口方向朝下，与图象不符，故C 选项错误；D 、由函数y ＝mx+m 的图象可知m ＜0，即函数y ＝﹣mx 2+2x+2开口方向朝上，对称轴为x ＝2b a -＝﹣212m m-= ＜0，则对称轴应在y 轴左侧，与图象相符，故D 选项正确； 故选D ．【点睛】本题主要考查了一次函数和二次函数的图象性质以及分析能力和读图能力，要掌握它们的性质才能灵活解题．一次函数和二次函数的图象所经过的象限的问题，关键是m 的正负的确定，9．D【解析】【分析】①．函数的对称轴为x ＝﹣2b a＝1，即可求解；②．新抛物线表达式为：y ＝ax 2+bx ＝ax 2﹣2ax ＝ax （x ﹣2），即可求解；③．x ＝﹣1时，y ＝a ﹣b +c ＜0，x ＝1时，y ＝a +b +c ＝2，即220b a a b c a b c =-⎧⎪++=⎨⎪-+<⎩，即可求解；④．∆＝4a 2﹣4a ＝4a （a ﹣1），而﹣1＜a ＜﹣12，故∆＞0，即可求解．【详解】解：①．函数的对称轴为x ＝﹣2b a＝1，解得：b ＝﹣2a ；故①正确； ②．此抛物线向下移动c 个单位后，新抛物线表达式为：y ＝ax 2+bx ＝ax 2﹣2ax ＝ax （x ﹣2）， 则x ＝2时，y ＝0，故抛物线过点（2，0），故②正确；③．x ＝﹣1时，y ＝a ﹣b +c ＜0，x ＝1时，y ＝a +b +c ＝2，即220b a a b c a b c =-⎧⎪++=⎨⎪-+<⎩，解得：﹣1＜a ＜﹣12，故③正确； ④．∵c ＜0，∴x 2﹣2x +1c＝0变形为cx 2﹣2cx +1＝0， ∵∆＝4c 2﹣4c ＝4c （c ﹣1），而1＜c ＜2， ∴∆＞0，故方程x 2﹣2x +1c ＝0有实数根，故④正确； 故选：D ．【点睛】此题考查的是二次函数图象及性质,掌握二次函数图象及性质与各项系数的关系是解决此题的关键．10．A【解析】【分析】观察图象：开口向下得到a ＜0；对称轴在y 轴的右侧得到a 、b 异号，则b ＞0；抛物线与y轴的交点在x 轴的上方得到c ＞0，所以abc ＜0；当x ＝﹣1时图象在x 轴上得到y ＝a ﹣b +c ＝0，即a +c ＝b ；对称轴为直线x ＝1，可得x ＝2时图象在x 轴上方，则y ＝4a +2b +c ＞0；利用对称轴x ＝﹣2b a＝1得到a ＝﹣12b ，而a ﹣b +c ＜0，则﹣12b ﹣b +c ＜0，所以2c ＜3b ；开口向下，当x ＝1，y 有最大值a +b +c ，得到a +b +c ＞am 2+bm +c ，即a +b ＞m （am +b ）（m ≠1）．【详解】解：开口向下，a ＜0；对称轴在y 轴的右侧，a 、b 异号，则b ＞0；抛物线与y 轴的交点在x 轴的上方，c ＞0，则abc ＜0，所以①不正确；当x ＝﹣1时图象在x 轴上，则y ＝a ﹣b +c ＝0，即a +c ＝b ，所以②不正确；对称轴为直线x ＝1，则x ＝2时图象在x 轴上方，则y ＝4a +2b +c ＞0，所以③正确； x ＝﹣2b a＝1，则a ＝﹣12b ，而a ﹣b +c ＝0，则﹣12b ﹣b +c ＝0，2c ＝3b ，所以④不正确； 开口向下，当x ＝1，y 有最大值a +b +c ；当x ＝m （m ≠1）时，y ＝am 2+bm +c ，则a +b +c ＞am 2+bm +c ，即a +b ＞m （am +b ）（m ≠1），所以⑤正确．故选：A ．【点睛】本题考查了二次函数图象与系数的关系：对于二次函数y=ax 2+bx+c （a ≠0）的图象，当a ＞0，开口向上，函数有最小值，a ＜0，开口向下，函数有最大值；对称轴为直线x=2b a -，a 与b 同号，对称轴在y 轴的左侧，a 与b 异号，对称轴在y 轴的右侧；当c ＞0，抛物线与y 轴的交点在x 轴的上方；当△=b 2-4ac ＞0，抛物线与x 轴有两个交点．11．B【解析】【分析】根据图像得出a ＜0，c ＜0，b ＞0，可判断①；再由图像可得对称轴在直线x=2右侧，可得22b a->，可判断②；再根据二次函数在y 轴右侧时的增减性，判断③；根据抛物线对称轴为直线x=3，得出6b a =-，再利用作差法判断④；最后根据AB≥3，则点A 的横坐标大于0且小于等于1，得出a+b+c≥0，再由当x=4时，得出16a+4b+c=0，变形为a=416b c +-，代入，可得4b+5c≥0，结合c 的符号可判断⑤.【详解】解：如图，抛物线开口向下，与y 轴交于负半轴，对称轴在y 轴右侧，∴a ＜0，c ＜0，02b a ->， ∴b ＞0，∴abc ＞0，故①正确；如图，∵抛物线过点B （4，0），点A 在x 轴正半轴，∴对称轴在直线x=2右侧，即22b a->， ∴42022b a b a a++=<，又a ＜0， ∴4a+b ＞0，故②正确；∵()11,M x y 与()22,N x y 是抛物线上两点，120x x <<，可得：抛物线2y ax bx c =++在02b x a<<-上，y 随x 的增大而增大， 在2b x a>-上，y 随x 的增大而减小， ∴12y y >不一定成立，故③错误；若抛物线对称轴为直线x=3，则32b a-=，即6b a =-， 则(3)(3)(3)a m m b m -+--=()()()3363a m m a m -++-=()()336a m m -+-=()23a m -≤0，∴(3)(3)(3)a m m b m -+≤-，故④正确；∵AB≥3，则点A 的横坐标大于0且小于等于1，当x=1时，代入，y=a+b+c≥0，当x=4时，16a+4b+c=0，∴a=416b c+-，则416b cb c+++≥-，整理得：4b+5c≥0，则4b+3c≥-2c，又c＜0，-2c＞0，∴4b+3c＞0，故⑤正确，故正确的有4个.故选B.【点睛】本题考查了二次函数的图像和性质，解题的关键是能根据图像得出二次函数表达式各系数的符号.12．D【解析】【分析】利用对称性得到抛物线对称轴为直线x＝1，根据点的坐标确定开口向下，最大值大于3，根据二次函数的性质即可判断D正确．【详解】解：∵抛物线y＝a（x﹣h）2＋k（a≠0）经过A（m﹣4，0），B（m﹣2，3），C（4﹣m，3）三点，其中m＜3，∴抛物线的开口向下，对称轴为直线x＝242m m-+-＝1，即a＜0，h＝1，∴k＞3，当x＜1时，y随x的增大而增大，故选：D．【点睛】本题考查二次函数图象与系数的关系，二次函数图象上点的坐标特征，熟练掌握二次函数的性质是关键．13．C【解析】【分析】根据二次函数的性质逐一进行判断即可【详解】解：∵x ＝1时，y ＝0，∴a ＋b ＋c ＝0，所以①正确；∵x ＝2b a＝－1，∴b ＝2a ，所以②错误； ∵点(1，0)关于直线x ＝－1对称的点的坐标为(－3，0)，∴抛物线与x 轴的交点坐标为(－3，0)和(1，0)，∴ax 2＋bx ＋c ＝0的两根分别为－3和1，所以③正确；∵抛物线与y 轴的交点在x 轴下方，∴c ＜0，∵a ＋b ＋c ＝0，b ＝2a ，∴c ＝－3a ，∴a －2b ＋c ＝－6a ，∵a ＞0，∴－6a ＜0∴a －2b ＋c ＜0，所以④错误．【点睛】本题考查的是二次函数图象与系数的关系，掌握二次函数的性质、灵活运用数形结合思想是解题的关键，解答时，要熟练运用抛物线的对称性和抛物线上的点的坐标满足抛物线的解析式.14．A【解析】【分析】由抛物线开口方向及与y 轴的交点位置可判断①；令y=1可判断②；由图像与x 轴的交点可判断③和④；由图像与x 轴的两个交点可求得对称轴，结合图像的开口方向，则可判断⑤；则可求得答案．【详解】抛物线开口方向、与y 轴的交点在x 轴的下方，∴00a c ><，，0ac <，故①正确；由图像可知当1x =时，0y <，∴0a b c ++<，故②不正确；由图像可知抛物线与x 轴交与(−1,0)和(3,0)两点，∴方程20ax bx c ++=的根是121,3x x =-=,且240b ac ->，故③、④正确；抛物线与x 轴交与(−1,0)和(3,0)两点，∴抛物线对称轴为直线1312x -+==，且抛物线开口向下， ∴当1x >时，y 随x 的增大而增大，故⑤正确；综上可知正确的结论有4个，故选A.【点睛】本题考查的知识点是二次函数图像与系数的关系，解题关键是利用数形结合得出各项符号． 15．C【解析】根据抛物线开口方向得a ＜0，由抛物线对称轴为直线x ＝﹣2b a＝1，得到b ＝﹣2a ＞0，即2a+b ＝0，即可判断①；根据二次函数的性质得当x ＝1时，函数有最大值a+b+c ，即可判断②；根据抛物线的对称性得到抛物线与x 轴的另一个交点在（﹣1，0）的右侧，则当x ＝﹣1时，y ＜0，所以a ﹣b+c ＜0，即可判断③；把b ＝﹣2a 代入a ﹣b+c ＜0可对④进行判断；把ax 12+bx 1＝ax 22+bx 2先移项，再分解因式得到（x 1﹣x 2）[a （x 1+x 2）+b]＝0，而x 1≠x 2，则a （x 1+x 2）+b ＝0，即x 1+x 2＝﹣b a ，然后把b ＝﹣2a 代入计算得到x 1+x 2＝2可对⑤进行判断． 【详解】∵抛物线开口向下，∴a ＜0，∵抛物线对称轴为直线x ＝﹣2b a＝1， ∴b ＝﹣2a ＞0，即2a+b ＝0，所以①正确；∵抛物线对称轴为直线x ＝1，∴函数的最大值为a+b+c ，∴a+b+c≥am 2+bm+c ，即a+b≥am 2+bm ，所以②正确；∵抛物线与x 轴的一个交点在（3，0）的左侧，而对称轴为直线x ＝1，∴抛物线与x 轴的另一个交点在（﹣1，0）的右侧，∴当x ＝﹣1时，y ＜0，∴a ﹣b+c ＜0，所以③错误；∵b ＝﹣2a ，a ﹣b+c ＜0，∴a+2a+c ＜0，即3a+c ＜0，所以④正确；∵ax 12+bx 1＝ax 22+bx 2，∴ax 12+bx 1﹣ax 22﹣bx 2＝0，∴a （x 1+x 2）（x 1﹣x 2）+b （x 1﹣x 2）＝0，∴（x 1﹣x 2）[a （x 1+x 2）+b]＝0，而x 1≠x 2，∴a （x 1+x 2）+b ＝0，即x 1+x 2＝﹣b a， ∵b ＝﹣2a ，∴x 1+x 2＝2，所以⑤正确．综上所述，正确的有①②④⑤共4个．故选：C ．【点睛】本题主要考查了二次函数的图象和性质，熟练掌握二次函数图象与解析式系数关系，与方程和不等式关系是解题的关键．16．D【解析】【分析】根据抛物线开口向上得出a ＞0，根据抛物线和y 轴的交点在y 轴的负半轴上得出c ＜0，根据图象与x 轴的交点坐标得出方程ax 2+bx+c=0的根，把x=1代入y=ax 2+bx+c 求出a+b+c ＜0，根据抛物线的对称轴和图象得出当x ＞1时，y 随x 的增大而增大，2a=-b ，根据图象和x 轴有两个交点得出b 2-4ac ＞0．【详解】∵抛物线开口向上，∴a ＞0，∵抛物线和y 轴的交点在y 轴的负半轴上，∴c ＜0，∴ac ＜0，∴①正确；∵图象与x 轴的交点坐标是（-1，0），（3，0），∴方程ax 2+bx+c=0的根是x 1=-1，x 2=3，∴②正确；把x=1代入y=ax 2+bx+c 得：a+b+c ＜0，∴③错误；根据图象可知：当x ＞1时，y 随x 的增大而增大，∴④正确；∵-2b a=1， ∴2a=-b ，∴2a+b=0，不是2a-b=0，∴⑤错误；∵图象和x 轴有两个交点，∴b 2-4ac ＞0，∴⑥正确；正确的说法有：①②④⑥．故答案为：D ．【点睛】本题考查了二次函数与系数的关系的应用，主要考查学生对二次函数的图象与系数的关系的理解和运用，同时也考查了学生观察图象的能力，本题是一道比较典型的题目，具有一定的代表性．17．C【解析】【分析】【详解】根据图像可得：a<0，b<0，c=0，即abc=0，则①正确；当x=1时，y<0，即a+b+c<0，则②错误； 根据对称轴可得：－2b a =－32，则b=3a ，根据a<0，b<0可得：a>b ；则③正确； 根据函数与x 轴有两个交点可得：2b －4ac>0，则④正确.故选C.【点睛】本题考查二次函数的性质.能通过图象分析a ，b ，c 的正负，以及通过一些特殊点的位置得出a ，b ，c 之间的关系是解题关键.18．D【解析】【分析】先根据一次函数的图象判断 , ,a b 的符号,再判断二次函数图象与实际是否相符,判断正误.【详解】A.由一次函数y ＝ax+a 的图象可得: a<0且a>0 ,两者矛盾,故A 错误;B ．由一次函数 y ＝ax+a 的图象可得: a<0,此时二次函数 y ＝(x －a)2的顶点(a, 0)的位置可推出a>0 ,两者矛盾,故B 错误;C.由一次函数 y ＝ax+a 的图象可得: a<0且a>0,两者矛盾,故C 错误;D.由一次函数y ＝ax+a 的图象可得:a>0 ,此时二次函数 y ＝(x －a)2的顶点(a, 0)的位置可推出a>0 ,故D 正确;故选:D.。

二次函数图像与系数关系70题-含答案

二次函数图像与系数关系70题-含答案

二次函数图像与系数关系70题1．（2020·湖南茶陵·初三零模）如图是二次函数y=ax 2+bx+c （a≠0）图象的一部分，直线x=-1是对称轴，有下列判断：①b-2a=0；②4a-2b+c ＜0；③a-b+c=-9a ；④若（-3，y 1），（32，y 2）是抛物线上两点，则y 1＞y 2，其中正确的个数是（ ）A ．1个B ．2个C ．3个D ．4个2．（2020·浙江杭州外国语学校初三月考）如图，直线1y kx =与抛物线22y ax bx c =++交于A 、B 两点，则2()y ax b k x c =+-+的图象可能是（ ）A ．B ．C ．D ．3．（2020·浙江杭州外国语学校初三月考）如图，二次函数y ＝ax 2+bx +c （a ≠0）图象与x 轴交于A ，B 两点，与y 轴交于C 点，且对称轴为x ＝1，点B 坐标为（﹣1，0）．则下面的四个结论：①2a +b ＝0；②4a ﹣2b +c ＜0；③b 2﹣4ac ＞0；④当y ＜0时，x ＜﹣1或x ＞2．其中正确的有（ ）A．4个B．3个C．2个D．1个4．（2020·福建省连江第三中学初三月考）在同一坐标系内，函数y＝kx2和y＝kx＋2（k≠0）的图象大致如图（）A．B．C． D．5．（2020·福建省连江第三中学初三月考）已知二次函数y＝ax2＋bx＋c（a≠0）的图象如图所示，则下列结论：①3a＋b＜0；②a﹣b＋c＜0；③c＞0；④a＋b＞0．其中正确的结论有（）A．仅①②③B．仅②③④C．仅①②④D．①②③④6．（2020·辽宁新宾·初三其他）抛物线y＝ax2+bx+c的图象如图所示，那么一次函数y＝bx+b2﹣4ac与反比例函数y＝()()a b c a b cx++-+在同一坐标系内的图象大致是（）A．B．C．D．7．（2020·湖南茶陵·初三期末）反比例函数kyx=-与二次函数2y kx k=-(0)k≠在同一直角坐标系的图像可能是（）A．B．C．D．8．（2020·兰西县红星乡第一中学校初二月考）在同一直角坐标系中，函数y mx m=+和函数222y mx x=-++(m是常数，且0m≠)的图象可能是( )A．B．C．D．9．（2020·福建省福州第十九中学初三其他）二次函数y＝ax2+bx+c的图象如图所示，则下列命题中：①b＝﹣2a；②此抛物线向下移动c个单位后过点（2，0）；③﹣1＜a＜﹣12；④方程x2﹣2x+1c＝0有实数根，结论正确的个数（）A ．1个B ．2个C ．3个D ．4个10．（2020·内蒙古海勃湾·初三期末）已知二次函数y ＝ax 2+bx +c （a ≠0）的图象如图所示，有下列5个结论： ①abc ＞0；②b ＜a +c ；③4a +2b +c ＞0；④2c ＜3b ；⑤a +b ＞m （am +b ）（m ≠1的实数）．其中正确的结论有（ ）A ．2个B ．3个C ．4个D ．5个11．（2020·湖北武汉·初三月考）如图，抛物线2y ax bx c =++与x 轴正半轴交于A ，B 两点，与y 轴负半轴交于点C ．若点(4,0)B ，则下列结论中：①0abc >；②40a b +>；③()11,M x y 与()22,N x y 是抛物线上两点，若120x x <<，则12y y >；④若抛物线的对称轴是直线3x =，m 为任意实数，则(3)(3)(3)a m m b m -+-；⑤若3AB ≥，则430b c +>，正确的个数是（ ）A ．5B ．4C ．3D ．212．（2020·陕西师大附中初三一模）已知抛物线y ＝a （x ﹣h ）2＋k （a ≠0）经过A （m ﹣4，0），B （m ﹣2，3），C （4﹣m ，3）三点，其中m ＜3，则下列说法正确的是（ ）A ．a ＞0B ．h ＜0C ．k ≥3D ．当x ＜0时，y 随x 的增大而增大 13．（2019·四川邛崃·初三三模）如图，是二次函数y ＝ax 2+bx +c （a ≠0）的图象的一部分，给出下列命题：①a +b +c ＝0；②b ＞2a ；③ax 2+bx +c ＝0的两根分别为﹣3和1；④a ﹣2b +c ＞0．其中正确的命题是（ ）A ．①②B ．②③C ．①③D ．①②③④14．（2019·陕西渭滨·初三二模）如图为二次函数y=ax 2+bx+c 的图象，在下列说法中：①ac ＜0；②a+b+c ＞0；③方程ax 2+bx+c=0的根是x 1=﹣1，x 2=3； ④b 2﹣4ac ＞0；⑤当x ＞1时，y 随x 的增大而增大；正确的说法有（ ）A ．4个B ．3个C ．2个D ．1个15．（2020·长沙市长郡梅溪湖中学初二期末）二次函数y ＝ax 2+bx+c （a≠0）的图象如图所示，下列结论：①2a+b ＝0；②若m 为任意实数，则a+b≥am 2+bm ；③a ﹣b+c ＞0；④3a+c ＜0；⑤若ax 12+bx 1＝ax 22+bx 2，且x 1≠x 2，则x 1+x 2＝2．其中正确的个数为（ ）A ．2B ．3C ．4D ．516．（2020·四川阿坝·初三期末）如图为二次函数2y ax bx c =++的图象，在下列说法中:①0ac <；②方程20ax bx c ++=的根是121,3x x =-=③ 0a b c ++>；④当1x >时，y 随x 的增大而增大；⑤20a b -=；⑥240b ac ->，正确的说法有（ ）A ．1B ．2C ．3D ．417．（2020·湖南雨花·初二期末）如图，已知二次函数y=ax 2+bx+c （a≠0）的图象如图所示，给出以下四个结论：①abc=0，②a+b+c＞0，③a＞b ，④4ac﹣b 2＜0；其中正确的结论有（ ）A ．1个B ．2个C ．3个D ．4个18．（2020·湖南雨花·初二期末）同一平面直角坐标系中，抛物线y ＝(x －a )2与直线y ＝ax +a 的图象可能是（ ）A ．B ．C ．D ．19．（2020·陕西碑林·西北工业大学附属中学初三一模）已知二次函数 y ＝ax 2＋bx ＋c ，其中 y 与 x 的部分对应值如表：下列结论正确的是（ ）A ．abc ＜0B ．4a ＋2b ＋c ＞0C ．若 x ＜－1 或 x ＞3 时，y ＞0D ．方程 ax 2＋bx ＋c ＝5 的解为 x 1＝－2，x 2＝3 20．（2020·湖南湘潭·初三期末）如图，二次函数2(0)y ax bx c a =++≠的图象，则下列结论正确的是（ ）①0b <；②240b ac ->；③a c b +<；④0c >A ．①②③B ．②③④C ．①③④D ．①②③④21．（2020·甘肃肃州·初三期末）已知二次函数y=2ax bx c ++（a≠0）的图像如图所示，对称轴为x= -1，则下列式子正确的个数是（ ）（1）abc ＞0（2）2a+b=0（3）4a+2b+c ＜0（4）b 2-4ac ＜0A ．1个B ．2个C ．3个D ．4个22．（2019·黑龙江甘南·初三期末）如图，已知抛物线y ＝ax 2+bx +c 经过点（﹣1，0），对称轴是x ＝1，现有结论：①abc ＞0 ②9a ﹣3b +c ＝0 ③b ＝﹣2a ④﹣1）b +c ＜0，其中正确的有（ ）A ．1个B ．2个C ．3个D ．4个23．（2020·湖南天心·长郡中学初二期末）二次函数2y ax bx c =++的图象如图所示，则下列结论正确的是（ ）A ．0abc >B ．0a b c ++=C ．420a b c -+<D ．240b ac -<24．（2020·全国初三课时练习）在同一平面直角坐标系中，函数y ＝ax 2＋b 与y ＝ax ＋b （ab ≠0）的大致图象可能是（ ）A ．B ．C ．D ．25．（2020·陕西旬阳·初三期末）已知二次函数2y ax bx c =++（a≠0）的图象如图所示，则下列结论：①b＜0，c ＞0；②a+b+c ＜0；③方程的两根之和大于0；④a ﹣b+c ＜0，其中正确的个数是（ ）A ．4个B ．3个C ．2个D ．1个26．（2019·无锡市南长实验中学初三月考）在同一平面直角坐标系中，函数2y ax bx =-与y bx a =+的图象可能是（ ）A ．B ．C ．D ．27．（2020·长沙麓山国际实验学校初三期末）如图为二次函数()20y ax bx c a =++≠的图象，则下列说法：①0a >；②20a b +=；③0a b c ++>；④0>；⑤420a b c -+<，其中正确的个数为（ ）A ．1B ．2C ．3D ．428．（2020·全国初三课时练习）如图，抛物线2(0)y ax bx c a =++≠与x 轴交于点(1,0)A -和B ，与y 轴交于点C ．下列结论：①0abc <；②20a b +<；③420a b c -+>；④30a c +>，其中正确的结论个数为（ ）A ．1个B ．2个C ．3个D ．4个29．（2020·云南昆明三中初二期末）下列图像中，当0ab >时，函数2y ax =与y ax b =+的图象时（ ）A ．B ．C ．D ．30．（2021·全国初三专题练习）已知二次函数y=ax 2+bx+c （a ，b ，c 是常数，且a≠0）的图象如图所示，则一次函数2b y cx a =+与反比例函数ab y x=在同一坐标系内的大致图象是（ ）A ．B ．C ．D ．31．（2020·全国初三单元测试）如图，抛物线2(0)y ax bx c a =++≠交x 轴于点A ，B ，交y 轴于点C ．若点A 坐标为(4,0)-，对称轴为直线1x =-，则下列结论错误的是（ ）A ．二次函数的最大值为a b c -+B ．0a b c ++>C ．240b ac ->D ．20a b +=32．（2020·甘肃兰州·中考真题）如图，已知二次函数()2y ax bx c a 0=++≠的图象如图所示，有下列5个结论 abc 0>①；b a c ->②；4a 2b c 0++>③；3a c >-④；()a b m am b (m 1+>+≠⑤的实数).其中正确结论的有( )A ．①②③B ．②③⑤C ．②③④D ．③④⑤33．（2019·四川雁江·初三其他）如图中实线所示，函数y=|a （x ﹣1）2﹣1|的图象经过原点，小明同学研究得出下面结论：①a=1；②若函数y 随x 的增大而减小，则x 的取值范围一定是x ＜0；③若方程|a （x ﹣1）2﹣1|=k 有两个实数解，则k 的取值范围是k ＞1；④若M （m 1，n ），N （m 2，n ），P （m 3，n ），Q （m 4，n ）（n ＞0）是上述函数图象的四个不同点，且m 1＜m 2＜m 3＜m 4，则有m 2+m 3﹣m 1=m 4．其中正确的结论有（ ）A ．4个B ．3个C ．2个D ．1个34．（2020·安徽初三其他）如图，已知函数y ＝﹣3x 与y ＝ax 2+bx （a ＞0，b ＞0）的图象交于点P ，点P 的纵坐标为1，则关于x 的方程ax 2+bx +3x＝0的解为（ ）A．x＝3 B．x＝1 C．x＝﹣3 D．无解35．（2020·广东福田·深圳实验学校初三三模）如图，二次函数y＝ax2+bx+c(a≠0)的图象经过点(﹣1，2)，且与x轴交点的横坐标分别为x1，x2，其中﹣2＜x1＜﹣1，0＜x2＜1，下列结论：①4a﹣2b+c＜0；②2a﹣b＜0；③a＜0；④b2+8a＞4ac，其中正确的有( )A．1个B．2个C．3个D．4个36．（2020·黑龙江甘南·初三期末）在同一平面直角坐标系中，一次函数y＝ax+b和二次函数y＝ax2+bx+c的图象可能为（）A．B．C．D．37．（2020·山西浑源·初三期末）在平面直角坐标系中，开口向下的抛物线y＝ax2+bx+c的一部分图象如图所示，它与x轴交于A（1，0），与y轴交于点B（0，3），对称轴是直线x= -1．则下列结论正确的是（）A ．ac ＞0B ．b 2－4ac ＝0C ．a －b ＋c ＜0D ．当-3＜x ＜1时，y ＞038．（2020·四川广安二中初三期末）抛物线y ＝ax 2＋bx ＋c(a≠0)的对称轴为直线x ＝－1，与x 轴的一个交点在(－3，0)和(－2，0)之间，其部分图象如图，则下列结论：①4ac －b 2＜0；②2a －b ＝0；③a ＋b ＋c ＜0；④点(x 1，y 1)，(x 2，y 2)在抛物线上，若x 1＜x 2，则y 1＜y 2 .正确结论的个数是( )A ．1B ．2C ．3D ．439．（2020·福建闽侯·初三一模）抛物线y ＝ax 2+bx+c 与直线y ＝ax+c （a≠0）在同一直角坐标系中的图象可能是（ ）A ．B ．C ．D ．40．（2020·宁夏金凤·初三其他）已知二次函数214y x bx c =-++的图象如下，则一次函数124y x b =--与反比例函数c y x=在同一平面直角坐标系中的图象大致是（ ）A ．B ．C ．D ．41．（2020·安徽铜陵·）抛物线2(0)y ax bx c a =++≠的对称轴为直线1x =，与x 轴的一个交点坐标为()4,0A ，其部分图象如图所示．下列叙述中：①24b ac <；②关于x 的方程20ax bx c ++=的两个根是122,4x x =-=；③20a b +=；④0a b c ++<；⑤当04x <<时，y 随x 增大而增大．正确的个数是（ ）A ．4B ．3C ．2D ．142．（2020·全国初三课时练习）如图，是二次函数2y ax bx c =++图象的一部分，下列结论中：①0abc >；②0a b c -+<；③210ax bx c +++=有两个相等．．的实数根；④4a 2a b -<<-.其中正确结论的序号为（ ）A ．①②B ．①③C ．②③D ．①④ 43．（2020·全国初三课时练习）如图是抛物线()210y ax bx c a =++≠图象的一部分，抛物线的顶点坐标()1,3A ，与x 轴的一个交点()4,0B ，直线()20y mx n m =+≠与抛物线交于A ，B 两点，下列结论： ①20a b +=；②0abc >；③方程23ax bx c ++=有两个相等的实数根；④抛物线与x 轴的另一个交点是()1,0-；⑤当14x <<时，有21y y <．其中正确结论的个数是（ ）A ．5B ．4C ．3D ．244．（2020·广东初三一模）如图是二次函数2y ax bx c =++图象的一部分，图象过点()5,0A -，对称轴为直线2x =-，给出四个结论：①0c >；②抛物线与轴的另一个交点坐标为()3,0；③40a b -=；④若()13,M y -与21,2N y ⎛⎫ ⎪⎝⎭是抛物线上两点，则12y y <．其中，正确结论的个数是（ ）A．1 B．2 C．3 D．445．（2020·北京八中初三月考）a≠0，函数y＝ax与y＝﹣ax2+a在同一直角坐标系中的大致图象可能是（）A．B．C．D．46．（2020·山东菏泽·初三月考）如图，抛物线y＝ax2＋bx＋c(a≠0)的对称轴为直线x＝1，与x轴的一个交点坐标为(－1，0)，其部分图象如图所示，下列结论：①4ac＜b2；②方程ax2＋bx＋c＝0的两个根是x1＝－1，x2＝3；③3a＋c＞0；④当y＞0时，x的取值范围是－1≤x＜3；⑤当x＜0时，y随x增大而增大．其中结论正确的个数是( )A．4个B．3个C．2个D．1个47．（2020·内蒙古扎鲁特旗·初三月考）如图，已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有下列5个结论：①abc＜0；②b＜a+c；③4a+2b +c＞0；④2c＜3b；⑤a+b＜m （am+b）（m≠1的实数）．其中正确结论的有（）A ．①②③B ．①③④C ．③④⑤D ．②③⑤ 48．（2020·全国初三课时练习）已知，二次函数y ＝ax 2+bx+c 满足以下三个条件：①2b a＞4c ，②a ﹣b+c ＜0，③b ＜c ，则它的图象可能是（ ）A ．B ．C ．D ．49．（2020·全国初三课时练习）已知二次函数2(0)y ax bx c a =++≠的图象如图所示，现给出下列结论：①0abc >；②930a b c ++=；③248b ac a -<；④50a b c ++>．其中正确结论的个数是（ ）A ．1B ．2C ．3D ．450．（2020·全国初三课时练习）已知二次函数y ＝ax 2+bx+c 的图象如图所示，下列结论：①ac ＜0，②b ﹣2a ＜0，③b 2﹣4ac ＜0，④a ﹣b+c ＜0，正确的是( )A ．①②B ．①④C ．②③D ．②④51．（2020·全国初三课时练习）抛物线2y ax bx c =++的对称轴是直线1x =-，且过点（1，0）.顶点位于第二象限，其部分图像如图所示，给出以下判断：①0ab >且0c <；②420a b c -+>；③8>0+a c ；④33c a b =-；⑤直线22y x =+与抛物线2y ax bx c =++两个交点的横坐标分别为12x x 、，则12125x x x x ++⋅=-.其中正确的个数有( )A ．5个B ．4个C ．3个D ．2个52．（2020·全国初三课时练习）已知：二次函数2(0)y ax bx c a =++≠的图象如图所示，下列结论中：①0abc >；②20a b +<；③()a b m am b +>+（1m ≠的实数）；④22()a c b +<；⑤1a >，其中正确的是（ ）A ．2个B ．3个C ．4个D ．1个53．（2020·全国初三课时练习）已知二次函数2(0)y ax bx c a =++≠的图象如下图，有下列5个结论：①0abc >；②b a c >+；③420a b c ++>；④23c b >；⑤()a b m am b +>+（1m ≠的实数）．其中正确结论的有（ ）A ．①②③B ．②③④C ．③④⑤D ．②③⑤54．（2020·广西南宁·三美学校初三学业考试）如图是抛物线()20y ax bx c a =++≠，其顶点为()1,n ，且与x轴的个交点在点()3,0和()4,0之间，则下列结论正确的个数是（ ）个①若抛物线与x 轴的另一个交点为(),0k ，则21k -<<-；②c a n -=；③若x m <-时，y 随x 的增大而增大，则1m ≥-．A ．0B ．1C ．2D ．355．（2020·辽宁铁岭·初三月考）如图，二次函数2(0)y ax bx c a =++≠的图象与x 轴交于点()1,0A -，其对称轴为直线1x =，下面结论中正确的是（ ）A ．0abc ＞B ．20a b -=C ．420a b c ++＜D ．930a b c ++=56．（2020·山东枣庄·初三其他）二次函数2y ax bx c =++的图象如图所示，对称轴是直线1x =．下列结论：①0abc <；②30a c +>；③()220a c b +-<；④()a b m am b +≤+(m 为实数)．其中结论正确的个数为( )A ．1个B ．2个C ．3个D ．4个57．（2019·黑龙江铁锋·初三三模）已知二次函数2y ax bx c =++的图象如图所示，则以下结论：①0abc >，②230b a +=，③0a b c -+<，④520a c +<．其中正确的有（ ）A ．1个B ．2个C ．3个D ．4个58．（2020·广东潮南·初三其他）平面直角坐标系中，二次函数()20y ax bx c a =++≠的图象如图所示，现给出下列结论：①0abc <；②20c a +>；③930a b c -+=；④2a b am bm -≤+（m 为实数）；⑤240ac b -<．其中正确的结论的个数是（ ）A ．2B ．3C ．4D ．559．（2020·山东历下·初三三模）如图是二次函数y ＝ax 2+bx+c （a≠0）的图象，下列结论正确的个数是（ ） ①对称轴为直线x ＝﹣1；②b 2﹣4ac ＞0；③方程ax 2+bx+c ＝0的解是x 1＝﹣3，x 2＝1；④不等式ax 2+bx+c ＞3的解为﹣2＜x ＜0．A ．4B ．3C ．2D ．160．（2020·全国初三课时练习）如图是二次函数y=ax 2+bx+c （a ，b ，c 是常数，a≠0）图象的一部分，与x 轴的交点A 在点（2，0）和（3，0）之间，对称轴是x=1．对于下列说法：①ab ＜0；②2a+b=0；③3a+c ＞0；④a+b≥m （am+b ）（m 为实数）；⑤当﹣1＜x ＜3时，y ＞0，其中正确的是（ ）A ．①②④B ．①②⑤C ．②③④D ．③④⑤61．（2020·全国初三课时练习）在同一坐标系内，一次函数y ax b =+与二次函数2y ax 8x b =++的图象可能是A ．B ．C ．D ．62．（2020·全国初三课时练习）已知抛物线y=ax 2+bx+c （a≠0）的对称轴为直线x=2，与x 轴的一个交点坐标为（4，0），其部分图象如图所示，下列结论：①抛物线过原点；②4a+b+c=0；③a ﹣b+c ＜0；④抛物线的顶点坐标为（2，b ）；⑤当x ＜2时，y 随x 增大而增大．其中结论正确的是（ ）A．①②③B．③④⑤C．①②④D．①④⑤63．（2020·全国初三课时练习）抛物线y＝ax2+bx+c的顶点为(﹣1，3)，与x轴的交点A在点(﹣3，0)和(﹣2，0)之间，其部分图象如图，则以下结论，其中正确结论的个数为()①若点P(﹣3，m)，Q(3，n)在抛物线上，则m＜n；②c＝a+3；③a+b+c＜0；④方程ax2+bx+c＝3有两个相等的实数根．A．1个B．2个C．3个D．4个64．（2020·湖北广水·初三期末）如图，二次函数y=ax2+bx+c的图象与x轴交于点A（﹣1，0），与y轴的交点B在（0，2）与（0，3）之间（不包括这两点），对称轴为直线x=2．下列结论：①abc＜0；②9a+3b+c＞0；③若点M（12，y1），点N（52，y2）是函数图象上的两点，则y1＜y2；④﹣35＜a＜﹣25；⑤c-3a＞0其中正确结论有（）A．2个B．3个C．4个D．5个65．（2020·河南太康·初三期末）如图，抛物线y ＝2ax ＋bx ＋c(a≠0)与x 轴交于点A(1，0)和B ，与y 轴的正半轴交于点C ．下列结论：①abc ＞0；②4a －2b ＋c ＞0；③2a －b ＞0；④3a ＋c ＞0.其中正确结论的个数为（ ）A ．1个B ．2个C ．3个D ．4个66．（2020·湖北广水·初三其他）二次函数y ＝2ax bx c ++（a ≠0）图象如图所示，下列结论：①abc ＞0；②2a b +＝0；③当m ≠1时，+a b ＞2am bm +；④a b c -+＞0；⑤若211ax bx +＝222ax bx +，且1x ≠2x ，则12x x +＝2．其中正确的有（ ）A ．①②③B ．②④C ．②⑤D ．②③⑤67．（2020·甘肃张掖·初三其他）小明从图所示的二次函数2y ax bx c =++的图象中，观察得出了下面四条信息：①230a b +=；②24b ac -＜0；③0a b c -+>；④方程20ax bx c ++=必有一个根在－1到0之间．你认为其中正确信息的个数有( )A ．1个B ．2个C ．3个D ．4个68．（2020·湖北广水·初三其他）如图，抛物线2y ax bx c =++的图象交x 轴于()2,0A -和点B ，交y 轴负半轴于点C ，且OB OC =，下列结论：①0a b c +<；②40a c +>；③12a =；④1acb +=； 其中正确的结论个数有（ ）A ．1个B ．2个C ．3个D ．4个69．（2020·重庆市荣昌区宝城初级中学初三其他）如图，抛物线2y ax bx c =++与x 轴交于点A(-1，0)，B(3，0)，交y 轴的正半轴于点C ，对称轴交抛物线于点D ，交x 轴与点E ，则下列结论：①2a+b=0；②b+2c>0；③a+b>am 2+bm （m 为任意实数）；④一元二次方程220ax bx c +++=有两个不相等的实数根；⑤当△BCD为直角三角形时，a 的值有2个；⑥若点P 为对称轴上的动点，则PB PC -有最大值，．其中正确的有（ ）A ．2个B ．3个C ．4个D ．5个70．（2020·内蒙古呼伦贝尔·初三二模）如图所示的抛物线y ＝ax 2+bx +c 的对称轴为直线x ＝1，则下列结论中错误的是（ ）A．ac＜0 B．b2﹣4ac＞0 C．2a﹣b＝0 D．9a+3b+c＝0参考答案1．C【解析】【分析】①根据直线x=-1是对称轴，确定b-2a 的值；②根据x=-2时，y ＞0确定4a-2b+c 的符号；③根据x=-4时，y=0，比较a-b+c 与-9a 的大小；④根据抛物线的对称性，得到x=-3与x=1时的函数值相等判断即可．【详解】解：①∵直线x=-1是对称轴，∴-2b a=-1，即b-2a=0，①正确； ②x=-2时，y ＞0，∴4a-2b+c ＞0，②错误；∵x=-4时，y=0，∴16a-4b+c=0，又b=2a ，∴a-b+c=-9a ，③正确；④根据抛物线的对称性，得到x=-3与x=1时的函数值相等，∴y 1＞y 2，④正确，故选C ．【点睛】本题考查二次函数图象与系数的关系．2．B【解析】【分析】根据题目所给的图像，首先判断1y kx =中k ＞0，其次判断22y ax bx c =++中a ＜0，b ＜0，c ＜0，再根据k 、b 、的符号判断2()y ax b k x c =+-+中b-k ＜0，又a ＜0，c ＜0可判断出图像．【详解】解：由题图像得1y kx =中k ＞0，22y ax bx c =++中a ＜0，b ＜0，c ＜0，∴b -k ＜0，∴函数2()y ax b k x c =+-+对称轴x=2b k a --＜0，交x 轴于负半轴， ∴当12y y =时，即2kx ax bx c =++，移项得方程2()0ax b k x c +-+=，∵直线1y kx =与抛物线22y ax bx c =++有两个交点， ∴方程2()0ax b k x c +-+=有两个不等的解，即2()y ax b k x c =+-+与x 轴有两个交点，根据函数2()y ax b k x c =+-+对称轴交x 轴负半轴且函数图像与x 轴有两个交点， ∴可判断B 正确．故选：B【点睛】本题考查二次函数与一次函数的图象与性质，解题的关键是根据图像判断k 、a 、b 、c 的正负号，再根据二次函数与一元二次方程的关系判断出正确图像．3．B【解析】【分析】根据二次函数的图象和二次函数的性质，可以判断各个小题中的结论是否成立，从而可以解答本题．【详解】∵二次函数y ＝ax 2+bx+c （a≠0）的对称轴为x ＝1， ∴﹣2b a＝1，得2a+b ＝0，故①正确； 当x ＝﹣2时，y ＝4a ﹣2b+c ＜0，故②正确；该函数图象与x 轴有两个交点，则b 2﹣4ac ＞0，故③正确；∵二次函数y ＝ax 2+bx+c （a≠0）的对称轴为x ＝1，点B 坐标为（﹣1，0），∴点A （3，0），∴当y ＜0时，x ＜﹣1或x ＞3，故④错误；故选B ．【点睛】本题考查二次函数图象与系数的关系、抛物线与x 轴的交点，解答本题的关键是明确题意，利用二次函数的性质和数形结合的思想解答．4．D【解析】【分析】分别利用函数解析式分析图象得出答案．【详解】解：由一次函数解析式为：y=kx+2可知，图象应该与y 轴交于正半轴上，故A 、B 、C 错误；D 符合题意；故选：D ．【点睛】此题主要考查了二次函数的图象以及一次函数的图象，得出直线交y 轴的正半轴是解题关键． 5．D【解析】【分析】由抛物线的开口方向判断a 与0的关系，由抛物线与y 轴的交点判断c 与0的关系，然后根据对称轴进行推理，进而对所得结论进行判断．【详解】解：抛物线开口方向向下，则a ＜0，∵对称轴是直线x=2b a=1，则b=-2a ， ∴3a+b=3a-2a=a ＜0，故①正确；当x=-1时，y ＜0，即a-b+c ＜0，故②正确；抛物线与y 轴交于正半轴，则c ＞0，故③正确；∵b=-2a ，∴a+b=a-2a=-a ，∵a ＜0，∴-a ＞0，∴a+b ＞0，故④正确．综上所述，正确的结论是：①②③④．故选：D ．【点睛】本题主要考查图象与二次函数系数之间的关系，会利用对称轴的范围求2a 与b 的关系，掌握“数形结合”数学思想的应用．6．D【解析】【分析】根据二次函数开口方向，可以判断出a 的正负，根据对称轴的位置和a 的正负，可以判断出b 的正负，再根抛物线与y 轴的交点，可以判断出c 的正负，然后根据a 、b 、c 的正负去判断一次函数和二次函数在坐标系中的位置即可.【详解】∵二次函数图象开口向上，∴a ＞0，∵对称轴为直线x ＝﹣2b a＞0， ∴b ＜0，当x ＝﹣1时，a ﹣b +c ＞0，当x ＝1时，a ﹣b +c ＜0，∴（a +b +c ）（a ﹣b +c ）＜0，∵抛物线与x 轴有两个交点，∴b 2﹣4ac ＞0，∴一次函数图象经过第一、二、四象限，反比例函数图象经过第二四象限．故选：D ．【点睛】本题考查了一次函数、二次函数、反比例函数的图像与系数的关系，根据二次函数抛物线求出a 、b 、c 的正负是解决本题的管家.7．C【解析】【分析】先根据反比例函数图象确定k 的值，再分析二次函数图象是否符合，逐一判断即可【详解】A 、由反比例函数图象知：k ＞0，因此二次函数图象应开口向上，且与y 轴交于负半轴，故此选项错误；B 、由反比例函数图象知：k ＜0，因此二次函数图象应开口向下，故此选项错误；C 、由反比例函数图象知：k ＜0，因此二次函数图象应开口向下，且与y 轴交于正半轴，故此选项正确；D 、由反比例函数图象知：k ＞0，因此二次函数图象应开口向上，故此选项错误； 故选Ｃ．【点睛】本题考查反比例函数、二次函数的图象与性质，比较基础．8．D【解析】【分析】先根据一次函数图像确定m 的符号，在依据二次函数y=ax 2+bx+c 图像性质进行判断，当a ＞0时，开口向上；当a ＜0时，开口向下．对称轴为x=2b a -，与y 轴的交点坐标为（0，c ）． 【详解】解：A 、由函数y ＝mx+m 的图象可知m ＜0，即函数y ＝﹣mx 2+2x+2开口方向朝上，与图象不符，故A 选项错误；B 、由函数y ＝mx+m 的图象可知m ＜0，对称轴为x ＝2b a -＝212m m -=＜0，则对称轴应在y 轴左侧，与图象不符，故B 选项错误；C 、由函数y ＝mx+m 的图象可知m ＞0，即函数y ＝﹣mx 2+2x+2开口方向朝下，与图象不符，故C 选项错误；D 、由函数y ＝mx+m 的图象可知m ＜0，即函数y ＝﹣mx 2+2x+2开口方向朝上，对称轴为x ＝2b a -＝﹣212m m-= ＜0，则对称轴应在y 轴左侧，与图象相符，故D 选项正确； 故选D ．【点睛】本题主要考查了一次函数和二次函数的图象性质以及分析能力和读图能力，要掌握它们的性质才能灵活解题．一次函数和二次函数的图象所经过的象限的问题，关键是m 的正负的确定，9．D【解析】【分析】①．函数的对称轴为x ＝﹣2b a＝1，即可求解；②．新抛物线表达式为：y ＝ax 2+bx ＝ax 2﹣2ax ＝ax （x ﹣2），即可求解；③．x ＝﹣1时，y ＝a ﹣b +c ＜0，x ＝1时，y ＝a +b +c ＝2，即220b a a b c a b c =-⎧⎪++=⎨⎪-+<⎩，即可求解；④．∆＝4a 2﹣4a ＝4a （a ﹣1），而﹣1＜a ＜﹣12，故∆＞0，即可求解．【详解】解：①．函数的对称轴为x ＝﹣2b a＝1，解得：b ＝﹣2a ；故①正确； ②．此抛物线向下移动c 个单位后，新抛物线表达式为：y ＝ax 2+bx ＝ax 2﹣2ax ＝ax （x ﹣2）， 则x ＝2时，y ＝0，故抛物线过点（2，0），故②正确；③．x ＝﹣1时，y ＝a ﹣b +c ＜0，x ＝1时，y ＝a +b +c ＝2，即220b a a b c a b c =-⎧⎪++=⎨⎪-+<⎩，解得：﹣1＜a ＜﹣12，故③正确； ④．∵c ＜0，∴x 2﹣2x +1c＝0变形为cx 2﹣2cx +1＝0， ∵∆＝4c 2﹣4c ＝4c （c ﹣1），而1＜c ＜2， ∴∆＞0，故方程x 2﹣2x +1c ＝0有实数根，故④正确； 故选：D ．【点睛】此题考查的是二次函数图象及性质,掌握二次函数图象及性质与各项系数的关系是解决此题的关键．10．A【解析】【分析】观察图象：开口向下得到a ＜0；对称轴在y 轴的右侧得到a 、b 异号，则b ＞0；抛物线与y轴的交点在x 轴的上方得到c ＞0，所以abc ＜0；当x ＝﹣1时图象在x 轴上得到y ＝a ﹣b +c ＝0，即a +c ＝b ；对称轴为直线x ＝1，可得x ＝2时图象在x 轴上方，则y ＝4a +2b +c ＞0；利用对称轴x ＝﹣2b a＝1得到a ＝﹣12b ，而a ﹣b +c ＜0，则﹣12b ﹣b +c ＜0，所以2c ＜3b ；开口向下，当x ＝1，y 有最大值a +b +c ，得到a +b +c ＞am 2+bm +c ，即a +b ＞m （am +b ）（m ≠1）．【详解】解：开口向下，a ＜0；对称轴在y 轴的右侧，a 、b 异号，则b ＞0；抛物线与y 轴的交点在x 轴的上方，c ＞0，则abc ＜0，所以①不正确；当x ＝﹣1时图象在x 轴上，则y ＝a ﹣b +c ＝0，即a +c ＝b ，所以②不正确；对称轴为直线x ＝1，则x ＝2时图象在x 轴上方，则y ＝4a +2b +c ＞0，所以③正确； x ＝﹣2b a＝1，则a ＝﹣12b ，而a ﹣b +c ＝0，则﹣12b ﹣b +c ＝0，2c ＝3b ，所以④不正确； 开口向下，当x ＝1，y 有最大值a +b +c ；当x ＝m （m ≠1）时，y ＝am 2+bm +c ，则a +b +c ＞am 2+bm +c ，即a +b ＞m （am +b ）（m ≠1），所以⑤正确．故选：A ．【点睛】本题考查了二次函数图象与系数的关系：对于二次函数y=ax 2+bx+c （a ≠0）的图象，当a ＞0，开口向上，函数有最小值，a ＜0，开口向下，函数有最大值；对称轴为直线x=2b a -，a 与b 同号，对称轴在y 轴的左侧，a 与b 异号，对称轴在y 轴的右侧；当c ＞0，抛物线与y 轴的交点在x 轴的上方；当△=b 2-4ac ＞0，抛物线与x 轴有两个交点．11．B【解析】【分析】根据图像得出a ＜0，c ＜0，b ＞0，可判断①；再由图像可得对称轴在直线x=2右侧，可得22b a->，可判断②；再根据二次函数在y 轴右侧时的增减性，判断③；根据抛物线对称轴为直线x=3，得出6b a =-，再利用作差法判断④；最后根据AB≥3，则点A 的横坐标大于0且小于等于1，得出a+b+c≥0，再由当x=4时，得出16a+4b+c=0，变形为a=416b c +-，代入，可得4b+5c≥0，结合c 的符号可判断⑤.【详解】解：如图，抛物线开口向下，与y 轴交于负半轴，对称轴在y 轴右侧，∴a ＜0，c ＜0，02b a ->， ∴b ＞0，∴abc ＞0，故①正确；如图，∵抛物线过点B （4，0），点A 在x 轴正半轴，∴对称轴在直线x=2右侧，即22b a->， ∴42022b a b a a++=<，又a ＜0， ∴4a+b ＞0，故②正确；∵()11,M x y 与()22,N x y 是抛物线上两点，120x x <<，可得：抛物线2y ax bx c =++在02b x a<<-上，y 随x 的增大而增大， 在2b x a>-上，y 随x 的增大而减小， ∴12y y >不一定成立，故③错误；若抛物线对称轴为直线x=3，则32b a-=，即6b a =-， 则(3)(3)(3)a m m b m -+--=()()()3363a m m a m -++-=()()336a m m -+-=()23a m -≤0，∴(3)(3)(3)a m m b m -+≤-，故④正确；∵AB≥3，则点A 的横坐标大于0且小于等于1，当x=1时，代入，y=a+b+c≥0，当x=4时，16a+4b+c=0，∴a=416b c+-，则416b cb c+++≥-，整理得：4b+5c≥0，则4b+3c≥-2c，又c＜0，-2c＞0，∴4b+3c＞0，故⑤正确，故正确的有4个.故选B.【点睛】本题考查了二次函数的图像和性质，解题的关键是能根据图像得出二次函数表达式各系数的符号.12．D【解析】【分析】利用对称性得到抛物线对称轴为直线x＝1，根据点的坐标确定开口向下，最大值大于3，根据二次函数的性质即可判断D正确．【详解】解：∵抛物线y＝a（x﹣h）2＋k（a≠0）经过A（m﹣4，0），B（m﹣2，3），C（4﹣m，3）三点，其中m＜3，∴抛物线的开口向下，对称轴为直线x＝242m m-+-＝1，即a＜0，h＝1，∴k＞3，当x＜1时，y随x的增大而增大，故选：D．【点睛】本题考查二次函数图象与系数的关系，二次函数图象上点的坐标特征，熟练掌握二次函数的性质是关键．13．C【解析】【分析】根据二次函数的性质逐一进行判断即可【详解】解：∵x ＝1时，y ＝0，∴a ＋b ＋c ＝0，所以①正确；∵x ＝2b a＝－1，∴b ＝2a ，所以②错误； ∵点(1，0)关于直线x ＝－1对称的点的坐标为(－3，0)，∴抛物线与x 轴的交点坐标为(－3，0)和(1，0)，∴ax 2＋bx ＋c ＝0的两根分别为－3和1，所以③正确；∵抛物线与y 轴的交点在x 轴下方，∴c ＜0，∵a ＋b ＋c ＝0，b ＝2a ，∴c ＝－3a ，∴a －2b ＋c ＝－6a ，∵a ＞0，∴－6a ＜0∴a －2b ＋c ＜0，所以④错误．【点睛】本题考查的是二次函数图象与系数的关系，掌握二次函数的性质、灵活运用数形结合思想是解题的关键，解答时，要熟练运用抛物线的对称性和抛物线上的点的坐标满足抛物线的解析式.14．A【解析】【分析】由抛物线开口方向及与y 轴的交点位置可判断①；令y=1可判断②；由图像与x 轴的交点可判断③和④；由图像与x 轴的两个交点可求得对称轴，结合图像的开口方向，则可判断⑤；则可求得答案．【详解】抛物线开口方向、与y 轴的交点在x 轴的下方，∴00a c ><，，0ac <，故①正确；由图像可知当1x =时，0y <，∴0a b c ++<，故②不正确；由图像可知抛物线与x 轴交与(−1,0)和(3,0)两点，∴方程20ax bx c ++=的根是121,3x x =-=,且240b ac ->，故③、④正确；抛物线与x 轴交与(−1,0)和(3,0)两点，∴抛物线对称轴为直线1312x -+==，且抛物线开口向下， ∴当1x >时，y 随x 的增大而增大，故⑤正确；综上可知正确的结论有4个，故选A.【点睛】本题考查的知识点是二次函数图像与系数的关系，解题关键是利用数形结合得出各项符号． 15．C【解析】根据抛物线开口方向得a ＜0，由抛物线对称轴为直线x ＝﹣2b a＝1，得到b ＝﹣2a ＞0，即2a+b ＝0，即可判断①；根据二次函数的性质得当x ＝1时，函数有最大值a+b+c ，即可判断②；根据抛物线的对称性得到抛物线与x 轴的另一个交点在（﹣1，0）的右侧，则当x ＝﹣1时，y ＜0，所以a ﹣b+c ＜0，即可判断③；把b ＝﹣2a 代入a ﹣b+c ＜0可对④进行判断；把ax 12+bx 1＝ax 22+bx 2先移项，再分解因式得到（x 1﹣x 2）[a （x 1+x 2）+b]＝0，而x 1≠x 2，则a （x 1+x 2）+b ＝0，即x 1+x 2＝﹣b a ，然后把b ＝﹣2a 代入计算得到x 1+x 2＝2可对⑤进行判断． 【详解】∵抛物线开口向下，∴a ＜0，∵抛物线对称轴为直线x ＝﹣2b a＝1， ∴b ＝﹣2a ＞0，即2a+b ＝0，所以①正确；∵抛物线对称轴为直线x ＝1，∴函数的最大值为a+b+c ，∴a+b+c≥am 2+bm+c ，即a+b≥am 2+bm ，所以②正确；∵抛物线与x 轴的一个交点在（3，0）的左侧，而对称轴为直线x ＝1，∴抛物线与x 轴的另一个交点在（﹣1，0）的右侧，∴当x ＝﹣1时，y ＜0，∴a ﹣b+c ＜0，所以③错误；∵b ＝﹣2a ，a ﹣b+c ＜0，∴a+2a+c ＜0，即3a+c ＜0，所以④正确；∵ax 12+bx 1＝ax 22+bx 2，∴ax 12+bx 1﹣ax 22﹣bx 2＝0，∴a （x 1+x 2）（x 1﹣x 2）+b （x 1﹣x 2）＝0，∴（x 1﹣x 2）[a （x 1+x 2）+b]＝0，而x 1≠x 2，∴a （x 1+x 2）+b ＝0，即x 1+x 2＝﹣b a， ∵b ＝﹣2a ，∴x 1+x 2＝2，所以⑤正确．综上所述，正确的有①②④⑤共4个．故选：C ．【点睛】本题主要考查了二次函数的图象和性质，熟练掌握二次函数图象与解析式系数关系，与方程和不等式关系是解题的关键．16．D【解析】【分析】根据抛物线开口向上得出a ＞0，根据抛物线和y 轴的交点在y 轴的负半轴上得出c ＜0，根据图象与x 轴的交点坐标得出方程ax 2+bx+c=0的根，把x=1代入y=ax 2+bx+c 求出a+b+c ＜0，根据抛物线的对称轴和图象得出当x ＞1时，y 随x 的增大而增大，2a=-b ，根据图象和x 轴有两个交点得出b 2-4ac ＞0．【详解】∵抛物线开口向上，∴a ＞0，∵抛物线和y 轴的交点在y 轴的负半轴上，∴c ＜0，∴ac ＜0，∴①正确；∵图象与x 轴的交点坐标是（-1，0），（3，0），∴方程ax 2+bx+c=0的根是x 1=-1，x 2=3，∴②正确；把x=1代入y=ax 2+bx+c 得：a+b+c ＜0，∴③错误；根据图象可知：当x ＞1时，y 随x 的增大而增大，∴④正确；∵-2b a=1， ∴2a=-b ，∴2a+b=0，不是2a-b=0，∴⑤错误；∵图象和x 轴有两个交点，∴b 2-4ac ＞0，∴⑥正确；正确的说法有：①②④⑥．故答案为：D ．【点睛】本题考查了二次函数与系数的关系的应用，主要考查学生对二次函数的图象与系数的关系的理解和运用，同时也考查了学生观察图象的能力，本题是一道比较典型的题目，具有一定的代表性．17．C【解析】【分析】【详解】根据图像可得：a<0，b<0，c=0，即abc=0，则①正确；当x=1时，y<0，即a+b+c<0，则②错误； 根据对称轴可得：－2b a =－32，则b=3a ，根据a<0，b<0可得：a>b ；则③正确； 根据函数与x 轴有两个交点可得：2b －4ac>0，则④正确.故选C.【点睛】本题考查二次函数的性质.能通过图象分析a ，b ，c 的正负，以及通过一些特殊点的位置得出a ，b ，c 之间的关系是解题关键.18．D【解析】【分析】先根据一次函数的图象判断 , ,a b 的符号,再判断二次函数图象与实际是否相符,判断正误.【详解】A.由一次函数y ＝ax+a 的图象可得: a<0且a>0 ,两者矛盾,故A 错误;B ．由一次函数 y ＝ax+a 的图象可得: a<0,此时二次函数 y ＝(x －a)2的顶点(a, 0)的位置可推出a>0 ,两者矛盾,故B 错误;C.由一次函数 y ＝ax+a 的图象可得: a<0且a>0,两者矛盾,故C 错误;D.由一次函数y ＝ax+a 的图象可得:a>0 ,此时二次函数 y ＝(x －a)2的顶点(a, 0)的位置可推出a>0 ,故D 正确;故选:D.。

二次函数图像与系数关系70题-含答案

二次函数图像与系数关系70题-含答案

二次函数图像与系数关系70题1．（2020·湖南茶陵·初三零模）如图是二次函数y=ax 2+bx+c （a≠0）图象的一部分，直线x=-1是对称轴，有下列判断：①b-2a=0；②4a-2b+c ＜0；③a-b+c=-9a ；④若（-3，y 1），（32，y 2）是抛物线上两点，则y 1＞y 2，其中正确的个数是（ ）A ．1个B ．2个C ．3个D ．4个2．（2020·浙江杭州外国语学校初三月考）如图，直线1y kx =与抛物线22y ax bx c =++交于A 、B 两点，则2()y ax b k x c =+-+的图象可能是（ ）A ．B ．C ．D ．3．（2020·浙江杭州外国语学校初三月考）如图，二次函数y ＝ax 2+bx +c （a ≠0）图象与x 轴交于A ，B 两点，与y 轴交于C 点，且对称轴为x ＝1，点B 坐标为（﹣1，0）．则下面的四个结论：①2a +b ＝0；②4a ﹣2b +c ＜0；③b 2﹣4ac ＞0；④当y ＜0时，x ＜﹣1或x ＞2．其中正确的有（ ）A．4个B．3个C．2个D．1个4．（2020·福建省连江第三中学初三月考）在同一坐标系内，函数y＝kx2和y＝kx＋2（k≠0）的图象大致如图（）A．B．C． D．5．（2020·福建省连江第三中学初三月考）已知二次函数y＝ax2＋bx＋c（a≠0）的图象如图所示，则下列结论：①3a＋b＜0；②a﹣b＋c＜0；③c＞0；④a＋b＞0．其中正确的结论有（）A．仅①②③B．仅②③④C．仅①②④D．①②③④6．（2020·辽宁新宾·初三其他）抛物线y＝ax2+bx+c的图象如图所示，那么一次函数y＝bx+b2﹣4ac与反比例函数y＝()()a b c a b cx++-+在同一坐标系内的图象大致是（）A．B．C．D．7．（2020·湖南茶陵·初三期末）反比例函数kyx=-与二次函数2y kx k=-(0)k≠在同一直角坐标系的图像可能是（）A．B．C．D．8．（2020·兰西县红星乡第一中学校初二月考）在同一直角坐标系中，函数y mx m=+和函数222y mx x=-++(m是常数，且0m≠)的图象可能是( )A．B．C．D．9．（2020·福建省福州第十九中学初三其他）二次函数y＝ax2+bx+c的图象如图所示，则下列命题中：①b＝﹣2a；②此抛物线向下移动c个单位后过点（2，0）；③﹣1＜a＜﹣12；④方程x2﹣2x+1c＝0有实数根，结论正确的个数（）A ．1个B ．2个C ．3个D ．4个10．（2020·内蒙古海勃湾·初三期末）已知二次函数y ＝ax 2+bx +c （a ≠0）的图象如图所示，有下列5个结论： ①abc ＞0；②b ＜a +c ；③4a +2b +c ＞0；④2c ＜3b ；⑤a +b ＞m （am +b ）（m ≠1的实数）．其中正确的结论有（ ）A ．2个B ．3个C ．4个D ．5个11．（2020·湖北武汉·初三月考）如图，抛物线2y ax bx c =++与x 轴正半轴交于A ，B 两点，与y 轴负半轴交于点C ．若点(4,0)B ，则下列结论中：①0abc >；②40a b +>；③()11,M x y 与()22,N x y 是抛物线上两点，若120x x <<，则12y y >；④若抛物线的对称轴是直线3x =，m 为任意实数，则(3)(3)(3)a m m b m -+-；⑤若3AB ≥，则430b c +>，正确的个数是（ ）A ．5B ．4C ．3D ．212．（2020·陕西师大附中初三一模）已知抛物线y ＝a （x ﹣h ）2＋k （a ≠0）经过A （m ﹣4，0），B （m ﹣2，3），C （4﹣m ，3）三点，其中m ＜3，则下列说法正确的是（ ）A ．a ＞0B ．h ＜0C ．k ≥3D ．当x ＜0时，y 随x 的增大而增大 13．（2019·四川邛崃·初三三模）如图，是二次函数y ＝ax 2+bx +c （a ≠0）的图象的一部分，给出下列命题：①a +b +c ＝0；②b ＞2a ；③ax 2+bx +c ＝0的两根分别为﹣3和1；④a ﹣2b +c ＞0．其中正确的命题是（ ）A ．①②B ．②③C ．①③D ．①②③④14．（2019·陕西渭滨·初三二模）如图为二次函数y=ax 2+bx+c 的图象，在下列说法中：①ac ＜0；②a+b+c ＞0；③方程ax 2+bx+c=0的根是x 1=﹣1，x 2=3； ④b 2﹣4ac ＞0；⑤当x ＞1时，y 随x 的增大而增大；正确的说法有（ ）A ．4个B ．3个C ．2个D ．1个15．（2020·长沙市长郡梅溪湖中学初二期末）二次函数y ＝ax 2+bx+c （a≠0）的图象如图所示，下列结论：①2a+b ＝0；②若m 为任意实数，则a+b≥am 2+bm ；③a ﹣b+c ＞0；④3a+c ＜0；⑤若ax 12+bx 1＝ax 22+bx 2，且x 1≠x 2，则x 1+x 2＝2．其中正确的个数为（ ）A ．2B ．3C ．4D ．516．（2020·四川阿坝·初三期末）如图为二次函数2y ax bx c =++的图象，在下列说法中:①0ac <；②方程20ax bx c ++=的根是121,3x x =-=③ 0a b c ++>；④当1x >时，y 随x 的增大而增大；⑤20a b -=；⑥240b ac ->，正确的说法有（ ）A ．1B ．2C ．3D ．417．（2020·湖南雨花·初二期末）如图，已知二次函数y=ax 2+bx+c （a≠0）的图象如图所示，给出以下四个结论：①abc=0，②a+b+c＞0，③a＞b ，④4ac﹣b 2＜0；其中正确的结论有（ ）A ．1个B ．2个C ．3个D ．4个18．（2020·湖南雨花·初二期末）同一平面直角坐标系中，抛物线y ＝(x －a )2与直线y ＝ax +a 的图象可能是（ ）A ．B ．C ．D ．19．（2020·陕西碑林·西北工业大学附属中学初三一模）已知二次函数 y ＝ax 2＋bx ＋c ，其中 y 与 x 的部分对应值如表：下列结论正确的是（ ）A ．abc ＜0B ．4a ＋2b ＋c ＞0C ．若 x ＜－1 或 x ＞3 时，y ＞0D ．方程 ax 2＋bx ＋c ＝5 的解为 x 1＝－2，x 2＝3 20．（2020·湖南湘潭·初三期末）如图，二次函数2(0)y ax bx c a =++≠的图象，则下列结论正确的是（ ）①0b <；②240b ac ->；③a c b +<；④0c >A ．①②③B ．②③④C ．①③④D ．①②③④21．（2020·甘肃肃州·初三期末）已知二次函数y=2ax bx c ++（a≠0）的图像如图所示，对称轴为x= -1，则下列式子正确的个数是（ ）（1）abc ＞0（2）2a+b=0（3）4a+2b+c ＜0（4）b 2-4ac ＜0A ．1个B ．2个C ．3个D ．4个22．（2019·黑龙江甘南·初三期末）如图，已知抛物线y ＝ax 2+bx +c 经过点（﹣1，0），对称轴是x ＝1，现有结论：①abc ＞0 ②9a ﹣3b +c ＝0 ③b ＝﹣2a ④﹣1）b +c ＜0，其中正确的有（ ）A ．1个B ．2个C ．3个D ．4个23．（2020·湖南天心·长郡中学初二期末）二次函数2y ax bx c =++的图象如图所示，则下列结论正确的是（ ）A ．0abc >B ．0a b c ++=C ．420a b c -+<D ．240b ac -<24．（2020·全国初三课时练习）在同一平面直角坐标系中，函数y ＝ax 2＋b 与y ＝ax ＋b （ab ≠0）的大致图象可能是（ ）A ．B ．C ．D ．25．（2020·陕西旬阳·初三期末）已知二次函数2y ax bx c =++（a≠0）的图象如图所示，则下列结论：①b＜0，c ＞0；②a+b+c ＜0；③方程的两根之和大于0；④a ﹣b+c ＜0，其中正确的个数是（ ）A ．4个B ．3个C ．2个D ．1个26．（2019·无锡市南长实验中学初三月考）在同一平面直角坐标系中，函数2y ax bx =-与y bx a =+的图象可能是（ ）A ．B ．C ．D ．27．（2020·长沙麓山国际实验学校初三期末）如图为二次函数()20y ax bx c a =++≠的图象，则下列说法：①0a >；②20a b +=；③0a b c ++>；④0>；⑤420a b c -+<，其中正确的个数为（ ）A ．1B ．2C ．3D ．428．（2020·全国初三课时练习）如图，抛物线2(0)y ax bx c a =++≠与x 轴交于点(1,0)A -和B ，与y 轴交于点C ．下列结论：①0abc <；②20a b +<；③420a b c -+>；④30a c +>，其中正确的结论个数为（ ）A ．1个B ．2个C ．3个D ．4个29．（2020·云南昆明三中初二期末）下列图像中，当0ab >时，函数2y ax =与y ax b =+的图象时（ ）A ．B ．C ．D ．30．（2021·全国初三专题练习）已知二次函数y=ax 2+bx+c （a ，b ，c 是常数，且a≠0）的图象如图所示，则一次函数2b y cx a =+与反比例函数ab y x=在同一坐标系内的大致图象是（ ）A ．B ．C ．D ．31．（2020·全国初三单元测试）如图，抛物线2(0)y ax bx c a =++≠交x 轴于点A ，B ，交y 轴于点C ．若点A 坐标为(4,0)-，对称轴为直线1x =-，则下列结论错误的是（ ）A ．二次函数的最大值为a b c -+B ．0a b c ++>C ．240b ac ->D ．20a b +=32．（2020·甘肃兰州·中考真题）如图，已知二次函数()2y ax bx c a 0=++≠的图象如图所示，有下列5个结论 abc 0>①；b a c ->②；4a 2b c 0++>③；3a c >-④；()a b m am b (m 1+>+≠⑤的实数).其中正确结论的有( )A ．①②③B ．②③⑤C ．②③④D ．③④⑤33．（2019·四川雁江·初三其他）如图中实线所示，函数y=|a （x ﹣1）2﹣1|的图象经过原点，小明同学研究得出下面结论：①a=1；②若函数y 随x 的增大而减小，则x 的取值范围一定是x ＜0；③若方程|a （x ﹣1）2﹣1|=k 有两个实数解，则k 的取值范围是k ＞1；④若M （m 1，n ），N （m 2，n ），P （m 3，n ），Q （m 4，n ）（n ＞0）是上述函数图象的四个不同点，且m 1＜m 2＜m 3＜m 4，则有m 2+m 3﹣m 1=m 4．其中正确的结论有（ ）A ．4个B ．3个C ．2个D ．1个34．（2020·安徽初三其他）如图，已知函数y ＝﹣3x 与y ＝ax 2+bx （a ＞0，b ＞0）的图象交于点P ，点P 的纵坐标为1，则关于x 的方程ax 2+bx +3x＝0的解为（ ）A．x＝3 B．x＝1 C．x＝﹣3 D．无解35．（2020·广东福田·深圳实验学校初三三模）如图，二次函数y＝ax2+bx+c(a≠0)的图象经过点(﹣1，2)，且与x轴交点的横坐标分别为x1，x2，其中﹣2＜x1＜﹣1，0＜x2＜1，下列结论：①4a﹣2b+c＜0；②2a﹣b＜0；③a＜0；④b2+8a＞4ac，其中正确的有( )A．1个B．2个C．3个D．4个36．（2020·黑龙江甘南·初三期末）在同一平面直角坐标系中，一次函数y＝ax+b和二次函数y＝ax2+bx+c的图象可能为（）A．B．C．D．37．（2020·山西浑源·初三期末）在平面直角坐标系中，开口向下的抛物线y＝ax2+bx+c的一部分图象如图所示，它与x轴交于A（1，0），与y轴交于点B（0，3），对称轴是直线x= -1．则下列结论正确的是（）A ．ac ＞0B ．b 2－4ac ＝0C ．a －b ＋c ＜0D ．当-3＜x ＜1时，y ＞038．（2020·四川广安二中初三期末）抛物线y ＝ax 2＋bx ＋c(a≠0)的对称轴为直线x ＝－1，与x 轴的一个交点在(－3，0)和(－2，0)之间，其部分图象如图，则下列结论：①4ac －b 2＜0；②2a －b ＝0；③a ＋b ＋c ＜0；④点(x 1，y 1)，(x 2，y 2)在抛物线上，若x 1＜x 2，则y 1＜y 2 .正确结论的个数是( )A ．1B ．2C ．3D ．439．（2020·福建闽侯·初三一模）抛物线y ＝ax 2+bx+c 与直线y ＝ax+c （a≠0）在同一直角坐标系中的图象可能是（ ）A ．B ．C ．D ．40．（2020·宁夏金凤·初三其他）已知二次函数214y x bx c =-++的图象如下，则一次函数124y x b =--与反比例函数c y x=在同一平面直角坐标系中的图象大致是（ ）A ．B ．C ．D ．41．（2020·安徽铜陵·）抛物线2(0)y ax bx c a =++≠的对称轴为直线1x =，与x 轴的一个交点坐标为()4,0A ，其部分图象如图所示．下列叙述中：①24b ac <；②关于x 的方程20ax bx c ++=的两个根是122,4x x =-=；③20a b +=；④0a b c ++<；⑤当04x <<时，y 随x 增大而增大．正确的个数是（ ）A ．4B ．3C ．2D ．142．（2020·全国初三课时练习）如图，是二次函数2y ax bx c =++图象的一部分，下列结论中：①0abc >；②0a b c -+<；③210ax bx c +++=有两个相等．．的实数根；④4a 2a b -<<-.其中正确结论的序号为（ ）A ．①②B ．①③C ．②③D ．①④ 43．（2020·全国初三课时练习）如图是抛物线()210y ax bx c a =++≠图象的一部分，抛物线的顶点坐标()1,3A ，与x 轴的一个交点()4,0B ，直线()20y mx n m =+≠与抛物线交于A ，B 两点，下列结论： ①20a b +=；②0abc >；③方程23ax bx c ++=有两个相等的实数根；④抛物线与x 轴的另一个交点是()1,0-；⑤当14x <<时，有21y y <．其中正确结论的个数是（ ）A ．5B ．4C ．3D ．244．（2020·广东初三一模）如图是二次函数2y ax bx c =++图象的一部分，图象过点()5,0A -，对称轴为直线2x =-，给出四个结论：①0c >；②抛物线与轴的另一个交点坐标为()3,0；③40a b -=；④若()13,M y -与21,2N y ⎛⎫ ⎪⎝⎭是抛物线上两点，则12y y <．其中，正确结论的个数是（ ）A．1 B．2 C．3 D．445．（2020·北京八中初三月考）a≠0，函数y＝ax与y＝﹣ax2+a在同一直角坐标系中的大致图象可能是（）A．B．C．D．46．（2020·山东菏泽·初三月考）如图，抛物线y＝ax2＋bx＋c(a≠0)的对称轴为直线x＝1，与x轴的一个交点坐标为(－1，0)，其部分图象如图所示，下列结论：①4ac＜b2；②方程ax2＋bx＋c＝0的两个根是x1＝－1，x2＝3；③3a＋c＞0；④当y＞0时，x的取值范围是－1≤x＜3；⑤当x＜0时，y随x增大而增大．其中结论正确的个数是( )A．4个B．3个C．2个D．1个47．（2020·内蒙古扎鲁特旗·初三月考）如图，已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有下列5个结论：①abc＜0；②b＜a+c；③4a+2b +c＞0；④2c＜3b；⑤a+b＜m （am+b）（m≠1的实数）．其中正确结论的有（）A ．①②③B ．①③④C ．③④⑤D ．②③⑤ 48．（2020·全国初三课时练习）已知，二次函数y ＝ax 2+bx+c 满足以下三个条件：①2b a＞4c ，②a ﹣b+c ＜0，③b ＜c ，则它的图象可能是（ ）A ．B ．C ．D ．49．（2020·全国初三课时练习）已知二次函数2(0)y ax bx c a =++≠的图象如图所示，现给出下列结论：①0abc >；②930a b c ++=；③248b ac a -<；④50a b c ++>．其中正确结论的个数是（ ）A ．1B ．2C ．3D ．450．（2020·全国初三课时练习）已知二次函数y ＝ax 2+bx+c 的图象如图所示，下列结论：①ac ＜0，②b ﹣2a ＜0，③b 2﹣4ac ＜0，④a ﹣b+c ＜0，正确的是( )A ．①②B ．①④C ．②③D ．②④51．（2020·全国初三课时练习）抛物线2y ax bx c =++的对称轴是直线1x =-，且过点（1，0）.顶点位于第二象限，其部分图像如图所示，给出以下判断：①0ab >且0c <；②420a b c -+>；③8>0+a c ；④33c a b =-；⑤直线22y x =+与抛物线2y ax bx c =++两个交点的横坐标分别为12x x 、，则12125x x x x ++⋅=-.其中正确的个数有( )A ．5个B ．4个C ．3个D ．2个52．（2020·全国初三课时练习）已知：二次函数2(0)y ax bx c a =++≠的图象如图所示，下列结论中：①0abc >；②20a b +<；③()a b m am b +>+（1m ≠的实数）；④22()a c b +<；⑤1a >，其中正确的是（ ）A ．2个B ．3个C ．4个D ．1个53．（2020·全国初三课时练习）已知二次函数2(0)y ax bx c a =++≠的图象如下图，有下列5个结论：①0abc >；②b a c >+；③420a b c ++>；④23c b >；⑤()a b m am b +>+（1m ≠的实数）．其中正确结论的有（ ）A ．①②③B ．②③④C ．③④⑤D ．②③⑤54．（2020·广西南宁·三美学校初三学业考试）如图是抛物线()20y ax bx c a =++≠，其顶点为()1,n ，且与x轴的个交点在点()3,0和()4,0之间，则下列结论正确的个数是（ ）个①若抛物线与x 轴的另一个交点为(),0k ，则21k -<<-；②c a n -=；③若x m <-时，y 随x 的增大而增大，则1m ≥-．A ．0B ．1C ．2D ．355．（2020·辽宁铁岭·初三月考）如图，二次函数2(0)y ax bx c a =++≠的图象与x 轴交于点()1,0A -，其对称轴为直线1x =，下面结论中正确的是（ ）A ．0abc ＞B ．20a b -=C ．420a b c ++＜D ．930a b c ++=56．（2020·山东枣庄·初三其他）二次函数2y ax bx c =++的图象如图所示，对称轴是直线1x =．下列结论：①0abc <；②30a c +>；③()220a c b +-<；④()a b m am b +≤+(m 为实数)．其中结论正确的个数为( )A ．1个B ．2个C ．3个D ．4个57．（2019·黑龙江铁锋·初三三模）已知二次函数2y ax bx c =++的图象如图所示，则以下结论：①0abc >，②230b a +=，③0a b c -+<，④520a c +<．其中正确的有（ ）A ．1个B ．2个C ．3个D ．4个58．（2020·广东潮南·初三其他）平面直角坐标系中，二次函数()20y ax bx c a =++≠的图象如图所示，现给出下列结论：①0abc <；②20c a +>；③930a b c -+=；④2a b am bm -≤+（m 为实数）；⑤240ac b -<．其中正确的结论的个数是（ ）A ．2B ．3C ．4D ．559．（2020·山东历下·初三三模）如图是二次函数y ＝ax 2+bx+c （a≠0）的图象，下列结论正确的个数是（ ） ①对称轴为直线x ＝﹣1；②b 2﹣4ac ＞0；③方程ax 2+bx+c ＝0的解是x 1＝﹣3，x 2＝1；④不等式ax 2+bx+c ＞3的解为﹣2＜x ＜0．A ．4B ．3C ．2D ．160．（2020·全国初三课时练习）如图是二次函数y=ax 2+bx+c （a ，b ，c 是常数，a≠0）图象的一部分，与x 轴的交点A 在点（2，0）和（3，0）之间，对称轴是x=1．对于下列说法：①ab ＜0；②2a+b=0；③3a+c ＞0；④a+b≥m （am+b ）（m 为实数）；⑤当﹣1＜x ＜3时，y ＞0，其中正确的是（ ）A ．①②④B ．①②⑤C ．②③④D ．③④⑤61．（2020·全国初三课时练习）在同一坐标系内，一次函数y ax b =+与二次函数2y ax 8x b =++的图象可能是A ．B ．C ．D ．62．（2020·全国初三课时练习）已知抛物线y=ax 2+bx+c （a≠0）的对称轴为直线x=2，与x 轴的一个交点坐标为（4，0），其部分图象如图所示，下列结论：①抛物线过原点；②4a+b+c=0；③a ﹣b+c ＜0；④抛物线的顶点坐标为（2，b ）；⑤当x ＜2时，y 随x 增大而增大．其中结论正确的是（ ）A．①②③B．③④⑤C．①②④D．①④⑤63．（2020·全国初三课时练习）抛物线y＝ax2+bx+c的顶点为(﹣1，3)，与x轴的交点A在点(﹣3，0)和(﹣2，0)之间，其部分图象如图，则以下结论，其中正确结论的个数为()①若点P(﹣3，m)，Q(3，n)在抛物线上，则m＜n；②c＝a+3；③a+b+c＜0；④方程ax2+bx+c＝3有两个相等的实数根．A．1个B．2个C．3个D．4个64．（2020·湖北广水·初三期末）如图，二次函数y=ax2+bx+c的图象与x轴交于点A（﹣1，0），与y轴的交点B在（0，2）与（0，3）之间（不包括这两点），对称轴为直线x=2．下列结论：①abc＜0；②9a+3b+c＞0；③若点M（12，y1），点N（52，y2）是函数图象上的两点，则y1＜y2；④﹣35＜a＜﹣25；⑤c-3a＞0其中正确结论有（）A．2个B．3个C．4个D．5个65．（2020·河南太康·初三期末）如图，抛物线y ＝2ax ＋bx ＋c(a≠0)与x 轴交于点A(1，0)和B ，与y 轴的正半轴交于点C ．下列结论：①abc ＞0；②4a －2b ＋c ＞0；③2a －b ＞0；④3a ＋c ＞0.其中正确结论的个数为（ ）A ．1个B ．2个C ．3个D ．4个66．（2020·湖北广水·初三其他）二次函数y ＝2ax bx c ++（a ≠0）图象如图所示，下列结论：①abc ＞0；②2a b +＝0；③当m ≠1时，+a b ＞2am bm +；④a b c -+＞0；⑤若211ax bx +＝222ax bx +，且1x ≠2x ，则12x x +＝2．其中正确的有（ ）A ．①②③B ．②④C ．②⑤D ．②③⑤67．（2020·甘肃张掖·初三其他）小明从图所示的二次函数2y ax bx c =++的图象中，观察得出了下面四条信息：①230a b +=；②24b ac -＜0；③0a b c -+>；④方程20ax bx c ++=必有一个根在－1到0之间．你认为其中正确信息的个数有( )A ．1个B ．2个C ．3个D ．4个68．（2020·湖北广水·初三其他）如图，抛物线2y ax bx c =++的图象交x 轴于()2,0A -和点B ，交y 轴负半轴于点C ，且OB OC =，下列结论：①0a b c +<；②40a c +>；③12a =；④1acb +=； 其中正确的结论个数有（ ）A ．1个B ．2个C ．3个D ．4个69．（2020·重庆市荣昌区宝城初级中学初三其他）如图，抛物线2y ax bx c =++与x 轴交于点A(-1，0)，B(3，0)，交y 轴的正半轴于点C ，对称轴交抛物线于点D ，交x 轴与点E ，则下列结论：①2a+b=0；②b+2c>0；③a+b>am 2+bm （m 为任意实数）；④一元二次方程220ax bx c +++=有两个不相等的实数根；⑤当△BCD为直角三角形时，a 的值有2个；⑥若点P 为对称轴上的动点，则PB PC -有最大值，．其中正确的有（ ）A ．2个B ．3个C ．4个D ．5个70．（2020·内蒙古呼伦贝尔·初三二模）如图所示的抛物线y ＝ax 2+bx +c 的对称轴为直线x ＝1，则下列结论中错误的是（ ）A．ac＜0 B．b2﹣4ac＞0 C．2a﹣b＝0 D．9a+3b+c＝0参考答案1．C【解析】【分析】①根据直线x=-1是对称轴，确定b-2a 的值；②根据x=-2时，y ＞0确定4a-2b+c 的符号；③根据x=-4时，y=0，比较a-b+c 与-9a 的大小；④根据抛物线的对称性，得到x=-3与x=1时的函数值相等判断即可．【详解】解：①∵直线x=-1是对称轴，∴-2b a=-1，即b-2a=0，①正确； ②x=-2时，y ＞0，∴4a-2b+c ＞0，②错误；∵x=-4时，y=0，∴16a-4b+c=0，又b=2a ，∴a-b+c=-9a ，③正确；④根据抛物线的对称性，得到x=-3与x=1时的函数值相等，∴y 1＞y 2，④正确，故选C ．【点睛】本题考查二次函数图象与系数的关系．2．B【解析】【分析】根据题目所给的图像，首先判断1y kx =中k ＞0，其次判断22y ax bx c =++中a ＜0，b ＜0，c ＜0，再根据k 、b 、的符号判断2()y ax b k x c =+-+中b-k ＜0，又a ＜0，c ＜0可判断出图像．【详解】解：由题图像得1y kx =中k ＞0，22y ax bx c =++中a ＜0，b ＜0，c ＜0，∴b -k ＜0，∴函数2()y ax b k x c =+-+对称轴x=2b k a --＜0，交x 轴于负半轴， ∴当12y y =时，即2kx ax bx c =++，移项得方程2()0ax b k x c +-+=，∵直线1y kx =与抛物线22y ax bx c =++有两个交点， ∴方程2()0ax b k x c +-+=有两个不等的解，即2()y ax b k x c =+-+与x 轴有两个交点，根据函数2()y ax b k x c =+-+对称轴交x 轴负半轴且函数图像与x 轴有两个交点， ∴可判断B 正确．故选：B【点睛】本题考查二次函数与一次函数的图象与性质，解题的关键是根据图像判断k 、a 、b 、c 的正负号，再根据二次函数与一元二次方程的关系判断出正确图像．3．B【解析】【分析】根据二次函数的图象和二次函数的性质，可以判断各个小题中的结论是否成立，从而可以解答本题．【详解】∵二次函数y ＝ax 2+bx+c （a≠0）的对称轴为x ＝1， ∴﹣2b a＝1，得2a+b ＝0，故①正确； 当x ＝﹣2时，y ＝4a ﹣2b+c ＜0，故②正确；该函数图象与x 轴有两个交点，则b 2﹣4ac ＞0，故③正确；∵二次函数y ＝ax 2+bx+c （a≠0）的对称轴为x ＝1，点B 坐标为（﹣1，0），∴点A （3，0），∴当y ＜0时，x ＜﹣1或x ＞3，故④错误；故选B ．【点睛】本题考查二次函数图象与系数的关系、抛物线与x 轴的交点，解答本题的关键是明确题意，利用二次函数的性质和数形结合的思想解答．4．D【解析】【分析】分别利用函数解析式分析图象得出答案．【详解】解：由一次函数解析式为：y=kx+2可知，图象应该与y 轴交于正半轴上，故A 、B 、C 错误；D 符合题意；故选：D ．【点睛】此题主要考查了二次函数的图象以及一次函数的图象，得出直线交y 轴的正半轴是解题关键． 5．D【解析】【分析】由抛物线的开口方向判断a 与0的关系，由抛物线与y 轴的交点判断c 与0的关系，然后根据对称轴进行推理，进而对所得结论进行判断．【详解】解：抛物线开口方向向下，则a ＜0，∵对称轴是直线x=2b a=1，则b=-2a ， ∴3a+b=3a-2a=a ＜0，故①正确；当x=-1时，y ＜0，即a-b+c ＜0，故②正确；抛物线与y 轴交于正半轴，则c ＞0，故③正确；∵b=-2a ，∴a+b=a-2a=-a ，∵a ＜0，∴-a ＞0，∴a+b ＞0，故④正确．综上所述，正确的结论是：①②③④．故选：D ．【点睛】本题主要考查图象与二次函数系数之间的关系，会利用对称轴的范围求2a 与b 的关系，掌握“数形结合”数学思想的应用．6．D【解析】【分析】根据二次函数开口方向，可以判断出a 的正负，根据对称轴的位置和a 的正负，可以判断出b 的正负，再根抛物线与y 轴的交点，可以判断出c 的正负，然后根据a 、b 、c 的正负去判断一次函数和二次函数在坐标系中的位置即可.【详解】∵二次函数图象开口向上，∴a ＞0，∵对称轴为直线x ＝﹣2b a＞0， ∴b ＜0，当x ＝﹣1时，a ﹣b +c ＞0，当x ＝1时，a ﹣b +c ＜0，∴（a +b +c ）（a ﹣b +c ）＜0，∵抛物线与x 轴有两个交点，∴b 2﹣4ac ＞0，∴一次函数图象经过第一、二、四象限，反比例函数图象经过第二四象限．故选：D ．【点睛】本题考查了一次函数、二次函数、反比例函数的图像与系数的关系，根据二次函数抛物线求出a 、b 、c 的正负是解决本题的管家.7．C【解析】【分析】先根据反比例函数图象确定k 的值，再分析二次函数图象是否符合，逐一判断即可【详解】A 、由反比例函数图象知：k ＞0，因此二次函数图象应开口向上，且与y 轴交于负半轴，故此选项错误；B 、由反比例函数图象知：k ＜0，因此二次函数图象应开口向下，故此选项错误；C 、由反比例函数图象知：k ＜0，因此二次函数图象应开口向下，且与y 轴交于正半轴，故此选项正确；D 、由反比例函数图象知：k ＞0，因此二次函数图象应开口向上，故此选项错误； 故选Ｃ．【点睛】本题考查反比例函数、二次函数的图象与性质，比较基础．8．D【解析】【分析】先根据一次函数图像确定m 的符号，在依据二次函数y=ax 2+bx+c 图像性质进行判断，当a ＞0时，开口向上；当a ＜0时，开口向下．对称轴为x=2b a -，与y 轴的交点坐标为（0，c ）． 【详解】解：A 、由函数y ＝mx+m 的图象可知m ＜0，即函数y ＝﹣mx 2+2x+2开口方向朝上，与图象不符，故A 选项错误；B 、由函数y ＝mx+m 的图象可知m ＜0，对称轴为x ＝2b a -＝212m m -=＜0，则对称轴应在y 轴左侧，与图象不符，故B 选项错误；C 、由函数y ＝mx+m 的图象可知m ＞0，即函数y ＝﹣mx 2+2x+2开口方向朝下，与图象不符，故C 选项错误；D 、由函数y ＝mx+m 的图象可知m ＜0，即函数y ＝﹣mx 2+2x+2开口方向朝上，对称轴为x ＝2b a -＝﹣212m m-= ＜0，则对称轴应在y 轴左侧，与图象相符，故D 选项正确； 故选D ．【点睛】本题主要考查了一次函数和二次函数的图象性质以及分析能力和读图能力，要掌握它们的性质才能灵活解题．一次函数和二次函数的图象所经过的象限的问题，关键是m 的正负的确定，9．D【解析】【分析】①．函数的对称轴为x ＝﹣2b a＝1，即可求解；②．新抛物线表达式为：y ＝ax 2+bx ＝ax 2﹣2ax ＝ax （x ﹣2），即可求解；③．x ＝﹣1时，y ＝a ﹣b +c ＜0，x ＝1时，y ＝a +b +c ＝2，即220b a a b c a b c =-⎧⎪++=⎨⎪-+<⎩，即可求解；④．∆＝4a 2﹣4a ＝4a （a ﹣1），而﹣1＜a ＜﹣12，故∆＞0，即可求解．【详解】解：①．函数的对称轴为x ＝﹣2b a＝1，解得：b ＝﹣2a ；故①正确； ②．此抛物线向下移动c 个单位后，新抛物线表达式为：y ＝ax 2+bx ＝ax 2﹣2ax ＝ax （x ﹣2）， 则x ＝2时，y ＝0，故抛物线过点（2，0），故②正确；③．x ＝﹣1时，y ＝a ﹣b +c ＜0，x ＝1时，y ＝a +b +c ＝2，即220b a a b c a b c =-⎧⎪++=⎨⎪-+<⎩，解得：﹣1＜a ＜﹣12，故③正确； ④．∵c ＜0，∴x 2﹣2x +1c＝0变形为cx 2﹣2cx +1＝0， ∵∆＝4c 2﹣4c ＝4c （c ﹣1），而1＜c ＜2， ∴∆＞0，故方程x 2﹣2x +1c ＝0有实数根，故④正确； 故选：D ．【点睛】此题考查的是二次函数图象及性质,掌握二次函数图象及性质与各项系数的关系是解决此题的关键．10．A【解析】【分析】观察图象：开口向下得到a ＜0；对称轴在y 轴的右侧得到a 、b 异号，则b ＞0；抛物线与y轴的交点在x 轴的上方得到c ＞0，所以abc ＜0；当x ＝﹣1时图象在x 轴上得到y ＝a ﹣b +c ＝0，即a +c ＝b ；对称轴为直线x ＝1，可得x ＝2时图象在x 轴上方，则y ＝4a +2b +c ＞0；利用对称轴x ＝﹣2b a＝1得到a ＝﹣12b ，而a ﹣b +c ＜0，则﹣12b ﹣b +c ＜0，所以2c ＜3b ；开口向下，当x ＝1，y 有最大值a +b +c ，得到a +b +c ＞am 2+bm +c ，即a +b ＞m （am +b ）（m ≠1）．【详解】解：开口向下，a ＜0；对称轴在y 轴的右侧，a 、b 异号，则b ＞0；抛物线与y 轴的交点在x 轴的上方，c ＞0，则abc ＜0，所以①不正确；当x ＝﹣1时图象在x 轴上，则y ＝a ﹣b +c ＝0，即a +c ＝b ，所以②不正确；对称轴为直线x ＝1，则x ＝2时图象在x 轴上方，则y ＝4a +2b +c ＞0，所以③正确； x ＝﹣2b a＝1，则a ＝﹣12b ，而a ﹣b +c ＝0，则﹣12b ﹣b +c ＝0，2c ＝3b ，所以④不正确； 开口向下，当x ＝1，y 有最大值a +b +c ；当x ＝m （m ≠1）时，y ＝am 2+bm +c ，则a +b +c ＞am 2+bm +c ，即a +b ＞m （am +b ）（m ≠1），所以⑤正确．故选：A ．【点睛】本题考查了二次函数图象与系数的关系：对于二次函数y=ax 2+bx+c （a ≠0）的图象，当a ＞0，开口向上，函数有最小值，a ＜0，开口向下，函数有最大值；对称轴为直线x=2b a -，a 与b 同号，对称轴在y 轴的左侧，a 与b 异号，对称轴在y 轴的右侧；当c ＞0，抛物线与y 轴的交点在x 轴的上方；当△=b 2-4ac ＞0，抛物线与x 轴有两个交点．11．B【解析】【分析】根据图像得出a ＜0，c ＜0，b ＞0，可判断①；再由图像可得对称轴在直线x=2右侧，可得22b a->，可判断②；再根据二次函数在y 轴右侧时的增减性，判断③；根据抛物线对称轴为直线x=3，得出6b a =-，再利用作差法判断④；最后根据AB≥3，则点A 的横坐标大于0且小于等于1，得出a+b+c≥0，再由当x=4时，得出16a+4b+c=0，变形为a=416b c +-，代入，可得4b+5c≥0，结合c 的符号可判断⑤.【详解】解：如图，抛物线开口向下，与y 轴交于负半轴，对称轴在y 轴右侧，∴a ＜0，c ＜0，02b a ->， ∴b ＞0，∴abc ＞0，故①正确；如图，∵抛物线过点B （4，0），点A 在x 轴正半轴，∴对称轴在直线x=2右侧，即22b a->， ∴42022b a b a a++=<，又a ＜0， ∴4a+b ＞0，故②正确；∵()11,M x y 与()22,N x y 是抛物线上两点，120x x <<，可得：抛物线2y ax bx c =++在02b x a<<-上，y 随x 的增大而增大， 在2b x a>-上，y 随x 的增大而减小， ∴12y y >不一定成立，故③错误；若抛物线对称轴为直线x=3，则32b a-=，即6b a =-， 则(3)(3)(3)a m m b m -+--=()()()3363a m m a m -++-=()()336a m m -+-=()23a m -≤0，∴(3)(3)(3)a m m b m -+≤-，故④正确；∵AB≥3，则点A 的横坐标大于0且小于等于1，当x=1时，代入，y=a+b+c≥0，当x=4时，16a+4b+c=0，∴a=416b c+-，则416b cb c+++≥-，整理得：4b+5c≥0，则4b+3c≥-2c，又c＜0，-2c＞0，∴4b+3c＞0，故⑤正确，故正确的有4个.故选B.【点睛】本题考查了二次函数的图像和性质，解题的关键是能根据图像得出二次函数表达式各系数的符号.12．D【解析】【分析】利用对称性得到抛物线对称轴为直线x＝1，根据点的坐标确定开口向下，最大值大于3，根据二次函数的性质即可判断D正确．【详解】解：∵抛物线y＝a（x﹣h）2＋k（a≠0）经过A（m﹣4，0），B（m﹣2，3），C（4﹣m，3）三点，其中m＜3，∴抛物线的开口向下，对称轴为直线x＝242m m-+-＝1，即a＜0，h＝1，∴k＞3，当x＜1时，y随x的增大而增大，故选：D．【点睛】本题考查二次函数图象与系数的关系，二次函数图象上点的坐标特征，熟练掌握二次函数的性质是关键．13．C【解析】【分析】根据二次函数的性质逐一进行判断即可【详解】解：∵x ＝1时，y ＝0，∴a ＋b ＋c ＝0，所以①正确；∵x ＝2b a＝－1，∴b ＝2a ，所以②错误； ∵点(1，0)关于直线x ＝－1对称的点的坐标为(－3，0)，∴抛物线与x 轴的交点坐标为(－3，0)和(1，0)，∴ax 2＋bx ＋c ＝0的两根分别为－3和1，所以③正确；∵抛物线与y 轴的交点在x 轴下方，∴c ＜0，∵a ＋b ＋c ＝0，b ＝2a ，∴c ＝－3a ，∴a －2b ＋c ＝－6a ，∵a ＞0，∴－6a ＜0∴a －2b ＋c ＜0，所以④错误．【点睛】本题考查的是二次函数图象与系数的关系，掌握二次函数的性质、灵活运用数形结合思想是解题的关键，解答时，要熟练运用抛物线的对称性和抛物线上的点的坐标满足抛物线的解析式.14．A【解析】【分析】由抛物线开口方向及与y 轴的交点位置可判断①；令y=1可判断②；由图像与x 轴的交点可判断③和④；由图像与x 轴的两个交点可求得对称轴，结合图像的开口方向，则可判断⑤；则可求得答案．【详解】抛物线开口方向、与y 轴的交点在x 轴的下方，∴00a c ><，，0ac <，故①正确；由图像可知当1x =时，0y <，∴0a b c ++<，故②不正确；由图像可知抛物线与x 轴交与(−1,0)和(3,0)两点，∴方程20ax bx c ++=的根是121,3x x =-=,且240b ac ->，故③、④正确；抛物线与x 轴交与(−1,0)和(3,0)两点，∴抛物线对称轴为直线1312x -+==，且抛物线开口向下， ∴当1x >时，y 随x 的增大而增大，故⑤正确；综上可知正确的结论有4个，故选A.【点睛】本题考查的知识点是二次函数图像与系数的关系，解题关键是利用数形结合得出各项符号． 15．C【解析】根据抛物线开口方向得a ＜0，由抛物线对称轴为直线x ＝﹣2b a＝1，得到b ＝﹣2a ＞0，即2a+b ＝0，即可判断①；根据二次函数的性质得当x ＝1时，函数有最大值a+b+c ，即可判断②；根据抛物线的对称性得到抛物线与x 轴的另一个交点在（﹣1，0）的右侧，则当x ＝﹣1时，y ＜0，所以a ﹣b+c ＜0，即可判断③；把b ＝﹣2a 代入a ﹣b+c ＜0可对④进行判断；把ax 12+bx 1＝ax 22+bx 2先移项，再分解因式得到（x 1﹣x 2）[a （x 1+x 2）+b]＝0，而x 1≠x 2，则a （x 1+x 2）+b ＝0，即x 1+x 2＝﹣b a ，然后把b ＝﹣2a 代入计算得到x 1+x 2＝2可对⑤进行判断． 【详解】∵抛物线开口向下，∴a ＜0，∵抛物线对称轴为直线x ＝﹣2b a＝1， ∴b ＝﹣2a ＞0，即2a+b ＝0，所以①正确；∵抛物线对称轴为直线x ＝1，∴函数的最大值为a+b+c ，∴a+b+c≥am 2+bm+c ，即a+b≥am 2+bm ，所以②正确；∵抛物线与x 轴的一个交点在（3，0）的左侧，而对称轴为直线x ＝1，∴抛物线与x 轴的另一个交点在（﹣1，0）的右侧，∴当x ＝﹣1时，y ＜0，∴a ﹣b+c ＜0，所以③错误；∵b ＝﹣2a ，a ﹣b+c ＜0，∴a+2a+c ＜0，即3a+c ＜0，所以④正确；∵ax 12+bx 1＝ax 22+bx 2，∴ax 12+bx 1﹣ax 22﹣bx 2＝0，∴a （x 1+x 2）（x 1﹣x 2）+b （x 1﹣x 2）＝0，∴（x 1﹣x 2）[a （x 1+x 2）+b]＝0，而x 1≠x 2，∴a （x 1+x 2）+b ＝0，即x 1+x 2＝﹣b a， ∵b ＝﹣2a ，∴x 1+x 2＝2，所以⑤正确．综上所述，正确的有①②④⑤共4个．故选：C ．【点睛】本题主要考查了二次函数的图象和性质，熟练掌握二次函数图象与解析式系数关系，与方程和不等式关系是解题的关键．16．D【解析】【分析】根据抛物线开口向上得出a ＞0，根据抛物线和y 轴的交点在y 轴的负半轴上得出c ＜0，根据图象与x 轴的交点坐标得出方程ax 2+bx+c=0的根，把x=1代入y=ax 2+bx+c 求出a+b+c ＜0，根据抛物线的对称轴和图象得出当x ＞1时，y 随x 的增大而增大，2a=-b ，根据图象和x 轴有两个交点得出b 2-4ac ＞0．【详解】∵抛物线开口向上，∴a ＞0，∵抛物线和y 轴的交点在y 轴的负半轴上，∴c ＜0，∴ac ＜0，∴①正确；∵图象与x 轴的交点坐标是（-1，0），（3，0），∴方程ax 2+bx+c=0的根是x 1=-1，x 2=3，∴②正确；把x=1代入y=ax 2+bx+c 得：a+b+c ＜0，∴③错误；根据图象可知：当x ＞1时，y 随x 的增大而增大，∴④正确；∵-2b a=1， ∴2a=-b ，∴2a+b=0，不是2a-b=0，∴⑤错误；∵图象和x 轴有两个交点，∴b 2-4ac ＞0，∴⑥正确；正确的说法有：①②④⑥．故答案为：D ．【点睛】本题考查了二次函数与系数的关系的应用，主要考查学生对二次函数的图象与系数的关系的理解和运用，同时也考查了学生观察图象的能力，本题是一道比较典型的题目，具有一定的代表性．17．C【解析】【分析】【详解】根据图像可得：a<0，b<0，c=0，即abc=0，则①正确；当x=1时，y<0，即a+b+c<0，则②错误； 根据对称轴可得：－2b a =－32，则b=3a ，根据a<0，b<0可得：a>b ；则③正确； 根据函数与x 轴有两个交点可得：2b －4ac>0，则④正确.故选C.【点睛】本题考查二次函数的性质.能通过图象分析a ，b ，c 的正负，以及通过一些特殊点的位置得出a ，b ，c 之间的关系是解题关键.18．D【解析】【分析】先根据一次函数的图象判断 , ,a b 的符号,再判断二次函数图象与实际是否相符,判断正误.【详解】A.由一次函数y ＝ax+a 的图象可得: a<0且a>0 ,两者矛盾,故A 错误;B ．由一次函数 y ＝ax+a 的图象可得: a<0,此时二次函数 y ＝(x －a)2的顶点(a, 0)的位置可推出a>0 ,两者矛盾,故B 错误;C.由一次函数 y ＝ax+a 的图象可得: a<0且a>0,两者矛盾,故C 错误;D.由一次函数y ＝ax+a 的图象可得:a>0 ,此时二次函数 y ＝(x －a)2的顶点(a, 0)的位置可推出a>0 ,故D 正确;故选:D.。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

二次函数系数a、b、c与图像的关系知识要点二次函数y=ax2+bx+c系数符号的确定：（1）a由抛物线开口方向确定：开口方向向上，则a＞0；否则a＜0．（2）b由对称轴和a的符号确定：由对称轴公式x=判断符号．（3）c由抛物线与y轴的交点确定：交点在y轴正半轴，则c＞0；否则c＜0．（4）b2-4ac的符号由抛物线与x轴交点的个数确定：2个交点，b2-4ac＞0；1个交点，b2-4ac=0；没有交点，b2-4ac＜0．（5）当x=1时，可确定a+b+c的符号，当x=-1时，可确定a-b+c的符号．（6）由对称轴公式x=，可确定2a+b的符号．一．选择题（共9小题）1．（2014•威海）已知二次函数y=ax2+bx+c（a≠0）的图象如图，则下列说法：①c=0；②该抛物线的对称轴是直线x=﹣1；③当x=1时，y=2a；④am2+bm+a＞0（m≠﹣1）．其中正确的个数是（）A．1B．2C．3D．4 2．（2014•仙游县二模）已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，给出以下结论：①a+b+c＜0；②a﹣b+c＜0；③b+2a＜0；④abc＞0．其中所有正确结论的序号是（）A．③④B．②③C．①④D．①②③3．（2014•南阳二模）二次函数y=ax2+bx+c的图象如图所示，那么关于此二次函数的下列四个结论：①a＜0；②c＞0；③b2﹣4ac＞0；④＜0中，正确的结论有（）A．1个B．2个C．3个D．4个4．（2014•襄城区模拟）函数y=x2+bx+c与y=x的图象如图，有以下结论：①b2﹣4c＜0；②c﹣b+1=0；③3b+c+6=0；④当1＜x＜3时，x2+（b﹣1）x+c＜0．其中正确结论的个数为（）A．1B．2C．3D．4 5．（2014•宜城市模拟）如图是二次函数y=ax2+bx+c图象的一部分，其对称轴为x=﹣1，且过点（﹣3，0）下列说法：①abc＜0；②2a﹣b=0；③4a+2b+c＜0；④若（﹣5，y1），（2，y2）是抛物线上的两点，则y1＞y2．其中说法正确的是（）A．①②B．②③C．②③④D．①②④6．（2014•莆田质检）如图，二次函数y=x2+（2﹣m）x+m﹣3的图象交y轴于负半轴，对称轴在y轴的右侧，则m的取值范围是（）A．m＞2 B．m＜3 C．m＞3 D．2＜m＜3 7．（2014•玉林一模）如图是二次函数y=ax2+bx+c图象的一部分，图象过点A（﹣3，0），对称轴为x=﹣1．给出四个结论：①b2＞4ac；②2a+b=0；③3a+c=0；④a+b+c=0．其中正确结论的个数是（）A．1个B．2个C．3个D．4个8．（2014•乐山市中区模拟）如图，抛物线y=ax2+bx+c与x轴交于点A（﹣1，0），顶点坐标为（1，n），与y轴的交点在（0，2）、（0，3）之间（包含端点）．有下列结论：①当x＞3时，y＜0；②3a+b＞0；③﹣1≤a≤﹣；④≤n≤4．其中正确的是（）A．①②B．③④C．①③D．①③④9．（2014•齐齐哈尔二模）已知二次函数y=ax2+bx+c（a＞0）的图象与x轴交于点（﹣1，0），（x1，0），且1＜x1＜2，下列结论正确的个数为（）①b＜0；②c＜0；③a+c＜0；④4a﹣2b+c＞0．A．1个B．2个C．3个D．4个10、（2011•重庆）已知抛物线y=ax2+bx+c（a≠0）在平面直角坐标系中的位置如图所示，则下列结论中，正确的是（）A、a＞0B、b＜0C、c＜0D、a+b+c＞011、（2011•雅安）已知二次函数y=ax2+bx+c的图象如图，其对称轴x=-1，给出下列结果①b2＞4ac；②abc＞0；③2a+b=0；④a+b+c＞0；⑤a-b+c＜0，则正确的结论是（）A、①②③④B、②④⑤C、②③④D、①④⑤12、（2011•孝感）如图，二次函数y=ax2+bx+c的图象与y轴正半轴相交，其顶点坐标为（12，1），下列结论：①ac＜0；②a+b=0；③4ac-b2=4a；④a+b+c＜0．其中正确结论的个数是（）A、1B、2C、3D、4答案一．选择题（共9小题）1．（2014•威海）已知二次函数y=ax2+bx+c（a≠0）的图象如图，则下列说法：①c=0；②该抛物线的对称轴是直线x=﹣1；③当x=1时，y=2a；④am2+bm+a ＞0（m≠﹣1）．其中正确的个数是（）A．1B．2C．3D．4考点：二次函数图象与系数的关系．分析：由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x 轴交点情况进行推理，进而对所得结论进行判断．解答：解：抛物线与y轴交于原点，c=0，（故①正确）；该抛物线的对称轴是：，直线x=﹣1，（故②正确）；当x=1时，y=a+b+c∵对称轴是直线x=﹣1，∴﹣b/2a=﹣1，b=2a，又∵c=0，∴y=3a，（故③错误）；x=m对应的函数值为y=am2+bm+c，x=﹣1对应的函数值为y=a﹣b+c，又∵x=﹣1时函数取得最小值，∴a﹣b+c＜am2+bm+c，即a﹣b＜am2+bm，∵b=2a，∴am2+bm+a＞0（m≠﹣1）．（故④正确）．故选：C．点评：本题考查了二次函数图象与系数的关系．二次函数y=ax2+bx+c（a≠0）系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点、抛物线与x轴交点的个数确定．2．（2014•仙游县二模）已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，给出以下结论：①a+b+c＜0；②a﹣b+c＜0；③b+2a＜0；④abc＞0．其中所有正确结论的序号是（）A．③④B．②③C．①④D．①②③考点：二次函数图象与系数的关系．专题：数形结合．分析：由抛物线的开口方向判断a的符号，由抛物线与y轴的交点判断c的符号，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．解答：解：①当x=1时，y=a+b+c=0，故①错误；②当x=﹣1时，图象与x轴交点负半轴明显大于﹣1，∴y=a﹣b+c＜0，故②正确；③由抛物线的开口向下知a＜0，∵对称轴为0＜x=﹣＜1，∴2a+b＜0，故③正确；④对称轴为x=﹣＞0，a＜0∴a、b异号，即b＞0，由图知抛物线与y轴交于正半轴，∴c＞0 ∴abc＜0，故④错误；∴正确结论的序号为②③．故选：B．点评：二次函数y=ax2+bx+c系数符号的确定：（1）a由抛物线开口方向确定：开口方向向上，则a＞0；否则a＜0；（2）b由对称轴和a的符号确定：由对称轴公式x=﹣判断符号；（3）c由抛物线与y轴的交点确定：交点在y轴正半轴，则c＞0；否则c＜0；（4）当x=1时，可以确定y=a+b+c的值；当x=﹣1时，可以确定y=a﹣b+c的值．3．（2014•南阳二模）二次函数y=ax2+bx+c的图象如图所示，那么关于此二次函数的下列四个结论：①a＜0；②c＞0；③b2﹣4ac＞0；④＜0中，正确的结论有（）A．1个B．2个C．3个D．4个考点：二次函数图象与系数的关系．专数形结合．题：分析：由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c 与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．解答：解：①∵图象开口向下，∴a＜0；故本选项正确；②∵该二次函数的图象与y轴交于正半轴，∴c＞0；故本选项正确；③∵二次函数y=ax2+bx+c的图象与x轴有两个不相同交点，∴根的判别式△=b2﹣4ac ＞0；故本选项正确；④∵对称轴x=﹣＞0，∴＜0；故本选项正确；综上所述，正确的结论有4个．故选D．点评：本题主要考查了二次函数的图象和性质，解答本题关键是掌握二次函数y=ax2+bx+c系数符号的确定，做题时要注意数形结合思想的运用，同学们加强训练即可掌握，属于基础题．4．（2014•襄城区模拟）函数y=x2+bx+c与y=x的图象如图，有以下结论：①b2﹣4c＜0；②c﹣b+1=0；③3b+c+6=0；④当1＜x＜3时，x2+（b﹣1）x+c ＜0．其中正确结论的个数为（）A．1B．2C．3D．4考点：二次函数图象与系数的关系．分析：由函数y=x2+bx+c与x轴无交点，可得b2﹣4c＜0；当x=﹣1时，y=1﹣b+c＞0；当x=3时，y=9+3b+c=3；当1＜x＜3时，二次函数值小于一次函数值，可得x2+bx+c＜x，继而可求得答案．解解：∵函数y=x2+bx+c与x轴无交点，答：∴b2﹣4ac＜0；故①正确；当x=﹣1时，y=1﹣b+c＞0，故②错误；∵当x=3时，y=9+3b+c=3，∴3b+c+6=0；③正确；∵当1＜x＜3时，二次函数值小于一次函数值，∴x2+bx+c＜x，∴x2+（b﹣1）x+c＜0．故④正确．故选C．点评：主要考查图象与二次函数系数之间的关系．此题难度适中，注意掌握数形结合思想的应用．5．（2014•宜城市模拟）如图是二次函数y=ax2+bx+c图象的一部分，其对称轴为x=﹣1，且过点（﹣3，0）下列说法：①abc＜0；②2a﹣b=0；③4a+2b+c＜0；④若（﹣5，y1），（2，y2）是抛物线上的两点，则y1＞y2．其中说法正确的是（）A．①②B．②③C．②③④D．①②④考点：二次函数图象与系数的关系．分析：根据抛物线开口方向得到a＞0，根据抛物线的对称轴得b=2a＞0，则2a﹣b=0，则可对②进行判断；根据抛物线与y轴的交点在x轴下方得到c＜0，则abc＜0，于是可对①进行判断；由于x=﹣2时，y＜0，则得到4a﹣2b+c＜0，则可对③进行判断；通过点（﹣5，y1）和点（2，y2）离对称轴的远近对④进行判断．解答：解：∵抛物线开口向上，∴a＞0，∵抛物线对称轴为直线x=﹣=﹣1，∴b=2a＞0，则2a﹣b=0，所以②正确；∵抛物线与y轴的交点在x轴下方，∴c＜0，∴abc＜0，所以①正确；∵x=2时，y＞0，∴4a+2b+c＞0，所以③错误；∵点（﹣5，y1）离对称轴要比点（2，y2）离对称轴要远，∴y1＞y2，所以④正确．故选D．点评：本题考查了二次函数图象与系数的关系：二次函数y=ax2+bx+c（a≠0），二次项系数a决定抛物线的开口方向和大小，当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口；一次项系数b和二次项系数a共同决定对称轴的位置：当a与b同号时（即ab＞0），对称轴在y轴左；当a与b异号时（即ab＜0），对称轴在y轴右．（简称：左同右异）．抛物线与y轴交于（0，c）．抛物线与x轴交点个数：△=b2﹣4ac＞0时，抛物线与x轴有2个交点；△=b2﹣4ac=0时，抛物线与x轴有1个交点；△=b2﹣4ac＜0时，抛物线与x轴没有交点．6．（2014•莆田质检）如图，二次函数y=x2+（2﹣m）x+m﹣3的图象交y轴于负半轴，对称轴在y轴的右侧，则m的取值范围是（）A．m＞2 B．m＜3 C．m＞3 D．2＜m＜3考二次函数图象与系数的关系．点：分析：由于二次函数的对称轴在y轴右侧，根据对称轴的公式即可得到关于m 的不等式，由图象交y轴于负半轴也可得到关于m的不等式，再求两个不等式的公共部分即可得解．解答：解：∵二次函数y=x2+（2﹣m）x+m﹣3的图象交y轴于负半轴，∴m﹣3＜0，解得m＜3，∵对称轴在y轴的右侧，∴x=，解得m＞2，∴2＜m＜3．故选：D．点评：此题主要考查了二次函数的性质，解题的关键是利用对称轴的公式以及图象与y轴的交点解决问题．7．（2014•玉林一模）如图是二次函数y=ax2+bx+c图象的一部分，图象过点A （﹣3，0），对称轴为x=﹣1．给出四个结论：①b2＞4ac；②2a+b=0；③3a+c=0；④a+b+c=0．其中正确结论的个数是（）A．1个B．2个C．3个D．4个考点：二次函数图象与系数的关系．分析：由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c 与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．解答：解：∵抛物线的开口方向向下，∴a＜0；∵抛物线与x轴有两个交点，∴b2﹣4ac＞0，即b 2＞4ac，①正确；由图象可知：对称轴x==﹣1，∴2a=b，2a+b=4a，∵a≠0，∴2a+b≠0，②错误；∵图象过点A（﹣3，0），∴9a﹣3b+c=0，2a=b，所以9a﹣6a+c=0，c=﹣3a，③正确；∵抛物线与y轴的交点在y轴的正半轴上，∴c＞0由图象可知：当x=1时y=0，∴a+b+c=0，④正确．故选C．点评：考查了二次函数图象与系数的关系，解答本题关键是掌握二次函数y=ax2+bx+c（a≠0）系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点、抛物线与x轴交点的个数确定．8．（2014•乐山市中区模拟）如图，抛物线y=ax2+bx+c与x轴交于点A（﹣1，0），顶点坐标为（1，n），与y轴的交点在（0，2）、（0，3）之间（包含端点）．有下列结论：①当x＞3时，y＜0；②3a+b＞0；③﹣1≤a≤﹣；④≤n ≤4．其中正确的是（）A．①②B．③④C．①③D．①③④考点：二次函数图象与系数的关系．分析：①由抛物线的对称轴为直线x=1，一个交点A（﹣1，0），得到另一个交点坐标，利用图象即可对于选项①作出判断；②根据抛物线开口方向判定a的符号，由对称轴方程求得b与a的关系是b=﹣2a，将其代入（3a+b），并判定其符号；③根据两根之积=﹣3，得到a=，然后根据c的取值范围利用不等式的性质来求a的取值范围；④把顶点坐标代入函数解析式得到n=a+b+c=c，利用c的取值范围可以求得n的取值范围．解答：解：①∵抛物线y=ax2+bx+c与x轴交于点A（﹣1，0），对称轴直线是x=1，∴该抛物线与x轴的另一个交点的坐标是（3，0），∴根据图示知，当x＞3时，y＜0．故①正确；②根据图示知，抛物线开口方向向下，则a＜0．∵对称轴x==1，∴b=﹣2a，∴3a+b=3a﹣2a=a＜0，即3a+b＜0．故②错误；③∵抛物线与x轴的两个交点坐标分别是（﹣1，0），（3，0），∴﹣1×3=﹣3，=﹣3，则a=．∵抛物线与y轴的交点在（0，2）、（0，3）之间（包含端点），∴2≤c≤3，∴﹣1≤≤，即﹣1≤a≤．故③正确；④根据题意知，a=，=1，∴b=﹣2a=，∴n=a+b+c=c．∵2≤c≤3，≤≤4，≤n≤4．故④正确．综上所述，正确的说法有①③④．故选D．点评：本题考查了二次函数图象与系数的关系．二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定．9．（2014•齐齐哈尔二模）已知二次函数y=ax2+bx+c（a＞0）的图象与x轴交于点（﹣1，0），（x1，0），且1＜x1＜2，下列结论正确的个数为（）①b＜0；②c＜0；③a+c＜0；④4a﹣2b+c＞0．A．1个B．2个C．3个D．4个考点：二次函数图象与系数的关系．分析：由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．解答：解：①∵y=ax2+bx+c（a＞0）的图象与x轴交于点（﹣1，0），（x1，0），且1＜x1＜2，∴对称轴在y轴的右侧，即：﹣＞0，∵a＞0∴b＜0，故①正确；②显然函数图象与y轴交于负半轴，∴c＜0正确；③∵二次函数y=ax2+bx+c（a＞0）的图象与x轴交于点（﹣1，0），∴a﹣b+c=0，即a+c=b，∵b＜0，∴a+c＜0正确；④∵二次函数y=ax2+bx+c（a＞0）的图象与x轴交于点（﹣1，0），且a ＞0，∴当x=﹣2时，y=4a﹣2b+c＞0，故④正确，故选D．点评：主要考查图象与二次函数系数之间的关系，会利用对称轴的范围求2a与b的关系，以及二次函数与方程之间的转换，根的判别式的熟练运用．。

相关文档
最新文档