cohesive-element-例子详细图解教学文案
Abaqus教程之cohesive单元损伤模拟全
然后我们结合具体的实例深入分析解读cohesive参数及设置,以及两种 不同的损伤演化准则之间的区别与联系
abaqus中 cohesive模型 的建立及设置
下面我们将给出abaqus不同模块下的实例设置步骤,方便快速理解和学习 Part模块:
Property模块:
Assembly模块:
Step模块:
Cohesive element理论
abaqus6.14在线帮助文档 http://ivt-abaqusdoc.ivt.ntnu.no:2080/v6.14/books/usb/default.htm
cohesive element是基于损伤力学理论,自己去帮助文档补充相关基础知识
cohesive单元的理解起来其实并没有那么复杂,使用起来也是非常高效的,它可以 模拟分层失效,也可以通过在模型中相邻的实体单元间批量插入cohesive单元来模 拟裂纹的随机扩展。
单元由于很多人并不理解cohesive的参数,导致总是调不出想要的开裂效果,多次尝试无果 导致失去信心,其实如果你掌握了abaqus中所有的模拟方法后,你会发现abaqus做断裂其实
没那么难,无非就是断裂力学LEFM和损伤力学而已,下面我详细分析cohesive的本构 及参数设置,而且结合实例验证设置的参数,并分析损伤演化的位移准则和能量 准则的区别与联系,让你在10分钟内掌握cohesive。
Stress2-位移U2曲线
从Stress2与位移U2中发现,当达到100MPa时开始损伤,cohesive张开达到1e-5mm时, cohesive单元完全失效,此时的SDEG=1,此时的cohesive不能再承受力将被删除掉, 这个与我们开始的预期是完全一致的。
PS:如果有需要批量插入cohesive插件的可以联系qq1057593923或微信maliweizhiyuan 插入的具体内容见技术邻https:///content/post/418489
abaqus 插入cohesive element 原理

abaqus 插入cohesive element 原理Abaqus中的Cohesive Element(粘结元素)是一种用于模拟材料中裂纹扩展和断裂行为的元素。
它可以模拟材料中的粘结和剪切行为,并允许裂纹在材料中传播。
Cohesive Element的原理基于断裂力学理论和粘结力学理论。
它将材料中的断裂行为建模为两个相邻表面之间的相互作用。
在裂纹扩展过程中,材料的断裂面上会产生粘结应力和剪切应力。
Cohesive Element通过施加粘结和剪切应力来模拟这种相互作用。
Cohesive Element的工作原理如下:1. 定义材料的弹性行为:首先,需要定义材料的弹性行为,即材料在无裂纹时的应力-应变关系。
可以使用线性弹性模型或非线性弹性模型来描述材料的弹性行为。
2. 定义粘结行为:接下来,需要定义材料的粘结行为。
这包括定义材料的粘结强度、粘结刚度和粘结应力-开裂位移关系。
通常会使用一个或多个粘结模型来描述材料的粘结行为,如弹簧-剪切模型、弹簧-弹性模型或弹簧-塑性模型。
3. 插入Cohesive Element:将Cohesive Element插入到模型中,以模拟裂纹的扩展。
Cohesive Element通常插入到两个相邻的节点之间,其中一个节点代表裂纹的一个端点,另一个节点代表裂纹的另一个端点。
CohesiveElement的属性包括弹性刚度、粘结强度和粘结模型。
4. 定义断裂准则:定义断裂准则以确定何时发生裂纹扩展。
常见的断裂准则包括最大切应力准则、最大切应变准则和能量释放率准则。
这些准则根据材料的断裂特性来确定裂纹扩展的条件。
5. 模拟裂纹扩展:通过施加加载条件(如拉伸、剪切或弯曲)来模拟裂纹的扩展。
在加载过程中,CohesiveElement会根据定义的粘结行为和断裂准则来计算裂纹的扩展。
总之,Abaqus中的Cohesive Element通过模拟材料中的粘结和剪切行为来模拟裂纹的扩展和断裂行为。
(完整版)cohesiveelement例子详细图解
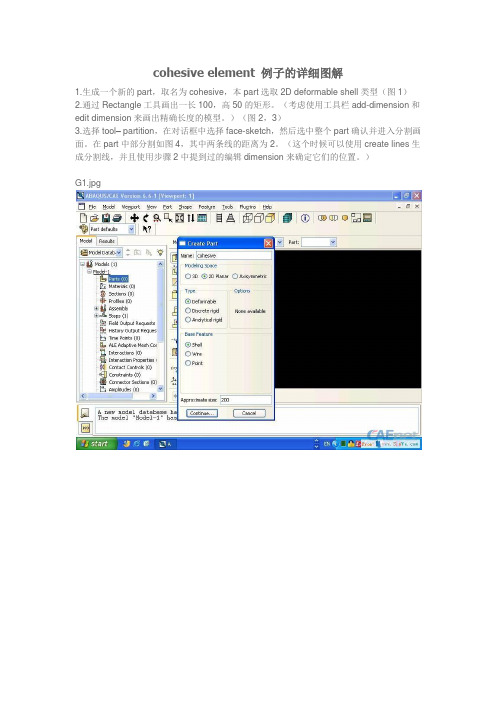
cohesive element 例子的详细图解1.生成一个新的part,取名为cohesive,本part选取2D deformable shell类型(图1)2.通过Rectangle工具画出一长100,高50的矩形。
(考虑使用工具栏add-dimension和edit dimension来画出精确长度的模型。
)(图2,3)3.选择tool– partition,在对话框中选择face-sketch,然后选中整个part确认并进入分割画面。
在part中部分割如图4,其中两条线的距离为2。
(这个时候可以使用create lines生成分割线,并且使用步骤2中提到过的编辑dimension来确定它们的位置。
)G1.jpgPicture3.jpg二(M5为第一个图)1.建立名为interface的材料,并且按照几图分别定义材料的damage initiation和damage evolution以及stiffness。
(相关材料的意义请认真查阅用户分析手册中Element--cohesive element章节)2.这里我们取damage initiation法则为Maxs,数值5e8,5e8,5e8;damage evolution选择energy,mode-independent,2e6。
3.选择mechanical-Elasticity-Elastic,type修改为traction将其中三项取为7e10)*另外建立名为Al的材料,杨式模量7e10,泊松彼0.3M5.jpgPicture6.JPGPicture7.JPGPicture8.JPG三、生成cohesive section,看图就很明了拉*另外生成一适合Al材料的sectionS5.JPGS6.JPG四part-section assignments,分别赋予section属性五Assembly--instance使用independent,然后进行mesh六设置mesh的seeds(看工具栏),然后选取工具栏上的mesh-->controls,将中间interface 部分Technique选为sweep,其他部分用系统默认设置。
cohesive-说明-2

zero thickness的cohesive section设定
abaqus所谓的zero-thickness,其实就是定义cohesive section的initial thickness=1.0。你可以在定义section的时候定义(specify),也可以用系统默认的thickness(也是1.0),这样有关cohesive element的计算当中,就有displacement(位移)=strain(应变)*thickness ( 1.0 )=strain的数值。
在6.5使用cohesive element,定义cohesive材料属性的时候主要步骤:
1.定义一个材料的名字,比如cohesive,不要去定义任何属性(弹性,弹塑性等等)。
2.打开工具栏model--edit keywords,在inp中手动添加材料的各种属性。
PS: 定义section的时候选cohesive,element control选sweep,element type选cohesive,这些是使用cohesive element的基本步骤。
我们知道从1914年Ingless和1921年Griffith提出断裂力学开始,一直到60年代都停留在线弹性断裂力学(LEFM)的层次。后来由於发现在裂纹尖端进入塑性区后用LEFM仍然无法解决stress singularity的问题。1960年由Barenblatt 和Dugdale率先提出了nonlinear/plastic fracture mechnics的概念,在裂纹前端引入了plastic zone,这也就是我们现在用的 cohesive fracture mechnics的前身。当时这个概念还没引起学术界的轰动。直到1966年Rice发现J-integral及随后发现在LEFM中J-integral是等于energy release rate的关系(赞大牛Rice一个,在读Ph.D期间就推导出对断裂力学有重要意义的J-integral了。。。 ,实令我辈汗颜)。随后在工程中发现了越来越多的LEFM无法解释的问题。cohesive fracture mechnics开始引起更多的关注。在研究以混凝土为代表的quassi-brittle material时,cohesive fracture mechnics提供了非常好的结果,所以在70年代到90年代,cohesive fracture mechnics被大量应用于混凝土研究中。目前比较常用的方法主要是fictitious crack approach和effective-elastic crack approach或是称为equivalent-elastic crack approach. 其中fictitious crack approach只考虑了Dugdale-Barenblatt energy mechanism而effective-elastic crack approach只考虑了基於LEFM的Griffith-Irwin energy dissipation mechanism,但作了一些修正。简单来说,我读了一下ABAQUS cohesive element的理论帮助,个人觉得ABAQUS的cohesive element采用的是广泛应用于混凝土的类似fictitious crack的方法。只考虑了Dugdale-Barenblatt energy mechanism。 这其中softening law 的影响是非常重要的。但ABAUQS似乎只提供了linear 或者exponential 的softening law,复杂的本构关系还需要另想办法。至於基於Griffith-Irwin energy dissipation mechanism的J-integral值可以在LEFM分析中单独算。(ABAQUS用的是Suo Zhigang 和Hutchinson在1990一篇论文中提出的方法) 目前cohesive fracture mechnics已经被应用于各种材料。不过在使用到纳米或者更小数量级的研究中碰到了不少问题,可能需要结合位错和分子动力学的一些理论,我现在的研究中也碰到类似的一些问题,希望和大家一起讨论。做裂纹ABAQUS有几种常见方法。最简单的是用debond命令, 定义*FRACTURE CRITERION, TYPE=XXX, 参数。。。** *DEBOND, SLAVE=XXX, MASTER=XXX, time increment=XX0,1, ……......time,0要想看到开裂特别注意需要在指定的开裂路径上定义一个*Nset, 然后在*INITIAL CONDITIONS, TYPE=CONTACT中定义master, slave, 及指定的Nset这种方法用途其实较为有限。另一种方法,在interaction模块,special, 定义crack seam, 网格最好细化,用collapse element模拟singularity. 这种方法可以计算J积分,应力强度因子等常用的断裂力学参数.裂尖及奇异性定义:在interaction-special,先定义crack, 定义好裂尖及方向, 然后在singularity选择:midside node parameter: 输入0.25, 然后选Collapsed element side, duplicate nodes,8节点单元对应(1/r)+(1/r^1/2)奇异性。这里midside node parameter选0.25对应裂尖collapse成1/4节点单元。如果midside nodes不移动到1/4处, 则对应(1/r)奇异性, 适合perfect plasticity的情况.网格划分:裂尖网格划分有一些技巧需要注意,partition后先处理最外面的正方形,先在对角线和边上布点,记住要点constraint, 然后选第三个选项do not allow the number of elements to change不准seed变化,密度可以自己调整. 最里面靠近圆的正方形可以只在对角线上布点. 也可以进一步分割内圆及在圆周上布点. 里面裂尖周围的内圆选free mesh, element type选cps6或者cpe6,外面四边形选sweep mesh, element type选cps8或者cpe8, 记住把quad下那个缩减积分的勾去掉。补充一下这种方法的几个常见问题,见不少朋友问过。主要是对断裂力学的理解问题,顺便一起回答一下。1.为什么我设置理想弹塑性(epp)分析的时候得到的xx,yy方向或者最大应力值Sxx, Syy会超过材料的屈服强度Sy呢, 这分析结果可能吗?这是因为在ABAQUS中对应等于材料的屈服强度的是von Mises等效应力Se=Sy,因此在平面应变的条件下,xx方向的应力Sxx=Sy*pi/SRQT(3)>Sy, 而Syy=Sy*(2+pi)/SRQT(3), 大概是3倍的屈服应力。所以得到大于材料的屈服强度的xx及yy方向应力是正常的。2.为什么设置collapse element的时候对弹性分析在中间就一个点而要把单元边上的中点移到1/4处,但弹塑性分析却要在中间设置一圈点并且保持单元边上的中点位置不变呢?这个其实不是随便定的,在有限元中分析裂纹时,对弹性分析需要模拟裂尖1/SQRT(r)的奇异性,这样在把单元边上的中点移到1/4处后计算出来的等参单元拉格郎日型函数对应的u field正好包含1/ SQRT(r)项,事实上这一方法在断裂力学的数值模拟发展史上是很巧妙的一个发现,至今仍然被广泛采用。至于理想弹塑性分析需要模拟裂尖1/r的奇异性, 这样大家都知道在把单元边上的点放在到1/2处后计算出来的正常的等参单元拉格郎日型函数对应的u field包含1/ r项, 可以模拟弹塑性分析需要的裂尖1/r的奇异性。所以在看似动手点几下就能实现的分析模式后面有很清楚漂亮的理论作支持。还有就是比较新的cohesive element单元。需要定义damage initiation和evolution的准则, softening准则目前只有linear和exponential,但对一般材料也够用了。然后通过设置后处理display group可以看到裂纹扩展情况。裂纹扩展不是ABAQUS的强项,目前比较方便的只能用cohesive element,我做过几个模型效果还可以,但对应的参数需要一定的实验数据支持,否则做出来了也不知道对不对。或者使用python控制seam尺寸,然后移动partition和网格,比较麻烦,我也没尝试过。但有一些学者有类似的结果:FRANC/FAM - A software system for the prediction of crack propagation.In: Journal of Structural Engineering 26, No. 1, 1999, pp. 39-48.再不就是用一些专业的断裂பைடு நூலகம்学软件如zencrack,感兴趣的可以自己看看:[url].au/publications/2355/DSTO-TR-1158.pdf[/url]还有自己编写cohesive Uel, 可以更加灵活的定义cohesive element的T-S law, 也有不少人做过,就不细说了。
Cohesive经典讲解

复合材料模型建模与分析1.Cohesive单元建模方法1.1几何模型使用内聚力模型(cohesivezone)模拟裂纹的产生和扩展,需要在预计产生裂纹的区域加入cohesive层。
建立cohesive层的方法主要有:方法一、建立完整的结构(如图1(a)所示),然后在上面切割出一个薄层来模拟cohesive 单元,用这种方法建立的cohesive单元与其他单元公用节点,并以此传递力和位移。
方法二、分别建立cohesive层和其他结构部件的实体模型,通过“tie”绑定约束,使得cohesive单元两侧的单元位移和应力协调,如图1(b)所示。
(a)cohesive单元与其他单元公用节点(b)独立的网格通过“tie”绑定图1.建模方法上述两种方法都可以用来模拟复合材料的分层失效,第一种方法划分网格比较复杂;第二种方法赋材料属性简单,划分网格也方便,但是装配及“tie”很繁琐;因此在实际建模中我们应根据实际结构选取较简单的方法。
1.2材料属性应用cohesive单元模拟复合材料失效,包括两种模型:一种是基于traction-separation 描述;另一种是基于连续体描述。
其中基于traction-separation描述的方法应用更加广泛。
而在基于traction-separation描述的方法中,最常用的本构模型为图2所示的双线性本构模型。
它给出了材料达到强度极限前的线弹性段和材料达到强度极限后的刚度线性降低软化阶段。
注意图中纵坐标为应力,而横坐标为位移,因此线弹性段的斜率代表的实际是cohesive单元的刚度。
曲线下的面积即为材料断裂时的能量释放率。
因此在定义cohesive的力学性能时,实际就是要确定上述本构模型的具体形状:包括刚度、极限强度、以及临界断裂能量释放率,或者最终失效时单元的位移。
常用的定义方法是给定上述参数中的前三项,也就确定了cohesive的本构模型。
Cohesive单元可理解为一种准二维单元,可以将它看作被一个厚度隔开的两个面,这两个面分别和其他实体单元连接。
Cohesive经典讲解
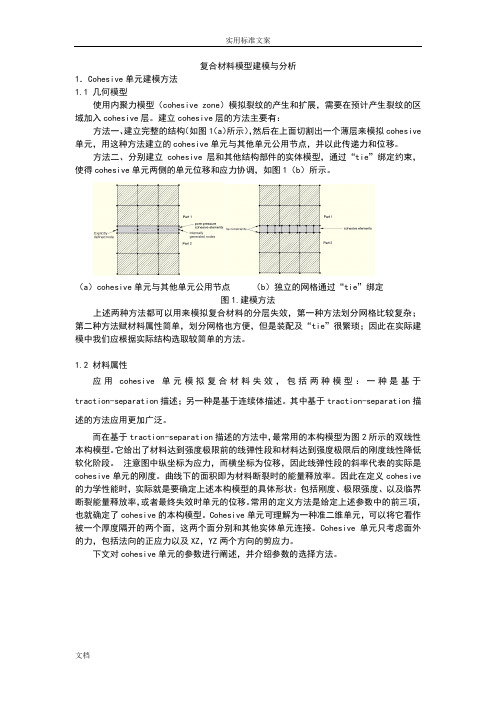
复合材料模型建模与分析1.Cohesive单元建模方法1.1 几何模型使用内聚力模型(cohesive zone)模拟裂纹的产生和扩展,需要在预计产生裂纹的区域加入cohesive层。
建立cohesive层的方法主要有:方法一、建立完整的结构(如图1(a)所示),然后在上面切割出一个薄层来模拟cohesive 单元,用这种方法建立的cohesive单元与其他单元公用节点,并以此传递力和位移。
方法二、分别建立cohesive层和其他结构部件的实体模型,通过“tie”绑定约束,使得cohesive单元两侧的单元位移和应力协调,如图1(b)所示。
(a)cohesive单元与其他单元公用节点(b)独立的网格通过“tie”绑定图1.建模方法上述两种方法都可以用来模拟复合材料的分层失效,第一种方法划分网格比较复杂;第二种方法赋材料属性简单,划分网格也方便,但是装配及“tie”很繁琐;因此在实际建模中我们应根据实际结构选取较简单的方法。
1.2 材料属性应用cohesive单元模拟复合材料失效,包括两种模型:一种是基于traction-separation描述;另一种是基于连续体描述。
其中基于traction-separation描述的方法应用更加广泛。
而在基于traction-separation描述的方法中,最常用的本构模型为图2所示的双线性本构模型。
它给出了材料达到强度极限前的线弹性段和材料达到强度极限后的刚度线性降低软化阶段。
注意图中纵坐标为应力,而横坐标为位移,因此线弹性段的斜率代表的实际是cohesive单元的刚度。
曲线下的面积即为材料断裂时的能量释放率。
因此在定义cohesive 的力学性能时,实际就是要确定上述本构模型的具体形状:包括刚度、极限强度、以及临界断裂能量释放率,或者最终失效时单元的位移。
常用的定义方法是给定上述参数中的前三项,也就确定了cohesive的本构模型。
Cohesive单元可理解为一种准二维单元,可以将它看作被一个厚度隔开的两个面,这两个面分别和其他实体单元连接。
(完整版)cohesive文摘介绍
关于cohesive element 中模量,厚度一些对应关系的理解与讨论dava,你可能看见了我在你那篇精华里面的留言,我发现这个问题还不是非常的清楚,现在单独的列出来,写一下我的理解以及一些还有疑问,需要和大家讨论的地方,供大家参考:1. 关于cohesive element的traction-separation law的定义:顾名思义,这个law给的是力与位移的关系,而不是平时常见的力与应变的关系,因此现在的曲线斜率(对于开始的线弹性阶段),是E/L而不是 E. (简单的推导:stress=E(modulus)*strain=E*L(original length)/L*strain=E/L*delta(位移),so stress/delta=E/L)。
2. 试验数据的输入:针对一种材料,或者一组试验数据得到的材料的young's modulus E, 中间的cohesive layer的厚度,当转换输入到ABAQUS中进行模拟的时候,对于cohesive layer,ABAQUS需要的是stiffness,也就是E/L,而不是E,所以使用者需要把试验材料的E除以试验得出的cohesive layer的厚度,输入到ABAQUS中去。
因此搞清楚这个关系也就明白了试验数据与模拟输入之间的转换。
3. 所谓的geometric thickness和constitutive thickness: geometric thickness,简单理解就是模型的尺寸,目的--让模型“显得”更真实。
constitutive thickness,就是参与内部运算的尺寸,目的--让结果“算的”更真实。
4. constitutive thickness在cohesive element的使用中起什么作用?(包含我的一些实践体会和疑问)a. 首先,参与运算,常用默认的1,可以使算得的位移等于应变值。
(可是这个到底有什么好处呢?我从手册上没有发现。
cohesive element 单元bk失效准则 -回复
cohesive element 单元bk失效准则-回复什么是单元BK失效准则?单元BK失效准则是指在材料力学和结构力学中,在材料的某一单元失效时,对该单元的边界条件和加载条件进行分析,以确定该单元的bk失效准则。
bk失效准则用于确定材料的失效点,并预测材料在实际应力状态下的强度和抗拉性能。
在材料的单元BK失效准则中,bk表示材料的强度。
根据材料的不同特性和应力状态,可以有多种不同的bk失效准则。
常见的单元BK失效准则有极限等效应力准则、极限应变准则和能量准则等。
一般来说,单元BK失效准则的分析流程可以分为以下几个步骤:第一步:确定应力状态和边界条件在进行单元BK失效准则的分析时,首先需要确定材料所处的应力状态和施加在单元上的边界条件。
这包括材料的外部载荷、约束条件以及加载路径等。
根据实际情况,可以选择不同的加载方式和加载路径。
第二步:选择合适的bk失效准则根据材料的特性和应力状态,选择适用的bk失效准则。
常见的bk失效准则有最大剪应力准则、最大主应力准则、von Mises准则等。
在选择bk失效准则时,需要考虑材料的强度特性以及应力分布的情况。
第三步:计算bk失效准则的准则值根据选定的bk失效准则,计算其对应的准则值。
准则值是衡量材料失效点的重要参数,可以通过实验数据和数值模拟等方法得到。
准则值的确定需要考虑材料的特性和试验条件等因素。
第四步:比较应力状态和准则值将材料所处的应力状态与bk失效准则的准则值进行比较。
如果应力状态满足准则值,则材料处于安全状态;如果应力状态超过准则值,则材料处于失效状态。
根据比较结果,可以评估材料的强度和抗拉性能。
第五步:优化设计和预测寿命根据单元BK失效准则的分析结果,可以对设计进行优化,改善材料的强度和抗拉性能。
同时,也可以根据分析结果预测材料的寿命和使用限制,以确保材料的安全和可靠性。
总结:单元BK失效准则是材料力学和结构力学中重要的分析方法。
通过对材料单元的边界条件和加载条件进行分析,可以确定材料的失效点,并预测材料在实际应力状态下的强度和抗拉性能。
(完整版)cohesive单元实例操作-01详解
今晚在仿真科技论坛上看见一个关于cohesive的帖子,真心觉得不错,原作者图文并茂的解说为初学者带来了福音,在此感谢原作者cheaxii的无私奉献!剥离臂AA5754-O:弹性模量74.7GPa 泊松比0.33粘合层ESP110:弹性模量5.72Gpa、泊松比0.40、极限应力99MPa、断裂能0.845mJ/mm2 (这里为保持单位一直,在输入参数时单位需要换算为MPa、mm、mJ/mm2)参数来源[1]Ph. Martinya, F. Lania, A.J. Kinlochb, T. Pardoenc.Numerical analysis of the energy contributions in peel tests[J]. International Journal of Adhesion & Adhesives 28 (2008) 222–236 文献中的实验结果如下:45°剥离,剥离强度16.7N/mm90°剥离,剥离强度6.05N/mm135°剥离,剥离强度4.11N/mm本算例模拟了90°剥离,结果和文献实验结果吻合很好。
以下是step by step:1;创建part,2维,deformable,尺寸如下:剥离臂长100mm,厚1mm。
(这里没有采用文献中的220mm的长度,因为这对结果没有影响,厚度一样就行);粘合层厚0.4mm,预制裂纹40mm,所以实际粘合部分长80mm。
这里只建立了半模型,就是说下面的基体没有建立,这里是因为基体厚10mm,相对来说比上剥离臂厚很多,认为它是刚性的,不发生变形,所以不需要建模,以减小计算量。
粘合层是在part模块下分割出来的,这样就可以为他们赋予不同的材料属性和截面特征了。
2,设置属性porperty这里创建两个属性:1、剥离臂;2、粘合层,如下图示3、创建两个截面section如下图4、为不同的分区赋予不同的截面属性如下图5、创建分析步这里因为有几何大变形,所以要打开几何大变形开关,将其从off调到on,其次为了最后的到载荷位移曲线的精确性,将增量步的大小做调整到0.002,这样就有500步,可以有500个采样点;6、调整场变量输出,在菜单栏output下拉菜单选择field output manage 点edit,勾选failure/fracture下面的SDEG和DMICRT,勾选state下面的status,这一步就不截图啦,很简单。
cohesive单元实例操作01详解
今晚在仿真科技论坛上看见一个关于cohesive的帖子,真心觉得不错,原作者图文并茂的解说为初学者带来了福音,在此感谢原作者cheaxii的无私奉献!剥离臂AA5754-O:弹性模量74.7GPa 泊松比0.33粘合层ESP110:弹性模量5.72Gpa、泊松比0.40、极限应力99MPa、断裂能0.845mJ/mm2 (这里为保持单位一直,在输入参数时单位需要换算为MPa、mm、mJ/mm2)参数来源[1]Ph. Martinya, F. Lania, A.J. Kinlochb, T. Pardoenc.Numerical analysis of the energy contributions in peel tests[J]. International Journal of Adhesion & Adhesives 28 (2008) 222–236 文献中的实验结果如下:45°剥离,剥离强度16.7N/mm90°剥离,剥离强度6.05N/mm135°剥离,剥离强度4.11N/mm本算例模拟了90°剥离,结果和文献实验结果吻合很好。
以下是step by step:1;创建part,2维,deformable,尺寸如下:剥离臂长100mm,厚1mm。
(这里没有采用文献中的220mm的长度,因为这对结果没有影响,厚度一样就行);粘合层厚0.4mm,预制裂纹40mm,所以实际粘合部分长80mm。
这里只建立了半模型,就是说下面的基体没有建立,这里是因为基体厚10mm,相对来说比上剥离臂厚很多,认为它是刚性的,不发生变形,所以不需要建模,以减小计算量。
粘合层是在part模块下分割出来的,这样就可以为他们赋予不同的材料属性和截面特征了。
2,设置属性porperty这里创建两个属性:1、剥离臂;2、粘合层,如下图示3、创建两个截面section如下图4、为不同的分区赋予不同的截面属性如下图5、创建分析步这里因为有几何大变形,所以要打开几何大变形开关,将其从off调到on,其次为了最后的到载荷位移曲线的精确性,将增量步的大小做调整到0.002,这样就有500步,可以有500个采样点;6、调整场变量输出,在菜单栏output下拉菜单选择field output manage 点edit,勾选failure/fracture下面的SDEG和DMICRT,勾选state下面的status,这一步就不截图啦,很简单。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
cohesive element 例子的详细图解
1.生成一个新的part,取名为cohesive,本part选取2D deformable shell类型(图1)
2.通过Rectangle工具画出一长100,高50的矩形。
(考虑使用工具栏add-dimension和edit dimension来画出精确长度的模型。
)(图2,3)
3.选择tool– partition,在对话框中选择face-sketch,然后选中整个part确认并进入分割画面。
在part中部分割如图4,其中两条线的距离为2。
(这个时候可以使用create lines生成分割线,并且使用步骤2中提到过的编辑dimension来确定它们的位置。
)
G1.jpg
Picture3.jpg
二(M5为第一个图)
1.建立名为interface的材料,并且按照几图分别定义材料的damage initiation和damage evolution以及stiffness。
(相关材料的意义请认真查阅用户分析手册中Element--cohesive element章节)
2.这里我们取damage initiation法则为Maxs,数值5e8,5e8,5e8;damage evolution选择energy,mode-independent,2e6。
3.选择mechanical-Elasticity-Elastic,type修改为traction将其中三项取为7e10)
*另外建立名为Al的材料,杨式模量7e10,泊松彼0.3
M5.jpg
Picture6.JPG
Picture7.JPG
Picture8.JPG
三、生成cohesive section,看图就很明了拉*另外生成一适合Al材料的section
S5.JPG
S6.JPG
四
part-section assignments,分别赋予section属性
五
Assembly--instance使用independent,然后进行mesh
六
设置mesh的seeds(看工具栏),然后选取工具栏上的mesh-->controls,将中间interface 部分Technique选为sweep,其他部分用系统默认设置。
在mesh-->element type中选择cohesive作为interface的单元类型。
*其他部分可以用系统默认的CPS4R
A1.JPG
七
使用工具栏mesh--〉edit,选择node-edit,点apply。
选取中间部分的节点,定义他们的纵坐标相同(可以选中点的纵坐标值。
通过tool-query可以查询节点坐标)。
注意勾掉progect to geometry选项。
八
建立一个Static, General类型的step,并且使用Nlgeom,其他用系统默认值
九
编辑field output,选中strains中的SDEG参数、failure\fracture中的DMICRT参数、state 中的STATUS参数。
十
剩下的其实就没什么了,无非就是加好正确的边界条件和加载条件。
我加的条件都在cae文件中,另外附上我的一个计算结果图和用tool-display group处理后的crack图
edit_mesh.JPG
edit mesh2.JPG
最后附上cae文件和结果图~~~ result.png
result2.png。
