必修一习题2.1(2)word
高中数学必修一第二章2.1.2指数函数及其性质习题(含答案)
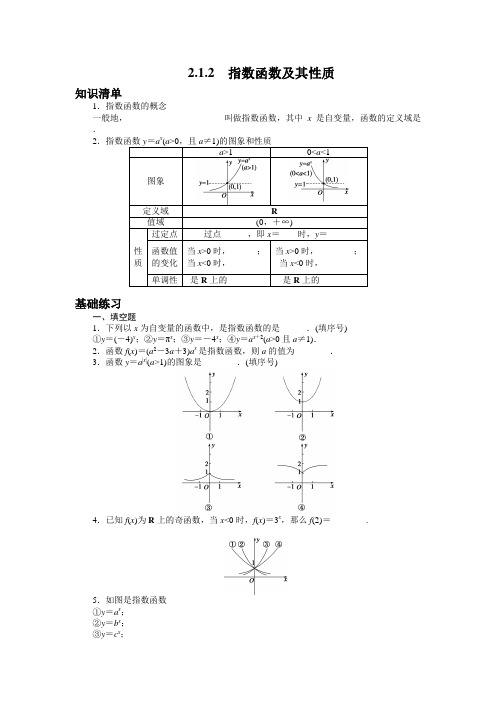
2.1.2 指数函数及其性质知识清单1.指数函数的概念一般地,______________________叫做指数函数,其中x 是自变量,函数的定义域是____.2.指数函数y =a x (a >0,且a ≠1)的图象和性质a >1 0<a<1图象定义域 R 值域 (0,+∞)性 质 过定点过点______,即x =____时,y =____函数值 的变化 当x >0时,______; 当x <0时,________ 当x >0时,________; 当x <0时,________单调性是R 上的________是R 上的________基础练习一、填空题1.下列以x 为自变量的函数中,是指数函数的是______.(填序号)①y =(-4)x ;②y =πx ;③y =-4x ;④y =a x +2(a >0且a ≠1). 2.函数f (x )=(a 2-3a +3)a x 是指数函数,则a 的值为________. 3.函数y =a |x |(a >1)的图象是________.(填序号)4.已知f (x )为R 上的奇函数,当x <0时,f (x )=3x,那么f (2)=________.5.如图是指数函数 ①y =a x ; ②y =b x ; ③y =c x ;④y =d x 的图象,则a 、b 、c 、d 与1的大小关系是________.6.函数y =(12)x -2的图象必过第________象限.7.函数f (x )=a x 的图象经过点(2,4),则f (-3)的值为____.8.若函数y =a x -(b -1)(a >0,a ≠1)的图象不经过第二象限,则a ,b 需满足的条件为________.9.函数y =8-23-x (x ≥0)的值域是________. 二、解答题10.比较下列各组数中两个值的大小:(1)0.2-1.5和0.2-1.7; (2)1314⎛⎫⎪⎝⎭和2314⎛⎫⎪⎝⎭; (3)2-1.5和30.2.11.2000年10月18日,美国某城市的日报以醒目标题刊登了一条消息:“市政委员会今天宣布:本市垃圾的体积达到50 000 m 3”,副标题是:“垃圾的体积每三年增加一倍”.如果把3年作为垃圾体积加倍的周期,请你完成下面关于垃圾的体积V (m 3)与垃圾体积的加倍的周期.(1) (2)根据报纸所述的信息,你估计3年前垃圾的体积是多少? (3)如果n =-2,这时的n ,V 表示什么信息?(4)写出n 与V 的函数关系式,并画出函数图象(横轴取n 轴). (5)曲线可能与横轴相交吗?为什么?12.定义运算a ⊕b =⎩⎪⎨⎪⎧a (a ≤b )b (a >b ),则函数f (x )=1⊕2x 的图象是________.(填序号)13.定义在区间(0,+∞)上的函数f (x )满足对任意的实数x ,y 都有f (x y )=yf (x ). (1)求f (1)的值;(2)若f (12)>0,解不等式f (ax )>0.(其中字母a 为常数).能力提升一、填空题1.设P ={y |y =x 2,x ∈R },Q ={y |y =2x ,x ∈R },则P 、Q 的关系为________. 2.函数y =16-4x 的值域是________.3.函数y =a 在[0,1]上的最大值与最小值的和为3,则函数y =2ax -1在[0,1]上的最大值是________.4.若函数f (x )=3x +3-x 与g (x )=3x -3-x 的定义域均为R ,则下列命题正确的是________.(填序号)①f (x )与g (x )均为偶函数;②f (x )为偶函数,g (x )为奇函数; ③f (x )与g (x )均为奇函数;④f (x )为奇函数,g (x )为偶函数.5.函数y =f (x )的图象与函数g (x )=e x +2的图象关于原点对称,则f (x )的解析式为________. 6.已知a =1335-⎛⎫ ⎪⎝⎭,b =1235-⎛⎫⎪⎝⎭,c =1243-⎛⎫ ⎪⎝⎭,则a ,b ,c 三个数的大小关系是________.7.春天来了,某池塘中的荷花枝繁叶茂,已知每一天新长出荷叶覆盖水面面积是前一天的2倍,若荷叶20天可以完全长满池塘水面,当荷叶刚好覆盖水面面积一半时,荷叶已生长了________天.8.已知函数f (x )是定义在R 上的奇函数,当x >0时,f (x )=1-2-x ,则不等式f (x )<-12的解集是________.9.函数y =2212x x-+⎛⎫ ⎪⎝⎭的单调递增区间是________.二、解答题10.(1)设f (x )=2u ,u =g (x ),g (x )是R 上的单调增函数,试判断f (x )的单调性; (2)求函数y =2212x x --的单调区间.11.函数f (x )=4x -2x +1+3的定义域为[-12,12].(1)设t =2x ,求t 的取值范围; (2)求函数f (x )的值域.12.函数y =2x -x 2的图象大致是________.(填序号)13.已知函数f (x )=2x-12x +1.(1)求f [f (0)+4]的值;(2)求证:f (x )在R 上是增函数;(3)解不等式:0<f (x -2)<1517.知识清单1.函数y =a x (a >0,且a ≠1) R 2.(0,1) 0 1 y >1 0<y <1 0<y <1 y >1 增函数 减函数 基础练习 1.②解析 ①中-4<0,不满足指数函数底数的要求,③中因有负号,也不是指数函数,④中的函数可化为y =a 2·a x ,a x 的系数不是1,故也不是指数函数. 2.2解析 由题意得⎩⎪⎨⎪⎧a 2-3a +3=1,a >0且a ≠1,解得a =2. 3.②解析 该函数是偶函数.可先画出x ≥0时,y =a x 的图象,然后沿y 轴翻折过去,便得到x <0时的函数图象.4.-19解析 当x >0时,-x <0,∴f (-x )=3-x ,即-f (x )=(13)x ,∴f (x )=-(13)x .因此有f (2)=-(13)2=-19.5.b <a <1<d <c解析 作直线x =1与四个指数函数图象交点的坐标分别为(1,a )、(1,b )、(1,c )、(1,d ),由图象可知纵坐标的大小关系. 6.二、三、四解析 函数y =(12)x 的图象上所有的点向下平移2个单位,就得到函数y =(12)x -2的图象,所以观察y =(12)x -2的图象可知.7.18解析 由题意a 2=4,∴a =2.f (-3)=2-3=18.8.a >1,b ≥2解析 函数y =a x -(b -1)的图象可以看作由函数y =a x 的图象沿y 轴平移|b -1|个单位得到.若0<a <1,不管y =a x 的图象沿y 轴怎样平移,得到的图象始终经过第二象限;当a >1时,由于y =a x 的图象必过定点(0,1),当y =a x 的图象沿y 轴向下平移1个单位后,得到的图象不经过第二象限.由b -1≥1,得b ≥2.因此,a ,b 必满足条件a >1,b ≥2. 9.[0,8)解析 y =8-23-x =8-23·2-x =8-8·(12)x=8[1-(12)x ].∵x ≥0,∴0<(12)x ≤1,∴-1≤-(12)x <0,从而有0≤1-(12)x <1,因此0≤y <8.10.解 (1)考察函数y =0.2x . 因为0<0.2<1,所以函数y =0.2x 在实数集R 上是单调减函数.又因为-1.5>-1.7,所以0.2-1.5<0.2-1.7.(2)考察函数y =(14)x .因为0<14<1,所以函数y =(14)x 在实数集R 上是单调减函数.又因为13<23,所以1314⎛⎫ ⎪⎝⎭>2314⎛⎫ ⎪⎝⎭1.(3)2-1.5<20,即2-1.5<1;30<30.2,即1<30.2,所以2-1.5<30.2.11.解 (1)由于垃圾的体积每3年增加1倍,24年后即8个周期后,该市垃圾的体积是50 000×28=12 800 000(m 3).(2)根据报纸所述的信息,估计3年前垃圾的体积是50 000×2-1=25 000(m 3).(3)如果n =-2,这时的n 表示6年前,V 表示6年前垃圾的体积. (4)n 与V 的函数关系式是V =50 000×2n ,图象如图所示.(5)因为对任意的整数n,2n >0,所以V =50 000×2n >0,因此曲线不可能与横轴相交. 12.①解析 由题意f (x )=1⊕2x=⎩⎪⎨⎪⎧1, x ≥0;2x , x <0.13.解 (1)令x =1,y =2,可知f (1)=2f (1),故f (1)=0.(2)设0<x 1<x 2,∴存在s ,t 使得x 1=(12)s ,x 2=(12)t ,且s >t ,又f (12)>0,∴f (x 1)-f (x 2)=f [(12)s ]-f [(12)t ]=sf (12)-tf (12)=(s -t )f (12)>0,∴f (x 1)>f (x 2).故f (x )在(0,+∞)上是减函数. 又∵f (ax )>0,x >0,f (1)=0, ∴0<ax <1,当a =0时,x ∈∅,当a >0时,0<x <1a ,当a <0时,1a<x <0,不合题意.故x ∈∅.综上:a ≤0时,x ∈∅;a >0时,不等式解集为{x |0<x <1a}.能力提升 1.Q P解析 因为P ={y |y ≥0},Q ={y |y >0},所以Q P . 2.[0,4)解析 ∵4x >0,∴0≤16-4x <16, ∴16-4x ∈[0,4). 3.3解析 函数y =a x 在[0,1]上是单调的,最大值与最小值都在端点处取到,故有a 0+a 1=3,解得a =2,因此函数y =2ax -1=4x -1在[0,1]上是单调递增函数,当x =1时,y max =3. 4.②解析 f (-x )=3-x +3x =f (x ),g (-x )=3-x -3x =-g (x ).5.f (x )=-e -x -2解析 ∵y =f (x )的图象与g (x )=e x +2的图象关于原点对称,∴f (x )=-g (-x )=-(e -x +2)=-e -x -2. 6.c <a <b解析 ∵y =(35)x 是减函数,-13>-12,∴b >a >1.又0<c <1,∴c <a <b . 7.19解析 假设第一天荷叶覆盖水面面积为1,则荷叶覆盖水面面积y 与生长时间的函数关系为y =2x -1,当x =20时,长满水面,所以生长19天时,荷叶布满水面一半. 8.(-∞,-1)解析 ∵f (x )是定义在R 上的奇函数, ∴f (0)=0.当x <0时,f (x )=-f (-x )=-(1-2x )=2x -1.当x >0时,由1-2-x <-12,(12)x >32,得x ∈∅;当x =0时,f (0)=0<-12不成立;当x <0时,由2x -1<-12,2x <2-1,得x <-1.综上可知x ∈(-∞,-1). 9.[1,+∞)解析 利用复合函数同增异减的判断方法去判断.令u =-x 2+2x ,则y =(12)u 在u ∈R 上为减函数,问题转化为求u =-x 2+2x 的单调递减区间,即为x ∈[1,+∞).10.解 (1)设x 1<x 2,则g (x 1)<g (x 2).又由y =2u 的增减性得()12g x<()22g x ,即f (x 1)<f (x 2), 所以f (x )为R 上的增函数.(2)令u =x 2-2x -1=(x -1)2-2, 则u 在区间[1,+∞)上为增函数.根据(1)可知y =2212x x --在[1,+∞)上为增函数. 同理可得函数y 在(-∞,1]上为单调减函数.即函数y 的增区间为[1,+∞),减区间为(-∞,1].11.解 (1)∵t =2x 在x ∈[-12,12]上单调递增,∴t ∈[22,2].(2)函数可化为:f (x )=g (t )=t 2-2t +3,g (t )在[22,1]上递减,在[1,2]上递增,比较得g (22)<g (2). ∴f (x )min =g (1)=2, f (x )max =g (2)=5-2 2.∴函数的值域为[2,5-22]. 12.①解析 当x →-∞时,2x →0,所以y =2x -x 2→-∞, 所以排除③、④.当x =3时,y =-1,所以排除②.13.(1)解 ∵f (0)=20-120+1=0,∴f [f (0)+4]=f (0+4)=f (4)=24-124+1=1517.(2)证明 设x 1,x 2∈R 且x 1<x 2, 则22x>12x>0,22x-12x>0,∴f (x 2)-f (x 1)=212121212121x x x x ---++ =()()()21212222121x x x x -++>0,即f (x 1)<f (x 2),所以f (x )在R 上是增函数.(3)解 由0<f (x -2)<1517得f (0)<f (x -2)<f (4),又f (x )在R 上是增函数,∴0<x -2<4,即2<x <6,所以不等式的解集是{x |2<x <6}.。
人教版必修一2.1.2热力环流

1. 地面受热不均,会引起近地面和高空等压面的变化。下列所示等
压面分布图中,正确的是
B
2. 读某沿海地区某时刻等压面分布示意图,探究以下问题。
(1) 该时刻近地面海洋与陆地,哪
个气压高?___海__洋____。近地面
风向是什么?(海风或陆风)
_海___风___。 (2) 该时刻是白天还是夜间?_白__天____ 人教版必修一2.1.2热力环流
B、高压、低压:
同一高度上,空气密度越大,气压值越大,称为高压; 空气密度越小,气压值越小,称为低压。
同一高度(水平面)上空气由高压向低压运动
C
B
地面
D
A
C、等压面: 大气中气压值相等的点所构成的面。
900hpa 2 1100hpa 1
B
高空
1000m
500m
A
C
地面
空间气压相等的 各点所组成的面。
等压面
地
面
低 1000(百帕)
1005 1010
高
(2).形成过程
高空
1020hpa
1060hpa
1100hpa
地面
C
A
高 度 升 高 , 气 压 减 小
B
若地面受热均匀,等压面应该是平行的。
B
A
C
冷却
受热
冷却
地面受热不均
高空
1020hpa
低压
1060hpa
1100hpa
地面
高压 C
冷却
等压面弯曲规律:
人教版必修一2.1.2热力环流
2、山谷风
山谷与其附近大气之间的温度差异引起的热力环流
人教版必修一2.1.2热力环流
(人教a版)数学必修一课时训练:2.1.2(第1课时)指数函数的图象及性质(含答案)

温馨提示:此套题为Word版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。
关闭Word文档返回原板块。
课时提升卷(十六)指数函数的图象及性质(45分钟 100分)一、选择题(每小题6分,共30分)1.若函数y=(2a-3)x是指数函数,则a的取值范围是( )A.a>B.a>,且a≠2C.a<D.a≠22.指数函数y=f(x)的图象经过点(-2,),那么f(4)·f(2)等于( )A.8B.16C.32D.643.(2013·黄冈高一检测)已知集合M={y|y=-x2+2,x∈R},集合M)∩N=( )N={y|y=2x,0≤x≤2},则(RA.[1,2]B.(2,4]C.[1,2)D.[2,4)4.当x>0时,指数函数f(x)=(a-1)x<1恒成立,则实数a的取值范围是( )A.a>2B.1<a<2C.a>1D.a∈R5.(2012·四川高考)函数y=a x-(a>0,a≠1)的图象可能是( )二、填空题(每小题8分,共24分)6.已知函数f(x)=则f(2)+f(-2)= .7.(2012·山东高考改编)若函数f(x)=a x(a>0,a≠1)在[-1,2]上的最大值为4,最小值为m,且函数g(x)=(1-4m)x2在[0,+∞)上是增函数,则a= .8.(2013·长沙高一检测)关于下列说法:(1)若函数y=2x的定义域是{x|x≤0},则它的值域是{y|y≤1}.(2)若函数y=的定义域是{x|x≥2},则它的值域是{y|y≤}.(3)若函数y=2x的值域是{y|0<y≤4},则它的定义域一定是{x|0<x≤2}.其中不正确的说法的序号是.三、解答题(9题,10题14分,11题18分)9.已知函数f(x)=a x+b(a>0,且a≠1).若f(x)的图象如图所示,求a,b 的值.10.(2013·长春高一检测)已知函数f(x)=a x-1(x≥0)的图象经过点(2,),其中a>0且a≠1.(1)求a的值.(2)求函数y=f(x)(x≥0)的值域.11.(能力挑战题)已知函数y=a x(a>0且a≠1)在[1,2]上的最大值与最小值之和为20,记f(x)=.(1)求a的值.(2)证明f(x)+f(1-x)=1.(3)求f()+f()+f()+…+f()的值.答案解析1.【解析】选B.由题意得2a-3>0,且2a-3≠1,所以a>,且a≠2.2.【解析】选D.设f(x)=a x(a>0且a≠1),由已知得=a-2,a2=4,所以a=2,于是f(x)=2x,所以f(4)·f(2)=24·22=26=64.3.【解析】选B.由题可知M=(-∞,2],N=[1,4],∴R M=(2,+∞),(RM)∩N=(2,4].【变式备选】若集合M={y|y=2-x},P={y|y=},则M∩P等于( ) A.{y|y>1} B.{y|y≥1}C.{y|y>0}D.{y|y≥0}【解析】选C.y=2-x的值域为{y|y>0},y=的值域为{y|y≥0},因此,其交集为{y|y>0}.故选C.4.【解题指南】结合指数函数的图象,若x>0时,(a-1)x<1恒成立,则必有0<a-1<1,进而求解.【解析】选B.∵x>0时,(a-1)x<1恒成立,∴0<a-1<1,∴1<a<2.5.【解析】选D.当a>1时,y=a x-在R上为增函数,且与y轴的交点为(0,1-),又0<1-<1,故排除A,B.当0<a<1时,y=a x-在R上为减函数,且与y轴的交点为(0,1-),又1-<0,故选D.6.【解析】f(2)+f(-2)=22+3-2=.答案:【举一反三】若对于本题中的函数f(x),有f(a)=16,试求a的值.【解析】当a≤1时,f(a)=3a≤3<16,故a>1,此时有f(a)=2a=16,所以a=4.7.【解析】当a>1时,有a2=4,a-1=m,此时a=2,m=,此时g(x)=-x2在[0,+∞)上是减函数,不合题意.若0<a<1,则a-1=4,a2=m,故a=,m=,检验知符合题意.答案:8.【解题指南】解答本题一方面要注意利用函数的单调性由定义域求值域,由值域求定义域;另一方面要注意结合函数的图象,弄清楚函数值与自变量的关系.【解析】(1)不正确.由x≤0得0<2x≤20=1,值域是{y|0<y≤1}.(2)不正确.由x≥2得0<≤,值域是{y|0<y≤}.(3)不正确.由2x≤4=22得x≤2,所以若函数y=2x的值域是{y|0<y≤4},则它的定义域一定是{x|x≤2}.答案:(1)(2)(3)9.【解析】由图象得,点(2,0),(0,-2)在函数f(x)的图象上,所以解得10.【解析】(1)∵函数f(x)=a x-1(x≥0)的图象经过点(2,),∴=a2-1,∴a=.(2)由(1)知f(x)=()x-1=2·()x,∵x≥0,∴0<()x≤()0=1,∴0<2·()x≤2,∴函数y=f(x)(x≥0)的值域为(0,2].11.【解析】(1)函数y=a x(a>0且a≠1)在[1,2]上的最大值与最小值之和为20,∴a+a2=20,得a=4或a=-5(舍去).(2)由(1)知f(x)=,∴f(x)+f(1-x)=+=+=+=+=1.(3)由(2)知f()+f()=1,f()+f()=1,…,f()+f()=1,∴f()+f()+f()+…+f()=++…+=1+1+…+1=1 006.关闭Word文档返回原板块。
2020-2021高中人教版化学必修一课时分层作业:2.1.2 分散系及其分类含解析

课时分层作业七分散系及其分类(40分钟70分)一、选择题(本题包括12小题,每小题4分,共48分)1.(2019·重庆江津中学高一检测)下列说法正确的是A.胶体不均一,不稳定B.胶体能通过半透膜C.利用丁达尔效应可以区别溶液和胶体D.胶体能发生电泳是因为胶体带电【解析】选C。
因胶体均一、在一定条件下能稳定存在,属于介稳体系,故A错误; 胶体中分散质粒子的直径处于1~100 nm,大于半透膜孔径,不能通过半透膜,故B错误;丁达尔效应是胶体的特征性质,可以用来区别溶液与胶体,故C正确;胶体不带电,胶粒因吸附带电离子而带电荷,故D错误。
2.下面做法或物质用途的叙述中错误的是( )A.盐卤可用于制豆腐B.活性炭作吸附剂C.以无水酒精作外科消毒剂D.明矾作净水剂【解析】选C。
盐卤的主要成分是电解质,能使豆浆胶体发生聚沉,A项正确;活性炭表面积大,可作吸附剂,B项正确;医用酒精为75%,不是无水酒精,C项错误;明矾溶于水可形成氢氧化铝胶体,吸附水中悬浮杂质而凝聚成沉淀,故可作净水剂,D项正确。
【方法规律】生活中常见的胶体有墨水、豆浆、淀粉溶液、蛋清溶液等。
3.下列关于胶体的叙述正确的是( )A.布朗运动是胶体微粒特有的运动方式,只用肉眼就可以把胶体、溶液和浊液区别开来B.分散质粒子直径大小介于1~10 nm之间的微粒称为胶体粒子C.用平行光照射NaCl溶液和Fe(OH)3胶体时,均产生丁达尔效应D.胶体粒子具有较大的表面积,能吸附阳离子或阴离子,故在电场作用下会产生电泳现象【解析】选D。
布朗运动是微粒普遍的运动方式,用肉眼不可以把胶体和溶液区别开来,故A错误;分散质粒子直径大小介于1~100 nm之间的微粒称为胶体粒子,故B错误;用平行光照射NaCl溶液和Fe(OH)3胶体时,只有Fe(OH)3胶体产生丁达尔效应,故C错误;胶体粒子具有较大的表面积,能吸附阳离子或阴离子,故在电场作用下会产生电泳现象,故D正确。
人教版高中化学必修一2.1《钠及其化合物》练习题含答

⼈教版⼈中化学必修⼈2.1《钠及其化合物》练习题含答案2.1《钠及其化合物》练习含答案⼀、选择题(单选题,共14个⼀题,每⼀题4分,共56分)1、⼀属钠是⼀种活泼⼀属,除了具有⼀属的⼀般性质外,还具有⼀⼀的特性。
下列关于钠的叙述中,正确的是()A.钠是银⼀⼀⼀属,熔点低,硬度⼀B.钠放置在空⼀中,会迅速被氧化⼀⼀成淡黄⼀的氧化钠C.在氧⼀中加热时,⼀属钠剧烈燃烧,发出黄⼀⼀焰D.⼀属钠着⼀可以⼀泡沫灭⼀器或⼀⼀燥的沙⼀灭⼀解析A中,钠的硬度⼀,可⼀⼀⼀切割;B中,放置在空⼀中,钠被缓慢氧化⼀成⼀⼀Na2O;D中,钠着⼀时⼀成Na2O2,泡沫灭⼀器释放的泡沫中有CO2、H2O会与Na和Na2O2反应⼀成H2、O2,故不能⼀泡沫灭⼀器灭⼀。
答案C2、将⼀块银⼀⼀的⼀属钠放在空⼀中会发⼀⼀系列的变化:表⼀迅速变暗―→“出汗”―→变成⼀⼀固体(粉末),下列有关叙述中正确的是()A. 表⼀迅速变暗是因为钠与空⼀中的氧⼀反应⼀成了过氧化钠B. “出汗”是因为⼀成的氢氧化钠吸收空⼀中的H2O在表⼀形成了溶液C. 最后变成碳酸氢钠粉末D. 该过程中的所有化学反应均为氧化还原反应解析钠露置在空⼀中表⼀迅速变暗,是因为Na与O2反应⼀成了Na2O,A项错误;Na2O与⼀反应⼀成NaOH,NaOH⼀吸收空⼀中的H2O和CO2,⼀成Na2CO3·10H2O,Na2CO3·10H2O逐渐风化脱⼀,最后变成Na2CO3粉末,B正确;该过程中只有钠的氧化是氧化还原反应,C错误,应该是碳酸钠,碳酸氢钠不稳定,D项错误。
答案B3、下列叙述中正确的是() A.过氧化钠是淡黄⼀固体,久置于空⼀中变成⼀⼀氢氧化钠固体B.过氧化钠中阴阳离⼀⼀例为1∶2 C.⼀过氧化钠漂⼀织物、麦秆等⼀久⼀逐渐变成黄⼀ D.Na2O与Na2O2都能和⼀反应⼀成碱,它们都是碱性氧化物解析过氧化钠久置于空⼀中变成⼀⼀碳酸钠固体,A错误;过氧化钠漂⼀是由于它的氧化性将有⼀物质永久漂⼀,C错误;碱性氧化物与酸反应⼀成盐和⼀,Na2O2与酸反应⼀成盐、⼀和氧⼀,不是碱性氧化物,属于过氧化物,D错误。
2020~2021学年人教版(2019)选择性必修一章节2.1.2 影响化学反应速率的因素(二)

2020—2.1.2 影响化学反应速率的因素(二)1.某温度下,体积一定的密闭容器中进行如下可逆反应:X(g)+Y(g)Z(g)+W(s);H >0下列叙述正确的是()A.增大升高温度,平衡逆向移动B.当容器中气体压强不变时,反应达到平衡C.加入少量W,逆反应速率增大D.平衡后加入X,上述反应的ΔH增大2.下列哪些是影响化学反应速率的主要因素( )A.压强B.温度C.催化剂D.反应物的性质3.把下列四种盐酸溶液分别加入四个盛有20mL 1mol/L的KOH溶液的烧杯中,均加水稀释到100mL,此时反应最快的是()A. 20℃ 20mL 3mol/L的盐酸B. 25℃ 30mL 2mol/L的盐酸C. 25℃ 10mL 5mol/L的盐酸D. 20℃ 10mL 2mol/L的盐酸4.对于密闭容器中进行的反应N 2(g)+O2(g)2NO(g),下列条件能加快其反应速率的是( )A.增大体积使压强减小B.体积不变,充入N2使压强增大C.体积不变,充入He使压强增大D.压强不变,充入气体Ne5.一定温度下用铁块与稀硫酸反应制取氢气,采取下列措施,①将铁块换成等质量的铁粉;②将稀硫酸换成浓硫酸;③加热;④加入少量KNO3固体;其中能够加快氢气产生速率的是( )A.①③④B.②④C.②③D.①③6.常温下,分别将四块形状相同、质量均为7 g的铁块同时投入足量下列四种溶液中。
铁块最快溶解完的是( )A.250.0 mL 21H SO溶液mol L-mol L-盐酸 B.150.0 mL 2124C.40.0 mL 51H SO溶液mol L-mol L-盐酸 D.20.0 mL18.41247.下列说法不正确的是( )A.加入正催化剂,活化分子百分数增大,化学反应速率一定增大B.熵增且放热的反应是自发反应C.任何条件下,化学反应的焓变都等于化学反应的反应热D.常温下硝酸铵能够溶于水,因为其溶于水是一个熵增大过程8.对可逆反应 2A(s)+3B(g)⇌C(g)+2D(g)△ H<0,在一定条件下达到平衡,下列有关叙述正确的是()①增加 A 的量,平衡向正反应方向移动②升高温度,平衡向逆反应方向移动,v 正减小③缩小容器体积,平衡不移动,v 正、v 逆增大④增大 B的浓度,v 正>v 逆⑤加入催化剂,平衡向正反应方向移动。
人教新课标版数学高一 数学必修一习题 2.1指数函数
习题课 指数函数及其基本性质基 础 过 关1.已知xy ≠0且4x 2y 2=-2xy ,则有( )A.xy <0B.xy >0C.x >0,y >0D.x <0,y <0 解析 ∵4x 2y 2=(2xy )2=2|xy |=-2xy ,∴xy <0.答案 A2.指数函数y =b ·a x 在[b ,2]上的最大值与最小值的和为6,则a =( )A.2B.-3C.2或-3D.-12 解析 由于函数是指数函数,因而b =1,又因为此函数在[1,2]上是单调函数,所以a +a 2=6,解得a =2或a =-3(舍去).答案 A3.函数y =xa x|x |(a >1)的图象的大致形状是( )解析 因为y =xa x |x |=⎩⎪⎨⎪⎧a x ,x >0,-a x ,x <0,又a >1,所以选B. 答案 B4.计算:0.25×⎝ ⎛⎭⎪⎫-12-4-4÷20-⎝ ⎛⎭⎪⎫116-12=________. 解析 原式=14×16-4÷1-⎝ ⎛⎭⎪⎫14-1=4-4-4=-4. 答案 -45.不等式22x -3>⎝ ⎛⎭⎪⎫127的解集是________. 解析 不等式变为2x -3>-7,得x >-2.答案 (-2,+∞)6.计算:823×100-12×⎝ ⎛⎭⎪⎫14-3×⎝ ⎛⎭⎪⎫1681-34. 解 原式=(23)23×(102)-12×(2-2)-3×⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫234-34=22×10-1×26×⎝ ⎛⎭⎪⎫23-3 =28×110×⎝ ⎛⎭⎪⎫323=4325. 7.已知函数f (x )=13x -1+12. (1)求f (x )的定义域;(2)讨论f (x )的奇偶性.解 (1)由3x -1≠0,得3x ≠1,即x ≠0,所以函数的定义域为{x ∈R |x ≠0}.(2)因为函数f (x )的定义域关于坐标原点对称,且f (-x )=13-x -1+12=3x 1-3x +12=3x +12(1-3x )=-3x +12(3x -1), 而f (x )=13x -1+12=3x +12(3x -1), 所以f (-x )=-f (x ),因此函数f (x )是奇函数.8.设0≤x ≤2,y =4x -12-3·2x +5,试求该函数的最值.解 令t =2x ,0≤x ≤2,∴1≤t ≤4.则y =22x -1-3·2x +5=12t 2-3t +5.又y =12(t -3)2+12,t ∈[1,4],∴y =12(t -3)2+12,t ∈[1,3]上是减函数;t ∈[3,4]上是增函数,∴当t =3时,y min =12;当t =1时,y max =52. 故函数的最大值为52,最小值为12.能 力 提 升9.设函数f (x )=⎩⎨⎧⎝ ⎛⎭⎪⎫12x -3,x ≤0,x 2,x >0,已知f (a )>1,则实数a 的取值范围是( )A.(-2,1)B.(-∞,-2)∪(1,+∞)C.(1,+∞)D.(-∞,-1)∪(0,+∞)解析 当a ≤0时,因为f (a )>1,所以⎝ ⎛⎭⎪⎫12a -3>1,解得a <-2;当a >0时,a 2>1,解得a >1,故实数a 的取值范围是(-∞,-2)∪(1,+∞).答案 B10.已知定义在R 上的奇函数f (x )和偶函数g (x )满足f (x )+g (x )=a x -a -x +2(a >0,且a ≠1),若g (2)=a ,则f (2)等于( )A.2B.154C.174D.a 2解析 ∵f (x )是奇函数,g (x )是偶函数,∴由 f (x )+g (x )=a x -a -x +2,①∴得f (-x )+g (-x )=-f (x )+g (x )=a -x -a x +2,②①+②,得 g (x )=2,①-②,得f (x )=a x -a -x .又g (2)=a ,∴a =2,∴f (x )=2x -2-x ,∴f (2)=22-2-2=154.答案 B11.若函数f (x )=2x 2+2ax -a -1的定义域为R ,则实数a 的取值范围是________. 解析 依题意,2x 2+2ax -a -1≥0对x ∈R 恒成立,即x 2+2ax -a ≥0恒成立,∴Δ=4a 2+4a ≤0,-1≤a ≤0.答案 [-1,0]12.已知f (x )=a x +b 的图象如图所示,则f (3)=________.解析 因为f (x )的图象过(0,-2),(2,0)且a >1.所以⎩⎪⎨⎪⎧-2=a 0+b ,0=a 2+b ,,所以a =3,b =-3. 所以f (x )=(3)x -3,f (3)=(3)3-3=33-3.答案 33-313.(2016·浙江湖州中学期中)已知f (x )是定义在[-1,1]上的奇函数,当x ∈[-1,0]时,函数的解析式为f (x )=14x -a 2x (a ∈R ).(1)试求a 的值;(2)写出f (x )在[0,1]上的解析式;(3)求f (x )在[0,1]上的最大值;解 (1)因为f (x )是定义在[-1,1]上的奇函数,所以f (0)=1-a =0,所以a =1.(2)设x ∈[0,1],则-x ∈[-1,0],所以f (x )=-f (-x )=-⎝ ⎛⎭⎪⎫14-x -12-x =2x -4x . 故当x ∈[0,1]时,f (x )=2x -4x .(3)由(2)知,f (x )=2x -4x ,x ∈[0,1],令t =2x ,则y =t -t 2,t ∈[1,2].又y =-⎝ ⎛⎭⎪⎫t -122+14在[1,2]上是减函数, ∴当t =1,即x =0时,y 有最大值0.故f (x )的最大值为0.探 究 创 新14.已知f (x )=a a 2-1(a x -a -x )(a >0且a ≠1). (1)判断f (x )的奇偶性;(2)讨论f (x )的单调性;(3)当x ∈[-1,1]时,f (x )≥b 恒成立,求实数b 的取值范围.解 (1)因为函数的定义域为R ,所以关于原点对称.又因为f (-x )=a a 2-1(a -x -a x )=-f (x ), 所以f (x )为奇函数.(2)当a >1时,a 2-1>0,y =a x 为增函数,y =-a -x 为增函数,从而y =a x -a -x 为增函数,所以f (x )为增函数,当0<a<1时,a2-1<0,y=a x为减函数,y=-a-x为减函数,从而y=a x-a-x为减函数,所以f(x)为增函数.故当a>0,且a≠1时,f(x)在定义域内单调递增.(3)由(2)知f(x)在R上是增函数,所以在区间[-1,1]上为增函数,所以f(-1)≤f(x)≤f(1),所以f(x)min=f(-1)=aa2-1(a-1-a)=aa2-1·1-a2a=-1,所以要使f(x)≥b在[-1,1]上恒成立,则只需b≤-1,故实数b的取值范围是(-∞,-1].。
高中地理学案(必修一)配套习题——2、1地壳的物质组成和物质循环(教师版)
第二章自然环境中的物质运动和能量交换2.1 地壳的物质组成和物质循环一、选择题下图为“某地地质构造简图”,读图完成1~4题。
1、图中岩层,最晚形成的是A.①B.②C.③D.④【解析】一般来讲,上边的岩层比下边的岩层形成晚;喷出型岩浆岩是岩浆喷出地表后冷却形成的,因此图示区域中由火山活动形成的岩浆岩是最晚的。
答案:A2、如果④是石灰岩,则⑤为A.花岗岩B.砂岩C.大理岩D.板岩【解析】石灰岩受高温或高压的作用发生变质而成为大理岩。
答案:C3、在地表形成的①岩石具有的特征是A.含有生物化石 B.具有较多的气孔 C.由方解石组成 D.由石英、云母、长石、方解石集合而成【解析】岩浆喷出地表形成喷出型岩浆岩,结构疏松,多气孔。
答案:B4、如果岩层③是由鹅卵石和粗砂组成的岩石,反映了该岩石的形成环境是A.海洋环境 B.湖泊沉积环境 C.山洪河流沉积环境 D.河流入海口泥沙沉积环境【解析】鹅卵石和粗砂应是由流速较快的水流携带、沉积形成的。
答案:C矿物是具有确定化学成分、物理属性的单质或者化合物,是化学元素在岩石圈中存在的基本单元。
常见的矿物如煤、石油、天然气、石英等。
据此完成5—7题。
5、下列地质名称按其形成及相互关系,排列正确的是①岩石②化学元素③矿床④矿物⑤矿产⑥地壳A.②—⑤—①—④ B.②—④—⑥—① C.②—④—①—⑥ D.②—④—③—⑤【解析】明确相关概念的含义可回答该问题。
答案:C6、下列关于矿物的叙述,错误的是①不同矿物的化学成分一定不同②常见的造岩矿物有长石、石英、云母、方解石等③所有矿物都为固体④在目前所知的矿物中,金刚石硬度最大A.①② B.②③ C.①③ D.②④【解析】不同矿物的化学成分有可能相同,例如,金刚石和石墨物理性质有很大差异,是两种性质不同的矿物,但它们的化学成分相同,都是由碳元素组成的。
矿物有不同的存在形式,并不都是固体,例如,天然气为气态矿物,石油和天然汞为液态矿物。
答案:C7、天然汞属于A.固态矿物 B.液态矿物 C.气态矿物 D.不是矿物【解析】自然界中天然汞呈液态,是液态矿物的一种。
人教版高中数学必修一2.1.2《指数函数及其性质》word教材分析1
《指数函数及其性质》一、教材分析(一)教材的地位和作用人民教育出版社《普通高中课程标准实验教科书••数学(1)》(人教A版)$2.1.2“指数函数”是在学生系统地学习了函数概念及性质,掌握了指数与指数幂的运算性质的基础上展开研究的。
作为重要的基本初等函数之一,指数函数既是函数近代定义及性质的第一次应用, 又对高中阶段研究对数函数、三角函数等完整的函数知识,初步培养函数的应用意识打下了良好的学习基础,也为今后研究其他函数提供了方法和模式。
指数函数在知识体系中起了承上启下的作用,同时在生活及生产实际中有着广泛的应用,因此它也是对学生进行情感价值观教育的好素材,所以指数函数应重点研究。
(二)课时划分指数函数的教学在中共分三个课时完成。
指数函数的图象及其性质,指数函数及其性质的应用(1),指数函数及其性质的应用(2)。
这是第一课时“指数函数的图象及其性质”。
“指数函数”第一课时是在学习了指数与指数幂的运算基础上学习指数函数的概念和性质,通过学习指数函数的定义,图象及性质,可以进一步深化学生对函数概念的理解与认识,使学生得到较系统的函数知识和研究函数的方法,并且为学习对数函数作好准备。
二、学情分析(一)有利因素通过初中学段的学习和高中对集合、函数等知识的系统学习,学生对函数和图象的关系已经构建了一定的认知结构,主要体现在三个层面:知识层面:对正比例函数、反比例函数、一次函数,二次函数等最简单的函数概念和性质已有了初步认识,能够从初中运动变化的角度认识函数初步转化到从集合与对应的观点来认识函数。
技能层面:学生对采用“描点法”描绘函数图象的方法已基本掌握,能够为研究《指数函数》的性质做好准备。
由观察到抽象的数学活动过程已有一定的体会,已初步了解了数形结合的思想。
情感层面:学生对数学新内容的学习有相当的兴趣和积极性。
(二)不利因素本节内容思维量较大,对思维的严谨性和分类讨论、归纳推理等能力有较高要求,学生学习起来有一定难度。
【金版教程】人教版高中数学必修一练习:2.1.2.1指数函数的基本内容(含答案解析)
1. [2015 ·福建六校高一联考 ]函数 f(x) = 2x 的图象 ( )
A.关于原点对称
B .关于直线 y= x 对称
C.关于 x 轴对称 D.关于 y 轴对称
答案 D
解析
f(x)
4x + =x
2
1 =
2x +
2-
x
.
f(-
x)
=
-
2
x+
2x=
f(x)
,
∴ f(x) 为偶函数,图象关于 y 轴对称. 2.如图是指数函数① y= ax,② y =bx,③ y = cx,④ y= dx 的图象,则 a, b, c, d 与 1
解法二:作直线 x= 1,与四个图象分别交于 A ,B, C,D 四点,由于 x= 1 代入各个函
数可得函数值等于底数的大小,所以四个交点的纵坐标越大,则底数越大,由图可知
b< a
< 1< d< c.故选 B.
3.若 a>1,- 1<b<0 ,则函数
y=
x
a
+限
B .第一、三、四象限
C.第二、三、四象限
D .第一、二、四象限
答案 A
解析 ∵ a>1,且- 1<b<0,故其图象如图所示.
ex +e- x
4.函数 y= ex- e- x的图象大致为 (
)
的大小关系是 ( )
A. a< b<1< c< d B. b< a< 1< d< c C. 1< a< b< c< d D. a< b<1< d< c 答案 B 解析 解法一:在 y 轴的右侧,指数函数的图象由下到上,底数依次增大. 由指数函数图象的升降,知 c> d>1, b< a< 1.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题2.1(2)
1.物体从静止开始下落,下落的距离与下落时间的平方成正比.已知开始下落的2 S 内,物体下落了 l 9.6 m ,求开始下落的3 S 内物体下落的距离.
2.某公司将进一批单价为8元的商品,若按10元/个销售,每天可卖出100 个;若销售价上涨l 元/个,则每天的销售量就减少l0个.
(1)设商品的销售价上涨x 元/个(0≤ x≤10,,x ∈N),每天的利润为y 元,试用列表法表示函数y=f(x);
(2)求销售价为l3元/个时每天的销售利润;
(3)如果销售利润为360元,那么销售价上涨了多少元?
3.设距地面高度x(单位:km)的气温为y(单位:℃),在距地面高度不超过 11 km 时,y 随着x 的增加而降低,且每升高l km ,大气温度降低6。
C ;高度超过ll km 时,气温可视为不变.设地面气温为22。
C ,试写出y=f(x)的 解析式,并分别求高度为3.5 km 和12 km 的气温.
4.建造一个容积为8 m 3、深为2m 的长方体形状的无盖水池,已知池底和池壁的造价分别为120元/m 2和80元/m 2,求总造价y(单位:元)关于底面 一边长x(单位:m)的函数解析式,并指出该函数的定义域.
5.画出函数f (x )=-x 2+x+1(一1≤x ≤1)的图象,并根据图象回答下列问题: (1)若一l≤x 1
〈x 2 ≤ 2
1 ,试比较f(x 1)与f(x 2)的大小; ‘
(2)是否存在x 。
∈[-1,1],使得f(x 0)= -2
6.已知A={1,2,3,4),B={1,3,5),试写出从A 到B 的两个函数
7已知函数⎩⎨⎧≥=0
x x 0x x x f 2〈,,)(试求,f(2).f(f(-2))的值. 8.画出函数Y=x 3
,(x ∈{2, -1. 5,一l ,一0.5,0,0.5,1,1.5,2})的图象.
9.某人去上班,先跑步,后步行.如果y 表示该人离单位的距离,x 表示出发后的时问,那么下列图象中符合此人走法的是( ).
10.请写出3个不同的函数y=f(x)的解析式,满足 f(1)=1,f(2)=4.
11.已知某皮鞋厂 一天的生产成本C(单位:元)与生产数量n(单位:双)之问 的函数关系式是C=4 000+50n .
(1)求一天生产1 000双皮鞋的成本;
(2)如果某天的生产成本是48 000元,那么这一天生产了多少双皮鞋?
(3)若每双皮鞋的售价为90元,且生产的皮鞋全部售出,试写出这一天的利润P 关于这一天生产数量n 的函数关系式,并求出每天至少生产多少皮鞋,才能不亏本。
12.2006年11月15日起,国内投寄首重100 g 以内的外埠信函的邮资标准是:每封信的重量不超过20 g 付邮资120分,超过20 g 而不超过40 g 付邮资240 分,超过40g 而不
超过60 g付邮资360分,依此类推.试画出每封不超过90 g 的信函应付邮资y(单位:分)与信函的重量x(单位:g)之削的函数关系的图象.
13.(开放题)已知一个函数的解析式为y=x,它的值域为[1,4],这样的函数有多少个?试写出其中两个函数.。
