12、小学奥数——转换法
12、小学奥数——转换法

小学奥数——转换法解答应用题时,通过转换(即转化)题中的情节,分析问题的角度、数据……从而较快找到解题思路,或简化解题过程的解题方法叫做转换法。
(一)转换题中的情节转换题中的情节是运用联想改变原题的某个情节,使题目变得易于解答。
1、一堆煤,上午运走它的72,上午运走它的72,下午运走余下的31还多6吨,最后剩下14吨。
这堆煤原来有多少吨?解:题中“下午运走余下的31还多6吨”,我们把这一情节变换为,下午正好运走余下的31,则最后剩下的煤是:14+6=20(吨)这20吨正好是余下的32,所以余下的的煤是:20÷32=30(吨) 30吨所对应的分率是:1-72=75 这堆煤原来的吨数是:30÷75=42(吨) 答略。
2、一项工程,甲、乙两队合做要用12天完成。
如果甲队先独做16天,余下的再由乙队独做6天完成。
如果全部工程由甲队独做,要用几天完成?解:求甲队独做要用几天完成全部工程,得先求出甲队的工作效率。
可是题中已知的是甲、乙合做要用的时间,和甲、乙一前一后独做的时间,很难求出甲的工作效率。
如果将“一前一后独做”这一情节变换为“先合做,后独做”就便于解题了。
可这样设想,从甲队的工作量中划出6天的工作量与乙队6天的工作量合并起来,也就是假定两队曾经合做了6天。
情节这样变动后,原题就变换成:一项工程,甲、乙两队合做要用12天完成,这项工程先由甲乙两队合做6天后,余下的工程由甲队单独做10天完成。
如果全部工程由甲队独做要用几天完成?这样就很容易求出甲队的工作效率是:(1-121×6)÷10=21÷10=201 甲队独做完成的时间是:1÷201=20(天) 答略。
(二)转换看问题的角度解应用题时,如果看问题的角度不适当就很难解出题。
如果转换看问题的角度,把原来从正面看问题转换为从侧面看或从反面看,把这一数量转换为另一数量进行分析,就可能找到解题思路。
四年级奥数之等价转换(含答案)

四年级奥数之等价转换(含答案)
介绍
本文档旨在介绍四年级奥数中的等价转换概念,并提供相关练
题和答案。
等价转换是指将数学问题中的数字、计量单位、图形等
以不同形式呈现,而其数值和含义保持不变的操作。
等价转换的概念
等价转换是数学问题中常用的策略之一,它能够使问题的解决
更加灵活和多样化。
通过等价转换,我们可以将问题中的数值、符
号或单位转换成其他等价的形式,从而更好地理解问题和解决问题。
例子
以下是一些等价转换的例子:
数字转换
1. 将10写成5+5的形式。
2. 将20写成10*2的形式。
计量单位转换
1. 将4千克转换为4000克。
2. 将3小时转换为180分钟。
图形转换
1. 将一个正方形转换为四个等边三角形的形式。
2. 将一个长方形转换为两个等面积的正方形的形式。
练题
请完成以下练题,并在下方标注答案:
1. 将15写成10+5的形式。
答案:15 = 10 + 5
2. 将30写成3*10的形式。
答案:30 = 3 * 10
3. 将6千克转换为6000克。
答案:6千克 = 6000克
4. 将4小时转换为240分钟。
答案:4小时 = 240分钟
5. 将一个长方形转换为两个等面积的正方形的形式。
答案:一个长方形 = 两个等面积的正方形
总结
等价转换是四年级奥数中常用的策略,通过将数值、符号或单位以不同形式呈现,我们可以更好地理解和解决数学问题。
希望这份文档对您有所帮助!。
六年级奥数培优 几何图形教案之等面积转换法
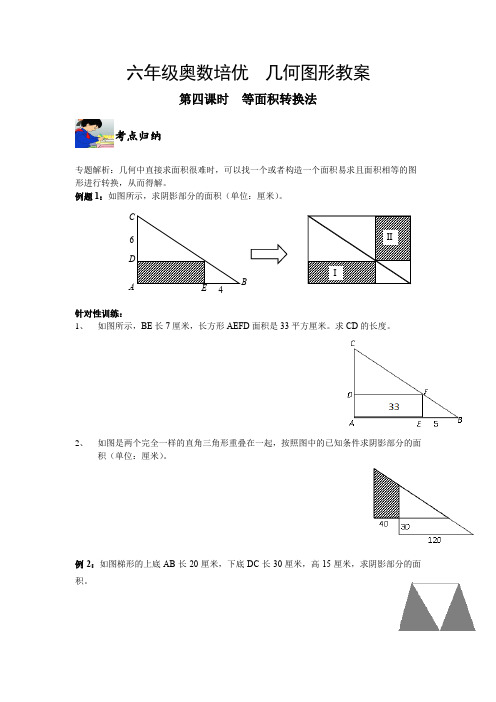
六年级奥数培优 几何图形教案第四课时 等面积转换法专题解析:几何中直接求面积很难时,可以找一个或者构造一个面积易求且面积相等的图形进行转换,从而得解。
例题1:如图所示,求阴影部分的面积(单位:厘米)。
针对性训练:1、 如图所示,BE 长7厘米,长方形AEFD 面积是33平方厘米。
求CD 的长度。
2、 如图是两个完全一样的直角三角形重叠在一起,按照图中的已知条件求阴影部分的面积(单位:厘米)。
例2:如图梯形的上底AB 长20厘米,下底DC 长30厘米,高15厘米,求阴影部分的面积。
B46考点归纳针对性训练:1、如图,E是平行四边形ABCD底边BC的中点,阴影部分的面积是3.1平方厘米,则平行四边形的面积是多少平方厘米?2、如图,E、F分别是平行四边形ABCD相邻两边的中点,求阴影部分的面积(单位:厘米)?3、如图,已知四条线段的长分别是:AB=2cm,CE=6cm,CD=5cm,AF=4cm,并且有两个直角。
求四边形ABCD的面积。
例3:如图,已知AB=BC=6厘米,三角形BCE的面积比三角形ADE的面积大3平方厘米,则AD长是多少厘米?针对性训练:1、如图,四边形ABCG 、DEFG 是长方形,那么三角形BCM 的面积与三角形DEM 的面积之差是多少(单位:厘米)?2、 如图,三角形ABC 的面积为36平方厘米,延长BA 到E,D 是AC 的中点,A 是BE 的三等分点,求三角形ADE 的面积。
3、如图,在三角形ABC 中,DC:BC=2:5,BO:OE=4:1,求AE:EC 的比是多少?1、如图,由两个完全一样的直角三角重叠在一起,则阴影部分的面积为 。
(单位:厘米)2、图中,ABCD 是正方形,三角形DEF 面积比三角形ABF的自我检测面积大6平方厘米,CD长4厘米。
则DE的长度为厘米。
3、如图是一块长方形草地。
长方形长12米,宽8米。
中间有三条宽2米的道路,一条是长方形,另两条是平行四边形。
小学数学解决问题教学中“转化法”的运用初探

小学数学解决问题教学中“转化法”的运用初探
转化法是小学数学解决问题的一种重要方法,它是指通过进行适当的转化,将原问题
转化为易于理解和解决的问题,从而帮助学生更好地理解和解决数学问题。
在小学数学教学中,教师可以通过以下几种方式运用转化法:
1. 数量转化:将原问题中的数量进行转化,使得问题更加简单。
将“小明有3个苹果,小红有比小明多2个苹果,小红有几个苹果?”的问题转化为“小红和小明一共有几个苹果?”的问题,进行简单的加法运算就可以解决。
2. 单位转化:将问题中的单位进行转化,使得问题更加明了。
将“一条绳子有多长?”的问题转化为“一米绳子有多少厘米?”的问题,通过将单位从米转化为厘米,将
问题转化为了一个更加熟悉且易于计算的问题。
4. 分类转化:将问题中的对象进行分类,使得问题更加简单。
将“连续10天每天读
1本书,一共读了多少本书?”的问题转化为“每天读了多少本书,最后乘以10?”的问题,通过将对象进行分类,问题的解决变得更加直观。
5. 数学模型转化:将实际问题转化为数学模型,使得问题的解决更加规范。
将“小
明买了3个苹果,每个苹果5元,他用了多少钱?”的问题转化为“3乘以5等于多少?”的问题,通过将实际问题转化为数学模型,问题的解决变得更加简单。
通过运用转化法,可以帮助学生更好地理解和解决数学问题,提高他们的问题解决能
力和数学思维能力。
在教学中,教师可以通过提问的方式引导学生进行思考和转化,培养
学生的转化能力和创造力。
教师还可以设计一些适合学生的练习和活动,让学生通过实际
操作来体验转化法的运用,进一步提高他们的问题解决能力。
六年级下册奥数讲义-奥数方法:类比转化法

我们在碰到一些较难的应用题时,有时难以理清数量之间的种种关系。
这时可以转换一个角度去思考,问题也往往迎刃而解了。
这种把要解决的问题变换为另一个与之有关系的问题去解答的方法就是类比转换法。
类比转化的方向是变繁为简,变生疏为熟悉,变隐含为显现,化难为易。
转化的对象是题知中的条件或图形,有时甚至是整个问题。
解题思路包括:审题、找类比转化模型、解答三个步骤,其中寻找模型最为关键。
进行转化的方法有两种,一种是等价转换法,一种是不等价转换法。
其中等价转换法是把问题A转化成新问题B后,两个问题的答案完全一样,而不等价转化法则是原问题A与转化后的新问题B并不等价,但通过解答问题B,很容易就可以找到原问题A的答案。
[例1] 分数的分子和分母同时加上一个相同的数,使分数变成问:这个加上的数是多少?思路剖析本题的要求是要我们求分子和分母同加上什么数,使分数的分母是分子的5倍。
因为分子和分母不管加上什么数,它们的差(71-3=)68是不变的,所以,根据这一特点,我们一定会想起本题和年龄问题相类似。
例如,儿子今年6岁,父亲33岁,问几年以后父亲的年龄正是儿子的4倍。
儿子今年6岁,父亲33岁,父子俩年龄差为(33-6=)27岁,因为儿子长几岁,父亲也长几岁,他们的年龄差不变。
几年后父亲的年龄是儿子的4倍,27岁相当于几年后儿子年龄的(4—1=)3倍。
用除法即可求出几年后儿子的年龄是(33-6)÷(4-1)=9岁,9-6=3年,也就是3年后父亲的年龄是儿子年龄的4倍。
从这道年龄问题的解题方法中,可以类比出原题的解题方法。
原题的分母与分子的差是(71-3=)68,分子和分母加上同一个数后,使分数变成即分母是分子的5倍,58相当于新分子的(5-l=)4 倍,用除法可求出新分子,进而再求出分子、分母同加上的是什么数。
解答(71-3)÷(5-1)-3=68÷4-3=17-3=14答:这个加上的数是14。
小学数学解题方法——转化法(1)计算中的转化

1、计算中的转化法方法点一运用运算性质、运算定律进行转化例1 883+(117-68)方法指导根据加法的运算性质,去掉算式中的括号,然后先计算883+117,再用所得的和减去68。
正确解答883+(117-68)=883+117-68=1000-68=932例2 1300÷25方法指导本题可以运用商不变的性质简算。
被除数和除数同时扩大4倍,除数25扩大4倍后得到一个整百数,这样原式就转化为“(1300×4)÷(25×4)”。
正确解答1300÷25=(1300×4)÷(25×4)=5200÷100=52例3方法指导本题可以应用乘法分配律进行简算。
先把拆分成的形式,再计算。
正确解答例4 2×5×4×25×8×125方法指导根据乘法交换律和乘法结合律可以把原式进行转化。
原式=(2×5)×(4×25)×(8×125)。
正确解答2×5×4×25×8×125=(2×5)×(4×25)×(8×125)=10×100×1000=1000000例5方法指导本题可以根据乘法分配律进行转化。
先把本题转化为的形式,再计算。
正确解答例6 99999×99999方法指导本题可以应用乘法分配律简算。
99999接近100000,所以先把99999看作是(100000-1),然后根据乘法分配律计算。
正确解答99999×99999=99999×(100000-1)=99999×100000-99999×1=9999900000-99999=9999800001例7 3333×3333+3333×6667方法指导本题可以应用提取公因数(即乘法分配律的逆运算)的方法进行转化凑整,两个乘法算式中都有3333,根据提取公因数的方法,原式=3333×(3333+6667)。
小学数学奥林匹克辅导及练习转化法(含答案)-.doc

转化法在解决一个数学问题时,常会出现一个题内有两个或两个以上的标准量,这就需要我们先统一标准(把所有各数量都用统一的标准来表示),从而使问题得到解决。
这种转化的思想在今后学习中会经常遇到。
(一)例题解析:例1. 学校食堂买来4把炒勺,5个高压锅共付832元,已知每个高压锅的价钱是炒勺的12倍,每个高压锅和每个炒勺各多少元?分析与解答:这个832元是4个炒勺和5个高压锅两种商品的总钱数。
如果是一种商品很容易解答,根据“总价÷数量=单价”可直接求出。
根据每个高压锅的钱数是炒勺的12倍,可以把“5个高压锅”转化成炒勺。
5个高压锅相当于(个)炒勺,那么832元就和(个)炒勺相对应。
列式:(个)(个)(元)(元)答:每个高压锅156元,每个炒勺13元。
例2. 用大小两辆汽车运煤,大汽车运了9次,小汽车运了10次,一共运了132吨,大汽车3次运的煤等于小汽车4次运的,大、小汽车的载重量各是多少吨?分析与解答:题目中“132吨”是由两辆大小不同的汽车运的,通过大、小汽车之间的关系,把“两辆”转化成“一辆”,问题便容易解决。
大汽车3次运的等于小汽车运4次的,那么大汽车9次运的就等于小汽车12次运的。
即:大车3次=小车4次大车9次+小车10次=132吨小车12次+小车10次=132吨这132吨相当于小汽车(12+10=)22次运的小汽车:(吨)大汽车:(吨)答:大汽车每次运8吨,小汽车每次运6吨。
例3. 篮球、排球、足球共83个,其中篮球数目是排球的2倍,排球比足球多5个,则篮球有多少个?分析与解答:三种球的数量关系是通过“倍数句”和“差比句”表现出来的,但倍数句是以排球个数为标准的,差比句是以足球个数为标准的,标准量不唯一,需要统一标准。
把足球少的5个补上,总个数就是88个,正好是排球个数的4倍(个)(个)(个)答:篮球有44个。
例4. 甲、乙、丙、丁与小华这五位同学下围棋,每两人不能多于一盘,已知甲、乙、丙、丁分别下了4、3、2、1盘,则小华下了多少盘?分析与解答:我们把这5个人用5个点来表示,两人下了棋,两人之间就连上一条线段。
小学奥数模块教程(五)转化法(一)

转化法(一)(2013.1.20五)有些数字谜问题按原来的说法往往难以解答,我们可以把题目的条件货问题换一种说法,或改变已知条件的组合,使问题转变的很容易解答,化难为易,化繁为简,这就是转化法的基本思路,本课我们主要研究已知条件的转化。
例1、学校组织学生去秋游,原计划用中巴若干辆,每辆车做25人,但有5名学生无座位;后来增加70名学生,学校决定改用大客车,每辆车可坐40人,但比中巴少一辆,结果还有5个空座位,问原计划有多少学生去秋游?用中巴几辆?答案:原计划有205个学生去秋游,用中巴8辆。
例2、甲乙两个书架,甲书架上书的册数是乙书架上的7倍,如果从甲书架上取出19册,而往乙书架上放15册,这时甲书架上书的册数是乙书架的3倍。
甲乙书架上原来有书多少册?答案:甲书架原有书112册,乙书架原有书16册。
例3、赵老师带领99名学生,要在操场的周围种100棵树。
赵老师先种了一颗,然后对同学们说:“男生每人种两颗,女生两人种一颗”。
说完,他把树苗分给了大家,正好按要求把树苗分完。
求有多少男生,多少女生?答案:男生有33人,女生有66人。
例4、某工程甲队独做50天可以完成,乙队独做75天可以完成,现在两队同时开工合作,但是中途乙队因另有任务调离了若干天,开工后40天才把这项工程做完,乙队中途离开了多少天?答案:乙队中途离开了25天。
例5、甲乙两人绕一长为80米,宽为60米的长方形操场跑步,甲从A,乙从B同时出发相向而跑,结果第一次在E处相遇,E离A处30米,(如图)问:甲乙能否再次在E处相遇?如果能,那是甲乙第几次相遇?答案:甲乙能在E处再次相遇,这是他们第9次相遇。
练习1、小明从家去学校,如果每分钟走80米,能在课前6分钟到校,如果每分钟走50米,就要迟到3分钟,那么小明的家到学校的路程多远?2、五六年级同学参加植树劳动,原定六年级的任务是五年级的4倍,后来考虑六年级任务太重,调拨了50棵树给五年级,这时六年级的任务是五年级的1.5倍。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小学奥数——转换法
解答应用题时,通过转换(即转化)题中的情节,分析问题的角度、数据……从而较快找到解题思路,或简化解题过程的解题方法叫做转换法。
(一)转换题中的情节
转换题中的情节是运用联想改变原题的某个情节,使题目变得易于解答。
1、一堆煤,上午运走它的72,上午运走它的72,下午运走余下的3
1还多6吨,最后剩下14吨。
这堆煤原来有多少吨?
解:题中“下午运走余下的31还多6吨”,我们把这一情节变换为,下午正好运走余下的3
1,则最后剩下的煤是:14+6=20(吨)
这20吨正好是余下的32,所以余下的的煤是:20÷3
2=30(吨) 30吨所对应的分率是:1-72=7
5 这堆煤原来的吨数是:30÷7
5=42(吨) 答略。
2、一项工程,甲、乙两队合做要用12天完成。
如果甲队先独做16天,余下的再由乙队独做6天完成。
如果全部工程由甲队独做,要用几天完成?
解:求甲队独做要用几天完成全部工程,得先求出甲队的工作效率。
可是题中已知的是甲、乙合做要用的时间,和甲、乙一前一后独做的时间,很难求出甲的工作效率。
如果将“一前一后独做”这一情节变换为“先合做,后独做”就便于解题了。
可这样设想,从甲队的工作量中划出6天的工作量与乙队6天的工作量合并起来,也就是假定两队曾经合做了6天。
情节这样变动后,原题就变换成:
一项工程,甲、乙两队合做要用12天完成,这项工程先由甲乙两队合做6天后,余下的工程由甲队单独做10天完成。
如果全部工程由甲队独做要用几天完成?
这样就很容易求出甲队的工作效率是:(1-121×6)÷10=21÷10=20
1 甲队独做完成的时间是:1÷20
1=20(天) 答略。
(二)转换看问题的角度
解应用题时,如果看问题的角度不适当就很难解出题。
如果转换看问题的角度,把原来从正面看问题转换为从侧面看或从反面看,把这一数量转换为另一数量进行分析,就可能找到解题思路。
1、某厂有工人1120名,其中女工占73,后来又招进一批女工,这时女工占总人数的15
7,求后来招进女工多少名?
一般都沿着女工占总人数的分率去寻找与之相对应的具体人数,但这样往往会误入歧途,难以找到正确答案。
不如根据女工所占分率,换一个角度,想一想男工的情况。
开始,女工占总人数的73,则男工占总人数的:1-73=7
4 男工的具体人数是:1120×7
4=640(人) 后来,招进一批女工,女工人数便占全体工人总数的15
7, 男工人数便占总人数的:1-157=15
8 这时全厂工人的总人数是:640÷15
8=1200(人) 后来招进女工的总人数是:1200-1120=80(人)
答略。
2、如图:求图中阴影部分的面积。
(单位:厘米)
解:如果直接计算图中阴影部分的面积,几乎是不可能的。
如果把角度转换为,从大扇形面积减去右面空白处的面积,就容易求出阴影部分的面积了。
41×3.14×16×16-(16×10-4
1×3.14×10×10) =200.96-81.5
=119.46(平方厘米)
答:阴影部分的面积是119.46平方厘米。
(三)转换题中的数据
转换题中的数据就是将题中已知的数据进行等价变换,从而协调各个数据之间的关系。
1、两辆汽车同时从相距465千米的两地相对开出,4.5小时后两车还相距120千米。
一辆汽车每小时行37千米。
另一辆汽车每小时行多少千米?
解:如果两地的距离减少120千米,两车经过4.5小时正好相遇,两车4.5小时行的路程是: 465-120=345(千米)
两车的速度之和是:345÷4.5=3
276(千米/小时) 另一辆汽车每小时行的路程是:3276-37=3
239(千米/小时) 综合算式:
(465-120)÷4.5-37
=345÷4.5-37 =3
276-37=
3
239(千米/小时) 答:另一辆汽车每小时行3239
千米。
2、某校三天共种70棵树,第一天种的棵树是第二天种的棵树是第三天的
6
5,三天各种多少棵树? 解:如果从分数角度分析,不易找出数量间的关系。
如果把分数转换为比来分析,就会得出,第一天与第二天种的棵数的比是3∶5,第二天与第三天种的棵数比是5∶6。
所以,第一、二、三天种的棵数的比是3∶5∶6。
第一天种:70×6
533++=15(棵) 第二天种:70×6
535++=25(棵) 第三天种:70×6
536++=30(棵) 答略。
(四)转换为统一标准
当题中两个或几个数量的单位“1”不统一,不便于解答时,如把某个数量作为标准单位“1”,把其他数量转化为以它为标准的分率,就会突破障碍,顺利解题。
1、甲、乙、丙、丁四人合买一批化肥。
甲付的钱是其他人所付钱数之 和的2
1,乙付的钱是其他人所付钱数之和的31,丙付的钱数是其他人所付钱数之和 的4
1,丁付260元,问:买这批化肥用了多少钱?
解:把甲、乙、丙、丁所付钱数统一为以总数量作为标准量的分率。
由 甲付的钱是其他人所付钱数之和的21可知,其他人所付钱数之和是:“1”,总数量是(1+2
1),甲乙丙所付的钱数分别占总数量的31、41、51。
丁所付的260元占总数量的(1-31-41-5
1)。
所以,买这批化肥用的钱数是: 260÷(1-31-41-51)=260÷60
13=1200(元) 答:略
2、某商店原有彩电是黑白电视机的43,黑白电视机卖出52台后,它的台数是彩色电视机的10
9,这个商店原来有黑白电视机和彩色电视机各多少台? 解:题中43和10
9的单位“1”不统一,不便于解题,因此彩色电视机的台数没有发生变化,我们以彩色电视机的台数作为单位“1”,这样就可以把“彩色电视机是黑白电视机的4
3”转化为“黑白电视机是彩色电视机的1÷43=3
4。
”两种电视机的单位“1”统一了,就容易看出,黑白电视机卖出52台时它的分率从34减少到109。
52台的对应分率是34-109=3013。
所以,彩色电视机的台数是:
52÷(1÷43-10
9)=120(台) 黑白电视机的台数是:
120÷43=160(台)或:120×10
9+52=160(台) 答:略
(五)转换隐蔽条件为明显条件
1、甲、乙二人分别从A 、B 两地同时出发,相向而行,在离B 点18千米的地方相遇。
相遇后二人继续往前行,甲到B 地和乙到A 地立即返回,在离A 地8千米的地方又相遇。
求A 、B 两地相距多少千米?
解:解答此题的条件十分隐蔽。
借助下图分析问题,可将隐蔽条件转换为明显条件。
(1)从开始出发到二人第一次相遇,甲、乙共同走完一个全程的路程,其中乙走了18千米。
这就
是说甲、乙二人共同走完一个全程的路程时乙走18千米,若共同走完三个全程,那么乙就走18×3千米的路程。
(2)甲、乙第二次相遇时,二人走了三个全程的路程,而乙走了一个全程加8千米。
(3)乙走的一个全程加8千米应等于18×3千米,所以,A 、B 两地的距离是:
18×3-8=46(千米)
答:甲乙两地相距46千米。
2、有两袋大米共重220千克,甲袋大米吃去31,乙袋大米吃去2
1时,甲袋剩下的米是乙的剩下米的5
31倍,求甲乙两袋米原来各有多少千克?
解:甲袋米吃去31,剩下(1-31);乙袋米吃去21,剩下(1-21)。
甲袋米的(1-31)是乙袋米的(1-2
1)的531倍,即甲袋米的32是乙袋米的21的5
31倍。
甲袋米的32是乙袋米的21的531倍,甲袋米的32=乙袋米×21×531。
即甲的32=乙的(21×5
8),甲的32等于乙的5
4。
甲袋米的重量是乙袋米重量的54÷32=5
11倍。
所以:220÷(1+5
11)=100(千克)……………………乙袋米重 220-100=120(千克)……………………甲袋米重
答略。
