和、差的变化规律
(完整版)和差积商的变化规律
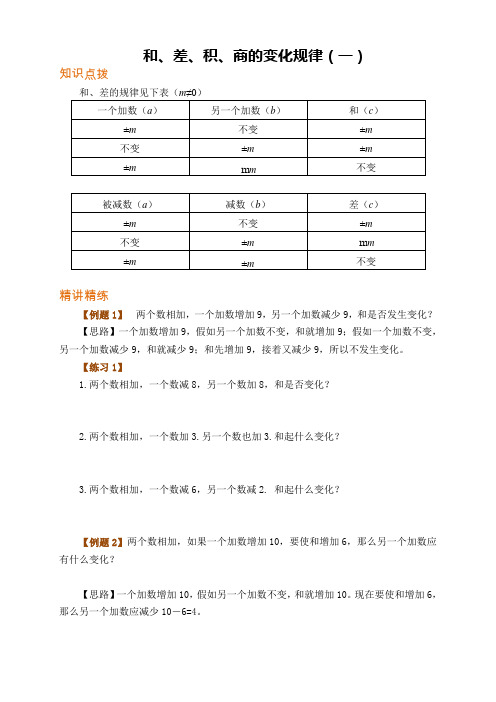
和、差、积、商的变化规律(一)知识点拨和、差的规律见下表(m≠0)精讲精练【例题1】两个数相加,一个加数增加9,另一个加数减少9,和是否发生变化?【思路】一个加数增加9,假如另一个加数不变,和就增加9;假如一个加数不变,另一个加数减少9,和就减少9;和先增加9,接着又减少9,所以不发生变化。
【练习1】1.两个数相加,一个数减8,另一个数加8,和是否变化?2.两个数相加,一个数加3.另一个数也加3.和起什么变化?3.两个数相加,一个数减6,另一个数减2. 和起什么变化?【例题2】两个数相加,如果一个加数增加10,要使和增加6,那么另一个加数应有什么变化?【思路】一个加数增加10,假如另一个加数不变,和就增加10。
现在要使和增加6,那么另一个加数应减少10-6=4。
【练习2】1.两个数相加,如果一个加数增加8,要使和增加15,另一个加数应有什么变化?2.两个数相加,如果一个加数增加8,要使和减少15,另一个加数应有什么变化?3.两个数相加,如果一个加数减少8,要使和减少8,另一个加数应有什么变化?【例题3】两数相减,如果被减数增加8,减数也增加8,差是否起变化?【思路】被减数增加8,假如减数不变,差就增加8;假如被减数不变,减数增加8,差就减少8。
两个数的差先增加8,接着又减少8,所以不起什么变化。
【练习3】1.两数相减,被减数减少6,减数也减少6,差是否起变化?2.两数相减,被减数增加12.减数减少12.差起什么变化?3.两数相减,被减数减少10,减数增加10,差起什么变化?【例题4】两数相乘,如果一个因数扩大8倍,另一个因数缩小2倍,积将有什么变化?【思路】如果一个因数扩大8倍,另一个因数不变,积将扩大8倍;如果一个因数不变,另一个因数缩小2倍,积将缩小2倍。
积先扩大8倍又缩小2倍,因此,积扩大了8÷2=4倍。
【练习4】1.两数相乘,如果一个因数缩小4倍,另一个因数扩大4倍,和是否起变化?2.两数相乘,如果一个因数扩大3倍,另一个因数缩小12倍,积将有什么变化?3.两数相乘,如果一个因数扩大3倍,另一个因数扩大6倍,积将有什么变化?【例题5】两数相除,如果被除数扩大4倍,除数缩小2倍,商将怎样变化?【思路】如果被除数扩大4倍,除数不变,商就扩大4倍;如果被除数不变,除数缩小2倍,商就扩大2倍。
小学数学四则运算的变化规则(和差积商变化规律)

四则运算的变化规则一、加法的变化规则(1)加法公式:加数+ 加数= 和加数= 和—另一个加数(2)加法的变化规则有:(一)如果一个加数增加几,另一个加数不变,那么和也增加几。
例如:13+5=18(13+2)+5=18+2题型1小丽在做一道加法题,一个加数十位上的4看作了7,个位上的5看作了2,算得的和是87。
正确的和是多少?一个加数十位4——7,个位5——2 增加 72-45=27另一个加数不变正确的和增加27即正确的和+27=87 => 正确的和=87-27=60(二)如果一个加数减少几,另一个加数不变,那么和也减少几。
例如:28+16=44(28-12)+16=44-12题型1小强在计算加法时,把一个加数十位上的7错写成1,把个位上的8错写成0,所得的和是285。
正确的和是多少?一个加数十位7——1,个位8——0 减少 78-10=68另一个加数不变正确的和减少68即正确的和-68=285 => 正确的和=285+68=353题型2两个数相加,一个加数减少29,另一个加数不变,和将有什么变化?一个加数减少29另一个加数不变和减少29题型3两个数相加,和是100,一个加数减少48,另一个加数不变,现在和是多少?一个加数减少48另一个加数不变和减少48即现在的和=100-48=52(三)如果一个加数增加几,另一个加数减少同样的几,那么和不变。
例如:112+23=135(112+3)+(23-3)=135题型1:两个加数的和是378,其中一个加数增加245,另一个加数减少245,现在这两个加数的和是(378 )。
题型2:一个加数增加6,要使和保持不变,另一个加数应(减少6 )。
(四)如果一个加数增加几,另一个加数增加另一个几,那么和增加了(几+另一个几)。
例如:35+48=83(35+12)+(48+5)=83+(12+5)题型1:小明在计算加法时,把一个加数十位上的0错写成8,把另一个加数个位上的6错写成9,所得的和是532。
小学数学四则运算的变化规则(和差积商变化规律)

四则运算的变化规则一、加法的变化规则(1)加法公式:加数+ 加数= 和加数= 和—另一个加数(2)加法的变化规则有:(一)如果一个加数增加几,另一个加数不变,那么和也增加几。
例如:13+5=18(13+2)+5=18+2题型1小丽在做一道加法题,一个加数十位上的4看作了7,个位上的5看作了2,算得的和是87。
正确的和是多少?一个加数十位4——7,个位5——2 增加 72-45=27另一个加数不变正确的和增加27即正确的和+27=87 => 正确的和=87-27=60(二)如果一个加数减少几,另一个加数不变,那么和也减少几。
例如:28+16=44(28-12)+16=44-12题型1小强在计算加法时,把一个加数十位上的7错写成1,把个位上的8错写成0,所得的和是285。
正确的和是多少?一个加数十位7——1,个位8——0 减少 78-10=68另一个加数不变正确的和减少68即正确的和-68=285 => 正确的和=285+68=353题型2两个数相加,一个加数减少29,另一个加数不变,和将有什么变化?一个加数减少29另一个加数不变和减少29题型3两个数相加,和是100,一个加数减少48,另一个加数不变,现在和是多少?一个加数减少48另一个加数不变和减少48即现在的和=100-48=52(三)如果一个加数增加几,另一个加数减少同样的几,那么和不变。
例如:112+23=135(112+3)+(23-3)=135题型1:两个加数的和是378,其中一个加数增加245,另一个加数减少245,现在这两个加数的和是(378 )。
题型2:一个加数增加6,要使和保持不变,另一个加数应(减少6 )。
(四)如果一个加数增加几,另一个加数增加另一个几,那么和增加了(几+另一个几)。
例如:35+48=83(35+12)+(48+5)=83+(12+5)题型1:小明在计算加法时,把一个加数十位上的0错写成8,把另一个加数个位上的6错写成9,所得的和是532。
和、差、积、商变化规律

(a≥b且a≥m,b>m)。
例如:
500-200=300→(500+100)-(200+100)=300,
500-200=300→(500-100)-(200-100)=300
积的变化规律:
积的变化规律
字母表示及举例
如果一个因数扩大到原来的几倍或缩小到原来的几分之一,另一个因数不变,那么它们的积也相应地扩大到
或(a÷n)÷b=c÷n
(a、c都是n的倍数)。
例如:
40÷5=8→ (40×5)÷5=8×5
或(40÷4)÷5=8÷4
如果被除数不变,除数扩大到原来的几倍或缩小到原来的几分之一,那么它们的商反而缩小到原来的几分之一或扩大到原来的几倍
用字母表示:
a÷b=c→ a÷(b×n)=c÷n
(a是b×n的倍数)
或a÷(b÷n)=c×n
(b是n的倍数)
例如:
120÷20=6→120÷(20×3)=6÷3
或120÷(20÷2)=6×2
商不变的性质:
在除法里,被除数和除数同时乘或除以相同的数(0除外),商不变。这个性质
通常被称为“商不变的性质”。
用字母表示:如果a÷b=c→ (a×n)÷(b×n)=c(n≠0),
减少)同一个数
字母表示:
a-b=c →(a+m)-b=c+m,
(a-m)-b=c-m(a≥m)。
例如:
100-60=40→(100+50) -60=40+50,
100-60=40→(100-10)-60=40-10
如果被减数不变,减数增加(或减
少)一个数,那么它们的差反而减
少(或增加)同一个数
和差积商的变化规律

和差积商的变化规律和差积商是数学中常见的运算方式,它们描述了数值之间的关系和变化规律。
在数学中,和表示两个数值的总和,差表示两个数值之间的差异,积表示两个数值的乘积,商表示两个数值的比率。
首先,我们来讨论和的变化规律。
当我们将两个数相加时,和的值会随着加数的增加而增大。
例如,1 + 2 = 3,2 + 3 = 5,3 + 4 = 7,可以看出和的值是逐渐增大的。
这是因为加法是一种累积运算,每次加上一个数,和的值就会增加相应的数量。
接下来,我们来探讨差的变化规律。
差表示两个数之间的差异,当我们计算两个数的差时,差的值会随着被减数的增加而减小。
例如,3 - 2 = 1,4 - 3 = 1,5 - 4 = 1,可以看出差的值是不断减小的。
这是因为减法是一种递减运算,每次减去一个数,差的值就会减少相应的数量。
然后,我们来研究积的变化规律。
积表示两个数相乘的结果,当我们计算两个数的积时,积的值会随着乘数的增加而增大。
例如,2 × 3 = 6,3 × 4 = 12,4 × 5 = 20,可以看出积的值是逐渐增大的。
这是因为乘法是一种倍增运算,每次乘上一个数,积的值就会增加相应的倍数。
最后,我们来讨论商的变化规律。
商表示两个数之间的比率,当我们计算两个数的商时,商的值会随着被除数的增加而减小。
例如,6 ÷ 2 = 3,12 ÷ 3 = 4,20 ÷ 4 = 5,可以看出商的值是不断减小的。
这是因为除法是一种递减运算,每次除以一个数,商的值就会减少相应的倍数。
综上所述,和差积商描述了数值之间的关系和变化规律。
和的值随着加数的增加而增大,差的值随着被减数的增加而减小,积的值随着乘数的增加而增大,商的值随着被除数的增加而减小。
这些变化规律在实际生活中有着广泛的应用,在解决问题和进行计算时都起到了重要作用。
四年级等差数列 (2)

四年级等差数列【专题导引】和、差的变化规律见下表(m ≠0)一个加数(a ) 另一个加数(b ) 和(c ) ±m 不变 ±m 不变 ±m±m ±m m 不变【典型例题】【C 1】两个数相加,一个加数增加3,另一个加数减少3,和是否会起变化?【试一试】1、两个数相加,一个加数增加5,另一个加数减少5,和是否会起变化?2、两个数相加,一个加数减少6,另一个加数增加2,和是否会起变化?【C 2】如果a -b=20,那么a -(b -2)=20+( )。
【试一试】1、如果a -b=18,那么(a+2)-b=18+( )。
2、如果a -b=18,那么(a -2)-b=18-( )。
【B 1】两个数相加,一个加数减少10,另一个加数增加10,和是否会起变化?【试一试】被减数(a )减数(b ) 差(c ) ±m 不变 ±m 不变 ±m m ±m±m不变 ++1、两个数相加,一个加数增加15,另一个加数减少15,和是否会起变化?2、两个数相加,一个加数增加6,另一个加数也增加6,和是否会起变化?】两个数相加,如果一个加数减少8,要使和增加8,另一个加数应有什么变化?【B2【试一试】1、两个数相加,如果一个加数增加9,要使和增加17,另一个加数应有什么变化?2、两个数相加,如果一个加数增加11,要使和减少11,另一个加数应有什么变化?【B】两数相减,如果被减数减少2,减数也减少2,差是否会起变化?3【试一试】(1)两数相减,如果被减数增加30,减数也增加30,差是否会起变化?(2)两数相减,如果被减数增加23,减数减少23,差是否会起变化?【A】两数相减,如果被减数增加20,要使差减少16,减数应有什么变化?1【试一试】(1)两数相减,被减数减少12,要使差增加8,减数应有什么变化?(2)两数相减,被减数减少36,要使差减少40,减数应有什么变化?】被减数、减数、差相加得2076,差是减数的一半。
和与差的变化规律.(精选)

和与差的变化规律一、和的变化规律(一)和不变的性质:一个加数增加几,另一个加数减少几,和不变举例:4+5=9 如果(4+3)+(5-3)则和等于9,不变(二)和的变化规律:(1)一个加数增加几,另一个加数也增加几,和增加它们的和举例:4+5=9 如果(4+3)+(5+4)则和增加3+4=7,即和9+7=16(2)一个加数减少几,另一个加数也减少几,和减少它们的和举例:4+5=9 如果(4-3)+(5-4)则和减少3+4=7,即和9-2=2 (3)一个加数增加几,另一个加数减少几,如果增加的多,则和增加,如果减少的多,则和减少举例:4+5=9 如果(4+3)+(5-2)则和增加3-2=1,即和9+1=10举例:4+5=9 如果(4+3)+(5-4)则和减少4-3=1,即和9-1=8二、差的变化规律(一)差不变的性质:被减数和减数同时增加或减少相同的数量,则差不变(二)差的变化规律:(1)被减数增加几,减数不变,则差增加几(2)被减数增加几,减数不变,则差减少几(3)被减数不变,减少增加几,则差反而减少几(4)被减数不变,减数减少几,则差反而增加几(5)被减数增加几,减数增加几,如果被减数增加的多,则差增加,如果减数增加的多,则差减少举例:9-5=4 如果(9+3)-(5+2)则差增加3-2=1,即差4+1=5举例:9-5=4 如果(9+3)-(5+5)则差减少5-3=2,即差4-2=2 (6)被减数减少几,减数减少几,如果被减数减少的多,则差减少,如果减数减少的多,则差增加举例:9-5=4 如果(9-3)-(5-2)则差减少3-2=1,即差4-1=3举例:9-5=4 如果(9-2)-(5-4)则差增加4-2=2,即差4+2=6最新文件仅供参考已改成word文本。
方便更改。
四年级和差变化规律

四年级和差变化规律
1、两个数相加,一个加数减少10,另一个加数增加10,和怎样变化?
2、两个加数相加,一个加数增加15,另一个加数减少15,和怎样变化?
3、两个数相加,一个加数增加12,另一个加数减少2,和有什么变化?
4、两个数相加,如果一个加数减少8,要使和增加8,另一个加数应怎样变化?
5、两数相加,如果一个加数增加9,要使和增加17,另一个加数应有什么变化?
6、两数相加,如果一个加数增加11,要使和减少11,另一个加数应有什么变化?
7、两数相加,如果一个加数减少16,要使和减少9,另一个加数应有什么变化?
8、两数相减,如果被减数减少10,减数也减少10,差怎样变化?
9、两数相减,如果被减数增加30,减数也增加30,差怎样变化?
10、两数相减,如果被减数增加23,减数减少23,差怎样变化?
11、两数相减,如果被减数减少18,减数增加18,差怎样变化?
12、两数相减,被减数增加20,要使差减少16,减数怎样变化?
13、两数相减,被减数减少12,要使差增加8,减数怎样变化?
14、两数相减,被减数减少36,要使差减少40,减数怎样变化?
15、两数相减,减数增加10,要使差减少15,被减数怎样变化?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
57+(356 )=413
257+( 156)=413
发展练习 一辆车从甲城开往乙城。在下表中填出 已行路程或剩下路程。
已行路程 ( km ) 剩下路程 ( km )
100 200
150 150
200 100
250 50
观察上表,你 发现了什么?
1、 一个加数减少10,另一个加数增加5, 和( 减少5 )。
780-123= 657
+10 +10 不变
780-123= 657
-20 -20 不变
790-133=(657) 780-123= 657
-20 不变 -20
760-103=( 657)
780-123= 657
不变 -20 +20
760-123=(637 )
780-103=(677)
两个数的差是185,这两个数同时减去126后,差 是( 185 )。
发展练习
填表。
小明父亲(岁) 小明(岁) 相差(岁)
35
10
40
15
45
20
25
25
观察上表,你 发现了什么?
25
拓展练习
在
里填合适的数字,使算式正确。
` 5
3 7
7
` 7
0
7
-2 9 5
- 7 3
2 4 2
3 3
被减数 减数
180 80 100Fra bibliotek280 180 100
380 280 100
480 380 100
差
被减数和减数(同时增加 或减少 同一个数 ), 差( 不变 )。
思考:1、如果被减数增加50,减数不变,差( 也增加50)
2、如果被减数减少23,减数不变,差( 也减少23 )
3、如果被减数不变,减数增加12,差( 反而减少12 ) 4、如果被减数不变,减数减少50,差( 反而增加50 )
308+107=( 415 )
1、一个加数增加13,另一个加数也增加13,和就 增加26 )。 ( 2、一个加数减少9,另一个加数也减少9,和就 ( 减少18 )。 3、一个加数增加20,另一个加数增加100,和就 ( 增加120 )。 4、一个加数增加35,另一个加数不变,和就 ( 增加35 )。 5、一个加数减少7,另一个加数增加18,和就 ( 增加11 )。 6、一个加数减少27,另一个加数不变,和就 减少27 )。 ( 7、一个加数增加15,另一个加数减少20,和 ( 减少5 )。
450+230 = 680
+5 -10 -5
450+ 230 = 680
-10
+20
+10
455+220=( 675 )
440+ 250=(690 )
2、一个加数增加20,另一个加数减少10, 和( 增加10 )。 3、一个加数减少30,另一个加数增加15, 和( 减少15 )。
加数 加数
10 300 310
20 400 420
30 500 530
40 600 640
和
两个数相加,第一个加数( 增加或减少一个数 ), 第二个加数( 增加 或减少 另一个数 ),和就 ( 增加 或减少 这两个数的和 )。
318+127= 445
+1 +1 +2
318+127= 445
-10 -20 -30
319+128=( 447 )
和 差的变化规律
START
表1 :
加数 加数 和 150 700 250 600 350 500 450 400
850
850
850
850
两个数相加,第一个加数(增加一个数 ), 第二个加数(减少同一个数),和 ( 不变 )。 157+ 256 =413 157+ 256 =413
-100 +100 不变 +100 -100 不变
