2019-2020年上海市复旦附中高三上开学考数学试卷及答案
2019届上海市复旦大学附属中学高三上学期10月月考数学试题(解析版)
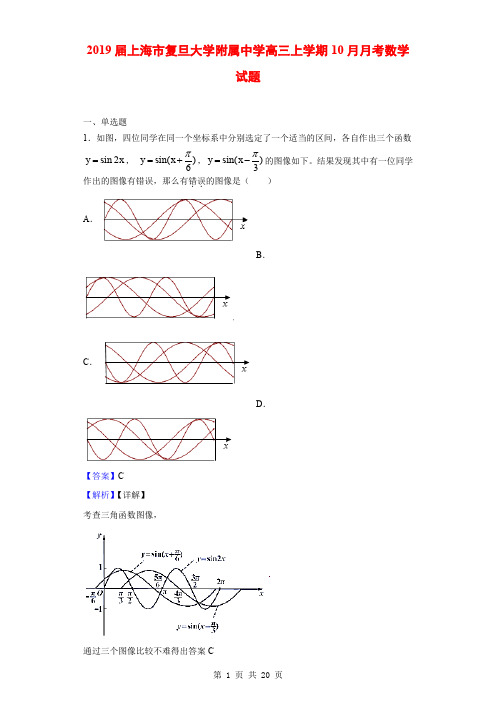
2019届上海市复旦大学附属中学高三上学期10月月考数学试题一、单选题1.如图,四位同学在同一个坐标系中分别选定了一个适当的区间,各自作出三个函数sin 2y x =, sin()6y x π=+,sin()3y x π=-的图像如下。
结果发现其中有一位同学作出的图像有错误,那么有错误..的图像是( ) A .B .C .D .【答案】C 【解析】【详解】 考查三角函数图像,通过三个图像比较不难得出答案C2.(2015新课标全国I 理科)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有A .14斛B .22斛C .36斛D .66斛【答案】B【解析】试题分析:设圆锥底面半径为r ,则,所以,所以米堆的体积为=,故堆放的米约为÷1.62≈22,故选B.【考点】圆锥的性质与圆锥的体积公式3.已知函数()12...201612 (2016)f x x x x x x x =+++++++-+-++-(x ∈R ),且集合2{|(2)(1)}M a f a a f a =--=+,则集合{()|}N f a a M =∈的元素个数有( ) A .2个 B .3个C .4个D .无数个【答案】D【解析】根据函数的几何意义可判断其为偶函数且在[]1,1x ∈-时,()f x C =(C 为常数),由此解出a 的范围,进而判断N 的元素个数即可 【详解】由题,()12...201612...2016f x x x x x x x =+++++++-+-++-的几何意义是:数轴上x 到点1,2,3,,2016±±±±的距离之和,则根据绝对值的几何意义可知()()f x f x -=,即()f x 是偶函数若2(2)(1)f a a f a --=+,则221a a a --=+或()221a a a --=-+,解得1a =-或3a =或1a =,同时,当[]1,1x ∈-时,()f x C =(C 为常数),则若2(2)(1)f a a f a --=+,满足2121111a a a ⎧-≤--≤⎨-≤+≤⎩即可,a ≤≤,{}11|1,322M a a ⎧⎪∴=≤≤⋃⎨⎪⎪⎩⎭∴{()|}N f a a M =∈的元素个数有无数个,故选:D 【点睛】本题考查函数的奇偶性,考查元素的个数,考查运算能力4.如图,长方形ABCD 的边2AB =,1BC =,O 是AB 的中点,点P 沿着边BC ,CD 与DA 运动,记BOP x ∠=.将动P 到A 、B 两点距离之和表示为x 的函数()f x ,则()y f x =的图像大致为( )A .B .C .D .【答案】B【解析】根据函数图象关系,利用排除法进行求解即可.解:当04x π≤≤时,tan ,BP x AP ===此时()tan f x x ,04x π≤≤,此时单调递增,当P 在CD 边上运动时,344ππ≤≤x 且2x π≠时, 如图所示,1tan tan()tan tan PQ POB POQ x POQ OQ OQπ∠=-∠==-∠=-=-, 1tan OQ x∴=-, 111,1tan tan PD AO OQ PC BO OQ x x∴=-=+=+=-,PA PB ∴+=当2x π=时,PA PB +=,当P 在DA 边上运动时,3,tan 4x PB x PA ππ≤≤+= 由对称性可知函数()f x 关于2x π=对称,且 42f f ππ⎛⎫⎛⎫>⎪ ⎪⎝⎭⎝⎭,且轨迹为非线型, 排除A ,C ,D , 故选:B . 【点睛】本题主要考查函数图象的识别和判断,根据条件先求出04x π≤≤时的解析式是解决本二、填空题5.集合{}0,2,A a =,{}21,B a =,若{}0,1,2,4,16A B ⋃=,则a 的值为 _____.【答案】4【解析】根据题意,由并集的计算方法,结合a 与a 2的关系,易得 2164a a ⎧=⎨=⎩,即可得答案. 【详解】∵A={0,2,a},B={1,a 2},A ∪B={0,1,2,4,16}∴2164a a ⎧=⎨=⎩ ∴a=4, 故答案为:4. 【点睛】本题考查了集合的并集运算,并用观察法得到相对应的元素,从而求得答案,本题属于容易题. 6.若复数312a ii++(a R ∈,i 为虚数单位)是纯虚数,则实数a 的值为_____________.【答案】6-【解析】解:因为复数312a ii++(a R ∈,i 为虚数单位)是纯虚数,故3(3)(12)6(32)6012556a i a i i a a ia i a ++-++-==∴+=+∴=- 7.线性方程组21{202x z x y y z -=-+=+=的增广矩阵是_________________.【答案】201112000112--⎛⎫ ⎪⎪ ⎪⎝⎭【解析】【详解】方程组21{202x z x y y z -=-+=+=化为20120002x y z x y z x y z +⨯-=-⎧⎪++⨯=⎨⎪⨯++=⎩,所以性方程组21{202x z x y y z -=-+=+=的增广矩阵是201112000112--⎛⎫⎪⎪ ⎪⎝⎭. 8.4(的展开式中33x y 的系数为 . 【答案】6【解析】224(1)c -=6。
上海市复旦附中2019-2020高三9月综合练习一数学

复旦附中高三数学综合练习(一)一. 填空题1. 在5(12)x +的展开式中,2x 的系数为 (用数字作答)2. 已知全集U =R ,集合{|2}A x x =<,{|0}B x x =<,那么U A C B =I3. 函数y =的定义域是4. 函数y (1x ≤-)的反函数是5. 不等式20ax bx c ++>的解集是1(,3)2-,则不等式20cx bx a ++<的解集为 6. 若集合2{|60}M x x x =+-=,{|10}N x ax =-=,且N M ⊆,则实数a 的值为7. 若函数234y x x =--的定义域为[0,]m ,值域为25[,4]4--,则m 的取值范围是 8. 已知222241a a x x x++≤+-对于任意的(1,)x ∈+∞恒成立,则a 的取值范围是9. 设关于x 的不等式0ax b +>的解集为(1,)+∞,则关于x 的不等式2056ax bx x +>--的解集为10. 已知函数()y f x =满足0xy >,且224936x y -=,则该函数的定义域是11. 设Q 是有理数,集合{|,,0}X x x a a b Q x ==+∈≠,在下列集合中:①|}x X ∈;②2{|}x X x∈;③1212{|,}x x x x X +∈;④1212{|,}x x x x X ∈; 与X 相等的集合的序号是12. 设集合{1,2,3,4,5}I =,若非空集合A 满足:①A I ⊆;②||min()A A ≤(其中||A 表示集合A 中元素的个数),min()A 表示集合A 中的最小元素),则称A 为I 的一个好子集,I 的所有好子集的个数为二. 选择题13. 已知实数a 、b 、c 满足c b a <<,那么“0ac <”是“ab ac >”成立的( ) A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件 D. 既不充分也不必要条件14. 已知原命题“如果||1a ≤,那么关于x 的不等式22(4)(2)10a x a x -++-≥的解集为∅”,那么原命题、逆命题、否命题和逆否命题是假命题的共有( ) A. 1个 B. 2个 C. 3个 D. 4个15. 已知平面α截一球面得圆M ,球中过小圆心M 的直径为AB ,过点M 且与AB 成30°角的平面β截该球面得圆N ,若该球的半径为4,圆M 的面积为4π,则圆N 的面积为( )A. 7πB. 9πC. 11πD. 13π16. 已知函数2()f x x =,[1,2]x ∈的反函数为1()f x -,则函数121[()](2)y f x f x --=+的值域是( )A. 1[,4]2- B. [1,4] C. [1+ D. [1++三. 解答题17. 设函数2()lg(2)f x x x =--的定义域为集合A ,函数()g x =B ,已知:x A B α∈I ,:x β满足20x p +<,且α是β的充分条件,求实数p 的取值范围.18. 已知函数y =R . (1)求实数m 的取值范围;(2)当m 变化时,若y 的最小值为()f m ,求函数()f m 的值域.19. 已知三棱柱111ABC A B C -中,1AA ⊥底面ABC ,90BAC ∠=︒,11AA =,AB =,2AC =,E 、F 分别为棱1CC 、BC 的中点.(1)求证:1AC A B ⊥; (2)求直线EF 与1A B 所成的角;(3)若G 为线段1AA 的中点,1A 在平面EFG 内的射影为H ,求1HA A ∠.20. 已知集合121212{(,)|0,0,}D x x x x x x k =>>+=(其中k 为正常数). (1)设12u x x =,求u 的取值范围; (2)求证:当1k ≥时,不等式21212112()()()2k x x x x k--≤-对任意12(,)x x D ∈恒成立; (3)求使不等式21212112()()()2k x x x x k--≥-对任意12(,)x x D ∈恒成立的k 的范围.21. 考虑下面两个定义域为(0,)+∞的函数()f x 的集合:1{()|f x Ω=对任何不同的两个正数1x 、2x ,都有211212()()0}x f x x f x x x ->-,2{()|f x Ω=对任何不同的两个正数1x 、2x ,都有22211212()()0}x f x x f x x x ->-, (1)已知32()2f x x ax bx =++,若1()f x ∈Ω,且2()f x ∉Ω,求实数a 和b 的取值范围; (2)已知0a b c <<<,1()f x ∈Ω且()f x 的部分函数值由下表给出:比较2d t +与4的大小关系;(3)对于定义域为D 的函数()g x ,若存在常数k ,使得不等式()g x k <对任何x D ∈都成立,则称k 为()g x (x D ∈)的上界,将2Ω中所有存在上界的函数()f x 组成的集合记作T ,判断是否存在常数M ,使得对任何()f x T ∈和(0,)x ∈+∞,都有()f x M <,若存在,求出M 的最小值,若不存在,说明理由.参考答案一. 填空题1. 402. [0,2)3. (3,2)-4. 1()2f x -=(0)x ≥5. 1(2,)3-6. 0或12或13-7. 3[,3]28. [3,1]-9. (1,1)(6,)-+∞ 10. (,3)(3,)-∞-+∞ 11. ①②④ 12. 12二. 选择题13. A 14. B 15. A 16. C三. 解答题 17. 6p <-18.(1)[0,1];(2) 19.(1)略;(2)4π;(3)6π20.(1)2(0,]4k ;(2)略;(3)21.(1)0a ≥,0b >;(2)24d t +<;。
2019-2020学年上海复旦附中高三上学期第一次月考数学试题

2019-2020学年上海复旦附中高三上学期第一次月考数学试题一、填空题1. 若集合,集合,则 .2.—个几何体的主视图、左视图、俯视图都是以为半径的圆,则该几何体的体积是 .3.已知是虚数单位,则的平方根是 .4.函数的反函数是 .5.设满足约束条件,则的最小值是 .6.如图,四个棱长为1的正方体排成一个正四棱柱,是一条侧棱,是上、下底面上其余十六个点,则的不同值的个数为 .7.数列满足,其前项和记为,若,那么.8.若是展开式中项的系数,则 .9.设函数,其中,若,且的最小正周期大于,则 .10.已知函数,设,若关于的不等式在上恒成立,则的{}23A x x =-<30x B xx -⎧⎫=>⎨⎬⎩⎭A B ⋃=a i 2-()()210f x x x =+<x y 、2330233030x y x y y +-≤⎧⎪-+≥⎨⎪+≥⎩2z x y =+AB ()1,2,,16i P i =()1,2,,16i AB AP i ⋅={}n a ()1213,5n n n a a a n a --=-≥=n n S 89S =100S =n a ()()*2,2,nx n N n x R +∈≥∈2x 2323222lim nx na a a →∞⎛⎫+++= ⎪⎝⎭()()2sin ,f x x x R ωϕ=+∈0,ωϕπ><5112,088f f ππ⎛⎫⎛⎫==⎪ ⎪⎝⎭⎝⎭()f x 2πϕ=()2,12,1x x f x x x x ⎧+<⎪=⎨+≥⎪⎩a R ∈x ()2x f x a ≥+R a取值范围是 .11.函数绕原点逆时针旋转,每旋转得到一个新的曲线,旋转一周共得到24条曲线(不包括未旋转时的曲线),请问从中任选其二,均不是函数图像的概率是 . 12.已知两正实数,满足,则的最大值为 .二、选择题13. 若为实数,则成立的一个充分不必要条件是( )A. B. C. D. 14. 已知是空间两条直线,是平面,以下结论正确的是( )A. 如果,则一定有;B. 如果,则一定有;C. 如果,则一定有;D. 如果,则一定有。
上海市2019-2020学年高三上学期期中数学试卷(理科)A卷

上海市2019-2020学年高三上学期期中数学试卷(理科)A卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分)(2018·吉林模拟) 设集合,则()A .B .C .D .2. (2分) (2017高二下·湖北期中) 命题“∃x0>0,使得(x0+1)>1”的否定是()A . ∀x>0,总有(x+1)ex≤1B . ∀x≤0,总有(x+1)ex≤1C . ∃x0≤0,总有(x0+1)≤1D . ∃x0>0,使得(x0+1)≤13. (2分)若定义在R上的偶函数f(x)在[0,+∞)上是减函数,则有()A . f(3)<f(﹣2)<f(1)B . f(1)<f(﹣2)<f(3)C . f(﹣2)<f(1)<f(3)D . f(3)<f(1)<f(﹣2)4. (2分)已知角α的终边与单位圆x2+y2=1交于P(, y0),则cos2α=()A . -B . 1C .D . -5. (2分)已知函数f(x)= ,则关于x的方程f2(x)﹣5(f(x)+4=0的实数根的个数为()A . 2B . 3C . 6D . 76. (2分) (2016高一下·抚州期中) 已知不等式m2+(cos2θ﹣5)m+4sin2θ≥0恒成立,则实数m的取值范围是()A . 0≤m≤4B . 1≤m≤4C . m≥4或m≤0D . m≥1或m≤07. (2分)(2018·临川模拟) 若,函数在处有极值,则的最大值是()A . 9B . 6C . 3D . 28. (2分)定义域为R的函数f(x)满足f(x+2)=2f(x)﹣2,当x∈(0,2]时,f(x)=,若x∈(0,4]时,t2﹣≤f(x)≤3﹣t恒成立,则实数t的取值范围是()A . [2,+∞)B . (1,)C . (2,)D . [1,2]9. (2分) (2017高三上·济宁期末) 已知函数y=f(x)的图象如图所示,则y=f(x)的解析式可能是()A . y=2x﹣x2﹣xB . y=C . y=(x2﹣2x)exD . y=10. (2分)若,则等于()A . 2B . -2C .D .11. (2分)(2017·吕梁模拟) 已知函数f(x)=sin(ωx+ )(ω>0),若f()=f(),且f(x)在区间(,)上有最小值,无最大值,则ω=()A .B .C .D .12. (2分)若函数满足且时,,函数,则函数在区间内的零点的个数为()A . 7B . 8C . 9D . 10二、填空题 (共5题;共5分)13. (1分) (2019高一上·龙江期中) 已知函数,对于任意的,恒成立,则的取值范围是________.14. (1分)使log2(﹣x)<x+1成立的x的取值范围是________15. (1分) (2019高三上·广东月考) 值为________.16. (1分) (2017高三下·上高开学考) 函数f(x)= ,则 f(x)dx的值为________.17. (1分)已知函数,若关于x的方程f(x)﹣k=0有唯一一个实数根,则实数k的取值范围是________三、解答题 (共6题;共55分)18. (10分) (2017高二下·邯郸期末) 设命题p:实数x满足x2﹣4ax+3a2<0,其中a>0;命题q:实数x 满足|x﹣3|≤1.(1)若a=1,且p∧q为真,求实数x的取值范围;(2)若¬p是¬q的充分不必要条件,求实数a的取值范围.19. (10分)(2019·南平模拟)(1)已知函数是上的增函数,求实数的取值范围;(2)试比较两数与的大小,并证明你得出的结论.20. (10分) (2019高一上·兰州期中) 计算下列各式的值:(1);(2)21. (10分)(2019·浙江模拟) 已知椭圆左顶点为,为原点,,是直线上的两个动点,且,直线和分别与椭圆交于,两点(1)若,求的面积的最小值;(2)若,,三点共线,求实数的值.22. (10分) (2018高二下·雅安期中) 设的导数为 ,若函数的图象关于直线对称,且 .(1)实数的值;(2)求函数的极值.23. (5分) (2017高三上·漳州期末) 已知函数f(x)=lnx+ax2 , g(x)= +x+b,且直线y=﹣是函数f(x)的一条切线.(Ⅰ)求a的值;(Ⅱ)对任意的x1∈[1, ],都存在x2∈[1,4],使得f(x1)=g(x2),求b的取值范围.参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共5题;共5分)13-1、14-1、15-1、16-1、17-1、三、解答题 (共6题;共55分) 18-1、18-2、19-1、19-2、20-1、20-2、21-1、21-2、22-1、22-2、23-1、。
上海市复旦大学附属中学青浦分校2019-2020学年高三下学期数学开学摸底考试卷( word版含答案)

复旦附中青浦分校2019学年第二学期高三年级开学摸底考数学试卷一.填空题(本大题共有12题,满分54分,第1~6题每题4分,第7~12题每题5分)1.抛物线214y x=-的准线方程是_____2. 若行列式12812x-=,则x=____3.函数()2sin1,,2f x x xππ⎡⎤=+∈⎢⎥⎣⎦的反函数1()f x-=____.4.“病毒无情人有情”.青浦某党支部要从2名女党员和4名男党员中选出4人担任某社区抗击新冠病毒疫情的志愿者工作,则在选出的志愿者中,男、女都有的概率为____. (结果用数值表示)5. 无穷等比数列{}n a的前n项和为,n S11limn a→∞=,则首项1a的取值范围是___.6.如图,已知扇形的圆心角为60°,半径为1,则扇形的内接矩形面积的最大值为___.7.设实数x、y满足约束条件360200,0x yx yx y--≤⎧⎪-+≥⎨⎪≥≥⎩,若目标函数z=ax+by(a> 0,b>0)的最大值为2,则2a + 3b的值为___.25218.(2)(1)xx+-的展开式中常数项为____.9.已知数列{},{}n na b满足*1121,1,()21nn n nnba ab b n Na+=+==∈-则2020b=___.10.在在平面直角坐标系中,O为坐标原点,M、N是椭圆22124x y+=上的两个动点,动点P满足2,OP OM ON=-u u u r u u u u r u u u r直线OM与直线ON斜率之积为-2,已知平面内存在两定点12,F F、使得12||||PF PF+为定值,则该定值为_____.11.已知向量,a brr满足||1,||2a b==rr,则||||a b a b++-r r rr的取值范围是___.12. 已知二元函数222222(,)()()(0)f x y x y x y a x a y a=++--+>26,则正实数a 的值为_____.二.选择题(本大题共有4题,满分20分,每题5分)13.对任意向量,a b ⋅r r 下列关系式中不恒成立的是( ).||||||A a b a b ⋅≤r r r r.||||||||B a b a b -≤-r r r r 22.()||C a b a b +=+r r r r 22.()()D a b a b a b +-=-r r r r r r14.一个学生期末数学的平时成绩为B 的标准为“平时的五次成绩均不小于80分”.根据甲、乙、丙、丁四位同学五次平时成绩的记录数据(记录数据都是正整数),平时成绩一定为B 的是( )A.甲同学:中位数为85,总体均值为82B.乙同学:众数为83,总体均值为82C.丙同学:总体均值为84,总体方差为6D.丁同学:中位数为83,总体方差为615.曲线C 是平面内与两个定点1(1,0)F -和2(1,0)F 的距离的积等于常数2(1)a a >的点的轨迹,给出下列三个结论:①曲线C 过坐标原点;②曲线C 关于坐标原点对称;③若点P 在曲线C 上,则22F PF V 的面积不大于21,2a 其中,所有正确结论的序号是( C )A.①②B.①③C.②③D.①②③ 16.设等差数列*12,,,(3,)n a a n a n ≥∈L N 的公差为d,满足121212|||||||1||1||1||2||2||2|n n n a a a a a a a a a m +++=-+-+-=++++++=L L L ,则下列说法正确的是(A)A. |d|≥3B. n 的值可能为奇数C.存在i ∈N *,满足21i a -<<D. m 的可能取值为11 三.解答题(本大题满分76分)本大题共有5题,解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.17. (本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.如图,已知多面体111111,,,ABC A B C A A B B C C -均垂直于平面ABC,∠ABC= 120°,1114,1, 2.A A C C AB BC B B =====(1)证明:1AB ⊥平面111A B C ;(2)求直线1AC 与平面1ABB 所成的角的正弦值.18. (本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.己知向量2,2),(cos ,cos ),222x x x m n ==u r r 函数().f x m n =⋅r r (1)求方程f(x)=0在区间[- 2π,2π]的解集;(2)在△ABC 中,角A 、B 、C 的对边分别是a 、b 、c,且满足(2a- c)cos B = bcosC,求f(A)的取值范围.19. (本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.我们称点p 到图形C 上任意一点距离的最小值为点P 到图形C 的距离,记作d(P, C).(1)求点P(3,0)到抛物线C 2:4y x =的距离d(P, C);(2)设l 是长为2的线段,求点集D={P|d(P, l)≤ 1}所表示图形的面积.20.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第三小题满分6分. 设a 为实数,函数2()||1()f x x x a a =+-+∈R(1)若函数y= f(x)是偶函数,求实数a 的值;(2)若a= 2 ,求f(x)的最小值;(3)对于函数y= m(x)和给定区间[a,b] ,若存在00(),x a x b <<满足0()()(),m b m a m x b a-=-则称函数m(x)是区间[ a,b]上的"平均值函数",0x 是它的一个"均值点",如函数2y x =是[-1,1]上的平均值函数, 0就是它的均值点,现有函数2()1g x x mx =-++是区间[ -1,1]上的平均值函数,求实数m 的取值范围.21.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分. 已知数列{}n a 是无穷数列,满足11lg |lg lg |(2,3,4,n n n a a a n +-=-=...) .(1)若122,3,a a ==求345,,a a a 的值;(2)求证:“数列{}n a 中存在*()k a k ∈N 使得lg 0k a =”是“数列{}n a 中有无数多项是1”的充要条件;(3)求证:存在正整数k,使得1 2.k a ≤<。
2022届上海市浦东复旦附中分校高三年级上册学期开学考试数学试题【含答案】

2022届上海市浦东复旦附中分校高三上学期开学考试数学试题一、填空题1.已知集合,,则__.{}23180A x x x =--≤(){}ln 2B x y x ==-A B = 【答案】(]2,6【分析】分别求出集合和集合,再求交集即可.A B 【详解】集合为不等式的解集,A 23180x x --≤,解得,23180x x --≤()()360x x ⇔+-≤36x -≤≤∴,{}{}2318036A x x x x x =--≤=-≤≤集合为函数的定义域,B ()ln 2y x =-由解得,20x ->2x >∴,(){}{}ln 22B x y x x x ==-=>∴.{}(]262,6A B x x ⋂=<≤=故答案为:.(]2,62.已知复数满足,其中为虚数单位,则_______.z (1)2zi i ⋅-=i z =【分析】首先化简复数,再求复数的模.21iz i =-【详解】,()()()2122211112i i i i z i i i i +-====-+--+.=【点睛】本题考查复数的化简和求复数的模,意在考查基本计算,属于基础题型.3.如图,已知长方体中,,,,则该长方体截去三棱锥1111ABCD A B C D -2AB =3BC =15AA =后,剩余部分几何体的体积为_______.111A AB D -【答案】25【解析】先根据,,,求得长方体的体积,利用,求2AB =3BC =15AA =111111113A A B D A B D V S AA -=⋅⋅ 得三棱锥的体积,然后作差即可.111A AB D -【详解】在长方体中,,,,1111ABCD A B C D -2AB =3BC =15AA =所以长方体的体积为,1111123530ABCD A B C D V AB BC AA -=⨯⨯=⨯⨯=三棱锥的体积为,111A AB D -11111111112355332A A B D A B D V S AA -=⋅⋅=⨯⨯⨯⨯= 所以剩余部分几何体的体积为,30525V =-=故答案为:254.设常数,函数.若的反函数的图象经过点,则___.R a ∈()()21og f x x a =+()f x ()31,=a 【答案】7【分析】由反函数的性质得函数f (x )=1og 2(x+a )的图象经过点(1,3),由此能求出a .【详解】∵常数a ∈R ,函数f (x )=1og 2(x+a ).f (x )的反函数的图象经过点(3,1),∴函数f (x )=1og 2(x+a )的图象经过点(1,3),∴log 2(1+a )=3,解得a=7.故答案为7.【点睛】本题考查实数值的求法,考查函数的性质等基础知识,考查运算求解能力,考查函数与方程思想,是基础题.5.设双曲线的方程为,过抛物线的焦点和点的直线为.若的C 22221(0,0)x y a b a b -=>>24y x =(0,)b l C 一条渐近线与平行,另一条渐近线与垂直,则双曲线的方程为_________.l l C【答案】221x y -=【解析】根据直线过抛物线焦点和点,可知该直线斜率为,由双曲线的一条渐近线与平l (0,)b b -l 行,另一条渐近线与垂直,可求得,从而得到双曲线方程.l 1a b ==【详解】双曲线的渐近线方程为,抛物线的焦点为,b y x a =±24y x =(1,0)所以直线过点和,斜率为,l (1,0)(0,)b 001b b-=--所以直线的方程为,即,l 0(1)y b x -=--y bx b =-+因为直线与双曲线的一条渐近线平行,一条渐近线垂直,l 所以,解得,1b b a b b a ⎧-=-⎪⎪⎨⎪-⋅=-⎪⎩1a b ==所以双曲线的方程为,221x y -=故答案为:221x y -=6.在的展开式中,含项的系数是__.23451(1)(1)(1)(1)(1)x x x x x ++++++++++2x 【答案】20【分析】直接根据二项式展开式的通项公式逐一进行求解即可.【详解】在的展开式中,23451(1)(1)(1)(1)(1)x x x x x ++++++++++含项的系数为.2x 22222345C C C C 1361020+++=+++=故答案为:207.中国宋代的数学家秦九韶曾提出“三斜求积术”,即假设在平面内有一个三角形,边长分别为、a 、,三角形的面积可由公式为三角形周长的一半,b c S S =p 这个公式也被称为海伦-秦九韶公式,现有一个三角形的边长满足,,则此()6a b cm +=()4c cm =三角形面积的最大值为________.2cm 【答案】【解析】计算得出,可得出的最大值.5p =S =S 【详解】由已知条件可得,()52a b cp cm ++==.)2cm S ∴=≤==当且仅当时,等号成立.()3a b cm==因此,该三角形面积的最大值为.2故答案为:【点睛】一是在应用基本不等式求最值时,要把握不等式成立的三个条件,就是“一正——各项均为正;二定——积或和为定值;三相等——等号能否取得”,若忽略了某个条件,就会出现错误.对于公式,要弄清它们的作用、使用条件及内在联系,两个公式a b +≥22a b ab +⎛⎫≤ ⎪⎝⎭也体现了和的转化关系.ab a b +8.已知参加某项活动的六名成员排成一排合影留念,且甲乙两人均在丙领导人的同侧,则不同的排法共有__种.【答案】480【分析】先只考虑甲乙丙三人的情况,其中甲乙两人均在丙领导人的同侧有4种,故甲乙两人均在丙领导人的同侧占总数的,则再考虑其他成员的情况即可迎刃而解.23【详解】甲乙丙的三个人顺序种,33A 6=其中甲乙两人均在丙的同侧有4种,在丙的两侧有2种,故甲乙两人均在丙领导人的同侧占总数的,23则甲乙两人均在丙领导人的同侧,则不同的排法共有种.662A 4803=故答案为:4809.黎曼函数(Riemannfunction )是一个特殊函数,由德国数学家黎曼发现并提出,黎曼函数定义在上,其定义为:[0,1].()[]1,,0,0,10,1q qx p q pp p R x x ⎧⎛⎫=⎪ ⎪=⎨⎝⎭⎪=⎩当都是正整数,是不可以再约分的真分数当或者上的无理数若函数是定义在上的奇函数,且,当时,,则()f x R ()(2)0f x f x +-=[0,1]x ∈()()f x R x =______.103310f f ⎛⎫⎛⎫+=⎪ ⎪⎝⎭⎝⎭【答案】730-【分析】先判断出是周期为的周期函数,然后根据函数的周期性以及的解析式,()f x 4()f x ()R x 求得的值.103310f f ⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭【详解】由知:关于对称,()(2)0f x f x +-=()f x (1,0)又为奇函数,图象关于原点对称 为周期函数,周期()f x ()f x ∴4T =103310f f ⎛⎫⎛⎫∴+ ⎪ ⎪⎝⎭⎝⎭1034310f R ⎛⎫⎛⎫=-+ ⎪ ⎪⎝⎭⎝⎭2121310310f f ⎛⎫⎛⎫=-+=-+⎪ ⎪⎝⎭⎝⎭21310R ⎛⎫=-+⎪⎝⎭11731030=-+=-故答案为:730-【点睛】本小题主要考查函数的奇偶性、周期性、对称性,考查分段函数的性质,属于中档题.10.设幂函数,数列满足:,且(),则数列的通项()3f x x ={}n a 12021a =()1n n a f a +=*n ∈N {}n a __.n a =【答案】132021n -【分析】将代入,得,两边同时取对数,构造等比数列求解即可.n a ()1n n a f a +=31n n a a +=【详解】∵,∴,()3f x x =()31n n na f a a +==∵,∴数列各项均为正数,且各项均不为,120210a =>{}n a 1∴,31ln ln 3ln n n n a a a +==∴数列各项均不为,∴,{}n a 1ln 0n a ≠∴,1ln 3ln n n a a +=∴数列是首项为,公比为的等比数列,{}ln n a 1ln ln 2021a =3∴,113ln 3ln 2021ln 2021n n n a --==∴.132021n n a -=故答案为:.132021n -11.已知函数,若方程恰有三个不同的实数根,则11ln ,01()1,12x x x f x x -+<≤⎧⎪=⎨>⎪⎩2()(1)()0f x a f x a +--=实数的取值范围是__.a 【答案】()0,1【分析】原方程化为,得或,作出函数的图象,数形结合可()()()1()0f x f x a +-=()1f x =-()f x a =求解.【详解】因为,所以,即或,2()(1)()0f x a f x a +--=()()()1()0f x f x a +-=()1f x =-()f x a =显然,函数在上单调递增,,且当时,; ()f x (0,1]max ()(1)1f x f ==0x →()f x →-∞函数在上单调递减,且当时,;()f x ()1,+∞x →+∞()0f x →作出函数的大致图象如图所示,方程只有1个实数根,()f x ()1f x =-方程恰有三个不同的实数根,则有2个不同的实数根,2()(1)()0f x a f x a +--=()f x a=所以函数与的图象要有两个交点,由图象得,()y f x =y a =01a <<所以实数的取值范围是.a ()0,1故答案为:.()0,1【点睛】方法点睛:已知函数有零点(方程有根)求参数值(取值范围)常用的方法:(1)直接法:直接求解方程得到方程的根,再通过解不等式确定参数范围;(2)分离参数法:先将参数分离,转化成求函数的值域问题加以解决;(3)数形结合法:先对解析式变形,进而构造两个函数,然后在同一平面直角坐标系中画出函数的图象,利用数形结合的方法求解.12.定义:若函数图像上的点到定点的最短距离小于3,则称函数是点的近点函数,()f x A ()f x A已知函数在上是增函数,且是点的近点函数,则实数的取值范围是2()2x af x x -+=-(2,)+∞(0,4)A -a ________.【答案】3(,4)2【分析】由函数在上是增函数,可知;由函数是点的近点函2()2x af x x -+=-(2,)+∞4a <()f x (0,4)A -数,可得,从而得到结果.32a >【详解】由题意可得:又函数在上是增函数,24()2,22x a a f x x x -+-==-+--2()2x af x x -+=-(2,)+∞∴4a <求出函数的导函数,()24()2af x x -'=-设函数图像上离A 最近的点()f x 004,22a P x x ⎛⎫--+ ⎪-⎝⎭则,()02004242412a x ax x --++--⋅=--令,即,0402a m x -=-<002+m 12mx x -⋅=--2200220,m m x x ++-=解得:(舍)或0m=2x -0x -∴=,即042a x --0x -20042a x x -=-∵函数是点的近点函数,()f x (0,4)A -∴22004292a x x ⎛⎫-++ ⎪-⎝⎭<,即,()220029x x +-<2002450x x --<∴()2450a --<∴32a >综上可得:3(,4)2a ∈故答案为3(,4)2【点睛】本题考查函数的单调性与最值,考查了转化能力与运算能力,属于难题.二、单选题13.已知,,,且都不为零,则“”是“与解集相同”的1a 1b 2a 2b R ∈1122a b a b =110a x b +>220a x b +>A .充分非必要条件B .必要非充分条件C .充要条件D .既非充分又非必要条件【答案】B【分析】根据充分条件和必要条件的定义,结合不等式的性质进行判断即可.【详解】若,取,,则与的解集不同,所以1122a b a b =111a b ==221a b ==-10x +>10x -->“”不是“与解集相同”的充分条件;1122a b a b =110a x b +>220a x b +>若,,,且都不为零,且与的解集相同,此时必有,1a 1b 2a 2b R ∈110a x b +>220a x b +>1212b ba a -=-所以成立,所以“”是“与解集相同”的必要条件.1122a b a b =1122a b a b =110a x b +>220a x b +>综上,“”是“与解集相同”的必要不充分条件.1122a b a b =110a x b +>220a x b +>故选:B.【点睛】本题主要考查充分条件和必要条件的判断,属于常考题.14.已知等差数列中,,则的前n 项和的最大值为( ){}n a 5470,0a a a >+<{}n a n S A .B .C .D .4S 5S 6S 7S 【答案】B【解析】根据已知条件判断时对应的的范围,由此求得的最大值.0n a >n n S 【详解】依题意,所以,556475600000a a a a a a a d >⎧>⎧⎪⇒<⎨⎨+=+<⎩⎪<⎩015n a n >⇒≤≤所以的前n 项和的最大值为.{}n a n S 5S15.已知f (x )=A sin(ωx+θ)(ω>0),若两个不等的实数x 1,x 2∈,且|x 1-x 2|min =π,则f (x )的最()2A x f x ⎧⎫=⎨⎬⎩⎭小正周期是( )A .3πB .2πC .πD .π2【答案】A【分析】由题意可得,求得的值,可得的最小正周期是的值123ππω⨯=ω()f x 2πω【详解】由题意可得的解为两个不等的实数,()1sin 2x ωθ+=1x 2x 且,求得123ππω⨯=23ω=故的最小正周期是()f x 23ππω=故选A【点睛】本题主要考查了的是三角函数的周期性及其图象,解题的关键根据正弦函数的图象求出的值,属于基础题ω16.已知圆心为,半径为1的圆上有不同的三个点,其中,存在实数满足O ,,A B C 0OA OB ⋅=,λμ,则实数的关系为0OC OA uOB λ++=,λμA .B .C .D .221λμ+=111λμ+=1λμ=1λμ+=【答案】A 【详解】由题意得,且.1OA OB OC === 0OA OB ⋅= 因为,即.平方得:.0OC OA uOB λ++= OC OA uOB λ=--221λμ+=故选A.三、解答题17.如图,在四棱锥中,底面为直角梯形,,,P ABCD -ABCD //AD BC AD DC ⊥,为的中点.PA PD PB ===122BC DC AD ===E AD(1)求二面角的正弦值;A PBC --(2)记的中点为,若在线段上,且直线与平面BC M N PE MN PAB 段的长.EN 【答案】(1)23(2)1或.195【分析】(1)利用空间向量的坐标运算求求二面角即可;(2)设,利用坐标运算表示出线面夹角EN t =的正弦值,解方程求解.【详解】(1)连接,则,BE 12BC AD DE ==因为,所以四边形为平行四边形,//AD BC BCDE 所以,2BE CD ==因为,,且为的中点,PA AD ==4=AD E AD所以,,PE AD ⊥4PE ===所以,即,222PE BE PB +=PE BE ⊥又,、平面,AD BE E = AD BE ⊂ABCD 所以平面.PE ⊥ABCD 以为原点,,,所在直线分别为轴建立如图所示的空间E EA EB EP ,,x y z 直角坐标系,则,(2,0,0),(0,2,0),(2,2,0),(0,0,4)-A B C P 所以,(2,2,0),(0,2,4),(2,0,0)AB PB BC =-=-=- 设平面的法向量为,则,即,PAB (,,)m x y z = 00m AB m PB ⎧⋅=⎪⎨⋅=⎪⎩ 220240x y y z -+=⎧⎨-=⎩令,则,,所以,2y =2x =1z =(2,2,1)m = 设平面的法向量为,则,即,PBC (,,)n a b c = 00n PB n BC ⎧⋅=⎪⎨⋅=⎪⎩ 24020b c a -=⎧⎨-=⎩令, 所以,2,0,1b a c ===(0,2,1)n =所以cos ,||||m n m n m m ⋅<>===⋅ 设二面角的平面角为,则,A PB C --α2sin 3α==故二面角的正弦值为.A PB C --23(2)设,,则,而,所以,EN t =(0,4)t ∈(0,0,)N t (1,2,0)M -(1,2,)NM t =-- 由(1)得平面的法向量为,PAB (2,2,1)m = 设直线与平面所成的角为,MN PAB θ则sin |cos ,||||||||MN m MN m MA m θ⋅=<>===⋅ 化简得,解得或,2524190t t -+=1t =195故线段的长为1或.EN 19518.的内角,,的对边分别为,,,已知.ABC A B C a b c tan cos tan sin A B A B =+(Ⅰ)若,的面积为6,求;8a c +=ABC sin B (Ⅱ)若,求.2252b a =sin 23B π⎛⎫- ⎪⎝⎭【答案】(1);(23sin 4B =【分析】(Ⅰ)由已知利用三角函数恒等变换的应用,正弦定理可得,进而可求,利a c =4a c ==用三角形的面积公式即可求得的值.sin B (Ⅱ)由(Ⅰ)可得,结合已知由余弦定理可得,利用同角三角函数基本关系式可求a c =cos B,利用二倍角公式可求,的值,进而根据两角差的正弦公式即可计算求解.sin B sin 2B cos 2B 【详解】解:(Ⅰ),tan cos tan sin A B A B =+ ,sin sin cos sin cos sin()sin A A B B A A B C ∴=+=+=由正弦定理可得,∴a c =又,8a c += ,4a c ∴==的面积为,ABC 116sin 44sin 22ac B B ==⨯⨯⨯解得:.∴3sin 4B =(Ⅱ)由(Ⅰ)可得,a c =又,2252b a =由余弦定理可得,∴2222222512cos 224a a a a c b B ac a +-+-===-,(0,)B π∈ ,,sin B ∴==sin 22sin cosB B B ==27cos 22cos 18B B =-=-∴17sin(2sin 2cos cos 2sin (()33328B B B πππ-=-=⨯--=19.我国西部某省4A 级风景区内住着一个少数民族村,该村投资了800万元修复和加强民俗文化基础设施,据调查,修复好村民俗文化基础设施后任何一个月内(每月按30天计算)每天的旅游人数与第x 天近似地满足(千人),且参观民俗文化村的游客人均消费近似地()f x 8()8f x x =+()g x 满足(元)()143|22|g x x =--(1)求该村的第x 天的旅游收入(单位千元,,)的函数关系;()p x 130x *x ∈N (2)若以最低日收入的20%作为每一天纯收入的计量依据,并以纯收入的5%的税率收回投资成本,试问该村在两年内能否收回全部投资成本?(一年以365天计)【答案】(1);(2)能.9688976122,()1320813122230,x x x N x p x x x x N x ⎧++≤≤∈⎪⎪=⎨⎪-++<≤∈⎪⎩【分析】(1)根据旅游收入等于每天的旅游人数与游客人均消费的乘积,然后去绝()p x ()f x ()g x 对值,从而得到所求;(2)分别研究每一段函数的最值,第一段利用基本不等式求最小值,第二段利用函数的单调性研究最小值,再比较从而得到日最低收入,最后根据题意可判断该村在两年内能否收回全部投资成本.【详解】解:(1)依据题意,有()8()()()8143|22|(130,*)p x f x g x x x x N x ⎛⎫=⋅=+⋅--∈ ⎪⎝⎭ 9688976,(122,*)132081312,(2230,*)x x x N x x x x N x ⎧++∈⎪⎪=⎨⎪-++<∈⎪⎩(2)当,时,1︒122x *x ∈N (当且仅当时,等号成立),968()89769761152p x x x =+++= 11x =因此,(千元).()(11)1152min p x p ==当,时,.2︒2230x < *x ∈N 1320()81312p x x x =-++求导可得,所以在上单调递减,21320()80p x x '=--<1320()81312p x x x =-++(22,30]于是(千元).()(30)1116min p x p ==又,所以日最低收入为1116千元.11521116>该村两年可收回的投资资金为(千元)(万元),111620%5%301228035.2⨯⨯⨯⨯⨯=803.52=因803.52万元万元,所以,该村两年内能收回全部投资资金.800>20.已知斜率为的直线与椭圆交于,两点,线段的中点k l 22:143x y C +=A B AB 为.(1,)(0)M m m >(1)证明:;12k <-(2)设为的右焦点,为上一点,且.证明:,,成等差数列;F C P C 0FP FA FB ++= ||FA ||FP ||FB (3)求(2)中数列的公差.【答案】(1)证明见解析(2)证明见解析.【分析】(1)设而不求,利用点差法以及中点坐标公式求出,再利用在椭圆内列不34k m =-(1,)M m 等式求解即可;(2)解出m ,进而求出点P 的坐标,得到,再由两点间距离公式表示出,,可证明,FP FA FB ||FA,成等差数列;||FP ||FB (3)先求出直线的方程,联立直线与椭圆方程由韦达定理进行求解.【详解】(1)设,因为线段的中点为,()()1122,,,A x y B x y AB (1,)M m 所以,,122x x +=122y y m +=将,代入椭圆中,得,A B 22:143x y C +=2211222234123412x y x y ⎧+=⎨+=⎩两式相减得,,121212123()()4()()0x x x x y y y y +-++-=即,所以,12126()8()0x x m y y -+-=12126384y y k x x m m -==-=--点在椭圆内,即,解得,(1,)M m 211,(0)43m m +<>302m <<所以.①3142k m =-<-(2)由题意得,设,则,,(1,0)F 33(,)P x y 1231110x x x -+-+-=1230y y y ++=由(1)及题设得,.3123()1x x x =-+=312()20y y y m =-+=-<又点在上,,所以,从而,.P C 214143m +=34m =3(1,2P -3||2FP = 于是.1||22x FA ===- 同理.所以,2||22x FB =- 121||||4()32FA FB x x +=-+= 故,即,,成等差数列.||||2||FA FB FP += ||FA ||FP ||FB (3)设该数列的公差为,d 则1212||||||||||2d FB FA x x =-=-= 将代入①得.34m =1k =-所以的方程为,代入的方程,并整理得.l 74y x =-+C 2171404x x -+=故,,代入②解得122x x +=12128x x=||d .21.已知为定义在实数集上的函数,把方程称为函数的特征方程,特22()1x m f x x -=+R 1()f x x =()f x 征方程的两个实根、(),称为的特征根.αβαβ<()f x (1)讨论函数的奇偶性,并说明理由;()f x (2)已知为给定实数,求的表达式;m ()()f f βα-(3)把函数,的最大值记作,最小值记作,研究函数,()y f x =[,]x αβ∈max ()f x min ()f x ()y f x =的单调性,令,若的取值范围.[,]x αβ∈()max ()min ()g m f x fx =-()g m ≤λ【答案】(1)非奇非偶函数;理由见解析(2)()()f f βα-=(3)2λ≥【分析】(1)当时,判断为奇函数;当时,取和,非奇非偶0m =0m ≠(1)(1)f f ≠-(1)(1)f f ≠--函数,得到答案.(2)根据韦达定理得到,代入表达式化简得到答案.,1m αβαβ+==-(3)先证明在内单调递增,,代入不等式得到答案.()f x (,)αβ()()()g m f f βα=-=【详解】(1)当时,,是奇函数0m =2()()()1x f x f x x --==--+22()1x f x x =+当时,,0m ≠22()1x m f x x -=+22(1),(1)22m m f f ---=-=且,是非奇非偶函数(1)(1)f f ≠-(1)(1)f f ≠--()f x ∴综上所述:时,为奇函数;时,是非奇非偶函数.0m =()f x 0m ≠()f x (2)恒成立221(),1040f x x mx m x =∴--=∴∆=+>,1||m αβαββα∴+==-∴-=()()222222()[()22]()()1111m m m f f βαβααβαββαβαβα---+-+-=-=++++()()f f βα∴-==(3)先证明上是递增函数,设(),[,]f x x αβ∈12x x αβ≤<≤()()()()()()21121221212222212122221111x x m x x x x x m x m f x f x x x x x -+-+⎡⎤--⎣⎦-=-=++++由(2)可知:、是方程的两个实根,αβ210x mx --=又2212112210,10x x x mx x mx αβ≤<∴--≤--≤≤ ()22121220x x m x x ∴+-+-≤()22221212121212222x x x x x x x x m x x <+∴<+++≤()1212220x x m x x ∴-+-<()()21212100x x x x f x f x ><∴-∴->在内单调递增 ,()f x (,)αβ()()()g m f f βα=-=恒成立≤λ∴≥=2λ≥【点睛】本题考查了函数的奇偶性,函数表达值,恒成立问题,判断函数的单调性是解题的关键.。
上海市复旦附中2019-2020学年高三上学期数学11月份综合练习09(简答)

复旦附中高三数学综合练习092019.11一. 填空题1. 1和4的等比中项为2. 函数1()3x f x -=(0x <)的反函数是1()f x -=3. 已知角θ的顶点在坐标原点,始边与x 轴的正半轴重合,若角θ的终边落在第三象限内, 且3cos()25πθ+=,则cos2θ= 4. 如图为某几何体的三视图,则其侧面积为 2cm5. 从集合{1,2,3,4,5,6,7,8,9,10}A =中任取两个数,欲使取到的一个数大于k ,另一个数小 于k (其中k A ∈)的概率是25,则k = 6. 方程1122log (95)log (32)2x x ---=-+的解为7. 已知集合[1,2]A =,2{|40}B x x ax =-+≥,若A B ⊆,则实数a 的取值范围是 8. 设等比数列{}n a 的各项均为正数,公比为q ,前n 项和为n S ,若对任何*n ∈N ,都有23n n S S <,则q 的取值范围是9. 已知α、β均为锐角,且sin cos()sin ααββ+=,则tan α的最大值是 10. 函数()sin f x x ω=(0ω>)的图像与其对称轴在y 轴右侧的交点从左到右依次记为1A ,2A ,3A ,⋅⋅⋅,n A ,⋅⋅⋅,在点列{}n A 中存在三个不同的点k A 、i A 、p A ,使得△k i p A A A 是等腰直角三角形,将满足上述条件的ω值从小到大组成的数列记为{}n ω,则2020ω=11. 已知函数2()|1||1|f x x x a x =+-++有两个不同的零点,则a 的取值范围是12. 设定义域为(0,)+∞的递增函数()f x 满足:对任意(0,)x ∈+∞,都有6()f x x>-,且6(())5f f x x+=,则(10)f =二. 选择题13. 若直线1l 和2l 是异面直线,1l 在平面α内,2l 在平面β内,l 是平面α与平面β的交线则下列命题一定正确的是( )A. l 与1l 、2l 都不相交B. l 与1l 、2l 都相交C. l 至多与1l 、2l 中的一条相交D. l 至少与1l 、2l 中的一条相交 14. 设2019220190122019(12)x a a x a x a x -=+++⋅⋅⋅+,则20191222019222a a a ++⋅⋅⋅+的值为( ) A. 2 B. 0 C. 1- D. 115. 已知{}n a 的前n 项和为n S ,则“2n S an bn c =++(0a ≠,*n ∈N )”是“{}n a 是等差数列”的( )A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件16. 设()f x 是定义域为R 的奇函数,()g x 是定义域为R 的偶函数,a 、b 是非零常数,若函数()()af x bg x +的值域为[1,3),则函数()()af x bg x -的值域为( )A. (3,1]--B. [1,3)C. 与a 、b 的取值有关D. 以上都不对三. 解答题17. 如图所示,已知长方体1111ABCD A B C D -的棱长2AB =,1BC =,12AA =,求: (1)异面直线1BC 与1CD 所成角的大小; (2)点B 到平面1ACD 的距离.18. 已知数列{}n a 和{}n b ,对任何正整数m ,记1122()||||||m m S m a b a b a b =-+-+⋅⋅⋅+-. (1)若21n a n =-,2n b n =-,求(1)S ,(3)S ;(2)若12n n a -=,213n b n =-,求()S m 关于m 的表达式.19. 已知函数()f x 、()g x 满足关系式()()()2g x f x f x π=⋅+.(1)设()cos sin f x x x =+,求()g x 的解析式;(2)当()|sin |cos f x x x =+时,存在12,x x ∈R ,对任意x ∈R ,12()()()g x g x g x ≤≤ 恒成立,求12||x x -的最小值.20. 已知函数2()f x x ax b =++(,a b ∈R ).(1)若不等式()0f x ≤的解集为[1,3],求实数a 和b 的值;(2)若对任意[1,1]a ∈-,都存在[2,3]x ∈-,使得()0f x >成立,求实数b 的范围; (3)已知集合{|()0}A x f x =≤,5{|(())}4B x f f x =≤,若A B =≠∅,求实数a 的取值范围.21. 对于定义域为R 的函数()g x ,若存在正常数T ,使得cos ()g x 是以T 为周期的函数, 则称()g x 为余弦周期函数,且称T 为其余弦周期,已知()f x 是以T 为余弦周期的余弦周期 函数,其值域为R ,设()f x 单调递增,(0)0f =,()4f T π=.(1)证明:()sin3xh x x =+是以6π为周期的余弦周期函数; (2)设a b <,证明对任意[(),()]c f a f b ∈,存在0[,]x a b ∈,使得0()f x c =;(3)证明:“0u 为方程cos ()1f x =在[0,]T 上的解”的充要条件是“0u T +为方程cos ()1f x =在[,2]T T 上有解”,并证明对任意[0,]x T ∈都有()()()f x T f x f T +=+.参考答案一. 填空题1. 2±2. 31log 1(0)3x x +<<3.7254. 4π5. 4或76. 27. (,4]-∞8. (0,1]9. 10. 40392π11. (3--- 12. 125二. 选择题13. D 14. C 15. D 16. A三. 解答题 17.(1);(218.(1)(1)0S =,(3)9S =;(2)当4m ≤,2393()212m m m S m -=-+;当5m ≥,2393()2772mm m S m -=-+.19.(1)()cos2g x x =;(2)34π.20.(1)5a =-,4b =;(2)(6,)-+∞;(3)∵A B =≠∅,∴05(())()()04f f x f x f x ≤⇒≤≤,即55(0)44f b =⇒=, ∴()0a f x -≤≤与()0f x ≤解集相同,∴254a a --≤且250a ∆=-≥,即a ∈21.(1)解:()6h x π是以为余弦周期的余弦周期函数 (2)证明:()()()()()()[]0,f a c f b f a c f b c f x c a b f x R ⎫≤≤⇒-⋅-≤⎡⎤⎡⎤⎪⎣⎦⎣⎦⇒-⎬⎪⎭在上必有解定义域值域都为()()[](),,,,c f a f b x a b f x c ∈∈=⎡⎤⎣⎦00故对于任意必存在使得(3)略。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 1 页 / 共 9 页
复旦大学附属中学2019学年第一学期
高三年级数学开学摸底考试卷
一、填空题
1. 已知
2|,|2x
AyyxByy
,则AIB____________
2. 设函数sincosfxxx,且1f,则sin2____________
3. 已知二元一次方程组
111
222
axbycaxbyc
的增广矩阵是111113,则此方程组的解是____________
4. 二项式
5
2
1
xx
的展开式中,x的系数为____________
5. 用半径1米的半圆形薄铁皮制作圆锥型无盖容器,其容积为____________立方米
6. 一个袋子中共有6个球,其中4个红色球,2个蓝色球,这些球的质地和形状一样,从中任意抽取2个
球,则所抽的球都是红色球的概率是____________
7. 在长方体
1111ABCDABCD中,若AB=BC=1,12AA,则异面直线1BD与1
CC
所成角的大小为
____________
8. 若双曲线两顶点的距离为6,渐近线方程为
3
2
yx
,则双曲线的标准方程为____________
9. 某人5次上班途中所花的时间(单位:分钟)分别为,,10,11,9xy,已知这组数据的平均数为10,方差
为2,则xy____________
10. 不等式
3
3
810
5011xxxx
的解集为____________
11. 已知,,abc都是实数,若函数
2
1
xxafxbaxcx
的反函数的定义域是,,则c的所
有取值构成的集合是____________
12. 已知函数
2
12fxxmx
两个零点差的绝对值为221pp,若p为质数,m为正整数,
则m=____________
二、选择题
13. 设
12
,zzC
,则“1z、2z均为实数”是“12zz是实数”的( )
A. 充分非必要条件 B. 必要非充分条件
C. 充要条件 D. 既非充分又非必要条件
第 2 页 / 共 9 页
14. 设,是两个不同的平面,l是一条直线,若l//,l//,Im,则( )
A. l与m平行 B. l与m相交 C. l与m异面 D. 以上三个答案均有可能
15. 已知数列na的通项公式为*11nanNnn,其前n项和910nS,则双曲线2211xynn
的渐近线方程为( )
A.
22
3
yx
B. 324yx C. 3210yx D. 103yx
16. 定义
,
aabFabbab
,已知函数fx、gx定义域都是R,给出下列命题:
(1)若fx、gx都是奇函数,则因函数,Ffxgx为奇函数;
(2)若fx、gx都是减函数,则函数,Ffxgx为减函数;
(3)若minmin,fxmgxn,则min,,FfxgxFmn;
(4)若fx、gx都是周期函数,则函数,Ffxgx是周期函数.
其中正确命题的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
三、解答题
17. 已知VABC的内角A,B,C的对边分别为,,abc.
(1)若,73Bb,VABC的面积332S,求ac值;
(2)若22cosCBABCABACc,求角C.
第 3 页 / 共 9 页
18. 如图,在直三棱柱
111ABCABC中,1
2CCACBC
,∠ACB=90°.
(1)下图给出了该直三棱柱三视图中的主视图,请据此画出它的左视图和俯视图;
(2)若P是1AA的中点,求四棱锥111BCAPC的体积.
19. 点P为ABC平面上一点,有如下三个结论:
①若0PAPBPC,则点P为ABC的____________;
②若sinsinsin0APABPBCPC,则点P为ABC的____________;
③若sin2sin2sin20APABPBCPC,则点P为ABC的____________.
回答以下两个小问:
(1)请你从以下四个选项中分别选出一项,填在相应的横线上
A. 重心 B. 外心 C. 内心 D. 垂心
(2)请你证明结论②
第 4 页 / 共 9 页
20. 已知椭圆
22
22
:10xyCabab
的右焦点为1,0F,短轴长为2,过定点P(0,2)的直线l交椭圆C
于不同的两点A、B(点B在点A,P之间).
(1)求椭圆C的方程;
(2)若PBPA,求实数的取值范围;
(3)若射线BO交椭圆C于点M(O为原点),求VABM面积的最大值.
21. 已知函数
2
327mxnhxx
为奇函数,13xmkx,其中m、nR.
(1)若函数hx的图像过点A(1,1),求实数m和n的值;
(2)若m=3,试判断函数11fxhxkx在3,x上的单调性并证明;
(3)设函数,39,3hxxgxkxx,若对每一个不小于3的实数1x,都恰有一个小于5的实数2x,使
得12gxgx成立,求实数m的取值范围.
第 5 页 / 共 9 页
参考答案
一、填空题
1. 0, 2. 0 3. 21xy 4. 10 5.324 6. 0.4 7.4 8.
22
18194xy
或22194yx 9. 4
10. ,11,2 11. 0 12. 9
二、选择题
13. A 14. A 15. C 16. B
三、解答题
17.(1)5ac (2)
3
C
18.(1)略
(2)2
19.(1)①重心②内心③外心
(2)
第 6 页 / 共 9 页
20.(1)
2
2
12xy
(2)
1
,13
(3)
2
max
7
2,2Sk
第 7 页 / 共 9 页
21.(1)30,0mn
(2)单调递增
(3)0,6m
第 8 页 / 共 9 页
第 9 页 / 共 9 页
