华中科技大学硕士研究生考试《电动力学习题集
电动力学习题集答案

电动力学第一章习题及其答案1、 当下列四个选项:(A 、存在磁单级, B 、导体为非等势体, C 、平方反比定律不精确成立,D 、光速为非普适常数)中的_ C ___选项成立时,则必有高斯定律不成立、 2、 若 a 为常矢量 , r= (x - x ')i + ( y - y ')j + (z -z ')k 为从源点指向场点的矢量 ,E 0 , k 为常矢量,则∇⋅(r 2 a) =∇⋅(r 2 a ) = (∇r ⋅a =2r ⋅a ,)⋅a ) = ddrr ∇r ⋅a = 2r r r2∇r = (i +j + k ) (x - x ') + (y - y ') + (z - z ') = i +j y-y' + k = rr∂ ∂x ∂ ∂y ∂ ∂z 2 2 2 x-x' r z-z' rr ⎛ ⎫ ⎪ 2(x -x ') = (x -x ') ,同理, ∂ ∂x(x -x ') 2+(y - y ') 2 +(z -z ') 2 = r 2 (x -x ')2+(y -y ')2+(z -z ')2⎝ ⎪⎪ ⎭(y -y ') (x -x ') +(y - y ') 2 +(z -z ') ∂ ∂y (x -x ') 2 +(y - y ') 2 +(z -z ') 2 = , ∂ ∂z 2 2 = (z -z ') r re e e x x x∇⋅r = ∂(x-x')∇⨯ r = + ∂(y-y') ∂y+ ∂(z-z') = 3∂z, ∂ ∂x ∂ ∂y ∂ ∂zx - x ' y - y ' z - z '= 0, ∂x∇⋅(a ⨯r )=a ⋅(∇⨯r ) = 0 ,) ⨯ r + r ∇ ⨯ r = ∇r 2r ⨯ r = ⨯ r = 0 r ∇ ⨯ rr = ∇( r1 1 3r a ,,∇ ( ⋅ ) = ∂[ a x (x -x' )]+ ∂[ a y (y - y')] j + [ a z ∂ (z -z')] = a r i k ∂x ∂y ∂z∇⋅ r =∇ ⋅ + ∇⋅ =- ⋅ + = r r r 1r 1 r r 3 r2 3 r ,∇ ⋅ (∇ ⨯ A ) = __0___、 r r∇ ⋅[E 0 sin(k ⋅r )] = k ⋅ E 0 cos(k ⋅ r )= __0__、 ∇ ⋅ (E 0 e ik ⋅r ) =, 当 r ≠ 0 时 , ∇ ⨯ = (r / r 3)ik ⋅ E 0 exp(ik ⋅r ) , ∇ ⨯ [rf (r )] = _0_、 ∇ ⋅ [ r f ( r)] 3f (r )+r df (r )drs3、 矢量场 f 的唯一性定理就是说:在以 为界面的区域V 内,若已知矢量场在V 内各点的旋度与散度,以及该矢量在边界上的切向或法向分量,则在 内唯一确定、 f V ∂ρ = 0 ,若 J为稳恒电流情况下的电流密度 ,则 J 满足4、 电荷守恒定律的微分形式为 ∇⋅ J + ∂t∇ ⋅ J = 0 、5、 场强与电势梯度的关系式为, E = -∇ϕ 、对电偶极子而言 ,如已知其在远处的电势为ϕ = P ⋅ r/(4πε 0r ⎛ 4πε 0 ⎝ ⎫ E = 1 3(P ⋅r )r- P3) ,则该点的场强为 ⎪ ⎪ 、 r 5 r 3⎭a (r > a ) 任意一点 D 的散度为 0,Q 6、 自由电荷 均匀分布于一个半径为 的球体内,则在球外内 (r < a )任意一点 D 的散度为 3Q / 4π a 3 、arbr 7、 已知空间电场为 E = + 3 (a ,b 为常数),则空间电荷分布为______、rr 2ar1 r 1 ∇ = - 3 ⇒ E = -b ∇ ⇒r r r 2 r 2 1 a ∇⋅r - 2r ⋅∇r + 4πb δ(r )]ρ = ε 0∇⋅E = ε 0(∇⋅ arr 2 -b ∇ r ) = ε 0[ r 2 r 33a 2r ⋅r + 4πb δ(r )]⇒ ρ = ε 0[ a 2 + 4πb δ(r )] = ε 0[ - r 2r 4 ra8、 电流 I 均匀分布于半径为 的无穷长直导线内,则在导线外 (r > a ) 任意一点 B 的旋度的大小为 0 , 导线内 (r < a )任意一点 B 的旋度的大小为 μ 0I / πa 2 、D ε9、 均匀电介质(介电常数为 )中 ,自由电荷体密度为 ρ f 与电位移矢量 的微分关系为∇ ⋅ D = ρ f , 束缚电荷体密度为 ρ P 与电极化矢量 的微分关系为 ∇ ⋅ P = - ρ P ,则P ρ = - ε - ε 0 ρ 、f ρ P 与 ρ f 间的关系为 P ε10、 无穷大的均匀电介质被均匀极化,极化矢量为 P ,若在σ = -(P - P )θ 21R= -(P cos θ - 0)介质中挖去半径为 R 的球形区域,设空心球的球心到球 P= - P ⋅R面某处的矢径为 R ,则该处的极化电荷面密度为R- P ⋅ R / R 、q ε 11、 电量为的点电荷处于介电常数为 的均匀介质中,则点电荷附近的极化电荷 为 (ε 0 / ε - 1)q 、H 12、 某均匀非铁磁介质中,稳恒自由电流密度为 J f ,磁化电流密度为 J M ,磁导率 ,磁场强度为 ,磁μ 化强度为M ,则∇⨯ H = Jf ,∇⨯ M =J M , JM 与J f 间的关系为J= (μ/ μ 0 - 1)J f、M13、 在 两 种 电 介 质 的 分 界 面 上 , D , E 所 满 足 的 边 值 关 系 的 形 式 为 n ⋅(D2- D1)=σf,- 1 -n ⨯(E2- E1)= 0、ε14、 介电常数为 的均匀各向同性介质中的电场为 E 、 如果在介质中沿电场方向挖一窄缝 ,则缝中电场强度大小为 E 、ε15、 介电常数为 的无限均匀的各项同性介质中的电场为 E ,在垂1 n2直于电场方向横挖一窄缝,则缝中电场强度大小为________、E⎧D 2n - D 1n = 0 ⇒ ⎧ ⎨ ⎩εE = ε 0E 缝 E 2τ = E 1 sin θ1 = 0 ⇒ E 缝 = εE / ε 0 , 、 E E⎨ E 2τ - E 1τ = 0 ⎩ 16、 在半径为 R 的球内充满介电常数为ε 的均匀介质,球心处放一点电荷,球面为接地导体球壳,如果挖去顶点在球 心的立体角等于 2的一圆锥体介质,则锥体中的场强与介 质中的场强之比为_1:1_、Eσ1nE2ε1Rσ 2极化电荷D 2n = D 1n = 0 ⇒E 1 = E 1τ = E 2τ = E 2 ⇒ E 1 : E 2 = 1:1自由电荷17、 在半径为 R 的球内充满介电常数为ε 的均匀介质,球心处放一点电荷,球面为接地导体球壳,如果挖去顶点在球心的立体角等于 2 的一圆锥体介质,锥体处导体壳上的自由电荷密度与介质 附近导体壳上的自由电荷密度之比为ε 0 / ε 、⎧ ⎨ ⎩ D 2n = D 1n = 0 E = E 1τ = E 2τ = E 2σ = σ 1D ε 0 D 2 ε 内球面上 ⇒ 1= ⇒ ε 0 2 ⇒ σ 1 :σ 2 = ε 0 :ε ε 118、 在 两 种 磁 介 质 的 分 界 面 上 , H , B 所 满 足 的 边 值 关 系 的 矢 量 形 式 为n ⨯ (H 2 - H 1)= α f ,n ⋅ B 2 - B = 0 、( ) 1I μ219、一截面半径为 b 无限长直圆柱导体,均匀地流过电流 I ,则储存在单位长度导 μ1体内的磁场能为__________________、rB ⋅ 2πr = μ 0I ππr 22⇒ B = bμ Ir2, 0 2πb22πrdr =⎰b 0 2μ0b W =⎰B μ I 2r 2 2 2πrdr =⎰ μ0I 2r 3dr4πb 4= μ0I 2b 4 16πb 4 = μ0I 216π12μ01 04π 2b 4 020、在同轴电缆中填满磁导率为 μ1,μ 2的两种磁介质,它们沿轴各占一半空间。
《电动力学》课后答案

(a ⋅ ∇ ) r = ( a x
∂ ∂ ∂ + ay + a z )[( x − x ' )e x + ( y − y ' )e y + ( z − z ' )e z ] ∂x ∂y ∂z = axe x + a y e y + az ez = a
4 ○
∇ ( a ⋅ r ) = r × (∇ × a ) + ( r ⋅ ∇ ) a + a × (∇ × r ) + (a ⋅ ∇ ) r 因为, a 为常向量,所以, ∇ × a = 0 , ( r ⋅ ∇) a = 0 , 又 ∵ ∇ × r = 0 ,∴ ∇( a ⋅ r ) = ( a ⋅ ∇) r = a ∇ ⋅ [ E0 sin( k ⋅ r )] = (∇ ⋅ E0 ) sin( k ⋅ r ) + E0 ⋅ [∇ sin( k ⋅ r )]
ez ex ey dA (3) ∇u × = ∂u / ∂x ∂u / ∂y ∂u / ∂z du dAx / du dAy / du dAz / du
dAy ∂u dAx ∂u dA ∂u dAz ∂u dAz ∂u dAy ∂u − )e x + ( x − )e y + ( − )e z du ∂y du ∂z du ∂z du ∂x du ∂x du ∂y ∂Ay (u ) ∂Ax (u ) ∂A (u ) ∂Ay (u ) ∂A (u ) ∂Az (u ) =[ z − ]e x + [ x − ]e y + [ − ]e z ∂y ∂z ∂z ∂x ∂x ∂y = ∇ × A(u ) =(
S S S S S S S S S
(1)
电动力学.习题

设 B(r , r ) 是 r 和 r 的矢量函数,计算 ∇ ⋅ B(r , r ) 。
∇ ⋅ B(r,r ) = = + ∂Bx ( r , r ) ∂x ∂Bx ( r , rc ) ∂x ∂r + + ∂By ( r , r ) ∂y ∂y + ∂y + ∂Bz ( r , r ) ∂z ∂Bz ( r , rc ) ∂z ∂y + ∂Bz ( rc , r ) ∂r ∂z ∂z
(9)
例5
证明
4
= (B ⋅ ∇ )A + (A ⋅ ∇ )B + B × (∇ × A) + A × (∇ × B )
∇(A ⋅ B )
[证明] 由 ∇ 的求导作用有
∇(A ⋅ B ) = ∇(A ⋅ Bc ) + ∇(Ac ⋅ B )
根据矢量公式
b (a ⋅ c ) = c a ⋅ b + a × b × c
a × b × c = b (a ⋅ c ) − c a ⋅ b
作调整得到
(
)
(
)
= Ac (∇ ⋅ B ) − (Ac ⋅ ∇ )B = A(∇ ⋅ B ) − (A ⋅ ∇ )B
∇ × (Ac × B ) = Ac (∇ ⋅ B ) − B (∇ ⋅ Ac )
]
[
(7)
交换 A 、 B 的顺序,由(7)式可以推出
由行列式可以看出混合积对 A 、 B 和 C 具有轮换对称性,即有:
Ai
Aj Bj Cj
Ak Bk Ck
A ⋅ ( B × C ) = C ⋅ ( A × B ) = B ⋅ ( C × A)
双重矢量积公式的证明
电动力学习题集答案-1

电动力学第一章习题及其答案1. 当下列四个选项:(A.存在磁单级, B.导体为非等势体, C.平方反比定律不精确成立,D.光速为非普适常数)中的_ C ___选项成立时,则必有高斯定律不成立.2. 若a为常矢量, k z z j y y i x x r )'()'()'(-+-+-=为从源点指向场点的矢量,k E,0为常矢量,则)(2a r ⋅∇=a r a r a r a r a r r r dr dr ⋅=⋅=⋅∇=⋅∇=⋅∇22))()(222,=⨯∇r0'''=---∂∂∂∂∂∂z z y y x x e e e zyxxxx, 3)z'-(z )y'-(y )x'-(x =++=⋅∇∂∂∂∂∂∂z y x r ,)()(=⨯∇⋅=⨯⋅∇r a r a ,0)(3211=⨯=⨯=⨯∇+⨯∇=⨯∇∇r r r r r r r r r rrr,a k j i r a za ya xa z y x =++=⋅∇∂∂∂∂∂∂)]z'-(z [)]y'-(y [)]x'-(x [)(,r r rr r rrr r r r 23113=+⋅-=⋅∇+⋅∇=⋅∇ ,=⨯∇⋅∇)(A __0___. =⋅⋅∇)]sin([0r k E )cos(0r k E k ⋅⋅, 当0≠r 时,=⨯∇)/(3r r __0__. =⋅∇⋅)(0r k i e E )exp(0r k i E k i ⋅⋅, =⨯∇)]([r f r _0_. =⋅∇)]([r f r dr r df r r f )()(3+3. 矢量场f的唯一性定理是说:在以s 为界面的区域V 内,若已知矢量场在V 内各点的旋度和散度,以及该矢量在边界上的切向或法向分量,则f在V内唯一确定.4. 电荷守恒定律的微分形式为0=∂∂+⋅∇tJ ρ,若J为稳恒电流情况下的电流密度,则J满足0=⋅∇J.5. 场强与电势梯度的关系式为,ϕ-∇=E.对电偶极子而言,如已知其在远处的电势为)4/(30r r P πεϕ ⋅=,则该点的场强为()⎪⎪⎭⎫ ⎝⎛-⋅=350341r P rr r P Eπε.6. 自由电荷Q 均匀分布于一个半径为a 的球体内,则在球外)(a r >任意一点D的散度为 0,内)(a r <任意一点D的散度为 34/3a Q π.7. 已知空间电场为b a rrb r r a E ,(32 +=为常数),则空间电荷分布为______.8. 电流I 均匀分布于半径为a 的无穷长直导线内,则在导线外)(a r >任意一点B的旋度的大小为 0 , 导线内)(a r <任意一点B的旋度的大小为20/a Iπμ.9. 均匀电介质(介电常数为ε)中,自由电荷体密度为f ρ与电位移矢量D的微分关系为f D ρ=⋅∇ , 束缚电荷体密度为Pρ与电极化矢量P 的微分关系为P P ρ-=⋅∇,则P ρ与f ρ间的关系为fP ρρεεε0--=.10. 无穷大的均匀电介质被均匀极化,极化矢量为P,若在介质中挖去半径为R 的球形区域,设空心球的球心到球面某处的矢径为R,则该处的极化电荷面密度为R R P /⋅-.11. 电量为q的点电荷处于介电常数为ε的均匀介质中,则点电荷附近的极化电荷为q )1/(0-εε.12. 某均匀非铁磁介质中,稳恒自由电流密度为f J,磁化电流密度为M J ,磁导率μ,磁场强度为H ,磁化强度为M ,则=⨯∇H f J ,=⨯∇M M J ,M J 与f J 间的关系为()f M J J1/0-=μμ.13. 在两种电介质的分界面上,E D ,所满足的边值关系的形式为()f D D n σ=-⋅12,()012=-⨯E E n.14. 介电常数为ε的均匀各向同性介质中的电场为E . 如果在介质中沿电场方向挖一窄缝,则缝中电场强度大小为E . 15. 介电常数为ε的无限均匀的各项同性介质中的电场为E ,在垂直于电场方向横挖一窄缝,则缝中电场强度大小为RR P P P P n n P ⋅-=--=--=)0cos ()(12θ,/0sin 00011201212εεθεετττE E E E E E E E D D n n =⇒⎩⎨⎧===⇒⎩⎨⎧=-=-缝缝. 16. 在半径为R 的球内充满介电常数为ε的均匀介质,球心处放一点电荷,球面为接地导体球壳,如果挖去顶点在球心的立体角等于2的一圆锥体介质,则锥体中的场强与介质中的场强之比为_1:1_.17. 在半径为R 的球内充满介电常数为ε的均匀介质,球心处放一点电荷,球面为接地导体球壳,如果挖去顶点在球心的立体角等于2的一圆锥体介质,锥体处导体壳上的自由电荷密度与介质附近导体壳上的自由电荷密度之比为εε/0.18. 在两种磁介质的分界面上, B H,所满足的边值关系的矢量形式为()fH H n α=-⨯12,()012=-⋅B B n.19. 一截面半径为b 无限长直圆柱导体,均匀地流过电流I ,则储存在单位长度导体内的磁场能为__________________.20. 在同轴电缆中填满磁导率为21,μμ的两种磁介质,它们沿轴各占一半空间。
华中科技大学硕士研究生入学考试试题(含答案)(1)

= e 2t ε (−t ) + e−2t ε (t ) ← → e2t ε (−t ) ← →
注
意是双边拉氏变换
−1 , Re[ s ] < 2 s−2
U R ( s) = X ( s) H (s ) = −1 < Re[ s ] < 2
−4 1 1 1 4 1 1 × =− × + × − ( s − 2)( s + 2) s + 1 3 s − 2 3 s +1 s + 2 1 4 u R (t ) = e 2t ε (−t ) + e −t ε (t ) − e −2t ε (t ) 3 3
−s −2 s 1 2 −t −2 t 1 2 zi1 −t −2 t 1 2 zi 2 −t 1 2 1 2 zs −t 1 2 1 zi1 zi 2 zs −t zs zi1 zi 2
= (2 + e − t )ε (t ) − (e− t + e−2t )ε (t ) − (e − t − e−2t )ε (t ) = (2 − e − t )ε (t )
()
1 ( z ) − z −1Yzs ( z ) = X ( z ) 3 z 1 zs h ( n) = ( ) n ε ( n) 1 3 1 + z −1 z − 3 3 Y ( z) z 1 2 Yzs ( z ) = X ( z ) H ( z ) X ( z ) = zs = x ( n) = ( ) n ε ( n) 1 H ( z) z − 2 2
其中
t e2τ e − (t −τ ) dτ , t < 0 1 1 ∫−∞ e2t ε (−t ) ∗ [e− t ε (t )] = 0 = e 2 t ε ( − t ) + e − t ε (t ) 3 ∫ e 2τ e − (t −τ ) dτ , t > 0 3 −∞
华科电气专业考研814电路历年真题全解
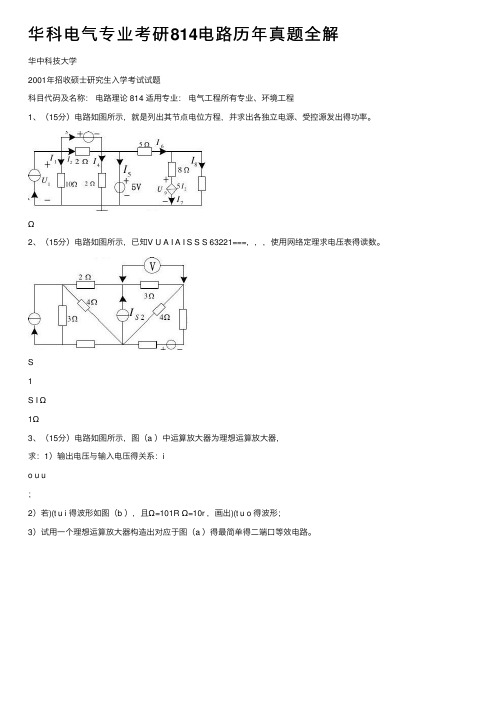
华科电⽓专业考研814电路历年真题全解华中科技⼤学2001年招收硕⼠研究⽣⼊学考试试题科⽬代码及名称:电路理论 814 适⽤专业:电⽓⼯程所有专业、环境⼯程1、(15分)电路如图所⽰,就是列出其节点电位⽅程,并求出各独⽴电源、受控源发出得功率。
Ω2、(15分)电路如图所⽰,已知V U A I A I S S S 63221===,,,使⽤⽹络定理求电压表得读数。
S1S I Ω1Ω3、(15分)电路如图所⽰,图(a )中运算放⼤器为理想运算放⼤器,求:1)输出电压与输⼊电压得关系:io u u;2)若)(t u i 得波形如图(b ),且Ω=101R Ω=10r ,画出)(t u o 得波形;3)试⽤⼀个理想运算放⼤器构造出对应于图(a )得最简单得⼆端⼝等效电路。
+-i u o)4、(15分)如图所⽰电路,在开关K 闭合前电路已达到稳态,试求:t ≥0时得相应)(t u c c18V5、(15分)电路如图所⽰,若在双⼝⽹络左端⼝加⼀电压源)(t u s 。
求:(1)⽹络函数) ()(s U s U H i o =;(2)冲激响应)(t u o ;(3)当t tus sin 3)(=伏时,电路得正弦稳态响应)(t u o 。
(t u S )(t u o6、(15分)如图所⽰为以正序对称三相电路,图中三相负载铭牌上标出:额定线电压为V 3220,额定有功功率为23、232kW ,额定功率因数为0、8(感性)。
当电源得交频率s rad 100=ω,电源得相电压V E A ο0220∠=?,线路阻抗为Ω+=)21(j Z L ,电源端对地电容为F C µ20000=,电源得中性点接得电感为mH L N )350(=。
求:(1)三相负载得参数;(2)线路上得电流A I ?,B I ?及C I ?(3)求当开关K 点闭合后,线路上得稳定电流A I ?,B I ?,C I ?以及接地电感N L 得电流LN I ?O7、(10分)如图所⽰电路,当V t u s 100)(=为直流电压源时,功率表得读数为400W ;将直流电压源)(t u s 换为⾮正弦电压源V t t u s )sin 290100()(ω+=时,安培表得读数为5A ,功率表得读数为670W ;此时若将电感L 断开,电压表读数为V 61618000,求参数1R ,2R ,L X 及1C X 。
华科2010到2013电路真题

华中科技大学2010年招收硕士研究生入学考试1.(18分)欲使下图所示电路中电阻Ω3的功率为3W ,求电流源?=SI 以及5V 电压源的功率。
+-+-23V5V5AΩ3Ω4Ω1Ω2SI2.(16分)电路如下图所示,设A1、A2为理想运放,试写出输出电压1o u 、2o u 、o u 与输入电压i u 的关系。
+-+∞+-+∞+-+-1o u2o u iu 1R 2R 3R 4R 5R3.(16分)求下图所示含互感的正弦稳态电路中的电压2∙U 。
+-+-Ω4+-Ω2V020∠V010∠2∙UΩ2j Ω3j Ω1j **4.(16分)电路如下图所示,已知端口*-11按理想电压源VU S 201=(1接电压源的正极性端)时,V U A I 5321=-=,;当端口*-11短路时,V U A I 3221==,。
问当端口*-11接电阻Ω=20R时,21U I 和各为多少?1N*1+-2U 1I5.(16分)在下图所示的正弦稳态电路中,已知S 闭合式,电压表的读数为50V ,功率表的读数为500W ;当S 打开时,电压表的读数仍为50V ,功率表的读数为750W ,A I C5=。
求参数1R 、1R 、2R 、L X 、C X 。
SI ∙**VS1R 2R LjX CI ∙CjX6.(18分)下图所示三相电路中,电压的线电压为380V ,频率为50Hz 。
对称三相感性负载的额定线电压为380V 、额定功率为500kW 、功率因数为0.71。
现欲在负载端并联电容,将电源侧的功率因数提高到0.9。
(1)不计线路阻抗的影响,即0=lZ ,计算并联电容值;(2)考虑线路阻抗的影响,且Ω=3j Z l ,试写出计算并联电容的详细步骤和每一步的表达式。
(3)上述两种情况下两个功率表读数的总和如何变化,予以定性说明,并简要说明理由。
**lZ l Z **lZC B A CCC对称三相负载2P1P7.(16分)如下图所示电路,已知Ω=====1,104321R R R R V U S,F C 11=,F C 22=,0=t 时开关S 闭合。
电动力学复习题库

一、单项选择题1. 学习电动力学课程的主要目的有下面的几条,其中错误的是( D )A. 掌握电磁场的基本规律,加深对电磁场性质和时空概念的理解B. 获得本课程领域内分析和处理一些基本问题的初步能力,为以后解决实际问题打下基础C. 更深刻领会电磁场的物质性,加深辩证唯物主义的世界观D. 物理理论是否定之否定,没有绝对的真理,世界是不可知的2. =⨯⋅∇)(B A ( C )A. )()(A B B A ⨯∇⋅+⨯∇⋅B. )()(A B B A ⨯∇⋅-⨯∇⋅C. )()(B A A B ⨯∇⋅-⨯∇⋅D. B A ⨯⋅∇)(3. 下列不是恒等式的为( C )。
A. 0=∇⨯∇ϕ B. 0f ∇⋅∇⨯= C. 0=∇⋅∇ϕ D. ϕϕ2∇=∇⋅∇4. 设222)()()(z z y y x x r '-+'-+'-=为源点到场点的距离,r 的方向规定为从源点指向场点,则( B )。
A. 0=∇r B. r r r ∇= C. 0=∇'r D. r r r'∇= 5. 若m 为常矢量,矢量3m R A R ⨯= 标量3m R R ϕ⋅= ,则除R=0点外,A 与ϕ应满足关系( A ) A. ▽⨯A =▽ϕ B. ▽⨯A =ϕ-∇ C. A =ϕ∇ D. 以上都不对6. 设区域V 内给定自由电荷分布)(x ρ,S 为V 的边界,欲使V 的电场唯一确定,则需要给定( A )。
A.S φ或S n ∂∂φ B. S Q C. E 的切向分量 D. 以上都不对 7. 设区域V 内给定自由电荷分布()ρx ,在V 的边界S 上给定电势s ϕ或电势的法向导数sn ϕ∂∂,则V 内的电场( A )A . 唯一确定 B. 可以确定但不唯一 C. 不能确定 D. 以上都不对 8. 导体的静电平衡条件归结为以下几条,其中错误的是( C )A. 导体内部不带电,电荷只能分布于导体表面B. 导体内部电场为零C. 导体表面电场线沿切线方向D. 整个导体的电势相等9. 一个处于x ' 点上的单位点电荷所激发的电势)(x ψ满足方程( C )A. 2()0x ψ∇=B. 20()1/x ψε∇=-C. 201()()x x x ψδε'∇=-- D. 201()()x x ψδε'∇=-10. 对于均匀带电的球体,有( C )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《电动力学》习题 集__________________一、思考题1、写出麦克斯韦方程组积分式和微分式,并说明建立方程组依据了哪些试验定律。
答:麦克斯韦方程组积分式为:⎰⎰⎰⎰⎰⎰⎰=•=••⎥⎦⎤⎢⎣⎡∂∂+=••∂∂-=•SVSL S L Ss d B dVs d E s d t E j l d B s d t B l d E 0100ρρρρρρρρρρρρρρεεμ 麦克斯韦方程组微分式为:000=•∇=•∇∂∂+=⨯∇∂∂-=⨯∇B E t E j B tB E ρρρρρρρερεμμ依据的试验定律为:静电场的高斯定理、静电场与涡旋电场的环路定理、磁场中的安培环路定理、磁场的高斯定理。
2、位移电流是怎样定义的?它与传导电流有何区别? 答:我们知道恒定电流是闭合的:()恒定电流.0=⋅∇J在交变情况下,电流分布由电荷守恒定律制约,它一般不再闭合。
一般说来,在非恒定情况下,由电荷守恒定律有.0≠∂∂-=⋅∇t J ρ现在我们考虑电流激发磁场的规律:()@.0J B μ=⨯∇ 取两边散度,由于0≡⨯∇⋅∇B ,因此上式只有当0=⋅∇J 时才能成立。
在非恒定情形下,一般有0≠⋅∇J ,因而()@式与电荷守恒定律发生矛盾。
由于电荷守恒定律是精确的普遍规律,故应修改()@式使服从普遍的电荷守恒定律的要求。
把()@式推广的一个方案是假设存在一个称为位移电流的物理量D J ,它和电流J 合起来构成闭合的量 ()()*,0=+⋅∇D J J 并假设位移电流D J 与电流J 一样产生磁效应,即把()@修改为 ()D J J B +=⨯∇0μ。
此式两边的散度都等于零,因而理论上就不再有矛盾。
由电荷守恒定律 .0=∂∂+⋅∇tJ ρ电荷密度ρ与电场散度有关系式 .0ερ=⋅∇E 两式合起来得:.00=⎪⎭⎫ ⎝⎛∂∂+⋅∇t E J ε与()*式比较可得D J 的一个可能表示式.0tEJ D ∂∂=ε 位移电流与传导电流有何区别:位移电流本质上并不是电荷的流动,而是电场的变化。
它说明,与磁场的变化会感应产生电场一样,电场的变化也必会感应产生磁场。
而传导电流实际上是电荷的流动而产生的。
3、分别写出电荷守恒定律的积分式和微分式,并由此写出恒定电流的连续性方程。
答:电荷守恒定律的积分式和微分式分别为:0=∂∂+•∇∂∂-=•⎰⎰t J dV t ds J S Vρρρρ恒定电流的连续性方程为:0=•∇J4、在有介质存在的电磁场中,极化强度矢量p 和磁化强度矢量M 各是怎样定义的?并写出P 与;M 与j ;E 、D 与p 以及B 、H 与M 的关系。
答:极化强度矢量p :由于存在两类电介质:一类介质分子的正电中心和负电中心不重和,没有电偶极矩。
另一类介质分子的正负电中心不重和,有分子电偶极矩,但是由于分子热运动的无规性,在物理小体积内的平均电偶极矩为零,因而也没有宏观电偶极矩分布。
在外场的作用下,前一类分子的正负电中心被拉开,后一类介质的分子电偶极矩平均有一定取向性,因此都出现宏观电偶极矩分布。
而宏观电偶极矩分布用电极化强度矢量P 描述,它等于物理小体积V ∆内的总电偶极矩与V ∆之比,.VpP i∆=∑ρi p 为第i 个分子的电偶极矩,求和符号表示对V∆内所有分子求和。
磁化强度矢量M :介质分子内的电子运动构成微观分子电流,由于分子电流取向的无规性,没有外场时一般不出现宏观电流分布。
在外场作用下,分子电流出现有规则取向,形成宏观磁化电流密度M J 。
分子电流可以用磁偶极矩描述。
把分子电流看作载有电流i 的小线圈,线圈面积为a ,则与分子电流相应的磁矩为: .ia m =介质磁化后,出现宏观磁偶极矩分布,用磁化强度M 表示,它定义为物理小体积V ∆内的总磁偶极矩与V ∆之比,.Vm M i∆=∑M B H P E D M j P M P ρρρρρρρρρ-=+=⨯∇=•∇=00,,,μερ5、写出导体表面的边界条件。
答:理想导体表面的边界条件为:.,0α=⨯=⨯H n E n ⎪⎪⎭⎫⎝⎛=•=•.0,B n D n σ。
它们可以形象地表述为:在导体表面上,电场线与界面正交,磁感应线与界面相切。
6、在球坐标系中,若电势ϕ不依赖于方位角φ,写出这种情形下拉氏方程的通解。
解:拉氏方程在球坐标中的一般解为:()()()φθφθφθϕm P R d R c m P R b R a R m n m n n nm nnm m n mn n nm n nm sin cos cos cos ,,,1,1∑∑⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=++ 式中nm nm nm nm d c b a 和,,为任意的常数,在具体的问题中由边界条件定出。
()θcos m n P 为缔合勒让德函数。
若该问题中具有对称轴,取此轴为极轴,则电势ϕ不依赖于方位角φ,这球形下通解为:()()θθϕcos ,cos 1n n n n n n n P P R b R a ∑⎪⎭⎫ ⎝⎛++=为勒让德函数,n n b a 和是任意常数,由边界条件确定。
7、研究磁场时引入矢势A 的根据是什么?矢势A 的意义?答:引入矢势A 的根据是:磁场的无源性。
矢势A 的意义为:它沿任一闭合回路的环量代表通过以该回路为界的任一曲面的磁通量。
只有A 的环量才有物理意义,而每点上的A (x )值没有直接的物理意义。
8、什么是平面时谐电磁波?平面时谐电磁波有那些性质?写出一般坐标系下平面电磁波的表达式。
答:平面时谐电磁波是交变电磁场存在的一种最基本的形式。
它是传播方向一定的电磁波,它的波阵面是垂直于传播方向的平面,也就是说在垂直于波的传播方向的平面上,相位等于常数。
平面时谐电磁波的性质:(1)电磁波为横波,E 和B 都与传播方向垂直; (2)E 和B 同相,振幅比为v ;(3 E 和B 互相垂直,E ×B 沿波矢k 方向。
9、电磁波在导体中和在介质中传播时存在那些区别?电磁波在导体中的透射深度依赖于哪些因素?答:区别:(1)在真空和理想绝缘介质内部没有能量的损耗,电磁波可以无衰减地传播;(2)电磁波在导体中传播,由于导体内有自由电子,在电磁波电场作用下,自由电子运动形成传导电流,由电流产生的焦耳热使电磁波能量不断损耗。
因此,在导体内部的电磁波是一种衰减波。
在传播的过程中,电磁能量转化为热量。
电磁波在导体中的透射深度依赖于:电导率和频率10、写出电磁场用矢势和标势表示的关系式。
答:电磁场用矢势和标势表示的关系式为:⎪⎩⎪⎨⎧∂∂--∇=⨯∇=t A E A B ϕ 11、写出推迟势的基本公式和达朗贝尔方程。
答:推迟势为:()()''0'0',4,4,,dvrc r t x J t x A dv rc r t x t x ⎰⎰⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-=πμπερϕ达朗贝尔方程为:⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎭⎫⎝⎛=∂∂+•∇-=∂∂-∇-=∂∂-∇011120222202222t c A t c Jt Ac A ϕερϕϕμ12、爱因斯坦建立狭义相对论的基本原理是什么?其内容如何?答:(1)相对性原理:所有的惯性参考系都是等价的。
物理规律对于所有惯性参考系都可以表为相同的形式。
(2)光速不变原理:真空中的光速相对于任何惯性系沿任一方向恒为c ,并与光源运动无关。
13、写出相对论时空坐标变换公式和速度变换公式。
答:坐标变换公式:222'''22'11cv x c v t t zz yy cv vt x x --===--=速度变换公式:⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧--=--=--=222'222'2'11111c vu c v u u c vu c v u u c vu v u u xz z xy y xx x 14、导出洛仑兹变换时,应用了哪些基本原理?还做了哪些附加假设?洛仑兹变换同伽利略变换二者的关系怎样?答:应用的基本原理为:变换的线性和间隔不变性。
基本假设为:光速不变原理(狭义相对论把一切惯性系中的光速都是c 作为基本假设,这就是光速不变原理)、空间是均匀的并各向同性,时间是均匀的、运动的相对性。
洛仑兹变换与伽利略变换二者的关系:伽利略变换是存在于经典力学中的一种变换关系,所涉及的速率都远小于光速。
洛仑兹变换是存在于相对论力学中的一种变换关系,并假定涉及的速率等于光速。
当惯性系'S (即物体)运动的速度c V <<时,洛伦兹变换就转化为伽利略变换,也就是说,若两个惯性系间的相对速率远小于光速,则它以伽利略变换为近似。
15、你学过哪些四维力学矢量?其形式如何?答:四维力学矢量为:(1)能量-动量四维矢量(或简称四维动量):⎪⎭⎫⎝⎛=W c i p p ,μ(2)速度矢量:dtdx d dx U μμμγτ==(3)动量矢量:μμU m p 0=(4)四维电流密度矢量:()ρρμμμic J J U J ,,0==(5)四维空间矢量:()ict x x ,=μ(6)四维势矢量:⎪⎭⎫⎝⎛=ϕμc i A A ,(7)反对称电磁场四维张量:νμμνμνx A x A F ∂∂-∂∂=(8)四维波矢量:⎪⎭⎫ ⎝⎛=c w i k k ,μ二、证明题1、试由毕奥-沙伐尔定律证明0=•∇B ρ证明:由式:()()''0'3'0144dv rx J dv r r x J B ∇⨯=⨯=⎰⎰πμπμ又知:()()''11x J r r x J ⨯⎪⎭⎫ ⎝⎛∇=⎥⎦⎤⎢⎣⎡⨯∇,因此 ()()⎰⎰=⨯∇=⨯∇=rdv x J A A dv rx J B ''0''04 4πμπμ式中由 ()0=⨯∇•∇=•∇A B 所以原式得证。
2、试由麦克斯韦方程组证明电磁场的边界条件()()().0;;0121212=-•=-•=-⨯B B n D D n E E n ρρρρρρρρρδ 解:()δδδρ=-=-⋅∴∆=⋅∆-⋅∆=•⎰⎰n n fVS D D D D n S D n S D n S dVs d D 121212.ρρρρρρρρρΘ即:对于磁场B ,把0=⋅⎰s d B Sρρ应用到边界上无限小的扁平圆柱高斯面上,重复以上推导可得:()01212=-⋅-B B n B B n n ρρρ即:作跨过介质分界面的无限小狭长的矩形积分回路,矩形回路所在平面与界面垂直,矩形长边边长为l ∆,短边边长为'l ∆。
因为⎰=⋅0dl E ,作沿狭长矩形的E 的路径积分。
由于'l ∆比l ∆小得多,当0'→∆l 时,E 沿'l ∆积分为二级小量,忽略沿'l ∆的路径积分,沿界面切线方向积分为:012=∆-∆l E l E t t 即:()*,012--t t E E 。
