角平分线的性质导学案
角平分线的性质(1)导学案

角平分线的性质【学习目标】:1.要求学生掌握角平分线的性质定理,会用这个定理解决一些简单问题。
3.能够作已知角的角平分线,并会熟练地写出已知、求作和作法,可以说明为什么所作的直线是角平分线。
3.会用全等知识证明角平分线的性质定理【学习重难点】:用全等知识证明角平分线性质定理。
【自学指导】:一、阅读P56---P57并回答下列问题:1)作已知角的平分线的方法是什么?在作法的第二步中,去掉“大于12MN的长”这个条件行吗?2)作∠AOP的平分线,要求保留作图痕迹并能说出作法。
3)点到直线的距离是什么?(点到直线的垂线段的长叫点到直线的距离)4)角平分线的性质:。
5)利用图(2)证明这个性质定理。
6)结合图(2)用几何语言表示这个定理:∵OP平分∠,AP⊥,BP⊥,∴PA= .7)由6)可知角平分线定理的作用是什么?应用该定理必须具备什么样的前提条件?二、自学检测:1.如图,在△ABC中,∠C=90°,AD是∠CAB的角平分线,DE⊥AB于点E,BC=8,BD=5,求DE的长。
2.如图:在△ABC中,∠C=90°AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;求证:CF=EB三、学会小结:1.定理的应用: 应用角平分线的性质定理所具备的前提条件是:有角的,有垂直 ;②若图中有角平分线,,可尝试添加辅助线的方法:向角的两边引 .2、该性质可以独立作为证明两条线段相等的依据.所以若遇到有关角平分线,又要证线段相等的问题,•我们可以直接利用性质解决问题.四、课堂作业△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别为E,F。
求证:EB=FC。
角平分线的性质导学案

12.3 角的平分线的性质导学案学习目标:1、会用尺规作已知角的平分线,知道作法的合理性;2、探索并证明角的平分线的性质定理;3、能用角的平分线的性质解决简单问题。
学习重点:探索并证明角的平分线的性质定理。
学习难点:角平分线性质定理的应用。
学习过程:一、情境导入问题:在S区有一个集贸市场P,它建在公路与铁路所成角的平分线上,要从P点建两条路,一条到公路,一条到铁路。
问题1:怎样修建道路最短?问题2:往哪条路走更近呢?P二、自学指导让学生先阅读课本48-49页内容,思考下面的问题:1、平分角的仪器怎么使用?2、用尺规如何平分已知角?3、角平分线的性质是4、角平分线的性质怎么证明?5、证明几何命题的一般步骤是:(1);(2);(3)。
三、自主探究合作展示探究(一):角平分仪平分角的道理:1、为什么角平分仪能平分一个角?(小组讨论回答)。
探究(二)如何作尺规作出一个角的平分线呢?1、分析角平分仪原理,你能利用圆规和直尺作角的平分线吗?(小组讨论)2、师生共同用尺规作角的平分线。
已知:∠AOB.求作:∠AOB的平分线.作法:(1)以O为圆心,适当长为半径作弧,分别交OA、OB于M、N.(2)分别以M、N为圆心,大于1MN的长为半径作弧.两弧在2∠AOB内部交于点C.(3)作射线OC。
射线OC 即为所求.3、让学生回答为什么射线OC 是∠AOB 的平分线。
4、在上面作法的第二步中,去掉“大于12MN 的长”这个条件行吗?探究(三)、探究角平分线的性质:如图4,OA 是∠BAC 的平分线,点O 是射线AM 上的任意一点. 操作测量:取点O 的三个不同的位置,分别过点O 作OE ⊥AB ,OD ⊥AC,点D 、E 为垂足,测量OD 、OE 的长.将三次数据填入下表:根据测量结果,猜想线段OD 与OE 的大小关系,猜想角平分线的性质结论是: 。
让学生用学过的知识证明此结论:教师引导学生分析这个文字命题的条件和结论,并找出结论中的隐含条件,最后让学生画出图形,用符号语言写出已知和求证,图4ODOE 第一次 第二次第三次BOAM并独立完成证明过程。
角平分线的性质导学案
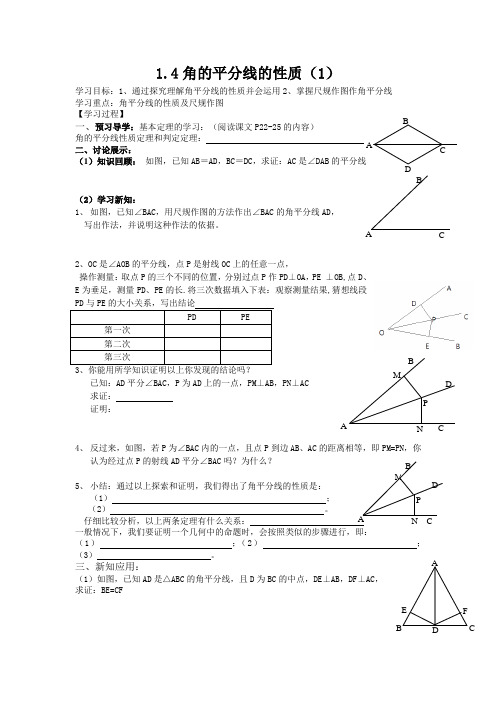
1.4角的平分线的性质(1)学习目标:1、通过探究理解角平分线的性质并会运用2、掌握尺规作图作角平分线 学习重点:角平分线的性质及尺规作图【学习过程】 一、预习导学:基本定理的学习:(阅读课文P22-25的内容)角的平分线性质定理和判定定理: 二、讨论展示:(1)知识回顾: 如图,已知AB =AD ,BC =DC ,求证:AC 是∠DAB 的平分线(2)学习新知:1、 如图,已知∠BAC ,用尺规作图的方法作出∠BAC 的角平分线AD ,写出作法,并说明这种作法的依据。
2、OC 是∠AOB 的平分线,点P 是射线OC 上的任意一点,操作测量:取点P 的三个不同的位置,分别过点P 作PD ⊥OA ,PE ⊥OB,点D 、E 为垂足,测量PD 、PE 的长.将三次数据填入下表:观察测量结果,猜想线段3、你能用所学知识证明以上你发现的结论吗? 已知:AD 平分∠BAC ,P 为AD 上的一点,PM ⊥AB ,PN ⊥AC 求证: 证明:4、 反过来,如图,若P 为∠BAC 内的一点,且点P 到边AB 、AC 的距离相等,即PM=PN ,你认为经过点P 的射线AD 平分∠BAC 吗?为什么?5、 小结:通过以上探索和证明,我们得出了角平分线的性质是:(1) ; (2) 。
仔细比较分析,以上两条定理有什么关系:一般情况下,我们要证明一个几何中的命题时,会按照类似的步骤进行,即:(1) ;(2) ;(3) 。
三、新知应用:(1)如图,已知AD 是△ABC 的角平分线,且D 为BC 的中点,DE ⊥AB ,DF ⊥AC , 求证:BE=CFA B D C A B C C A B CN M P D A B C N M P D。
角平分线性质2
求证:
证明:
完成知识技能2:
1、认真阅读21页例题的解题过程并能独立完成。
2、思考点P在∠A的平分线上吗?你会证明吗?
3、由此说明三角形的三条角平分线有什么关系?
二、记录预习中存在的问题:
三、课堂学习:
(一)完善并整理自学内容
(二)以小组为单位合作交流自学中存在的问题
(三)汇报展示自学效果
(四)质疑与教师精讲
八年级数学导学案课题:11.3角的平分线的性质(2)
主备人:备课时间:月日学科领导签字:上课时间:月日
1分工预设
人员
分配
任务
2学情预设
3知识点:
学习目标:
1、掌握角平分线上点的判定。
2、能初步应用判定解决实际问题。
3、提高综合运用三角形全等的有关知识解决问题的能力。
4、初步了解角的平分线的判定在生活、生产中的应用。
4关键点:
5易错点
6.拓展变式
7.注意问题
8.反思提高
重点:角平分线上点的判定的证明及运用
难点:角平分线上点的判定的探究
学习过程:
一自主学习完成知识技能1:
1、阅读教材第21页思考你想怎么做?
2、操作(保留作图痕迹):
3、从上述操作中你能发现什么结论?试加以证明:
4、结论(文字描述):
几何语言:
已知:
(五)课堂练习课堂练习(12分钟)
1、教材22页1题:2、22页练习:
(六)课堂小结:八)课堂检测(10分钟)
1.如图ll.3—9, 且DE=CE,下列结论错误的是( ).
, ,
2.如图11.3—10,已知0为 的平分线的交点,0E_kAC于E,若0E=2
求0到AB与0到CD的距离之和.
角平分线的性质

隆回县雨山中学八年级下数学导学案第7课时 角的平分线的性质(1)班级_______姓名 _____ 主备人 徐娟学习目标:1、通过探究理解角平分线的性质并会运用2、掌握尺规作图作角平分线 学习重点:角平分线的性质及尺规作图一、预习导学:(阅读课文P22-24的内容)1.角的平分线性质定理和判定定理:2.如图,已知AB =AD ,BC =DC ,求证:AC 是∠DAB 的平分线二、合作探究、展示点评1、 如图,已知∠BAC ,用尺规作图的方法作出∠BAC 的角平分线AD , 写出作法,并说明这种作法的依据。
2、OC 是∠AOB 的平分线,点P 是射线OC 上的任意一点, 操作测量:取点P 的三个不同的位置,分别过点P 作PD ⊥OA ,PE ⊥OB,点D 、E 为垂足,测量PD 、PE 的长.将三次数据填入下表:观察测量结果,猜想线段已知:如图AD 平分∠BAC ,P 为AD 上的一点,PM ⊥AB ,PN ⊥AC 求证:证明:4、 反过来,如图,若P 为∠BAC 内的一点,且点P 到边AB 、AC 的距离相等,即PM=PN ,你认为经过点P 的射线AD 平分∠BAC 吗?为什么?ABCA BN MP D ABC5、 小结:通过以上探索和证明,我们得出了角平分线的性质是:(1) ; (2) 。
仔细比较分析,以上两条定理有什么关系: 一般情况下,我们要证明一个几何中的命题时,会按照类似的步骤进行,即:(1) ;(2) ;(3) 。
三、新知应用:(1)如图,已知AD 是△ABC 的角平分线,且D 为BC 的中点,DE ⊥AB ,DF ⊥AC , 求证:BE=CF(2)如图:△ABC 的角平分线BM 、CN 相交于点P 。
求证:点P 到三边AB 、BC 、CA 的距离相等。
探究:点P 在∠A 的平分线上吗?为什么?四.课堂小结: 五.当堂测评1、在△ABC 中∠C=90°,∠A 的平分线交BC 于D ,BC=14CM , BD :DC :=4:3,则点D 到AB 的距离为___________。
角的平分线的性质(一)
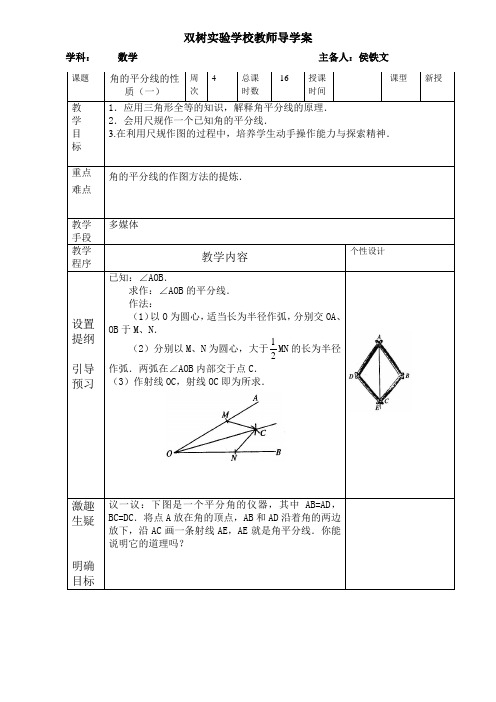
双树实验学校教师导学案学科:数学主备人:侯铁文课题角的平分线的性质(一)周次4 总课时数16 授课时间课型新授教学目标1.应用三角形全等的知识,解释角平分线的原理.2.会用尺规作一个已知角的平分线.3.在利用尺规作图的过程中,培养学生动手操作能力与探索精神.重点难点角的平分线的作图方法的提炼.教学手段多媒体教学程序教学内容个性设计设置提纲引导预习已知:∠AOB.求作:∠AOB的平分线.作法:(1)以O为圆心,适当长为半径作弧,分别交OA、OB于M、N.(2)分别以M、N为圆心,大于12MN的长为半径作弧.两弧在∠AOB内部交于点C.(3)作射线OC,射线OC即为所求.激趣生疑明确目标议一议:下图是一个平分角的仪器,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线.你能说明它的道理吗?展示交流精讲释疑演示角平分仪器的操作过程,使学生直观了解得到射线AC的方法.AB=ADBC=DCAC=AC所以△ABC≌△ADC(SSS).所以∠CAD=∠CAB.即射线AC就是∠DAB的平分线.老师再提出问题:通过上述探究,能否总结出尺规作已知角的平分线的一般方法.自己动手做做看.然后与同伴交流操作心得.已知:∠AOB.求作:∠AOB的平分线.作法:(1)以O为圆心,适当长为半径作弧,分别交OA、OB于M、N.(2)分别以M、N为圆心,大于12MN的长为半径作弧.两弧在∠AOB内部交于点C.(3)作射线OC,射线OC即为所求.教师根据学生的叙述,作多媒体课件演示,使学生能更直观地理解画法,提高学习数学的兴趣1.在上面作法的第二步中,去掉“大于12MN的长”这个条件行吗?2.第二步中所作的两弧交点一定在∠AOB的内部吗?(设计这两个问题的目的在于加深对角的平分线的作法的理解,培养数学严密性的良好学习习惯)盘点收获总结提升本节课中我们利用已学过的三角形全等的知识,•探究得到了角平分线仪器的操作原理,由此归纳出角的平分线的尺规画法,进一步体会温故而知新是一种很好的学习方法.巧设练习达标检测任意画一角∠AOB,作它的平分线.作业布置板书设计教学反思。
角平分线的性质导学案

1.4 角平分线的性质与判定导学案(一)【导学目标】1、掌握角平分线的性质定理及判定定理;2、理解原命题、逆命题、逆定理的概念及关系。
【导学重点】掌握角平分线的性质定理及判定定理;【导学难点】掌握角平分线的性质定理及判定定理;【强基导学】1、判定三角形全等的方法有哪些?判定直角三角形全等的方法呢?2、斜边、直角边定理的内容是什么?3、什么是角平分线?4、点到直线的距离的定义,完成任务1:【自主探学】阅读教材P22【任务1】如图,在∠AOB的平分线OC上任取一点P,作PD⊥OA ,PE⊥OB,垂足分别为点D,E,试问PD与PE相等吗?请写出证明过程。
【归纳】角平分线的性质定理:角平分线上的点到。
几何语言描述角平分线的性质定理:∵∴,完成任务2:【带问自学】阅读教材P23【任务2】如图,点P在∠AOB的内部,作PD⊥OA,PE⊥OB,垂足分别为点D,E. 若PD= PE,那么点P在∠AOB的平分线上吗?请说明理由。
【归纳】角平分线的判定定理:角的内部到角的两边距离相等的点 。
用几何语言描述角平分线的判定定理:∵∴【互动帮学】例1 如图,∠BAD =∠BCD = 90°,∠1=∠2. (1)求证:点B 在∠ADC 的平分线上; (2)求证:BD 是∠ABC 的平分线.【知识梳理】1、角平分线的性质定理是 。
2、角平分线的判定定理是 。
【达标评学】1. 如图,在△ABC 中,∠B =90°,AD 平分∠BAC 交BC 于D ,BC =10cm ,CD =6cm ,则点D 到AC 的 距离是: 。
2、如图,在Rt △ABC 中,AC =4,BC =3,AB =5, 点D 是三角形内角平分线的交点,则点D 到AB 的 距离是: 。
A3、如图,在△ABC中,∠C=90°,点D在AC上,DE⊥AB于E,且DC=DE,∠CBD:∠A=2:1,则∠A的度数为。
【布置作业】教材P26A组1、2题BEADC第3题图。
角平分线的性质和判定定理

角平分线的性质及判定定理导学案课前准备:1.我们学过哪些与“角的平分线”有关的结论:2.什么是“点到直线的距离”:3.我们学过的证明线段和角相等的方法有哪些: 学习目标:1.通过经历自主证明角平分线的性质和判定定理的过程,理解并掌握定理,会用符号语言描述定理;2.通过例题和针对练习,进一步理解定理,会解决与定理有关的问题,发展推理能力,体会演绎思想;3.掌握角平分线应用中常见辅助线的作法,体会建模思想。
一、交流与发现活动①:搭档合作,自主证明角平分线的性质定理(1分钟)活动②:针对练习1.见PPT.2.如图,在⊿ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,BC=15, CD:BD=1:2,AB=20,求S⊿ABD面积。
二、交流与发现活动①:搭档合作,共同证明角平分线的判定定理(1分钟)活动②:针对练习1.见PPT.2.已知,如图,BN、CP是⊿ABC的两条角平分线,交点为点O,求证:。
证明:三、学以致用例、已知,如上图,AM、BN,CP是⊿ABC的三条角平分线。
探究性结论1:探究性结论2:针对练习(思维延伸):1.已知:如图,⊿ABC两个相邻外角的平分线BD、CE相交于点P,求证:点P在∠A的平分线上。
探究性结论3:2.加油站位置在哪儿?课堂小结:我学到了①、②、③、④、┅┅拓展提升:一图二问1.如图,在Rt ⊿ ABC中,∠ C为直角, BD平分∠ ABC,且AC=8, BC=6,AB=10,求CD的长。
(温馨提示:等面积求高)2.如上图,在Rt ⊿ ABC中,∠ C为直角, BD平分∠ ABC,DE ⊥ AB于点E,而且AC=8,BC=6,AB=10,求⊿ADE的周长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
角平分线的性质(1)导学案
学习目标:
1.会用尺规作图作角平分线。
2.探究理解角平分线的性质并会应用。
一、自主学习
角平分线:从一个的顶点引出一条,把这个角分成两个的角,这条叫做这个角的角平分线。
二、探究活动
活动1:
不利用工具,请你将一张用纸片做的角分成两个相等的角。
你有什么办法?
活动2:
如果前面活动中的纸片换成木板、钢板等没法折的角,又该怎么办呢?
你能用三角形全等的知识说明角平分仪的工作原理吗?
活动3:
如何用尺规作角的平分线?
探究验证:
1.操作测量:在上图的角平分线oc上取点P的三个不同的位置,分别过点P作PD⊥OA,PE ⊥OB,点D、E为垂足,测量PD、PE的长.将三次数据填入下表:
PD PE
第一次
第二次
第三次
2.观察测量结果,猜想线段PD与PE的大小关系,PD PE
3.得出结论:
证明结论:
已知:
求证:
证明:
活动4:
师生共同总结证明命题的步骤A
D
O
B
E
P
C
O
A
C
B
三、例题讲解:
例:在△OAB 中,OE 是∠ AOB 的角平分线,且EA=EB ,EC 、ED 分别垂直OA ,OB ,垂足为C ,D ,求证:AC=BD 。
四、课堂达标:
1.如图,OC 是∠AOB 的平分线,点P 在OC 上,PD ⊥OA,PE ⊥OB,垂足分别是D 、E,PD=4cm,则PE=__________cm.
2.如图,OC 平分∠AOB , PM ⊥OB 于点M ,PN ⊥OA 于点N , △POM 的面积为6,OM=6,则PN=_______。
3:如图,在△ABC 中,∠C =900,AD 平分∠BAC 交BC 于点D ,若BC =8,BD =5,则点D 到AB 的距离为?
O
A
B
E
C D
A D
O
B
E
P
C
A
C
D
B
E
E
A
B
M
N
P C。
