等级相关系数

合集下载

各种相关系数介绍与对比

各种相关系数介绍与对比各种相关系数介绍与对比按照变量的不同测量层次对各种相关系数简单介绍：1、定类变量——定类变量用于测量两个定类变量的相关系数，主要有Lambda 与T au-y两种。

（1）Lambda（λ）系数分为：对称形式——用于测量两个变量间的关系是对等的，即无自变量与因变量之分。

非对称形式——测量两个变量间的关系有自变量与因变量之分。

（2） Tau-y系数：用于测量变量间非对称关系的。

2、定序变量——定序变量如果测量两个定序尺度变量间的关系，可用Gamma系数、dyx系数和斯皮尔曼等级相关系数。

（1）Gamma（G）系数：分析两个变量间的对等关系，即无自变量与因变量之分。

（2）dyx系数：等级相关系数，两个变量间的关系是非对称的。

（3）斯皮尔曼(Spearman)等级相关系数(ρ)：考虑单个个案在两个变量上的等级差异，测量两变量间对等相关关系。

3、定距变量——定距变量测量两个定距变量相关系数的最常用指标是皮尔森（Pearson）相关系数（γ）。

（要求N≥50而且两个变量的分布应近似于正态分布。

）4、定类变量——定距变量两个变量中，自变量为定类变量，因变量为定距变量时，采用相关比率来测量两者间相关程度。

（又称eta平方系数 E）5、定类变量——定序变量对一个定类变量例如性别，与一个定序变量例如收入水平关系的分析：第一，用theta系数（θ），专门测量定类变量与定序变量间关系有无和强度，非对称关系。

第二，采用λ系数和Tau-y系数，即将定序变量作为定类变量处理。

6、定序变量——定距变量处理一个定序变量例如教育水平，与一个定距变量如年均收入之间的关系，采用二种办法：第一，将定序变量看作定类变量，采用相关比例测量法。

第二，将定序变量看作定距变量，采用γ相关系数。

小结：在分析两个变量关系时，选择哪种相关系数，主要考虑两个方面：1、变量的测量层次；2、变量关系的类别，即是对等的还是非对称的。

斯皮尔曼相关系数公式

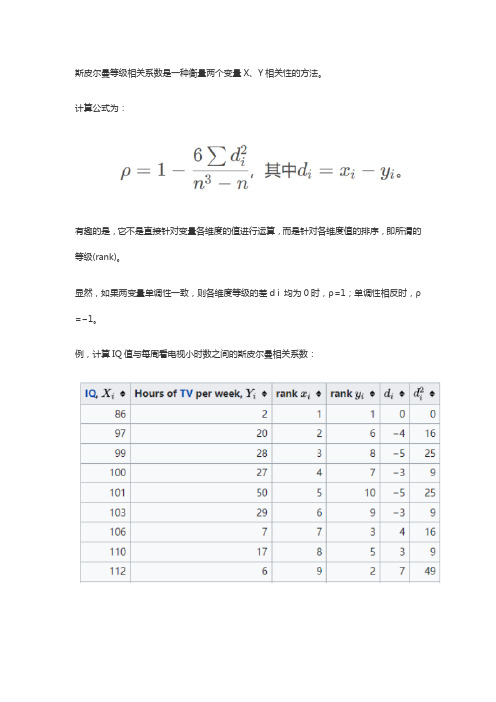
斯皮尔曼等级相关系数是一种衡量两个变量X、Y相关性的方法。

计算公式为：
有趣的是，它不是直接针对变量各维度的值进行运算，而是针对各维度值的排序，即所谓的等级(rank)。

显然，如果两变量单调性一致，则各维度等级的差d i 均为0时，ρ=1；单调性相反时，ρ=−1。

例，计算IQ值与每周看电视小时数之间的斯皮尔曼相关系数：
斯皮尔曼等级相关系数以Charles Spearman命名，并经常用希腊字母ρ（rho）表示其值。

斯皮尔曼等级相关系数用来估计两个变量X、Y之间的相关性，其中变量间的相关性可以使用单调函数来描述。

如果两个变量取值的两个集合中均不存在相同的两个元素，那么，当其中一个变量可以表示为另一个变量的很好的单调函数时（即两个变量的变化趋势相同），两个变量之间的ρ可以达到+1或-1。

操作篇 09_等级相关系数的计算与检验

计算机辅助英语教学与研究（操作篇）浙江师范大学外语学院夏建新第9讲用Excel计算等级相关系数目次9.1 等级相关的概念 (1)9.2 适用条件与计算公式 (1)9.3 操作练习 (1)9.4 课堂练习 (3)9.5 积差相关与等级相关比较 (4)9.6 肯德尔和谐系数的计算 (5)9.7 Task 9 (6)9.1 等级相关的概念等级相关是指以等级次序排列或以等级次序表示的变量之间的相关。

主要包括斯皮尔曼(Spearman)二列等级相关及肯德尔和谐系数(the Kandall Coefficient of Concordance)多列等级相关。

9.2 适用条件与计算公式z当测量到的数据不是等距或等比数据，而是具有等级顺序的测量数据；z（或）得到的数据是等距或等比的测量数据，但其所来自的总体分布不是正态的;z（或）样本容量不一定大于50（或30）在无法满足积差相关系数的适用条件时，只要满足上述三个条件中的任何一个，都可以计算其等级相关系数。

由于该系数并不要求总体是否呈正态分布，也不要求N>50（或N>30），所以应用范围较广。

斯皮尔曼等级相关系数r R的计算公式为：在该式中，D = (Rx – Ry)，它表示对偶等级之差。

9.3 操作练习计算下表的相关系数。

学号学习潜能自学能力199901 71 7199902 68 7199903 84 2199904 64 9199905 76 5199906 69 8199907 90 3199908 71 8199909 66 10199910 71 6(注：自学能力是按能力高低从小往大的数字打的，即数值越小，说明自学能力越强)步骤一：先用Excel中的“排序”工具对“学习潜能”进行等级赋值，操作步骤如下所示：数据→ 排序 → 主要关键字 → 学习潜能 → 递减 → 有标题行→ 确定结果如下：学号学习潜能自学能力19990790 319990384 219990576 519990171 719990871 819991071 619990669 819990268 719990966 1019990464 9然后对“学习潜能”进行赋值，结果如下：序号学号学习潜能等级1 自学能力1 19990790 1 32 19990384 2 23 19990576 3 55 19990171 5 74 199908715 86 19991071 5 67 19990669 7 88 19990268 8 79 19990966 9 1010 19990464 10 9说明：因4、5、6号三位学生的“学习潜能”分相等，其赋值取三者的平均等级5（计算方法为名次的总和除以同名次人数，即(4+5+6)/3=5）。

等级相关系数计算公式及其

的作用。今考文献
陈启光，沈其君．医学统计学．苏科学技术出版社，９江１”：
１ ·２．７２１８
写“ 等级相关” 一节时，采用对双变盆（，编写的ｘＹ）秩次Ｒ、：Ｒ直接作Ｐｎ积差相关系数公式计算等级相关系数。：ｅ拼ｏ
这样，教师讲授其计算公式时只需简单回顾一下Ｐ明。ｅ。积差相关系数的计算公式即可计算时只需将两变且的对应秩
７３
由表２可得：二，，；Ｔ０Ｔ二１同时将表２行数据代人公下
式得：
几二
由此可见，当ｘ与Ｙ中相同秩次较多时，二ｒ。、。
［１１）一０１一（护一０历］（＋）刃二住８７１１了［１１）一ｘ了［１１巧〕Ｚｆ（护一０历〕Ｚｏ（护一０一ｘ）
０（时前ｒ０得ｒ钾、〕。、＜时此校正．＜，到｝１｝１，．孙。：）。，［即ｔ
综上所在ｘ与Ｙ中无相同秩次的情况下，：ｒ，述．．ｒ二。、；ｘＹ在与中有较多相同秩次的情况下，＞二即 ‘ 、与；正，
相关校正后可使相关系数绝对值减小，尸值增大；相关校负正后可使相关系数绝对值增大，尸值减小。因此，建议在编次摘人计算器或０吧系列组件Ｅｅ即能求得等级相关系伍ｃｃｘｌ数，学生更容易理解，更容易掌握，起到触类旁通和融会贯通
ＹＲ＿Ｒ，
ｌ．ｒ ” 恶
乡约号
．且内 ‘ ，｝４．曰６７已６，
么，上述３个
当Ｘ与Ｙ中相同秩次较多时，应计算ｒ的校正值：，

pearson相关系数分段

pearson相关系数分段
Pearson相关系数是用来衡量两个变量之间线性相关程度的一个指标，其取值范围在-1到1之间。

根据相关系数的取值范围，可以将相关程度分为以下几个等级：
1.完全正相关：当相关系数为1时，表示两个变量之间存在完全正线性关系，即一个变量的变化会完全引起另一个变量的相同方向变化。

2.高度正相关：当相关系数在0.8至0.99之间时，表示两个变量之间存在高度正线性关系，即一个变量的变化大部分会引起另一个变量的相同方向变化，但可能存在一些离群值或噪声。

3.中等程度相关：当相关系数在0.4至0.6之间时，表示两个变量之间存在中等程度的相关性，即一个变量的变化对另一个变量的影响介于强和弱之间。

4.弱相关：当相关系数在0.2至0.4之间时，表示两个变量之间存在弱相关性，即一个变量的变化对另一个变量的影响较小。

5.极弱相关或无相关：当相关系数在-1至0.2之间时，表示两个变量之间存在极弱相关性或无相关性，即一个变量的变化对另一个变量的影响很小或没有影响。

需要注意的是，Pearson相关系数的取值范围并不是严
格划分好的，有些情况下可能会有一定的重叠。

此外，相关系数的显著性检验也是非常重要的，只有当相关系数显著时，才能认为两个变量之间存在真正的线性关系。

怎么算等级相关系数的方法

怎么算等级相关系数的方法
等级相关系数（Spearman's Rank Correlation Coefficient）是一种用于衡量两个变量之间等级顺序相关性的统计方法。

它不要求变量服从正态分布，适用于有序变量或等级数据。

以下是计算等级相关系数的步骤：
1. 首先，对两个变量的数据进行排序，将其转换为等级数据。

如果有相同的数值，则使用平均排名。

2. 计算每个变量的等级之差（D）。

对于每一对等级（X和Y），计算Y的等级减去X的等级，得到差值D。

3. 计算每个D的平方值（D^2）。

4. 计算等级差值的和（SigmaD）。

5. 使用以下公式计算等级相关系数：
等级相关系数= 1 - [6 * SigmaD^2 / (n^3 - n)]
其中，n表示样本的数量。

等级相关系数的取值范围为-1到1。

当相关系数接近1时，表示变量的等级顺序高度一致；当相关系数接近-1时，表示变量的等级顺序完全相反；当相关系数接近于0时，表示变量的等级顺序无关。

请注意，以上是计算等级相关系数的传统方法。

在某些统计软件中，也可以直接使用相应的函数来计算等级相关系数。

Chapter 5-4---等级相关系数

等级相关

等级相关的应用场合
斯皮尔曼等级相关肯德尔等级相关（肯德尔Ｗ系数）

作业：6、7
肯德尔等级相关（肯德尔Ｗ系数）

肯德尔(Kendall)和谐（W）系数无相同等级有相同等级

有相同等级

Ri为评定对象获得的K个等级之和, n为相同等级的数目例5－7
无相同等级

Ri为评定对象在K个评价者那里获得的等级之和 N代表被评定对象的数目 K为评定者的数目例5－6
肯德尔(Kendall)和谐（W）系数

1、用于衡量两个以上评定者等级评定的一致程度。这种一致程度要用多列等级变量的相关系数表示 2、适用这种方法的数据资料一般是采用等级评定的方法收集的，即让K个评委（被试）评定N件事物，或1个评委（被试）先后K次评定N件事物。 3、等级评定法每个评价者对N件事物排出一个等级顺序，最小的等级序数为1 ，最大的为N，若并列等级时，则平分共同应该占据的等级。

4、可用积差相关计算的资料若用等级相关来计算，则精确度降低了。
无相同等级时的计算公式
6 D 2
i 1 n
rR 1
N ( N 1)
2
N : 成对等级个数； D=R X -R Y:二列成对变量的等级差数

例题5－3
有相同等级时的计算公式

N: 成对数据的数目 n为各列变量内的相同等级数，注意求和注意相同等级的等级赋值参见例

等级相关的应用场合

等级数据间的相关或总体分布非正态时不满足积ቤተ መጻሕፍቲ ባይዱ相关条件。
因为对总体分布不作要求，又称为非参数的相关方法。

斯皮尔曼等级相关系数二

Pearson（皮尔逊）相关系数相关系数：考察两个事物（在数据里我们称之为变量）之间的相关程度。

如果有两个变量：X、Y，最终计算出的相关系数的含义可以有如下理解：(1)、当相关系数为0时，X和Y两变量无关系。

(2)、当X的值增大（减小），Y值增大（减小），两个变量为正相关，相关系数在0.00与1.00之间。

(3)、当X的值增大（减小），Y值减小（增大），两个变量为负相关，相关系数在-1.00与0.00之间。

相关系数的绝对值越大，相关性越强，相关系数越接近于1或-1，相关度越强，相关系数越接近于0，相关度越弱。

通常情况下通过以下取值范围判断变量的相关强度：相关系数0.8-1.0 极强相关0.6-0.8 强相关0.4-0.6 中等程度相关0.2-0.4 弱相关0.0-0.2 极弱相关或无相关Pearson（皮尔逊）相关系数1、简介皮尔逊相关也称为积差相关（或积矩相关）是英国统计学家皮尔逊于20世纪提出的一种计算直线相关的方法。

假设有两个变量X、Y，那么两变量间的皮尔逊相关系数可通过以下公式计算：公式一：公式二：公式三：公式四：以上列出的四个公式等价，其中E是数学期望，cov表示协方差，N表示变量取值的个数。

2、适用范围当两个变量的标准差都不为零时，相关系数才有定义，皮尔逊相关系数适用于：(1)、两个变量之间是线性关系，都是连续数据。

(2)、两个变量的总体是正态分布，或接近正态的单峰分布。

(3)、两个变量的观测值是成对的，每对观测值之间相互独立。

3、Matlab实现皮尔逊相关系数的Matlab实现（依据公式四实现）：[cpp]view plainc opy1.function coeff = myPearson(X , Y)2.% 本函数实现了皮尔逊相关系数的计算操作3.%4.% 输入：5.% X：输入的数值序列6.% Y：输入的数值序列7.%8.% 输出：9.% coeff：两个输入数值序列X，Y的相关系数10.%11.12.13.if length(X) ~= length(Y)14. error('两个数值数列的维数不相等');15.return;16.end17.18.fenzi = sum(X .* Y) - (sum(X) * sum(Y)) / length(X);19.fenmu = sqrt((sum(X .^2) - sum(X)^2 / length(X)) * (sum(Y .^2) - sum(Y)^2 /length(X)));20.coeff = fenzi / fenmu;21.22.end %函数myPearson结束也可以使用Matlab中已有的函数计算皮尔逊相关系数：[cpp]view plainc opy1.coeff = corr(X , Y);文案编辑词条B 添加义项?文案，原指放书的桌子，后来指在桌子上写字的人。

斯皮尔曼等级相关系数斯皮尔曼等级相关系数

n6
n8
n9
Gamma等级相关
测度定序变量xi与定序变量yi之间是否存在等级相关，相关程度有多大？计算公式为
n n G n n
s s

1.
2.
d d
ns: 同序对的数目 nd: 异序对的数目 Gamma系数的使用不受样本容量限制 G的取值：［－1 ，＋1］ G系数具有减少误差比例（PRE）的性质
rs的统计检验
1. 当n<30时，使用统计量t进行检验
t rs n2 1 rs
2
～ t (n2)
2. 当n≥30时，使用统计量Z进行检验
z
a等级相关
Gamma等级相关几个名词
两个定序变量,
n
同序对ns：如果xi >xj , 则异序对nd：如果xi >xj , 则
yi >yj yi <yj
n
怎么计算同序对和异序对
同序对 ns=n1(n5+n6+n8+n9)+n2(n6+n9)+n4(n8+n9)+n5(n9)
异序对 nd= n7(n2+n3+n5+n6)+n8(n3+n6)+n4(n2+n3)+n5(n3)
y
高
n
n
x
高 n1
中 n4
低 n7
中
低
n2
n3
n5
Gamma系数的检验
1. 当n≥10时，使用Z统计量进行检验
Z G 1 G
2
n n
s
d
n
～ N (0，1)

ns: 同序对的数目 nd: 异序对的数目 n越大，Z越趋近N (0，1)

等级相关系数.

(2) Gamma 等级相关系数 G
若同序对ns 较多，表示变量x与变量y呈正相关；若异序对nd 较多，表示变量x与变量y呈负相关；则同序对数目与异序对数目之差反映了相关程度。
G ns nd ns nd
G系数的取值范围为 [-1，1].
(3) Gamma 等级相关系数的检验
H0 : γ 0 H1 : γ 0 (总体等级相关是否为0).
a、同序对ns 若 xi x j (或xi x j ) 时，yi y j (或yi y j )称AB为同序对. b、异序对nd 若 xi x j (或xi x j ) 时，yi y j (或yi y j )称AB为异序对. c、同分对
若 xi x j (且yi y j ) 时，称AB为x的同分对. Tx 若 yi y j (且xi x j ) 时，称AB为y的同分对. Ty 若 xi x j (且yi y j )时，称AB为xy的同分对. Txy
H0为真时，
t rs
n2 1 rs2
:
t(n 2)
给定显著性水平 α ；
拒绝域为：(,ta (n 2)) U(ta (n 2),)
2
2
计算样本统计量的值 t S ;若落在拒绝域,则可以认
为两变量之间存在相关关系；否则，不存在。
2、Gamma 等级相关系数 G
(1)、名词
A : ( xi , yi ); B : ( x j , yj ). i j
Z G
ns nd : N (0,1)
1 G2
n
给定显著性水平 α ；
拒绝域为：(, Za ) U(Za , )
2
2
计算样本统计量的值 Z S;若落在拒绝域，则可以
认为两变量之间存在等级相关关系；否则，不存在。

四大相关系数

四大相关系数四大相关系数是指皮尔逊相关系数、斯皮尔曼等级相关系数、判定系数和点双相关系数。

这些系数是用于衡量两个变量之间相关关系的统计指标。

下面将对这四大相关系数进行详细介绍。

一、皮尔逊相关系数皮尔逊相关系数是最常用的一种相关系数，用于衡量两个连续变量之间的线性相关程度。

它的取值范围在-1到1之间，越接近1表示两个变量正相关性越强，越接近-1表示两个变量负相关性越强，而接近0则表示两个变量之间没有线性相关性。

二、斯皮尔曼等级相关系数斯皮尔曼等级相关系数是一种非参数的相关系数，用于衡量两个变量之间的单调关系，不要求变量的分布形态。

它通过将原始数据转换为等级数据，然后计算等级数据之间的皮尔逊相关系数来得到最终的相关系数。

斯皮尔曼等级相关系数的取值范围也在-1到1之间，其含义和皮尔逊相关系数相似。

三、判定系数判定系数又称为决定系数，用于衡量因变量的变异程度可以由自变量解释的比例。

它的取值范围在0到1之间，表示自变量对因变量的解释程度。

判定系数越接近1，说明自变量对因变量的解释程度越高；而越接近0，说明自变量对因变量的解释程度越低。

四、点双相关系数点双相关系数是一种用于衡量三个变量之间关系的相关系数。

它用于度量两个自变量对因变量的联合影响程度，同时消除了两个自变量之间的相关性。

点双相关系数的取值范围也在-1到1之间，其含义和皮尔逊相关系数相似。

四大相关系数是用于衡量变量之间相关关系的重要统计指标。

皮尔逊相关系数适用于连续变量之间的线性相关性分析，斯皮尔曼等级相关系数适用于非参数的单调关系分析，判定系数适用于衡量自变量对因变量解释程度，而点双相关系数适用于评估两个自变量对因变量的联合影响程度。

在实际应用中，根据具体问题选择合适的相关系数进行分析，可以更准确地理解和描述变量之间的关系。

三大相关系数

三大相关系数三大相关系数，又称为Pearson等距系数、Spearman等级系数和Kendalltau相关系数，简称三大相关系数，是统计学中用来评估两个变量间的关联性的一种统计指标。

它们提供的信息包括两个变量之间的相关性大小以及变量之间的关系的方向和强度。

三大相关系数是建立在统计学研究背景下的可用来评价两个变量相关性的三种指标，可用于分析和描述两个变量之间的关系和依赖性。

它们是Pearson等距系数、Spearman等级系数以及Kendallτ相关系数。

Pearson等距系数，又称为Pearson相关系数，也可以称为线性相关系数，它是指探究变量间某种线性关系的统计量。

它是用来判断两个变量之间是否存在线性关系，并对其关系的强度进行量化的工具。

其值的范围是-1到1，值越大表明变量间存在较强的线性关系，若值等于0则表示变量之间没有线性关系。

Spearman等级系数，是另一种测量变量间相关性的统计量。

它主要用于分析非线性的等级相关，并能用来检验两个变量的关系是否符合等级关系。

它的值也介于-1到1之间，其值越大，变量间的关系越强，若值等于0，则表明两个变量之间没有等级关系。

Kendall关系数，是一种判断两组数据之间关系的参数，也可以称为非线性相关系数，它主要用于衡量变量之间的非线性关系，例如，两个变量之间是否存在非线性关系或曲线型关系，其值的范围仍然是-1 1，值越高表明变量间存在较强的关系，值等于0时则表示变量之间没有任何关系。

在实际应用中，三大相关系数常用来在某一领域测量变量之间的相关性，从而分析影响因子的强度并最大程度地提高预测模型的准确性。

三大相关系数也可以用来比较一组样本的变量之间的相关性，从而弄清楚不同变量之间的关系。

总之，三大相关系数是统计学中用来评估变量之间的相关性的重要指标，可用于分析变量之间的关系以及辅助提高模型的准确性。

不论是在研究的设计还是模型的建立中，三大相关系数都是不可或缺的重要工具。

斯皮尔曼等级相关系数比皮尔逊相关系数适用范围

斯皮尔曼等级相关系数比皮尔逊相关系数适用范围
斯皮尔曼等级相关系数和皮尔逊相关系数是两种常用的相关系数计算方法。

虽然它们都可以用于衡量两个变量之间的相关性，但是它们适用的范围有所不同。

皮尔逊相关系数适用于度量两个连续变量之间的线性相关性。

这意味着两个变量的关系必须是线性的，即随着一个变量的增加，另一个变量也会相应地增加或减少。

此外，皮尔逊相关系数还要求两个变量的分布必须是正态分布的。

而斯皮尔曼等级相关系数适用于度量两个变量之间的相关性，其中至少有一个变量是顺序变量。

顺序变量是有序的，但并不一定是连续的，例如一个学生的成绩排名。

斯皮尔曼等级相关系数不要求变量的分布必须是正态分布的，因此它在处理非正态分布的数据时更加适用。

总的来说，当两个变量之间的关系是线性的且分布是正态的时，应该使用皮尔逊相关系数。

而当两个变量之间的关系不一定是线性的或者分布不是正态分布时，应该使用斯皮尔曼等级相关系数。

- 1 -。

spearman相关系数

解释
斯皮尔曼相关系数表明X(独立变量)和Y(依赖变量)的相关方向。如果当X增加时，Y趋向于增加，斯皮尔曼相关系数则为正。如果当X增加时，Y趋向于减少，斯皮尔曼相关系数则为负。斯皮尔曼相关系数为零表明当X增加时Y没有任何趋向性。当X和Y越来越接近完全的单调相关时，斯皮尔曼相关系数会在绝对值上增加。当X和Y完全单调相关时，斯皮尔曼相关系数的绝对值为1。完全的单调递增关系意味着任意两对数据Xi，Yi和Xj，Yj，有 Xi−Xj和Yi−Yj总是同号。完全的单调递减关系意味着任意两对数据Xi，Yi和Xj，Yj，有Xi−Xj和Yi−Yj总是异号。
一致性分析
经典的一致性分析是一种统计方法，它给两个标称变量赋给一个分数。通过这种方法，两个变量间的皮尔逊相关系数被最大化了。
有一种被称为级别相关分析的等价方法，它最大化了斯皮尔曼相关系数或肯德尔相关系数。
谢谢观看
如果F(r)是r的Fisher变换，则
是r的z-值，其中，r在统计依赖(ρ=0)的零假设下近似服从标准正态分布。
显著性为
其在零假设下近似服从自由度为n−2的t分布。一般地，斯皮尔曼相关系数在有三个或更多条件的情况下是有用的。并且，它预测观测数据有一个特定的顺序。例如，在同一任务中，一系列的个体会被尝试多次，并预测在多次尝试过程中，性能会得到提升。在这种情况下，对条件间趋势的显著性检验由发展了，并通常称为给定序列下的Page趋势测验。
相关度量

度量一对观测数据的统计依赖性还有其他的几种度量指标:在相关性和依赖性中有谈及。其中最常用的是皮尔逊积矩相关系数。
斯皮尔曼相关也可称为"级别相关";也就是说，被观测数据的"等级"被替换成"级别"。在连续的分布中，被观测数据的级别，通常总是小于等级的一半。然而，在这个案例中，级别和等级相关系数是一致的。更一般的，被观测数据的"级别"与估计的总体样本的比值小于给定的值，即被观测值的一半。也就是说，它是相应的等级系数的一种可能的解决方案。虽然不常用，"级别相关"还是仍然有被使用。

斯皮尔曼相关系数优点

斯皮尔曼相关系数优点（最新版）目录1.斯皮尔曼相关系数的定义与背景2.斯皮尔曼相关系数的优点3.斯皮尔曼相关系数与其他相关系数的比较4.斯皮尔曼相关系数在实际应用中的案例5.斯皮尔曼相关系数的局限性正文一、斯皮尔曼相关系数的定义与背景斯皮尔曼相关系数，又称为等级相关系数，是一种用来衡量两个变量之间相关关系的统计指标。

该系数由英国统计学家查尔斯·斯皮尔曼（Charles Spearman）于 1904 年提出，适用于非正态分布的数据，以及等级数据和连续数据之间的相关性分析。

二、斯皮尔曼相关系数的优点1.适用范围广泛：斯皮尔曼相关系数不仅适用于正态分布的数据，还适用于非正态分布的数据，以及等级数据和连续数据之间的相关性分析。

2.较强的稳健性：斯皮尔曼相关系数对数据分布的形状没有严格的要求，因此具有较强的稳健性。

当数据分布发生变化时，斯皮尔曼相关系数仍能较好地反映变量之间的相关关系。

3.可处理缺失值：与其他相关系数不同，斯皮尔曼相关系数可以处理缺失值。

当数据中存在缺失值时，斯皮尔曼相关系数仍能计算得出，并且具有较好的稳定性。

4.计算简便：斯皮尔曼相关系数的计算方法较为简单，可以通过计算等级差数的方法进行。

对于小样本数据，还可以通过查表的方式获取斯皮尔曼相关系数的近似值。

三、斯皮尔曼相关系数与其他相关系数的比较斯皮尔曼相关系数与皮尔逊相关系数（Pearson correlation coefficient）是统计学中最常用的两种相关系数。

它们之间的主要区别在于适用的数据类型和计算方法。

皮尔逊相关系数适用于正态分布的数据，并且其值范围为 -1 到 1。

当皮尔逊相关系数为 1 时，表示两个变量完全正相关；当皮尔逊相关系数为 -1 时，表示两个变量完全负相关；当皮尔逊相关系数为 0 时，表示两个变量之间不存在线性相关关系。

斯皮尔曼相关系数适用于非正态分布的数据，以及等级数据和连续数据之间的相关性分析。