8.6 平面图及图的着色
合集下载
8.6x14.6 七层城中村自建房出租房设计图平面户型图布局图效果图

C0909
D
M0921 杂物间 10.0 m² M0921
D
1400
C
1300 3120 14600
1200
260x18= 4160
大厅车库 65.9 m²
C1518
C
上
B
C1518
C
M3630
M3635
4580
1300
±0.000
A
B
B
4300 8600 4300
1
2
一层平面图
1 : 100
3
A
A 说明:未注墙厚200mm,未注门跺尺寸为120mm,墙、 柱未注位置为中心对齐或者边线对齐。卫生间、厨房 标高相对楼板面标高低30mm。 1 2
桂林云合房屋设计室
校核 制图 3 已审 林应海
项目
普通民房 PF0916-7T01 一层平面图 A0 页码 02 5
编号 图名 2015-12-7 版本 4
1
主卧 21.2 m²
杂物间 7.6 m²
1400
D
D
M1021 楼梯间 11.9 m² 过厅 3.8 m²
1400
下
C
14600
16.200
上
2820
B
客厅 35.2 m²
M2427B2800源自C2418C3018
1300
厨房 9.2 m²
1300
1350
餐厅 13.6 m²
2130
C
C
A
B
2900
1500 8600
E
D
1360
C0909
房间 16.3 m²
M0921
1400
建筑施工图识图1

附图7
8.4.5 建筑立面图的绘制方法与步骤
立面图的画法和步骤与建筑平面图基本相同,同 样先选定比例和图幅,经过画底图和加深两个步骤, 如图8.6
第一步 第二步 第三步,画墙面细部,如阳台、窗台、楣线、
第四步,检查无误后,按立面图的线型要求进
第五步,标注标高、首尾轴线,书写墙面装修 文字、图名、比例等,说明文字一般用5号字,图名 用10号字。
附图10
8.5.4 建筑剖面图的绘制方法与步骤
比例、图幅的选择与建筑平面图、立面图相同, 剖面图的具体画法、步骤如下:
第一步,画被剖切到的墙体定位轴线、墙体、 楼板面等,如图8.8(a
第二步,在被剖切的墙上开门窗洞口以及可见
第三步,画剖开房间后向可见方向投影所看到 部分的投影,如图8.8(b
第四步,按建筑剖面图的图示方法加深图线, 标注标高与尺寸,最后画定位轴线,书写图名和比 例,如附图10所示。
建筑施工图识图1
本章内容
8.1 施工图首页 8.2 总平面图 8.3 建筑平面图 8.4 建筑立面图 8.5 建筑剖面图 8.6 建筑详图
8.1.3 工程做法表
工程做法表主要是对建筑各部位构造做法用表 格的形式加以详细说明。
在表中对各施工部位的名称、做法等详细表达 清楚,如采用标准图集中的做法,应注明所采用标 准图集的代号、做法编号,如有改变,在备注中说 明。
(4)表示电梯、楼梯的位置及楼梯上下行方向 及主要尺寸。
(5)表示阳台、雨篷、台阶、斜坡、烟道、通 风道、管井、消防梯、雨水管、散水、排水沟、花
(6)画出室内设备,如卫生器具、水池、工作 (7)表示地下室、地坑、地沟、墙上预留洞、 (8)在底层平面图上还应画出剖面图的剖切符
(9) (10)综合反映其他工种如水、暖、电、煤气 等对土建工程的要求:各工种要求的水池、地沟、 配电箱、消火栓、预埋件、墙或楼板上的预留洞等
第十七章 平面图及图的着色
注意观察K5与K3,3的特点!
K5 的特点每三个点构成一个面! 而K3,3每四个点构成一个面
4.库拉托斯基定理判别法
定义
如果两个图G1和G2是同构的,或者通过反复插入或删
除度为2的结点,它们能变成同构的图,则称G1 和G2 在度为2的结
点内同构(同胚)。
K3,3与K5称为库拉托夫斯基(Kuratowski)图, 它们有
例5
利用定理判别图G是否非平面图。
解法一与 K3,3同胚
图G 去掉图G中边:{a,c},{a,d},{d,e},{b,e},与 K3,3同胚
可以去边吗?
边少时非平面图,边多时更不是平面图
解法二 去掉图中边{d,f}和{e,g},为K5
练习
1.用简单、直观判别法判断下图所给出的两个图a,b是否平面图。
3. 欧拉公式判断法
定义设G是一个连通平面图,G的边将G所在的平面划分成若干个区
面积有限的区域称为有限面。包围每个面的所有边构成的回路称为 面的边界。它的长度称为面的度(次数)(degree)。
域,每一个区域称为G的一个面。其中面积无限的区域称为无限面。
例3
定理 一个有限平面图,面的次数之和等于其边数的两倍. 证明:因为任何一条边,或者是二个面的公共边,或者在 一个面中作为边界被重复计算两次,故面的次数之和等于 其边数的两倍。 如右图中,
若v1 和v3 同属于一个G(RY)的连通分支,那么从v1到v3 必有一 条通路,其各顶点被红、黄两色相间着色。这条通路连同v0便构 成回路: C:v0, v1,…, v3, v0,
C把BW分成两部分,一部分在回路C之外,一部分在C之内。 于是,BW生成的G的子图也被分成了两个互不连通的部分,一 部分在C外,一部分在C内,这就使v2,v4 处于BW生成的G的子 图的两个不同连通分支,同上将v2所在分支作颜色对换,以便给 v0着上白色,完成对G的5-着色。
第九章-平面图与图的着色课件

部面。
单连通区域是指能够收缩到一个点的区域
5
2、平面图的面数、顶点数、边数之间的关系。
f3
f2 v
f1
u
f4
0
1
3
2
4
5
平面图的每个内部面都是G的某个圈围成的单连通区 域。
没有圈的图没有内部面,只有一个外部面。
6
2、平面图的面数、顶点数、边数之间的关系。
如果用V表示多面体的顶点,用E表示棱,用F表示 面数。
定理9.1.1(欧拉公式) 如果一个平面连通图 有p个顶点、q条边、f个面,则:p-q+f=2
11
3、最大(极大)可平面图
一个图称为最大可平面图,如果这个可平面图再 加入一条边,新图必然是不可平面的。
观察下面两个图,他1不是最大可平面图 图2是最大可平面图
12
4、最大(极大)平面图的性质
q=10≤3p-6=9,这是不成立的
所以K5不是可平面图。
最大可平面图
17
4、最大(极大)平面图的性质
如果K3,3是平面图 在偶图中每个圈的长至少为4
如果K3,3是平面图 K3,3应满足q≤2p-4 K3,3中p=6,q=9 9≤8
K3,3不是平面图
K33
18
4、最大(极大)平面图的性质
推论9.1.6 每个平面图G中顶点度的最小值不超过5,即 (G)≤5
图1 推论9.1.4 若G是任一有p个顶点q条边的可平面图 p≥3,则q≤3p-6,若G是2-连通的且没有三角形,则 q≤2p-4
15
4、最大(极大)平面图的性质
推论9.1.4 若G是任一有p个顶点q条边的可平面图 p≥3,则q≤3p-6,若G是2-连通的且没有三角形,则 q≤2p-4
《平面图的面着色》课件

平面图的表示方法
总结词
平面图的表示方法有多种,包括几何表 示法和代数表示法等。
VS
详细描述
平面图的表示方法有多种,其中最常用的 是几何表示法。几何表示法是将平面图中 的顶点和边用几何图形表示出来,例如点 表示顶点,线段表示边。此外,代数表示 法也是一种常用的表示方法,它将平面图 中的顶点和边用代数符号表示出来,通过 建立代数方程来表示平面图的性质和关系 。
03
平面图面着色的算法
贪心算法
总结词
贪心算法是一种在每一步选择中都采取当前最优的选择,从而希望导致结果是全 局最优的算法。
详细描述
在平面图面着色问题中,贪心算法会从图的某个顶点开始,尽可能地使用最小数 量的颜色对所有面进行着色,直到无法继续进行。贪心算法并不保证得到最优解 ,但在某些情况下可以获得接近最优解的结果。
电路板的设计
要点一
总结词
电路板的设计中,平面图面着色被广泛应用于标识不同功 能的电路区域,提高电路板的可维护性和可靠性。
要点二
详细描述
在电路板设计中,不同功能的电路区域通常会使用不同的 颜色进行标识。这样可以帮助工程师快速识别和定位特定 电路区域,提高电路板的可维护性和可靠性,减少错误和 故障的发生。
详细描述
平面图是指将图形放置在平面上,使得图形中的点、线、面 等元素在平面上有对应的表示。平面图通常由顶点和边组成 ,顶点表示图形中的点,边表示图形中的线段。
平面图的性质
总结词
平面图的性质包括连通性、无环性、简单性等。
详细描述
平面图具有一些重要的性质,这些性质决定了图形的表示方式和可操作性。其中,连通性是指平面图中的任意两 点都可以通过一条路径相连;无环性是指平面图中不存在环路,即不存在一条路径可以从起点回到起点;简单性 是指平面图中的边和顶点都没有额外的标记或属性。
平面图及着色
例2 指出下图所示平面图的面、面的边界及 面的度数。
e1
f5
3
1
e10
2
e7 f3 e6
f2 e8
f1 e4
f4 e5
4
e2 e3
5
e9
6
7
解:面f1,其边界1e15e24e43e72e101,d(f1)=5. 面f2,其边界1e102e87e91,d(f2)=3. 面f3,其边界2e73e67e82,d(f3)=3. 面f4,其边界3e44e57e63,d(f4)=3. 外部面f5, 其边界1e15e24e36e34 e57e91,d(f5)=6.
R是E(G)-E(H)上的等价关系。R确定E(G)-E(H) 上的一个划分设为S={ S1、S2、…Sm}由Si导出的 G-E(H)的子图
B1、B2、…Bm 称为G的H片。
定义2.若H1和H2都是图G的子图,称V(H1) V(H2)为H1 和H2在G中的接触点集。记作VG(H1,H2).
定在义 G的3平设面H是表可示平G~面,图使GH的~子 图G~,H称~是H~H的是平G容面许表的示。,若存
证明:只要对极大平面图G来证明定理即可(简单平面图是 极大平面图的子图).当v=3时,G是三角形,定理显然成立. 假设定理对所有阶数小于v的极大平面图成立,并设G是 三角剖分图.选取xV(G)使x不是外部剖面边界上的点.取 边{x,y}.则边{x,y}仅是某两个内部三角形的公共边.不妨 设这两个三角形分别为z1xy和z2xy.如图(b)所示.收缩边 {x,y},且结点x和y收缩为P,得图G’(图c).显然G’是平面图, 且有E(G’)= E(G)-3=3(V(G)-1)-6= 3V(G)-9 = 3V(G’)-6,即G’是v-1阶极大平面图,由归纳假设,G’
房屋建筑工程图集-平面图立面图剖面图详图
结合实际看图。
1111
(二)、阅读房屋建筑工程图的方法 先读首页图 读总平面图 读建筑施工图 读结构施工图 读设备施工图 读图时注意工种之间的联系,前后照应。
1212
8.2 总平面图
一、总平面图的形成和用途及表示方法
总平面图的形成 将新建工程四周一定范围内的新建、拟建、原有和拆除的建筑物、
99
五、建筑设计总说明
设计依据:立项,规划许可证 建筑规模 占地面积——建筑物底层外墙皮以内所有面积之和 建筑面积——建筑物外墙皮以内各层面积之和 标高 相对标高———以建筑物底层室内地面为零的标高 绝对标高——以青岛黄海平均平面的高度为零点的标高 装修做法:地面、楼面、墙面的装修做法 施工要求 1)严格执行施工验收规范中规定 2)对图纸中不详之处的说明
2、建筑平面图表达的内容 建筑平面图反映新建建筑的平面形状、房间的位置、大小、相互关
系、墙体的位置、厚度、材料、柱的截面形状与尺寸大小,门窗的位 置及类型。 3、建筑平面图的用途
是施工放线、砌墙、安装门窗、室内外装修及编制工程预算的重要依 据,是建筑施工中的重要图纸。
2323
二、建筑平面图的图示方法
1818
5.等高线
1)地形——地面上高低起伏的形状,地形用等高线表示 2)等高线的绘制 假想用间隔相等的若干水平面把山头从某一高度顶一层一层地剖开, 在山头表面上便出现一条一条的截交线,把这些截交线投射到水平投影 面上,就得到一圈一圈的封闭曲线,即为等高线。 3)由等高线分析地形的高低起伏状况: A 等高线间距越大,地面越平坦,间距越小,地面越陡峭 B 数值由外圈向内圈增大,地形上凸;数值由外向内减小,地形下凹 6、 道路:标注道路中心控制点,道路的标高及平面位置
着色匹配平面图
定理:对任意的图G 均有 c ≤Δ+1
证明:对图G 的点数υ用归纳法。 当υ=1 时。 =1,Δ≥0,满足 ≤Δ+1。 对υ≥2 的图G , 取 u∈V(G), 设 G’=G-u 。由归纳假设 χ (G’)≤Δ(G’)+1,从而存在 G’ 的 (Δ(G’)+1)-着色φ 。因 Δ(G’)≤Δ(G), 所以 φ 也是 G’ 的(Δ(G) +1 ) - 着色。 设 dG(u) = k, G 中与 u 相邻的点为 v1,v2,…,vk。因 | {φ(v1), …, φ(vk)} | ≤k ≤ Δ(G)+1, 所以存在 j ∈ {1,2,…,Δ(G)+1} 满足 j ≠φ(v1), …, φ(vk), 令φ(u)= j, 则 φ 被扩充为 G 的一个(Δ(G)+1)-着色,所以
对 M2,点v1是的饱和点,点v2是非饱和点。
例中的M1 和M2既不是最大匹配,也不是完美匹配, 而M3是最大匹配,也是完美匹配。
着色、匹配、平面图
关系:完美匹配必是最大匹配,而最大匹配不一定是完美匹 配。一个图的最大匹配必存在,但完美匹配不一定存在。易 知,图G存在完美匹配的一个必要条件是 G 的点数为偶。
着色、匹配、平面图 Welsh-Powell算法
该算法较前述算法优。该算法要求顶点序列v1, v2,…, vn满足: d(v1)≥d(v2)≥…≥d(vn) 其余步骤同算法1。
用最大度数优先算法对上例中的图着色,结果 如下图所示。V3 V1 V6
V5
V2
V4
着色、匹配、平面图 偶图
定义:若图 G = (V, E) 的点集能划分为两个互不相 交的非空子集 V1 与 V2(V1∪V2 = V),使任意的 e∈E,e 的两端点分属于 V1 与 V2,则称 G为偶图 (或二部图、二分图),记为G = (V1, V2, E)。
证明:对图G 的点数υ用归纳法。 当υ=1 时。 =1,Δ≥0,满足 ≤Δ+1。 对υ≥2 的图G , 取 u∈V(G), 设 G’=G-u 。由归纳假设 χ (G’)≤Δ(G’)+1,从而存在 G’ 的 (Δ(G’)+1)-着色φ 。因 Δ(G’)≤Δ(G), 所以 φ 也是 G’ 的(Δ(G) +1 ) - 着色。 设 dG(u) = k, G 中与 u 相邻的点为 v1,v2,…,vk。因 | {φ(v1), …, φ(vk)} | ≤k ≤ Δ(G)+1, 所以存在 j ∈ {1,2,…,Δ(G)+1} 满足 j ≠φ(v1), …, φ(vk), 令φ(u)= j, 则 φ 被扩充为 G 的一个(Δ(G)+1)-着色,所以
对 M2,点v1是的饱和点,点v2是非饱和点。
例中的M1 和M2既不是最大匹配,也不是完美匹配, 而M3是最大匹配,也是完美匹配。
着色、匹配、平面图
关系:完美匹配必是最大匹配,而最大匹配不一定是完美匹 配。一个图的最大匹配必存在,但完美匹配不一定存在。易 知,图G存在完美匹配的一个必要条件是 G 的点数为偶。
着色、匹配、平面图 Welsh-Powell算法
该算法较前述算法优。该算法要求顶点序列v1, v2,…, vn满足: d(v1)≥d(v2)≥…≥d(vn) 其余步骤同算法1。
用最大度数优先算法对上例中的图着色,结果 如下图所示。V3 V1 V6
V5
V2
V4
着色、匹配、平面图 偶图
定义:若图 G = (V, E) 的点集能划分为两个互不相 交的非空子集 V1 与 V2(V1∪V2 = V),使任意的 e∈E,e 的两端点分属于 V1 与 V2,则称 G为偶图 (或二部图、二分图),记为G = (V1, V2, E)。
二部图及其匹配
2.Euler公式 Euler在1750年研究多面体时发现,多面体的 面数等于多面体的棱数减去顶点数加2,后来 发现连通平面图的面数与其节点数、边数 之间也有同样的关系. Theorem (Euler公式)任意(n, m)连通平面图 的面数r = m – n +2. Proof 对面数r归纳. r = 1. r 2 回路C. 去掉C上的一条边e. G – {e}.
v1
v2
v3
v4
v5
v6
v7
v8
K 3, 4
V1 {v1 , v2 , v3 , v4 , v5},
V2 {v6 , v7 , v8 }.
Remark 互补节点集合不是唯一的.
下面的定理给出了简单无向图是二部图的 充要条件. Theorem 8-15 设G为阶数 2的简单无向图, 则G是二部图的充要条件是G中任意圈的长 度为偶数. Proof () ()取v V, 令V1 = {u|u V, d(u, v)是偶数}, V2 = V - V1.
v
v1 v2
v3
R(3, 3) = 6(1930), 其他Ramsey数?
8.7 二部图及其匹配
在诸如人员分配、资源分配等问题的讨论 中,经常涉及到二部图及其匹配. 本节仅对简单无向图进行讨论.
1. 二部图 Definition V划分为V1和V2, 任意边关联的两 个节点中一个在V1中, 一个在V2中.
c2 c1
c6 c5
c3
c3
c4 c3
c5
c1
c4
c1 c1 c2 c c c 3 3 4 c4 c3 c2 c2 c2 c2 c1 c1
【新教材课件】2021学年高中数学人教A版必修第二册:8.6.3+第2课时 平面与平面垂直的性质
又∵E 是 PC 的中点,∴O 是 AC 的中点. 又∵AB∥CD,∴△ABO∽△CDO. 又∵AO=OC,∴AB=CD, 这与 CD=2AB 矛盾,
∴假设不成立.故平面 EBD 不能垂直于平面 ABCD.
课堂达标练经典
1.设两个平面互相垂直,则 ( C ) A.一个平面内的任何一条直线垂直于另一个平面 B.过交线上一点垂直于一个平面的直线必在另一平面上 C.一个平面内过交线上一点垂直于交线的直线,必垂直于 另一个平面 D.分别在两个平面内的两条直线互相垂直 解析:由面面垂直的性质可知,选 C.
四边形 ABCD 是∠DAB=60°的菱形,侧面 PAD 为正三角形,其 所在平面垂直于底面 ABCD.若 G 为 AD 边的中点,求证:BG⊥ 平面 PAD.
[分析] 解答本题可先由面面垂直依据面面垂直的性质定 理得线面垂直.
[证明] 连接 BD, ∵四边形 ABCD 是菱形且∠DAB=60°, ∴△ABD 是正三角形. ∵G 是 AD 的中点,∴BG⊥AD. 又平面 PAD⊥平面 ABCD,平面 PAD∩平面 ABCD=AD, ∴BG⊥平面 PAD.
要点整合夯基础 课堂达标练经典
典例讲练破题型 课时作业
要点整合夯基础
知识点 平面与平面垂直的性质定理
[填一填] 1.文字语言:两个平面垂直,如果一个平面内有一直线垂 直于这两个平面的交线,那么这条直线与另一个平面 垂直.
2.符号语言:
α⊥β aα⊂∩αβ=l⇒a⊥β a⊥l
3.图形语言:
解:平面 EBD 不能垂直于平面 ABCD.理由如下: 假设平面 EBD 垂直于平面 ABCD, 过 E 作 EO⊥BD 于 O,连接 AO、CO. ∵EO⊂平面 EBD,EO⊥BD,平面 EBD∩平面 ABCD=BD, ∴EO⊥平面 ABCD. 又∵PA⊥平面 ABCD,∴EO∥PA. ∵A、O、C 是 PC 上三点 P、E、C 在平面 ABCD 上的投影, ∴P、E、C 三点的投影均在直线 AC 上, ∴A、O、C 三点共线.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)m*=m(3)r*=Fra bibliotekk+1
三、自对偶图 定义8.8 图。 设G*是平面图G的对偶图,若G*G,则称G为自对偶
在n1(n4)边形Cn1 内放置1个顶点,使这个顶点与Cn1 上的 所有的顶点均相邻,所得n阶简单图称为n阶轮图。记为Wn。 n为奇数的轮图称为奇阶轮图。 n为偶数的轮图称为偶阶轮图。
i 1
于是,对(8.1)的两边同时求和得
2k (ni mi ri ) ni mi ri n m r k 1
i 1 i 1 i 1 i 1 k k k k
经整理得 n-m+r = k+1。
2、 与欧拉公式有关的定理 定理8.10 设G为连通的平面图,且每个面的次数至少为 l(l 3),则 G的边数与顶点数有如下关系:
m
证明
l ( n 2) l2
由定理8.4(面的次数之和等于边数的2倍)及欧拉公式得
2m deg( Ri ) l r l (2 m n)
l ( n 2) 解得 m l2
i 1 r
推论 K5, K3,3不是平面图。
证明
若K5是平面图,由于K5中无环和平行边,所以每个面的次数 均大于或等于l≥3,由定理17.10可知边数10应满足
离 散 数 学
8.6 平面图
周金明 zjmjz@
说明
–平面图的基本概念
–欧拉公式
–平面图的判断 –平面图的对偶图 –顶点着色及点色数 –地图的着色与平面图的点着色
8.1 平面图的基本概念
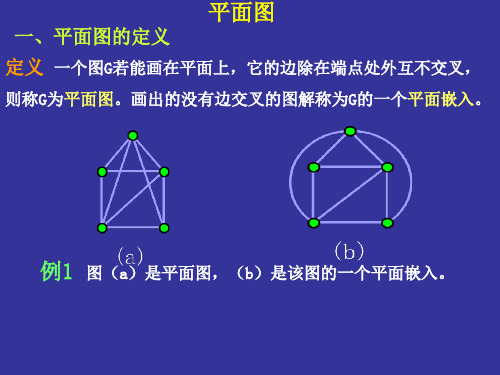
一、关于平面图的一些基本概念 1、 平面图的定义 定义8.1 G可嵌入曲面S——如果图G能以这样的方式画在曲面S上 ,即除顶点处外无边相交。 G是可平面图或平面图——若G可嵌入平面。
R1
R0 R2
R3
平面图有4个面,deg(R1)=1, deg(R2)=3, deg(R3)=2, deg(R0)=8。
定理8.4 平面图G中所有面的次数之和等于边数m的两倍,即
deg( R ) 2m
证 明
i 1 i
r
其中r为G的面数
本定理中所说平面图是指平面嵌入。
e∈E(G),
当e为面Ri和Rj(i≠j)的公共边界上的边时,在计算Ri和Rj的次 数时,e各提供1。 当e只在某一个面的边界上出现时,则在计算该面的次数时 ,e提供2。
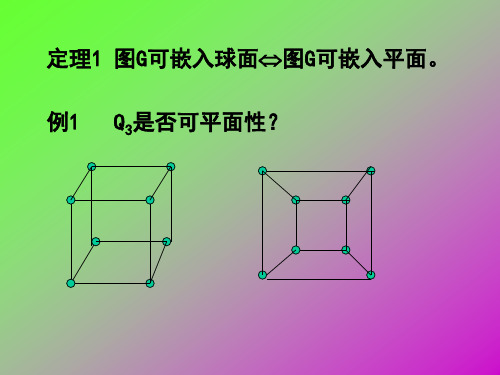
定理8.2 设GG,若G为非平面图,则G也是非平面图。 推论 Kn(n5)和K3,n(n3)都是非平面图。 定理8.3 若G为平面图,则在G中加平行边或环所得图还是 平面图。 即平行边和环不影响图的平面性。
二、平面图的面与次数(针对平面图的平面嵌入) 1、 定义 定义8.2 设G是平面图, G的面——由G的边将G所在的平面划分成的每一个区域。
上面两个图分别与K3,3, K5同胚 。
二、两个判断定理 定理8.15(库拉图斯基定理1) 图G是平面图当且仅当G中既不含 与K5同胚子图,也不含与K3,3同胚子图。
8.4 平面图的对偶图
一、对偶图的定义 定义8.7 设G是平面图,构造G的对偶图G*如下: 在G的面Ri中放置G*的顶点vi* 。 设e为G的任意一条边,
2m= d (vi ) 6n
n i 1
因而m 3n,这与定理8.12矛盾。 所以,假设不成立,即G的最小度(G)5。
说 明
本定理在图着色理论中占重要地位。
定理8.7 设G为n(n3) )阶简单连通的平面图,G为极大平面图 当且仅当G的每个面的次数均为3。(仅证充分性)
证 明
由定理17.4可知,
m l (n k 1) l 2
定理8.12 设G为n(n3)阶m条边的简单平面图,则m3n6。
证明
设G有k(k1)个连通分支, 若G为树或森林,当n3时,m=n-k3n6为真。
若G不是树也不是森林,则G中必含圈,又因为G是简单图 ,所以,每个面至少由l(l3)条边围成,又在l=3达到最大 值,由定理8.11可知
由于n3, 又G必为简单平面图,可知,G每个面的次数均3。
因为G为平面图,又为极大平面图。可证G不可能存在次数>3
的面。
s
S-
假设存在面Ri的次数deg(Ri)=s≥4, 如图所示。 在G中,若v1与v3不相邻,在Ri内加边(v1,v3)不破坏平面性,这 与G是极大平面图矛盾,因而v1与v3必相邻,由于Ri的存在, 边(v1,v3)必在Ri外。 类似地,v2与v4也必相邻,且边(v2,v4)也必在Ri外部,于是必 产生(v1,v3)与(v2,v4)相交于Ri的外部,这又矛盾于G是平面图, 所以必有s=3,即G中不存在次数大于或等于4的面,所以G的 每个面为3条边所围,也就是各面次数均为3。
(3)设m=k(k≥1)时成立,当m=k+1时,对G进行如下讨论。 若G是树,则G是非平凡的,因而G中至少有两片树叶。 设v为树叶,令G'=G-v,则G'仍然是连通图,且G'的边数 m'=m-1=k,n'=n-1,r'=r。 由假设可知 n'-m'+r'=2,式中n',m',r'分别为G'的顶点数, 边数和面数。 于是n-m+r=(n'+1)-(m'+1)+r'=n'-m'+r'=2 若G不是树,则G中含圈。
m l 2 (n k 1) (1 )(n k 1) 3(n 2) 3n 6 l 2 l 2
定理8.13 设G为n(n3)阶m条边的极大平面图,则m=3n6。
证明
由于极大平面图是连通图,由欧拉公式得:
r=2+m-n
(8.4)
又因为G是极大平面图,由定理17.7的必要性可知,G的每个 面的次数均为3,所以:
小节结束
8.3 平面图的判断
1、 插入2度顶点和消去2度顶点 定义8.5 设e=(u,v)为图G的一条边,在G中删除e,增加新的顶点w, 使u、v均与w相邻,称为在G中插入2度顶点w。 设w为G中一个2度顶点,w与u、v相邻,删除w,增加新边 (u,v),称为在G中消去2度顶点w。
2、图之间的同胚 定义8.6 若两个图G1与G2同构,或通过反复插入或消去2 度顶点后是同构的,则称G1与G2是同胚的。
于是每条边在计算总次数时,都提供2,因而deg(Ri)=2m。
三、极大平面图 1、 定义 定义8.3 若在简单平面图G中的任意两个不相邻的顶点之间 加一条新边所得图为非平面图,则称G为极大平面图。
注意:若简单平面图G中已无不相邻顶点,G显然是极大平 面图,如K1(平凡图), K2, K3, K4都是极大平面图。
从定义不难看出G的对偶图G*有以下性质: G*是平面图。 G*是连通图。 若边e为G中的环,则G*与e对应的边e*为桥,若e为桥, 则G*中与e对应的边e*为环。 在多数情况下,G*为多重图(含平行边的图)。
同构的平面图的对偶图不一定是同构的。
二、平面图与对偶图的阶数、边数与面数之间的关系。 定理8.16 设G*是连通平面图G的对偶图,n*、m*、r*和n、 m、r分别为G*和G的顶点数、边数和面数,则 (1)n*= r
若e在G的面Ri 与Rj 的公共边界上,做G*的边e*与e相交, 且e*关联G*的位于Ri与Rj中的顶点vi*与vj*,即e*=(vi*,vj*) ,e*不与其它任何边相交。
若e为G中的桥且在面Ri的边界上,则e*是以Ri中G*的顶点 vi*为端点的环,即e*=(vi*,vi*)。
实线边图为平面图,虚线边图为其对偶图。
设边e在G中某个圈上,令G'=G-e,则G'仍连通且m'=m-1=k , n'=n,r'=r-1。
由假设有 n'-m'+r'=2。 于是 n-m+r=n'-(m'+1)-(r'+1)=n'-m'+r'=2
定理8.9 对于具有k(k≥2)个连通分支的平面图G,有 n-m+r = k+1 其中n,m,r分别为G的顶点数,边数和面数。
证明
设G的连通分支分别为G1、G2、…、Gk,并设Gi的顶点数、 边数、面数分别为ni、mi、ri、i=1,2,…,k。
由欧拉公式可知: ni-mi+ri = 2,i=1,2,…,k 易知, m mi,n ni
i 1 i 1 k k
(8.1)
由于每个Gi 有一个外部面,而G只有一个外部面,所以G的面数 k r ri k 1
2、极大平面图的主要性质 定理8.5 极大平面图是连通的。 定理8.6 n(n3)阶极大平面图中不可能有割点和桥。
定理8.7 设G为n(n3) )阶简单连通的平面图,G为极大平面图 当且仅当G的每个面的次数均为3。
证 明 思 路
本节只证明必要性,即设G为n(n3) )阶简单连通的平面图,G 为极大平面图,则G的每个面的次数均为3。
(2)m*=m
(3)r*=n
证 明
(1)、(2)由G*的构造可知是显然的。 (3)由于G与G*都连通,因而满足欧拉公式: n-m+r = 2 n*-m*+r* = 2
由(1)、(2))可知, r* = 2+m*-n* = 2+m-r = n
定理8.17 设G*是具有k(k2)个连通分支的平面图G的对 偶图, n*, m*, r*, n, m, r分别为G*和G的顶点数、边数和 面数, (1)n*= r
10≤(3/(3-2))(5-2) = 9
这是个矛盾,所以K5不是平面图。 若K3,3是平面图,由于K3,3中最短圈的长度为l≥4,于是边数9 应满足 9≤ (4/(4-2))(6-2) = 8
