假设检验-例题讲解剖析
假设检验练习试题-答案解析

假设检验练习题1. 简单回答下列问题:1)假设检验的基本步骤?答:第一步建立假设 (通常建立两个假设,原假设H0 不需证明的命题,一般是相等、无差别的结论,备择假设H1,与H0对立的命题,一般是不相等,有差别的结论)有三类假设第二步选择检验统计量给出拒绝域的形式。
根据原假设的参数检验统计量:对于给定的显著水平样本空间可分为两部分:拒绝域W 非拒绝域A拒绝域的形式由备择假设的形式决定H1: W为双边H1: W为单边H1: W为单边第三步:给出假设检验的显著水平第四步给出零界值C,确定拒绝域W有了显著水平按照统计量的分布可查表得到临界值,确定拒绝域。
例如:对于=0.05有的双边 W为的右单边 W为的右单边 W为第五步根据样本观测值,计算和判断计算统计量 Z 、 t 、当检验统计量的值落在W内时能拒绝,否则接受(计算P值 227页 p值由统计软件直接得出时拒绝,否则接受计算1-a的置信区间置信区间由统计软件直接得出统计量落入置信区间接受,否则接受)2)假设检验的两类错误及其发生的概率?答:第一类错误:当为真时拒绝,发生的概率为第二类错误:当为假时,接受发生的概率为3)假设检验结果判定的3种方式?答:1.计算统计量 Z 、 t 、当检验统计量的值落在W内时能拒绝,否则接受2.计算P值 227页 p值由统计软件直接得出时拒绝,否则接受3.计算1-a的置信区间置信区间由统计软件直接得出,落入置信区间接受,否则接受4)在六西格玛A阶段常用的假设检验有那几种?应用的对象是什么?答:连续型(测量的数据):单样本t检验 -----比较目标均值双样本t检验 -----比较两个均值方差分析 -----比较两个以上均值等方差检验 -----比较多个方差离散型(区分或数的数据):卡方检验 -----比较离散数2.设某种产品的指标服从正态分布,它的标准差σ=150,今抽取一个容量为26 的样本,计算得平均值为1 637。
问在5%的显著水平下,能否认为这批产品的指标的期望值μ = 1600。
假设检验例题 (3)

假设检验例题引言假设检验是统计学中常用的一种方法,用于通过对样本数据进行推断来判断某个假设是否成立。
在实际应用中,假设检验可以用于验证某个新的产品是否与现有产品相同、进行医学研究是否有显著的治疗效果等。
本文将通过一个例题来介绍假设检验的基本概念和步骤,并以Markdown文本格式输出。
例题描述假设某个公司改变了产品包装的设计,认为新的包装可以提高产品的销售量。
为了验证这个假设,该公司进行了一项实验,在两个不同的市场中随机选择了一部分店铺,其中一部分店铺使用新的包装,另一部分店铺继续使用旧的包装。
经过一段时间的实验,记录下两组店铺的销售量。
以下是两组店铺的销售量数据:新包装店铺销售量:50, 52, 55, 48, 57, 55, 54, 53, 51, 56旧包装店铺销售量:45, 46, 44, 46, 42, 48, 43, 41, 47, 44现在的问题是,是否可以通过这些数据来判断新的包装是否显著地提高了产品的销售量?假设检验步骤进行假设检验的步骤如下:步骤1:建立零假设和备择假设在这个例题中,零假设表示新的包装不会显著地提高产品的销售量,备择假设表示新的包装显著地提高了产品的销售量。
假设检验的目标是通过样本数据来决定是拒绝零假设还是接受备择假设。
零假设 (H0):新的包装不会显著地提高产品的销售量。
备择假设 (H1):新的包装显著地提高了产品的销售量。
步骤2:选择显著性水平显著性水平是假设检验中的一个重要概念,用于决定拒绝或接受零假设的标准。
通常情况下,我们会选择一个合适的显著性水平,常见的显著性水平有0.05和0.01。
在这个例题中,我们选择显著性水平为0.05,表示要求95%的置信水平。
步骤3:计算检验统计量假设检验的目标是通过样本数据来计算一个统计量,并与一个期望的分布进行比较。
在这个例题中,我们可以使用两组店铺的平均销售量作为检验统计量。
步骤4:计算p值p值是一个概率值,表示当零假设为真时,观察到比检验统计量更极端结果的概率。
假设检验的习题及详解包括典型考研真题

§假设检验基本题型Ⅰ 有关检验统计量和两类错误的题型【例8.1】u 检验、t 检验都是关于 的假设检验.当 已知时,用u 检验;当 未知时,用t 检验.【分析】 由u 检验、t 检验的概念可知,u 检验、t 检验都是关于均值的假设检验,当方差2σ为已知时,用u 检验;当方差2σ为未知时,用t 检验. 【例8.2】设总体2(,)XN u σ,2,u σ未知,12,,,n x x x 是来自该总体的样本,记11ni i x x n ==∑,21()ni i Q x x ==-∑,则对假设检验0010::H u u H u u =↔≠使用的t 统计量t = (用,x Q 表示);其拒绝域w = . 【分析】2σ未知,对u 的检验使用t 检验,检验统计量为(1)x t t n ==-对双边检验0010::H u u H u u =↔≠,其拒绝域为2{||(1)}w t t n α=>-.【例8.3】设总体211(,)XN u σ,总体222(,)Y N u σ,其中2212,σσ未知,设112,,,n x x x 是来自总体X 的样本,212,,,n y y y 是来自总体Y 的样本,两样本独立,则对于假设检验012112::H u u H u u =↔≠,使用的统计量为 ,它服从的分布为 .【分析】记1111n i i x x n ==∑,2121n i i y y n ==∑,因两样本独立,故,x y 相互独立,从而在0H 成立下,()0E x y -=,221212()()()D x y D x D y n n σσ+=+=+,故构造检验统计量(0,1)x yu N =.【例8.4】设总体2(,)XN u σ,u 未知,12,,,n x x x 是来自该总体的样本,样本方差为2S ,对2201:16:16H H σσ≥↔<,其检验统计量为 ,拒绝域为 .【分析】u 未知,对2σ的检验使用2χ检验,又由题设知,假设为单边检验,故统计量为222(1)(1)16n S n χχ-=-,从而拒绝域为221{(1)}n αχχ-<-.【例8.5】某青工以往的记录是:平均每加工100个零件,由60个是一等品,今年考核他,在他加工零件中随机抽取100件,发现有70个是一等品,这个成绩是否说明该青工的技术水平有了显著性的提高(取0.05α=)?对此问题,假设检验问题应设为 【 】()A 01:0.6:0.6H p H p ≥↔<. ()B 01:0.6:0.6H p H p ≤↔>. ()C 01:0.6:0.6H p H p =↔≠. ()D 01:0.6:0.6H p H p ≠↔=.【分析】一般地,选取问题的对立事件为原假设.在本题中,需考察青工的技术水平是否有了显著性的提高,故选取原假设为0:0.6H p ≤,相应的,对立假设为1:0.6H p >,故选()B .【例8.6】某厂生产一种螺钉,标准要求长度是68mm ,实际生产的产品,其长度服从2(,3.6)N u ,考察假设检验问题01:68:68H u H u =↔≠.设x 为样本均值,按下列方式进行假设检验:当|68|1x ->时,拒绝原假设0H ;当|68|1x -≤时,接受原假设0H . (1)当样本容量36n =时,求犯第一类错误的概率α; (2)当样本容量64n =时,求犯第一类错误的概率α;(3)当0H 不成立时(设70u =),又64n =时,按上述检验法,求犯第二类错误的概率β. 【解】(1)当36n =时,223.6(,)(,0.6)36xN u N u =,000{|68|1|}{67|}{69|}P x H P x H P x H α=->=<+>成立成立成立67686968()[1()]( 1.67)[1(1.67)]0.60.6--=Φ+-Φ=Φ-+-Φ 2[1(1.67)]2[10.99575]0.095=-Φ=-=.(2)当64n =时,223.6(,)(,0.45)64xN u N u =000{|68|1|}{67|}{69|}P x H P x H P x H α=->=<+>成立成立成立67686968()[1()]0.450.45--=Φ+-Φ 2[1(2.22)]2[10.9868]0.0264=-Φ=-=.(3)当64n =,又70u =时,2(70,0.45)xN ,这时犯第二类错误的概率(70){|68|1|70}{6769|70}P x u P x u β=-≤==≤≤=69706770()()( 2.22)( 6.67)0.450.45--=Φ-Φ=Φ--Φ- (6.67)(2.22)10.98680.0132=Φ-Φ=-=.【评注】01(1)(2)的计算结果表明:当n 增大时,可减小犯第一类错误的概率α;02 当64n =,66u =时,同样可计算得到(66)0.0132β=.03 当64n =,68.5u =时,2(68.5,0.45)xN ,则(68.5){6769|68.5}P x u β=≤≤= 6968.56768.5()()(1.11)( 3.33)0.450.45--=Φ-Φ=Φ-Φ-0.8665[10.9995]0.8660=--=.这表明:当原假设0H 不成立时,参数真值越接近于原假设下的值时,β的值就越大. 【例8.7】设总体2(,)XN u σ,12,,,n x x x 是来自该总体的样本,对于检验01:0:0H u H u ≤↔>,取显著性水平α,拒绝域为:{}w u u α=>,其中u =,求:(1)当0H 成立时,求犯第一类错误的概率()u α; (2)当0H 不成立时,求犯第二类错误的概率()u β. 【解】(1)当0H 成立时,0u ≤,则(){|0}|0}u P u u u P u u ααα=>≤=>≤()|0}1()(0)P x u u u u u αα=->≤=-Φ≤因0u ≤,故()()1u u αααΦ≥Φ=-,从而()1()1(1)u u αααα≤-Φ=--=,即犯第一类错误的概率不大于α.(2)(){|0}()|0}u P u u u P x u u u ααβ=≤>=-≤>()(0)u u α=Φ>因0u >,故当u →+∞时,()0u β→,即u 与假设0H 偏离越大,犯第二类错误的概率越小;而当0u +→时,()1u βα→-,即当u 为正值且接近0时,犯第二类错误的概率接近1α-.基本题型Ⅱ 单个正态总体的假设检验【例8.8】某天开工时,需检验自动包装机工作是否正常,根据以往的经验,其包装的质量在正常情况下服从正态分布2(100,1.5)N (单位:kg ),先抽测了9包,其质量为: 99.3,98.7,100.5,101.2,98.3,99.7,99.5,102.0,100.5 问这天包装机工作是否正常?【分析】 关键是将这一问题转化为假设检验问题.因检验包装机工作是否正常,化为数学问题应为双边检验01:100:100H u H u =↔≠.【解】由题意,提出假设检验问题:01:100:100H u H u =↔≠, 选取检验统计量(0,1)x u N =当0.05α=时,0.02521.96u u α==,又20.04 1.96u u α==<=,即接受原假设0H ,认为包装机工作正常.【例8.9】已知某种元件的寿命服从正态分布,要求该元件的平均寿命不低于1000h ,现从这批元件中随机抽取25知,测得平均寿命980X h =,标准差65S h =,试在水平0.05α=下,确定这批元件是否合格.【解】由题意,2σ未知,在水平0.05α=下检验假设0010:1000:1000H u u H u u ==↔<=属于单边(左边)t 检验.构造检验统计量 (1)x t t n =-,其中25,65,980n S X h ===,查t 分布表可得:0.05(1)(251) 1.7109t n t α-=-=,又0.05|| 1.538(24) 1.7109x t t ===<=.即接受原假设0H ,认为这批元件是合格的.【例8.10】某厂生产的一中电池,其寿命长期以来服从方差225000()σ=小时的正态分布,现有一批这种电池,从生产的情况来看,寿命的波动性有所改变,现随机地抽取26只电池,测得寿命的样本方差229200()S =小时,问根据这一数据能否推断这批电池寿命的波动性较以往有显著性的变化(取0.02α=).【解】 检验假设2201:5000:5000H H σσ=↔≠,选取统计量2222(1)(1)n S n χχσ-=-,由0.02α=,26n =,查2χ分布表可得220.012(1)(25)44.314n αχχ-==,220.0912(1)(25)11.524n αχχ--==, 又统计量2220.012(1)46(25)44.314n S χχσ-==>=,故拒绝原假设0H ,即认为这批电池寿命的波动性较以往有显著性的变化.【例8.11】 某种导线,要求其电阻的标准不得超过0.005(欧姆),今在生产的一批导线中取样品9根,测得0.007S =(欧姆),设总体为正态分布,问在水平0.05α=下,能否认为这批导线的标准差显著性地偏大?【解】本题属于总体均值未知,正态总体方差的单边检验问题0010:0.005:0.005H H σσσσ==↔>=选取统计量2222(1)(1)n S n χχσ-=-当0.05α=,9n =时,查2χ分布表可得:220.05(1)(8)15.507n αχχ-==,又题设0.007S =,则统计量22220.0522(1)80.00715.68(8)15.5070.005n S χχσ-⨯===>=. 故拒绝原假设0H ,认为这批导线的标准差显著性地偏大.【例8.12】 机器自动包装食盐,设每袋盐的净重服从正态分布,规定每袋盐的标准重量为500克,标准差不超过10克.某天开工以后,为了检查机器工作是否正常,从已包装好的食盐中随机抽取9袋,测得其重量(克)为:497,507,510,475,484,488,524,491,515问这天自动包装机工作是否正常(显著性水平0.05α=)? 【解】 设每袋盐重量为随机变量X ,则2(,)XN u σ,为了检查机器是否工作正常,需检验假设:01:500H u =及202:100H σ≤.下面现检验假设0111:500:500H u H u =↔≠ 由于2σ未知,故构造统计量(1)x t t n =-由于0.05α=,查t 分布表可得0.0252(1)(8) 2.306t n t α-==,又由题设计算可得499,16.03X S ==,故统计量取值0.025||0.187(8) 2.306x t t ===<=即接受原假设01H ,认为机器包装食盐的均值为500克,没产生系统误差.下面在检验假设220212:100:100H H σσ≤↔>选取统计量2222(1)(1)n S n χχσ-=-,由于0.05α=,查2χ分布表可得220.05(1)(8)15.5n αχχ-==,而统计量2220.052(1)20.56(8)15.5n S χχσ-==>=,故拒绝原假设02H ,接受12H ,即认为其标准差超过了10克.由上可知,这天机器自动包装食盐,虽没有产生系统误差,但生产不够稳定(方差偏大),从而认为这天自动包装机工作不正常.基本题型Ⅲ 两个正态总体的假设检验【例8.13】 下表给出了两个文学家马克·吐温(Mark Twain )的8偏小品文以及斯诺·特格拉斯(Snodgrass )的10偏小品文中由3格字母组成的词比例.马克·吐温: 0.225,0.262,0.217,0.240,0.230,0.229,0.235,0.217斯诺·特格拉斯:0.209,0.205,0.196,0.210,0.202,0.207,0.224,0.223,0.220,0.201 设两组数据分别来自正态分布,且两总体方差相等,两样本相互独立,问两个作家所写的小品文中包含由3格字母组成的词的比例是否有显著性的差异(0.05α=)?【分析】首先应注意题中的“比例”即“均值”的含义,因而本题应属于未知方差,却知其相等的两正态母体,考虑它们的均值是否相等的问题.【解】设题中两正态母体分别记为,X Y ,其均值分别为12,u u ,因而检验问题如下:012112::H u u H u u =↔≠选取统计量(2)X Y T t n m =+-,其中8,10n m ==,()()22122112wn S m S Sn m -+-=+-,在0.05α=时,查t 分布表可得()()/20.025216 2.1199t n m t α+-==由题设样本数据计算可得22120.2319,0.2097,0.00021,0.00009X Y S S ====,0.119w S ===.从而t统计量值为()0.025|| 3.964316 2.1199X Y T t ===>=,因而拒绝原假设0H ,认为两个作家所写的小品文中包含由3格字母组成的词的比例有显著性的差异.【例8.14】据专家推测:矮个子的人比高个子的人的寿命要长一些,下面给出了美国31个自然死亡的总统的寿命.矮个子(身高小于5英尺8英寸)总统 Modison Van Buren B.Harrison J.Adams J.Q.Adams 身高 5’4” 5’6” 5’6” 5’7” 5’7” 寿命 85 79 67 90 80高个子(身高大于5英尺8英寸)总统 W.Harrison Plok Tayler Crant Hayes Truman Fillmore Pierce A.Johson 身高 5’8” 5’8” 5’8”5’8.5” 5’8.5” 5’9” 5’9” 5’10” 5’10” 寿命 68 53 65 63 70 88 74 64 66 总统 T.Roosevelt Coolidge Eisenhower Cleveland Wilson Hoover Monroe Tyler 身高 5’10” 5’10” 5’10” 5’11” 5’11” 5’11” 6’ 6’ 寿命 60 60 78 71 67 90 73 71 总统 Buchanan Taft Harding Jaskon Washington Arthur F.Roosevelt 身高 6’ 6’ 6’ 6’1” 6’2” 6’2” 6’2” 寿命77 72 57 78 67 56 63设两个寿命总体均为正态分布且方差相等,试问以上数据是否符合上述推测(0.05α=)? 【解】设矮个子总统寿命为X ,高个子总统寿命为Y ,需检验012112::H u u H u u =↔>.由于22212σσσ==未知,故选用统计量(2)X Y T t n m =+-,其中5,26n m ==,()()22122112wn S m S Sn m -+-=+-.由题设样本数据可得80.2,69.15,X Y ==22124294.8,252183.215S S ==,故()()221221185.4492wn S m S Sn m -+-==+-,从而统计量|| 2.448X Y T ==,又当0.05α=时,查t 分布表可得()()0.05229 1.6991t n m t α+-==,即()0.05|| 2.44829 1.6991T t =>=,故拒绝原假设0H ,即推测是正确的,认为矮个子的人比高个子的人的寿命要长一些 【例8.15】总体21(,)XN u σ,22(,)Y N u σ,112,,,n x x x 与212,,,n y y y 分别时来自总体,X Y 的样本,试讨论检验问题012112::H u u H u u δδ-≤↔->.【解】取统计量12(2)X Y T t n n =+-,其中()()221122212112wn S n S S n n -+-=+-, 则检验统计量为X Y T =,当1H 成立时,t 有偏大的趋势,故取拒绝域为12{(2)}w t t n n α=>+-.【例8.16】甲乙相邻地段各取了50块和25块岩心进行磁化率测定,算出两样本标准差分别是210.0139S =,220.0053S =,问甲乙两段的标准差是否有显著性差异(0.05α=)?【解】作假设001:H σσ=,由题设有250211501500.0139()0.01425014949i i S X X =⨯⨯-===-∑, 252221521520.0053()0.00545215151ii S Y Y =⨯⨯-===-∑ 从而统计量21112222(1)0.01422.630.0054(1)n S n F n S n -===-,当0.05α=,查F 分布表可得0.0252(501,521)(501,521) 1.7494F F α--=--=,0.97512(501,521)(501,521)0.5698FF α---=--=,因为0.0252.63(49,51) 1.7494F F =>=,故拒绝原假设0H ,即认为甲乙两段的标准差有显著性差异.【例8.17】在集中教育开课前对学员进行了测试,过来一段时间后,又对学员进行了与前一次同样程度的考查,目的是了解上次的学员与这次学员的考试分类是否有显著性差别(0.05α=),从上次与这次学员的考试中随机抽取12份考试成绩,如下表考试次数 考分 合计平均分 (1) 80.5,91.0,81.0,85.0,70.0,86.0,69.5,74.0,72.5,83.0,69.0,78.5940 78.5 (2)76.0,90.0,91.5,73.0,64.5,77.5,81.0,83.5,86.0,78.5,85.0,96080.073.5【解】此为双正态总体的假设检验,两总体均值未知,先检验假设2222012112::H H σσσσ=↔≠.选取统计量211222(1,1)S F F n n S =--,由题设可计算得221253.15,60.23S S ==,则统计量212253.150.882560.23S F S ===,取0.05α=,查F 分布表可得0.0252(11,11)(11,11) 3.43F F α==,0.97510.02521(11,11)(11,11)0.2915(11,11)FF F α-===.由于122(11,11)0.8825(11,11) 3.43FF F αα-<=<=,故在0.05α=下,接受0H ,即认为两次考试中学员的成绩的方差相等. 再假设012112::H u u H u u =↔≠.构造统计量12(2)X YT t n n =+-,其中()()221122212112wn S n S S n n -+-=+-,1212,12n n ==.由样本数据可得78.5,80.0,X Y ==221253.1515,60.2273S S ==,故()()2211222121156.68942wn S n S Sn n -+-==+-,从而统计量||0.488X Y T ==,在0.05α=下,查t 分布表可得()()120.0252222 2.0739t n n t α+-==.由于()0.025||0.48822 2.0739T t =<=,即认为两次考试中学员的平均成绩相等,从而认为两次考试中学员的成绩无显著性差异.基本题型Ⅳ 非正态总体参数假设检验【例8.18】某产品的次品率为0.17,现对此产品进行了新工艺试验,从中抽取400件检查,发现次品56间,能否认为这项新工艺显著性地影响产品质量(0.05α=)? 【解】检验问题01:0.17:0.17H p H p =↔≠由题设可知56ˆ0.14400m pn ===,构造统计量 1.597u ===-,当0.05α=时,查正态分布表可得0.025 1.96u =,因为0.025|| 1.96u u <=,故接受原假设0H ,认为新工艺显著性地影响产品质量.【评注】本题的理论依据时中心极限定理:当n 充分大时,在0H 成立时,u =(0,1)N 分布.【例8.19】 已知某种电子元件的使用寿命X 服从指数分布()E λ,现抽查100个元件,得样本均值950()x h =,能否认为参数0.01λ=(0.05α=)? 【解】由题设()XE λ,故211,EX DX λλ==,当n 充分大时,1((0,1)1x u x N λλ-==-,现在检验问题01:0.001:0.001H H λλ=↔≠,则((0.0019501)0.5u x λ=-=⨯-=,当0.05α=时,查正态分布表可得0.025 1.96u =,因为0.025|| 1.96u u <=,故接受原假设0H ,认为参数0.01λ=.【评注】总体()X F x ,2,EX u DX σ==,则当n充分大时,u =从(0,1)N 分布.【例8.20】对某干洗公司去除污点的比例做下列假设检验01:0.7:0.9H p H p =↔=,选出100个污点,设其中去除的污点数为x ,拒绝域为{82}w x =>. (1)当0.7p =时,求犯第一类错误的概率α; (2)当0.9p =时,求犯第二类错误的概率β. 【解】(1)由题设有{82|0.7}1P x p α=>==-Φ1(2.62)10.99560.0044=-Φ=-=.(2){82|0.9}P x p β=≤==Φ( 2.67)1(2.67)10.99620.0038=Φ-=-Φ=-=.【评注】从计算分析,这一检验法的α,β皆很小,是较好的检验.§历年考研真题评析1、【98.1.4】设某次考试的考生成绩服从正态分布,从中随机地抽取36位考生的成绩,计算得到平均成绩为66.5,标准差为15分,问在显著性水平0.05下,是否可以认为这次考试全体考生平均成绩为70分?并给出检验过程.【解】设该次考试的考生成绩为X ,则2(,)XN ,设X 为从总体X 抽取的样本容量为n 的样本均值,S 为样本标准差,根据题意建立假设001:70;:70H H .选取统计量 07036X X TnSS在70时,2(70,),(35)X T t .选取拒绝域{||}R T ,其中满足{||}0.05P T ,即{||}0.95P T .即0.975(35) 2.0301t . 由036,66.5,70,15n xs 可以计算得统计量T 的值|66.570|||361.42.030115T .因此不能拒绝0H ,即在显著性水平0.05下可以认为全体考生的平均成绩为70分.§习题全解1、在正常情况下,某炼钢厂的铁水含碳量(%)2(4.55,)XN σ.一日测得5炉铁水含碳量如下:4.48,4.40,4.42,4.45,4.47在显著性水平0.05α=下,试问该日铁水含碳量得均值是否有明显变化. 【解】设铁水含碳量作为总体X ,则2(4.55,)XN σ,从中选取容量为5的样本,测得24.444,0.0011X S ==.由题意,设原假设为0: 4.55H u = 构造检验统计量 ||(4)X u t t S -=,则7.051t ==在显著性水平0.05α=下,查表可得0.97512(4)(4) 2.77647.051tt α-==<,拒绝原假设0H ,即认为有显著性变化.2、根据某地环境保护法规定,倾入河流的废物中某种有毒化学物质含量不得超过3ppm.该地区环保组织对某厂连日倾入河流的废物中该物质的含量的记录为:115,,x x .经计算得15148ii x==∑, 1521156.26i i x ==∑.试判断该厂是否符合环保法的规定.(该有毒化学物质含量X 服从正态分布)【解】设有毒化学物质含量作为总体X ,则2(,)XN u σ,从中选取容量为15的样本,测得1511 3.215i i X x ===∑,22221111()()0.1911n ni i i i S x x x nx n n ===-=-=--∑∑.由题意,设原假设为0:3H u <,备择假设为1:3H u >.构造检验统计量(14)X t t =,则 1.777t ==,在显著性水平0.05α=下,查表可得10.95(14)(14) 1.7613 1.777t t α-==<,即拒绝原假设0H ,接受备择假设1H ,认为该厂不符合环保的规定.3、某厂生产需用玻璃纸作包装,按规定供应商供应的玻璃纸的横向延伸率不应低于65.已知该指标服从正态分布2(,)N μσ, 5.5σ=.从近期来货中抽查了100个样品,得样本均值55.06x =,试问在0.05α=水平上能否接受这批玻璃纸? 【解】设玻璃纸的横向延伸率为总体X ,则2(,5.5)XN u ,从中选取容量为100的样本,测得55.06x =.由题意,设原假设为0:65H u >,备择假设为1:65H u <.构造检验统计量||(0,1)X u U N σ-=,则|55.0665|18.07275.5U -==在显著性水平0.05α=下,查表可得10.95 1.644918.0727U U α-==<,即拒绝原假设0H ,接受备择假设1H ,不能接受该批玻璃纸..4、某纺织厂进行轻浆试验,根据长期正常生产的累积资料,知道该厂单台布机的经纱断头率(每小时平均断经根数)的数学期望为9.73根,标准差为1.60根.现在把经纱上浆率降低20%,抽取200台布机进行试验,结果平均每台布机的经纱断头率为9.89根,如果认为上浆率降低后均方差不变,问断头率是否受到显著影响(显著水平α=0.05)?【解】设经纱断头率为总体X ,则9.73u EX ==, 1.6σ==,从中选取容量为200的样本,测得9.89x =.由题意,设原假设为0:9.73H u =,备择假设为1:9.73H u ≠. 构造检验统计量(0,1)X U N =,则 1.4142U ==在显著性水平0.05α=下,查表可得0.975121.96 1.4142UU α-==>,即接受原假设0H ,认为断头率没有受到显著影响.5、某厂用自动包装机装箱,在正常情况下,每箱重量服从正态分布2(100,)N σ.某日开工后,随机抽查10箱,重量如下(单位:斤):99.3,98.9,100.5,100.1,99.9,99.7,100.0,100.2,99.5,100.9.问包装机工作是否正常,即该日每箱重量的数学期望与100是否有显著差异?(显著性水平α=0.05) 【解】设每箱重量为总体X ,则2(100,)XN σ,从中选取容量为10的样本,测得99.9x =,20.34S =.由题意,设原假设为0:100H u =,备择假设为1:100H u ≠.构造检验统计量||(9)X u t t S -=,则0.5423t ==,在显著性水平0.05α=下,查表可得0.97512(9)(9) 2.26220.5423tt α-==>,即接受原假设0H ,认为每箱重量无显著差异.6、某自动机床加工套筒的直径X 服从正态分布.现从加工的这批套筒中任取5个,测得直径分别为15,,x x (单位m μ:),经计算得到51124ii x==∑, 5213139i i x ==∑.试问这批套筒直径的方差与规定的27σ=有无显著差别?(显著性水平0.01α=) 【解】设这批套筒直径为总体X ,则2(,)XN u σ,从中选取容量为5的样本,测得151124.815i i X x ===∑,22221111()()15.9511n ni i i i S x x x nx n n ===-=-=--∑∑. 由题意,设原假设为20:7H σ=,备择假设为21:7H σ≠.构造检验统计量2222(1)(4)n S χχσ-=,则2415.959.11437χ⨯==,在显著性水平0.01α=下,查表可得220.99512(4)(4)14.86αχχ-==,220.0052(4)(4)0.2070αχχ==,从而222122(4)(4)ααχχχ-<<. 即接受原假设0H ,认为这批套筒直径的方差与规定的27σ=无显著差别.7、甲、乙两台机床同时独立地加工某种轴,轴的直径分别服从正态分布211(,)N μσ、222(,)N μσ(12,μμ未知).今从甲机床加工的轴中随机地任取6根,测量它们的直径为16,,x x ,从乙机床加工的轴中随机地任取9根,测量它们的直径为19,,y y ,经计算得知:61204.6ii x==∑, 6216978.9i i x ==∑,91370.8i i y ==∑,92115280.2i i y ==∑.问在显著性水平0.05α=下,两台机床加工的轴的直径方差是否有显著差异? 【解】设两台机床加工的轴的直径分别为总体,X Y ,则211(,)XN μσ、222(,)YN μσ,从总体X 中选取容量为6的样本,测得61134.16i i X x ===∑222211111()()0.40811n ni i i i S x x x nx n n ===-=-=--∑∑. 从总体Y 中选取容量为9的样本,测得91141.29i i Y y ===∑222221111()()0.40511n ni i i i S y y y ny n n ===-=-=--∑∑ 由题意,设原假设为22012:H σσ=,备择假设为22112:H σσ≠.构造检验统计量2122(5,8)S F F S =,则0.4081.0070.405F ==,在显著性水平0.05α=下,查表可得0.97512(5,8)(5,8) 6.76FF α-==,0.0252(5,8)(5,8)0.1479F F α==,从而122(5,8)(5,8)F F Fαα-<<.即接受原假设0H ,认为两台机床加工的轴的直径方差无显著差异.8、某维尼龙厂根据长期正常生产积累的资料知道所生产的维尼龙纤度服从正态分布,它的标准差为0.048.某日随机抽取5根纤维,测得其纤度为1.32,1.55,1.36,1.40,1.44.问该日所生产得维尼龙纤度的均方差是否有显著变化(显著性水平α=0.1)? 【解】设维尼龙纤度为总体X ,则2(,0.048)XN u ,从中选取容量为5的样本,测得511 1.4145i i X x ===∑,2211()0.00781n i i S x x n ==-=-∑.由题意,设原假设为0:0.048H σ=,备择假设为1:0.048H σ≠.构造检验统计量2222(1)(4)n S χχσ-=,则2240.007813.542(0.048)χ⨯==在显著性水平0.1α=下,查表可得220.9512(4)(4)9.487713.542αχχ-==<.即拒绝原假设0H ,认为维尼龙纤度的均方差有显著变化.9、某项考试要求成绩的标准差为12,先从考试成绩单中任意抽出15份,计算样本标准差为16,设成绩服从正态分布,问此次考试的标准差是否符合要求(显著性水平α=0.05)? 【解】 设考试成绩为总体X ,则2(,12)XN u ,从中选取容量为15的样本,测得16S =.由题意,设原假设为0:12H σ=,备择假设为1:12H σ≠. 构造检验统计量2222(1)(14)n S χχσ-=,则222141619.055612χ⨯==.在显著性水平0.05α=下,查表可得220.97512(14)(14)26.1189αχχ-==,220.0252(14)(14) 5.6287αχχ==,从而222122(14)(14)ααχχχ-<<.即接受原假设0H ,认为此次考试的标准差符合要求.10、某卷烟厂生产甲、乙两种香烟,分别对他们的尼古丁含量(单位:毫克)作了六次测定,获得样本观察值为:甲:25,28,23,26,29,22; 乙:28,23,30,25,21,27.假定这两种烟的尼古丁含量都服从正态分布,且方差相等,试问这两种香烟的尼古丁平均含量有无显著差异(显著性水平α=0.05,)?对这两种香烟的尼古丁含量,检验它们的方差有无显著差异(显著性水平α=0.1)?【解】设这两种烟的尼古丁含量分别为总体,X Y ,则211(,)X N μσ、222(,)Y N μσ,从中均选取容量为6的样本,测得61125.56i i X x ===∑,22111()7.51n i i S x x n ==-=-∑, 61125.66676i i Y y ===∑,22211()11.06671n i i S y y n ==-=-∑, 由题意,在方差相等时,设原假设为012:H u u =,备择假设为112:H u u ≠.构造检验统计量12(2)X Y t t n n =+-,其中222112212(1)(1)9.2834(2)wn S n S S n n -+-==+-.则0.0948t ==,在显著性水平0.05α=下,查表可得120.97512(2)(10) 2.22810.0948tn n t α-+-==>.即接受原假设0H ,认为这两种香烟的尼古丁平均含量无显著差异.由题意,在方差待定时,设原假设为22012:H σσ=,备择假设为22112:H σσ≠.构造检验统计量2122(5,5)S F F S =,则7.50.677711.0667F ==,在显著性水平0.1α=下,查表可得0.9512(5,8)(5,5) 5.0503FF α-==,0.052(5,8)(5,5)0.1980F F α==,由122(5,5)(5,5)F F Fαα-<<.即接受原假设0H ,认为它们的方差无显著差异.§同步自测题及参考答案一、选择题1、关于检验水平α的设定,下列叙述错误的是 【 】()A α的选取本质上是个实际问题,而非数学问题. ()B 在检验实施之前, α应是事先给定的,不可擅自改动.()C α即为检验结果犯第一类错误的最大概率. ()D 为了得到所希望的结论,可随时对α的值进行修正.2、关于检验的拒绝域W,置信水平a ,及所谓的“小概率事件”,下列叙述错误的是 【 】()A a 的值即是对究竟多大概率才算“小”概率的量化描述. ()B 事件021|),,,{(H W X X X n ∈ 为真}即为一个小概率事件.()C 设W 是样本空间的某个子集,指事件}|),,,{(021为真H W X X X n ∈ . ()D 确定恰当的W 是任何检验的本质问题.3、设总体22),,(~σσμN X 未知,通过样本n X X X ,,,21 检验假设00:μμ=H ,此问题拒绝域形式为 【 】()A }C >. ()B }/100{C n S X <-. ()C }10/100{C S X >- . ()D }{C X >.4、设n X X X ,,,21 为来自总体2(,)N μσ的样本,若μ未知, 100:20≤σH ,21:100,H 0.05a ,关于此检验问题,下列不正确的是 【 】()A 检验统计量为100)(12∑=-ni iX X. ()B 在0H 成立时,)1(~100)1(22--n x S n . ()C 拒绝域不是双边的. ()D 拒绝域可以形如})({12∑=>-ni i k X X .5、设总体服从正态分布2(,3)XN μ,12,,,n x x x 是X 的一组样本,在显著性水平0.05α=下,假设“总体均值等于75”拒绝域为12{,,,:74.0275.98}n w x x x x x =<⋃>,则样本容量n = 【 】()A 36. ()B 64. ()C 25. ()D 81.二、填空题1、为了校正试用的普通天平,把在该天平上称量为100克的10个试样在计量标准天平上进行称量,得如下结果:99.3, 98.7, 100.5, 101,2, 98.399.7 99.5 102.1 100.5, 99.2 假设在天平上称量的结果服从正态分布,为检验普通天平与标准天平有无显著差异,0H为 .2、设样本2521,,,X X X 来自总体μμ),9,(N 未知,对于检验0010::H H μμμμ=↔= 取拒绝域形如k X ≥-0μ,若取05.0=a ,则k 值为 .3、设12,,,n x x x 是正态总体2(,)XN μσ的一组样本.现在需要在显著性水平0.05α=下检验假设2200:H σσ=.如果已知常数u ,则0H 的拒绝域1w =______________;如果未知常数u ,则0H 的拒绝域2w =______________.4、在一个假设检验问题中令0H 是原假设,1H 时备择假设,则犯第一类错误的概率{______________}P ,犯第二类错误的概率{______________}P .三、解答题1、某批矿砂的5个样本中的镍含量,经测定为(%)3.25,3.27,3.24,3.26,3.24设测定值总体服从正态分布,问在0.01α=下,能否接受假设:这批矿砂的含量的均值为3.25.2、已知精料养鸡时,经若干天鸡的平均重量为4公斤.今对一批鸡改用粗料饲养,同时改善饲养方法,经同样长的饲养期后随机抽取10只,的其数据如下:3.7,3.8,4.1,3.9,4.6,4.7,5.0,4.5,4.3,3.8已知同一批鸡的重量X 服从正态分布,试推断:这一批鸡的平均重量是否显著性提高.试就0.01α=和0.05α=分别推断.3、测定某种溶液中的水份,它的10个测定值给出0.037%S =,设测定值总体为正态分布,2σ为总体方差,试在水平0.05α=下检验假设01:0.04%:0.04%H H σσ=↔<.4、在70年代后期,人们发现在酿造啤酒时,在麦芽干燥过程中形成致癌物质亚硝基二甲胺(NDMA ).到了80年代初期开发了一种新的麦芽干燥过程,下面给出了在新老两种干燥过程中形成的NDMA 的含量(以10亿份中的份数计)老过程 6,4,5,5,6,5,5,6,4,6,7,4 新过程2,1,2,2,1,0,3,2,1,0,1,3设两样本分别来自正态总体,且两总体的方差相等,两样本独立,分别以12,u u 记对应于老、新过程的总体均值,试检验假设(0.05α=)0111:2:2H u u H u u -=↔->.5、检验了26匹马,测得每100毫升的血清中,所含的无机磷平均为3.29毫升,标准差为0.27毫升;又检验了18头羊,每100毫升血清中汗无机磷平均值为3.96毫升,标准差为0.40毫升.设马和羊的血清中含无机磷的量均服从正态分布,试问在显著性水平0.05α=条件下,马和羊的血清中无机磷的含量有无显著性差异?6、某种产品的次品率原为0.1,对这种产品进行新工艺试验,抽取200件发现了13件次品,能否认为这项新工艺显著性地降低了产品的次品率(0.05α=)?7、设n X X X ,,,21 为总体(,4)XN a 的样本,已知对假设01:1: 2.5H a H a =↔=,0H 的拒绝域为{2}w X =>.(1)当9u =时,求犯两类错误的概率α和β; (2)证明:当n →∞时,0α→,0β→.同步自测题参考答案 一、选择题1.()D .2. ()C .3. ()C .4. ()B .5. ()A . 二、填空题1.100=μ.2. 1.176.3. 222210.0250.97522110011{()()()()}nniii i w x u n x u n χχσσ===->⋃-<∑∑;222220.0250.975220(1)(1){(1)(1)}n S n S w n n χχσσ--=>-⋃<- .4.10{|}P H H 接受成立,01{|}P H H 接受成立.三、解答题 1、接受0H .2、0.01α=时,显著性提高;0.05α=时,没有显著性提高 .3、 接受0H .4、拒绝0H ,接受1H .5、方差无显著性差异,均值有显著性差异,故有显著性差异.6、 拒绝0H .7、(1)0.0668α=,0.2266β=,(2)102α=-Φ→,(04β=Φ-→()n →∞.。
假设检验流程案例分析

假设检验流程案例分析一、假设检验的基本概念。
1.1 什么是假设检验呢?简单来说,这就像是一场法庭审判。
我们有一个“被告”,也就是我们要检验的假设。
比如说,我们想知道一种新的减肥方法是不是真的有效,那“这种减肥方法有效”就是我们的假设。
我们不能轻易就相信这个说法,得拿出证据来。
1.2 这里面有个很重要的东西叫“显著性水平”。
这就好比是我们判断事情的一个标准。
如果把生活中的事情比作考试,那显著性水平就是及格线。
一般我们会设定一个值,像0.05或者0.01。
如果计算出来的结果小于这个值,那就像考试不及格一样,我们就有理由怀疑我们的假设是错的。
2.1 案例背景。
咱就说有个工厂,他们生产的灯泡,以前一直说平均使用寿命是1000小时。
但是最近呢,工人换了新的生产工艺,老板就想知道,这新的工艺下,灯泡的平均使用寿命是不是还是1000小时。
这时候我们的假设就出来了。
原假设就是“新工艺下灯泡平均使用寿命还是1000小时”,那备择假设就是“新工艺下灯泡平均使用寿命不是1000小时”。
2.2 收集数据。
这就好比破案要找线索一样。
我们得去收集灯泡使用寿命的数据。
从新生产的灯泡里随机抽取一些,比如抽取了50个灯泡,然后测试它们各自的使用寿命。
这一步可得认真,要是数据不准确,那就好比地基没打好,后面全是白搭。
2.3 选择检验统计量并计算。
这里就有点技术含量了。
根据我们的问题和数据类型,选择合适的检验统计量。
就像我们要开锁,得选对钥匙一样。
对于这个灯泡的例子,可能会用到t检验或者z 检验。
计算出这个统计量的值之后,就像是我们算出了一个“关键指标”。
2.4 做出决策。
计算出统计量的值后,我们就可以根据显著性水平来做决定了。
如果这个值落在了我们事先设定的“拒绝域”里,那就像证据确凿一样,我们就拒绝原假设。
就好比我们发现这个新生产工艺下灯泡的平均使用寿命和1000小时相差太多,那我们就有理由相信原假设不成立了。
要是不在拒绝域里,那我们就没有足够的证据拒绝原假设,只能暂时认为原假设是对的。
假设检验案例分析
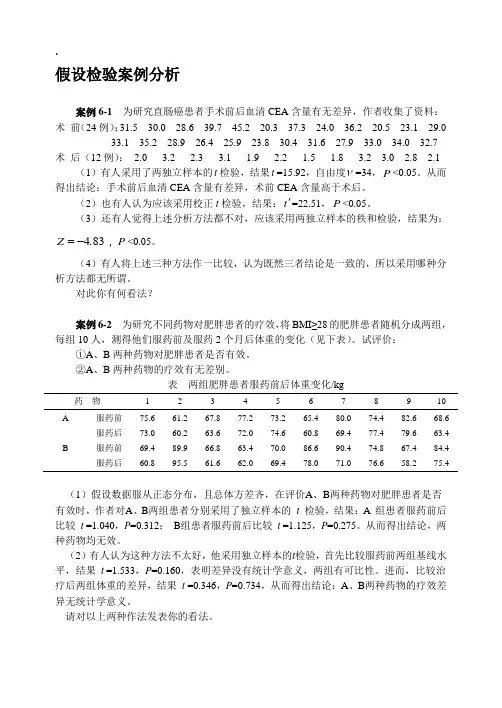
.假设检验案例分析案例6-1 为研究直肠癌患者手术前后血清CEA含量有无差异,作者收集了资料:术前(24例):31.5 30.0 28.6 39.7 45.2 20.3 37.3 24.0 36.2 20.5 23.1 29.033.1 35.2 28.9 26.4 25.9 23.8 30.4 31.6 27.9 33.0 34.0 32.7 术后(12例):2.0 3.2 2.3 3.1 1.9 2.2 1.5 1.8 3.2 3.0 2.8 2.1 (1)有人采用了两独立样本的t检验,结果t=15.92,自由度ν=34,P<0.05。
从而得出结论:手术前后血清CEA含量有差异,术前CEA含量高于术后。
(2)也有人认为应该采用校正t检验,结果:t'=22.51,P<0.05。
(3)还有人觉得上述分析方法都不对,应该采用两独立样本的秩和检验,结果为:=,P<0.05。
Z-834.(4)有人将上述三种方法作一比较,认为既然三者结论是一致的,所以采用哪种分析方法都无所谓。
对此你有何看法?案例6-2 为研究不同药物对肥胖患者的疗效,将BMI≥28的肥胖患者随机分成两组,每组10人,测得他们服药前及服药2个月后体重的变化(见下表)。
试评价:①A、B两种药物对肥胖患者是否有效。
②A、B两种药物的疗效有无差别。
表两组肥胖患者服药前后体重变化/kg药物 1 2 3 4 5 6 7 8 9 10 A 服药前75.6 61.2 67.8 77.2 73.2 65.4 80.0 74.4 82.6 68.6服药后73.0 60.2 63.6 72.0 74.6 60.8 69.4 77.4 79.6 63.4 B 服药前69.4 89.9 66.8 63.4 70.0 86.6 90.4 74.8 67.4 84.4服药后60.8 95.5 61.6 62.0 69.4 78.0 71.0 76.6 58.2 75.4(1)假设数据服从正态分布,且总体方差齐,在评价A、B两种药物对肥胖患者是否有效时,作者对A、B两组患者分别采用了独立样本的t 检验,结果:A 组患者服药前后比较t =1.040,P=0.312;B组患者服药前后比较t =1.125,P=0.275。
假设检验问题讲解(ppt 47页)

其样本均值为2.8965,样本标准为0.148440135,
你可以拒绝原假设吗?
拒绝域为:
x3
s
t0.05(n1)
H0: 3 H1: > 3
H0: 3 H1: 3
Rejection Regions
0 0
Critical Value(s)
/2
0
P-值的应用
p=Pr(t<-3.118)=0.0028
0.45
0.4
0.35 比它小的概率 0.3 是多少?P-值
0.25
0.2
0.15
比它小的概率是0.05
0.15
0.1
0.05
0
-1
0
31-c0 2
3
4
5
6
7
8
大样本下的解决方案(3)
如果2未知,则
x ~ N (0 , 1) s n
选择拒绝域为
x3
s
z 0 . 05
n
假定由36听罐头所组成的一个样本的样 本均值 x 2.92 磅,样本标准差 s=0.18 ,你能拒绝原假设吗?
x
s
3
2.92 0.18
影响 b 的因素
True Value of Population Parameter
Increases When Difference Between Hypothesized Parameter & True Value Decreases
第八章 假设检验-案例分析
在 = 0.05的水平上不拒绝H0 不能认为该机器的性能未达到 设计要求
0 12.40
39.36
2
1.4 -0.9 -0.5 -0.2 -0.6
-0.6 1.3 0 -1.9 1.1
绿色
健康饮品
例题分析
H0: 2 = 1 H1: 2 1 = 0.05 df = 25 - 1 = 24 临界值(s):
/2 =.05
统计量: 2 ( n 1 ) s 2 2 0
决策: 结论:
双侧检验
例题分析
H0: = 0.081 H1: 0.081 = 0.05 n = 200 检验统计量:
z
x 0
n
0.076 0.081 0.025 200
2.83
临界值(s):
拒绝 H0
.025
决策:
在 = 0.05的水平上拒绝H0
拒绝 H0
.025
结论:
结论:
-1.96
0
1.96
Z
该市老年人口比重为14.7%
【例7.7】某厂商生产出一种新 0.3 -0.4 -0.7 型的饮料装瓶机器,按设计要 求 , 该 机 器 装 一 瓶 一 升 -0.3 -1.5 0.6 1 (1000cm3) 的 饮 料 误 差 上 下 不 -1.3 0.7 超过1cm3。如果达到设计要求 -0.6 0.7 -1.5 ,表明机器的稳定性非常好。 -0.5 1 -0.2 现从该机器装完的产品中随机 抽取25瓶,分别进行测定(用样 本减1000cm3),得到如下结果 绿色 。检验该机器的性能是否达到 健康饮品 设计要求 (=0.05) 双侧检验
假设检验案例辨析及参考答案
第5章假设检验案例辨析及参考答案案例5-1 为了比较一种新药与常规药治疗高血压的疗效,以血压下降值为疗效指标,有人作了单组设计定量资料均数比较的检验,随机抽取25名患者服用了新药,以常规药的疗效均值为,进行检验,无效假设是,对立假设是,检验水平α=1%。
结果值很大,拒绝了无效假设。
“拒绝了无效假设”意味着什么?下面的说法你认为对吗?(1)你绝对否定了总体均数相等的无效假设。
(2)你得到了无效假设为真的概率是1%。
(3)你绝对证明了总体均数不等的备择假设。
(4)你能够推论备择假设为真的概率是99%。
(5)如果你决定拒绝无效假设,你知道你将犯错误的概率是1%。
(6)你得到了一个可靠的发现,假定重复这个实验许多次,你将有99%的机会得到具有统计学意义的结果。
提示:就类似的问题,Haller和Kruss(2002)在德国的6个心理系问了30位统计学老师、44位统计学学生和39位心理学家。
结果所有的统计学学生、35位心理学家和24位统计学老师认为其中至少有一条是正确的;10位统计学老师、13位心理学家和26位统计学学生认为第4题是正确的。
(见Statistical Science, 2005, 20(3):223-230.)案例辨析6个选择均不正确。
(1)可能犯Ⅰ类错误。
(2)α=1%是表示在无效假设成立的条件下,犯Ⅰ类错误的概率。
(3)可能犯Ⅰ类错误。
(4)α=1%是表示在无效假设成立的条件下,犯Ⅰ类错误的概率,而不是推论备择假设为真的概率是99%。
(5)在无效假设成立的条件下,就该例拒绝无效假设犯错误的概率是。
(6)在无效假设成立的条件下,还可能犯错误,并不是完全“可靠”的发现;1-=99%是指无效假设成立的条件下不犯错误的概率是99%。
正确做法“拒绝了无效假设”意味着在无效假设成立的条件下,推断犯错误的概率为。
案例5-2 某工厂生产的某医疗器械的合格率多年来一直是80.0%。
最近从该厂一次抽取20个该器械检测,合格13个,计算得到合格率为65.0%;一周后又抽取15个器械检测,合格10个,计算得到合格率为66.7%,分别进行检验,得到两总体率相等的结论,表明合格率没下降,两个合格率的平均值为65.85%,进行检验,得到两总体率不等的结论,表明合格率下降了。
关于假设检验的详细总结与典型例题
关于假设检验的详细总结与典型例题假设检验是数一考生普遍反映非常头疼的一块内容,因为它入门较难,其思想在初次复习时理解起来较难。
虽然这一部分在历年真题中考查次数很少,但为了做到万无一失,我们也应该准备充分,何况相对来说这一部分内容的难度和变化并不大。
为了让各位考生对假设检验有一个全面深入的理解和掌握,我们给出如下总结与例题。
对于假设检验,首先要理解其基本原理,即小概率原理,假设检验的方法即是从此原理衍生而来;其次,要掌握其步骤,会根据显著性水平α,即第一类心理学考研错误,来求拒绝域与接收域,其求法要根据不同的条件来套用公式,能根据理解推导公式是上策,如果时间不够,可以选择记忆各种不同条件下的求拒绝域的公式。
最后,相比之下两个正态总体参数的假设检验的考查可能性要低于一个正态总体参数的假设检验。
假设检验的基本概念数理统计的基本任务是根据样本推断总体,对总体的分布律或者分布参数作某种假设,然后根据抽得的样本,运用统计分析的方法来检验这一假设是否正确,从而作出接受假设或者拒绝假设的决定,这就是假设检验.根据实际问题提出的假设0H 称为原假设,其对立假设1H 称为备择假设. 假设检验中推理的依据是小概率原理:小概率事件在一次试验中实际上不会发生. 假设检验中的小概率α称为显著性水平,通常取0.05α=或者0.01α=.假设检验中使用的推理方法是:为了检验原假设0H 是否成立,我医学考研论坛们先假定原假设0H 成立. 如果抽样的结果导致小概率事件在一次试验中发生了,根据小概率原理,有理由怀疑0H 的正确性,从而拒绝0H ,否则接受0H .假设检验的步骤⑴根据实际问题提出原假设0H 和备择假设1H ; ⑵确定检验统计量T ;⑶根据给定的显著水平α,查概率分布表,确定拒绝域W ;⑷利用样本值计算统计量T 的值t ,若t W ∈,则拒绝0H ,否则接受0H .假设检验中可能犯的两类错误由于小概率事件还是可能发生的,根据小概率作出的判断可能是错误的. 事件0H 真而拒绝0H ,称为第一类(弃真)错误,犯第一类错误的概率为{}0P t W H α∈≤,因此显著性水平α是用来控制犯第一类错误的概率的. 0H 假而接受0H ,称为第二类(纳伪)错误,犯第二类错误的概率为{}1P t W H ∉,记作β.典型例题1.136,,X X 是取自正态总体(,0.04)N μ的简单随机样本,检验假设0:0.5H μ=,备择假设11:0.5H μμ=>,检验的显著水平0.05α=,取否医学考研论坛定域为X c >,则c = ,若10.65μ=,则犯第二类错误的概率β= .解 ⑴0H 成立时,0.04~(0.5,)36X N , {}00.50.051()0.1/3c P X c H αΦ-==>=-,0.5()0.95(1.645)0.1/3c ΦΦ-==,0.51.6450.1/3c -=,得0.5548c =.⑵1H 成立时,0.04~(0.65,)36X N{}10.55480.65()( 2.856)0.1/3P X c H βΦΦ-=≤==-.1(2.856)10.99790.0021Φ=-=-=2.设总体20~(,)X N μσ,20σ已知,检验假设00:H μμ=,备择假设10:H μμ>,取否定域为X c >,则对固定的样本容量n ,犯第一类错误的概率α随c 的增大而 .(减小)解 0H 成立时,200~(,)X N nσμ,犯第一类(弃真)错误的概率{}001(/P X c H nαΦσ=>=-,故犯第一类错误的概率α随c 的增大而减小.一个正态总体2(,)N μσ参数的假设检验 ⑴ 2σ已知,关于μ的检海文考研验(u 检验) 检验假设00:H μμ= 统计量X U =拒绝域2U u α>检验假设00:H μμ>统计量X U =拒绝域U u α<-检验假设00:H μμ<统计量X U =拒绝域U u α>⑵2σ未知,关于μ的检验(t 检验) 检验假设00:H μμ=统计量X t =拒绝域2(1)t t n α>-检验假设00:H μμ> 统计量0/X t S n = 拒绝域(1)t t n α<--检验假设00:H μμ< 统计量0/X t S n=拒绝域(1)t t n α>-⑶μ未知,关于2σ的检验(2χ检验) 检验假设2200:H σσ=统计量2220(1)n S χσ-=拒绝域222(1)n αχχ>-或者2212(1)n αχχ-<-检验假设2200:H σσ>统计量2220(1)n S χσ-=拒绝域221(1)n αχχ-<-检验假设2200:H σσ< 统计量2220(1)n S χσ-= 拒绝域22(1)n αχχ>-▲拒绝域均采用上侧分位数.两个正态总体21(,)N μσ、22(,)N μσ参数的假设检验.⑴两个正态总体21(,)N μσ、22(,)N μσ均值的假设检验(t 检验) 检验假设012:H μμ=统计量X Yt =拒绝域122(2)t t n n α>+-检验假设012:H μμ>统计量X Yt =拒绝域12(2)t t n n α<-+-检验假设012:H μμ<统计量X Yt =拒绝域12(2)t t n n α>+-⑵两个正态总体211(,)N μσ、222(,)N μσ方差的假设检验(F 检验) 检验假设22012:H σσ=统计量2122S F S = 拒绝域122(1,1)F F n n α>--或者1212(1,1)F F n n α-<--检验假设22012:H σσ>统计量2122S F S = 拒绝域112(1,1)F F n n α-<--检验假设22012:H σσ< 统计量2122S F S = 拒绝域12(1,1)F F n n α>--▲拒绝域均采用上侧分位数. 典型例题1.设n X X X ,,,21 是来自正态总海文考研体2(,)N μσ的简单随机样本,其中参数2,μσ未知,记22111,(),n ni i i i X X Q X X n ====-∑∑则假设0:0H μ=的t 检验使用统计量t = .解 统计量2(1)//(1)n n XX nXt S n Q n -===-2.某酒厂用自动装瓶机装酒,每瓶规定重500克,标准差不超过10克,每天定时检查,某天抽取9瓶,测得平均重X =499克,标准差S =16.03克. 假设瓶装酒的重量X 服从正态分布.问这台机器是否工作正常?(05.0=α).解 先检验0H :500μ=,统计量X t =, 拒绝域0.025(8) 2.3060t t >=,4995000.18716.03/3X t -===-,接受0H ;再检验0H ':2210σ≤,统计量222(1)10n S χ-=, 拒绝域220.05(8)15.507χχ>=, 22222(1)816.0320.5571010n S χ-⨯===,拒绝220:10H σ'≤, 故该机器工作无系统误差,但不稳定3.设127,,,X X X 是来自正态总体211(,)N μσ的简单随机样本,设128,,,Y Y Y 是来自正态总体222(,)N μσ的简单随机样本,且两个样本相互独立,它们的样本均值分别为13.8,17.8X Y ==,样本标准差123.9, 4.7S S ==,问在显著性水平0.05下,是否可以认为12μμ<?解 先检验0H :2212σσ=,检验统计量2122S F S =,拒绝域0.025(6,7) 5.12F F >=或者0.9750.02511(6,7)(7,6) 5.70F F F <==,221222 3.90.68854.7S F S ===,接受0H ; 再检验0H ':12μμ<,统计量1211w X Yt S n n =+, 拒绝域0.05(13) 1.7709t t >=,1.7773X Yt ==-,接受0H ',即可以认为12μμ<. ▲检验两个正态总体均值相等时,应先检验它们的方差相等.。
假设检验例题讲解
假设检验例题讲解引言假设检验是统计学中一种重要的推断方法,用于根据样本数据对总体参数进行推断。
在实际应用中,我们经常需要对某个总体参数是否满足某个假设进行检验,以此来判断某种情况的发生是否是偶然的还是具有统计学意义的。
在本文中,我们将通过一个具体的例子来详细讲解假设检验的步骤和方法。
例题描述某公司通过市场调研,推出了一种新的产品,并声称该产品的平均寿命超过了现有市场上的同类产品。
为了验证这一声称,该公司随机选取了30台该产品进行了测试,并记录了它们的寿命(以小时为单位)。
假设该产品的寿命服从正态分布,现在我们想要对该声称进行检验。
步骤1:建立假设在进行假设检验之前,首先需要明确我们的原假设和备择假设。
原假设(H0):该产品的平均寿命不超过现有市场上同类产品的平均寿命,即μ ≤ μ0(μ0为现有产品的平均寿命)。
备择假设(H1):该产品的平均寿命超过现有市场上同类产品的平均寿命,即μ> μ0。
在本例中,我们要采用单侧检验,因为我们关心的是新产品平均寿命是否超过现有产品的平均寿命。
步骤2:选择显著性水平显著性水平(α)是在进行假设检验时事先设定的一个值,它规定了我们对收集到的样本数据作出判断的临界点。
常用的显著性水平有0.05和0.01两种。
在本例中,我们选择α = 0.05作为显著性水平。
步骤3:计算样本统计量根据收集到的样本数据,我们需要计算出一个样本统计量,用来对总体参数进行估计。
在本例中,我们要计算平均寿命的样本均值和样本标准差。
假设样本的平均寿命为x̄,样本标准差为s。
步骤4:计算检验统计量在假设检验中,我们需要计算一个检验统计量来判断样本数据和原假设是否一致。
在本例中,我们要计算t检验统计量,其公式为: t统计量其中,x̄为样本均值,μ0为原假设的参数值,s为样本标准差,n为样本容量。
步骤5:计算P值在假设检验中,P值是一个重要的指标,用于评估样本数据在原假设为真时出现的概率。
在本例中,我们要计算P值,即检验统计量大于等于观察到的t检验统计量的概率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
假设检验
一、单样本总体均值的假设检验 .................................................... 1 二、独立样本两总体均值差的检验 ................................................ 2 三、两匹配样本均值差的检验 ........................................................ 4 四、单一总体比率的检验 ................................................................ 5 五、两总体比率差的假设检验 .. (7)
一、单样本总体均值的假设检验
例题:
某公司生产化妆品,需要严格控制装瓶重量。
标准规格为每瓶250 克,标准差为1 克,企业的质检部门每日对此进行抽样检验。
某日从生产线上随机抽取16 瓶测重,以95%的保证程度进行总体均值的假设检验。
x t μ-=
data6_01 样本化妆品重量 SPSS 操作:
(1)打开数据文件,依次选择Analyze (分析)→Compare Means (比较均值)→One Sample T Test (单样本t 检验),将要检验的变量置入Test Variable(s)(检验变量);
(2)在Test Value (检验值)框中输入250;点击Options (选项)按钮,在
Confidence Interval(置信区间百分比)后面的框中,输入置信度(系统默认为95%,对应的显著性水平设定为5%,即0.05,若需要改变显著性水平如改为0.01,则在框中输入99 即可);
(3)点击Continue(继续)→OK(确定),即可得到如图所示的输出结果。
图中的第2~5 列分别为:计算的检验统计量t 、自由度、双尾检验p-值和样本均值与待检验总体均值的差值。
使用SPSS 软件做假设检验的判断规则是:p-值小于设定的显著性水平Ɑ时,要拒绝原假设(与教材不同,教材的判断标准是p<Ɑ/2)。
从图中可以看到,p-值为0.01,小于0.05,故检验结论是拒绝原假设、接受备择假设,认为当天生产的全部产品平均装瓶重量与250 克有显著差异(拒绝原假设),不符合规定的标准。
图中表格的最后两列,是样本均值与待检验总体均值差值(xi-250)1-Ɑ置信区间的下限与上限,待检验的总体均值Test Value 加上这两个值,就构成了总体均值的1-Ɑ置信区间。
通过这个置信区间也可以做假设检验:若这个区间不包含待检验的总体均值,就要在Ɑ水平上拒绝原假设。
本例中样本均值与待检验总体均值差值95%置信区间的下限与上限均为负值,因此所构造的总体均值的95%置信区间不可能包含待检验的总体均值250,因此要在0.05 的水平上拒绝原假设、接受备择假设,与依据p-值得出的检验结论一致。
注意:除非给出明确结果,SPSS没有单侧检验,SPSS中的p值均为双侧检验的概率p值,如果要进行要单侧检验,将软件给出的p值与2倍的显著性水平进行比较即可,如要求Ɑ=0.05,单侧比较时,p值与2Ɑ=0.1进行比较.
二、独立样本两总体均值差的检验
例题:
某品牌时装公司在城市中心商业街的专卖店中只销售新款产品且价格不打折,打折的旧款产品则统一在城郊购物中心的折扣店销售。
公司销售部门为制订更合理的销售价格及折扣方法,对购买该品牌时装的顾客做了抽样调查。
分别从光顾城中心专卖店的顾客中随机抽取了36 人,从光顾折扣店的顾客中随机抽取了25 人。
调查发现,光顾专卖店的顾客样本平均月收入水平为1.35 万元,而光顾折扣店的顾客样本平均月收入水平为1.24 万元。
现在需要判断:光顾这两种店的顾客的总体收入水平是否也存在明显的差异?
(“data6_03样本顾客月收入水平”)
()()
x x t ---=
SPSS 操作:
(1)打开数据文件,依次选择Analyze (分析)→Compare Means (比较均值)→IndependentSample T Test (独立样本t 检验),将要检验的变量置入Test Variable(s)(检验变量),将分组变量置入Grouping Variable (分组变量),并点击Define Groups (定义组)输入两个组对应的变量值;
(2)点击Options (选项)按钮,在Confidence Interval (置信区间百分比)后面的框中,输入置信度(系统默认为95%,对应的显著性水平为5%即0.05,若需要改变显著性水平如改为0.01,则在框中输入99 即可);
(3)点击Continue (继续)→OK (确定)。
得到如图所示的输出结果。
三、两匹配样本均值差的检验
例题:
中学生慢跑试验的例子。
表6-3 是30 名学生慢跑锻炼前后脉搏恢复时间及差值数据,试以0.05 的显著性水平检验:学生慢跑锻炼前后脉搏恢复时间是否具有显著差异。
/d d d t s μ-=
data6_04 学生慢跑锻炼前后脉搏恢复时间及差值
SPSS 操作:
(1)打开数据文件,依次选择Analyze (分析)→Compare Means (比较均值)→Paired-Sample T Test (匹配样本t 检验),将要检验的两个变量分别置入
Paired Variables(成对变量)下面的Variable1(变量1)和Variable2(变量2);
(2)点击Options(选项)按钮,在Confidence Interval(置信区间百分比)后面的框中输入置信度(系统默认为95%,对应的显著性水平为5%,即0.05,若需要改变显著性水平如改为0.01,则在框中输入99 即可);
(3)点击Continue(继续)→OK(确定),即得到如图所示的输出内容。
拒绝原假设、接受备择假设
方法二:
对d进行单样本t检验,原假设:检验值为0
四、单一总体比率的检验
例题:
甲企业产品中使用的微型电动机采购自专门制造这种电动机的乙企业。
合同规定,若一批电动机的次品率不高于5%,甲企业应当接收;若次品率高于5%,则产品要退回,乙企业同时还要承担相应的运输、检验费用和损失。
现有一批电动机到货,抽取100 件进行检验,发现有6 件次品,样本次品率为6%。
试以0.05 的显著性水平检验:该批产品的次品率是否明显地高于规定的标准。
/d d d t s μ-=
data6_06 产品合格率检验
SPSS 操作:
比率属于二项分布,使用SPSS 软件做单一总体比率的检验时,可以选择非参数检验(Nonparametric Tests )中的二项分布检验(Binomial Test )或卡方检验(Chi-Square Test )来做。
下面给出利用SPSS 实现中单一总体比率的二项分布检验过程。
注意:数据文件需要整理为图6-12
所示的形式(见所附数据集“data6_06 产品合格率检验”),检验结果1代表合格品、2代表次品。
五、两总体比率差的假设检验
例题:
某省一项针对女性社会地位的调查结果显示:被调查的1200 名20 至30 岁青年女性中,拥有大专及以上学历者为390 人,占32.5%;被调查的1000 名20 至30 岁青年男性中,拥有大专及以上学历者为306 人,占30.6%。
试以0.05 的显著性水平检验:该省30 岁以下青年女性中,拥有大专及以上学历的比率是否显著地高于青年男性的这一比率。
p p Z -=
data6_07 样本的性别及学历情况
SPSS 操作:
检验统计a
学历 Mann-Whitney U 264.000 Wilcoxon W 564.000 Z
-.766 渐近显著性 (双尾) .443
a. 分组变量:性别
不能拒绝原假设。
